PROBLEMA 4

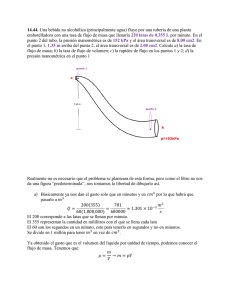
PROBLEMA 4
Un tanque esta lleno de agua hasta una altura H y se hace
un orificio a una profundidad h respecto a su superficie
libre. a) Encontrar la distancia desde el pie de la pared del
estanque hasta el lugar donde el chorro de agua choca
inicialmente con el suelo. b) Cuál debe ser la profundidad h
para que dicha distancia sea máxima, y cuanto vale dicha
distancia. Se supone el orificio de área despreciable frente a
la del estanque.
h
H
SOLUCION
a)
Partimos de la aproximación de
que el área del agujero ”S2” es
despreciable frente a la del estanque
”S2”. De aquí aplicamos la condición de
que la velocidad del agua en el estanque
“V1”es despreciable respecto de la que
lleva al salir el chorro de agua “V2”,
esto implica que podemos suponer que
la velocidad “V1” es cero.
Suponemos energía potencial=0 en (H-h) (altura del agujero)
Aplicamos la ecuación de Bernoulli entre la parte superior del deposito y el orificio de
salida:
2
2
P1 + 1/2 ρ (V1) + ρ g h = P2 + 1/2 ρ (V2) + 0
Pero P1 = P2 =cte. = presión atmosférica. Además, 1/2 ρ (V1)
2
=0
según la
aproximación antes indicada. Por lo tanto la ecuación de Bernoulli se simplifica a:
ρ g h = (1/2) ρ (V2)
Despejando V2: V2 = √ (2gh)
2
(1)
Ahora todo se reduce a un caso similar a un tiro horizontal, cuyas ecuaciones son:
X = V2* t
(2)
Y = (H- h) – (1/2)gt
2
Para la ecuación de la componente “Y” ponemos como condición “Y=0” momento en el
que el agua llega al suelo
2
0= (H - h) - 1/2gt
⇒
t = √ [ 2(H - h)/g]
(3)
Ahora sustituimos la V2 de la ecuación (1) y el tiempo de la ecuación (3) en el alcance
de la ecuación (2) :
X = √ (2gh))
√ [ 2(H - h)/g] ⇒
X = √[4h (H - h)]
(4)
b)
Este apartado es un sencillo problema de optimización que consiste en derivar la
expresión respecto de h e igualarla a cero (ver para que valor de h, la X es máxima).
Como
X = √[4h (H - h)]
[4(H -h)- 4h] = 0
⇒
⇒
d X /dh = (1/2) [4(H -h)- 4h] / √ [4h (H - h)] = 0 ⇒
h = H/2
Finalmente sustituimos este valor de h en la ecuación (4):
X = √[4 (H/2) (H – (H/2))]
⇒
X=H
PROBLEMA 6
Del deposito de la figura sale agua continuamente. La altura del
punto 1 es de 10 m, la de los puntos 2 y 3 es de 1 m. La sección
2
2
transversal en el punto 2 es de 0.04 m y en el punto 3 0.02 m .
El área del deposito es muy grande comparada con las secciones
del tubo. Calcular: a) la presión manométrica en los puntos 2 y 3
b) el gasto.
1
2 3
SOLUCION
a)
Aplicamos Bernouilli entre los puntos 1 y 3:
2
2
P1 + ρgH1 + 1/2 ρV1 = P3 + ρgH3 + 1/2 ρ V3
P1 = P atmosférica = 101300 Pa = P3
La sección en el punto 3 es muy pequeña comparándola con el punto 1 por lo que ,
aplicando continuidad la velocidad V1 es despreciable comparada a V3.
Simplificando los términos de la ecuación:
2
gH1 = gH2 + 1/2 ρ V3 è V3= √(2g(H1-H2)) = 13.288 m/sg
Aplicamos continuidad entre 2 y 3:
A2V2 =
A3V3
0.04 V2 = 0.02 13.28 è V2 = 6.644 m/sg
Aplicamos Bernouilli entre 1 y 2:
2
2
P1 + ρgH1 + 1/2 ρV1 = P2 + ρgH2 + 1/2 ρV2
De nuevo, la sección en 1 es mucho más grande que en 2 por lo que V1 es despreciable
frente a V2
2
La ecuación nos queda:
P1 + ρgH1 = P2+ ρgH2 + 1/2ρ V2
Además:
P1 = P atmosférica = 101300 Pa
2
Introduciendo este valor de P1 y despejando:
P2 = P1 + ρg (H1 - H2) - 1/2ρ V2
Sustituyendo datos:
P2 = 167519 Pa
P absoluta = P manométrica + P atmosférica
P manométrica = P absoluta – P atmosférica
P manométrica = 167519Pa – 101300 Pa è
P manométrica = 66219 Pa
b)
Q3 = V3 S3 = 13.288 0.02
3
è Q3 = 0.2658 m /s