3 diapositivas por página

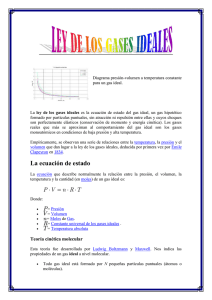
Electricidad y calor
Webpage: http://paginas.fisica.uson.mx/qb
©2007 Departamento de Física
Universidad de Sonora
Temas
3. Gases ideales y estados
termodinámicos.
i.
ii.
Concepto y características del gas ideal.
Ley de Boyle, Ley de Charles, Ley de Gay-Lussac
e hipótesis de Avogadro.
iii. Ecuación de estado del gas ideal pV = nRT y su
aplicación en la determinación de los diferentes
estados termodinámicos y su representación
grafica de presión vs. volumen.
Gases
Una sustancia se considera gas
cuando las fuerzas interatómicas (o
intermoleculares) entre los distintos
átomos (o moléculas) que la forman
son tan pequeñas que la sustancia no
adopta, ni forma, ni volumen fijo,
tendiendo a expandirse todo lo posible
para ocupar el recipiente que lo
contiene.
Refiriéndose a los gases, las condiciones normales de presión
y temperatura (CNPT) para la determinación de sus propiedades
son, por acuerdo internacional: 0ºC (273.15K) y 1 atm (ó 105 Pa,
como recomienda la International Union of Pure and Applied
Chemistry, IUPAC), con la salvedad de que los medidores de
gasto volumétrico se calibran a 25ºC.
1
Gases
Es importante mencionar que un gas es una sustancia que se
encuentra en ese estado a temperatura y presión normales,
mientras que “vapor” es la forma gaseosa de cualquier sustancia
que normalmente es líquida o sólida a condiciones normales.
En condiciones normales de presión y temperatura (CNPT)
existen elementos que son gaseosos como los del grupo 8A, (las
moléculas de) O2, N2, H2, F2 y Cl2.
„ El O2 es esencial para la vida.
„ H2S y HCN son venenos mortales.
„ CO, NO2, O3, y SO2, son tóxicos.
„ El He, Ar y Ne son químicamente inertes.
Gases
Presión de un Gas
Los gases ejercen presión sobre
cualquier superficie con la que
entren en contacto, dado que las
moléculas gaseosas están en
constante movimiento y chocan
con la superficie del recipiente que
los contienen.
Gases ideales y Ecuación de estado
Una vez revisadas algunas ideas básicas sobre los
gases, veamos qué es un gas ideal.
Se define un gas ideal como aquel en el que todas
las colisiones entre los constituyentes (átomos y
moléculas) son perfectamente elásticos y en el
cual no hay fuerzas atractivas intermoleculares.
Este concepto implica que las moléculas del gas
no interactúan excepto en las colisiones, y que el
volumen molecular es despreciable comparado
con el volumen del recipiente.
Un gas real se puede considerar como ideal si la
interacción entre sus moléculas es despreciable,
lo cual se logra manteniéndolo a una presión
baja.
2
Gases ideales y Ecuación de estado
Para estudiar un gas de masa m, confinado en un
recipiente de volumen V a una presión p y
temperatura T, es importante conocer la relación
entre estas cantidades.
En general, esta relación conocida como
Ecuación de estado es bastante complicada; sin
embargo, para el caso de un gas ideal es muy
simple y se puede encontrar experimentalmente.
Antes de construir la ecuación de estado,
revisemos tres leyes empíricas que se observa son
satisfechas por los gases (de baja presión).
Leyes empíricas de los gases: Ley de Boyle
En 1662, el irlandés Robert Boyle
(1627-1691) enuncia la hoy
conocida como Ley de BoyleMariotte*, que establece:
“Cuando el gas se mantiene a
temperatura constante, su presión
es inversamente proporcional a su
volumen”.
P1V1 = P2V2
* En 1660, el francés Edme Mariotte (1620-1684) emprendió investigaciones sobre las deformaciones
elásticas de los sólidos e, independientemente de su colega Robert Boyle, enunció una ley relacionada con la
compresibilidad de los gases. En su tratado De la naturaleza del aire (1676) formuló la ley de
compresibilidad de los gases: "a temperatura constante, el volumen de un gas varía en razón inversa a su
presión".
Leyes empíricas de los gases: Ley de Charles
En 1787, el francés Jacques
Alexandre César Charles (17461823) enuncia la hoy conocida
como ley de Charles, que
establece:
“Cuando la presión del gas se
mantiene constante, su volumen es
directamente proporcional a su
temperatura”.
V1/T1 = V2/T2
3
Leyes empíricas de los gases: Ley de Gay-Lussac
En 1802, el francés Joseph Louis
Gay-Lussac (1778-1850) enuncia la
hoy conocida como Ley de GayLussac, que establece:
“Cuando el gas se mantiene en un
recipiente a volumen constante, la
presión
experimentada
es
directamente proporcional a su
temperatura”.
P1/T1 = P2/T2
Leyes empíricas de los gases: Ley general e hipótesis
de Avogadro.
La unificación de estas tres leyes da lugar a lo que se llama ley general
del estado gaseoso, a saber
pV
= constante
T
donde p es la presión, V es el volumen y T es la temperatura.
Un gas ideal se modela como un gas de esferas duras sin volumen y que
solo interaccionan mediante choques perfectamente elásticos.
• La energía interna de un gas es la energía cinética total de las
moléculas
• Todo cambio de energía interna va acompañado de un cambio en la
temperatura
Leyes empíricas de los gases: Ley general e hipótesis
de Avogadro.
En 1811, el italiano Amedeo Avogadro
(1776-1856) establece la llamada hipótesis
de Avogadro: “A presión y temperatura
constantes, el volumen de un gas es
directamente proporcional al número de
moles del gas presente”, lo que se puede
escribir como
V
= constante
n
donde n es el número de moles y V es el
volumen. Es importante mencionar que
este resultado es independiente de su
naturaleza química y características físicas
Esta constante se llama número de
Avogadro (NA) y tiene un valor de
6.02214x1023mol-1.
4
Gases ideales y Ecuación de estado
En el estudio de los gases una cantidad muy importante es el número de
moles n, y que se define como el cociente entre la masa m del gas y su
correspondiente masa molar M, es decir
n =
m
M
Con la anterior definición, la ecuación de estado de un gas ideal se
escribe como
pV = nRT
R = 8.3143 J / mol ⋅ K
donde p es la presión en pascales, V es el volumen en m3, n es número de
moles, R es la constante universal de los gases y T es la temperatura en K.
Gases ideales y Ecuación de estado
En ocasiones, la ecuación de estado del gas ideal se escribe en términos
del número de moléculas N en lugar del número de moles n, en tal caso
se tiene
pV = NkBT
k B = 1.38065 x10−23 J / K
donde p es la presión en Pascales, V es el volumen en m3, N es número de
moléculas, kB es la constante de Boltzmann y T es la temperatura en
Kelvins.
Finalmente, es importante señalar que a las cantidades p, V y T se les
llama variables termodinámicas y nos permiten caracterizar el estado de
un gas, de manera análoga al papel que juegan en mecánica: la posición,
la velocidad y la aceleración.
Ecuación de estado del gas ideal: Resumen
Presión
pV = nRT
Volumen
n=
m
M
Número de moles
R = N A kB
N A = 6.02214 × 1023 mol −1
Temperatura
R = 8.3143 J / mol º K
R = 0.08214 atm ⋅ l / mol º K
Constante de los gases
k B = 1.38065 × 10−23 J / K
Constante de Boltzmann
Número de Avogadro
5
Ecuación de estado y diagrama p-V
Para terminar, introduciremos una herramienta muy útil en
termodinámica: el diagrama p-V, empleado para estudiar sistemas
termodinámicos, como los gases ideales.
De la ecuación de estado del
gas ideal podemos escribir
p=
nRT
V
Si fijamos el valor de la
temperatura T (pV=constante),
podemos graficar la expresión
anterior en un sistema de
coordenadas p vs. V, resultando
lo que se conoce como
diagrama p-V.
Ecuación de estado y diagrama p-V
La trayectoria seguida por un gas (o sistema) en un diagrama pV, al pasar
de un estado inicial (i) a un estado final (f) representa un proceso
termodinámico. En el ejemplo recién mostrado, el proceso seguido por
el gas recibe el nombre de isotérmico, ya que la temperatura permaneció
constante.
Dependiendo de la variable de
estado que permanece sin cambio,
podemos hablar de procesos:
Estado inicial (i)
• isotérmicos (ΔT = 0);
Estado final (f)
• isobáricos (Δp = 0);
• isocóricos (ΔV = 0); y
• adiabáticos (ΔQ = 0).
Ecuación de estado y diagrama p-V
Los diferentes procesos termodinámicos pueden ser representados de
manera muy precisa en un diagrama pV.
A continuación se muestran diagramas característicos de cada tipo de
proceso termodinámico.
isotérmicos (ΔT = 0)
Ley de Boyle
isobáricos (Δp = 0)
Ley de Charles
isocóricos (ΔV = 0)
Ley de Gay-Lussac
adiabático (ΔQ = 0)
Para terminar, observa que mientras la isoterma es una hipérbola, debido a que
cuando la temperatura es constante p es función de (1/V), la adiabática NO lo es.
6
Gases ideales: Ejercicios.
a) De la ecuación de estado, podemos escribir
b) Para conocer el número de moléculas, podemos usar la relación
existente entre el número de moles n y el número de Avogadro NA, a
saber
Gases ideales: Ejercicios.
Aplicando la ecuación de estado, y considerando que todo el He pasa a
los N globos (manteniendo la temperatura constante), podemos escribir
donde hemos considerado que el
volumen de un globo es
De esta expresión despejamos el número de globos N, es decir
= 884.1941
Por lo que podemos inflar 884 balones y nos queda un poco de He sin
usar.
Gases ideales: Ejercicios.
(a) En esta parte tenemos un proceso isocórico (mismo volumen)
p
p2= 18atm
T2
p1=6atm
T1
si aplicamos la Ley de Gay-Lussac, podemos
despejar la temperatura final T2
V1
V
(b) En esta parte tenemos un proceso, por ejemplo, como el mostrado
p
si aplicamos la Ley general obtenemos para T2
p2
(= 2p1)
p1
T1
V1
T2
V2 (= 2V1)
V
7
Gases ideales: Tarea.
(c) Con los datos presentados, ¿podrías calcular el volumen inicial del
gas V1? En caso afirmativo, hazlo; de lo contrario, ¿qué dato hace
falta?
Gases ideales: Tarea (solución).
(c) Con los datos presentados, ¿podrías calcular el volumen inicial del
gas V1?
Si, usando la ecuación de estado podemos despejar el volumen
V=
(1mol )(0.08214atm ⋅ l / mol ⋅ K )(300 K )
nRT
=
= 4.107l
p
6atm
El volumen de un mol de oxígeno a una presión de 6.00atm y 27ºC (300K)
de temperatura es 4.107 litros.
Gases ideales: Tarea (solución).
Considerando a la burbuja como un gas ideal, podemos aplicar la ecuación
general, de donde despejamos el volumen V2
( P + ρ gh ) V1T2 Aquí hemos usado la Ley de Pascal
PV
1 1T2
= atm
para calcular las presiones p1 y p2.
T1 Patm
T1 P2
Numéricamente
(101,300 Pa + (1025 kg m3 )(9.806 m s 2 )(25.0m) )(1.00cm3 ) ( 293.15K )
V2 =
( 278.15K )(101,300 Pa )
de tal forma que el volumen final de la burbuja es
V2 = 3.6684cm3
V2 =
8
Teoría cinética de los gases
Antes de 1908 no se aceptaba de manera
general la teoría atómica a pesar de la
existencia de evidencias físicas y químicas,
como por ejemplo:
• Tabla periódica de los elementos
• Leyes de la química (Ley de Dalton, etc.)
• Pesos moleculares y atómicos
• Teoría cinética de los gases y del calor
Esta última trata de explicar las propiedades de
los gases, tales como la existencia de la presión,
temperatura ó su volumen, considerando su
composición molecular y su movimiento.
Teoría cinética de los gases
Sin embargo, con la teoría de
Einstein, para el movimiento
browniano, Perrin en 1908 fue
capaz de determinar de
manera
experimental
el
número de Avogadro.
N A = 6.023 × 1023
Con lo anterior, y hasta entonces, fue aceptada
universalmente la teoría atómica de la materia.
Teoría cinética de los gases: Bases
1. Un gas ideal consta de partículas que siguen un movimiento
aleatorio y que obedecen las leyes de la mecánica clásica.
2. El número total de moléculas es muy grande.
3. El volumen ocupado por las moléculas es una fracción muy
pequeña del que ocupa el gas.
4. La única fuerza que actúa sobre las moléculas es la debida a
las colisiones, ya sean con otras moléculas o con las paredes
del contenedor.
5. Todas las colisiones son elásticas y de muy corta duración.
9
Teoría cinética de los gases: Resultados
L
•
A1
•
•
2 ⎛ N ⎞⎛ 1
2 ⎞
⎜ ⎟⎜ m v ⎟
3 ⎝ V ⎠⎝ 2
⎠
⎛ N ⎞⎛ 1
2 ⎞
p = ⎜ ⎟⎜ m v ⎟
⎝ V ⎠⎝ 3
⎠
p=
•
•
A2
•
Presión:
•
•
Energía cinética
•
Masa de cada molécula: m
G
Velocidad de cada molécula: v = ( vx , v y , vz )
Ec = N
m v2
2
=
3
Nk BT
2
Teoría cinética de los gases: Resultados
Teorema de equipartición de la energía.
Establece que “la energía (interna) U de un sistema en equilibrio térmico
se divide en cantidades iguales para cada grado de libertad ( f )”.
Lo anterior permite establecer que por cada grado de libertad, en un
sistema formado por N moléculas, se tiene una contribución dada por
(1/2)NKBT a su energía interna. Es importante mencionar que, además de
los grados de libertad traslacionales, también hacen su contribución los
correspondientes a rotaciones y vibraciones de las moléculas.
U=
f
f
Nk BT = nRT
2
2
⎧gas monoatómico →
⎪
considere que ⎨ gas diatómico
→
⎪ gas poliatómico →
⎩
f =3
f =5
f =6
Para un gas ideal la energía interna depende sólo de la temperatura del
gas (y del número de moles).
Teoría cinética de los gases: Resultados
Un ejercicio
[21S10] Un recipiente de 5.00 litros contiene gas nitrógeno a 27.00C y 3.00atm.
Encuentre (a) el número de moles, (b) la energía cinética traslacional total de las
moléculas del gas, y (c) la energía cinética promedio por molécula.
(a) Usando la ecuación de estado del gas ideal, el número de moles es
n=
pV
(3.00atm)(5.00lt )
=
= 0.6084moles
RT (0.08214atm ⋅ lt / mol ⋅ K )(300.15K )
(b) Usando la Ecuación de estado del gas ideal y la expresión para la presión tenemos
Por otro lado, la energía cinética total se puede escribir como
así que
(c) Usando la definición de energía cinética y el teorema de equipartición de la energía
tenemos
10