Una nueva métrica para números fuzzy

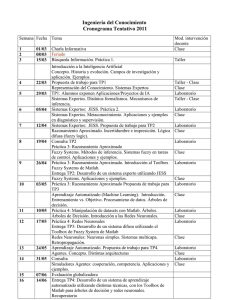
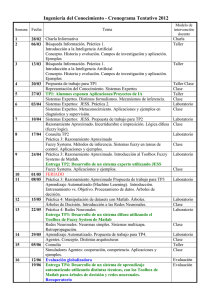
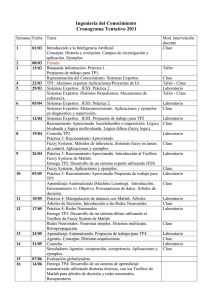
Beatriz Sinova Fernández
Estadística e Investigación
Operativa
Address:
Dept. de Estadística e Investigación Operativa
Universidad de Oviedo
Facultad de Ciencias - Campus de Llamaquique
Calvo Sotelo s/n, 33007 Oviedo, Spain
E-mail:
[email protected]
Congreso Jóvenes Investigadores RSME
Soria, 5 9 de septiembre de 2011
Una nueva métrica para números fuzzy
Para modelar muchos experimentos de la vida real, se usa la escala de números fuzzy porque permite
una representación más adecuada y exible de la imprecisión que los números reales, y mayor expresividad,
capacidad computacional y tratamiento matemático que los valores categóricos. Pueden citarse un buen
número de ejemplos y aplicaciones que involucran valoraciones, juicios o percepciones con una imprecisión
subyacente en campos muy dispares, desde las ingeniería del control a las ciencias del comportamiento.
e : R → [0, 1] tal que
U
e
e
para cada α ∈ (0, 1] el α−nivel correspondiente Uα = {x ∈ R : U (x) ≥ α} es un intervalo compacto no
e0 = {x ∈ R : U
e (x) > 0}. Para cada x ∈ R, el valor U
e (x) representa el `grado de compatibilidad
vacío y U
e
de x con la propiedad que caracteriza a U ' (o también puede interpretarse como el `grado de posibilidad
e ). Fc (R) denotará el espacio de números fuzzy. Cada número fuzzy vendrá
de la armación x es `U
Un número fuzzy se formaliza, en su acepción más general, como una aplicación
caracterizado indistintamente, entre otros, en términos de:
•
•
α-niveles;
eα = (inf U
eα + sup U
eα )/2 = centro de U
eα ) y la semiamplitud (spr U
eα =
U
eα − inf U
eα )/2 = radio de U
eα ) de todos sus α-niveles;
(sup U
e1 , y la semiamplitud izquierda (lsprU
eα =midU
e1 − inf U
eα ) y la
• o el punto medio del 1-nivel, midU
e
e
e
semiamplitud derecha (rsprUα = sup Uα −midU1 ) de todos sus α-niveles.
el ínmo y el supremo de todos los
o el punto medio (mid
En cuanto a la aritmética entre los números fuzzy, las operaciones más importantes desde un punto de
vista estadístico son la suma y el producto por escalares. La aritmética fuzzy usual, basada en el Principio
de Extensión de Zadeh (1975), equivale a la aritmética intervalar usual nivel a nivel. Esto es, dados dos
e , Ve ∈ Fc (R)
U
cada α ∈ [0, 1]
números fuzzy
tal que para
e + Ve )α =
(U
y el producto de
e
U
y un número real
γ ∈ R,
suma de Minkowski de
por el escalar
γ
se dene como
la suma de
eα
U
y
e
U
y
Ve
se dene como
e + Ve ∈ Fc (R)
U
eα , z ∈ Veα }
Veα = {y + z : y ∈ U
e ∈ Fc (R)
γ·U
tal que para cada
α ∈ [0, 1]
eα }.
e )α = γ · U
eα = {γ · y : y ∈ U
(γ · U
Una observación importante es que el espacio
Fc (R)
con estas dos operaciones no es lineal, sino que
tiene una estructura semilineal cónica.
Una de las ventajas del empleo de números fuzzy frente al de datos categóricos es que entre los
primeros tiene sentido medir la `proximidad'. Al respecto, se han denido en la literatura varias métricas
(cf. Diamond y Kloeden, 1999, Trutschnig et al., 2009).
En recientes estudios motivados por la necesidad de establecer medidas y estimadores más robustos
que la media tipo Aumann de un conjunto de datos fuzzy (o de un número fuzzy aleatorio, en un contexto
probabilístico general) se ha hecho patente la conveniencia de considerar métricas tipo
L1
que permitieran
introducir una extensión de la noción de mediana (habida cuenta de la no existencia de un orden total
universalmente aceptable entre los números fuzzy).
La representación mid1/lspr/rspr coincide con la
representación mid/spr para números fuzzy simétricos y, en consecuencia, para intervalos.
Con inspiración parcial en la métrica de Hausdor para intervalos y en las métricas
L2
de Trutschnig
et al. (2009) y de Yang y Ko (1996) para números fuzzy, se introduce, a continuación, una nueva distancia
1
JIRSME: Beatriz Sinova Fernández
2
entre números fuzzy basada en la caracterización mid1/lspr/rspr. Dados dos números fuzzy
y un valor
θ>
e1 − midVe1 | + θ ·
= |midU
2
e , Ve )
D1θ (U
Entre
ρ1
sus
ventajas,
propuesta
pacio
de
e , Ve ∈ Fc (R)
U
0, la distancia D1θ entre ellos se dene como:
por
números
reseñar
Diamond
fuzzy
y
en
que
Z
eα − lsprVeα |dα + θ ·
|lsprU
2
(0,1]
se
Kloeden
un
cono
trata
y
de
que
cerrado
una
métrica
también
y
convexo
eα − rsprVeα |dα.
|rsprU
(0,1]
topológicamente
permite
{funciones vectoriales de tres dimensiones de tipo L1 con dominio
Z
del
un
encaje
espacio
(0, 1]}.
de
equivalente
a
la
isométrico
del
es-
funciones
H1
=
También es interesante señalar
que esta métrica va a permitir garantizar la existencia de un concepto de mediana operativo, lo cual no
podía armarse en general cuando se utilizaba una métrica
L1
basada en la caracterización mid/spr e
2
inspirada en la métrica L de Trutschnig et al. (2009).
References
[1] Diamond, P., Kloeden, P., 1999. Metric spaces of fuzzy sets. Fuzzy Sets Syst. 100, 6371.
[2] Trutschnig, W., González-Rodríguez, G., Colubi, A., Gil, M.A. 2009. A new family of metrics for
compact, convex (fuzzy) sets based on a generalized concept of mid and spread. Inform. Sci. 179,
39643972.
[3] Yang, M.S., Ko, C.H., 1996. On a class of fuzzy c-numbers clustering procedures for fuzzy data.
Fuzzy Sets Syst. 84, 4960.
[4] Zadeh, L.A., 1975. The concept of a linguistic variable and its application to approximate reasoning,
Part 1. Inform. Sci. 8, 199249; Part 2. Inform. Sci. 8, 301353; Part 3. Inform. Sci. 9, 4380.