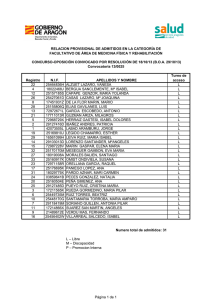
Tema 3.

Tema 3
Scheduling
Introducción
Caracterización de tareas
Planificadores
Análisis de planificabilidad
Tareas aperiódicas
Uso de recursos
Modelo extendido
Maria Isabel Alfonso Galipienso. 2006
1
Indice
„ Introducción
„ Caracterización de tareas
„ Planificadores
„ Análisis de planificabilidad
„ Tareas aperiódicas
„ Uso de recursos
„ Modelo extendido
Maria Isabel Alfonso Galipienso. 2006
2
1
Introducción (I)
„
Un sistema de tiempo real debe ser PREDECIBLE
Capacidad del sistema para poder determinar con antelación las
características de respuesta del mismo
„
Existen muchas secuenciaciones posibles de las
tareas, pero solamente algunas de ellas cumplen las
restricciones temporales del sistema
„
Un esquema de scheduling proporciona
„
„
Un algoritmo para determinar el orden de uso de los recursos
del sistema (procesadores) PLANIFICADOR
Una forma de predecir el tiempo de respuesta del sistema en
el peor de los casos cuando se aplica el algoritmo de
scheduling TEST DE PLANIFICABILIDAD
Maria Isabel Alfonso Galipienso. 2006
3
Introducción (II)
El sistema debe:
„
Procesar las actividades periódicas:
„
„
„
Requeridas a intervalos regulares
Completar el trabajo antes de un plazo (deadline)
Responder a eventos esporádicos:
„
„
„
Requeridos a intervalos irregulares
Completar el trabajo antes de un plazo (deadline )
Minimizar la respuesta temporal media
„
Garantizar que los requerimientos temporales críticos
se cumplen durante una sobrecarga transitoria
„
Garantizar la consistencia de recursos compartidos,
como estructuras de datos y dispositivos de I/O
Maria Isabel Alfonso Galipienso. 2006
4
2
Introducción (III)
+ Tests de Planificabilidad
Scheduler
Factores de utilización
Prioridades
Ejecutivo cíclico
Estáticas
Tiempos de respuesta
Dinámicas
Fixed-Priority
Scheduling
FPS
Rate Monotonic
RM
Deadline
Monotonic
DM
Maria Isabel Alfonso Galipienso. 2006
Earliest
Deadline First
EDF
5
Indice
„ Introducción
„ Caracterización de tareas
„ Planificadores
„ Análisis de planificabilidad
„ Tareas aperiódicas
„ Uso de recursos
„ Modelo extendido
Maria Isabel Alfonso Galipienso. 2006
6
3
Notación estándar
C: Tiempo de ejecución en el peor de los casos (WCET)
D: Deadline del proceso (tarea)
I : Tiempo de interferencia para el proceso
J: Release jitter para el proceso
N: Número de procesos en el sistema
P: Prioridad asignada al proceso
R: Tiempo de respuesta en el peor de los casos
T: Periodo del proceso
U: Factor de utilización de cada proceso (igual a C/T)
7
Maria Isabel Alfonso Galipienso. 2006
Caracterización de las tareas (I)
Tiempo de respuesta (R)
Interferencia (I)
Interferencia (I)
T = 10
C=3
I=5
R=8
D=9
Deadline (D)
Periodo (T)
Determinan sus restricciones temporales de
τi =(Ci, Ti, Di, Ii, Ri)
ejecución
Maria Isabel Alfonso Galipienso. 2006
8
4
Caracterización de las tareas (II)
Prioridad → P
ττii==(Ci,
(Ci,Ti,
Ti,Di)
Di)
τ1 = {20,100,100)
τ2 = {40,150,150)
τ3 = {100,300,300)
τ1
T1
1
τ2
T2
2
τ3
T3
3
2
τT1
1
3
1
τT2
2
2
τT3
3
1
3
τT1
1
3
τT2
2
2
τT3
3
1
Maria Isabel Alfonso Galipienso. 2006
9
Modelo de procesos básico (I)
(A1) Conjunto fijo de tareas
(A2) Tareas periódicas con periodos conocidos
(A3) Tareas independientes
(A4) Se ignora overhead del procesador (cambios de
contexto, etc. tienen coste 0)
(A5) Los periodos son iguales a los deadlines (Ti =Di)
(A6) Tiempo de cómputo (C) conocido y fijo
Maria Isabel Alfonso Galipienso. 2006
10
5
Otras asunciones
„ Cada tarea se invoca periódicamente mediante la
ocurrencia de un evento particular
„ Una tarea es “lanzada” (released) cuando está
preparada para ejecución
Instante crítico (máxima carga del procesador)
„ Una tarea puede ser interrumpida (preeempted) si una
tarea de mayor prioridad está preparada para su
ejecución
Maria Isabel Alfonso Galipienso. 2006
11
Indice
„ Introducción
„ Caracterización de tareas
„ Planificadores
„ Análisis de planificabilidad
„ Tareas aperiódicas
„ Uso de recursos
„ Modelo extendido
Maria Isabel Alfonso Galipienso. 2006
12
6
Planificadores (schedulers)
„
Un planificador proporciona un algoritmo de uso de
recursos del sistema por parte de los procesos
„
Planificador óptimo
Si puede planificar todos los conjuntos de procesos que
cualquier otro puede
„
Planificacion INTERRUMPIBLE (Preemptive
scheduling)
„
Instante crítico: cuando todos los procesos son
activados simultáneamente (máxima carga del
procesador)
Maria Isabel Alfonso Galipienso. 2006
13
Planificadores estáticos
„ Analizan estáticamente las tareas para
determinar sus propiedades temporales
„ Orden de ejecución fijo determinado off-line
„ Se puede crear una tabla de ejecución que
cubra un tiempo igual al mcm de los periodos de
las tareas
„ Ejemplos:
„
„
Ejecutivo cíclico
Planificadores de prioridad fija (FPS)
Maria Isabel Alfonso Galipienso. 2006
14
7
Ejecutivo cíclico
„ Se crea una tabla secuencial de llamadas a
procedimientos
„ Se "simula" la ejecución de varias tareas
concurrentes utilizando un único proceso
„ Ventajas:
„
„
No es posible el acceso concurrente a datos
No necesita test de planificabilidad
„ Inconvenientes:
„ Dificultad de incorporar procesos esporádicos, con
largos periodos, o procesos nuevos
„ Dificultad de implementación
15
Maria Isabel Alfonso Galipienso. 2006
Ejecutivo cíclico. Ejemplo 1
t
0
5
10 15 20 25 30 35 40 45
Temp_Control
pH_Control
Level_Control
t
0
5
10 15 20 25 30 35 40 45
Temp_Control
pH_Control
Maria Isabel Alfonso Galipienso. 2006
Level_Control
loop
Temp_Control;
pH_Control ;
Level_Control;
PERIOD := PERIOD + T ;
delay until PERIOD ;
end loop;
loop
Temp_Control ;
if ((cnt mod 2) = 0) then
pH _Control ;
Level_Control;
end if ;
cnt := cnt + 1 ;
PERIOD := PERIOD + T ;
delay until PERIOD ;
end loop;
16
8
Ejecutivo cíclico. Ejemplo 2
Tarea
a
b
c
d
e
T=D
25
25
50
50
100
Interrupción
a
0
b
c
loop
esperar_interrupción;
proc_a;
proc_b;
proc_c;
esperar_interrupción;
proc_a;
proc_b;
proc_d;
proc_e;
esperar_interrupción;
proc_a;
proc_b;
proc_c;
esperar_interrupción;
proc_a;
proc_b;
proc_d;
end loop;
C
10
8
5
4
2
Interrupción
a
b
Interrupción
de
a
25
Maria Isabel Alfonso Galipienso. 2006
b
c
50
Interrupción
aa
bb dd
75
TIEMPO
17
Fixed Priority Scheduling (FPS)
RM: Rate Monotonic
p La prioridad se asigna en función del PERIODO
p A menor periodo → mayor prioridad
Ti < Tj ⇒ Pi > Pj
p Es una asignación ÓPTIMA
DM: Deadline Monotonic
p La prioridad se asigna en función del DEADLINE
p A menor deadline → mayor prioridad
Di < Dj ⇒ Pi > Pj
p Es una asignación ÓPTIMA
Maria Isabel Alfonso Galipienso. 2006
18
9
Ejemplos RM y DM
RM
DM
T
D
P
a
20
5
4
3
b
15
7
3
4
c
10
10
2
d
105 1
d
20
20
1
e
75
Tarea
T
P
a
25
5
b
60
c
42
Tarea
2
Maria Isabel Alfonso Galipienso. 2006
19
Planificadores dinámicos
„ Analizan dinámicamente las tareas para
determinar sus propiedades temporales
„ Orden de ejecución determinado on-line
„ Se obtienen secuenciaciones más flexibles
„ Comprenden los siguientes pasos:
Análisis de factibilidad, scheduling, dispatching.
„ Ejemplos:
„ EDF
Maria Isabel Alfonso Galipienso. 2006
20
10
Earliest Deadline First (EDF)
„ Selecciona la siguiente tarea a ejecutar
dependiendo de su deadline absoluto
„ Se elige la tarea con deadline absoluto más
cercano
„ La decisión se realiza en tiempo de ejecución
„ Es una asignación óptima
21
Maria Isabel Alfonso Galipienso. 2006
Ejemplo EDF
EDF
Tarea
a
0
5
10
T=D
C
a
5
2
b
7
4
15
20
25
30
35
b
0
7
14
21
28
35
TIEMPO
Maria Isabel Alfonso Galipienso. 2006
22
11
Indice
„ Introducción
„ Caracterización de tareas
„ Planificadores
„ Análisis de planificabilidad
„ Tareas aperiódicas
„ Uso de recursos
„ Modelo extendido
Maria Isabel Alfonso Galipienso. 2006
23
Tests de Planificabilidad
„ Son métodos utilizados para determinar si el
sistema cumplirá con las restricciones
establecidas
„ Ejemplos:
„
Utilización de diagramas de tiempo
„
Test basado en factores de utilización
„
Test basado en tiempos de respuesta
Maria Isabel Alfonso Galipienso. 2006
24
12
Factores de utilización
Se denomina factor de utilización U de un
conjunto Γ de N tareas periódicas a la fracción de
tiempo utilizado por el procesador para ejecutar
dicho conjunto de tareas
N
Ci
i =1 Ti
U =∑
Existe un valor máximo de U por encima del
cual Γ no es planificable
25
Maria Isabel Alfonso Galipienso. 2006
Test factores de utilización (RM)
Dado un conjunto Γ de N tareas periódicas
secuenciadas según RM, Γ será
planificable SI:
N
1
Ci
∑ T ≤ N (2 N −1)
i =1 i
N
1
2
3
4
...
∞
U
100 %
82,8 %
78,0 %
75,7 %
...
69,3%
Se trata de una condición SUFICIENTE
Maria Isabel Alfonso Galipienso. 2006
26
13
Test factores de utilización (RM). Ejemplo 1
Tarea
a
C
T=D P
U
20
100 3
0,2
b
40
150 2
0,267
c
100
350 1
0,286
RM
n
U(n)
1
1.000
2
0.828
3
0.779
4
0.756
5 0.743
...
...
∞ 0.693
Uso total 75.3 % ≤ U(3) = 77.9 %
Un 24.7 % de la CPU se puede utilizar para
cálculos sin requerimientos temporales, a más
baja prioridad.
a
b
OK!
c
0
100
150
200
300
350
27
Maria Isabel Alfonso Galipienso. 2006
Test factores de utilización (RM). Ejemplo 2
C
T=D P
a
40
80
1
0,50
b
10
40
2
0,25
c
5
20
3
0,25
Tarea
RM
U
Uso total 100 %
Falla el
test!
a
b
OK!
c
0
10
20
30
Maria Isabel Alfonso Galipienso. 2006
40
50
60
70
80
35
28
14
Test factores de utilización (DM)
Dado un conjunto Γ de N tareas periódicas
secuenciadas según DM, Γ será
planificable SI:
N
1
Ci
∑ D ≤ N (2 N −1)
i =1
i
Se trata de una condición SUFICIENTE
Maria Isabel Alfonso Galipienso. 2006
29
Test factores de utilización (EDF)
Dado un conjunto Γ de N tareas periódicas
secuenciadas según EDF, Γ será
planificable SI Y SOLO SI:
N
Ci
∑ T ≤1
i =1 i
Se trata de una condición SUFICIENTE y
NECESARIA
Maria Isabel Alfonso Galipienso. 2006
30
15
Test factores de utilización (EDF)
Ejemplo 1
C
T=D U
a
40
80
0,50
b
10
40
0,25
c
5
20
0,25
Tarea
Uso total 100 %
EDF
a
b
OK!
c
0
10
20
30
40
50
60
70
80
35
31
Maria Isabel Alfonso Galipienso. 2006
Test factores de utilización (EDF) Ejemplo
2
C
T=D U
a
2
5
0,40
b
4
7
0,57
Tarea
EDF
Uso total 97 %
a
0
5
10
15
20
25
30
35
b
0
RM
7
14
21
28
a
35
Falla!
b
0
7
Maria Isabel Alfonso Galipienso. 2006
14
21
28
35
32
16
Tiempos de respuesta
„ Instante crítico de una tarea τi: es el tiempo
en el que la activación de dicha tarea da
lugar a un tiempo de respuesta máximo para
τi
„ El tiempo máximo de respuesta Ri para una
tarea periódica τi se calcula, en su instante
crítico, como:
Ri = Ci + Ii
33
Maria Isabel Alfonso Galipienso. 2006
Cálculo de Ri
„ Tiempo máximo de respuesta de una tarea en
su instante crítico:
⎡ Ri ⎤
Ri = Ci + ∑ ⎢ ⎥ ⋅ C j
j∈hp(i ) ⎢T j ⎥
Solución de la ecuación:
k +1
i
R
Maria Isabel Alfonso Galipienso. 2006
⎡ Rik ⎤
= Ci + ∑ ⎢ ⎥ ⋅ C j
j∈hp( i ) ⎢ T j ⎥
34
17
Test tiempos respuesta (RM)
Dado un conjunto Γ de N tareas periódicas
secuenciadas según RM, Γ será
planificable SI Y SÓLO SI:
Ri ≤ Ti , ∀i = 1..N
Se trata de una condición SUFICIENTE y
NECESARIA
35
Maria Isabel Alfonso Galipienso. 2006
Test tiempos respuesta (RM) Ejemplo (I)
C
T=D P
a
40
80
1
b
10
40
2
c
5
20
3
Tarea
Tarea c
RM
Rc0 = 5
Rc1 = 5
Rc0 = Rc1 = 5 ≤ 20
Maria Isabel Alfonso Galipienso. 2006
OK!
36
18
Test tiempos respuesta (RM) Ejemplo
(II)
C
T=D P
a
40
80
1
b
10
40
2
c
5
20
3
Tarea
RM
Tarea b
Rb0 = 10
⎡10⎤
Rb1 = 10 + 5 ⋅ ⎢ ⎥ = 10 + 5 = 15
⎢ 20⎥
⎡15⎤
Rb2 = 10 + 5 ⋅ ⎢ ⎥ = 10 + 5 = 15
⎢ 20⎥
Rb1 = Rc2 = 15 ≤ 40 OK!
37
Maria Isabel Alfonso Galipienso. 2006
Test tiempos respuesta (RM)
Ejemplo (III)
Tarea
a
RM
C
40
T=D P
1
80
b
10
40
2
c
5
20
3
Tarea a
Ra0 = 40
⎡ 40 ⎤
⎡ 40 ⎤
Ra1 = 40 + 10 ⋅ ⎢ ⎥ + 5 ⋅ ⎢ ⎥ = 40 + 10 + 10 = 60
⎢ 40 ⎥
⎢ 20 ⎥
⎡ 60 ⎤
⎡ 60 ⎤
Ra2 = 40 + 10 ⋅ ⎢ ⎥ + 5 ⋅ ⎢ ⎥ = 40 + 20 + 15 = 75
⎢ 40 ⎥
⎢ 20 ⎥
⎡ 75 ⎤
⎡ 75 ⎤
Ra3 = 40 + 10 ⋅ ⎢ ⎥ + 5 ⋅ ⎢ ⎥ = 40 + 20 + 20 = 80
⎢ 40 ⎥
⎢ 20 ⎥
⎡ 80 ⎤
⎡ 80 ⎤
Ra4 = 40 + 10 ⋅ ⎢ ⎥ + 5 ⋅ ⎢ ⎥ = 40 + 20 + 20 = 80
⎢ 40 ⎥
⎢ 20 ⎥
Maria Isabel Alfonso Galipienso. 2006
OK!
38
19
Test tiempos respuesta (RM)
Ejemplo (IV)
C
T=D P
a
40
80
1
b
10
40
2
c
5
20
3
Tarea
RM
a
Ra = 80
b
Rb = 15
c
0
10
20
30
40
50
60
70
80
Rc = 5
Maria Isabel Alfonso Galipienso. 2006
35
39
Test tiempos respuesta (DM)
Dado un conjunto Γ de N tareas periódicas
secuenciadas según DM, Γ será
planificable SI Y SÓLO SI:
Ri ≤ Di , ∀i = 1..N
Se trata de una condición SUFICIENTE y
NECESARIA
Maria Isabel Alfonso Galipienso. 2006
40
20
Resumen tests planificabilidad
Prioridades estáticas
N
C
i=1
i
Di = Ti
Di≤ Ti
RM
DM
1
∑Ti ≤ N(2 N −1)
Ri ≤ Di , ∀i =1..N
Ri ≤ Ti , ∀i =1..N
EDF
Prioridades dinámicas
N
C
i=1
i
∑Ti ≤1
41
Maria Isabel Alfonso Galipienso. 2006
Cambios de contexto
„
Tiempo de salvar el contexto de la tarea en ejecución
+ atención a la interrupción
+ resolución
+ selección de la tarea a ejecutar
+ recuperación del estado de la tarea
Csb
Planificar y recuperar el contexto
Tarea 1
Tarea 2
Peor caso: 2 cambios por cada expulsión
Csa
Salvar el contexto
Maria Isabel Alfonso Galipienso. 2006
42
21
Cambios de contexto
Ejemplo (I)
Cs = 2 ms
C1 = 20 + 4 T1 = 100 U1 = 0.24
C2 = 40 + 4 T2 = 150 U2 = 0.293
C3 =100 + 4 T3 = 350 U3 = 0.297
No cumple
el test 1
U = 0.831 > U(3) = 0.779
Tarea 1: W1 = C1 = 24
0
W = C + 0 = 24 ≤ T
1
1
1
1
= 100
BIEN
W = C = 44
0
Tarea 2:
2
2
⎡
⎤
⎡ 44 ⎤
W = C + ∑ ⎢⎢W ⎥⎥ = 44+ ⎢⎢100⎥⎥24 = 68
⎢T ⎥
⎡
⎤
⎡ 68 ⎤
W = C + ∑ ⎢⎢W ⎥⎥ = 44+ ⎢⎢100⎥⎥24 = 68
T
⎢
⎥
=
=
68
≤
=
W W
T 150 BIEN!
0
1
2
2
2
∀j∈{1}
j
1
2
2
2
2
1
2
2
2
∀j∈{1}
j
2
43
Maria Isabel Alfonso Galipienso. 2006
Cambios de contexto
Ejemplo (I)
Cs = 2 ms
C1 = 20 + 4 T1 = 100 U1 = 0.24
C2 = 40 + 4 T2 = 150 U2 = 0.293
C3 =100 + 4 T3 = 350 U3 = 0.297
W =C
3
= 104
W =C
3
+
0
3
Tarea 3:
1
3
+
3
W =C
3
3
En cambio, con un T3 = 250
no cumpliria el test.
∀j∈{1, 2}
W =C
2
3
3
⎡
∑ ⎢W
⎢⎢ T
⎡
∑ ⎢W
⎢⎢ T
⎡
∑ ⎢W
⎢⎢ T
+
∀j∈{1, 2}
∀j∈{1, 2}
0
3
j
⎤
⎡104 ⎤
⎡104 ⎤
24 + ⎢
44 = 196
⎥ = 104 + ⎢
⎢100 ⎥⎥
⎢150 ⎥⎥
⎥⎥
⎤
⎡196 ⎤
⎡196 ⎤
24 + ⎢
44 = 240
⎥ = 104 + ⎢
⎢100 ⎥⎥
⎢150 ⎥⎥
⎥
j ⎥
1
3
2
3
j
⎤
⎡ 240 ⎤
⎡ 240 ⎤
24 + ⎢
44 = 264
⎥ = 104 + ⎢
⎢ 100 ⎥⎥
⎢ 150 ⎥⎥
⎥⎥
⎡ 264 ⎤
⎡ 264 ⎤
W34 = 104 + ⎢
24 + ⎢
44 = 264
⎥
⎢ 100 ⎥
⎢ 150 ⎥⎥
Cumple
W33 = W34 = 264 < T3 = 350
el test 2
Maria Isabel Alfonso Galipienso. 2006
44
22
Indice
„ Introducción
„ Caracterización de tareas
„ Planificadores
„ Análisis de planificabilidad
„ Tareas aperiódicas
„ Uso de recursos
„ Modelo extendido
Maria Isabel Alfonso Galipienso. 2006
45
Tareas aperiódicas (I)
Se pueden producir en cualquier instante.
Se ejecutan bajo petición explicita mediante una
interrupción al sistema
Pueden ser de dos tipos:
Críticas: se transforman en periódicas, con un
período que depende de plazo de entrega
deseado y la separación.
No Críticas: se pretende ofrecer buenos tiempos de
respuesta mediante un servicio aperiódico.
Manejador de interrupción
Resolución Servidor “background”
Servidor por consulta ("polling")
Servidor “diferido” ("deferred")
Maria Isabel Alfonso Galipienso. 2006
46
23
Rutina de interrupción
0
5
10
15
20
25
30
35
40
TT11::(P
(P11=15,
=15, DD11=5,
=5, CC11=1)
=1)
TT22::(P
(P22=8,
=8, DD22=8,
=8, CC22=2)
=2)
TT33::(P
(P33=5,
=5, DD33=15,
=15, CC33=6)
=6)
Distorsiona totalmente
el esquema de prioridades.
0
5
10
15
20
25
30
35
40
Tiempo de respuesta
inmediato
47
Maria Isabel Alfonso Galipienso. 2006
Background server
Se puede asumir que las tareas aperiódicas se ejecutan con la
prioridad más baja de todas y con una política de FCFS.
(Servidor de background)
El problema fundamental es el tiempo de respuesta
de las tareas aperiódicas: impredecible
(P11=15,
=15, DD11=5,
=5, CC11=1)
=1)
TT11::(P
(P22=8,
=8, DD22=8,
=8, CC22=2)
=2)
TT22::(P
(P33=5,
=5, DD33=15,
=15, CC33=6)
=6)
TT33::(P
0
5
10
15
20
25
30
35
40
TT44::(P
(P44=∞
=∞, ,DD44=∞,
=∞,CC44==∞)
∞)
Maria Isabel Alfonso Galipienso. 2006
48
24
Polling server
Se le puede asignar una prioridad mayor y limitarle el tiempo
de cómputo (Servidor de consulta). Cada período se rellena el
tiempo de cómputo.
La tarea tiene un tiempo de cómputo Cs máximo, un período y
una prioridad, con lo que se puede incorporar en el análisis de
planificabilidad del sistema.
0
5
10
15
20
25
30
35
40
En el peor caso
se comportará
así
planificable
49
Maria Isabel Alfonso Galipienso. 2006
Deferrable server
0
Factor de
utilización máximo
del servidor
CDS
Ds_Util_max = ——≤
TDS
5
10
15
20
25
30
35
40
U +2
ln P————
2UP + 1
Cs
Tiempo disponible del servidor
Mientras al servidor le quede tiempo atiende las peticiones de
servicio aperiódico que se presenten. Cuando ya no tiene tiempo, ha
de esperar al siguiente período para recargar Cs.
Si al final no ha conseguido ejecutarlo se pierde.
Maria Isabel Alfonso Galipienso. 2006
50
25
Tests planificabilidad (RM)
Condición suficiente
POLLING SERVER
Test para actividades PERIÓDICAS
U p + US ≤ U (n + 1)
para 1 servidor:
1
Ci CS
⎡
+
≤ (n + 1) ⋅ 2 ( n+1) − 1⎤
∑
⎢⎣
⎥⎦
TS
i =1 Ti
n
para m servidores:
m
UP + ∑
CSj
J =1 TSj
≤ U (n + m)
51
Maria Isabel Alfonso Galipienso. 2006
Tests planificabilidad (RM)
DEFERRABLE SERVER
Condición suficiente
Test para actividades
PERIÓDICAS
para 1 servidor:
Maria Isabel Alfonso Galipienso. 2006
⎛ U +2 ⎞
⎟⎟
U P ≤ ln⎜⎜ S
U
2
⋅
+
1
S
⎝
⎠
52
26
Indice
„ Introducción
„ Caracterización de tareas
„ Planificadores
„ Análisis de planificabilidad
„ Tareas aperiódicas
„ Uso de recursos
„ Modelo extendido
Maria Isabel Alfonso Galipienso. 2006
53
Uso de recursos
Las tareas interactuan mediante:
p Datos protegidos
p Directamente (cita)
Pueden producirse bloqueos de tareas:
p
bloqueo directo: cuando se llama a otra tarea
ocupada
p
bloqueo indirecto: una tarea se bloquea por
que otra tarea está utilizando el recurso de
modo exclusivo
Maria Isabel Alfonso Galipienso. 2006
27
Bloqueo de tareas
„ Las tareas más prioritarias se pueden
retrasar debido a otras de menor prioridad
„
Ejemplo: cuando una tarea de menor prioridad
está consumendo un recurso compartido y otra
tarea de mayor prioridad es "activada"
„ Un proceso que espera a otro proceso de
menor prioridad, se dice que está bloqueado
(inversión de prioridades)
55
Maria Isabel Alfonso Galipienso. 2006
Inversión de prioridades
T4
T3
T2
T1
0
2
4
6
8
Ejecutando
Interrumpido
Q bloqueado
Bloqueado
V bloqueado
10
12
14
16
18
Tarea Prioridad Sec. ejecución Activación
T4
4
EEQVE
4
T3
T2
T1
3
2
1
EVVE
EE
EQQQQE
2
2
0
Maria Isabel Alfonso Galipienso. 2006
28
Políticas de planificación
„ Para limitar el efecto de la inversión de
prioridad derivada de un esquema puro de
prioridades estáticas se utilizan:
„
„
„
Herencia de prioridades (No es óptimo)
Techo de prioridades (OCCP)
Techo de prioridades inmediato (ICCP)
La prioridad de un proceso ya no es estática
57
Maria Isabel Alfonso Galipienso. 2006
Herencia de prioridades
T4
T3
T2
T1
0
2
18
Ejecutando
Q bloqueado
4
6
Interrumpido
Bloqueado
V bloqueado
8
10
12
14
16
Tarea Prioridad Sec. ejecución Activación
T4
4
EEQVE
T3
3
EVVE
4
2
T2
2
EE
2
T1
1
EQQQQE
0
Maria Isabel Alfonso Galipienso. 2006
29
Herencia de prioridad. Bloqueos (I)
„ Bloqueo que puede sufrir una tarea i:
K
Bi = Σ (uso(k,i) C(k))
k=1
„ uso(k,i) = 1 si el recurso k se utiliza al menos
por un proceso con una prioridad < Pi y al
menos por un proceso con prioridad ≥ a Pi. En
otro caso será 0.
„ C(k) es el tiempo de ejecución de la sección
crítica k en el peor caso
59
Maria Isabel Alfonso Galipienso. 2006
Herencia de prioridad. Bloqueos (II)
Ambos tests son
condición suficiente
i
Test de factores de
Ck Bi
⎛⎜ 2 1i − 1⎞⎟
∀
≤
≤
+
≤
⋅
i
,
1
i
n
,
i
∑
utilización (Di= Ti):
⎝
⎠
Ti
k =1 Tk
Test de garantía
(Di ≤ Ti):
∀i, Ri = Ci + Bi +
Cálculo del bloqueo:
Bi = min(Bil , Bis )
Maria Isabel Alfonso Galipienso. 2006
Bil =
⎡ Ri ⎤
∑ ⎢ ⎥ ⋅ C j ≤ Di
j∈hp(i ) ⎢ Tj ⎥
∑ max[D
j∈lp(i )
m
k
j,k
: C(Sk ) ≥ Pi
]
Bis = ∑ max[D j,k : C(Sk ) ≥ Pi ]
k =1
j∈lp( i )
60
30
Protocolos de techo de prioridad (I)
El techo de prioridad de un recurso compartido es la
prioridad de la tarea de más alta prioridad que puede
bloquear el recurso.
Ventajas:
„
Una tarea solamente puede ser bloqueada como
mucho una sóla vez durante su ejecución por un
proceso de menor prioridad.
„
No se producen interbloqueos.
„
Se evitan bloqueos transitivos (transitive blocking)
„
Se asegura acceso en exclusión mutua a los recursos
Maria Isabel Alfonso Galipienso. 2006
OCPP
p Cada
tarea tiene una prioridad estática asignada por
defecto.
p Cada
recurso tiene definido un techo de prioridad:
máxima prioridad de la tarea que lo usa
p Cada
tarea tiene una prioridad dinámica: máximo entre
su propia prioridad estática y cualquiera que herede
debido a que bloquea a tareas más prioritarias. La
prioridad máxima que puede heredar es la del techo del
recurso.
p Una
tarea puede bloquear un recurso solamente si su
prioridad dinámica es mayor que el techo de cualquier
recurso actualmente bloqueado por otras tareas.
Maria Isabel Alfonso Galipienso. 2006
31
OCPP.Ejemplo
T4
T3
T2
T1
0
2
4
6
8
Ejecutando
Interrumpido
Q bloqueado
Bloqueado
V bloqueado
10
12
14
16
18
Tarea Prioridad Sec. ejecución Activación
T4
4
EEQVE
4
T3
3
EVVE
2
T2
2
EE
2
T1
1
EQQQQE
0
Maria Isabel Alfonso Galipienso. 2006
OCPP. Bloqueos (I)
„ Bloqueo que puede sufrir una tarea i:
K
Bi = max (uso(k,i) C(k))
k=1
„ Cálculo del tiempo de respuesta Ri = Ci + Bi + Ii
„ Se permite un primer bloqueo de un recurso en
el sistema
„ Se asegura que un segundo recurso será
bloqueado solamente si no existe un proceso de
mayor prioridad que usa ambos recursos
Maria Isabel Alfonso Galipienso. 2006
64
32
OCPP. Bloqueos (II)
Ambos tests son
condición suficiente
Test de factores de
utilización (Di= Ti):
Test de garantía
(Di ≤ Ti):
i
1
Ck Bi
+ ≤ i ⋅ ⎛⎜ 2 i − 1⎞⎟
⎝
⎠
Ti
k =1 Tk
∀i,1 ≤ i ≤ n, ∑
∀i, Ri = Ci + Bi +
Cálculo del bloqueo:
⎡ Ri ⎤
∑ ⎢T ⎥ ⋅ C
j∈hp( i )
⎢
j
⎥
j
≤ Di
{
Bi = max Dj,k Pj < Pi , C(Sk ) ≥ Pi
j ,k
Maria Isabel Alfonso Galipienso. 2006
}
65
ICPP
z
Cada tarea tiene una prioridad estática por
defecto asignada.
z
Cada recurso tiene un techo de prioridad
asignado (máxima prioridad de las tareas que lo
usan).
z
Cada tarea tiene una prioridad dinámica que es
igual al máximo entre su prioridad estática y los
valores “techo” de cualquier recurso que en ese
momento esté bloqueado.
Maria Isabel Alfonso Galipienso. 2006
33
ICPP.Ejemplo
T4
T3
T2
T1
0
2
18
Ejecutando
Q bloqueado
4
6
Interrumpido
Bloqueado
V bloqueado
8
10
12
14
16
Tarea Prioridad Sec. ejecución Activación
T4
4
EEQVE
4
T3
3
EVVE
2
T2
2
EE
2
T1
1
EQQQQE
0
Maria Isabel Alfonso Galipienso. 2006
ICPP. Características
„ El tiempo de respuesta en el peor de los
casos se calcula igual que para OCPP
„ Es más fácil de implementar que un OCPP
„ Provoca menos cambios de contexto
„ Requiere más “cambios” de prioridad (OCPP
solamente cambia la prioridad si ocurre un
bloqueo real)
Maria Isabel Alfonso Galipienso. 2006
68
34
Indice
„ Introducción
„ Caracterización de tareas
„ Planificadores
„ Análisis de planificabilidad
„ Tareas aperiódicas
„ Uso de recursos
„ Modelo extendido
69
Maria Isabel Alfonso Galipienso. 2006
Release jitter (I)
„ La variación máxima en el “lanzamiento” de un proceso se
denomina JITTER (J)
„ Las tareas esporádicas suelen sufrir jitter
P. ej. en el caso de una tarea S esporádica que es lanzada por una
tarea periódica L desde otro procesador
„
TL= 20 La primera ejecución
L
t
S
t+15
t+20
Js
RL= 15
de L termina en RL
CL=1
La segunda ejecución
de L termina después
de CL
L y S NO comparten un
instante crítico
Máxima variación Js = 15
t
t+15
Maria Isabel Alfonso Galipienso. 2006
t+21
70
35
Release jitter (II)
„ Tiempo de respuesta en el peor de los casos:
Ri = Bi + Ci + ∑
Ri + Ji
Cj
Tj
j∈hp(i)
„ Las tareas periódicas pueden sufrir “jitter”
dependiendo de la granularidad del “reloj” del
sistema
Ri periódica = Ri + Ji
71
Maria Isabel Alfonso Galipienso. 2006
Deadlines arbitrarios
„ Di puede ser mayor que el periodo Ti
„ Para cada lanzamiento se define una ventana w(q)
n
win+1(q) = Bi + (q+1)Ci + ∑ wi (q)
j∈hp(i)
Ri(q) = win(q) - qTi
T
Cj
j
„ El número de lanzamientos está limitado por el valor más
pequeño de q que cumple la relación: Ri(q) ≤ Ti
„ El peor tiempo de respuesta el por lo tanto asociado al máximo
valor encontrado para cada q:
Ri = maxq=0,1,2,... Ri(q)
Maria Isabel Alfonso Galipienso. 2006
72
36
Deadlines arbitrarios
„ Si queremos tener en cuenta el efecto del Jitter,
modificaremos el análisis anterior incrementando el factor
que representa la inferencia
win+1(q)
= Bi + (q+1)Ci + ∑
j∈hp(i)
win(q)+Jj
Tj
Cj
„ Si un proceso puede sufrir jitter, entonces dos ventanas
consecutivas pueden solapar si el tiempo de respuesta más
el jitter es mayor que el periodo
Ri(q) = win(q) - qTi + Ji
Maria Isabel Alfonso Galipienso. 2006
73
Asignación de prioridades
„ Teorema:
Si a un proceso P se le asigna la menor prioridad y es factible,
entonces, si existe una ordenación de prioridades factible para el
conjunto completo de procesos, existirá una ordenación en la que a
P se le asigne la menor prioridad
procedure assign_pri (set: in out process_set; N:natural;
ok: out:boolean);
begin
for k in 1..N loop
for next in k..N loop
swap (set, K, next);
process_test (set, k, ok);
end loop;
exit when not ok;
end loop;
end assign_pri;
Maria Isabel Alfonso Galipienso. 2006
74
37
Prioridades en Ada (I)
Hay que asociar prioridades a las tareas.
El sistema proporciona lo siguiente una rango de prioridades
(0..32) y una por defecto (16).
Se definen mediante pragma
task Controller is
pragma Priority(10);
end Controller;
Prioridad base
task type Productor(pid: INTEGER; prio: System.Priority) is
pragma Priority(prio);
end Productor;
Maria Isabel Alfonso Galipienso. 2006
Prioridades en Ada (II)
„ Prioridad BASE: prioridad asignada mediante
"pragmas"
„ Prioridad ACTIVA: es el máximo entre entre la
prioridad base y cualquier otra prioridad heredada
„ Formas de heredar prioridades:
„
Mediante el uso de objetos protegidos
„ Durante la activación: se hereda la prioridad activa del
padre
„ Durante una cita: la tarea que realiza el "accept" hereda la
prioridad activa de la tarea que realiza la llamada a la
entrada (si es mayor que la propia)
Maria Isabel Alfonso Galipienso. 2006
76
38
Prioridades Ceiling Locking
„ Los objetos protegidos necesitan mantener la consistencia de
sus datos
„ La exclusión mutua puede garantizarse mediante el uso del
modelo de prioridades de Ada
„ Cada objeto protegido tiene asignado un techo de prioridad
que es mayor o igual que la prioridad más alta de cualquiera
de las tareas que lo llaman
„ Cuando una tarea llama a una operación protegida, su
prioridad se convierte automáticamente en la del objeto
protegido
„
Si una tarea que quiere acceder a un objeto protegido está en ejecución
entonces el objeto protegido no puede estar ya ocupado
Maria Isabel Alfonso Galipienso. 2006
77
Ceiling Locking (ICCP)
„ A cada objeto protegido se le asigna una prioridad mediante
un pragma
„ Si se omite el prama, se asume Priority'Last
„ La excepción Program_Error es lanzada si la tarea que
llama tiene una prioridad activa mayor que el techo
„ Utilizando ceiling locking, una implementación efectiva usará
el hilo de ejecución de la tarea que llama para ejecutar no
solamente la operación protegida sino también para ejecutar
el código de cualqueir otra tarea que tenga que ser lanzada
(activada) como resultado de la llamada
Maria Isabel Alfonso Galipienso. 2006
78
39