tm99207. - Universidad de los Andes

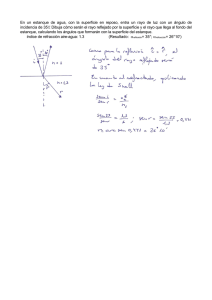
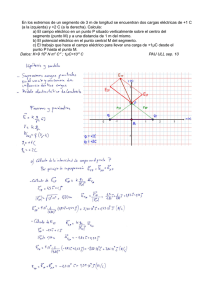
Estudio de la exposición de estructuras delgadas mediante el Modelo de Progresión del
Líder
Jorge Eliécer Forero Aponte, Universidad de los Andes
e_mail: [email protected]
Agosto de 1999
Resumen
El propósito de este trabajo de investigación
es
realizar
una
implementación
computacional del Modelo de Progresión del
Líder (M.P.L.) para estudiar la exposición de
estructuras delgadas a las descargas eléctricas
atmosféricas (DEAT’S). En este trabajo se
desarrollaron las expresiones matemáticas de
campo eléctrico y potencial debidos a un
segmento recto de carga inclinado, con los
cuales se simula la trayectoria de los líderes
del rayo. El programa permite obtener la
distancia lateral máxima (DLM) entre el eje
de la estructura y el primer líder descendente
que finaliza en un rayo descendente con
impacto a tierra. La aplicación práctica del
modelo es servir como herramienta de
análisis y diseño de apantallamiento de
estructuras en general y de líneas de
transmisión.
Palabras clave:
Modelo,
Rayo,
Líder,
Electrostática,
Apantallamiento.
1 Introducción.
Este trabajo de investigación es puramente
teórico y está enfocado en la implementación
del MPL en un programa computacional
llamado “Simulación de la Trayectoria del
Líder” (SITRALID), el cual sirve para
estudiar la exposición de estructuras delgadas
a las DEAT’S. El programa fue realizado
utilizando la técnica de la programación
orientada a objetos dado su relativo gran
tamaño. En la tesis de pregrado titulada
“Simulación de una Descarga Eléctrica
Atmosférica Basada en el Modelo De Progresión
Del Líder” [1] se hizo una primera
implementación del MPL, en la cual se hizo
una simplificación de la representación de la
estructura y no se utilizaron los segmentos de
carga
adecuados
para
simular
el
desplazamiento de carga en los canales
líderes del rayo. La importancia de este
trabajo radica en que se hizo una
implementación completa del MPL utilizando
segmentos rectos de carga que siguen la
dirección de avance de los líderes y haciendo
una representación más precisa de la
estructura delgada.
Inicialmente se hizo una revisión de la teoría
electrostática y del cálculo diferencial e
integral con el propósito de facilitar el
desarrollo de las expresiones de campo
eléctrico y potencial para un segmento recto
de carga inclinado. Con el fin de validar las
expresiones desarrolladas, se hizo un estudio
comparativo de resultados obtenidos con
estas y con las expresiones ya conocidas de
campo y potencial para una carga puntual.
Finalmente, se implementó el modelo en el
programa SITRALID, en el cual se hizo
énfasis en la disminución del tiempo de
simulación. Usando el programa se
estudiaron tres estructuras delgadas, para las
cuales se calcularon las distancias máximas
laterales como función de la corriente pico
del rayo. Los resultados obtenidos son los
esperados desde el punto de vista teórico.
2 Contenido.
El propósito fundamental de este trabajo de
investigación es hacer una implementación
completa y adecuada del MPL para evaluar la
exposición de estructuras delgadas a las
DEAT’S. Como consecuencia de este trabajo
se puede tener una visión más clara de la
aplicación práctica que podría tener este
modelo.
Ecuaciones de campo eléctrico y
potencial para segmentos rectos
inclinados de carga.
En la figura 2.1.1 se muestra la configuración
segmento inclinado - plano para la cual se
encontraron las expresiones de campo y
potencial. En la figura 2.1.2 se muestra el
significado de las variables involucradas en
las expresiones para el campo y el potencial
de las cargas en cuestión.
EH = K




⋅ A ⋅ 



 (ro − H P )⋅ u 2

 ( ro − H P )⋅ u 1
 
1
1


+ 1 −
+ 1 − 


D
P
D
P
2


2

 
u2 + D P
u1 + D P

 ( ro − H N )⋅ v 2

 ( ro − H N )⋅ v 1
 
1
1


+ 1  +
+ 1  


D
N
D
N

 
v22 + D N 
v1 2 + D N 
2.1
Ec. 2.1.1
En donde:
K=
G = z2 − z1
H = r 2 − r1
λ
4 ⋅π ⋅ε
O
I = G × H; J = H 2 × r 0 + G 2 × r 2
L = G2 + H2
P=
Segmento
recto de
carga.
J − I× z 2 ;
L
Q=
I× z0
L
I × (r 0 − r 2 ) + H 2 × z 2
H2 × z 0
D=
; E=
L
L
Plano de
potencial
cero.
HP = P + Q
D P = ( D − E )2
Figura 2.1.1
HN = P − Q
DN = ( D + E )2
z
u1 = r1 − H P
u2 = r2 − H P
( r1, z1 )
λ × dl
( r, z )
v1 = r1 − HN
v2 = r2 − HN
( r2, z2 )
( r o, zo )
dE
r
Figura 2.1.2.
La componente horizontal de campo eléctrico
en el punto de coordenadas (r0 , z0 ) en la con
figuración segmento inclinado - plano está
determinada por la ecuación 2.1.1.
La componente vertical de campo eléctrico
en la misma configuración se presenta en la
ecuación 2.1.2
EV =





K ⋅B ⋅




1
u2 2 + DZP





(zo − HZP )⋅ u +  −
1
2
DZP
1
u12 + DZP

2
( zo + HZN )⋅ v −  +
1
DZN
v2 2 + DZN
1




Ec. 2.1.2
En donde:




1
v1 2 + DZN


(zo − HZP ) ⋅u +  − 
1 
1
DZP




1
( zo + HZN ) ⋅v
DZN



−1 

G 2 ⋅ z0
L
HZP = D + N
HZN = D − N
I ⋅z0
G 2 ⋅ (r 0 − r 2 ) + I ⋅ z 2
R=
; Q=
L
L
2
D Z P = (R − Q )
N
=
D Z N = (R + Q )
campo eléctrico, este es prácticamente el
mismo para ambas fuentes de carga.
Campoeléctrico para segmento y carga puntual en z=197
1.8
1.6
PUNTO: P = (15,200)
1.4
SEGMENTO: Pi = (14,202)
Pf = (16,198)
1.2
2
1
E [kV / cm]
0.8
0.6
u2 = z1− HZP
u1= z2 − HZP
0.4
0.2
0
0
5
10
15
20
25
30
r [m]
v2 = z1 − HZN
v1= z2 − HZN
La expresión matemática para el potencial
eléctrico se presenta en la ecuación 2.1.3
Φ= K⋅ln
(r2−HP) 2 +DP+( r2 −HP) ( r1−HN) 2 +DN +(r1−HN)
⋅
(r1−HP) 2 +DP+( r1− HP) ( r2 −HN) 2 +DN +(r2−HN)
Ec. 2.1.3
2.2
Comparación del campo eléctrico
debido a una carga puntual y del
debido a un segmento inclinado.
En la figura 2.2.1 se presentan las curvas de
campo eléctrico para una carga puntual y para
un segmento recto de carga, las cuales fueron
obtenidas evaluando el campo eléctrico en
varios puntos a lo largo de la recta horizontal
cuya ecuación es z=197. El valor de ambas
cargas es igual a 100 µC y sus coordenadas
de localización en el sistema rz son: (15, 200)
para el punto, y ((14, 202), (16, 198)) para
los puntos extremos del segmento. Se observa
la asimetría del campo eléctrico debido al
segmento, el cual tiene una pendiente
negativa igual a dos. Por otra parte se ve más
claramente que cuanto más alejados del
segmento estén los puntos de evaluación del
Figura 2.2.1
2.3
Representación de la estructura
delgada.
La estructura delgada es un mástil vertical
aterrizado. Para asegurar que la condición de
aterrizado se cumpla siempre es necesario
evaluar la carga inducida en cada paso de
avance de los líderes. La configuración de
carga utilizada para simular la carga inducida
residente en la superficie consta de dos
segmentos rectos de carga, los cuales
modelan el cuerpo de la estructura y cuatro
cargas puntuales ubicadas en un arco circular
en la parte superior. En la figura 2.3.1 se
muestra la representación de la estructura
delgada.
Cargas puntuales
Segmentos Rectos
de Carga
Puntos de contorno.
Cuerpo de la
estructura.
Figura 2.3.1
El valor de cada una de las cargas usadas en
la estructura se calcula resolviendo un
sistema de siete ecuaciones lineales
simultáneas. Cada ecuación corresponde a un
punto de contorno en la estructura, en el que
la suma de los potenciales debidos a cada una
de las cargas en el interior de la estructura,
debe ser igual a la suma de los potenciales
debidos a cada una de las cargas externas a la
estructura. Las cargas externas son los anillos
unipolares de carga usados para representar la
nube y los segmentos rectos de carga con los
que se representa el avance de los líderes. El
siguiente es el sistema de ecuaciones lineales
con el que se calcula el valor de cada una de
las cargas que modelan la estructura
aterrizada:
[P] × [Q]
7 ×7
7 x1
[ ]
= − V 7 x1
Ec. 2.3.1
En donde P es la matriz de coeficientes de
potencial, Q es el vector de cargas
desconocidas y V es el vector de potencial.
Aplicación del MPL a la exposición de
estructuras delgadas.
El estudio de la exposición de estructuras
delgadas a las descargas atmosféricas
requiere de la realización de repetidas
simulaciones con el fin de determinar la
distancia lateral máxima. La distancia lateral
máxima es aquella distancia horizontal entre
el eje de la estructura y el canal del líder
descendente, para la cual ocurre el primer
rayo a tierra, después de haber incrementado
la distancia lateral comenzando con una en la
cual ocurre un rayo descendente con impacto
en la estructura.
La comparación de los resultados del modelo
con los reales se hace determinando el
número de rayos que hacen impacto en la
estructura, conociendo la densidad de rayos a
tierra de la zona en la cual está la estructura.
Entonces el número de rayos se determina
así:
Ns = Ng ∗ Aeq
Ec. 3.3.1
Aeq es el área equivalente que tiene en
cuenta la probabilidad de ocurrencia de la
corriente del rayo y la distancia lateral
máxima relevante a la estructura bajo estudio.
El área equivalente se calcula así:
Aeq = ∫ 0∞ DL
2
( I ) ∗ p ( I ) ∗ dI
Ec. 3.3.2
4
Resultados.
El estudio realizado con el programa
SITRALID consistió en encontrar las
distancias laterales máximas para tres
estructuras diferentes. En la tabla 3.1 se
resumen los resultados obtenidos:
3
I [kA]
10
60
140
Altura de la estructura [m]
H = 20 m H = 35 m H = 50 m
45.5
90.5
133.5
111.5
147.5
172.5
132.5
172.5
205.5
Tabla 4.1
Como era de esperarse los resultados
corresponden a los predichos por la teoría
electromagnética. En las tres estructuras
estudiadas se observa que a medida que crece
la corriente del rayo se obtienen distancias
laterales mayores. También se esperaba que a
medida que crece la altura de la estructura
delgada se obtienen distancias laterales
máximas mayores. Estos resultados se
representan gráficamente en la figura 4.1.
DISTANCIA LATERAL MÁXIMA Vs. CORRIENTE DEL RAYO
250
200
DL [m]
150
100
50
0
10
H = 20 m
60
I [kA]
H = 35 m
140
H = 50 m
Figura 4.1
5 Conclusiones.
A través de las diferentes simulaciones
realizadas con el programa SITRALID y del
mismo desarrollo del programa, se pone de
manifiesto la necesidad de seguir estudiando
la manera de implementar el M.P.L en un
algoritmo que sea rápido y que tenga la
precisión adecuada para las estimaciones que
el modelo hace de la exposición de
estructuras y de líneas de transmisión.
De todas maneras con el trabajo desarrollado
es evidente que el modelo tiene grandes
limitaciones debidas principalmente a la
cantidad de cálculos que es necesario hacer
para simular una descarga atmosférica, los
cuales aumentan si el número de objetos en el
piso crece.
Todavía no es claro y evidente si el M.P.L.
arroja resultados más aproximados a la
realidad que los obtenidos con el Método
Electrogeométrico, y si es así, que tan
aproximados son y que facilidad existe para
ser aplicado. Si los resultados del M.P.L. son
mucho más cercanos a la realidad y si es
relativamente más fácil de aplicar, entonces
estaríamos hablando de un cambio de
paradigma en cuanto la metodología para
estudiar la exposición de estructuras y líneas
de transmisión.
Una de las recomendaciones para continuar
con el estudio es la comparación de los
resultados de exposición que arroja el modelo
con datos reales de mediciones de campo,
para lo cual es necesario revaluar los
parámetros que usa el modelo, ya que estos
en su mayoría son de tipo local, es decir
varían con las condiciones climáticas de la
zona en la cual se está haciendo el estudio.
Del estudio realizado es importante resaltar
que los resultados obtenidos son lógicos
desde la óptica de la teoría electrostática y del
orden de magnitud esperado en tales sucesos,
lo cual se constituye en una importante
justificación para continuar estudiando el
modelo.
Nuevamente es necesario resaltar los aportes
que se hicieron en este trabajo, los cuales son:
el desarrollo de las ecuaciones de campo
eléctrico y potencial para segmentos rectos de
carga inclinados y la representación de un
objeto en el piso usando varias cargas de
diferente tipo. Estos dos aportes se
implementaron en el programa realizado.
6
Referencias
[1]
BERNARDI M., BONDIOU A.,
COOREY
V.,
GALLIMBERTI
I.,PEDERSEN A. y RUHLING F. Lightning
exposure of structures and interception
efficiency of air terminals. En: CIGRE
TF33.01.03. Italia. (Abril 1997); p. 1-50.
[2] CORTINA, R.; GARBAGNATI, E.;
SERRAVALLI, W.; DELLERA, L.; PIGINI,
A. y THIONE, L. Some aspects of the
evaluation of the lightning performance of
electrical systems.
En : International
conference on large high voltage electric
systems. Paris. En: CIGRE TF33.13. Italia.
(1980); 21p.
[3] DELLERA, L.; GARBAGNATI, E. and
PIGINI A. A lightning model based on the
similarity between lightning fenomena and
long laboratory sparks.
En : The 16th
International Conference on Lightning
Protection. ( Jun. 1981, Szeged). Hungary :
CESI. 17 p.
[4] Dellera, L. and Garbagnati, E. Lightning
stroke simulation by means of the leader
progression model - Part I : Description of
the model and evaluation of exposure of freestanding structures. En : IEEE. Transactions
on power delivery. Vol. 5, No. 4 (oct. 1990);
p. 2009 - 2022.
[5] __
______.________ Part II: Exposure
shielding failure evaluation of overhead
with assessment of application graphs.
IEEE Transactions on Power Delivery.
5, No. 4 ( oct. 1990); p. 2023 - 2029
and
lines
En :
Vol.
[6] ________ . Shielding failure evaluation :
application of the leader progression model.
En : The international conference on
lightning and power systems. (Jun. 1984,
London) UK : IEE. 6 p.
[7] DELLERA, L.; GARBAGNATI, E. and
PIGINI A. Lightning simulation by means of
a leader progression model.
En : The
International Aeroespace Conference on
Lightning and Static Electricity. (Mar. 1982,
Oxford); 9 p.
[8] FORERO A., Jorge Eliécer y GÓMEZ
P., Manuel José. Simulación de una descarga
eléctrica atmosférica basada en el Modelo de
Progresión del Líder. Santafé de Bogotá,
1997, 162 p. Trabajo de grado (Ingeniero
Electricista) Universidad Nacional de
Colombia.
Facultad
de
Ingeniería.
Departamento de Ingeniería Eléctrica.
[9] GEORGE B. Thomas y ROSS L. Finney.
Cálculo con Geometría Analítica. 6 ed.
Madrid: Addisson Wesley Iberoamericana,
1987. p. 483-493.
[10]
JOHNK, Carl T. A.
Ingeniería
Electromagnética : Campos y Ondas.
México : Limusa,1993. p. 49, 223-239, 265269.
[1] ANDREWS Mark. Aprenda Visual C++
Ya. Madrid (España): McGraw – Hill, 1997.
397 p.
[2] BECERRA SANTAMARIA Cesar A.
C++ una herramienta para programación
orientada a objetos. Santafé de Bogotá:
Editorial Kimpres Ltda., 1994. 606 p.
[3] KRUGLINSKI David J. Progrese con
Visual C++. Madrid (España): McGraw –
Hill, 1994. 664 p.
[4] PERRY Greg. Moving from C to C++.
Indianapolis (USA): SAMS Publishing, 1991.
404 p.
[5] TORRES, H. y CASTAÑO, O. El rayo.
Bogotá : ICONTEC, 1994. 154 p.
[6]
UMAN, Martin.
The lightning
discharge. Orlando: Academic Press, 1987.
368 p. (International Geophysics series; vol.
39)