O1 O2 T1 T2

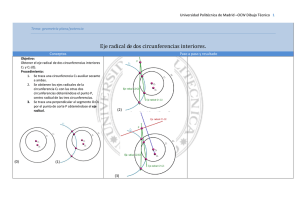
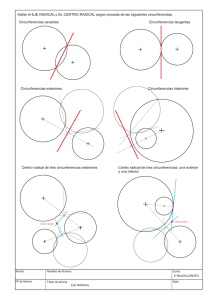
EJE RADICAL DE DOS CIRCUNFERENCIAS
Se denomina eje radical de dos circunferencias de centros O1 y O2 al lugar geométrico de los puntos del plano que
tienen igual potencia respecto de ambas circunferencias
CIRCUFERENCIAS SECANTES (ilustración nº 7)
El ejej radical e de dos circunferencias secantes viene definido por la recta que une sus puntos comunes M y N. Resulta ser, siempre, perpendicular a la recta que une sus centros O1 y O2.
CIRCUFERENCIAS TANGENTES (ilustración nº 8)
Como caso límite del anterior, el ejej radical e de dos circunferencias tangentes será la recta perpendicular al segmento
que une de los centros, por el punto de tangencia.
e
e
e
M
O1
O2
O1
O2
O1
O2
N
ILUSTRACIÓN Nº 7
ILUSTRACIÓN Nº 8
CIRCUFERENCIAS EXTERIORES O INTERIORES (ilustración nº 9)
Cuando dos circunferencias no tienen ningún punto en común, el eje radical e sigue siendo perpendicular a la recta que
une sus centros y pasará por un punto que cumpla la condición de tener igual potencia respecto a ambas.
Para determinar (Q) emplearemos una circunferencia auxiliar secante a las dadas. El punto común a los ejes radicales
(e1 y e2) con las dadas, determina el punto Q y con ello, el eje radical e buscado.
Las tangentes trazadas a dos circunferencias exteriores desde cualquier punto del eje radical tienen igual longitud
(PTt3 = PT4), por tanto el punto de intersección del eje radical con una recta tangente a las dos circunferencias exteriores será su punto medio (T1M = T2M).
En el caso de dos circunferencias interiores las tangentes trazadas desde un punto (P) del eje radical a los dos circunferencias también tendrán la misma magnitud (PT1 = PT2 = PT3 = PT4).
e
e
T3
T4
O2
O1
O1
O3
T1
T1
O2
T2
T2
ILUSTRACIÓN Nº 9
CENTRO RADICAL DE TRES CIRCUNFERENCIAS. (Ilustración nº 10)
Dadas tres circunferencias de centros O1, O2 y O3, se llama centro radica al punto C desde el cual la potencia, respecto
de la tres circunferencias, es la misma.
El centro radical es el punto de intersección de los ejes radicales de las circunferencias tomadas de dos en dos. Dicho
centro será impropio (situado en el infinito) cuando los ejes radicales de los pares de circunferencias sean paralelos,
por tanto los centros de las circunferencias estarán alineados.
O'
O
ER
O'
O
O'
CR
O
O''
O''
ER
O''
ER
ILUSTRACIÓN Nº 10
TANGENTES TRAZADAS DESDE UN PUNTO DEL EJE RADICAL (Ilustración nº 11)
Dado que el eje radical de dos circunferencias es el lugar geométrico de puntos de igual potencia con relación a ambas, los segmentos de tangente trazados desde un punto cualquiera de dicho eje, tienen la misma longitud.
Por tanto, y en particular en el caso de circunferencias tangentes entre sí (interiores o exteriores), se tendrá que verificar que los segmentos tangentes (PT), trazados desde cualquier punto P del eje radical, son iguales.
T3
e
T2
O1
T3
P
e
T1
O1
O2
O2
T1
P
T2
ILUSTRACIÓN Nº 11
TANGENTES TRAZADAS DESDE EL CENTRO RADICAL (Ilustración nº 12)
Para cualquier posición relativa
entre circunferencias, y, en particular, si las tres son tangentes entre
sí, o lo son dos a dos, o lo son dos
pares, los segmentos de las tangentes (CT) trazadas desde el centro
radical (C) son iguales.
Como consecuencia, también lo
son las trazadas desde C a las circunferencias auxiliares empleadas
para obtener el centro radical. CT1
= CT2 = CT3…..
e12
e12
O2
T1
T2
O1
e13
O3
O2
e23
e23
T2
T3
T1
O1
CR
T3
ILUSTRACIÓN Nº 12
T4
O3