Descargar - Ministerio de Trabajo y Promoción del Empleo
Anuncio

BOLETÍN DE
ECONOMÍA
LABORAL
33
Año 9
Abril 2006
Análisis de la Distribución del Ingreso Laboral en Lima
Metropolitana, 1990 - 2004
1
MINISTERIO DE TRABAJO Y PROMOCIÓN DEL EMPLEO
C A R L OS A L M ER Í V E R A M E N D I
Ministro
B L A N C A E L E NA M E D I A N ER O B UR G A
Viceministro de Trabajo (e)
W A L T E R FR A N C IS C O G A G O R O D R I G U E Z
Viceministro de Promoción del Empleo y de la Micro y Pequeña Empresa
B L A N C A E L E NA M E D I A N ER O B UR G A
Secretaria General
DIRECCIÓN NACIONAL DE PROMOCIÓN DEL EMPLEO Y FORMACIÓN
PROFESIONAL
A S T R I D S A N C H EZ F A L ER O
Directora Nacional (e)
PROGRAMA DE ESTADÍSTICAS Y ESTUDIOS LABORALES
Coordinadora
T A T I A NA V EL A Z C O P OR T O C A R R E R O
Equipo Técnico
E DG A R D A B A N T O M I L LO N E S
V I V IA N A S A LG A DO PO R T U GA L
2
ÍNDICE
Introducción
1. Aspectos metodológicos
a. Sobre la Encuesta de Hogares
Especializada de Niveles de
Empleo del MTPE
b. Medición de los ingresos a partir de la Encuesta de Hogares
c. Medición de indicadores de desigualdad
2. Características de la distribución del ingreso en Lima Metropolitana,
2001 – 2004
3. Evolución de la desigualdad del ingreso laboral 1990 – 2004
a. Principales indicadores de desigualdad
b. Descomposición de la Desigualdad, a partir del índice de Theil
c. Factores que influyen en la desigualdad: la descomposición de
Fields
4. Modelización de los retornos de
capital humano sobre los ingresos
laborales a partir de la Regresión Cuantílica
a. Método de regresión cuantílica (MRC)
b. Resultados
Conclusiones
Bibliografía
Anexos
3
ANÁLISIS DE LA DISTRIBUCIÓ DEL INGRESO LABORAL EN LIMA
METROPOLITANA, 1990 - 2004
Introducción
El presente artículo tiene como objetivo analizar la evolución de la
distribución
de
ingresos
y
sus
indicadores
de
dispersión
en
Lima
Metropolitana, durante los años 1990 – 2004. De acuerdo a los resultados
encontrados, se muestra que la desigualdad del ingreso laboral ha venido
reduciéndose en los últimos años. Por ello resulta de interés conocer los
cambios operados en los factores que lo explican: el nivel educativo,
estructura de mercado, categoría ocupacional, entre otras variables de
interés.
En primer lugar se examina las fuentes de información utilizadas así como
diversos aspectos metodológicos. En segundo lugar, se presenta el análisis
no paramétrico de la distribución del ingreso. Así, se evaluará el cambio de
la distribución de los ingresos de los ocupados en Lima Metropolitana en el
año 2004 respecto al 2001, a través del método de estimación de funciones
empíricas de densidad de Kernel. Este instrumento permite explorar si para
alguna población se observa un cambio en la distribución empírica de
ingresos. Además, se comprueba la existencia de valores extremos,
también
conocidos
como
outliers,
lo
cual
se
manifiesta
en
el
comportamiento heterogéneo de los indicadores de posición.
En tercer lugar, se explora la evolución de los indicadores de desigualdad y
se presta particular atención a la descomposición de los principales factores
que influyen en la desigualdad, para ello se utiliza el índice de Theil. En
cuarto lugar, se evalúa los retornos de los activos, tales como educación,
experiencia, género u otras sobre la distribución del ingreso laboral.
Diversos estudios parten de la hipótesis que en los últimos años se ha
observado un incremento significativo, en el ingreso principalmente,
originado por diferenciales en educación y experiencia laboral. Para ello se
emplea la ecuación de ingresos tipo Mincer y se aplica la técnica semi paramétrica
de
regresión
cuantílica,
la
cual
permite
capturar
4
heterogeneidad de comportamiento de los ingresos laborales debido a la
presencia de observaciones outliers.
La información estadística utilizada proviene de las Encuestas de Hogares
Especializada en Niveles del Empleo, ejecutadas por el
Ministerio de
Trabajo y Promoción del Empleo en Lima Metropolitana en el periodo 1990 –
2004.
5
1. Aspectos Metodológicos
En el Perú, existen estadísticas laborales desde fines de la década de los 50,
las cuales han venido siendo ejecutadas por el Ministerio de Trabajo y
Promoción del Empleo (MTPE), principalmente mediante encuestas a
empresas y hogares. Las primeras son la base de las estimaciones del
empleo y remuneraciones del sector formal urbano, mientras que las
encuestas a hogares se utilizan para medir las principales variables
relacionadas a todo el mercado de trabajo, por ello éstas se han constituido
en la principal fuente de información para el análisis del mercado laboral
peruano.
a. La Encuesta de Hogares Especializada de Niveles de Empleo del
MTPE
La Encuesta de Hogares Especializada en Niveles de Empleo es el
instrumento estadístico más importante que cuenta el MTPE para la
obtención de información relacionada a la dinámica del mercado laboral,
empleo e ingresos. Su alcance geográfico ha variado con el tiempo, en
función de razones operativas y presupuestales. Actualmente la información
es
representativa
a
las
principales
ciudades
del
país.
Para
Lima
Metropolitana, el tamaño de la muestra es, aproximadamente, 2,500
viviendas. Asimismo, la ENAHO del MTPE permite contar con información
sobre la estructura y tendencias de cambio en la fuerza laboral del sector a
través de
variables socio demográficas y económicas proveniente de los
hogares. La población en estudio está constituida por todos los residentes
habituales del hogar1.
En el presente artículo se utilizará la Encuesta de Hogares aplicada en el
período 1990 – 2004 en Lima Metropolitana. Ésta encuesta tiene como
característica entrevistar a todos los miembros del hogar, a aquellos que se
encuentran laborando se les pregunta sobre sus remuneraciones netas. Así,
las cifras captadas por esta encuesta son las emitidas por los propios
1
Se denomina residente habitual a aquellos individuos que habitan en el hogar por lo menos
los ultimas 30 días antes de la ejecución de la encuesta.
6
trabajadores. Según MTPE (1996), una limitación importante de esta
manera de recoger información, radica en que las declaraciones de ingresos
pueden presentar problemas de subestimación. Asimismo, debe tenerse en
cuenta la dificultad de captar correctamente los ingresos netos de los
trabajadores informales y de los conductores de microempresas,
b. La Medición del Ingreso a partir de las Encuestas de Hogares
Las variables de ingreso utilizadas en este artículo son:
Ingreso familiar, que está constituido por todos los ingresos mensuales
del hogar sea cual sea su procedencia: laboral y no laboral. Éste último
compuesto por las transferencias corrientes, rentas de la propiedad, y otros
ingresos extraordinarios2.
Ingreso laboral, está constituido por los ingresos laborales mensuales
(monetarios o en especie) que percibe el trabajador por su ocupación
principal y secundaria.
Ingreso laboral horario, está constituido por los ingresos laborales que
percibe el trabajador por una hora de trabajo por su ocupación principal y
secundaria.
Las variables utilizadas para este análisis son el Ingreso familiar, el ingreso
laboral mensual y el ingreso laboral horario, donde:
2
Cabe mencionar que no son considerados miembros del hogar
trabajadores del hogar.
los no parientes ni los
7
Ingreso laboral
= Ingreso laboral de la ocupación principal
Ingreso
+
laboral de la ocupación secundaria.
Usualmente se considera el ingreso labora
mensual
Ingreso
familiar
=
Ingreso
laboral
(Transferencias
+
Ingreso
corrientes,
no
laboral
rentas
de
propiedad y otros ingresos extraordinarios)
Ingreso laboral horario= Ingreso laboral mensual/ Número de horas
normales de trabajo al mes
8
2. Distribución del ingreso en Lima Metropolitana, 2001 - 2004
En esta sección se analizan de manera descriptiva los ingresos totales del
hogar y los laborales, a partir de información proveniente de la Encuestas
de Hogares del Ministerio de
Trabajo y Promoción del Empleo (MTPE).
Asimismo, se especifica su función densidad, e
identifica los principales
parámetros de los ingresos, de tal manera que permita un mejor
entendimiento de la distribución de los ingresos.
El análisis de los ingresos se hará a través del método de estimación de
funciones empíricas de densidad de Kernel. Este instrumento permite
explorar si para algún año se observa un cambio en la distribución empírica
de ingresos.
Las variables utilizadas para este análisis son el Ingreso familiar, el ingreso
laboral mensual y el ingreso laboral horario.
a. Estimación y adecuación de los modelos a los datos empíricos
En esta sección se analiza los ingresos de la Población Económicamente
Activa (PEA) ocupada que recibe algún tipo de remuneración. Así, el análisis
se inicia con un análisis descriptivo de los datos, haciendo referencia a las
siguientes medidas:
1. Posición central. Corresponde al valor de la media y de la mediana.
2. Dispersión. Desviación típica y Gini
3. Forma. Coeficiente de asimetría y coeficiente curtosis
4. Estimadores robustos. M-Estimadores3
3
David C. Hoaglin. « Understanding Robust and Exploratory Data Analysis ». Las medias
ajustados o Trimmed means, proporcionan estimadores robustos de posición y se basan en
estadísticas de orden, este ajuste consiste en recortar los extremos de la variable, que son
consideradas como puntos outliers y así obtener un indicador más estable. El valor α permite
identificar el porcentaje que es ajustado en cada extremo de la muestra ordenada. Así, el
20%trimmed (ajuste del 20%) de una muestra de tamaño 10, es un promedio simple de 6
observaciones quitando 2 observaciones en cada extremo.
El α - trimmed means, denotado por T(α) es formulado de la siguiente manera:
T (α ) =
n − g −1
1
(1 − r ) X ( g +1) + X ( n− g ) + ∑ X ( i )
n(1 − 2α )
i= g +2
[
]
9
El cuadro N° 1 se presentan las estadísticas descriptivas del ingreso. Así,
para el año 2004, el ingreso laboral promedio mensual de los hogares
limeños ascendió a S/. 2,020 con una mediana de S/. 1,320. Por otro lado,
el ingreso laboral promedio mensual y por hora de los individuos fue de
S/.1,039 y S/. 4.8 nuevos soles, respectivamente. En todos los casos se
aprecia un alto grado de dispersión, dado por el coeficiente de variación4.
Asimismo, con el objetivo de encontrar un promedio más robusto a
observaciones atípicas se recortan en cada cola de la distribución, el 10, 15
y 20 % de los datos, reduciéndose sustancialmente los promedios en todas
las variables de análisis. Así, considerando el 80% de los datos centrales, el
ingreso laboral promedio mensual de los hogares descendió a S/. 1,856, el
ingreso laboral individual, a S/. 800 y el ingreso laboral por hora, a S/. 3.6;
este comportamiento se repite para los siguientes niveles sin lograr que
converjan a un valor estable, esto es una evidencia de una alta dispersión
de los datos y la existencia de datos extremos en la distribución de las
variables, además de confirmar la asimetría de distribución como también lo
sugieren los indicadores de asimetría y curtosis, que se encuentran lejos de
cero.
El análisis anterior es importante porque permite distinguir la presencia de
una alta dispersión de los datos y la presencia de “puntuaciones” extremas
que pueden alterar la correlación de las variables. La distorsión que
producen estos datos, normalmente es aumentar de forma espurea el grado
de relación lineal, por ello se hace necesario la utilización de técnicas de
estimación robustas y que capturen el efecto real de los parámetros sin la
influencia de los datos atípicos. Bajo esta observación las estimaciones
utilizadas en este estudio se basan en el método de regresión cuantílica
(MRC), metodología que puede capturar, en caso de existir, heterogeneidad
de comportamiento a través del modelo, que puede tornarse más rica en la
medida en que los datos presenten alta heterocedasticidad o una elevada
proporción de observaciones outliers.
4
El Coeficiente de Variación (CV) se obtiene de la división entre desviación estándar y la
media.
10
Cuadro N° 1
Lima Metropolitana: Estadísticas Descriptivas del Ingreso, 2004
Ingreso
familiar
Ingreso
individual
Ingreso
Individual
por hora
Media
2,020
1,038
4.8
Mediana
1,320
714.4
3.1
Desviación
Estándar
2,861
1,319
6.7
8
6.6
9.6
111
75.9
178.7
Trimmed 0.1
1,856
798
3.6
Trimmed 0.15
1,488
770
3.5
Trimmed 0.20
1,444
750
3.3
Asimetría
Curtósis
Media
Ajustada
Fuente: MTPE - Encuesta de Hogares Especializada en Niveles de Empleo, 2004 – III trimestre.
Elaboración: MTPE – Programa de Estadísticas y Estudios Laborales
Nota: En los cálculos se ha excluido a los trabajadores familiares no remunerados.
b. Función densidad estimada de la variable ingresos
De acuerdo a Deaton (1997), la función de densidad se estima mediante el
método no paramétrico de Kernels. Este método genera una estimación
consistente de la densidad de los ingresos. Este método es esencialmente
no paramétrico, dado que se puede producir estimaciones de la distribución
del ingreso sin suponer ninguna forma funcional para la misma.
Así, para calcular la distribución de densidad empírica de los ingresos f(x),
mediante el estimador de Kernel, consideremos que x1,… xn es una variable
aleatoria x con función de densidad f(x); donde se define una función de
distribución empírica:
Fn ( x) =
# obs ≤ x
n
11
La cual es un estimador de la función de distribución acumulada F(x) de X.
Considerando que la función de densidad f(x) es la derivada de la función de
distribución F(x) y usando aproximación para derivada se tiene que:
1 n x − xi
fˆ ( x) =
∑ K
nh i =1 h
Donde K, es la función Kernel. Aquí se utilizará la función Kernel Gaussiana
definida por:
K ( z) =
1
1
exp( z 2 )
2
2π
Como se ha señalado en la metodología antes descrita, a modo de
comparación, se calcula la función de densidad empírica para el ingreso,
representándose de manera conjunta los años 2001 y 2004.
12
Gráfico Nº 1
Lima Metropolitana: Funciones de densidad de los ingresos, 2001 y
2004
.6
Lima Metropolitana: Logarítmo del Ingreso laboral 2001 y 2004
2001
2004
2001
2004
densidad
.3
0
0
.1
.2
.2
densidad
.4
.4
.5
Lima Metropolitana: Logarítmo del Ingreso Familiar 2001-2004
0
5
0
10
5
10
15
Log(Ingreso laboral)
Log(Ingreso familiar)
2001
2004
0
.2
densidad
.4
.6
Lima Metropolitana: Logarítmo del Ingreso laboral por hora 2001 y 2004
-5
0
5
Log(Ingreso laboral por hora)
Fuente: Convenio MTPE - INEI. Encuesta Nacional de Hogares, 2001 – III trimestre;
MTPE - Encuesta de Hogares Especializada de Niveles de Empleo 2004 - III trimestre.
Elaboración: MTPE – Programa de Estadísticas y Estudios Laborales
Tal como se mencionó en el punto 1.b, el ingreso familiar resulta de sumar
los ingresos laborales y no laborales de todos los miembros de la familia.
Una adecuada medición del ingreso familiar es importante dado que nos
permitirá conocer alguna disminución o mejora en el bienestar de las
familias. Como es usual, para distribuciones de ingreso de otros países, la
función de densidad del logaritmo del ingreso tiene forma de “campana
invertida” (o en términos técnicos, forma aproximadamente normal), lo cual
tiene un corolario importante: la distribución de los ingresos - no de sus
logaritmos- presenta una gran acumulación de individuos en los niveles de
ingreso medio-bajos y muy pocos en los altos. Es decir, la distribución del
ingreso es asimétrica, con una cola derecha larga y un ingreso medio
superior al mediano.
13
Así, de acuerdo al Gráfico Nº 1, para los años 2001 y 2004 la distribución
de los ingresos laborales familiares, individuales y por hora se ha mantenido
constante en estos dos períodos. Mendoza y García (2006) afirman que un
crecimiento económico generalizado y sostenido es condición suficiente para
reducir la pobreza y mejorar los ingresos a lo largo del tiempo. Sin
embargo, persisten afirmaciones tales como ..” en nuestro país, el
crecimiento económico registrado en los últimos años no ha tenido un
correlato
en el bienestar macroeconómico, dado que el patrón de
crecimiento actual no ha permitido trasladar los frutos del crecimiento
económico hacia los sectores más pobres de la población. Según esta
visión, el crecimiento económico actual también habría acentuado la
desigualdad al beneficiar más a los sectores más ricos”. Ante ello Mendoza y
García (2006) encuentran que en términos teóricos,
resulta complicado
sustentar que un proceso de crecimiento económico generalizado, no haya
contribuido a la reducción de la pobreza. Asimismo, muestran que las
afirmaciones anteriores tanto las vinculadas al “patrón de crecimiento”
como a las de la pobreza e incluso las relativas al tema de desigualdad, no
guardan correspondencia con lo observado.
14
3. Desigualdad del ingreso en Lima Metropolitana, 1990 - 2004
Según Gasparini (2000), uno de los objetivos centrales de toda sociedad es
la equidad. En términos económicos ese objetivo se traduce en una
asignación equitativa de los bienes y servicios. Sin embargo, aunque existe
consenso en este amplio objetivo social, al momento de hacerlo más
específico y de evaluar sus consecuencias económicas prácticas, aparecen
fuertes divergencias. Así, existen dos nociones de equidad contrapuestas:
igualdad en resultados e igualdad en oportunidades. Pese a que la última
tiene mayor consenso, su implementación política es compleja. Por esta
razón, la mayoría de estudios sobre equidad analizan la desigualdad de la
distribución de resultados, en particular del ingreso.
El análisis de la desigualdad es importante por razones de eficiencia
económica, sociales e incluso morales (Sen, 1992). Independientemente del
grado de desigualdad entre países, resulta importante comprender los
procesos que han dado lugar a las actuales diferencias de ingresos entre los
individuos, lo cual es una meta relevante para el diseño de políticas públicas
para el desarrollo.
a. Evolución de los principales indicadores de desigualdad
En esta sección, el análisis de las tendencias de la desigualdad en Lima
Metropolitana en el periodo 1990
- 2004, se llevará a cabo a través de
índices que resuman la forma en que se distribuyen los ingresos. Así, se
utilizarán el coeficiente de Gini y el índice de Theil5. Este último posee una
interesante propiedad, puede descomponerse linealmente por grupos, de tal
forma que se puede investigar la importancia de cualquier clasificación de la
población en la desigualdad total.
5
El coeficiente de Gini mide el grado en el que coinciden las distribuciones de frecuencia de
los individuos y la de sus ingresos. Es un número entre 0 y 1, donde 0 significa igualdad
perfecta (todos tienen el mismo ingreso) y 1 significa desigualdad perfecta. El índice de Theil
representa una medida de las distancias entre los distintos ingresos a lo largo de la
distribución del ingreso; corresponde a la familia de medidas de entropía generalizada.
15
Al respecto, el grafico Nº 2 muestra la evolución del coeficiente de Gini para
Lima Metropolitana, el cual muestra niveles de inequidad en la distribución
del ingreso laboral. En el caso de la ciudad de Lima y para el período 19902004, este coeficiente se encuentra en un rango entre 0.429 (año 2004) y
0.554 (año 1990). Asimismo, del gráfico se desprende que la desigualdad
en los ingresos medido por el coeficiente de Gini ha tenido una evolución
que se puede dividir en tres etapas, una en la que se registra una
disminución en la desigualdad (período 1990-1996), otra en la que la
desigualdad se incrementa hasta alcanzar un coeficiente de Gini de 0.552
en el año 2001, y desde el 2002 se registra una caída en el índice de Gini.
Gráfico Nº 2
Lima Metropolitana: Evolución1 del índice de Gini2, 1990 2004
0.600
0.580
0.560
0.540
0.520
0.500
0.480
0.460
0.440
0.420
0.400
1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004
Fuente: MTPE - Encuesta de Niveles de Empleo 1990-1995.
Convenio MTPE-INEI, Encuesta Nacional de Hogares 1996-2001
MTPE, Encuesta de Hogares Especializada en Niveles de Empleo 2002-2004.
Elaboración: MTPE – Programa de Estadísticas y Estudios Laborales
Nota:
1/ Se empleo la técnica del bootstrap para estimar los intervalos de confianza.
2/ Para el cálculo del índice de Gini se empleo el ingreso laboral mensual.
El análisis tradicional de la distribución del ingreso está vinculado más con
el tema de la pobreza, por lo que las variables involucradas además del
ingreso laboral son: el tamaño de la familia y el ingreso no laboral. En los
cálculos efectuados en esta sección se analiza la distribución de los ingresos
desde una perspectiva individual y laboral, es decir las unidades de análisis
son los trabajadores que perciben ingresos.
16
Asimismo, es preciso señalar dos cuestiones acerca del indicador; en primer
lugar, los cambios en la
desigualdad utilizando el coeficiente de Gini,
incluso cuando las curvas de Lorenz se crucen entre si.
En segundo lugar, dado que los coeficientes fueron obtenidos de encuestas
a hogares (los cuales no forman un panel de datos), las diferencias de estos
indicadores (aumento o disminución) podrían deberse a cambios en la
distribución del ingreso, o simplemente al hecho de que la muestra cambió,
o a ambos factores, por lo que la conclusión de que la distribución se ha
vuelto más o menos desigual no es necesariamente correcta, siendo
necesario acompañar a los coeficientes de Gini de sus respectivos intervalos
de confianza.
Asimismo, al analizar la distribución de los ingresos familiares se obtiene un
índice de Gini superior en relación al calculado para el ingreso laboral. Lo
anterior indicaría que los ingresos no laborales están mas desigualmente
distribuidos. Según lo señalan las respectivas curvas de Lorenz trazadas
para los años 2001
y 2004, parece no haberse registrado cambios
significativos los cuales prácticamente se superponen con una leve mejora
en la distribución registrada en el año 2004. En la misma línea, se puede
mencionar que el índice de Gini, indicador que resume la información
reflejada por la curva de Lorenz, es de 0.523 para el 2004 y 0.536 para el
2001, por lo que es muy probable que estadísticamente esto signifique que
el nivel de desigualdad sea el mismo para ambos años.
17
Gráfico N° 1
Lima Metropolitana: Distribución del ingreso familiar a través de la
Curva de Lorenz
Fuente: Convenio MTPE - INEI. Encuesta Nacional de Hogares, 2001 – III trimestre;
MTPE - Encuesta de Hogares Especializada de Niveles de Empleo 2004 - III trimestre.
Elaboración: MTPE – Programa de Estadísticas y Estudios Laborales
Nota:
*/ La variable de análisis es el ingreso familiar.
Por otro lado, así como ha cambiado la desigualdad de ingresos laborales,
la importancia de cada uno de los factores que la explican también ha
evolucionado en el tiempo. Por ejemplo, a pesar de que aún
persisten
diferencias importantes de ingresos laborales entre hombres y mujeres, la
importancia de esta diferencia en la explicación de la desigualdad total cayó
57% entre 1990 y 2004.
Por otro lado, en el terreno macroeconómico, Mendoza y García (2006),
sostienen que el PBI per cápita creció en 9,3% en el periodo 2001-2004, lo
cual se relaciona con una disminución de 2,7% en el índice agregado de
pobreza; sin embargo, la pobreza extrema disminuyó en 5%. Como
resultado de dicho proceso, la desigualdad en el país se habría reducido.
Así, según cálculos de los autores mencionados, el coeficiente de Gini
(estimado a partir del gasto familiar) habría pasado de 0.53 en el 2001, se
ha reducido 0.525 en el 2004. Con lo cual se, muestra que el incremento
del bienestar de la población está favoreciendo a segmentos de menores
ingresos, sin embargo es necesario perseverar en este crecimiento
económico que genera ingresos mayores para las familias pobres.
18
b. Perfiles de la Desigualdad de ingresos laborales
De acuerdo a la evolución de la desigualdad de ingreso laborales entre 1990
y 2004, analizada en la sección anterior, ésta no ha cambiado de manera
significativa en los últimos 15 años. Sin embargo, los factores que la
explican si habrían registrado
evidencia
empírica
cambios importantes. Así, de acuerdo a la
encontrada,
es
posible
afirmar
que
factores
demográficos como el sexo y la edad han perdido importancia mientras que
factores económicos, como la informalidad en el trabajo, se han convertido
en determinantes importantes de la dispersión de los ingresos.
La desigualdad de ingresos, medida a través del índice de Theil, se puede
descomponer en dos componentes: la diferencia de ingresos entre grupos
poblacionales
y
las
diferencias
al
interior
de
dichos
grupos.
Tradicionalmente, los distintos grupos en los que se puede dividir a
población, tales como
la
edad, genero, educación, ocupación, rama de
actividad económica, grupo y categoría ocupacional, y la informalidad
logran explicar algo más de la mitad de la dispersión total del ingreso.
Pascó – Font y Saavedra (2001) analizaron la importancia de los
componentes intra y entre grupos, tanto para el área urbana y rural en el
Periodo 1985 – 2000. En el caso de las zonas urbanas, los autores utilizan
como variable de análisis el ingreso laboral por hora, la cual se asocia a
características de capital humano acumulado por los trabajadores, así como
a otras variables asociadas a la inserción laboral de los individuos, tales
como la rama de actividad o la categoría ocupacional.
Mediante los resultados de la Encuesta de Hogares Especializada de Niveles
de Empleo del MTPE, ejecutada en Lima Metropolitana en el periodo 1990 –
2004, se obtuvo la descomposición del índice de Theil, obtenido a partir de
la distribución del ingreso laboral horario de la PEA ocupada remunerada. El
índice de Theil permite su descomposición por grupos definidos de la
población (Shorrocks 1980), y desagrega esta medida de desigualdad por
diferencias al interior de cada uno de los grupos y por la diferencias entre
grupos. Así, se estimaron las diferencias de ingreso entre los trabajadores
19
agrupados según variables educativas, de edad, género y otras ligadas al
ámbito y funciones laborales que desempeñan, para mayores detalles
metodológicos de la descomposición del índice de Theil ver el anexo Nº I.
En el cuadro Nº 2 se muestran la evolución del componente entre grupos;
así, las diferencias de ingreso entre trabajadores remunerados según su
nivel educativo, explica entre 9% y 25% de la dispersión total. Lo cual, es
consistente con la evolución de los retornos
a la educación y los
diferenciales de ingreso por niveles educativos encontrados en Saavedra
(1997). En el gráfico Nº 2 se aprecia la evolución de los retornos o premios
a la educación, la cual presentan una tendencia creciente en la primera
mitad de la década de los noventa. Así, se evidencia una alta correlación, en
cada año, del logaritmo del salario por hora del trabajador, y su número de
años de estudio, condicional en los años de experiencia y los años de
experiencia al cuadrado. En los últimos años, el retorno a la educación ha
crecido 45%, lo cual implica que, en la actualidad, una persona esperaría
una mayor motivación de realizar estudios universitarios.
Gráfico N° 2
Evolución de los Retornos a la Educación, 1997
- 2004
Retornos a la educación
0.160
0.140
0.120
0.100
0.080
0.060
1997
1998
1999
2000
Hombre
2001
Mujer
2002
2003
2004
Total
Fuente: Convenio MTPE - INEI. Encuesta Nacional de Hogares, 1997 –
Encuesta de Hogares Especializada de Niveles de Empleo 2002
trimestre.
Elaboración: MTPE - Programa de Estadísticas y Estudios Laborales
Nota:
1/ Las estimaciones proceden de ecuaciones de ingreso del tipo Mincer, y
aumento en el ingreso horario que se deriva de tener un año adicional
condicional en los años de experiencia y los años de experiencia al cuadrado.
2001, MTPE al 2004, III
representan el
de educación,
20
Asimismo, la experiencia, aproximada por la edad, representa un valor en el
mercado y es uno de los determinantes de las brechas de ingreso entre los
individuos. Según Ortega (2003), la experiencia está asociada a la
acumulación de destrezas en labores especificas. En Lima Metropolitana, en
el periodo 1997 – 2004, el valor de la especialización que proporciona la
experiencia laboral registra una tendencia creciente, en el gráfico Nº 3 se
aprecia la evolución del retorno a la experiencia estimada como la
sensibilidad del salario a un incremento de un año en la experiencia laboral,
controlada por una caída esperada hacia la vejez y por los años de
escolaridad de la persona6.
Gráfico N° 3
Evolución de los Retornos a la Experiencia
Potencial, 1997 - 2004
0.025
0.020
0.015
0.010
0.005
1997
1998
1999
2000
Hombre
2001
Mujer
2002
2003
2004
Total
Fuente: Convenio MTPE - INEI. Encuesta Nacional de Hogares, 1997 – 2001, MTPE Encuesta de Hogares Especializada de Niveles de Empleo 2002 al 2004, III
trimestre.
Elaboración: MTPE - Programa de Estadísticas y Estudios Laborales
Nota:
1/ Las estimaciones proceden de ecuaciones de ingreso del tipo Mincer, y representan el
aumento en el ingreso horario que se deriva de tener un año adicional de experiencia,
condicional en los años de estudio.
Al considerar otras variables de capital humano, como la edad, y otras
características como el género de los trabajadores, es posible llegar a un
rango de explicación de la desigualdad del ingreso que oscila entre 12 y
30% de la desigualdad, principalmente por la contribución explicativa de la
6
La experiencia se define como la edad, menos seis, menos el número de años de estudio.
21
edad. Otras características asociadas al empleo, como la distribución de la
PEA ocupada según tipo de actividad económica, el grupo ocupacional
(profesionales,
técnicos,
gerentes,
vendedores,
artesanos,
etc.),
se
incrementa considerablemente las diferencias entre grupos, ya que es
posible explicar entre el 32 y 49% del índice de Theil. Sin embargo, al
incorporar en el análisis la categoría ocupacional (asalariados, trabajadores
independientes, etc.) se logra explicar entre el 47 y 55%, y al incorporar la
división de la PEA ocupada según informalidad en el trabajo, se logra
explicar entre el 50 al 63% de la desigualdad de los ingresos laborales.
22
Cuadro N° 2
L im a M e tro p o lita n a : D e s c o m p o s ic ió n d e l Ín d ic e d e T h e il p a ra e l in g re s o la b o ra l p o r h o ra : 1 9 9 0 / 2 0 0 4
T o ta l
T o ta l
1990
In tra
E n tre
0 .6 6 5
T o ta l
1995
In tra
E n tre
0 .5 6 0
T o ta l
2000
In tra
E n tre
T o ta l
2004
In tra
E n tre
0 .4 5 9
0 .5 04
N iv e l e d u c a tiv o
N iv el
E stru ctu ra
0 .6 0 2
9 0 .6 %
0 .0 6 3
9 .4 %
0 .4 4 9
8 0 .2 %
0 .1 1 1
1 9 .8 %
0 .3 8 0
7 5 .5 %
0 .1 2 3
2 4 .5 %
0 .3 5 5
7 7 .4 %
0 .1 0 4
2 2 .6 %
N iv e l e d u c a tiv o y e d a d
N iv el
E stru ctu ra
0 .5 7 9
8 7 .1 %
0 .0 8 6
1 2 .9 %
0 .3 9 0
6 9 .7 %
0 .1 7 0
3 0 .3 %
0 .3 6 8
7 3 .0 %
0 .1 3 6
2 7 .0 %
0 .3 3 8
7 3 .6 %
0 .1 2 1
2 6 .4 %
N iv e l e d u c a tiv o , e d a d y g é n e ro
N iv el
0 .5 6 5
E stru ctu ra
8 5 .0 %
0 .1 0 0
1 5 .0 %
0 .3 7 8
6 7 .6 %
0 .1 8 2
3 2 .4 %
0 .3 6 3
7 2 .0 %
0 .1 4 1
2 8 .0 %
0 .3 2 9
7 1 .8 %
0 .1 3 0
2 8 .2 %
0 .3 6 3
6 4 .9 %
0 .1 9 7
3 5 .1 %
0 .3 4 9
6 9 .3 %
0 .1 5 5
3 0 .7 %
0 .3 1 6
6 8 .9 %
0 .1 4 3
3 1 .1 %
N iv e l e d u c a tiv o , e d a d y g é n e ro , ra m a d e a c tiv id a d y g ru p o o c u p a c io n a l
N iv el
0 .4 5 0
0 .2 1 5
0 .2 9 6
0 .2 6 4
E stru ctu ra
6 7 .7 %
3 2 .3 %
5 2 .9 % 4 7 .1 %
0 .2 7 7
5 5 .1 %
0 .2 2 6
4 4 .9 %
0 .2 3 3
5 0 .8 %
0 .2 2 6
4 9 .2 %
N iv e l e d u c a tiv o , e d a d y g é n e ro , ra m a d e a c tiv id a d , g ru p o o c u p a c io n a l y c a te g o ría o c u p a c io n a l
N iv el
0 .3 5 2
0 .3 1 3
0 .2 6 0
0 .3 0 0
0 .2 4 3
0 .2 6 1
E stru ctu ra
5 2 .9 %
4 7 .1 %
4 6 .5 % 5 3 .5 %
4 8 .2 % 5 1 .8 %
0 .2 0 7
4 5 .0 %
0 .2 5 2
5 5 .0 %
N iv e l e d u c a tiv o , e d a d y g é n e ro , ra m a d e a c tiv id a d , g ru p o o c u p a c io n a l, c a te g o ría o c u p a c io n a l e In fo rm a lid a d
N iv el
0 .3 2 8
0 .3 3 7
0 .2 3 8
0 .3 2 2
0 .2 2 5
0 .2 7 9
0 .1 7 3
E stru ctu ra
4 9 .4 %
5 0 .6 %
4 2 .5 % 5 7 .5 %
4 4 .6 % 5 5 .4 %
3 7 .7 %
0 .2 8 6
6 2 .3 %
N iv e l e d u c a tiv o , e d a d y g é n e ro y ra m a d e a c tiv id a d
N iv el
0 .5 2 8
0 .1 3 7
E stru ctu ra
7 9 .5 %
2 0 .5 %
Fuente: MTPE - Encuesta de Niveles de Empleo en Lima Metropolitana 1990 – 1995, Convenio MTPE - INEI. Encuesta Nacional de Hogares, 1996 – 2001, MTPE - Encuesta de
Hogares Especializada de Niveles de Empleo 2002 al 2004, III trimestre.
Elaboración: MTPE - Programa de Estadísticas y Estudios Laborales
Notas:
1/ La variable de análisis es el ingreso laboral horario de la PEA ocupada que percibe ingresos.
23
Cuadro N° 3
Lima Metropolitana: Contribuciones bruta y marginal a la desigualdad del ingreso laboral por hora, 1990 - 2004(como
porcentaje del índice de Theil)
1990
Índice de Theil
Nivel educativo
Grupo de edad
Género
Rama de actividad
Grupo ocupacional
Categoría ocupacional
Informalidad
Contribución bruta
1995
2000
2004
0.665
0.560
0.504
0.459
9.4%
3.3%
2.5%
2.1%
12.8%
1.3%
0.1%
19.8%
7.3%
2.7%
1.6%
23.7%
1.4%
3.5%
24.5%
3.3%
0.6%
0.8%
24.7%
5.1%
11.3%
22.6%
4.8%
1.1%
2.2%
32.4%
7.2%
16.8%
1990
9.4%
3.5%
2.1%
5.5%
11.8%
14.8%
3.5%
Contribución marginal
1995
2000
19.8%
10.5%
2.2%
2.7%
12.0%
6.4%
4.0%
24.5%
2.5%
1.0%
2.7%
14.2%
6.9%
3.6%
2004
22.6%
3.8%
1.8%
2.8%
18.1%
5.8%
7.3%
Fuente: MTPE - Encuesta de Niveles de Empleo en Lima Metropolitana 1990 – 1995, Convenio MTPE - INEI. Encuesta Nacional de Hogares, 1996 – 2001,
MTPE - Encuesta de Hogares Especializada de Niveles de Empleo 2002 al 2004, III trimestre.
Elaboración: MTPE - Programa de Estadísticas y Estudios Laborales
Notas:
1/ La variable de análisis es el ingreso laboral horario de la PEA ocupada que percibe ingresos.
24
Ahora bien, según contribuciones bruta y margina7l de las variables
empleadas a la desigualdad del ingreso laboral, se muestran en el cuadro
Nº 3. De acuerdo a la contribución marginal se encuentra que las
variables con mayor poder explicativo son el nivel educativo y el grupo
ocupacional, en Pascó – Font y Saavedra (2001) se señala que la
disminución en la dispersión en el ingreso evidenciada en los últimos
años se debería al mayor acceso a la educación durante los últimos 30
años; sin embargo, a pesar de ser la educación una de las variables más
importantes para determinar el ingreso de las personas, ésta aún recibe
escasa atención estatal.
Similar a lo encontrado en Pascó – Font y Saavedra (2001) la
contribución marginal de variables ligadas a la inserción laboral de los
individuos en el mercado de trabajo, como la ocupación y la rama de
actividad
económica
8
informalidad
en
el
es
elevada.
trabajo,
la
Especial
cual
ha
atención
registrado
merece
la
incrementos
importantes en los últimos años, a la par con el crecimiento del sector
informal en Lima Metropolitana.
Factores de género
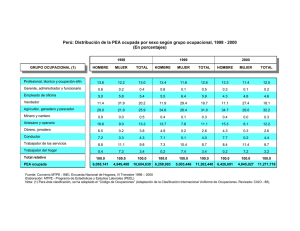
Según resultados de las Encuestas de Hogares del MTPE, en 1990 las
mujeres representaban el 38.1% de la población perceptora de ingresos
laborales, sin embargo su participación en el ingreso laboral era de
33.4%, mientras que los hombres representaban el 61.9% de la
población perceptora de ingresos y recibían el 66.6%. En el 2004, las
mujeres pasaron a ser el 39.5% y a recibir el 40.2% de los ingresos
laborales, mientras que los hombres pasaron a representar solo el 60.5%
y a percibir el 59.8% de los ingresos laborales.
7
La contribución bruta se define como la proporción de la desigualdad explicada por la variable que
determina los grupos de análisis. Adicionalmente, es posible calcular la parte explicada por la
combinación de dos (o más) variables, lo que determina la contribución bruta (bij) al utilizar grupos
definidos por las variables j e i. Luego, se define la contribución marginal de la variable j como la
diferencia entre la contribución entre la contribución bruta conjunta de ambas variables (bij) y la
contribución bruta de la variable j. Para mayores detalles, ver anexo Nº 1. y marginal se definen como
8
Se considera la definición de informalidad empleada por MTPE. Así, se considera trabajadores
informales a: los provenientes de las microempresas, independientes no profesionales, trabajadores no
remunerados y a los trabajadores del hogar.
25
Uno de los cambios más interesantes en términos de la distribución de
los ingresos en Lima Metropolitana es la disminución, aunque ligera, en
la importancia del género en la desigualdad de los
ingresos laborales,
ver grafico Nº 4. A ello ha contribuido la creciente participación femenina
en el mercado de trabajo registrada en las ultimas tres décadas,
logrando así una progresiva disminución de las brechas de genero desde
el orden del 40% a inicios de los años 70, hasta menos del 20% a inicios
de la presente década.
Gráfico N° 4
Lima Metropolitana: Importancia del género en la
Desigualdad de Ingresos Laborales, 1990 - 2004
3.0%
2.5%
2.7%
2.5%
2.0%
1.5%
1.1%
1.0%
0.6%
0.5%
0.0%
1990
1995
2000
2004
Fuente: MTPE - Encuesta de Niveles de Empleo 1990-1995.
Convenio MTPE-INEI, Encuesta Nacional de Hogares 1996-2001
MTPE, Encuesta de Hogares Especializada en Niveles de Empleo 2002-2004.
Elaboración: MTPE - Programa de Estadísticas y Estudios Laborales
Nivel educativo
Según diversos autores, la educación es un determinante primordial en la
generación de los ingresos del trabajo. Asimismo, la teoría económica
permite relacionar los ingresos del trabajo con el capital humano de las
personas. Así, los ingresos laborales son explicados por variables que
miden productividad, donde la productividad está asociada a la educación
y experiencia laboral del individuo. Esto permite medir la importancia de
la educación y de la experiencia laboral en la determinación de los
ingresos laborales. Además, es posible establecer una relación entre
educación e ingresos del hogar debido a que los ingresos laborales
representan una fracción importante de los ingresos familiares, lo cual
26
permite establecer una relación entre educación y distribución del
ingreso. Dado que los ingresos laborales representan alrededor del 80%
del ingreso total de los hogares, entonces es posible medir el impacto de
la educación sobre la distribución de los ingresos.
Mediante esta estrategia, la evidencia indica que la educación resulta ser
la variable más importante al momento de explicar la desigualdad del
ingreso laboral pues explica cerca del 30% de su dispersión.
Gráfico N° 5
Lima Metropolitana: Importancia de la Educaciòn en la
Desigualdad de Ingresos Laborales, 1990 - 2004
35.0%
30.0%
30.0%
27.2%
27.6%
1995
2000
25.0%
20.0%
15.0%
11.5%
10.0%
5.0%
0.0%
1990
2004
Fuente: MTPE - Encuesta de Niveles de Empleo 1990-1995.
Convenio MTPE-INEI, Encuesta Nacional de Hogares 1996-2001
MTPE, Encuesta de Hogares Especializada en Niveles de Empleo 2002-2004.
Elaboración: MTPE - Programa de Estadísticas y Estudios Laborales
Grupo ocupacional
Esta clasificación está relacionada con las labores que realiza la persona
en su ocupación. Para obtener una clasificación que sea comparable con
estadísticas internacionales, se ha adoptado el “Código Nacional de
Ocupaciones” (Adaptación de la Clasificación Internacional Uniforme de
Ocupaciones Revisada: CIUO - 88). La ocupación es uno de los factores
mas importantes para la explicación de la desigualdad laboral, debido a
que existen niveles de remuneraciones diferentes para ocupaciones
distintas. El anexo Nº 5 muestra la contribución de la ocupación a la
desigualdad laboral. La ocupación puede verse como una característica
que
complemente
el
nivel
educativo
y
la
edad
como
medidas
aproximadas de la especialización del capital humano.
27
Informalidad en el Empleo
Según la definición que utiliza el Ministerio de Trabajo, se clasifica como
empleo informal, a los siguientes segmentos de la PEA ocupada:
1.
Trabajadores independientes, no profesionales;
2.
Trabajadores en unidades económicas
de 2 a 9 empleados, es
decir los que laboran en microempresas;
3.
Trabajo domestico y el trabajador familiar no remunerado TFNR.
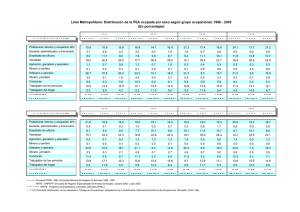
De acuerdo a estadísticas de MTPE, en Lima Metropolitana,
en el año
1990, la microempresa estuvo conformada por el 17.8% de la PEA
ocupada, mientras que en el 2004 dicho segmento de mercado
representa el 20.8%. Asimismo, los trabajadores independientes pasaron
de 30.9% a representar el 34.8%. Mientras que los trabajadores de las
pequeñas y medianas empresas, registraron una menor participación en
el 2004, al pasar de 29.8% a 27.1%.
Lo anterior configura la principal característica del mercado de trabajo en
la capital, el 54.8% de la ocupados desarrollan sus actividades en la
microempresa o como trabajadores independientes.
De acuerdo al gráfico Nº 6 se aprecia el incremento en la participación de
la desigualdad de la variable estructura de mercado, logrando explicar el
7% de la desigualdad de los ingresos en el 2004.
28
Gráfico N° 6
Lima Metropolitana: Evolución de la informalidad en el Empleo,
1990 - 2004
2004
2003
2002
2001
2000
1999
1998
1997
1996
1995
1994
1993
1992
1991
1990
20%
35%
50%
Informal
65%
80%
Formal
Fuente: MTPE - Encuesta de Niveles de Empleo 1990-1995.
Convenio MTPE-INEI, Encuesta Nacional de Hogares 1996-2001
MTPE, Encuesta de Hogares Especializada en Niveles de Empleo 2002-2004.
Elaboración: MTPE - Programa de Estadísticas y Estudios Laborales
29
c. Factores que influyen en la desigualdad: La descomposición de
Fields
De acuerdo a la metodología planteada por Fields (Fields, 2002; Fields y
Gyeongjoon, 1999) y extendida por Yun (2002), las variaciones de
ingreso
se
pueden
descomponer
en
componentes
asociados
a
características personales y del puesto de trabajo que desempeñan los
trabajadores.
La descomposición de Fields se basa en la estimación de ecuaciones de
ingresos bajo un modelo semilogarítmico y puede ser escrita de la
siguiente manera:
n
n
j =0
j =0
ln Yi = ∑ Bj * Xj + ei = ∑ Bj * Zj
(1)
donde:
Bj =[B0, B1, …, Bn, 1]
y
Zj =[1, X1, …, Xn, e]
lnYi es el logaritmo del ingreso laboral mensual, las Xj son las variables j
asociadas con la persona i. Los coeficientes Bj miden los precios o
premios salariales por cada variable X. El residual ei es la parte de la
variación en las remuneraciones entre los trabajadores que no puede ser
explicada por la variación entre las variables incluidas en la ecuación.
Se puede ilustrar la derivación de la descomposición de Fields utilizando
la varianza del logaritmo de los ingresos como una medida de dispersión.
Dada la ecuación de remuneración, la varianza del logaritmo de las
remuneraciones puede ser escrita como:
30
n
n
j =0
j =0
Var (ln Y ) = Cov (ln Y , ln Y ) = Cov (∑ Bj * Zj , ln Y ) = ∑ Cov( Bj * Zj , ln Y )
(2)
Dividiendo la ecuación (2) por la varianza del logaritmo de las
remuneraciones.
n
∑ Cov(Bj * Zj, ln Y )
n
∑S
j
=
j =0
Var (ln Y )
j =0
=1
(3)
Si bien se pueden usar los Sj para medir la contribución de cada variable
j al nivel de desigualdad, para medir el impacto de cada variable a las
diferencias en la desigualdad entre periodos, es necesario utilizar algo
más que los Sj.
De acuerdo a esta metodología, si I(t) es la medida de desigualdad en el
período o país t, el cambio en la desigualdad entre períodos o grupos 1 y
2 puede ser escrito como:
n
I (1) − I (2) = ∑ {I (2) * S j 2 − I (1) * S j1 }
(4)
j =0
la contribución de la j-ésimo variable al cambio en una medida de
desigualdad
particular
entre
el
país/grupo/tiempo
1
y
el
país/grupo/tiempo 2 está dada por
Π j ( I (⋅)) =
[ S j , 2 * I (2) − S j ,1 * I (1)]
(5)
[ I (2) − I (1)]
Las variables utilizadas en el análisis de la desigualdad de los ingresos
son: grado de educación, horas de trabajo expresadas en
logaritmo,
trabajo independiente, sector formal, sexo, ocupación y experiencia. El
residual es la parte de la variación en las remuneraciones entre los
trabajadores que
no puede
ser explicada por
la variación entre las
variables incluidas en la ecuación.
31
El cuadro N º 4 se presenta los Sjt, o la proporción de la desigualdad
en
las remuneraciones que es explicada por variables asociadas con
características del
Los
resultados
mercado de trabajo
muestran
que
la
y
características personales.
educación
se
ha
incrementado
sustancialmente: de 4.5 % en 1990 a 12.9% en el 2004, convirtiéndose
así en el principal factor de desigualdad.
Podemos destacar según estos resultados, que mientras a inicios de los
90 los principales factores de desigualdad eran, sexo, horas de trabajo y
ocupación, en los últimos años, la educación, horas de trabajo, el
trabajar independientemente y estar dentro de la formalidad, están más
asociadas a la desigualdad total.
La desigualdad asociada con
las características medidas
llegaron a
explicar como máximo un 30% de la desigualdad total en 1990, 54%, en
el 2000
y 53% en el 2004, siendo el complemento explicado por el
residual de la ecuación de remuneración. La parte de la desigualdad
"explicado" por el residual resulta de la desigualdad entre personas con
la
misma
educación,
sexo,
horas
trabajadas,
sector
formal,
independientes y experiencia.
32
Cuadro N° 4
Lima Metropolitana: Descomposición de Fields de la
desigualdad de los ingresos laborales 1990,2000 y 2004
1990
2000
2004
Contribución de cada factor a la
desigualdad de los ingresos
Educación
Horas de trabajo
Independientes
(independientes=1)
4.5%
10.2%
12.9%
8.4%
18.8%
11.7%
-0.2%
7.0%
7.9%
Sector formal (formal=1) 1/.
0.9%
5.8%
6.0%
Sexo
9.0%
2.2%
4.0%
Ocupación 2/.
5.2%
2.1%
3.8%
Experiencia
1.9%
-0.4%
0.8%
70.3%
54.4%
53.1%
100.0%
100.0%
100.0%
0.67
0.50
0.46
0.03
0.05
0.06
0.06
0.09
0.05
Otros
Total
Índice de theil
Contribución de cada factor al
índice de Theil
Educación
Horas de trabajo
Independientes
(independientes=1)
0.00
0.04
0.04
Sector formal (formal=1) 1/.
0.01
0.03
0.03
Sexo
0.06
0.01
0.02
Ocupación 2/.
0.03
0.01
0.02
Experiencia
0.01
0.00
0.00
Otros
0.47
0.27
0.24
0.67
0.50
0.46
-13.5%
-17.1%
-24.0%
91.2%
-22.6%
-2.0%
Total
Contribución de cada factor al
cambio de la desigualdad 3/.
Educación
Horas de trabajo
Independientes
(independientes=1)
Sector formal (formal=1) 1/.
-14.4%
3.7%
Sexo
30.2%
-15.8%
Ocupación 2/.
14.7%
-14.5%
9.3%
-13.2%
Experiencia
Otros
Total relativo
120.3%
67.6%
100.0%
100.0%
Total
-0.16
-0.05
Fuente: MTPE - Encuesta de Niveles de Empleo 1990.
Convenio MTPE-INEI, Encuesta Nacional de Hogares 2000
MTPE, Encuesta de Hogares Especializada en Niveles de Empleo 2004.
Elaboración: MTPE – Programa de Estadísticas y Estudios Laborales
Notas técnicas:
1/. El sector informal incluye: microempresa (2 a 9 trabajadores),
independiente no profesional, TFNR , trabajadores del hogar y resto.
2/. La variable ocupación corresponde al grupo ocupacional.
3/. Las diferencias encontradas en estos períodos no son estadísticamente
significativas, es decir, según los datos no hay evidencia estadística para
afirmar que se hubiera presentado un cambio en el valor del indicador de un
período a otro, esto al 95 % de confianza
33
Esta metodología también permite indagar cómo se explican las
diferencias en la desigualdad del ingreso entre un año y otro. Es decir,
cuánto de las diferencias en la desigualdad del ingreso entre un año y
otro es atribuible a cada determinante.
Se observa que el aporte dinámico de una variable al incremento o
decremento de la desigualdad del ingreso depende conjuntamente tanto
de la dirección de la variación de la variable en cuestión, como de la
variación del índice de Theil. Así, en el periodo 1990-2000 la desigualdad
del ingreso pasó de 0.67 a 0.50, de igual manera que el factor educación
también se contrajo. Por lo tanto, hay evidencia que entre 1990 y 2000
los cambios en la educación (-13%) fueron a favor de una disminución de
la desigualdad del ingreso. Los mismo se presenta en el siguiente
periodo, 2004-2000, donde la educación aporta el -17% del cambio de la
desigualdad.
Asimismo, la variable trabajador independiente influye sobre el indicador
de manera directa, mientras el resto de variables experimentan una
trayectoria volátil respecto a la explicación de la desigualdad del ingreso.
34
3. Modelización de los retornos de capital humano sobre los
ingresos a partir de la Regresión Cuantílica
Según la literatura económica, el capital humano está conformado
principalmente por la combinación de dos factores: educación y/o
experiencia laboral. La mayoría de las personas poseen algún grado de
ambos. La hipótesis que subyace, consistente en que la tasa de ganancia
de un individuo se incrementa con los años de educación ha sido
confirmada empíricamente por diversos investigadores. De la misma
forma, la proposición que la tasa de ganancia incrementa con los años de
experiencia, hasta un cierto punto en el ciclo de vida, y posteriormente
desciende, es también una generalización empírica establecida. Ambas
proposiciones se combinan en la ecuación de ingresos tipo Mincer.
En esta sección se procede a cuantificar los impactos en el ingreso
laboral analizándolo desde una óptica distribucional, con el objetivo de
determinar los cambios no solamente sobre la media condicional, sino
sobre cada cuantíl de distribución. Así, resulta interesante preguntarse
cuestiones tales como:
• ¿Responde de manera distinta el ingreso laboral frente a iguales
cambios en alguna variable educativa través de diferentes cuantiles de su
distribución?
• ¿Son iguales los retornos de la educación derivadas de los efectos
sobre el capital humano, a través de los distintos cuantíles de la
distribución ingreso , o bien, tienden a ser más acentuadas en los
cuantíles superiores?.
Estas preguntas pueden abordarse mediante el enfoque MRC; que es
además un enfoque especialmente adecuado debido a la presencia de
valores extremos, también conocidos como outliers.
35
a. Método de regresión cuantílica (MRC)
Un avance teórico y empírico significativo, que ha enriquecido el análisis
de desigualdades socioeconómicas, lo constituye el método de regresión
cuantílica (MRC), que describe el modo en que los cuantíles de la variable
dependiente
del
modelo
responden
a
cambios
en
las
variables
explicativas, a diferencia del enfoque dado por MCO, que describe cómo
el valor medio de la variable explicada responde a cambios en las
variables explicativas.
La regresión por (MCO), es el método más utilizado debido a su
simplicidad y facilidad de cálculo. La medida de error de este método es
el cuadrado de la desviación de los datos de la línea de regresión
respecto a los Y observados (∑e2). El objetivo es minimizar la sumatoria
de los errores al cuadrado obteniéndose la mejor línea de ajuste. La
desventaja del método es que es muy sensible a valores atípicos.
El método de regresión cuantílica es muy similar al método de mínimos
cuadrados. La diferencia radica en que, la medida de error de este
método es el valor absoluto de la desviación de los datos de la línea de
regresión respecto a los Y observados (∑|e|). Aunque parece un método
más simple de describir al error, su proceso de minimización es
complicado. Los algoritmos iterativos que reducen al mínimo el error se
basan en la programación lineal. Este método es menos sensible a
outliers si se compara con el método de MCO. Cuando el criterio de
minimización es alcanzado el 50% de los residuos son negativos. En
forma análoga al modelo de regresión simple, en la que la esperanza de
Y dado X viene a ser la recta de mejor ajuste (E(Y/X)=X’B), en este tipo
de modelos la recta estimada es la mediana de Y condicionada a X
(Q(Y/X)0.50= X’B).
En lo que sigue se define un cuantíl como un valor Yτ de la muestra que
deja a un porcentaje τ de las observaciones por sobre Yτ y a un
porcentaje (1- τ) por debajo de este. De este modo, si τ=0,5, Y0.5
corresponderá a la mediana de la muestra, y por lo tanto un 50% de las
36
observaciones quedarán por sobre Y0.5, y otro 50% por debajo9 Así, el
MRC permite estimar o ajustar distintas regresiones para distintos
valores de τ, ocupando toda la información muestral, pero captando las
diferencias entre el porcentaje superior e inferior separado por Yτ.
Esta metodología puede capturar, en caso de existir, heterogeneidad de
comportamiento a través del modelo, que puede tornarse más rica en la
medida en que los datos presenten alta heterocedasticidad o una elevada
proporción de observaciones outliers.
En la aplicación práctica, también nos interesará analizar en qué medida
el haber accedido a cursos de capacitación tiene un efecto positivo sobre
los ingresos. En la medida que es necesario aislar el efecto de la
capacitación técnica sobre los ingresos, del efecto que tiene la educación
formal (primaria, secundaria, secundaria o superior no universitaria)
sobre los mismos, es útil sistematizar estos efectos a través de la
estimación de una ecuación de ingresos del tipo Mincer (1974) de la
forma:
Y= a + b*D+b*X+e
donde Y es el logaritmo del ingreso laboral horario, D es una variable
ficticia que toma el valor de 1 para el caso de las mujeres y 0 en el caso
de los hombres, X es un vector de atributos individuales que involucra
dummies
acumulativas
para
educación,
sexo,
experiencia
laboral,
capacitación para el trabajo, ocupación independiente y jefe de hogar
b. Resultados
Así, según los resultados del cuadro Nº 5, se comprueba que los
rendimientos
de
la
educación
superior,
son
menores
cuando
se
condiciona la ecuación de ingresos hacia los cuantíles bajos, y al
condicionar hacia los altos, los rendimientos son crecientes, lo cual
confirma la hipótesis de que la tasa de ganancia de un individuo se
incrementa con los años de educación, lo cual ha sido confirmada
9
En tanto que si τ=0,8, entonces Y0.8 será el valor de Y en la muestra que las
observaciones arriba de Y0.8 y un 80% de ellas bajo este valor.
37
empíricamente en diferentes estudios. Asimismo, la capacitación para el
trabajo confirma lo anterior al redituar ingresos hasta de 27.9% en el
cuantíl superior, ver Grafico Nº 7.
De la misma forma, la proposición que la tasa de ganancia se incrementa
con los años de experiencia hasta un cierto punto en el ciclo de vida y
posteriormente desciende, es también una generalización empírica
establecida. Ambas se combinan en la ecuación de ganancias de Mincer.
En cuanto al género, se muestra la brecha de ingresos, la cual disminuye
en los cuantíles superiores. Así, en el cuantíl 25, la brecha es del 23.9%
mientras que en el cuantíl 75, la brecha es de 17.6%. Una posible
explicación de lo anterior se debe a que el acceso a la educación por
parte de las mujeres, pese a que se ha incrementado en los últimos
años, este acceso aún no es homogéneo. Además, es posible detectar
imperfecciones en el mercado de trabajo que es necesario corregir con la
finalidad de que la productividad sea igualmente remunerada en el caso
de los hombres y mujeres.
38
Cuadro N° 5
1
Lima Metropolitana: Ecuación Cuantílica de Ingresos
2004
Variables2
Superior
Cuantil 25
Coeficientes
Cuantil 50
Cuantil 75
MCO
0.651
0.766
0.813
0.032
0.034
0.033
0.715
0.026
Experiencia
0.023
0.023
0.025
0.022
0.003
0.003
0.003
0.003
Experiencia2 (x100)
-0.034
-0.033
-0.035
-0.030
0.000
0.000
0.000
0.000
Mujer
-0.239
-0.235
-0.176
-0.219
0.031
0.033
0.032
0.025
Jefe
0.079
0.077
0.078
0.051
0.034
0.036
0.036
0.028
Independiente
-0.375
-0.357
-0.305
-0.367
0.029
0.031
0.030
0.024
Capacitación para el
trabajo
0.175
0.186
0.279
0.214
0.030
0.032
0.031
0.024
Constante
0.519
0.863
1.192
0.915
0.038
0.040
0.040
0.031
0.151
0.179
0.198
0.300
Pseudo R2
Fuente: MTPE - Encuesta de Hogares Especializada de Niveles de Empleo, 2004
Elaboración: Ministerio de Trabajo - Programa de Estadísticas y Estudios Laborales
Nota:
1/ La variable dependiente es el logaritmo del ingreso laboral horario de la ocupación
principal.
2/ Se registra cada coeficiente y su respectivo error estándar.
39
Gráfico N° 7
Lima Metropolitana: Retornos de la Educaciòn Superior y la Capacitaciòn para
el trabajo, 2004
0.300
0.800
0.250
0.700
0.600
0.200
0.500
0.150
0.400
0.300
0.100
0.200
0.050
0.100
0.000
Retorno según acceso a
capacitación para el
trabajo
Retorno según acceso a
educación superior
0.900
0.000
Cuantil 25
Cuantil 50
Capacitación para el trabajo
Cuantil 75
MCO
Acceso a Educación Superior
Fuente: MTPE - Encuesta de Hogares Especializada de Niveles de Empleo, 2004
Elaboración: Ministerio de Trabajo - Programa de Estadísticas y Estudios Laborales
Nota:
1/ Dichos retornos fueron obtenidos a partir de una ecuación de ingresos tipo Mincer, donde la variable dependiente es el
logaritmo del ingreso laboral horario. Los retornos expresan el incremento el incremento en el logaritmo del ingreso
laboral horario según variables dummies de acceso a la educación superior y a algún curso de capacitación para el trabajo.
40
Conclusiones
•
Para el año 2004, el ingreso laboral promedio mensual de los
hogares limeños
ascendió a S/. 2,020 con una mediana de S/.
1,320. Por otro lado, el ingreso laboral promedio mensual y por
hora de los individuos fue de
S/.1,039 y S/. 4.8 nuevos soles,
respectivamente. En todos los casos se registra un elevado grado
de dispersión, medida por el coeficiente de variación. Asimismo,
con el objetivo de encontrar un promedio más robusto a
observaciones atípicas se recortan en cada cola de la distribución,
el 10, 15 y 20 % de los datos, reduciéndose sustancialmente los
promedios en todas las variables de análisis. Así, se registra una
alta dispersión de los datos y la existencia de datos extremos en la
distribución de las variables, además se confirma la forma
asimétrica de la distribución de los ingresos laborales, tanto
familiares como individuales.
•
A partir de los resultados de la Encuesta de Hogares Especializada
de Niveles de Empleo del MTPE, con inferencia para Lima
Metropolitana en el periodo 1990 – 2004 y utilizando como
variable de análisis el ingreso laboral por hora se puso de
manifiesto que en los últimos años no se registra un cambio
significativo en la desigualdad de los ingresos. Sin embargo, los
factores que la explican si lo han hecho de manera significativa.
Así, de acuerdo a la evidencia empírica encontrada, es posible
afirmar que factores demográficos como el sexo y la edad han
perdido importancia mientras que factores económicos, como la
informalidad del trabajo, el grupo ocupacional, e incluso los niveles
educativos, se han convertido en determinantes importantes de la
dispersión de los ingresos.
•
Mediante el índice de Theil, fue posible
descomponer a la
desigualdad del ingreso en dos componentes: la diferencia de
ingresos entre grupos poblacionales y la diferencia al interior de
dichos grupos. Así, para el año 2004, la división de la población en
41
grupos definidos por: el nivel educativo, grupos de edad, género,
rama de actividad económica, grupos y categoría ocupacionales, y
la informalidad en el trabajo lograron explicar el 63% de la
desigualdad de los ingresos, siendo las variables con mayor
contribución marginal el nivel educativo, los grupos ocupacionales
y la informalidad. En relación a los niveles educativos, dicho grupo
explica el 25% de la desigualdad del ingreso, lo cual es consistente
con la evolución de los retornos a la educación y la experiencia
laboral, los cuales muestran una tendencia creciente ya que ambas
son determinantes de las brechas de ingreso entre los individuos.
•
De acuerdo al capitulo 2, se evidenció que la distribución del
ingreso laboral registra valores extremos, también conocidos como
“outliers”. Por ello, al cuantificar los impactos en el ingreso laboral,
resulta conveniente determinar los cambios no solamente sobre la
media condicional (obtenidos en una regresión lineal simple o
MCO) sino sobre cada cuantíl de distribución. Así, se estimó una
ecuación de ingreso tipo Mincer mediante el método de regresión
por cuantíles, la cual permite explorar la forma de la distribución
condicional; esto es de gran interés ya que permite determinar sí
los ingresos de los individuos que pertenecen a los cuantíles
inferiores se ven influenciados en menor medida por diversas
variables educativas y socioeconómicas, que los individuos que
pertenecen a los cuantíles superiores. Así, de acuerdo a diversas
estimaciones se halló que el ingreso laboral responde de manera
distinta frente a iguales cambios en los años de estudios a través
de diferentes cuantíles de su distribución, con lo cual
se
demuestra que los retornos de la educación derivadas de los
efectos sobre el capital humano, a través de los distintos cuantíles
de la distribución ingreso, tienden a ser más acentuadas en los
cuantíles superiores.
42
BIBLIOGRAFÍA
Bustelo, M. (2004); “Caracterización de los cambios de la desigualdad y
la pobreza en Argentina haciendo uso de técnicas de descomposiciones
microeconométricas (1992
- 2001)”, Documento de Trabajo N° 13.
Centro de Estudios Distributivos, Laborales y Sociales, CEDLAS.
Contreras, D. (1997); Distribución del ingreso en Chile: Nuevos hechos y
algunos mitos. Universidad de Chile.
Chumacero,
R.(2002);
Characterizing
Income
Distribution:
ocy
implications for poverty and inequality. Banco Central de Chile.
Díaz, J. (1997);
Evolución de la estructura de ingresos en Lima
Metropolitana: Un análisis de los factores de oferta y demanda, 1986 –
1995. En: Investigaciones Breves No. Lima: CIES.
Espino J. (2001); “Dispersión salarial, capital humano y segmentación
laboral
en
Lima”.
Investigaciones
Breves
N°
13.
Consorcio
de
Investigación Económica y Social - CIES.
Gasparini
L.
(2002);
La
Distribución
del
ingreso
en
Argentina.
Universidad Nacional de la Plata. Argentina
Gamero J. (2006); Crecimiento y Empleo. Proyecto Elecciones Perú 2006.
Consorcio de Investigación Económica y Social - CIES.
Hoaglin D. (1983); Understanding robust and Exploratory Data Análisis.
Ministerio de Trabajo y Promoción del Empleo (2004); “Distribución
funcional del ingreso”. En Boletín de Economía Laboral N° 27.
Ministerio de Trabajo y Promoción del Empleo (2003); “Tendencias del
empleo e ingresos de los trabajadores asalariados e independientes
43
durante la última década en Lima Metropolitana”. En Boletín de Economía
Laboral N° 25.
Mincer, S. (1974); Schooling, Experience and Earnings. Columbia
Universiity Press. New York.
Ortega, D. (2003); Descripción y perfiles de desigualdad de ingresos en
Venezuela: 1975 – 2002. PNUD. Documentos para discusión. Informe de
Desarrollo Humano
Parodi C. (2004); Economía de las políticas sociales. Centro de
Investigación de la Universidad del Pacífico.
Pascó Font y Saavedra J. (2001); Reformas estructurales y Bienestar:
Una mirada al Perú de los noventa. Grupo de Análisis para el Desarrollo.
Ramos L. (2005); La distribución salarial del mercado de trabajo en
México: un análisis de la informalidad. Tesis doctoral. Universidad
Autónoma de Barcelona.
Saavedra J. y Maruyama E. (1998); “Retornos a le educación y a la
experiencia en el Perú: 1985 - 1997”. En Pobreza y Economía Social.
Análisis de la Encuesta de Condiciones de Vida ENNIV 1997. Instituto
Cuanto.
Saavedra, J. y Díaz J. (1999); Distribución del ingreso antes y después
de las reformas estructurales. Serie Reformas Económicas Nº 32. CEPAL.
Shack N. (1999); La Pobreza, la desigualdad y la Educación en el Perú de
hoy: Una aproximación cuantitativa. Estudio de caso N° 32. Universidad
de Chile
Tribín A. (2004); Evolución y causas de la desigualdad salarial en Bogotá.
Pontificia Universidad Javeriana. Departamento de Economía. Colombia
Sen, A (2002); La desigualdad económica. Fondo de Cultura Económica
44
Yamada, G. (2004); Economía Laboral en el Perú: Avances recientes y
agenda pendiente. Centro de Investigación de la Universidad del Pacífico.
Yamada, G.
(2004); Caminos entrelazados, la realidad del empleo
urbano en el Perú.
Centro de Investigación de la Universidad del
Pacífico.
Zárate H. (2002); Cambios en la estructura salarial: una historia desde la
regresión cuantílica. Banco de la República. Colombia
45
ANEXOS
ANEXO I:
Descomposición lineal del Índice de Theil10
El índice de Theil (IT) corresponde pertenece a la clases de índices de
entropía generalizada. Es un indicador que puede oscilar entre 0
(perfecta igualdad) y Log(N) (perfecta desigualdad), el cual refleja los
niveles de desigualdad de una población de tamaño N. Sin embargo,
como advierte Shack (1999), esta medida estar influenciada por el
tamaño N, de la población. El índice de Theil tiene la siguiente forma:
n
Índice de Theil:
T=
Yi
∑ Y log(
i =1
Yi N
)
Y
El índice de Theil tiene la propiedad de poder descomponerse de forma aditiva,
lo cual
representa una interesante propiedad para medidas de desigualdad.
Así, es posible descomponerlo en11:
Descomposición del Índice:
T=
Yi
Yi
Yi / Y
)
i /N
∑ Y T + ∑ Y log( N
i
i
i
Donde Yi representa el ingreso total del grupo i, Ti el Theil de cada grupo
y Ni la población de cada grupo. El primer componente de la suma
representa la contribución de la dispersión al interior de los grupos,
mientras que la segunda expresa la contribución de la dispersión entre
grupos a la desigualdad total.
En esta especificación el componente “entre” grupos es considerado
como la proporción de la desigualdad explicada por la variable i que
determina los grupos de análisis, mientras que el componente “al
10
Para la elaboración de esta sección se revisaron los apuntes señalados en Ortega
(2003), Shack (1999), y Pascó – Font y Saavedra (2001).
46
interior” de los grupos es considerada como la parte no explicada por
dicha variable. La parte explicada por la variable i se denomina
comúnmente contribución bruta a la desigualdad, denotada por bi.
Adicionalmente, es posible calcular la parte explicada por la combinación
de dos (o más) variables, lo que determina la contribución bruta bij al
utilizar grupos definidos por las variables j e i. luego se define la
contribución marginal de la variable j como la diferencia entre la
contribución entre la contribución bruta conjunta de ambas variables (bij)
y la contribución bruta de la variable j:
Mj/i= bij - bi
47
ANEXO II: Medición de indicadores de desigualdad
El grado de concentración de la distribución
de ingresos
puede ser
medido a partir de diversos indicadores, los cuales, según la CEPAL,
deben de cumplir algunas propiedades básicas12:
1. Principio de transferencia débil: el cual implica que la transferencia
de ingreso de un hogar rico a un hogar pobre, el indicador debe
reflejar una disminución del grado de desigualdad.
2. Independencia de escala: el indicador no debe variar ante
transformaciones proporcionales de los ingresos o cambios de
escala, tales como modificaciones en la unidad de medida del
ingreso.
3. Principio de población: la concentración del ingreso en dos
poblaciones con idénticas curvas de Lorenz, debe ser la misma,
independiente de su tamaño.
4. Descomposición aditiva: La concentración del ingreso en una
población debe ser igual a la suma ponderada de la desigualdad en
todos los subgrupos que la conforman.
5. Principio de la transferencia fuerte: ante una transferencia de
ingreso de un hogar rico a un hogar pobre, la disminución en la
desigualdad será más pronunciada a medida que aumente a la
distancia entre los ingresos de ambos hogares.
Entre los indicadores más comunes, algunos reflejan de mejor forma
los cambios ocurridos en los grupos extremos mientras otros
privilegian las modificaciones que se producen en la parte media de la
distribución.
Por
ello
es
recomendable
utilizar
los
índices
de
desigualdad de manera complementaria y analizar sus resultados en
forma conjunta.
c.1) Coeficiente de Gini
12
Panorama social de América Latina 2002 -2003, página 78.
48
Es el indicador mas conocido en la medición de la desigualdad. Este
indicador se basa en la curva de Lorenz, la que se obtiene ordenando
toda la población de menores a mayor ingreso y graficando el
porcentaje acumulado de la población contra el porcentaje acumulado
del ingreso que se apropia cada individuo. El coeficiente de Gini
resume la información representada por esta curva, relacionando el
área que esta entre la curva de Lorenz y la línea de 45 grados
(igualdad perfecta) con el área total que esta debajo de ella. Este
indicador toma valores entre 0 y 1, donde 0 representa una sociedad
con igualdad perfecta, mientras que un valor igual a 1 se obtendría
en el caso que un individuo en la sociedad concentrara todo el
ingreso.
A decir de varios autores, el estudio privilegia las modificaciones que
se producen en la parte media de la distribución, sin asignar, como si
lo hacen otros indicadores, una ponderación mayor en su parte baja.
c.2) Comparación entre participaciones de grupos de una
misma población
Existe otra forma de presentar las diferencias de ingresos entre los
individuos, la cual consiste en reportar la proporción de ingresos de la
que se apropian las personas u hogares, ordenados en orden
decreciente de acuerdo a su nivel de ingresos, y divididos luego en
grupos de igual tamaño. La división de la población por decíles o
quintiles aporta mucha información sobre la manera en que esta
distribuido el ingreso entre toda la población. Así, los índices de este
tipo mas utilizados son las relaciones que comparan la proporción de
ingresos del 10% más rico respecto al 10% mas pobre.
c.3) Indicadores que asignan importancias relativas diferentes
a determinados grupos
Dos índices bastante utilizados en la literatura de desigualdad son el
índice de Theil y el de Atkinson, similares en cuanto ambos grupos
49
asignan mayor importancia relativa a
los hogares de ingresos más
bajos, considerando que para algunos analistas incrementar la
ponderación de la parte inferior es deseable desde el punto de vista
teórico.
El índice de Theil, otorga mas importancia a las transferencias que se
realizan en la parte baja de la distribución, tiene la ventaja de
permitir su descomposición aditiva, el valor mínimo que puede
alcanzar es cero (equidad absoluta) y su valor máximo es log(N),
donde N representa el tamaño de la población. Su formula viene dado
por:
1 n Yi
y
T = ∑ log( i )
N i =1 µ
µ
El índice de Atkinson por su parte fluctúa entre los valores 0 y 1, y
posee la especial característica de un parámetro de aversión a la
desigualdad (e), que indica la ponderación que se le asigna a las
observaciones de la parte baja de la distribución, su formula viene
dada por:
y
1
Ae = 1 − ∑ ( i )1−e
n i=1 µ
n
1
1− e
50
ANEXO III:
Anexo Estatístico
Anexo Nº 1
Lima Metropolitana: Distribución del ingreso laboral por hora,
según quintiles, 1990 -2004
Quintil
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
I
II
3.2%
4.1%
4.6%
4.3%
4.1%
4.2%
5.3%
4.4%
4.2%
3.6%
3.9%
2.9%
4.2%
5.0%
5.1%
III
7.0%
8.2%
8.7%
8.7%
8.4%
8.7%
10.3%
9.4%
9.2%
8.0%
8.8%
8.0%
8.7%
8.9%
9.3%
11.5%
12.9%
13.3%
13.4%
12.8%
12.7%
14.6%
13.8%
13.0%
11.9%
12.8%
12.0%
12.6%
12.5%
13.6%
IV
18.5%
20.9%
19.9%
20.3%
19.9%
18.9%
20.3%
19.9%
18.2%
17.9%
18.4%
17.6%
18.2%
17.9%
20.4%
V
59.8%
54.0%
53.5%
53.3%
54.8%
55.5%
49.5%
52.5%
55.4%
58.6%
56.1%
59.5%
56.3%
55.7%
51.6%
Fuente: MTPE - Encuesta de Niveles de Empleo en Lima Metropolitana 1990 – 1995,
Convenio MTPE - INEI. Encuesta Nacional de Hogares, 1996 – 2001, MTPE Encuesta de Hogares Especializada de Niveles de Empleo 2002 al 2004, III
trimestre.
Elaboración: MTPE - Programa de Estadísticas y Estudios Laborales
Notas:
1/ La variable de análisis es el ingreso laboral horario de la PEA ocupada remunerada.
51
Anexo Nº 2
Lima Metropolitana: Distribución del ingreso laboral por hora1, según decíles, 1990 - 2004
Décil
I
II
Porcentaje acumulado del Ingreso
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
1.0%
0.7%
1.0%
1.0%
1.1%
1.0%
1.4%
1.0%
1.1%
0.9%
1.0%
0.6%
1.2%
1.4%
1.5%
III
2.2%
1.2%
1.8%
1.9%
2.0%
2.1%
2.7%
2.4%
2.4%
2.2%
2.3%
1.8%
2.3%
2.7%
2.8%
IV
3.0%
1.6%
2.4%
2.6%
2.7%
2.9%
3.6%
3.3%
3.4%
3.0%
3.3%
2.9%
3.3%
3.4%
3.6%
V
4.0%
2.1%
3.0%
3.3%
3.5%
3.6%
4.4%
4.2%
4.2%
3.8%
4.1%
3.7%
4.1%
4.0%
4.3%
VI
5.2%
2.7%
3.6%
4.1%
4.2%
4.5%
5.2%
5.1%
5.0%
4.5%
4.9%
4.6%
4.8%
4.8%
5.0%
VII
6.3%
3.3%
4.4%
4.9%
5.1%
5.3%
6.2%
6.1%
5.8%
5.5%
5.8%
5.5%
5.7%
5.7%
6.4%
VIII
8.0%
4.3%
5.4%
6.0%
6.4%
6.5%
7.1%
7.2%
6.9%
6.6%
7.0%
6.6%
6.8%
6.8%
7.7%
10.3%
5.5%
6.6%
7.6%
8.1%
8.1%
8.7%
8.9%
8.4%
8.5%
8.4%
8.1%
8.4%
8.3%
9.3%
IX
15.1%
7.7%
9.0%
10.4%
11.4%
11.3%
11.3%
12.1%
11.8%
12.8%
11.6%
11.3%
12.2%
11.4%
12.5%
Fuente: MTPE - Encuesta de Niveles de Empleo en Lima Metropolitana 1990 – 1995, Convenio MTPE - INEI. Encuesta Nacional de Hogares, 1996 – 2001,
MTPE - Encuesta de Hogares Especializada de Niveles de Empleo 2002 al 2004, III trimestre.
Elaboración: MTPE - Programa de Estadísticas y Estudios Laborales
Notas:
1/ La variable de análisis es el ingreso laboral horario de la PEA ocupada remunerada.
52
Anexo Nº 3
Lima Metropolitana: Importancia de la Estructura de Mercado en
la Desigualdad de ingresos laborales, 1990 - 2004
25.0%
20.0%
15.0%
10.0%
5.0%
0.0%
1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004
Estructura de mercado
Fuente: MTPE - Encuesta de Niveles de Empleo en Lima Metropolitana 1990 – 1995,
Convenio MTPE - INEI. Encuesta Nacional de Hogares, 1996 – 2001, MTPE Encuesta de Hogares Especializada de Niveles de Empleo 2002 al 2004, III
trimestre.
Elaboración: MTPE - Programa de Estadísticas y Estudios Laborales
Notas:
1/ La variable de análisis es el ingreso laboral horario de la PEA ocupada remunerada.
Anexo Nº 4
Lima Metropolitana: Importancia de la Rama de Actividad
en la Desigualdad de Ingresos Laborales, 1990 - 2004
18.0%
16.0%
14.0%
12.0%
10.0%
8.0%
6.0%
4.0%
2.0%
0.0%
1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004
Fuente: MTPE - Encuesta de Niveles de Empleo en Lima Metropolitana 1990 – 1995,
Convenio MTPE - INEI. Encuesta Nacional de Hogares, 1996 – 2001, MTPE Encuesta de Hogares Especializada de Niveles de Empleo 2002 al 2004, III
trimestre.
Elaboración: MTPE - Programa de Estadísticas y Estudios Laborales
Notas:
1/ La variable de análisis es el ingreso laboral horario de la PEA ocupada remunerada.
53
Anexo Nº 5
Lima Metropolitana: Importancia del Grupo Ocupacional en la
Desigualdad de Ingresos Laborales, 1990 - 2004
40.0%
35.0%
30.0%
25.0%
20.0%
15.0%
10.0%
5.0%
0.0%
1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004
Fuente: MTPE - Encuesta de Niveles de Empleo en Lima Metropolitana 1990 – 1995,
Convenio MTPE - INEI. Encuesta Nacional de Hogares, 1996 – 2001, MTPE Encuesta de Hogares Especializada de Niveles de Empleo 2002 al 2004, III
trimestre.
Elaboración: MTPE - Programa de Estadísticas y Estudios Laborales
Notas:
1/ La variable de análisis es el ingreso laboral horario de la PEA ocupada remunerada.
54
Anexo Nº 6
Lima Metropolitana: PEA ocupada por categoría ocupacional según estructura demográfica, 1990 - 2004
(en porcentajes)
Asalariados
Año
Empleador
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
4.8
5.8
5.2
6.1
5.9
5.8
5.2
5.3
6.6
5.7
4.8
5.7
5.4
4.9
4.1
Total
54.1
54.0
52.6
54.3
54.0
54.0
52.0
50.4
54.1
53.1
49.4
49.2
48.3
51.1
50.7
Trabajador
Privados Públicos independiente
42.8
42.2
42.7
44.3
46.0
44.8
43.9
43.6
45.5
44.5
40.8
39.6
39.3
43.3
42.9
11.3
11.8
9.9
10.0
8.0
9.2
8.1
6.8
8.6
8.6
8.6
9.6
9.0
7.8
7.8
Trabajador
Trabajador
Resto
familiar no
del hogar
remunerado
30.9
31.7
33.2
29.4
30.1
30.6
33.0
33.0
28.8
29.4
34.4
32.7
34.7
33.9
34.8
5.0
3.5
4.0
5.3
5.3
4.8
4.9
5.5
4.7
4.6
5.6
5.3
5.0
3.8
4.6
5.1
4.8
4.9
4.6
4.6
4.7
4.2
5.0
5.4
6.7
5.3
6.5
5.3
6.3
5.8
0.1
0.1
0.1
0.2
0.2
0.2
0.7
0.8
0.4
0.6
0.5
0.6
1.2
-
Total
Cifras
expandidas
Casos
2,334,478
2,327,776
2,333,813
2,536,478
2,611,321
2,846,028
2,782,669
3,037,861
3,157,355
3,254,494
3,264,790
3,411,790
3,334,304
3,361,308
3,366,936
3,136
3,045
3,238
3,314
3,438
3,989
3,957
2,997
1,673
2,072
2,236
3,272
3,739
3,021
4,121
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
Fuente: MTPE - Encuesta de Niveles de Empleo en Lima Metropolitana 1990 – 1995,
Convenio MTPE - INEI. Encuesta Nacional de Hogares, 1996 – 2001, MTPE Encuesta de Hogares Especializada de Niveles de Empleo 2002 al 2004, III
trimestre.
Elaboración: MTPE - Programa de Estadísticas y Estudios Laborales
Notas:
1/ La variable de análisis es el ingreso laboral horario de la PEA ocupada remunerada.
Anexo Nº 7
Lima Metropolitana: PEA total por nivel educativo según estructura demográfica, 1990 - 2004
(en porcentajes)
Primaria
Sin Nivel
nivel
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999 (*)
2000
2001
2002
2003
2004
2.3
1.5
1.9
1.7
1.2
1.2
2.3
1.8
1.0
6.2
1.3
1.7
1.0
1.3
0.6
Secundaria
Incompleta
Completa
Incompleta
7.6
6.8
6.2
5.8
5.8
6.7
6.8
6.3
4.7
5.2
5.9
4.0
4.4
4.2
12.9
11.6
12.2
10.5
11.0
9.5
9.2
9.4
9.1
7.5
7.7
9.0
7.9
6.9
7.0
18.0
14.1
16.0
13.7
13.8
16.8
17.2
17.7
19.7
15.4
16.1
15.9
14.1
12.9
13.3
Completa
33.2
34.8
38.0
38.7
36.5
35.7
31.7
33.8
34.5
33.7
38.5
34.6
36.1
41.5
41.1
Superior no universitaria
Incompleta
3.2
3.8
2.3
3.1
3.3
3.4
5.0
5.1
4.4
4.3
4.5
4.7
4.0
4.7
4.7
Completa
5.9
9.8
8.4
9.8
11.1
7.0
10.5
7.8
6.8
8.3
9.3
8.9
10.5
9.1
11.2
Superior universitaria
Incompleta
6.3
5.2
3.2
5.0
4.9
7.5
6.5
6.5
6.6
7.9
5.2
5.9
6.2
5.1
5.1
Total
Completa
10.7
12.3
11.7
11.7
12.4
12.2
10.7
11.7
13.3
16.8
12.3
13.4
16.1
14.0
12.8
Cifras
Casos
expandidas
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
2,551,668
2,471,050
2,576,846
2,814,241
2,867,350
3,062,621
2,998,128
3,323,259
3,391,372
3,591,506
3,542,784
3,742,357
3,693,324
3,747,307
3,761,351
Fuente: MTPE - Encuesta de Niveles de Empleo en Lima Metropolitana 1990 – 1995,
Convenio MTPE - INEI. Encuesta Nacional de Hogares, 1996 – 2001, MTPE Encuesta de Hogares Especializada de Niveles de Empleo 2002 al 2004, III
trimestre.
Elaboración: MTPE - Programa de Estadísticas y Estudios Laborales
Notas:
1/ Para el año 1999 sin instrucción incluye primaria incompleta.
55
3,421
3,231
3,570
3,673
3,777
4,300
4,263
3,295
1,810
2,277
2,427
3,595
4,138
3,365
4,640
Anexo Nº 8
Lima Metropolitana: PEA ocupada por grupo ocupacional según estructura demográfica, 1990 - 2004
(en porcentajes)
Profesional,
técnico y
ocupación
afín
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999 (*)
2000
2001
2002
2003
2004
13.4
16.7
13.8
16.9
16.3
16.1
15.9
16.9
19.6
21.2
19.5
19.3
18.3
19.7
18.3
Gerente,
Administrador y
funcionario
3.5
4.5
4.0
1.7
3.1
2.5
2.2
1.5
0.9
0.3
0.7
1.7
-
Empleado
de
oficina
Vendedor
12.6
9.9
10.3
10.0
10.7
9.2
9.9
8.7
10.1
12.7
8.5
8.8
10.7
9.0
8.0
26.2
26.5
28.2
26.7
27.5
25.1
26.0
26.0
23.7
22.8
23.3
24.3
24.4
23.1
26.5
Agricultor,
ganadero y
pescador
1.4
1.0
1.0
0.8
0.3
0.7
0.9
1.0
0.3
0.3
0.3
1.2
0.8
1.2
0.8
Minero y
cantero
Artesano y
operario
0.1
0.1
0.1
0.1
0.1
0.1
0.1
-
25.7
24.0
23.6
21.9
20.3
22.5
20.2
18.2
15.7
15.8
18.7
14.6
18.3
16.3
18.5
Obrero,
jornalero
1.0
1.0
1.1
2.0
2.7
1.9
1.8
2.7
3.3
2.9
2.1
2.7
3.0
3.5
2.9
Conductor
4.0
4.1
4.7
5.3
4.4
5.7
5.9
6.1
5.9
5.4
6.7
6.4
6.5
7.1
7.6
Trabajador
de los
del
servicios hogar
6.9
7.5
8.4
9.9
10.1
11.6
12.9
14.0
15.0
12.1
15.3
15.6
11.1
14.6
11.9
5.1
4.8
4.9
4.6
4.6
4.7
4.2
5.0
5.4
6.7
5.3
6.4
5.3
5.6
5.5
Fuente: MTPE - Encuesta de Niveles de Empleo en Lima Metropolitana 1990 – 1995,
Convenio MTPE - INEI. Encuesta Nacional de Hogares, 1996 – 2001, MTPE Encuesta de Hogares Especializada de Niveles de Empleo 2002 al 2004, III
trimestre.
Elaboración: MTPE - Programa de Estadísticas y Estudios Laborales
Notas:
1/ Para el año 1999 profesionales, técnicos y ocupaciones afines incluye gerentes,
administrativos y funcionarios.
2/ Para el año 2003 y 2004, profesionales, técnicos y ocupaciones afines incluye gerentes,
administrativos y funcionarios.
56
Total
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
100.0
Cifras
expandidas
2,334,478
2,327,776
2,333,813
2,536,478
2,611,322
2,846,029
2,782,669
3,037,864
3,157,355
3,254,494
3,264,790
3,411,790
3,334,304
3,361,308
3,366,936