Construcción de modelos

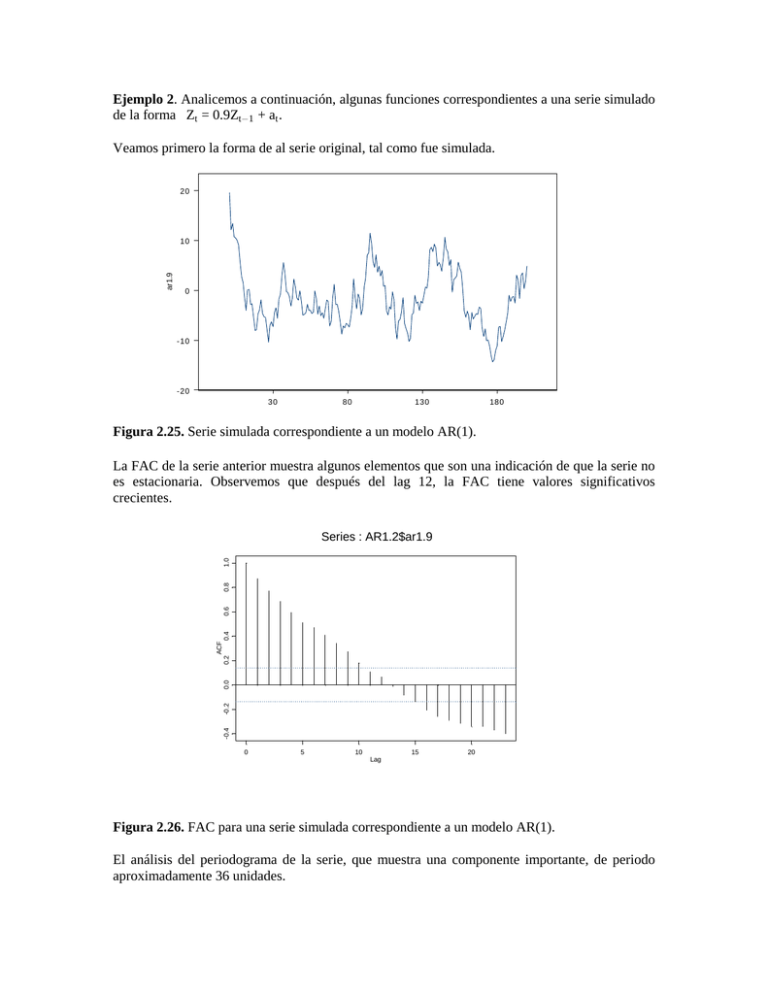
Ejemplo 2. Analicemos a continuación, algunas funciones correspondientes a una serie simulado
de la forma Zt = 0.9Zt1 + at .
Veamos primero la forma de al serie original, tal como fue simulada.
20
ar1.9
10
0
-10
-20
30
80
130
180
Figura 2.25. Serie simulada correspondiente a un modelo AR(1).
La FAC de la serie anterior muestra algunos elementos que son una indicación de que la serie no
es estacionaria. Observemos que después del lag 12, la FAC tiene valores significativos
crecientes.
-0.4
-0.2
0.0
0.2
ACF
0.4
0.6
0.8
1.0
Series : AR1.2$ar1.9
0
5
10
15
20
Lag
Figura 2.26. FAC para una serie simulada correspondiente a un modelo AR(1).
El análisis del periodograma de la serie, que muestra una componente importante, de periodo
aproximadamente 36 unidades.
Periodogram Values
Spectral analysis:
3500
3500
3000
3000
2500
2500
2000
2000
1500
1500
1000
1000
500
500
0
0
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16
Frequency
Figura 2.27. Periodograma correspondiente a un modelo AR(1) simulado.
Log (Periodogram)
Log Periodogram
9
9
8
8
7
7
6
6
5
5
4
4
3
3
2
2
1
1
0
0
-1
-1
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16
Frequency
Figura 2.28. Log-Periodograma de una serie simulada correspondiente a un proceso AR(1).
Observemos que en este grafico es posible visualizar el peso relativo del resto de las
componentes
periódicas de la serie.
Analizaremos a continuación la fuención de densidad espectral de la serie. Al igual que una
función de densidad de probabilidad de una variable aleatoria, esta función nos muestra la
densidad del espectro para ciertas frecuencias, pudiendo visualizar en ella el espectro de
frecuencias en las que las señales son de mayor intensidad.
Spectral Density
Densidad Espectral
1800
1800
1600
1600
1400
1400
1200
1200
1000
1000
800
800
600
600
400
400
200
200
0
0
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16
Frequency
Figura 2.29. Densidad espectral. Observemos que esta función nos muestra una ventana, entre
0.01 y 0.03,
donde se encuentran las más altas frecuencias.
Lo mismo que el logaritmo del periodograma, el logaritmo de la densidad espectral nos permite
visualizar otras ventanas de frecuecias que pudieran aparecer ocultas dada la gran intensidad de
las señales en la ventana de frecuencias entre 0.01 y 0.03.
Log (Spectral Density)
Log Densidad Espectral
8
8
7
7
6
6
5
5
4
4
3
3
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16
Frequency
Figura 2.30. Logaritmo de la densidad espectral. Observemos que esta función nos muestra una
ventana,
entre 0.01 y 0.03, donde se encuentran las más altas frecuencias.
CAPITULO III
CONSTRUCCION DE MODELOS
3.1. Introducción.
En una primera etapa, nos preocuparemos de la construcción de modelos usando la metodología
propuesta por Box y Jenkins para los modelos conocidos como ARIMA. Es necesario destacar
que esta metodología de ajuste difiere diametralmente de los modelos estructurales, construidos
en torno a la teoría de los filtros de Kalman. En esos casos, se busca precisamente modelar las
componentes de tendencia, estacionalidad, etc., al contrario, de los modelos de Box y Jenkins
que veremos a continuación, para los que supondremos que disponemos de series estacionarias;
es decir, series en las que se han removido sus componentes estacionales, tendencias y promedio.
En el caso que no se indique en forma específica que este procedimiento se ha realizado,
supondremos que es posible hacerlo sin mayores dificultades.
El estudio de los modelos de Box y Jenkins, se inicia habitualmente con la construcción de
modelos sencillos, para los cuales es necesario definir previamente la estrategia de ajuste. En este
curso, seguiremos los criterios habituales de ajuste los que contemplan, al menos, las siguientes
etapas:
Etapa 0. Exploración y validación.
Esta etapa consta de los procedimientos habituales de verificación de la calidad de la
información, en cuanto a cumplimiento de supuestos, detección de valores atípicos, etc. Se apoya
fuertemente en el análisis gráfico de la información.
Etapa 1. Identificación de una familia de modelos.
Si la etapa anterior nos ha permito definir el problema como uno relacionado con el ajuste de
modelos de series de tiempo, deberemos indentificar la familia de modelos a la cual,
tentativamente, pertenecería el modelo a ajustar. Esta identificación permitirá seleccionar el tipo
de estrategia de estimación a utilizar. La identificación de un modelo pasa por obtener en forma
previa algunos estimadores de funciones asociadas con la estructura autocorrelativa de las series,
como son las de autocorrelación (FAC), autocorrelación parcial (FACP) y de correlación cruzada
(FCC), que veremos en detalle más adelante.
Etapa 2. Estimación de parámetros.
Una vez definida la familia de modelos a sjustar, procedemos a obtener estimadores de los
parámetros del modelo, mediante métodos de ajustar generalmente disponibles en programas
computacionales. Esta etapa es la que generalmente requiere de menor intervención de parte del
investigador, por cuanto es sólo computacionalmente intensiva, habiéndose, durante los últimos
años, facilitando mucho mediante la incorporación de computadores personales.
Entre los paquetes disponibles que otorgan mayor diversidad de opciones para el ajuste de este
tipo de modelos están: BMDP, STATGRAPHICS, TS, ETS y SAS. Para efectos de este curso,
utilizaremos principalmente los tres primeros. Las características básicas de estos tres programas
son las siguientes:
BMDP: Es el de mayor flexibilidad para el ajuste de modelos de funciones de transferencia y
por lo tanto será utilizado intensivamente en la última etapa del curso.
STATGRAPHICS: Es el que dispone de mayor capacidad gráfica y por lo tanto es muy útil en el
análisis exploratorio inicial y en la etapa de la identificación de la familia de modelos a ajustar.
TS: Es el programa más sencillo, pero al mismo tiempo el más simple de utilizar, particularmente
en la etapa de estimación de parámetros de modelos ARIMA.
Etapa3. Diagnóstico.
Esta etapa está destinada a verificar la calidad de los modelos identificados y ajustados en las
etapas anteriores. Se apoya principalmente en algunos tests estadísticos específicos y en un
análisis gráfico de los resultados obtenidos del proceso de ajuste. Es la etapa más importante de
todo el proceso, pues aquí se deben tomar decisiones sobre la calidad del proceso de ajuste y por
tanto sobre su aceptación definitiva. Requiere, generalmente de un mayor entrenamiento.
Etapa 4. Predicción.
En la mayoría de los casos, el objetivo final del proceso de ajuste de este tipo de modelos es
precisamente, realizar algún tipo de predicción, pudiendo por tanto, ser esta etapa final de todo el
proceso. La calidad de la predicción depende casi exclusivamente de la calidad de los modelos
ajustados y por lo tanto de las cuatro etapas anteriores.
Etapa 5. Simulación.
Como complemento a la predicción es frecuente detectar la necesidad de lograr una
representación del proceso que se está modelando mediante un proceso de simulación basado en
algunas de las características distribucionales de las series manejadas. El procedimiento se basa
generalmente en el método Montecarlo y se apoya en algún tipo de generador de números
aleatorios.
Las etapas reseñadas completan el proceso de ajuste de modelos. Sin embargo, frecuentemente,
ellas necesitan de otras áreas del estudio de las series de tiempo como es el caso, por ejemplo, del
análisis espectral, el que, si bien apunta hacia otros aspectos de la serie sobre los cuales aún no
hemos comentado, son también de gran importancia en su estudio y sirven de complemento a lo
ya revisado. En la medida que ello sea necesario, revisaremos los conceptos más importantes
relacionados con este tipo de análisis.
OBSERVACION. Adicionalmente a la condición de estacionariedad del proceso que se está
modelando, existen dos condiciones indispensables que debe cumplir la información, para que el
proceso de construcción de los modelos sea adecuado. La primera es que la observación del
proceso a modelar debe ser a intervalos equiespaciados, lo que asegura una adecuada evaluación
de la autodependencia y la segunda, que deriva de la primera, es que no deben existir
observaciones perdidas. La falta de una o más observaciones podría inducir a asignar
erróneamente, niveles de dependencia a una o más observaciones. El concepto de observación
secuencial, involucra ambas restricciones.
3.2. Identificación de modelos.
3.2.1 Modelos autoregresivos.
Consideremos una sucesión de (valores) impactos at , at1 ,... tal que at µ RBN(0, 5a2 ) que
llamaremos Ruido Blanco. Este proceso de ruido {at } puede ser transformado en el proceso (serie
de tiempo) zt mediante la operación de filtro lineal
zt = at +<1 at1 + <2 at2 + ...
= D_
j=0 < (B) atj
con < (B) = 1 + <1 B + <2 B2 + ... , en la función de transferencia del filtro y los valores <1 , <2 , ...
definen la función de respuesta al impulso. A esta representación la llamaremos proceso lineal
general y nos permite representar zt como una suma ponderada de valores presentes y pasados de
un proceso de ruido blanco at . Este proceso puede ser considerado como una serie de impactos
que dirigen el proceso y que consiste de variables aleatorias no correlacionadas con media cero y
varianza constante; esto es, E(at ) = 0 y Var(at ) = 5a2 , lo que denotamos, at µ RB(0, 5a2 ).
Dado que estas variables aleatorias son no correlacionadas, su función de autocovarianza es de la
forma
5 2 k=0
#k = E(at at-k ) = œ a
0 kÁ0
por lo que la función de autocorrelación tiene la forma simple
1 k=0
3k = œ
0 kÁ0
La estructura del proceso lineal general definido, sirve de base para la construcción de un
conjunto de modelos de Box y Jenkins han agrupado en la clase de los modelos ARMA. De esta
familia de modelos estudiaremos primero algunos casos especiales, que normalmente son los de
uso más frecuente.
Definición: Un modelo se dice autorregresivo si puede ser utilizado en la representación de
procesos que corresponden a una combinación lineal de valores previos (consecutivos) del
mismo.
Denotemos los valores del proceso en los instantes t, t 1, t 2,... , por zt , zt1 , zt2 ,... ,
entonces
zt = 91 zt1 + 92 zt2 + ... + 9p ztp + at
(1)
con at µ RBN(0, 5a2 ), se llama modelo Autorregresivo de Orden p, AR(p).
Si definimos el operador autorregresivo como
p
9(B) = 1 91 B 92 B2 ... 9p B ,
podemos escribir
9(B)zt = at .
(2)
Este es un modelo con p+2 parámetros desconocidos (incluyendo . y 5 2 ). Observemos que
zt
= 91 zt1 + 92 zt2 + ... + 9p ztp + at
zt1
= 91 zt2 + 92 zt3 + ... + 9p ztp + at1
zt2
zt(p1)
= 91 zt3 + 92 zt4 + ... + 9p ztp2 + at2
ã
= 91 ztp + at(p1)
ztp
= a t p .
Luego reemplazando
zt = 91 (91 zt2 + 92 zt3 + ... + 9p ztp + at1 )
+ 92 (91 zt3 + 92 zt4 + ... + 9p ztp2 + at2 )
+ ... + 9p atp + at
y así hasta obtener una expresión del tipo
zt = < (B) at ,
Observación: Una condición necesaria y suficiente para que el proceso sea estacionario es que
<1 , <2 , ..., sea una serie convergente.
Consideremos ahora nuevamente el proceso AR(p)
Zt = 91 Zt1 + 92 Zt2 + ... + 9p Ztp + at
o escrito de otra forma
Zt 91 Zt1 ... 9p Ztp = at
(1 91 B ... 9p Bp )Zt = at
9(B)Zt = at
"
Zt = 9(B)
at
= 91 (B)at .
a 9(B) se le llama Operador Autoregresivo y es a diferencia de la función de transferencia del
filtro lineal, un operador con un número finito de términos y, más aún, un operador que
trataremos de que sea lo más parsimonioso posible (con el menor número de términos posible).
Veamos, a modo de ejemplo la representación como filtro lineal, de un proceso AR(1)
(1 91 B)Zt = at
Zt = 1"9 B at
1
Esta expresión tiene desarrollo en serie de la forma.
= at + 91 at1 + 912 at2 + ...
Zt = D_
j=0 91 atj
j
(2a)
que corresponde a, como definieraramos inicialmente, un filtro lineal con función de
transferencia
< (B) = (1 91 B)1
j j
= D_
j=0 91 B
Para asegurar estacionariedad, < (B) debe converger para lBl Ÿ 1 Ê l91 l 1 y dado que la raíz
del polinomio en B
1 91 B = 0, es B = 911 , ello es equivalente a tener que la raíz de
1 91 B = 0 esté fuera del círculo unitario.
Para el caso general AR(p); Zt = 91 (B)at
9(B) = (1 :1 B)(1 :2 B) ... (1 :p B)
Ê 91 (B) = Dpi=1 (1": B) .
j
La ecuación equivalente es 9(B) = 0 y se llama ecuación característica del proceso y como la
serie 9(B) es finita, no se requiere restricciones sobre 9i para asegurar la estacionariedad.
Funciones de autocovarianza y autocorrelación de un proceso AR(p)
Zt = 91 Zt1 + 92 Zt2 + ... + 9p Ztp + at
Ztk Zt = 91 Ztk Zt1 + 92 Ztk Zt2 + ... + 9p Ztk Ztp + Ztk at
#k = 91 #k1 + 92 #k2 + ... + 9p #kp + 0 ; k 0
/ Ztk
/E
(3)
9(B)#k = 0
Si dividimos la expresión anterior por #0 , obtenemos la función de autocorrelación,
3k = 91 3k1 + 92 3k2 + ... + 9p 3kp ; 5 0
(4)
Ê
9(B)3k = 0
Lo anterior significa que podemos expresar los parámetros del modelo AR(p), en términos de 3k ,
de la forma
31 = 91 + 92 31 + ... + 9p 3p1
32 = 91 31 + 92 + ... + 9p 3p2
ã
3p = 91 3p1 + 92 3p2 + ... + 9p ,
de donde podemos deducir el siguiente sistema de ecuaciones, conocido como Ecuaciones de
Yule-Walker, las que nos permiten obtener estimadores de los parámetros 9i , precisamente en
términos de la autocorrelación.
9=
Ô 91 ×
ã
Õ 9p Ø
;
3p =
Ô 31 ×
ã
;
Õ 3p Ø
Pp =
Ô 1
31
Õ 3p1
31
1
3p2
â 3p1 ×
â 3p2
1 Ø
â
Ê 9 = Pp1 3p
(5)
Para obtener los estimadores, reemplamos 3k por su estimador muestral rk ,obteniendo.
^
Ô 91 ×
^=Ö ã Ù
9
^ Ø
Õ9
;
p
Ô r1 ×
rp = ã
;
Õ rp Ø
Ô 1
Rp = r1
Õ rp1
r1
1
rp2
â
â
â
r p 1 ×
rp2
1 Ø
^ = R 1 r
Ê 9
p
p
(5)
Varianza de un proceso AR(p).
Cuando k=0 el término correspondiente a
E(Ztk at ) = E[Zt at ] = E[a2t ] = 5a2
luego
#0 = 91 #1 + 92 #2 + ... + 9p #p + 5a2
/ #0 = 5z2 y como #z = #z
52
1 = 91 31 + 92 32 + ... + 9p 3p + 5a2
z
de donde
5a2
= 1 91 31 ... 9p 3p
5z2
52
5z2 = 19 3 a 9 3
1 1 ? ... ? p p
(6)
Función de Autocorrelación Parcial (FACP).
La función de autocorrelación parcial, como hemos visto, permite cuantificar la dependencia de
cada valor de la serie respecto de sus valores anteriores, para cada uno de los rezagos k, desde
k=0, que corresponde a la varianza de la serie, hasta k=n, este valor como máximo. Sin
embargo, producto de la persistencia de la serie, los valores observados de la AC en cada
desfase, están mezclados con la serialidad de la correlación; esto es, Yt depende de Yt1 , pero
como Yt" depende a su vez de Yt2 , entonces Yt1 depende también de Yt2 , y asi
sucesivamente. Necesitamos entonces corrregir esta autocorrelación serial, de modo de obtener
sólo la medida exacta de la dependencia entre Yt y Yt1 , es decir no contaminada por la
dependencia entre Yt1 y Yt2 . Con este objeto, definimos la Función de Autocorrelación
Parcial (FACP).
Sea 9kj el j-ésimo coeficiente de un proceso AR(k) de modo que 9kk es el último coeficienteà
/sto es,
3j = 9k1 3j1 + ... + 9k(k1) 3jk+1 +9kk 3jk
j = 1, 2, ..., k
luego las ecuaciones de Yule-Walker pueden ser escritas de la forma
31
1
ã
3k-2
Ô 1
Ö 31
Ö
ã
Õ 3k-1
â
â
ã
â
3k1 ×Ô 91 × Ô 31 ×
3k2 ÙÖ 92 Ù Ö 32 Ù
ÙÖ
Ù= Ö Ù Í Pk 9k = 3k
ã
ã
ã
1 ØÕ 9kk Ø Õ 3k Ø
resolviendo
911 = 31
1
º3
922 = 1
1
º3
933 =
1
â
â1
â
â 31
â
â 32
â
â1
â
â 31
â
â 32
31
32 º
31
1º
=
31
1
31
31
1
31
â
31 â
â
32 â
â
33 â
â
32 â
â
31 â
â
1â
32 312
1 312
9kk es la Función de Autocorrelación Parcial (FACP) para k = 1,2,....
Para un proceso AR(p), 9kk Á 0, k Ÿ p
y 9kk = 0 si k p.
La FACP puede también ser considerada como la correlación entre Z1 y Zk+1 ajustada por los
valores intermedios Z2 ,..., Zk en otras palabras, corresponde a la correlación entre los residuos
obtenidos de las regresiones Xk+1 y X1 sobre X2 ,..., Xk .
Así por ejemplo. Si Zt = .9Zt1 + %t se tiene
9kk = Corr(Z2 , Z1 )
= Corr(.9Z1 + %2 , Z1 ) = .9.
Una estimación de estos valores puede ser obtenida de las ecuaciones de Yule-Walker,
reemplazando 3j por su estimador rj .
Métodos de estimación.
Un método recursivo propuesto por Durbin, basado en los valores rj , nos da
rj = 9k1 rj1 + 9k2 rj2 + ... + 9k(k1) rjk+1 + 9kk rjk
Los estimadores Yule Walker para k = 2 y 3 son
Para k = 2
s 21 r1 + 9
s 22
r2 = 9
s 21 + 9
s 22 r1
r1 = 9
r
si definimos R2 = ” 1
1
Ÿ
1
r1 •
entonces
s 21
r2
9
” r • = R2 – s — Ê
1
922
s 21
r
9
= R21 ” 2 •
–9
r1
s 22 —
(1)
Para k=3,
s 31 r2 + 9
s 32 r1 9
s 33
r3 = 9
s 31 r1 + 9
s 32 9
s 33 r1
r2 = 9
s
s
s 33 r2
r1 = 931 + 932 r1 9
(2)
(3)
Ÿ
luego, de (3) obtenemos
r2
–r
1
s 33 r1
s r
9
9
= – 31 1
—
s 33 r2
s 31
9
9
lo que es equivalente a
s
9
= R2 – 31 —
s 32
9
de donde obtenemos
s 32
9
s 32 r1 —
9
s 31
9
r
œ R21 – 2
–9
s —
r
1
32
s 33 r1
9
s 33 r2 —
9
s 31
9
r
s 33 R1 ” r1 •
= R21 ” 2 • 9
2
–9
s —
r1
r2
32
pero, de (1) podemos reemplazar para obtener
s 31
s
9
9
s 33 R1 ” r1 •
= – 21 — 9
2
–9
—
s
s
r2
9
32
22
pero, de (1) podemos reemplazar para obteneer
s 31
s 21
s
9
9
s 33 922
9
=
–9
–9
s 32 — – 9
s 22 —
s 21 —
(4)
Ahora podemos expresar (4) como el sistema
s 31 = 9
s 21 9
s 33 9
s 22
9
s 32 = 9
s 22 9
s 33 9
s 21
9
Ÿ
Si sustituimos en (4) obtenemos
s 33 =
9
s 21 r2 9
s 2# r1
r3 9
s 21 r1 9
s 22 r1
19
s 33 como función de 9
s 21 y 9
s 22 .
lo que quiere decir que podemos calcular 9
Una forma recursiva general, a partir de la expresión anterior, es
s p+1,j = 9
s pj 9
s p+1 9
s p,pj+1 ; j= 1,2,..., p
9
sp+1,:" =
9
s rp+1?j
rp+1 Dpj=1 9
pj
p s
1D 9 rj
j=1 pj
Varianza de la FACP.
La varianza asociada a la FACP tiene la forma
s kk ) ¸
Var (9
"
n
, k p+1
Asumiendo distribución normal, podemos definir intervalos de confianza del tipo
s kk „ Z1! /2 É " .
9
n
Espectro de un proceso AR(p).
Si consideramos el operador autorregresivo 9(B) del modelo
9(B)zt = at , de forma que
< (B) = 91 (B), con 9(B) = 1 91 B .... 9p Bp
Recordemos que la forma general del espectro es
p(f) = 25a2 a l< (ei21f )l2
Luego, para un proceso AR(p), podemos escribir,
p(f) =
25a2
l191 ei21f ...9p ei2p1f l2
0 f 1/2
(7)
Veamos a continuación la forma de las funciones de autocorrelación y espectrales para algunos
modelos particulares y de uso más frecuente.
Proceso Autorregresivo de primer orden (Proceso de Markow).
De acuerdo con la definición (1) de un proceso
condiciones de estacionariedad tiene la forma;
zt
= 91 zt1 + at
zt1
= 91 zt2 + at1
zt(p1)
= 91 zt3 + at2
ã
= 91 ztp + at(p1)
ztp
= a t p .
zt2
de tipo AR(p), un proceso AR("), bajo
Luego reemplazando zt1
zt = 91 (91 zt2 + at1 ) + at
y ahora reemplazando zt2
zt = 91 (91 (91 zt3 + at2 ) + at1 ) + at
hasta obtener
zt = at + 91 at1 + 912 at2 + ...
1 91 1
que, como se mostrara en (2a), corresponde a una representación como modelo de filtro lineal de
la forma,
zt = < (B) at ,
Función de autocorrelación.
k0
3k = 91 3k1
31 = 91
32 = 91 31
32 = 91 91 = 912
33 = 91 3p1
ã
3p = 91 3p1
33 = 913
ã
3k = 9k Ê decaimiento exponencial.
Varianza
52
5z2 = 13a 9
1 1
=
5a2
1312
.
Espectro.
252
p(f) = l19 ea?i21f l2 ;
1
i=È1
eix = cos x + sen x
eix = cos x i sen x
p(f) =
25a2
2
1+91 291 cos
21 f
0 Ÿ f Ÿ 1/2.
Proceso autorregresivo de segundo orden - AR(2).
De acuerdo con la definición (1) de un proceso
condiciones de estacionariedad tiene la forma
de tipo AR(p), un proceso AR(2), bajo
Zt = 91 Zt1 + 92 Zt2 + at .
en que el término at corresponde a un proceso de ruido blanco,
Para que el proceso sea estacionario e invertible, las raices del polinomio deben estar fuera del
círculo unitario, lo que implica que la ecuación
9(B) = 1 91 B 92 B2 = 0
debe tener raices que cumplan con
# 9" #.
1 92 1.
92 + 91 1
92 91 1
Función de autocorrelación de un proceso AR(2).
De la expresión general planteada en (3), podemos obtener
3k = 91 3k1 + 92 3k2 ,
; k 0.
Del mismo modo las ecuaciones de Yule-Walker son de la forma
31 = 91 + 92 31
32 = 91 3" + 9#
Ÿ 91 =
31 (132 )
9
Ê 31 = 119 .
1312
2
Varianza.
5a2
5z2 =
5z2 =
131 91 32 92
5a
"92
1+92 {(192 )2 912 } .
2
Espectro.
252
p(f) = l19 e?i21f a 9 e?i41f l2 .
1
2
Ejemplos. Analicemos a continuación, algunos ejemplos de series y revisemos sus funciones
de autocorrelación y funciones espectrales.
Serie N12.
SERIE EL NIÑO 12
30
TEMPERATURA EN oC
28
26
24
22
20
18
1950
1960
1970
1980
1990
2000
Figura 3.1. Serie N12 mostrando evidencia de estacionalidad
FUNCION DE AUTOCORRELACION PARA NIÑO12
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
-1.0
Conf. Limit
-0.5
0.0
0.5
1.0
FUNCION DE AUTOCORRELACION PARCIAL PARA NIÑO12
ANOM
(Standard errors assume AR order of k-1)
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
-1.0
Conf. Limit
-0.5
0.0
0.5
1.0
Figura 3.2. Función de autocorrelacion y autocorrelacion parcial para la serie N12. La FAC
muestra la falta de estacionariedad de la serie, la incluye una clara componente de 12 meses,
correspondiente al ciclo estacional anual.
Periodogram Values
PERIDOGRAMA SERIE N12
No. of cases: 638
2500
2500
2000
2000
1500
1500
1000
1000
500
500
0
0
50
100
150
200
250
300
350
400
450
500
550
600
650
0
700
Period
Log (Spectral Density)
SERIE N12
7
7
6
6
5
5
4
4
3
3
2
2
1
1
0
0
-1
0
50
100
150
200
250
300
350
400
450
500
550
600
650
-1
700
Period
Figura 3.3. Periodograma y log. de la densidad espectral para la serie N12. Se muestra la
componente estacional de doce meses.
Luego de examinada la serie y sus funciones de autocorrelación y autocorrelación parcial. se
removieron las componentes estacionales obteniéndose los siguientes resultados.
SERIE DE ANOMALIAS DE N12
5
4
3
ANOM12
2
1
0
-1
-2
-3
1950
1960
1970
1980
1990
2000
Figura 3.4. Serie de anomalias de N12. No aparecen as componentes periódicas, pero si son
evidentes los eventos El Niño de los últimos 50 años.
FAC PARA SERIE DE ANOMALIAS DE NIÑO12
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
-1.0
Conf. Limit
-0.5
0.0
0.5
1.0
FACP PARA LA SERIE DE ANOMALIAS DE NIÑO12
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
-1.0
Conf. Limit
-0.5
0.0
0.5
1.0
Figura 3.5. Función de autocorrelacion y autocorrelacion parcial para la serie N12. La FAC
muestra la falta de estacionariedad de la serie, la incluye una clara componente de 12 meses,
correspondiente al ciclo estacional anual.
Periodogram Values
ANOMALIAS DE NIÑO12
100
100
80
80
60
60
40
40
20
20
0
0
50
100
150
200
250
300
350
400
450
500
550
600
650
0
700
Period
Spectral Density
DENSIDAD ESPECTRAL PARA ANOM. DE NOÑO12
60
60
50
50
40
40
30
30
20
20
10
10
0
0
50
100
150
200
250
300
350
400
450
500
550
600
650
0
700
Period
Figura 3.6. Periodograma y log. de la densidad espectral para la serie N12. Se muestra la
componente estacional de doce meses.
La FAC, muestra los resultados de la corrección por estacionalidad. La serie aún muestra señales
de falta de estacionariedad, que se reflejan en la persistencia de la señal después de los doce
meses. Esta componente, que pudiera ser periódica se puede examinar en las funcionnes
espectrales, las que muestran una mayor actividad en la ventana de los 48 meses. La FACP,
muestra una fuerte señal de una autocorrelación significativa con desfase uno, aunque aparecen
otros desfases también significativos..
Serie del Indice de Oscilación del Sur (SOI)
SERIE ANOMALIAS DE SOI
6
4
2
ANOMALIAS
0
-2
-4
-6
-8
-10
1950
1960
1970
1980
1990
AÑO
Figura 3.7. Serie de anomalías de SOI.
FAC de SOI
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
-1.0
Conf. Limit
-0.5
0.0
0.5
1.0
FACP de SOI
(Standard errors assume AR order of k-1)
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
-1.0
Conf. Limit
-0.5
0.0
0.5
1.0
Figura 3.8. Función de autocorrelacion y autocorrelacion parcial para la serie SOI
2000
Periodogram Values
SOI
120
120
100
100
80
80
60
60
40
40
20
20
0
0
50
100
150
200
250
300
350
400
450
500
550
600
0
650
Period
Log (Spectral Density)
SOI
5
5
4
4
3
3
2
2
1
1
0
0
-1
0
50
100
150
200
250
300
350
400
450
500
550
600
-1
650
Period
Figura 3.9. Periodograma correspondiente log. de la función de densidad espectral para la serie
de SOI (anomalías)
Las funciones de esta serie muestran signos simuilares a los de N12, aunque algo menos
marcados.La FACP, muestra una fuerte señal de una autocorreleción significativa con desfase
uno y dos y algo menos significativa en el desfase tres.No aparecen otros desfases también
significativos.
Serie de radiación de onda larga (OLR).
Esta serie es significativamente más corta que las dos anteriores, ya que tiene valores
continuados válidos sólo a partir del año 1978.
SERIE OLR
80
70
60
50
OLR
40
30
20
10
0
-10
Figura 3.10. Serie de radiación de onda larga (OLR).
Autocorrelation Function
OLR
(Standard errors are white-noise estimates)
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
-1.0
Conf. Limit
-0.5
0.0
0.5
1.0
0.5
1.0
FACP OLR
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
-1.0
Conf. Limit
-0.5
0.0
Figura 3.11. Función de autocorrelacion y autocorrelacion parcial para la serie OLR.
OLR
1.6E6
1.4E6
1.4E6
1.2E6
1.2E6
Periodogram Values
1.6E6
1E6
1E6
8E5
8E5
6E5
6E5
4E5
4E5
2E5
2E5
0
0
50
100
150
200
250
300
350
0
400
Period
Log (Spectral Density)
OLR
16
16
14
14
12
12
10
10
8
8
6
6
4
0
50
100
150
200
250
300
350
4
400
Period
Figura 3.12. Periodograma y log de la densidad espectral.
La FAC muestra un claro decaimiento exponencial lo que es una indicación de que se
trata de un proceso AR. Sin embargo, la FACP, a pesar de que muestra un valor muy
significativo para el rezago uno, muestra una componente periódica de cinco meses que
no aoperece clara en la FAC. Las funciones espectrales no muestran esta periodicidad.
Ellas muestran, sin embargo, componentes periódicas en loos 30 y 60 meses. La densidad
espectral, muestra que la ventana de frecuencias registra su mayor energía precisamente
en la banda de 30 a 60 meses.
3.2.2. Procesos de Medias Móviles.
La característica principal de los procesos AR revisados hasta aquí, es que ellos representan las
relaciones de autodependencia de la serie, permitiendo la construcción de modelos cuyos
parámetros son estimados en base a las relaciones de dependencia de cada observación con sus
valores pasados, hasta un cierto nivel de desfase, el que es controlado por la función de
autocovarianza. A este esquema sólo hemos agregado una sucesión de impactos aleatorios con la
distribución de ruido blanco usual. Sin embargo, la definición de una serie de tiempo como
modelo de filtro lineal, sugiere que es posible modelar la serie sólo en función de su dependencia
con una sucesión impactos aleatorios definidos. En particular, podemos pensar que existe una
estructura de dependencia finita respecto de valores pasados de la sucesión de impactos
mencionados. Esta relación de dependencia es la que nos permite definir la siguiente familia de
modelos, llamada de medias móviles (que no tiene relación, con las medias móviles definidas
hasta aquí, como una forma de filtro de ruido de alta frecuencia - tipo filtro paso bajo).
Definición: Modelos de Medias Móviles.
Un proceso que puede ser representado de la forma
Yt = at )1 at?1 )2 at?2 ... )q at?q
se llama proceso de media móviles finito.
Si definimos como )(B) al operador de medias móviles de orden q,
) (B) = 1 )1 B ... )q Bq , podemos escribir
Yt = ) (B)at
el que también contiene q+2 parámetros desconocidos.
Función de Autocorrelación y espectro de un modelo MA(q).
Si consideramos nuevamente el modelo MA(q)
Yt = at )1 at?1 )2 at?2 ... )q at?q ,
la FACV correspondiente es de la forma #k = E[Yt Yt?k ], por lo que reemplazando obtenemos
#k = E[(at )1 at?1 ... )q at?q )(at?k )1 at?k?1 ... )q at?k?q )]
luego, si k=0 Ê #0 = (1+)12 + )22 + ... + )q2 ) 5a2 ß y si k 0,
ya que la covarianza para todos los productos cruzados es cero, dado que at es un proceso de
ruido blanco.
#k = œ
( ? )k + )1 )k+1 + )2 )k+2 + ... + )q?k )q )5a2 si k=1,2,...,q
si k P q.
0,
Luego 3k = ?)k + )1 )k+1 + ... + )q?k )q
1 + )12 + )22 + ... + )q2
0
k=1,2,...,q
si k P q
En este caso, las ecuaciones de Yule-Walker no pueden aplicarse y que, excepto el caso q=1, que
veremos más adelante, este sistema debe ser resuelto iterativamente por ser de tipo no lineal.