2. Conceptos básicos.

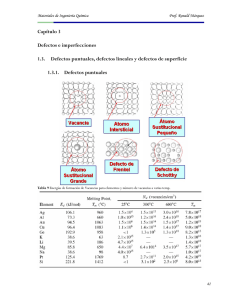
2.
Conceptos básicos.
En este capitulo se pretende hacer una introducción a las redes cristalinas y sus
propiedades. Consideraremos primero a los átomos en su posición de equilibrio en redes perfectas. Luego le introduciremos a estas redes ”perf ectas” los defectos, ya que como sabemos las
redes cristalinas son idealizaciones que no encontramos en la realidad. Los materiales poseen
en su estructura cantidades de defectos que dependen de numerosos factores.
2.1. Sistemas cristalinos y redes de Bravais.
La mayor parte de los sólidos de la naturaleza son cristalinos lo que signica que
los átomos, moléculas o iones que los forman se disponen ordenados geométricamente en el
espacio. Esta estructura ordenada no se aprecia en muchos casos a simple vista porque están
formados por un conjunto de microcristales orientados de diferentes maneras formando una
estructura policristalina, aparentemente amorfa. Esta disposición reticular se opone al desorden
que se maniestan en los gases o líquidos. Cuando un mineral no presenta estructura cristalina
se denomina amorfo. Las redes cristalinas se caracterizan fundamentalmente por un orden
o periodicidad. La estructura interna de los cristales viene representada por la llamada cela
unidad que se repite una y otra vez en las tres direcciones del espacio. El tamaño de esta celda
viene determinado por la longitud de sus tres aristas (a, b, c), y la forma por el valor de los
ángulos entre dichas aristas (α, β, γ) ver Fig.(1a).
(a)
(b)
Figura 1: (a) Red espacial de un solido cristalino ideal y (b) celda unitaria mostrando las constantes de la red.
Combinando las dos traslaciones y el ángulo que forman entre sí, sólo hay cinco posibles formaciones de redes planas: paralelogramo, rectángulo, cuadrado, hexágono y rombo. Si
formamos una red espacial apilando estas redes planas, sólo existen catorce posibles formaciones
que representan las formas más sencillas en que puede descomponerse la materia cristalina sin
que por ello pierdan sus propiedades originales, son las llamadas redes de Bravais1 . Las celdas
de bravais tridimensionales pueden verse en la Figura (2). Desde el punto de vista geométrico
y cristalográco una red de Bravais es una disposición de puntos cuya estructura es invariante
bajo cierto grupo de traslaciones. En la mayoría de casos también se da una invariancia bajo
1 August
Bravais (1811-1863). Cristalográco francés que estableció los 14 posibles ordenamientos de puntos
en el espacio.
6
Figura 2: Las 14 celdas de Bravais según los sistemas cristalinos.
rotaciones o simetría rotacional. Estas propiedades hacen que en todos los puntos de la red de
Bravais se tenga la misma perspectiva de la red. Decimos entonces que todos los puntos de la
red son equivalentes. Una red unidimensional es el caso mas elemental, simplemente consiste
en una secuencia de nodos equidistantes entre si. En dos o tres dimensiones las cosas se hacen
un poco mas complicadas y la variedad de formas obliga a denir ciertas estructuras patrón
para trabajar (Figura (2)). Para generar dichas redes, normalmente se utiliza en concepto de
celda primitiva. Las celdas unitarias, son paralelogramos en (2D) o paralelepípedos en (3D)
que constituyen la menor subdivisión de una red cristalina que conserva las características en
toda su retícula. Una red típica de Bravais se representa de la siguiente manera
R=
n
X
vi a~i |vi ∈ Zn ,
(1)
i=1
donde ai es la base de la red y n la dimensión espacial que se considere.
2.2. Defectos en Materiales cristalinos.
En realidad no existen cristales perfectos pues contienen varios tipos de defectos
que afectan a muchas de las propiedades físicas y mecánicas, que a su vez afectan a muchas
propiedades importantes de los materiales para la ingeniería, como la conformación en frío
de aleaciones, la conductividad eléctrica de semiconductores, la velocidad de migración de los
átomos en aleaciones y corrosión. Todas las redes cristalinas reales contienen imperfecciones,
las cuales pueden ser puntuales, ocurriendo en un solo punto de la red; lineales, ocurriendo a lo
7
largo de una la de átomos; o defectos planos, ocurriendo en un plano 2D de la red. Las mismas
perturban localmente la disposición regular de la red atómica. Su presencia puede modicar
signicativamente las propiedades eléctricas y mecánicas de los sólidos cristalinos. Si bien es
quizás intuitivo pensar en los defectos como cosas malas, por el contrario, son necesarios.
Muchas, o quizá todas, las ramas de la ciencia que estudian las diferentes propiedades de los
materiales depende de la existencia de algún tipo de defectos. Los defectos en la red cristalina
se clasican según su forma y geometría. Los tres grupos principales son: 1) defectos puntuales
o de dimensión cero, 2) defectos de linea o de una dimensión (dislocaciones) y 3) defectos de
dos dimensiones que incluyen supercies externas y supercies limite de grano. Los defectos
macroscopicos tridimensionales o de volumen también pueden incluirse. En este trabajo nos
centraremos en las dislocaciones, pero en este apartado haremos un breve recorrido por los
distintos tipos de defectos para luego enfocarnos en las dislocaciones.
2.2.1.
Defectos Puntuales.
El defecto puntual mas sencillo es de vacante, un sitio atómico en el que he de desaparecido el átomo que lo ocupaba (Figura 3a). Las vacantes pueden producirse durante la
solidicación como resultado de perturbaciones locales durante el crecimiento de los cristales,
o por las reordenaciones atómicas en un cristal ya existente debido movilidad de los átomos.
En los metales, la concentración de vacante en el equilibrio, raramente excede de aproximadamente 1 átomo en 10000. Las vacantes son defectos en equilibrio y su energía de formación
es del orden de 1 eV. En los metales pueden introducirse vacante adicionales durante la deformación plástica, por el enfriamiento rápido desde elevadas temperaturas y por bombardeo
de partículas a alta energía, como son los neutrones. Las vacantes que no están en equilibrio
tienden a formar aglomerados , formando divacantes o trivacantes. Las vacantes pueden moverse intercambiando su posición con sus vecinas. Este proceso es importante en la migración o
difusión de átomos en estado solido, particularmente a temperaturas elevadas donde la movilidad de los átomos es mayor. Algunas veces un átomo de un cristal puede ocupar un hueco
intersticial entre los átomos de su entorno que ocupan posiciones atómicas normales (Figura
(3b)). Este tipo de defectos puntuales se llama autointersticial o intersticialidad. Estos defectos
no ocurren generalmente de forma natural por la distorsion estructural que provocan, pero se
pueden introducir en la estructura por irradiacion. En cristales iónicos los defectos puntuales
son más complejos debido a la necesidad de mantener la neutralidad eléctrica. Cuando dos
iones de carga opuesta faltan en un cristal iónico, se crea una divacante aniónica-catiónica
que se conoce como defecto de Schottky (Figura (4)). Si un catión se mueve a un hueco
intersticial del cristal iónico, se crea una nueva vacante catiónica en la posición inicial del
catión. Este par defectos vacante-intersticio se llama defecto de Frenkel (Figura (4)). La
presencia estos defectos en los cristales iónicos, aumenta la actividad eléctrica. Los átomos de
impurezas de tipo sustitucional o intersticial son también defectos puntuales y se pueden presentar en cristales con enlaces metálicos o covalentes. Por ejemplo, cantidades muy pequeñas
de impurezas sustitucionales en silicio puro, pueden afectar mucho su conductividad eléctrica
para su uso en dispositivos electrónicos. Las impurezas iónicas son también defectos puntuales
en cristales iónicos.
8
(a)
(b)
Figura 3: (a) Vacante. (b) Intersticial o autointersticial, defectos puntuales en una red metalica compacta.
Figura 4: Representacion en dos dimenciones de un cristal ionico ilustrando un defecto de Schottky y un defecto de Frenkel.
2.2.2.
Defectos planos.
Los defectos que se remiten a un plano, es decir 2D, son por ejemplo supercies
externas, limites de grano, maclas, bordes de ángulo, borde de ángulos abierto, torsiones y
fallas de apilamiento. La supercie libre o externa de cualquier material es el tipo más común
de defecto de plano. Las supercies externas se consideran defectos debido a que los átomos de
la supercie están enlazados a otros átomos solo por un lado. Por consiguiente, los átomos de
la supercie tienen un menor número de vecinos. Como resultado de ello, estos átomos tienen
un mayor estado de energía en comparación con los átomos situados dentro del cristal, con un
número óptimo de vecinos. La mayor energía asociada con los átomos de la supercie de un
material hace a la supercie susceptible a la erosión y a reaccionar con elementos del ambiente.
Este punto ilustra con mayor claridad la importancia de los defectos en el desempeño de los
materiales. Los límites de grano son una clase de defectos en la supercie de los materiales
policristalinos donde se separan los granos (cristales) de diferentes orientaciones. En los metales,
los limites de grano se originan durante la solidicación, cunado los cristales formados desde
9
diferentes núcleos crecen simultáneamente juntándose unos con otros (Figura (5))2 . La forma
de los límites de grano esta determinada por la restricción impuesta por el crecimiento de
los granos vecinos. El límite de grano es una región estrecha entre dos granos de entre dos y
cinco diámetros atómicos de ancho, y es una región de átomos no alineados entre dos granos
adyacentes. El ordenamiento atómico en los límites de grano es menor que en los granos debido
a esa falta. Los límites de grano tienen átomos en posiciones pensionadas, lo que provoca un
aumento de energía en la región del límite de grano. Entre mayor sea la energía en los limites de
grano y su estructura sea mas abierta, estos se convertirían en una región mas favorable para
la nucleación y el crecimiento de precipitados. El menor orden atómico en los límites de grano
también permite una difusión atómica más rápida en esas regiones. A temperatura ordinaria,
los límites de grano disminuyen la plasticidad dicultando el movimiento de las dislocaciones
en la región del límite de grano.
Figura 5: Esta micrografía de relativamente baja resolución muestra la estructura de límite de grano para una lámina muy
delgada de aluminio.
(a)
(b)
Figura 6: (a) Dislocaciones de borde en un haz que forma un limite inclinado en ángulo pequeño. (b) Esquema de límite
doblado en ángulo pequeño.
Cuando en un arreglo de dislocaciones de borde éstas se originan en un cristal de
manera tal que dos regiones del cristal parecen desorientarse o inclinarse (Figura (6a)), se
forma un defecto bidimensional llamado limite de inclinación en ángulo agudo. Puede ocurrir
2 Imagen
obtenida por el laboratorio de Cavendish de la Universidad de Cambridge.
10
un fenómeno similar cuando una red de dislocaciones helicoidales crea un limite de torsión en
ángulo agudo (Figura (6b). El ángulo de desorientación θ de un limite de ángulo agudo suele
ser menor a 10 grados. A medida que aumenta la densidad de las dislocaciones en los limites
en ángulo agudo (inclinación o torsión), aumenta el ángulo de desorientación θ. Si θ es mayor
que 20 grado, el limite ya no se caracteriza como ángulo agudo, sino como un limite general de
grano. De manera similar a las dislocaciones, los borde de ángulo agudo son regiones de alta
energía debido a las distorsiones locales de la red tienden a endurecer a un metal.
Una red atómica de Brabais puede formarse a partir de un apilamiento de capas de
átomos en una secuencia regular. Por ejemplo una red BCC puede formarse a partir de apilar
planos (100) o (110) en la dirección 111. De la ruptura de esta regularidad se desprende otro
defecto de tipo 2D, el cual denominamos fallo de apilamiento. La presencia de de este tipo de
(a)
(b)
Figura 7: Defecto de apilamiento en una estructura cubica centrada en las caras (F CC). La secuencias normal de apilamiento
en los planos (111) es ABCA..., los planos en sin defectos son separados por la distancia 4, mientras que con el error se
separan por 5: (a) defecto de apilamiento intrínseco (b) defecto de apilamiento extrínseco.
fallos juega un rol importante en la plasticidad de los cristales. En redes con estructura tipo
F CC dos posibles fallos de este tipo don posibles, no referiremos a ellos como intrínseco y
extrínseco. Estos se deben al cambio resultante de remover o introducir una capa extra. En la
Figura (7a) parte de la capa C fue removida. En la Figura (7b), en cambio, una capa extra es
introducida entre las capas A y B .
Es importante señalar que, en términos generales, de los defectos bidimensionales que
se comentaron anteriormente, los limites de grano son los mas ecaces para endurecer a un
metal.
2.2.3.
Defectos de Volumen.
Precipitados, huecos y burbujas son defectos de este tipo que pueden ocurrir bajo
ciertas circunstancias y tienen importantes efectos sobre la propiedad de los sólidos cristalinos.
Los nanohuecos los podemos pensar como un conjunto de vacancias puntuales. Al rededor de
nanohuecos es donde se originan o nuclean otro tipo de defecto tales como las dislocaciones.
Publicaciones recientes muestran que la interacción entre las dislocaciones y los precipitados
tienen una rol vital en el desarrollo de aleaciones de altas resistencias.
11
2.3. Dislocaciones.
Los defectos lineales o dislocaciones es los sólidos cristalinos son defectos que provocan una distorsión de la red centrada a lo largo de una línea. Auque hoy hay muchas técnicas
disponibles para la visualización de este tipo de defectos de línea, es decir para ver las dislocaciones en un material, la existencia de estos defectos fue deducida entre los años 1934 a
comienzos de la década de los 50. Fuerte evidencia surgió de intentar explicar las diferencias
entre los valores teóricos y los resultados experimentales de la tensión de corte necesaria para
deformar plásticamente un cristal. Hoy sabemos que esta deformación existe por que en el
cristal se encuentran defectos que permiten que planos atómicos deslicen respecto a otros posibilitando esta deformación. En un cristal perfecto, es decir, en ausencia de dislocaciones, la
tensión requerida para hacer que haya un deslizamiento en un plano de átomos respecto a otro
en un movimiento que mantenga la red invariante fue calculada por primera vez por Frenkel
en 1926. La situación es ilustrada en la Figura (8). Asumiendo que hay una fuerza constante
periódica requerida para mover la la de átomos de arriba a lo largo de la la inferior es una
función sinusoidal de la siguiente forma
τ=
2πx
Gb
sen
,
2πa
b
(2)
donde τ es la tensión de corte aplicada, G es el modulo de corte, b es el espaciado entre
los átomos en la dirección de la tensión de corte, a es el espaciamiento entre las o planos
(si consideramos 3D) de átomos y x es la traslación entre las dos las desde una posición de
minima energía a otra posición de equilibrio. El termino derecho de la ecuación (2) es periódico
Figura 8: Esquema utilizado para estimar la tensión de corte máxima teórica para un deslizamiento.
en b y se reduce a la ley de Hooke para pequeñas deformaciones x/a, es decir, que en pequeñas
deformaciones sen(2πx/b) ≈ (2πx/b). El valor máximo de τ es entonces la máxima tensión
critica teórica
b
τth = f racG2π,
a
(3)
Como b ≈ a, la resistencia teórica de corte es una considerable fracción del modulo
de elasticidad. Usando expresiones mas realistas para la fuerza como una función del campo
de desplazamiento, se obtienen valores teóricos de τth ≈ G/30. De todas formas estas aproximaciones muestran que τth es de algunos ordenes de magnitud mayor que los valores obtenidos
en mediciones reales. Esta llamativa diferencia entre la predicción y los valores experimentales
12
fueron explicados y asociados a la presencia de dislocaciones por Orowan, Polanyi y Taylor
en 1934. Luego de aquel entonces fue posible producir cristales en forma de bras de pequeño
diámetro (llamados W hiskers) los cuales poseen un alto grado de perfección en su estructura
cristalina. Estos materiales pueden llegar a fabricarse libres de dislocaciones y su resistencia es
muy cercana al valor teórico. Otra evidencia la cual contribuyó apreciablemente a la aceptación
(a)
(b)
Figura 9: (a) Modelo esquemático de una dislocación de borde DC en un red cúbica simple formada por el plano extra de
átomos ABCD. (b) Representación de una dislocación del tipo helicoidal.
universal de la existencia de dislocaciones en cristales, fue la reconciliación de la teoría clásica
de crecimiento en cristales con las observaciones experimentales. Si consideramos un cristal
perfecto con facetas irregulares que crecen en un vapor sobresaturado. Para un grado bajo de
13
Figura 10: Esquema que de una dislocación mixta en un cristal. La línea de dislocación AB es del tipo helicoidal pura cuando
entra en el cristal a la izquierda y del tipo arista o borde pura cuando deja el cristal.
sobresaturación, el crecimiento ocurre por la deposición de átomos sobre las regiones imperfectas o irregulares del cristal. La deposición preferencial en las regiones imperfectas resulta en
la formación de caras más perfecta que consiste en arreglos de planos de máxima capacidad o
densidad de átomos. Además del crecimiento luego se requiere la nucleación de nuevas capas
de átomos sobre una supercie suave. Este es un proceso mucho mas dicultoso, y la teoría de
nucleación predice que para que el crecimiento ocurra se requiere un grado de sobresaturación
de aproximadamente un 50 %. Esta predicción es muy dispar a algunas observaciones experimentales muestran que el crecimiento ocurre a una sobresaturación de 1 %. La dicultad fue
luego resuelta cuando se demostró que la presencia de dislocaciones en el cristal durante el crecimiento genera escalones sobre las caras del cristal los cuales no se eliminan por la deposición
preferencial, como en un cristal perfecto. Estos escalones proveen sitios para la deposición y así
eliminar la dicultad para el proceso de nucleación. Para que se produzca deformación plástica
en los cristales metálicos grandes a baja tensión de cizalladura, es necesaria una alta densidad
de dislocaciones. Un gran numero de estas (≈ 106 cm/cm3 ) se forman durante la solidicación
del metal, pero se generan muchas mas durante la deformación del metal; debido a esto, un
metal severamente deformado puede alcanzar un densidad de hasta (1012 cm/cm3 ).
2.3.1.
Geometría de las dislocaciones.
En este apartado haremos una descripción de la geometría básica de una dislocación
tipo tornillo o helicoidal y una dislocación de borde o arista. Estos términos provienen del ingles
screw y edge respectivamente. Consideremos una red cristalina cúbica simple, por conveniencia
asumimos que los enlaces pueden ser representados por muelles exibles entre átomos vecinos.
Hay que destacar que el enlazamiento en los sólidos reales es mas complejo y, de hecho, la
naturaleza de los enlaces determina la disposición de los átomos alrededor de una dislocación.
14
En la Figura (9a) vemos que la disposición de una dislocación de borde puede ser simulada
suponiendo que los enlaces sobre la supercie ABCD son rotos y las supercies del cristal a
ambos lados del plano son separadas y un plano extra de átomos es disertado en la ranura.
La deexión y distorsión de los enlaces decrece cuando incrementamos la distancia desde la
línea de dislocación. Esta línea DC es llamada dislocación de borde. La disposición de átomos
alrededor de una dislocación del tipo helicoidal se ve claramente en la Figura (9b). La dislocación helicoidal se forma a partir de un cristal perfecto aplicando esfuerzos cortantes hacia
arriba y hacia abajo a los lados del plano que rompe los enlaces entre átomos. La región distorsionada del cristal no es bien denida y tiene cuanto menos varios átomos de de diámetro.
Esta cuestión la veremos en los apartados siguientes. Con frecuencia los cristales exhiben mezcla de las dislocaciones anteriores. Su vector de Burgers, concepto que introduciremos en el
siguiente apartado, no es ni perpendicular ni paralelo a la línea de dislocación, pero mantiene
una orientación ja en el espacio. La estructura atómica local en torno a la dislocación mixta
es difícil de visualizar, pero el vector de Burgers proporciona una descripción conveniente y
sencilla. Una representación de este tipo de dislocación se muestra en la Figura (10).
2.3.2.
Vector y circuito de Burgers.
La denición mas utilizada de una dislocación es dada en términos del circuito de
Burgers. Un circuito de Burgers es una trayectoria cerrada tomada en un cristal que contiene
dislocaciones, la cual se hace de átomo a átomo. Tal trayectoria es ilustrada en la Figura
(11a), es decir M N OP Q. Si la misma trayectoria átomo a átomo se hace en un cristal libre
de dislocaciones, Figura (11b), y la trayectoria no es cerrada, luego el primer circuito, Figura
(11a), contiene una o mas dislocaciones. El vector requerido para completar o cerrar el circuito
es llamado vector de burgers. Cuando el circuito de Burgers es dibujado alrededor de una
(a)
(b)
Figura 11: (a) Circuito de Burgers alrededor de una dislocación tipo borde perpendicular al folio. (b) El mismo circuito de
Burgers en un cristal perfecto libre de defectos. El error de cierre es el vector de Burgers b.
dislocación tipo tornillo (Figura (9b)), nuevamente con un circuito cerrado en un cristal que
contiene la dislocación, el vector de Burgers QM es paralelo a la línea de dislocación. Esto
conduce a dos reglas importantes,
a) El vector de Burgers de una dislocación de borde es normal a la línea de la dislocación.
15
Figura 12: Tres dislocaciones formando un nodo.
b) El vector de burgers de una dislocación helicoidal o de tornillo es paralelo a la línea de
la dislocación.
De todas formas como de se ve en la Figura (10) la dislocación generalmente es una mezcla de los dos tipos, y su vector de Burgers forma un ángulo arbitrario con la línea de la
dislocación. Aun así, el vector de Burgers de una sola dislocación se mantiene jo en longitud
y dirección, y es independiente de la posición y orientación de la línea de dislocación.
Los vectores de Buergers son los vectores mas cortos de traslación de la red entre dos
puntos en la red. Una dislocación La cual tenga asociada un vector de Burgers es conocida
como dislocación perfecta o dislocación de unidad. El vector de Buerges generalmente se describe en función al igual que las direcciones dentro de un deslizamiento. Por ejemplo, para
una estructura cúbica centrada en el cuerpo si consideramos una terna ortogonal con origen
en el átomo central y sus ejes perpendiculares a tres de sus caras con un vértice en común, √la
notación usada para el vector de Burgers es b = 21 [111]. Su modulo o magnitud será b = a 2 3
siendo a el parámetro de la red (la longitud de sus lados). Si consideramos la Figura (12) vemos
que en el nodo la suma de los vectores de Burgers debe ser nula, esto es b1 + b2 + b3 = 0, o
mas generalmente
n
X
bi = 0.
1
16
(4)