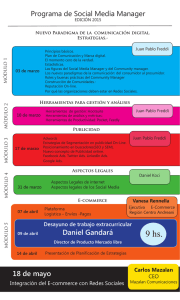
Movimiento Browniano a partir de la Dualidad Norma/Gravedad

Movimiento Browniano a partir de la
Dualidad Norma/Gravedad
Alberto Güijosa
Departamento de Física de Altas Energías
Instituto de Ciencias Nucleares, UNAM
Mensaje Principal
En el contexto de la dualidad
norma/gravedad,
¡¡Hawking = Brown!!
Quark en el Plasma

Quark pesado en plasma
SYM N  4
D7-branas
z  zm
z  zh
desde z  z hasta z  z
 Cuerda
sobre brana negra en AdS
m
h
Quark en el Plasma

Quark pesado en plasma
SYM N  4
D7-branas
z  zm
z  zh
desde z  z hasta z  z
 Cuerda
sobre brana negra en AdS
m
h
Plan
•
•
•
•
T>0 con tiempo real: Schwinger-Keldysh
Schwinger-Keldysh con AdS/CFT
Movimiento Browniano y Ec. de Langevin
Movimiento Browniano a partir de AdS/CFT
Basado en:
Herzog & Son, hep-th/0212072
Son & Teaney, arXiv:0901.2338
de Boer, Hubeny, Rangamani & Shigemori,arXiv:0812.5112
Giecold, Iancu & Mueller, arXiv:0903.1840
Schwinger-Keldysh
Conocemos conexión cuantización canónica vs. funcional
f e
 iH ( t f ti )
 ( t f )  f
i 

 ( ti ) 
que tras rotación de Wick
i  dt  d 3 x L

D ( x , t ) e
i
t  i implica que

 H ( f  i )
 
 D ( x)  e
 
 ( i )  (
H

Z( )  Tr e 
con
  d  d 3 x LE

D ( x , ) e
f
)
   f  i
(t f  ti  i )
Schwinger-Keldysh
Por otro lado, funcional generatriz involucra tiempo real
i  d 4 x L  i  dt  d 3 x J ( x ) ( x )


 T  ( x1 ) ( xn )  

D ( x) e

i J ( x1 ) i J ( xn )
t
ti
ti  i
tf
Schwinger-Keldysh
Entonces, para funciones de correlación a temperatura finita,
Tr T  ( x1 ) ( xn ) e
 H
i  d 4 x L  i  dt  d 3 x J ( x ) ( x )


 

D ( x) e

i J ( x1 ) i J ( xn )
t
ti
ti  i
ti  i
tf
t f  i
Resultado NO depende de 
Schwinger-Keldysh
Más en detalle, insertamos fuentes en AMBOS segmentos,
tf
 tf

3
3
exp i  dt  d x 1 ( x) J1 ( x) i  dt  d x 2 ( x) J 2 ( x) 
 ti

ti

1 ( x)   (t , x )
ti
ti  i
ti  i
t
tf
 t  i
2 ( x)   (t  i , x ) f
Schwinger-Keldysh
y podemos entonces calcular propagador de S-K
1  2 ln Z [ J1 , J 2 ]
iGcd ( x  y )  2
, c, d  1, 2
i  J c ( x) J d ( x)
qué está relacionado p.ej. con propagador retardado
G R (k )   d 4 x eik x ( x)  ( x),  (0) 

G A (k )   d 4 x eik x ( x)  (0),  ( x)   G R* (k )

Schwinger-Keldysh



Im G R (k )
a través de G11 (k )  Re GR (k )  i coth
2
 (   )
2
ie
 (k )
G12 (k ) 
Im
G
R
 
1 e

2
ie
 (k )
G 21 (k ) 
Im
G
R
1  e 



G22 (k )   Re GR (k )  i coth
Im G R (k )
2
En AdS/CFT, consideramos funciones de correlación NO de
los campos básicos de SYM N  4, sino de operadores
invariantes de norma (p.ej. Tr F 2 , T ,  )
S-K con AdS/CFT

SYM SU ( Nc ) N  4
Cuerdas IIB en SchwAdS5 ( R, zh )
a temp. finita T  TH  1/  zh

Plasma de gluones
(+ escalares y
fermiones adjuntos)
z0

x
z
z  zh
Brana negra en AdS

2
R
dz

4
 
ds 2      1  zz 4 dt 2  dx 2 
4

h
z
z
  
1  z4
h

2
 
 




S-K con AdS/CFT

SYM SU ( Nc ) N  4
Cuerdas IIB en SchwAdS5 ( R, zh )
a temp. finita T  TH  1/  zh

h( x, z  0)  J ( x)
h( x, z )
Funciones de correlación caso euclideano a T=0
[Gubser,Klebanov,Polyakov; Witten]
Receta para GR ( x  y) propuesta por
[Son,Starinets]
z
S-K con AdS/CFT
Para reproducir S-K, necesitamos diagrama de Penrose
completo para SchwAdS:
z  zh
z0
z  zh
S-K con AdS/CFT
Para reproducir S-K, necesitamos diagrama de Penrose
completo para SchwAdS:
t 
t 0
t  
S-K con AdS/CFT
Para reproducir S-K, necesitamos diagrama de Penrose
completo para SchwAdS:
t '  
t 
t'0
t'
t  
S-K con AdS/CFT
Para reproducir S-K, necesitamos diagrama de Penrose
completo para SchwAdS:
t '  
SYM
N 4
t'
t 
SYM N
4
t  
S-K con AdS/CFT
Receta para funciones de correlación S-K
t '  
h( x, z '  0)  J 2 ( x)
t'
[Herzog,Son;
Son,Teaney]
t 
h( x, z  0)  J1 ( x)
t  
Langevin a partir de S-K
Consideremos ahora partícula NR acoplada a baño térmico
Z

Dx
(
t
)
Dx
(
t
)
e
2
 1



i dt1 M 0 x12  i dt2 M 0 x22  i dt1 F1x1  i dt2 F2 x2
Si partícula es pesada (fuerza pequeña), esto es aprox.
Z   Dx1 (t ) Dx2 (t ) e 


i dt1 M 0 x12  i dt2 M 0 x22  12 dtdt ' xc (t ) Fc (t ) Fd (t ') xd (t ')
Z   Dx1 (t ) Dx2 (t ) e 


i dt1 M 0 x12  i dt2 M 0 x22  12 dtdt ' xc ( t ) Gcd ( t ,t ') xd ( t ')
Langevin a partir de S-K
Reescrito en términos de “formalismo ra”
x1  x2
F1  F2
xr 
, xa  x1  x2 , Fr 
, Fa  F1  F2 ,
2
2
Z   Dxr (t ) Dxa (t ) exp  i  dt M 0 xa xr 
exp    dtdt ' xa (t )iGR (t , t ') xr (t ')  12  dtdt ' xa (t )Gsim (t , t ') xa (t ') 
donde
i
iGR  G11  G22  G21  G12  ,
2
i
Gsim  G11  G22  G21  G12  (  0)
4
Langevin a partir de S-K
En términos de transformada de Fourier xr,a ( )
 d

Z   Dxr ( ) Dxa ( ) exp  i 
xa  M 0 2  G R xr 
 2

 1 d 



exp   2 
xa Gsim xa 
2




Como último truco, usamos
 1 d 
exp   2 
xa Gsim xa
2

 

d

d



 ( ) exp i



D

x



a


 

2 Gsim 
 2
Langevin a partir de S-K
para obtener
 

d


Z   Dxr ( ) Dxa ( ) D ( ) exp   12 
 
2

G
sim 

 d

2





exp  i 
xa  M 0 xr  GR xr   
 2

 

d


Z   Dxr ( ) D ( ) exp   12 


2

Gsim 

  M  2 x  G x  


0
r

R r

Langevin a partir de S-K
es decir, tenemos trayectorias clásicas con fuerza aleatoria
M 0 2  G R  xr  ,
   G

sim
M 0 xr   dt ' GR (t , t ') xr (t ')   (t ),
 (t ) (t ')  Gsim (t , t ')
 

d


Z   Dxr ( ) D ( ) exp   12 


2

Gsim 

  M  2 x  G x  

0
r
R r

Langevin a partir de S-K
es decir, tenemos trayectorias clásicas con fuerza aleatoria
M 0 2  G R  xr  ,
M 0 xr   dt ' GR (t , t ') xr (t ')   (t ),
fricción no local
   G

sim
 (t ) (t ')  Gsim (t , t ')
ruido de color
Ec. de Langevin generalizada
Langevin a partir de S-K
es decir, tenemos trayectorias clásicas con fuerza aleatoria
M 0 2  G R  xr  ,
M 0 xr   dt ' GR (t , t ') xr (t ')   (t ),
A bajas frecuencias
   G

sim
 (t ) (t ')  Gsim (t , t ')
G R ()  i  M  2 , G sim  2T 
 M 0  M  xr (t )   xr (t )   (t ),  (t ) (t ')
fricción local ruido blanco
Ec. de Langevin original
 2T  (t  t ')
Langevin a partir de Hawking
Pequeñas fluctuaciones (“modos cuasinormales”) por encima
de cuerda estática en SchwAdS completo:
t '  
t 
X ref (t , z)  0
x2 (t )
t'
x1 (t )
t  
Langevin a partir de Hawking
Función de partición para cuerda (c/acción cuadratizada)
(2)
(2)

Z   Dx1 (t ) Dx1 (t , z) Dx2 (t ) Dx2 (t , z)exp iS NG,1  iS NG,2 
Integrando sobre encaje en el bulto (aprox. semiclásica)
se obtiene [Son,Teaney]
 d

2

Z   Dxr ( ) Dxa ( ) exp  i 
xa  M 0  GR xr 
 2


 
 1 d 

exp   2 
xa Gsim xa  ,
 M 0 

2
2 zm 





que como vimos da lugar a ec. generalizada de Langevin
Langevin a partir de Hawking
M 0 xr   dt ' GR (t , t ') xr (t ')   (t ),  (t ) (t ')  Gsim (t , t ')
 ()  i  M  2 , G  2T 
A bajas frecuencias G
R
sim
 M 0  M  xr (t )   xr (t )   (t ),  (t ) (t ')
con
T
M  
2
 2
  T
2
 2T  (t  t ')
[Herzog,Karch,Kovtun,Kozcaz,Yaffe]
[Herzog,Karch,Kovtun,Kozcaz,Yaffe;
Gubser;
Casalderrey-Solana,Teaney]
Langevin a partir de Hawking
La conexión con radiación de Hawking se da través de
elección de c.b. en horizonte (térmicas)
t '  
t 
x2 (t )
x1 (t )
t'
t  
Langevin a partir de Hawking
Posible deducir mov. Browniano (ec.Langevin generalizada) a
partir de números de ocupación térmicos para fluctuaciones
en hoja de mundo [de Boer,Hubeny,Rangamani,Shigemori]
t '  
t 
x2 (t )
x1 (t )
t'
t  
Langevin a partir de Hawking
Además, si solo integramos grados de libertad de cuerda
dentro de “horizonte estirado”…
t 
t '  
z  zh
x2 (t )
t'
z  zh (1   ) x1 (t )
t  
Langevin a partir de Hawking
Además, si solo integramos grados de libertad de cuerda
dentro de “horizonte estirado”…
… se encuentra ec. de mov. estocástica para extremo de la
cuerda en horizonte estirado [Son,Teaney]
 z xr (t , ze )   xr (t )   e (t ),
 e (t ) e (t ')  2T  (t  t ')
La ec. de mov. clásica de cuerda hace que estas
fluctuaciones se propaguen hasta el extremo en z  zm ,
reproduciendo resultado anterior
Extensiones
Posible generalizar análisis a pequeñas fluctuaciones
alrededor de cuerda dual a quark con v=cte.
[Giecold,Iancu,Mueller]
Ese caso es más interesante, porque horizonte en
espaciotiempo z  zh NO coincide con horizonte en
hoja de mundo z  zh (1  v 2 )1/4
Radiación de Hawking relevante proviene de horizonte
en hoja de mundo (se observa clara anisotropía
entre direcciones paralela y perpendiculares a
velocidad)
Incluso a T=0 existe horizonte en hoja de mundo
[Chernicoff,AG]
(cuando quark se acelera)
Queremos explorar fluctuaciones asociadas (cuánticas,
NO térmicas)…