Sección de trabajo2 parte 2

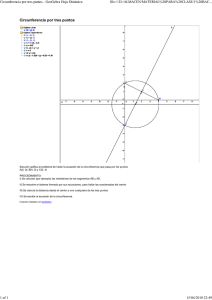
¡Hay un problema interesante
que quisiera saber!...
¿Cuál es la mínima cantidad de
puntos que determinan una curva
¡Para darte la respuesta voy
a citar los siguientes
ejemplos!...
Sabemos que por un punto
pueden pasar una infinidad
de rectas, en cambio, dados
dos puntos, solo hay una
recta que pasa por ambos,
en el caso de la circunferencia,
por uno y por dos puntos
pueden pasar una infinidad
de circunferencias, en
cambio, por tres puntos no
alineados sólo puede
pasar una circunferencia
ya que tres puntos
determinan un
triángulo.
¡Recuerda! Que centro de la circunferencia circunscrita a un triángulo es el
punto donde se cortan las mediatrices del triángulo, este punto se llama circun centro.
Sabemos que las tresmediatrices se cortan en un punto, así que basta
encontrar dos de ellas y calcular el punto de intersección.
¡Veamos!
un Ejemplo.
1.- Encontrar la circunferencia que pasa por los
puntos A(2 , 1), B(- 4 , 3) y C(- 6 , 5). Debemos encontrar
dos de las mediatrices del triángulo ABC. Calcularemos
cada una de ellas por métodos distintos.
104
109
Debemos encontrar dos de lasmediatrices del triángulo ABC. Calcularemos
cada una de ellas por métodos distintos.
M
C
B
A
El empleo de las letras fue introducido,
o por lo menos generalizado, en álgebra
por Francisco Viéte, Este autor utilizaba
las consonantes para representar las
cantidades conocidas y las vocales para
representar las cantidades desconocidas.
Circunferencia que pasa por tres puntos.
Tres puntos:
Mediatriz de AB:
Encontramos el punto medio P, del segmentoAB
P
2 - 4
2
, 1 + 3
2
=
( - 1 , 2)
Encontramos la pendiente, m, del segmento AB
m = 3 - 1 = 2 = - 1
-4-2
- 6
3
Entonces, la mediatriz pasa por P y tiene pendiente - 1 = 3
3
y - 2 = 3(x + 1)
es decir,
y = 3x + 5
mediatriz de AC
Encontramos los puntos (x , y) que equidisten de A y C, es decir, (x , y) debe
satisfacer.
d(x , y) ,A) = d((x , y) , C)
sustituyendo las coordenadas de los puntos en la fórmula de la distancia entre dos
puntos obtenemos.
2
(x - 2)2 + (y - 1)
=
2
(x + 6) + (y - 5)
2
105
110
Elevamos al cuadrado ambos lados de la ecuación y efectuamos las
operaciones para obtener:
y = 2x + 7
Ya que tenemos dosmediatrices, las resolvemos simultánea mente para
encontrar su intersección. Como en ambas tenemos despejada la y lo más fácil es
resolverlos por igualación:
3x + 5 = 2x + 7
de donde obtenemos:
x = 2
Sustituyendo este valor en cualquiera de las dos mediatrices encontramos
el valor de:
x = 2
Sustituyendo este valor en cualquiera de las dos matrices encontramos el
valor de:
y = 11
Así que el circun centro es:
M (2 , 11)
El radio de la circunferencia es la distancia del circun centro a cualquiera de
los puntos A , B o C
r = d(M,A) =
2
(2 - 2) + (11 - 1)
2
= 10
Así que la ecuación de la circunferencia que pasa por A , B y C es la circunferencia
con centro en M y radio r:
(x - 2)2 + (y - 11)2 = 100
o en la forma general es:
x + y - 4x - 22y + 25 = 0
2
2
111
106
CIRCUNFERENCIA:
Un satélite espía, fotografía una base militar enemiga de producción de armas
químicas. La base militar comprende de 3 galpones ubicados en las siguientes
coordenadas: P1 (- 3 , 9); P2 (- 4 , 6) y P3 (- 6 , 8), medidas de la base militar aliada
como muestra de la figura. Un bombardero aleado es enviado a destruir los 3 galpones
GALPONhallar
1
enemigos, el cual lleva una sola bomba de alto poder. se desea
la coordenada
donde debe lanzar la bomba para que el impacto en los tres galpones se d e igual
magnitud, y la ecuación de la circunferencia que pasa por las tres coordenadas, para
verificar que otras zonas son afectadas con la misma magnitud (de explosión de la bomba)
Solución:
Buscamos el punto donde debe caer
11
la bomba, es decir el circun centro de la
circunferencia que se forma al unir las tres
coordenadas (para que queden afectadas
GALPON 3
P3
de igual forma).
GALPON 1
P1
10
9
8
7
GALPON 3
6
P2
5
Debemos hallar también la circunferencia
4
LAGO KING
que pasa por las tres coordenadas P1 , P2 , P3 :
2
Comenzaremos hallando lasmediatrices del
triángulo
P1 , P2 , P3 :
3
1
-6 -5 -4
-3 -2 -1
1 2 3 4 5 6 7 8
MEDIATRIZ DE P2P3:
Buscamos el puntomediodelsegmento P2 P3.
P -4 - 6
, 6 + 8 = ( - 5 , 7)
2
2
Encontramos la pendiente, m, del segmento P2 P3.
6 - 8
-2
m =
=
= -1
- 4 -(-6)
2
La mediatriz que pasa por P, tiene pendiente -
1
= 1
m
es decir la ecuación de
la mediatriz es: y - 7 = 1 (x - (-5))
y - 7 = x + 5
y = x + 12
108
Mediatriz de P1 P3: (otra forma de hallar lamediatriz)
Buscamos los puntos (x , y) que equidistan de P1 y P3, es decir, (x , y) debe
satisfacer:
d( (x , y), P1) = d( (x , y), P3 )
Sustituyendo las coordenadas de los puntos P1 y P3 en la ecuación de la distancia
entre dos puntos obtenemos:
2
2
(x - (-3)) + (y - 9)
2
=
(x - (- 6)) + (y - 8)
2
Elevando al cuadrado a ambos lados de la ecuación.
2
2
2
(x + 3) + (y - 9) = (x + 6) + (y - 8)
2
x2 + 6x + 9 y2 - 18y + 81 = x2 + 12x + 36 + y2 - 16y + 64
- 18y + 16y = - 6x + 12x - 9 - 81 + 36 + 64
- 2y = 6x + 10
y = - 3x - 5
Con las dos mediatrices anteriores hallamos su intersección para hallar
así finalmente el punto donde caer la bomba, es decir, el circun centro del
triángulo.
y = - 3x - 5
x + 12 = - 3x - 5
x + 3x = - 5 - 12
4x = - 17
x = - 17
4
= - 4,25
Hallamos la pendiente y
y = - 3x - 5
y = - 3 - 17
4
51
y =
-5
4
y =
-5
31
= 7,75
4
109
por llo tanto la bomba debe caer en la coordenada circun centro.
M - 17 , 31 = M (- 4, 25 ; 7, 75)
4
4
El Radio de la circunferencia es la distancia del circun centro a cualquier
a los 3 puntos (p1 ; p2 ; p3)
- 17 - ( - 3)
4
r = d(19 , p1) =
2
+
31
4
- 9
2
= 1,768
Así la ecuación de la circunferencia que pasa por p1 , p2 , p3
en la
circunferencia con centro en M y Radio r
x +
17
4
2
+
y -
31
4
2
=
25
8
2
2
x + y + 17 x - 31 y + 75 = 0
2
4
110
115