Apuntes - Carlos Pitta

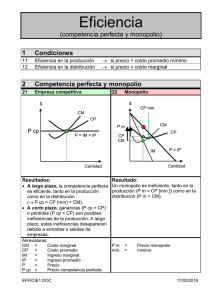
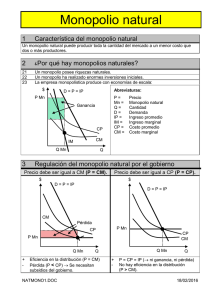
Capítulo 13
MODELOS DE MONOPOLIO
1
Monopolio
• Un monopolio se da cuando existe un
único oferente en un mercado
• Esta firma puede elegir cuánto producir,
y de hecho puede seleccionar producir
cualquier nivel, en cualquier punto de la
curva de demanda
2
Barreras a la Entrada
• La razón por la que existen los
monopolios es que otras firmas pueden
encontrar poco atractivo o imposible
entrar a dicho mercado
• Las barreras a la entrada son la fuente
de todo poder monopólico
– Generalmente existen 2 tipos
• Barreras técnicas
• Barreras legales
3
Barreras Técnicas a la entrada
• La producción de un bien puede exhibir
costos marginales y promedio
decrecientes
– En esta situación, firmas grandes son las
que pueden producir a menor costo
• Algunas firmas pueden ganar sacando a otras
firmas de la industria, bajando sus precios
• Esta situación es llamada monopolio natural
• Una vez que se establece un monopolio, la
entrada de nuevas firmas puede ser muy difícil
4
Barreras Técnicas a la entrada
• Otra barrera técnica a la entrada es el
conocimiento especial de alguna
técnica productiva con menores costos
• También puede ocurrir que la firma sea
la propietaria de un recurso único que
sea esencial para el negocio (de Beers)
5
Barreras Legales a la
Entrada
• Muchos monopolios puros son creados
por ley
– Con una patente, la tecnología básica para
la producción es asignada a una sola firma
– Los gobiernos pueden premiar a las firmas
con franquicias exclusivas para servir un
determinado mercado
6
Creación de Barreras
• Algunas barreras a la entrada son el resultado
de acciones tomadas por la firma
– Investigación y desarrollo de nuevos productos o
tecnologías
– Compra de recursos únicos
– Cabildeo político para ganar poder monopólico
• Lo intentos por parte de un monopolista por
crear barreras a la entrada pueden general
grandes costos
7
Maximización de Ganancias
• Para maximizar ganancias, un
monopolista escogerá el nivel de
producción tal que su ingreso marginal
sea igual a su costo marginal
– El ingreso marginal es menor que el precio
debido a que el monopolista enfrenta una
curva de demanda con pendiente negativa
• Debe bajar su precio en todas las unidades
vendidas si quiere generar la demanda extra
para la última unidad
8
Maximización de Ganancias
• Dado que IMg = CMg al nivel de
producción que maximiza los beneficios,
y P > IMg para un monopolista, este
establecerá un precio mayor que el
costo marginal
9
Maximización de Ganancias
CMg
Precio
El monopolista maximiza
ganancias en IMg = CMg
CP
P*
C
IMg
Q*
D
La firma cobrará un precio
de P*
El beneficio
extraordinario se
encuentra en el
rectángulo gris
Cantidad
10
La regla de la Inversa de la Elasticidad
• La brecha entre el precio de la firma y su
costo marginal se encuentra relacionado
inversamente a la elasticidad precio de la
demanda que enfrenta:
P  MC
1

P
eQ,P
Donde eQ,P es la elasticidad precio de la
demanda para todo el mercado
11
La regla de la Inversa de la Elasticidad
• Conclusión General sobre los
mecanismos de precios bajo monopolio:
– Un monopolio elegirá operar solamente en
regiones en donde la curva de demanda sea
elástica
• eQ,P < -1
12
Beneficios Monopólicos
• Los beneficios del monopolio serán
positivos siempre que P > AC
• Los beneficios monopolistas
continuarán en el largo plazo debido a
que nuevas entradas no son posibles
– Algunos economistas llaman a lo que el
monopolio gana en el largo plazo rentas
monopólicas
• Es el pago al factor singular que forma la base
13
del monopolio
Beneficios Monopólicos
• El tamaño de los beneficios
monopólicos en el largo plazo
dependerá de la relación entre costos
promedios y la demanda de mercado
para el producto
14
Beneficios Monopólicos
precio
precio
MC
MC
AC
AC
P*=AC
P*
C
MR
Q*
D
MR
cantidad
Beneficios positivos
Q*
Sin beneficios
D
cantidad
15
Curva de Oferta Monopólica
• Con una curva de demanda de mercado
fija, la curva de oferta para un
monopolista será únicamente un punto
– Aquella combinación precio-producto en
donde MR = MC
• Si la curva de demanda cambia, la curva
de ingreso marginal cambia y se elige un
nuevo nivel de producción maximizadora
del beneficio
16
Monopolio con Demanda Lineal
• Suponga que la demanda por frisbees
es lineal y de la forma
Q = 2,000 - 20P
ó
P = 100 - Q/20
• El costo total para el productor de
frisbee está dado por
C(Q) = 0.05Q2 + 10,000
17
Monopolio con Demanda Lineal
• Para maximizar el beneficio, el
monopolista escoge producir en donde
MR = MC
• Necesitamos encontrar el ingreso total
TR = PQ = 100Q - Q2/20
• Por lo tanto, el ingreso marginal es:
MR = 100 - Q/10
Mientras que el costo marginal es:
MC = 0.01Q
18
Monopolio con Demanda Lineal
• Así, MR = MC en
100 - Q/10 = 0.01Q
Q* = 500
P* = 75
• Y, en dicho nivel de producción,
C(Q) = 0.05(500)2 + 10,000 = 22,500
AC = 22,500/500 = 45
 = (P* - AC)Q = (75 - 45)500 = 15,000
19
Monopolio con Demanda Lineal
• Para verificar la regla de la inversa de la
elasticidad, calculamos la elasticidad de
la demanda en el nivel de producción
que maximiza los beneficios del
monopolista:
eQ,P
Q P
 75 

  20
  3
P Q
 500 
20
Monopolio con Demanda Lineal
• La regla inversa de la elasticidad
establece que:
P  MC
1
1


P
eQ,P 3
• Dado que P* = 75 y MC = 50, esta
relación se verifica
21
Monopolio y la Distribución
de los Recursos
• Para evaluar los electos en la
distribución de recursos de un
monopolio, usaremos como base de
comparación una industria
perfectamente competitiva
– La curva de oferta de largo plazo de la
industria es infinitamente elástica con un
precio igual tanto al costo marginal como
al costo promedio
22
Monopolio y la Distribución
de los Recursos
precio
Si el mercado fuera competitivo, se
produciría Q* y el precio sería P*
Bajo monopolio, la producción será Q** y
el precio subirá a P**
P**
MC=AC
P*
D
MR
Q**
Q*
cantidad
23
Monopolio y la Distribución
de los Recursos
Precio
El excedente del consumidor (EC) cae
El excedente del productor (EP) sube
EC cae más de lo que el EP
sube.
P**
MC=AC
P*
Por lo que hay una
pérdida neta a consecuencia
del monopolio
D
MR
Q**
Q*
Cantidad
24
Pérdida de Bienestar y Elasticidad
• Asuma que el costo marginal (y
promedio) constante para un
monopolista está dado por c y que la
curva de demanda compensada tiene
una elasticidad constante:
Q = Pe
donde e es la elasticidad precio de la
demanda (e < -1)
25
Pérdida de Bienestar y Elasticidad
• El precio competitivo en este mercado
será
Pc = c
mientras que el precio monopólico está
dado por
Pm 
c
1
1
e
26
Pérdida de Bienestar y Elasticidad
• El excedente del consumidor asociado
con cualquier precio (P0) puede ser
calculado como:


P0
P0
EC   Q( P)dP   P dP
e
e 1 
P0e1
P
EC 

e 1 P
e 1
0
27
Pérdida de Bienestar y Elasticidad
• Por lo tanto, bajo competencia perfecta
c e1
ECc  
e 1
y bajo monopolio


 c 


1 1 


ECm    e 
e 1
e 1
28
Pérdida de Bienestar y Elasticidad
• Tomando el cociente de estas dos
medidas de excedente tenemos:


ECm  1 


ECc  1  1 


 e
e 1
• Si e = -2, dicho cociente es ½
– El excedente del consumidor bajo monopolio es la
mitad que el EC bajo competencia perfecta
29
Pérdida de Bienestar y Elasticidad
• Los beneficios monopólicos son:


 c

m  PmQm  cQm  
 c Qm
 1 1



e


e
 c  



    c 
 c 
  

m   e   
 1 1   1 1 
 1 1 

 



e 
e
e


e 1
1

e
30
Pérdida de Bienestar y Elasticidad
• Para encontrar las transferencias de
excedente del consumidor hacia
beneficios monopólicos podemos dividir a
estas últimas por el EC competitivo:


 m  e  1  1 



ECc  e  1  1 


 e
e 1
 e 


1 e 
• Si e = -2, este cociente es ¼
e
31
Monopolio y Calidad del Producto
• El poder de mercado de que disfruta un
monopolio puede ser ejercido en formas
diferentes al precio de sus productos
– Tipo, calidad o diversidad de bienes
• Que un monopolio produzca un bien de
alta o de baja calidad (que un bien que se
produciría bajo competencia perfecta)
dependerá de la demanda y los costos de
la firma.
32
Monopolio y Calidad del Producto
• Suponga que la disposición a pagar de un
consumidor por calidad (X) está dada por
la función inversa de demanda P(Q,X)
donde
P/Q < 0 y P/X > 0
• Si los costos están dados por C(Q,X), el
monopolio escogerá Q y X para
maximizar
 = P(Q,X)Q - C(Q,X)
33
Monopolio y Calidad del Producto
• Las CPO para un máximo son:

P
 P (Q, X )  Q
 CQ  0
Q
Q
– MR = MC para la decisión de producción

P
Q
 CX  0
X
X
– El ingreso marginal de incrementar la calidad
en una unidad será igual al costo marginal de
34
producir tal incremente de la calidad
Monopolio y Calidad del Producto
• El nivel de calidad del producto que será
escogido bajo competencia perfecta es
aquel que maximiza el bienestar social
neto:
Q*
SW   P(Q, X )dQ  C(Q, X )
0
• Maximizando con respecto a X
Q*
SW
  PX (Q, X )dQ  C X  0
0
X
35
Monopolio y Calidad del Producto
• La diferencia entre la elección de calidad
de una industria competitiva y el
monopolista es:
– El monopolista observa la valoración
marginal de una unidad adicional de calidad
asumiendo que Q se encuentra ya en su
nivel que maximiza las ganancias
– La industria competitiva observa el valor
marginal de la calidad promediada a través
de TODOS los niveles de producción.
36
Monopolio y Calidad del Producto
• Aun si un monopolio y una empresa
perfectamente competitiva escogiesen
el mismo nivel de producto, pueden
optar por diferentes niveles de calidad
– Cada uno se preocupa de un margen
diferente en su proceso de toma de
decisiones
37
FIN DE
CLASE
38
Discriminación de Precios
• Un monopolio practica discriminación de
precios si es capaz de vender unidades
idénticas de producto a precios diferentes
• El que dicha estrategia de precios sea factible
o no dependerá de la inhabilidad de los
compradores a practicar arbitraje
– Un intermediario en su búsqueda de ganancias
destruiría cualquier esquema de discriminación de
precios que pudiese existir
• La discriminación de precios es posible si la reventa es
sumamente costosa
39
Discriminación de Precios Perfecta
• Si cada comprador puede ser
identificado de manera separada por el
monopolista, puede ser posible cobrar a
cada uno el precio máximo que está
dispuesto a pagar por el bien
– Discriminación Perfecta o de Primer Grado
• Extrae todo el excedente del consumidor
• No hay pérdida neta
40
Discriminación de Precios Perfecta
precio
Bajo discriminación de precios perfecta, el
monopolista cobra un precio diferente a cada
comprador
El primer comprador paga P1 por Q1
P1
El segundo comprador paga P2 por Q2-Q1
P2
MC
D
Y el monopolista continua
de esta forma hasta que
cobrar el precio máximo al
consumidor marginal
cantidad
Q1 Q2
41
Discriminación de Precios Perfecta
• Recuerde el ejemplo del productor de
frisbees
• Si este monopolista deseara practicar
discriminación de precios perfecta,
querrá producir la cantidad por la cual el
comprador marginal paga un precio
exactamente igual a su costo marginal
42
Discriminación de Precios Perfecta
• Por lo tanto,
P = 100 - Q/20 = MC = 0.1Q
Q* = 666
• Los Ingreso y costos totales serán:
IT  
Q*
0
2 666
Q
P(Q)dQ  100Q 
40
 55,511
0
c(Q)  0.05Q 2  10,000  32,178
• Las ganancias son mucho mayores
(23,333 > 15,000) que cuando MR=MC
43
Separación de Mercados
• La discriminación de precios perfecta requiere
que el monopolista conozca la función de
demanda para cada comprador potencial
• Un requisito menos restrictivo será asumir que el
monopolio puede separar a sus compradores en
unos pocos mercados localizados
– Entonces, puede seguir una política de precios
diferente para cada mercado
– Esto es llamado discriminación de precios de tercer
grado
44
Separación de Mercados
• Todo lo que el monopolista necesita
saber son las elasticidades precio de la
demanda para cada mercado
– Y entonces fija sus precios de acuerdo a la
regla de la inversa de la elasticidad
• Si es costo marginal es el mismo en
todos los mercados, entonces,
1
1
Pi (1  )  Pj (1  )
ei
ej
45
Separación de Mercados
• Esto implica qué:
1
)
ej
Pi

Pj (1  1 )
ei
(1 
• El precio que maximiza las ganancias
será menor en los mercados donde la
demanda es más elástica
46
Separación de Mercados
Si existen dos mercados separados, las ganancias
máximas son logradas poniendo precios distintos en cada
mercado
precio
Al mercado con la
demanda menos elástica
se le cobrará el precio
más alto
P1
D menos
elástica
P2
MC
MC
D
Q en Mercado 1
D
MR
MR
Q1*
0
Q2*
D más
elástica
Q en Mercado 2
47
Discriminación de Precios
de Tercer Grado
• Suponga que las curvas de demanda
en dos mercados separados son
Q1 = 24 – P1 → P1 = 24 –Q1
Q2 = 24 – 2P2 → P2 = 12 – 1/2P2
• Suponga que MC = 6
• La maximización de profits requiere:
MR1 = 24 – 2Q1 = 6 = MR2 = 12 – Q2
48
Discriminación de Precios
de Tercer Grado
• Las cantidades y precios óptimos son:
Q1 = 9
P1 = 15
Q2 = 6
P2 = 9
• Las ganancias del monopolio son:
 = (P1 - 6)Q1 + (P2 - 6)Q2 = 81 + 18 = 99
49
Discriminación de Precios
de Tercer Grado
• El impacto distributivo de esta política
puede ser evaluado al calcular las pérdidas
netas en los dos mercados
– La producción de competencia perfecta
sería18 en el mercado 1 y 12 en el mercado 2
PN1 = 0.5(P1-MC)(18-Q1) = 0.5(15-6)(18-9) = 40.5
PN2 = 0.5(P2-MC)(12-Q2) = 0.5(9-6)(12-6) = 9
50
Discriminación de Precios
de Tercer Grado
• Si este monopolio usara una política de
un solo precio, usaría la función de
demanda
Q = Q1 + Q2 = 48 – 3P
• Su ingreso marginal sería
MR = 16 – 2Q/3
• Y la maximización ocurriría en
Q = 15
P = 11
51
Discriminación de Precios
de Tercer Grado
• La Pérdida Neta es menor con un precio
que con dos: (función lineal, triángulo)
PN = 0.5(P-MC)(30-Q) = 0.5(11-6)(15) = 37.5
52
Tarifas en dos Partes
• Una tarifa lineal en dos partes ocurre cuando
los compradores deben pagar una cuota fija
por el derecho a consumir un bien, y
adicionalmente un precio uniforme por cada
unidad consumida
T(q) = a + pq
• Aquí, el objetivo del monopolista es escoger
a y p para maximizar sus ganancias, dada la
demanda por su producto
53
Tarifas en dos Partes
• Debido a que el precio promedio
pagado por un comprador es
p’ = T/q = a/q + p
esta tarifa solo es factible si aquellos
que pagan precios promedio bajos
(para quienes q es grande) no pueden
revender el bien a aquellos que deben
pagar precios promedio bajos (para
quienes q es pequeña)
54
Tarifas en dos Partes
• Una manera de maximizar los beneficios
será que la firma iguale p = MC y
después fije a igual al excedente del
consumidor de aquel comprador que
menos valora al bien
– Pero este podría no ser el método que
brinde más beneficios
– En general, los esquemas de precio óptimo
dependerán de una gran variedad de
55
factores
Tarifas en dos Partes
• Suponga que hay dos tipos diferentes de
consumidores con funciones de demanda
como siguen:
q1 = 24 - p1
q2 = 24 - 2p2
• Si MC = 6, una manera en que el monopolista
podría implementar una tarifa en dos partes
sería igualar p1 = p2 = MC = 6
q1 = 18
q2 = 12
56
Tarifas en dos Partes
• Con este precio marginal, el comprador
2 obtendrá un excedente de 36
– Este sería el monto máximo de la tarifa de
entrada que podría ser cobrada sin
ocasionar que el consumidor salga del
mercado
• Esto significa que la tarifa en dos partes
sería, en este caso:
T(q) = 36 + 6q
57
Regulación del Monopolio
• Los Monopolios naturales tales como
los servicios públicos, las
comunicaciones y las industrias de
transporte se encuentran altamente
regulados en muchos países
58
Regulación del Monopolio
• Muchos economistas creen que es
importante que los precios de los monopolios
regulados reflejen de manera precisa los
costos marginales de producción
• Establecer una política fuerte de que el
monopolio venda al valor de su costo
marginal causará pérdidas para el monopolio
– Los monopolios naturales muestran costos
promedio decrecientes para muchos niveles de
producción
59
Regulación del Monopolio
Dado que los monopolios naturales muestran
costos decrecientes, MC cae por debajo de AC
precio
Un monopolio no regulado
maximizará en Q1 y P1
P1
C1
C2
AC
P2
MR
Q1
Pero si el ente
regulador fuerza al
monopolio a cobrar P2,
la firma perderá porque
P2 < C2
MC
Q2 D
cantidad
60
Regulación del Monopolio
precio
Suponga que la comisión reguladora permite al
monopolio cobrar P1 a algunos compradores
Otros compradores podrán pagar el precio
menor de P2
Las ganancias sobre las ventas a los
clientes a quienes se les cobra un precio
alto son suficientes para
cubrir las pérdidas sobre las ventas a los
clientes que se les cobró un bajo precio
P1
C1
C2
AC
MC
P2
Q1
Q2 D
cantidad
61
Regulación del Monopolio
• Otro método seguido en muchas situaciones
de regulación es permitir al monopolio cobrar
un precio por arriba de su costo marginal lo
suficiente para concretar una tasa de retorno
“justa” sobre su inversión
– Si esta tasa de retorno es mayor que la que
existiría en un mercado competitivo, habrán
incentivos para usar relativamente más capital
que aquel que en realidad minimizaría los costos
62
Regulación del Monopolio
• Suponga que una compañía de servicios
públicos tiene una función de producción de
la forma:
q = f (k,l)
• La tasa de retorno real del capital se define
cómo:
pf (k, l )  wl
s
k
63
Regulación del Monopolio
• Suponga que s está restringida por la
regulación a ser igual a s0, entonces el
problema de la firma es maximizar su
nivel de ganancias
 = pf (k,l) – wl – vk
sujeto a ésta restricción s = s0
• El langrangeano para este problema es:
L = pf (k,l) – wl – vk + [wl + s0k – pf (k,l)]
64
Regulación del Monopolio
• Si =0, la regulación no es efectiva y el
monopolio se comporta como cualquier
firma maximizadora de beneficios
• Si =1, el Langrangeano se reduce a:
L = (s0 – v)k
lo cual (asumiendo que s0>v), significa
que el monopolio contratará niveles
infinitos de capital – lo que es un
resultado absurdo
65
Regulación del Monopolio
• Por lo tanto, 0<<1 y las condiciones de
primer orden para un máximo son:
L
 pfl  w  (w  pfl )  0
l
L
 pfk  v  (s0  pfk )  0
k
L
 wl  s0  pf (k, l )  0

66
Regulación del Monopolio
• Dado que s0>v y <1, esto significa
qué:
pfk < v
• La firma contratará más capital de lo
que contrataría si no estuviese sujeta a
la regulación
– También logrará una menor productividad
marginal del capital
67
Visión Dinámica del Monopolio
• Muchos economistas han enfatizado el
papel benéfico que las ganancias
monopólicas pueden jugar durante el
proceso de desarrollo económico
– Esas ganancias proveen fondos que pueden
ser invertidos en investigación y desarrollo
– La posibilidad de lograr o mantener una
posición monopólica provee un incentivo
para mantenerse siempre adelante de los
68
competidores
¡Puntos Importantes!
• El nivel de producción más lucrativo
para el monopolista es aquel para el
cual el costo marginal es igual al
ingreso marginal
– En este nivel de producción, los precios
serán mayores que el costo marginal
– La rentabilidad del monopolista
dependerá de la relación entre precios y
costos promedio
69
¡Puntos Importantes!
• En relación a la competencia perfecta,
el monopolio implica una pérdida de
excedente del consumidor para los
compradores
– Parte de ella se transfiere al monopolista,
mientras que otra parte representa una
pérdida neta en bienestar económico
– Esto es un signo de ineficiencia a lo
Pareto
70
¡Puntos Importantes!
• Los monopolios pueden elegir
diferentes niveles de calidad que los
que elegirían las firmas perfectamente
competitivas
• Los monopolistas que producen bienes
durables pueden estar restringidos por
los mercados de bienes usados
71
¡Puntos Importantes!
• Un monopolio puede ser capaz de
incrementar sus ganancias a través de
la discriminación de precios –
cobrando precios diferentes a
diferentes categorías de compradores
– La factibilidad de que el monopolista
practique discriminación de precios
dependerá de su habilidad para prevenir
el arbitraje entre compradores.
72
¡Puntos Importantes!
• Los gobiernos eligen, a menudo,
regular los monopolios naturales
(empresas con costos promedios
decrecientes sobre un amplio rango de
niveles de producción)
– El tipo de mecanismo regulador que se
adopte puede afectar el comportamiento
de la firma sujeta a la regulación
73