Descargar - Matestay Design by Carlos Estay F.

Relaciones: Ejercicios Propuestos
1. Sean A = {a, b, c}, B = {1, 2}, C = {4, 5, 6}.
Prof. Carlos Estay Fuentes.
a) Dé la lista de los elementos de A × B, B × A, A × C.
b) Dé ejemplos de relaciones de A en B y de B en A, con 4 elementos
cada una.
2. Sea R una relación en A = {2, 3, 4, 5} definida por “x e y son primos
relativos”, esto es “el único divisor común de x e y es 1”
i) Escribir R como un conjunto de pares ordenados.
ii) Representar R en un diagrama de coordenadas A × A.
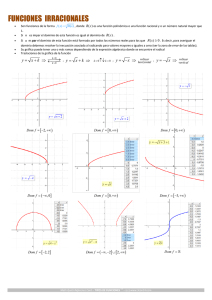
3. Sea R una relación definida en los naturales,
R = {(x, y) : 2x + 3y = 13; x, y ∈ N }
i) Escribir R como un conjunto de pares ordenados.
ii) Hallar el dominio y recorrido de R.
ta
y
iii) Determine R−1
4. Considere las siguientes relaciones
R1 = (a, b) ∈ A 2 / a = b con A = {1,2,3}
R2 = ( x, y ) ∈ N 2 / 2 x + y = 9
R4
R5
2
2
}
at
2
es
}
/ a divide a b
}
M
R3
{
{
= { ( a, b) ∈ A
= { ( x, y ) ∈ A
= { ( a, b) ∈ A
} si
A = {1,2,3,4,5}
/ xy ≥ 0 si A = {− 2,−1,0,1,2,3}
/ a 2 + b 2 > 3 si A = {− 1,0,1,2,3}
}
a) Determine por extensión la relación Ri , i = 1,2,3,4,5
b) Determine dom( Ri ) , rec( Ri )
c) Determine por extensión Ri−1
5. Sea R : N → N una relación definida por:
R = {(n, m)/n + 3m = 12; n, m ∈ N}
a) Exprese R como un conjunto de pares ordenados
b) Hallar Dom R y el Rec R
c) Determine R−1
6. Sean R y S dos relaciones dadas por
R = {(a, 1), (a, 2), (a, 3), (b, 2), (b, 3), (c, 3)}
S = {1, x), (2, x), (3, y)}
Determine: S ◦ R , R−1 ◦ S −1 y S −1 ◦ R−1
Instituto Nacional
1/4
Prof. Carlos Estay Fuentes.
Relaciones: Ejercicios Propuestos
7. Considere las siguientes relaciones definidas en Z
R1 = (a, b) / a = b 2
R2 = (a, b) / a + a 2 = b + b 2
R3 = {( x, y ) / x − y es multiplo de 3}
R4 = { (a, b) / ∃ m ∈ Z tal que a = mb}
−1
Determine por comprensión Ri
R5 = { (a, b) / ∃ k ∈ Z tal que a − b = 2k }
{
{
}
}
8. Sean A = {1, 2, 4}, B = {1, 3, 4}. Sean R = {(1, 3), (1, 4), (4, 4)} una
relación de A en B, S = {(1, 1), (3, 4), (3, 2)} una relación de B en A y
T = ∅ una relación de A en B. Encuentre:
b) Dom(S)
c) Dom(T ).
d) Im(R)
e) Im(S)
f) Im(T ).
g) S ◦ R
h) R ◦ S.
j) Im(S ◦ R).
k) Dom(R ◦ S)
l) Im(R ◦ S).
m) R−1
n) S −1 .
o) IA
p) IB .
q) R−1 ◦ S −1
r) S −1 ◦ R−1 .
u) T −1
w) (R ◦ S) ◦ R
es
at
M
s) (R ◦ S)−1
ta
i) Dom(S ◦ R)
y
a) Dom(R)
t) (S ◦ R)−1 .
v) IB−1 .
x) R ◦ (S ◦ R).
9. Sean A, B, C conjuntos cualesquiera. Demuestre
a) n( A × B) = n( A) ⋅ n( B)
b) A × B = φ ⇔ ( A = φ ∨ B = φ )
c) A ⊆ B ⇒ A × C ⊆ B × C ∀C
d) A × ( B − C ) = A × B − A × C
e) ( A ∩ B) × C = ( A × C ) ∩ ( B × C )
10. Sean A, B y C conjuntos no vacı́os. Demostrar que
a) (A ∩ B) × C = (A × C) ∩ (B × C)
b) (A − B) × C = (A × C) − (B × C)
Instituto Nacional
2/4
Prof. Carlos Estay Fuentes.
Relaciones: Ejercicios Propuestos
11. Sean S, T relaciones de X → Y , pruebe que:
a) (S −1 )−1 = S
b) (S ∩ T )−1 = S −1 ∩ T −1
12. En R se dan las relaciones
R = {(x, y)/y ≥ x2 }
S = {(x, y)/x2 + y 2 ≤ 1}
a) Grafique: R ∩ S, R−1 , S −1 y R−1 ∩ S −1
b) Determine: Dom (R ∩ S), Rec (R ∩ S)
13. Sea R una relación de R en R definida por:
i) R = {(x, y) (−2 ≤ x < 2 ∧ −2 ≤ y ≤ 2) ∨ (−5 < x < −1) ∧
(−1 < y ≤ −3)}
iv) R = {(x, y) : x2 + 2y < 1 }
es
v) R = {(x, y) : x + y ≥ 0 }
ta
iii) R = {(x, y) : x2 + y 2 − 2x ≤ 0 }
y
ii) R = {(x, y) : x2 + y 2 ≤ 16 }
M
at
Representar cada relación en un diagrama de coordenadas R × R y
determine su dominio y recorrido.
14. Sean R ⊆ N × N y S ⊆ N × N dos relaciones definidas por:
R = { (n, m) : n + m = 17 }; S = { (n, m) : n m = 36 }
Encuentre el dominio y recorrido de: R, S y R ∩ S.
15. Sea R ⊆ A × B = {( x, y ) / p ( x, y )} una relación. Demuestre que:
a) dom( R) ⊆ A ; rec( R) ⊆ B
b) ( R −1 ) −1 = R
c) dom( R −1 ) = rec( R) ; rec( R −1 ) = dom( R)
{
16. Sean las relaciones definidas en ℜ : R = {( x, y ) / y = 2 x} , S = ( x, y ) / y = 2 x 3
Determine: a) S o R b) R o S
Instituto Nacional
3/4
}
Prof. Carlos Estay Fuentes.
Relaciones: Ejercicios Propuestos
17. Sean A, B, C, D conjuntos. Demuestre o de contraejemplos para las
siguientes conjeturas.
a) A × (B ∪ C) = (A × B) ∪ (A × C)
b) A × (B ∩ C) = (A × B) ∩ (A × C)
c) (A × B) ∩ (Ac × B) = ∅
d) (A ⊆ B ∧ C ⊆ D) −→ A × C ⊆ B × D
e) A ∪ (B × C) = (A ∪ B) × (A ∪ C)
f) A ∩ (B × C) = (A ∩ B) × (A ∩ C)
g) (A × B) ∩ (C × D) = (A ∩ C) × (B ∩ D)
h) A × (B − C) = A × B − A × C
18. Sean A, B conjuntos y R, S relaciones de A en B. Demuestre:
c) Im(R ∪ S) = Im(R) ∪ Im(S)
at
es
d) Im(R ∩ S) ⊆ Im(R) ∩ Im(S)
ta
b) Dom(R ∩ S) ⊆ Dom(R) ∩ Dom(S)
y
a) Dom(R ∪ S) = Dom(R) ∪ Dom(S)
M
19. Considere las relaciones R ⊆ A × B , S ⊆ B × C
Demuestre que ( S o R ) −1 = R −1 o S −1
20. Se define el par ordenado (a, b) por: (a, b) = {{a}, {a, b}}. Demuestre
que con la definición anterior se tiene:
(a, b) = (c, d) ←→ (a = c ∧ b = d).
21. Sean R una relación de A en B y S una relación de B en C. Muestre
que:
a) Dom(S ◦ R) ⊆ Dom(R).
b) Im(S ◦ R) ⊆ Im(S).
c) Im(R) ⊆ Dom(S) implica Dom(S ◦ R) ⊆ Dom(R).
Instituto Nacional
4/4
Prof. Carlos Estay Fuentes.