CAPITULO Nº2

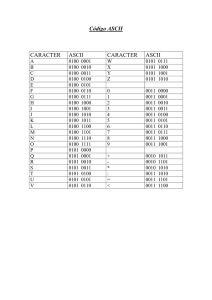
CAPITULO Nº2
CÓDIGOS.
2.1 Definiciones.
Funciones de la codificación:
•
•
•
•
Transmitir en forma fácil, rápida y segura los datos.
Facilitar el procesamiento de datos.
Descubrir y corregir errores.
Mantener en secreto información.
Capacidad : Número de valores diferentes que puede representar un código. Depende del
número de dígitos usados.
Palabra : Representación válida dentro de un código.
Distancia: Número de dígitos diferentes que existen entre dos palabras del código.
Código adyacente: Cuando las palabras vecinas tienen una distancia unitaria.
2.2 Códigos ponderados.
En estos códigos, cada dígito tiene una ponderación establecida.
Palabra : dn-1 dn-2 ... d1 d0
Ponderaciones : pn-1 pn-2 ...p1 p0
El número que representan se calcula como:
N dec= dn-1 * pn-1 + dn-2 * pn-2 +... + d1 * p1 + d0 * p0
Código BCD (Binary Coded Decimal).
Código ponderado en que cada cifra decimal se representa por 4 cifras binarias con
cierta ponderación.
La ponderación más usada es la 8421, en que los dígitos 0 ... 9 son representados
por su respectivo binario de 4 dígitos (en este caso cada dígito puede ser 0 ó 1).
Tabla BCD 8421
Dec
0
1
2
3
4
5
6
7
8
9
d3 (p3=8)
0
0
0
0
0
0
0
0
1
1
d2(p2=4)
0
0
0
0
1
1
1
1
0
0
d1(p1=2)
0
0
1
1
0
0
1
1
0
0
d0(p0=1)
0
1
0
1
0
1
0
1
0
1
Desarrollo
0*8+0*4+0*2+0*1=0
0*8+0*4+0*2+1*1=1
0*8+0*4+1*2+0*1=2
0*8+0*4+1*2+1*1=3
0*8+1*4+0*2+0*1=4
0*8+1*4+0*2+1*1=5
0*8+1*4+1*2+0*1=6
0*8+1*4+1*2+1*1=7
0*8+0*4+0*2+0*1=8
1*8+0*4+0*2+1*1=9
Otras ponderaciones son BCD 2421, BCD1224, BCD 7421.
Decimal
0
1
2
BCD
8421
0000
0001
0010
3
4
5
0011
0100
0101
6
0110
7
0111
8
9
1000
1001
BCD
2421
0000
0001
0010
1000
0011
1001
0101
1011
0110
1100
0111
1101
1110
1111
Se observa que en BCD 2421 no hay representación única.
En BCD 8421 si hay representación única.
2.3 Códigos autocomplementados.
Un código es auto complementado cuando el complemento a la base disminuida de una
palabra es también parte del código.
Recordar que en caso binario se obtiene cambiando el valor de los bits o dígitos.
Decimal
0
1
2
BCD
8421
0000
0001
0010
Exceso
3
0011
0100
0101
3
4
5
0011
0100
0101
0110
0111
1000
6
0110
1001
7
0111
1010
8
9
1000
1001
1011
1100
BCD
2421
0000
0001
0010
1000
0011
1001
0101
1011
0110
1100
0111
1101
1110
1111
Según la tabla anterior se pueden realizar las siguientes observaciones:
•
El código exceso 3 se obtiene sumando 0011 al código BCD 8421.
•
Códigos exceso 3 y BCD 2421 son autocomplementados.
•
Código BCD 8421 no es auto complementado.
2.4 Códigos adyacentes.
2.4.1 Conceptos.
Un código es adyacente cuando las palabras vecinas tienen distancia 1.
Los más utilizados son el código GRAY y el REFLEJADO EXESO 3.
Decimal BCD GRAY Reflejado
8421
Exceso 3
0
0000 0000
0010
1
0001 0001
0110
2
0010 0011
0111
3
0011 0010
0101
4
0100 0110
0100
5
0101 0111
1100
6
0110 0101
1101
7
0111 0100
1111
8
1000 1100
1110
9
1001 1101
1010
2.4.2 Método de transformación de binario(BCD 8421) a gray.
Se utiliza función binaria XOR (Or exclusivo)
0 xor 0 = 0
0 xor 1 = 1
1 xor 0 = 1
1 xor 1 = 0
Cifras iguales resultado 0
Cifras distintas resultado 1
Se parte del dígito binario menos significativo y se aplica la siguiente relación:
gray (i) = bin (i) xor bin (i+1)
Ejemplo: Convertir el binario 1100 a gray.
b3 b2 b1 b0
1 1 0 0
g0 = b0 xor b1 = 0 xor 0 = 0
g1 = b1 xor b2 = 0 xor 1 = 1
g2 = b2 xor b3 = 1 xor 1 = 0
g3 = b3 xor b4 = 1 xor 0 = 1
g3 g2 g1 g0
1 0 1 0
2.4.3 Método de transformación de gray a binario.
•
Método 1
Partiendo del dígito más significativo:
bMS = gMS
b(i + 1)
b(i) = 
b(i + 1)
Con
si g(i) = 0
si g(i) = 1
bMS = Binario más significativo.
gMS = Gray más significativo.
Ejemplo : Transformar a binario el gray 1010gray
•
Gray
:
1
0
1
0
Binario
: 1xxx , 11xx , 110x , 1100
Método 2
Del mismo modo que el anterior, se parte del dígito del dígito más significativo, y se
aplica la siguiente relación:
b MS = g MS



b(i) = b(i + 1) exor g(i)


Ejemplo : Transformar a binario el gray 1010gray
Gray
:
g3 g2 g1 g0
1 0 1 0
b3= g3 = 1
b2= b3 exor g2 = 1 exor 0 = 1
b1= b2 exor g1 = 1 exor 1 = 0
b0 = b1 exor g0 = 0 exor 0 = 0
b3 b2 b1 b0 = 1 x x x
b3 b2 b1 b0 = 1 1 x x
b3 b2 b1 b0 = 1 1 0 x
b3 b2 b1 b0 = 1 1 0 0
2.5 Códigos detectores de error.
2.5.1 Conceptos.
El esquema de comunicación más básico contempla 3 elementos importantes: El
transmisor (Tx), el medio por el que se transmiten los datos y el receptor (Rx).
En el caso de la transmisión de datos, es posible que la palabra transmitida no sea la
misma que la palabra recibida, esto es, se ha producido un error de transmisión, lo cual en
algunos casos se debe a imperfecciones en el medio de transmisión.
Para la transmisión digital (se transmiten palabras binarias), existen técnicas basadas
en la codificación que permiten detectar si ha existido un error de transmisión, es decir,
permiten detectar diferencias en la palabra transmitida y la recibida.
La detección de errores considera que el receptor es capaz de detectar que se ha
producido un error de transmisión, pero no es capaz de saber que dígito binario es el que
está errado, es decir, a través de la detección no se puede conocer la posición del error.
En general, para la detección de errores como para la corrección de ellos, esta última
considera la ubicación de bit errado, es necesario agregar información redundante que sirva
para los propósitos anteriores, es decir, no sólo basta con transmitir la palabra deseada, sino
que además se deben transmitir otros bits.
Cuando el sistema detecta un error, la solución al problema consiste en volver a
transmitir hasta que el error no se produzca.
Las técnicas de detección de errores a estudiar son básicamente tres: El uso del bit
de paridad, los códigos m de n y los códigos m de n ponderados.
2.5.2 Bit de paridad.
Bit de paridad: Es un bit que se agrega a la palabra para verificar la paridad de unos.
Paridad par: El número de unos en la palabra más el bit de paridad deben ser pares.
Paridad impar: El número de unos en la palabra más el bit de paridad deben ser
impares.
Ejemplo: Para el número de 7 bits 1001010 encontrar bit de paridad par e impar.
Paridad bp b6 b5 b4
Par
0
1 1 0
Impar
0
0 1 0
b3 b2 b1 b0
1 0 1 0
1 0 1 0
Según lo anterior, se pueden realizar las siguientes observaciones:
•
Este método es capaz de detectar un número impar de errores.
•
Si existe en la transmisión un número par de errores, la cuenta de paridad
es correcta.
2.5.3 Códigos m de n
Estos códigos mantienen “m” unos en una palabra de n dígitos.
Verificando la cantidad de “1s” en la palabra recibida se observa si ha ocurrido un
error.
Típicamente se utilizan los códigos 2 de 5.
Código 2 de 5 Walking Code.
Decimal
0
1
2
3
4
5
6
7
8
9
Walking Code
00011
00101
00110
01010
01100
10100
11000
01001
10001
10010
2.5.4 Códigos m de n ponderados
Código 2 de 5 ponderado 50-43210 y 10-86420
Dec
0
1
2
3
4
5
6
7
8
9
50-43210
01-00001
01-00010
01-00100
01-01000
01-10000
10-00001
10-00010
10-00100
10-01000
10-10000
10-86420
01-00001
10-00001
01-00010
10-00010
01-00100
10-00100
01-01000
10-01000
01-10000
10-10000
2.6 Códigos correctores de errores.
2.6.1 Conceptos.
La detección de errores considera que el sistema es capaz de darse cuenta que existe
un error. En el caso de la corrección de errores, además de lo anterior, involucra la
capacidad de saber la posición exacta del bit erroneo.
Se presentan a continuación dos método para corregir errores en la transmisión: La
Transmisión en bloque y el Código Hamming.
2.6.2 Transmisión en bloques.
Se transmite un conjunto o bloque de palabras con un código detector de error (bit de
paridad o código m de n).
Junto con transmitir las palabras deseadas, se transmite una palabra de validación de
paridad por columnas.
Ejemplo: Transmitir los dígitos 1, 2, 4, 5, 9 en BCD 8421 con bit de paridad par, con
paridad par por columnas.
Dec bp
1
1
2
1
4
1
5
0
9
0
V
1
b3
0
0
0
0
1
1
b2
0
0
1
1
0
0
b1
0
1
0
0
0
1
b0
1
0
0
1
1
1
Al producirse un error de transmisión se altera la paridad por filas y por columnas.
La intersección de errores de paridad por filas y columnas indican el bit del bloque
que está errado.
Ejemplo de error de transmisión:
Dec bp
1
1
2
1
4
1
5
0
9
0
V
1
b3
0
1
0
0
1
1
b2
0
0
1
1
0
0
b1
0
1
0
0
0
1
b0
1
0
0
1
1
1
error
error
Con este método es posible corregir varios errores.
La cantidad de errores posibles de detectar y además corregir dependerá de la
cantidad par o impar de errores que se produzcan en una fila o columna.
2.5.2 Código Hamming.
Para poder detectar o corregir errores es necesario introducir bits redundantes. Si se
quiere corregir un error, es necesario identificarla posición del error.
En una palabra de “n” bits, “m” bits de datos y “k” dígitos de redundancia se cumple
que:
n=m+k
Con “k” bits de redundancia se pueden direccionar 2k –1 posiciones. Luego debe
cumplirse que
2k -1 ≥ n = m + k
k: Bits de corrección.
n: Bits totales del código.
m: bits de datos en el código.
m
1
2
3
4
5
n
3
5
6
7
9
k
2
3
3
3
4
Hamming propuso ubicar los bits redundantes o de validación en posiciones
potencias de 2 y en las restantes posiciones ubicar los datos.
Bits P de validación
Bits D de datos.
1
P1
2
P2
3
D3
4
P4
5
D5
6
D6
7
D7
8
P8
9
D9
10
D10
11
D11
Cada bit de validación Pi debe producir paridad par (o impar) en determinadas
posiciones según la siguiente tabla:
P1: 1, 3, 5, 7, 9, 11, 13, 17, ...
P2: 2, 3, 6, 7, 10, 11, 14, 15, 18, ...
P4: 4, 5, 6, 7, 12, 13, 14, 15, 20, ...
P8: 8, 9, 10, 11, 12, 13, 14, 15, 24, ...
Ejemplo: Codificar en Hamming el equivalente a 7 decimal en BCD 8421,
utilizando para verificación paridad par.
7(10) = 0 1 1 1 (BCD8421)
4 bits de datos implican 3 bits de redundancia
1 3 5 7
(P1 , 0 , 1 , 1 ) => P1 = 0
2 3 6 7
(P2 , 0 , 1 , 1 ) => P2 = 0
4 5 6 7
(P4, 1 , 1 , 1) => P4 = 1
P1
0
P2
0
D3
0
P4
1
D5
1
D6
1
D7
1
Si existe un error de transmisión, el análisis de la información de los datos
recepcionados indicará la posición del error.
Tx
P1
0
P2
0
D3
0
P4
1
D5
1
P1
0
P2
0
D3
0
P4
1
D5
1
D6
D7
1
D6
D7
1
1
Rx
0
Para obtener la posición del error se revisa la paridad de las posiciones anteriores
incluyendo el bit P correspondiente.
1 3 5 7
( 0 , 0 , 1 , 1 ) => E1 = 0
2 3 6 7
(0 , 0 , 0 , 1 ) => E2 = 1
4 5 6 7
( 1, 1 , 0 , 1 )
=> E4 = 1
La posición del error es la formada por los bits E de la siguiente forma:
E4 E2 E1 = 1 1 02 = 610
En caso de no existir error los valores Ei son todos ceros.
2.7 Códigos alfanuméricos.
Son necesarios códigos alfanuméricos cuando no sólo se desean transmitir números,
sino que caracteres.
Los códigos alfanuméricos más usados son:
ASCII (American Standard Code for Information Interchange).
EBCDIC (Extended BCD Interchange). Usado por IBM.
Para los códigos anteriores, ambos son de 8 bits. En el caso del ASCII el bit más
significativo corresponde al bit de paridad (par o impar).
Tabla de Códigos Ascii y EBCDIC
Carácter
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
0
1
2
3
4
5
6
7
8
9
Espacio
.
(
+
$
*
)
/
,
=
ASCII
100
100
100
100
100
100
100
100
100
100
100
100
100
100
100
101
101
101
101
101
101
101
101
101
101
101
011
011
011
011
011
011
011
011
011
011
010
010
010
010
010
010
010
010
010
010
010
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
0000
1110
1000
1011
0100
1010
1001
1101
1111
1100
1101
EBCDIC
1100
1100
1100
1100
1100
1100
1100
1100
1100
1101
1101
1101
1101
1101
1101
1101
1101
1101
1110
1110
1110
1110
1110
1110
1110
1110
1111
1111
1111
1111
1111
1111
1111
1111
1111
1111
0100
0100
0100
0100
0101
0101
0101
0110
0110
0110
0111
0001
0010
0011
0100
0101
0110
0111
1000
1001
0001
0010
0011
0100
0101
0110
0111
1000
1001
0001
0010
0011
0100
0101
0111
1000
1001
0000
0001
0010
0011
0100
0101
0110
0111
1000
0001
0000
1011
1101
1110
1011
1100
1101
0000
0001
1011
1110