direcciones sobre una superficie

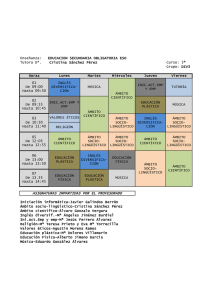
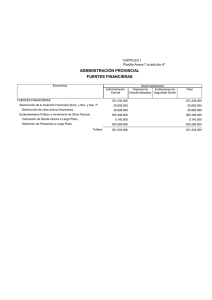
SUPERFICIES-2
Carlos S. Chinea
DIRECCIONES SOBRE UNA
SUPERFICIE
Líneas de curvatura principal. Direcciones
principales.
Nota: las nociones básicas que se manejan en este artículo
(formas fundamentales, curvatura normal, teorema de
Meusnier) pueden ser consultadas en la primera parte,
Superficies_1, en esta misma web
(http://personales.ya.com/casanchi/mat/superficies01.htm).
Sabemos que las direcciones sobre una superficie S en un determinado punto P de
r
la misma, presentan distinta curvatura k , y también, por consiguiente, distinta
r
r
curvatura normal K n , proyección sobre el vector normal N del vector de curvatura
r
k en dicho punto P.
El sentido del vector de curvatura normal puede ser el mismo que el sentido del
vector normal o bien puede ser de sentido contrario, esto es, puede ser la
proyección positiva, negativa o nula,
dependiendo de las dos formas
fundamentales, ya que sabemos que es
Kn =
l du 2 + 2l12 du1 du 2 + l 22 du 22
II
= 11 12
I
g11 du1 + 2 g 12 du1 du 2 + l 22 du 22
r r
Como I siempre es positiva ( I = dr .dr = ds > 0 ) el signo de K n viene determinado
2
por la segunda forma fundamental II. Así, se tienen tres casos posibles:
1) II > 0 → K n > 0. El punto P se llama punto elíptico.
2) II = 0 → K n = 0. El punto P se llama punto parabólico.
3) II < 0 → K n < 0. El punto P se llama punto hiperbólico.
Para poder determinar de qué forma es el contacto con el plano tangente a la
superficie en el punto P, en cada uno de estos tres casos, debemos establecer el
1
SUPERFICIES-2
Carlos S. Chinea
grado de aproximación de la superficie al plano tangente en cada situación. Esto lo
podemos conseguir con el siguiente teorema.
Teorema 06:
Si es T el plano tangente a la superficie S en el punto P y es q un punto de S
infinitamente próximo a P, entonces la distancia de q al plano tangente es igual a la
mitad de II más un infinitésimo de tercer orden:
d ( q, T ) =
Demostración:
1
II + θ 3
2
r
(r − rr ).N = 0 la ecuación
r r
Siendo rp , rq los vectores de posición de ambos puntos y r
p
r r
r 1 2r 1 3r
del plano tangente, es rq = rp + dr + d r + d r + ... , y la distancia del punto q al
2
3!
plano tangente es
r r 1 r r 1 r r
r r r
d (q, T ) = (rq − rp ).N = dr.N + d 2 r .N + d 3 r .N + ... =
2
3!
r r
r r
1 r r
1
= 0 + r11 .N .du12 + r12 .N .du1 du 2 + r22 .N .du 22 + θ 3 = II + θ 3
2
2
(
)
Teorema 07:
1) En un punto elíptico toda la superficie S está a un lado del plano tangente en
dicho punto.
2) En un punto parabólico P se cumple que la dirección en la que II=0 es
asintótica y tiene el mayor contacto posible con el plano tangente.
3) En un punto hiperbólico la superficie corta al plano tangente.
Demostración:
2
SUPERFICIES-2
Carlos S. Chinea
1) Si es II > 0 , la distancia es siempre positiva: d ( q, T ) =
1
II + θ 3 > 0 , y por
2
consiguiente, los puntos de la superficie S se encuentran a un lado del plano
tangente.
2) Si es II = 0 , la distancia es un infinitésimo de orden 3: d ( q, T ) = θ 3 → 0 y la
superficie S está en la mayor proximidad posible al plano tangente T en la
dirección en la que se anula la segunda forma fundamental. (dirección
asintótica).
3) Si es II < 0 , la segunda forma fundamental es indefinida y la superficie no
está totalmente del mismo lado del plano tangente, es decir, lo corta.
El ejemplo más clásico de superficie en la que se distinguen los tres tipos de puntos
es el toro.
1) Los puntos exteriores de la superficie,
engendrados al rotar ABC, son elípticos.
2) Los puntos de las circunferencias que
definen tanto el movimiento del punto A
como el movimiento del punto C, son
parabólicos.
3) Los puntos interiores, engendrados al
rotar el arco ADC, son hiperbólicos.
De lo anterior inferimos que en cada punto P de la superficie pueden haber
direcciones en donde se anula la curvatura normal (direcciones asintóticas de
puntos parabólicos), direcciones en donde la curvatura normal es positiva (puntos
elípticos) y direcciones en donde la curvatura normal es negativa (puntos
hiperbólicos).
Podemos también tratar de encontrar aquellas direcciones en las que la curvatura
normal presenta valor máximo o valor mínimo (presenta un extremo). Tales
3
SUPERFICIES-2
Carlos S. Chinea
direcciones se llaman principales y las correspondientes curvaturas se denominan
curvaturas principales.
Para encontrar el valor máximo o mínimo de la curvatura normal emplearemos el
cálculo diferencial, derivando e igualando a cero la curvatura normal con respecto a
 du 
2
 .
la variable dirección 
du
 1
Si hacemos x =
du 2
II
en K n =
:
du1
I
K n ( x) =
l11 + 2l12 .x + l 22 .x 2
g11 + 2 g12 .x + g 22 .x 2
Bastará obtener los valores de x para los cuales
(
)
dK n ( x)
= 0.
dx
(
)
dK n ( x) (2l12 + 2l 22 x ) g 11 + 2 g12 x + g 22 x 2 − (2 g12 + 2 g 22 x ) l11 + 2l12 x + l 22 x 2
=
=0⇒
2
dx
g11 + 2 g12 x + g 22 x 2
(
⇒ (l12 + l 22 x ) g 11 + 2 g12 x + g 22 x 2
(
) − (g
12
(
)
)
+ g 22 x ) l11 + 2l12 x + l 22 x 2 = 0
[1]
de lo cual:
l12 + l 22 x
l11 + 2l12 x + l 22 x 2
l + l x + (l12 + l 22 x )x
=
= 11 12
= kp
2
g12 + g 22 x g11 + 2 g12 x + g 22 x
g11 + g12 x + (g12 + g 22 x )x
[2]
ordenando [1] con respecto a las potencias de x:
(l12 g11 − l11 g12 ) + (l22 g11 − l11 g 22 )x + (l22 g12 − l12 g 22 )x 2 = 0
y los valores de x =
du 2
que hacen extrema la curvatura normal son las soluciones
du1
de dicha ecuación de 2º grado:
x1 =
x2 =
l11 g 22 − l22 g11 +
(g11l22 − g 22l11 )2 − 4(g12l22 − g 22l12 )(g11l12 − g12l 11 )
2( g12l22 − g 22l12 )
l11 g 22 − l22 g11 −
(g11l22 − g 22l11 )2 − 4(g12l22 − g 22l12 )(g11l12 − g12l 11 )
2( g12l22 − g 22l12 )
que, por lo demás, cumplen que:
x1 + x2 = −
l22 g11 − l11 g 22
l22 g12 − l12 g 22
x1.x2 =
l12 g11 − l11 g12
l22 g12 − l12 g 22
[3]
4
SUPERFICIES-2
Carlos S. Chinea
Veamos como obtener los valores máximo y mínimo de la curvatura normal
mediante el siguiente teorema.
Teorema 08:
Los valores de las curvaturas principales son las soluciones Kp de la ecuación de
segundo grado
l11 − g 11 k p
l12 − g 12 k p
l12 − g12 k p
=0
l 22 − g 22 k p
Demostración:
De la igualdad [2] y teniendo en cuenta la conocida equivalencia de proporciones:
A C
A A + r.C
= ⇔ =
B D
B B + r.D
r real
se tiene:
l12 + l 22 x
l + l x + (l12 + l 22 x )x
l +l x
l +l x
= 11 12
= k p ⇒ 12 22 = 11 12 = k p
g12 + g 22 x g11 + g12 x + (g 12 + g 22 x )x
g 12 + g 22 x g11 + g12 x
de lo cual:
l12 − g 12 k p + (l 22 − g 22 k p ) x = 0
l11 − g 11 k p + (l12 − g 12 k p ) x = 0
y siendo x =
 l11 − g11 k p

l − g k
12 p
 12
du 2
, podemos escribir
du1
l12 − g12 k p  du1   0 

= 
l 22 − g 22 k p  du 2   0 
de donde, finalmente:
l11 − g 11 k p
l12 − g12 k p
l12 − g 12 k p
l 22 − g 22 k p
=0
[4]
Asimismo podemos obtener la ecuación de las líneas de curvatura principal de la
superficie S en un punto P.
Teorema 09:
Las ecuación de las líneas de curvatura principal viene dada por
(g11l12 − g12 l11 ).du12 + (g11l 22 − g 22 l11 ).du1du 2 + (g 22 l12 − g12 l 22 ).du 22 = 0
Demostración:
De [1]:
(l12 + l 22 x )(g11 + 2 g12 x + g 22 x 2 ) − (g12 + g 22 x )(l11 + 2l12 x + l 22 x 2 ) = 0
⇒
⇒ ( g11l12 − g12 l11 ) + ( g11l 22 − g 22 l11 )x + ( g12 l 22 − g 22 l12 )x 2 = 0
5
SUPERFICIES-2
Carlos S. Chinea
y sustituyendo x =
du 2
:
du1
(g11l12 − g12 l11 ).du12 + (g11l 22 − g 22 l11 ).du1du 2 + (g 22 l12 − g12 l 22 ).du 22 = 0
que puede considerarse el desarrollo del determinante
du 22
g11
− du1 du 2
g12
l11
l12
du 22
g 22 = 0
l 22
Teorema 10:
Las líneas de curvatura son perpendiculares.
Demostración:
du 2
du 2*
, x 2 = * . Las direcciones las determinan los vectores:
Sean x1 =
du1
du1
r r
r
dr = r1 .du1 + r2 .du 2 ,
r
r
r
dr * = r1* .du1* + r2* .du 2*
Veamos que su producto interior es nulo:
r r
r r
r r
r r
r r
dr .dr * = r1 .r1* .du1 .du1* + r1 .r2* .du1 .du 2* + r2 .r1* .du 2 .du1* + r2 .r2* .du 2 .du 2* =
= g11 .du1 .du1* + g12 du1 .du 2* + g12 du 2 .du1* + g 22 du 2 .du 2* =
= g11 .du1 .du1* + g12 (du1 .du 2* + du 2 .du1* ) + g 22 du 2 .du 2* =
= g11 + g12 (
du 2* du 2
du 2 du 2*
+
+
= g11 + g12 ( x1 + x 2 ) + g 22 .x1 .x 2
g
)
.
.
22
du1 du1*
du1* du1
Sustituyendo las expresiones
[3]: x1
+ x2 = −
l 22 g11 − l11 g 22
l 22 g12 − l12 g 22
x1 .x 2 =
l12 g 11 − l11 g12
l 22 g 12 − l12 g 22
Resulta:
 l g −l g
r r
dr .dr = g11 + g12 ( x1 + x 2 ) + g 22 .x1 .x 2 = g11 + g 12  − 22 11 11 22
 l 22 g 12 − l12 g 22

 l g −l g
 + g 22  12 11 11 12

 l 22 g12 − l12 g 22
= g11 (l 22 g12 − l12 g 22 ) + g12 (− l 22 g11 + l11 g 22 ) + g 22 (l12 g11 − l11 g12 ) = 0
y las direcciones principales son, efectivamente, perpendiculares.
6

 =

SUPERFICIES-2
Carlos S. Chinea
Teorema 11:
Si son proporcionales los coeficientes de ambas formas fundamentales, entonces no
hay direcciones principales. Es decir:
lij = c.g ij , i, j = 1,2 ⇒ k n = k1 = k 2 = c
Demostración:
Bastará sustituir en [4]:
l11 − g11 k p
l12 − g12 k p
⇒
l12 − g12 k p
c.g11 − g11 k p
=0⇒
l 22 − g 22 k p
c.g12 − g12 k p
c.g12 − g12 k p
=0⇒
c.g 22 − g 22 k p
g11 (c − k p ) g12 (c − k p )
2 g
= 0 ⇒ (c − k p ) . 11
g12 (c − k p ) g 22 (c − k p )
g12
g12
= 0 ⇒ (c − k p ) 2 = 0 ⇒ k p = c (doble)
g 22
(Estos puntos se denominan puntos umbílicos)
Corolario:
Si
lij = 0, i, j = 1,2 ⇒ k n = k1 = k 2 = 0
Demostración: trivial. (los puntos se dicen umbílicos parabólicos. Todos los puntos
de un plano son umbílicos parabólicos).
Teorema 12:
La condición necesaria y suficiente para que las líneas paramétricas, du1=0 y du2=0,
sean líneas de curvatura es que
g12 = l12 = 0
Demostración:
-
Veamos que es condición necesaria:
Si las líneas paramétricas, du1=0 y du2=0, son líneas de curvatura, esto implica
que son perpendiculares por el teorema 10, luego g 12 = 0 .
Y de ser g 12 l 22 − l12 g 22 = 0 ⇒ l12 = 0
-
Veamos que es condición suficiente:
7
SUPERFICIES-2
Carlos S. Chinea
Sustituyendo en la ecuación de las líneas de curvatura principal:
(g11l12 − g12 l11 ).du12 + (g11l 22 − g 22 l11 ).du1du 2 + (g 22 l12 − g12 l 22 ).du 22 = 0 ⇒
⇒ 0 + ( g11l 22 − g 22 l11 ).du1 du 2 + 0 = 0 ⇒ ( g11l 22 − g 22 l11 ).du1 du 2 = 0 ⇒ du1 = du 2 = 0
Bibliografía:
ABELLANAS, Pedro, “Geometría Básica”, Ediciones Romo, Madrid, 1969
STRUICK, D.J., “Geometría Diferencial clásica”, Aguilar Ediciones, Madrid, 1961
LELONG-FERRAND, Jacqueline, “Geometrie Differentielle”, Masson and Cie., Paris,
1963
CHOQUET-BRUHAT, Yvonne, “Geometrie Differentielle et systemes exterieurs”,
Dunod, París, 1968
CARTAN, Elie, ‘’La theorie des groupes finis et continus et la geometrie differentielle
traitées par le methode du repere mobile’’, Gauthiers-Vilars. París, 1937
Carlos S. Chinea
[email protected]
8