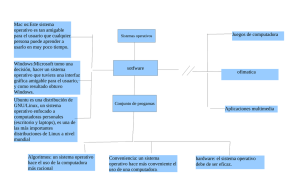
análisis comparativo del uso de memoria en linux y windows

ANÁLISIS COMPARATIVO DEL USO DE MEMORIA EN LINUX Y WINDOWS
Miguel Sánchez de León Peque Antón Kalinov Iliev Estadística, ETSI Industriales, Universidad Politécnica de Madrid
Enero de 2009
ANÁLISIS COMPARATIVO DEL USO DE MEMORIA ENTRE LOS SISTEMAS
OPERATIVOS LINUX Y WINDOWS
1. LA IDEA
1
2. LOS DATOS
2
3. ANÁLISIS
5
3.1
3.2
3.3
Diagnosis
Modelo de estudio
Definición de un nuevo modelo; análisis de resultados
4. CONCLUSIÓN
Anexo: Dónde encontrar el archivo de datos original y el utilizado en el estudio
AGRADECIMIENTOS
REFERENCIAS
5
8
10
18
20
21
21
1. LA IDEA
La nuestra, como muchas otras “grandes ideas”, comenzó en la servilleta de una cafetería.
Debíamos encontrar un tema para nuestro trabajo de estadística y pensábamos en algo actual,
interesante y nuevo. Seguro que a muchos usuarios de Linux la batalla entre el software libre y el
propietario no les parece nada nuevo, pero para aquellos que no sepan muy bien de qué va el asunto
y por qué hemos decidido tratar este tema, daremos una pequeña explicación de lo que es el
fantástico mundo del software libre.
Software libre es como denominamos a una clase de programas no sólo gratuitos, sino
abiertos al público para que éste los revise, modifique y distribuya libremente (eso sí, siempre
ajustándose a unas licencias del software libre que tienen sus características distintivas). De modo
más preciso, se refiere a cuatro libertades que se otorgan a los usuarios del software:
•
•
•
•
la libertad de usar el programa, con cualquier propósito
la libertad de estudiar el funcionamiento del programa y adaptarlo a las necesidades
la libertad de distribuir copias
la libertad de mejorar el programa y hacer públicas las mejoras, de modo que toda la
comunidad se beneficie.
Es todo un fenómeno cultural, pues cada vez más gente utiliza y/o elabora este tipo de
software, que muchas veces no es sólo igual sino mejor que sus alternativas comerciales.
Mucho se puede hablar de los orígenes del software libre, pero realmente la popularización
de esta ideología tuvo lugar a la par que la revolución de internet, lo cual tiene sentido, pues internet
lo que hizo y sigue haciendo es promover la libertad de expresión, algo muy relacionado con las
ideas detrás del software libre.
En los años 60 y 70 del siglo XX, antes del gran boom que experimentó la informática, en
ambientes universitarios y empresariales, que eran los que tenían acceso a las computadoras de la
época, era común que los programadores compartieran libremente sus programas. Sin embargo, con
la llegada de los años 80, la situación cambió radicalmente. Surgieron y crecieron empresas de
software que forzaron a los usuarios a aceptar condiciones restrictivas del uso de software. Se
negaban a proporcionar el código fuente (es decir, el archivo que contiene las instrucciones que
sigue un programa y que revela el funcionamiento del mismo), con lo cual nadie podía mejorar un
programa a pesar de estar capacitado y motivado para hacerlo. Así se inició el movimiento que
buscaba la creación de software libre para todos, una idea algo romántica, pero que ha ido cogiendo
fuerza y asentándose con el paso del tiempo.
Las motivaciones detrás del movimiento del software libre son:
•
•
La motivación ética: que argumenta que el software es conocimiento y debe poderse
difundir sin trabas. Su ocultación es una actitud antisocial y la posibilidad de modificar
programas es una forma de libertad de expresión.
La motivación pragmática, que argumenta ventajas técnicas y económicas.
No es oportuno hablar del software libre sin mencionar Linux, un sistema operativo creado
con esa mentalidad. Gente capaz e inconformista ha hecho posible que desde sus inicios cuando
Linus Torvalds, un estudiante de la universidad de Helsinki, empezó a promover un proyecto que
trataba de realizar una mejora sobre un sistema basado en Unix, se convirtiera en una fuerte
1
comunidad con millones de usuarios en todo el mundo. Se acabó por desarrollar un sistema
operativo completamente diferente, nuevo y de libre distribución que hiciera competencia a los
sistemas Windows.
Desde entonces no ha dejado de evolucionar y ahora Linux tiene un lugar clave en las filas
del software libre en su lucha contra el monopolio de Microsoft y, en menor proporción, el resto de
los sistemas operativos comerciales como Mac OSX.
En los últimos años, el uso de Linux ha incrementado en cifras importantes y la tendencia
es que siga siendo así. Muchos gobiernos, universidades y entornos empresariales han descubierto
las ventajas no sólo económicas sino de rendimiento que puede proporcionar Linux.
Hoy en día disponemos de una gran variedad de distribuciones de Linux, lideradas por
diferentes grupos de trabajo o asociaciones, pudiendo escoger de entre todas ellas la que mejor se
adapte a nuestras necesidades o gustos personales. Cada distribución sigue su propia filosofía, pero
compartiendo el mismo espíritu y los logros realizados.
Sabiendo ya qué estamos tratando y las diferencias entre el software libre y el propietario, la
pregunta que muchos nos hacemos es ¿qué es mejor?. Lo cierto es que es una pregunta complicada,
ya que para llegar a una respuesta habría que analizar muchos factores (algunos de ellos subjetivos),
por lo que no podríamos llegar a una solución que satisficiera a todos. Por eso en nuestro caso
hemos escogido analizar un aspecto comparable de forma objetiva entre los dos sistemas
operativos: el consumo de memoria “base”, es decir, excluyendo el consumo de memoria que hacen
las aplicaciones que no corren por defecto al arrancar el ordenador (procesos del sistema,
antivirus...). Con esto no nos referimos al consumo mínimo posible para que funcione nuestro
sistema operativo, sino al consumo permanente (al que hemos llamado “base”), que permanece
desde un principio y mientras realizamos cualquier actividad con nuestro ordenador.
Escogimos cuatro factores que consideramos podían ser influyentes en la variable respuesta
“consumo de memoria base”:
•
•
•
•
Sistema operativo (Linux // Windows)
Antigüedad del sistema operativo (2007 o posterior // anterior al 2007)
Memoria RAM total
Memoria virtual total
2. LOS DATOS
Una vez teníamos clara nuestra idea, debíamos pensar en cómo íbamos a recoger los datos.
Lo primero que pensamos fue hacerlo vía correo electrónico, con mensajes en cadena, pero era
complicado conseguir que la gente respondiera a estos correos y, sobre todo, era difícil la gestión de
todos los datos con este método. La solución fue realizar una encuesta en lenguaje HTML y
colgarla en los servidores de la escuela para que estuvieran accesibles y resultase más cómodo
responder a las preguntas que en ella se planteaban.
Realizamos un modelo de encuesta para cada sistema operativo:
http://wiki.dii.etsii.upm.es/etsii/windows.html (para usuarios de Windows)
http://wiki.dii.etsii.upm.es/etsii/linux.html (para usuarios de Linux)
2
Ambas tenían una estructura similar, en la que se pedía al usuario que introdujese los
siguientes datos:
⁻
⁻
⁻
⁻
⁻
⁻
⁻
Antigüedad de su sistema operativo
Tamaño de la memoria RAM del equipo
Tamaño del archivo de paginación / SWAP / memoria virtual
Consumo de memoria RAM (o disponible en el caso de Windows, por facilitar la tarea al
usuario)
Consumo de memoria virtual
Memoria usada por el navegador de internet
Memoria usada por la aplicación de monitorización de recursos del sistema
Además, y aunque no utilicemos estos datos en nuestro estudio, en la encuesta para usuarios
de Linux pedimos que se seleccione de una lista:
⁻
⁻
Distribución de Linux (Debian, Fedora, Mandriva, Suse, Ubuntu, otra)
Escritorio (GNOME, KDE, XFCE, otro)
De esta forma estos datos estarían disponibles para, por ejemplo, hacer un estudio del
consumo de memoria dentro de las diferentes distribuciones de Linux o los diferentes escritorios.
Con esta encuesta, podíamos disponer de todos los datos necesarios para realizar nuestro
estudio: los cuatro factores de forma directa (el sistema operativo, su antigüedad y la memoria
RAM y virtual totales) y la variable respuesta, calculada restando al consumo total de memoria
(consumo de la memoria RAM + consumo de la memoria virtual) la memoria consumida por las
dos aplicaciones abiertas (el navegador de internet y la aplicación de monitorización de recursos del
sistema). Por supuesto, la encuesta incluye comentarios con todas las instrucciones para rellenarla
de forma correcta y asegurarnos que el encuestado no se olvidaba de, por ejemplo, cerrar
aplicaciones que tuviese abiertas como el reproductor de música o el cliente de mensajería
instantánea.
Teniendo el diseño de la encuesta sólo faltaba encontrar el método para lograr almacenar y
organizar todos los datos de forma sencilla y compacta. Para ello, utilizamos en la encuesta un
script en PHP llamado “apgForm 1.7”, que traduce los resultados de una encuesta o formulario a un
formato de hoja de cálculo.
El día 19 de diciembre de 2008, colgamos en el servidor la primera versión de la encuesta y
lo anunciamos vía correo electrónico a personas cercanas. Con el paso de los días, vimos los errores
que tenía la encuesta (principalmente por falta de explicaciones para rellenarla correctamente), así
que realizamos un nuevo modelo que colgamos el día 29 (cuando habíamos recibido 75 datos). Tras
hacerlo, nos pusimos a publicitarla en diferentes sitios, como los foros de las principales
distribuciones de Linux, algunos de Windows y otros foros poco relacionados con la informática
pero con gran participación de personas.
A día 9 de enero de 2009 y tras sólo 11 días desde la publicación de la nueva encuesta,
comenzamos a purgar los 1573 datos que teníamos para comenzar el estudio con una muestra que
ya consideramos sería significativa.
3
Para “limpiar” estos datos debíamos, antes de nada, eliminar aquellas encuestas que
estuvieran incompletas, cosa que no fue difícil teniendo los datos en una hoja de cálculo. Lo
segundo que teníamos que hacer era procesar los datos numéricos. Estos datos tenían un formato
muy dispar: había quien respondía en MB y quien lo hacía en KB o GB (a pesar de nuestra expresa
petición de hacerlo en MB), había quien ponía puntos para indicar la separación entre las centenas y
los millares y quien lo hacía para indicar la separación entre las cifras enteras y los decimales, quien
utilizaba la coma para hacer esta separación y quien ponía alguna explicación o comentario en el
resultado. La idea de depurar los datos uno por uno fue descartada inmediatamente, así que
decidimos realizar un programa que lo hiciese lo mejor posible.
El programa fue escrito en Pascal (muy cómodo para manejar archivos y conjuntos) y
realizaba un proceso muy sencillo. En primer lugar, debíamos copiar las columnas de datos
numéricos a un archivo nuevo y guardarlo como tipo texto (.txt) para poder manejarlo con facilidad.
Puesto que esta tabla sólo debían aparecer datos numéricos, el algoritmo del programa era el
siguiente:
1. Realizaba una copia del archivo original exceptuando caracteres no numéricos, signos de
puntuación y los caracteres 'g' o 'G' (que permanecerían en los pocos datos que tuvieran la
indicación de GB tras la cifra numérica).
2. Realizaba otra copia de este archivo. En este caso realizaba la siguiente comprobación: si se
encontraba un signo de puntuación:
a) Si los tres caracteres siguientes son numéricos entonces no copia el signo de
puntuación (interpretamos que se trata de una separación entre las centenas y los
millares).
b) Si no ocurre esto, interpreta que se trata de un carácter de separación entre las cifras
enteras y decimales para programas configurados en castellano (escribe en el archivo
una coma ','). Debemos recordar que entre dato y dato existe un carácter de
tabulación o un salto de línea.
Con este sencillo algoritmo, conseguimos tener los datos casi a punto. Los copiamos de
nuevo a la tabla original y los ordenamos para que tengamos agrupados los datos que no sean de
tipo numérico en las columnas en las que debieran serlo. De esta forma, terminamos la limpieza
añadiendo tres ceros en los pocos datos que tenemos que tienen una G (de GB) al final, y borramos
la G.
Nos queda por hacer dos comprobaciones: unidades e incoherencias.
₋
₋
4
Para la primera hemos supuesto que no puede haber diferencias de tres órdenes de magnitud
entre datos de la misma clase (ej.: un ordenador con 64MB de RAM y otro con 64GB), de
esta forma con la hoja de cálculo realizamos una sencilla operación lógica: si pasa de un
límite que establezcamos, dividimos la cifra entre 1000 porque estará en KB, si no, dejamos
la cifra como está.
La segunda comprobación también es sencilla manejando la hoja de cálculo: consiste en
comprobar incoherencias del tipo “el ordenador consume más memoria de la que dispone”
(aplicado a la RAM y la memoria virtual). Debemos tener en cuenta que los datos de
Windows representaban la memoria RAM disponible, luego tenemos que crear una columna
de datos resultante de la diferencia entre la memoria RAM total y la disponible para saber
cuánta memoria está consumiendo.
Ahora ya disponemos de una tabla de datos limpia y coherente, pero nos queda una cosa más
que hacer: eliminar las respuestas claramente incorrectas. Para eso ordenamos columna por
columna los datos y vemos qué valores extremos podemos considerar incorrectos, como quien dice
tener (respuesta textual) 545446465559999987777777888888888888888888888888899999999777777
de memoria RAM o quien responde a todo 0.
Tras realizar esta limpieza, descubrimos que nos quedaban de los 1573 datos originales,
1102. Lo cierto es que entraba dentro de nuestras previsiones, pues pensábamos analizar en torno a
1000 datos.
3. ANÁLISIS
Para realizar el estudio, utilizaremos el programa Statgraphics. Para comenzar, importamos
la tabla de datos. Una vez hecho esto, seleccionamos la opción de ANOVA factorial en la pestaña
de comparación, sección de análisis de la varianza. De esta forma realizaremos un análisis del
modelo para múltiples factores.
Puesto que no estamos realizando un estudio de regresión, clasificamos los factores “RAM”
y “memoria virtual” en distintos niveles (dos en nuestro caso):
•
•
RAM:
Virtual:
nivel 1, <= 1024 MB
nivel 1, <= 1535 MB
nivel 2, > 1024 MB
nivel 2, > 1535 MB
El no realizar más divisiones en cada factor es debido a la dificultad para encontrar datos
que correspondan, por ejemplo, al tratamiento de mucha memoria RAM y poca memoria virtual.
Seleccionamos entonces como variable dependiente o variable respuesta el consumo de memoria
base y como factores: el sistema operativo (Windows // Linux), la antigüedad (new: del 2007 o
posterior // med: anterior al año 2007), la RAM (1: <= 1024 MB // 2: > 1024 MB) y la memoria
virtual (1: <= 1535 MB // 2: > 1535 MB). Es importante tener claro estas clasificaciones para
comprender bien el análisis. La distinción en la antigüedad del sistema operativo supone, en el caso
de Windows, la división entre la versión Vista y XP.
Al disponer de cuatro factores, deberemos analizar la influencia de todos ellos como factores
principales y también la influencia de las interacciones: de segundo orden (combinaciones de dos
factores), de tercero (de tres) y de cuarto orden.
Teniendo un modelo desequilibrado como el nuestro (en el que no disponemos del mismo
número de réplicas por cada cruce) y además de más de tres factores, no mencionaremos gran parte
de la base matemática del estudio, por su carácter poco didáctico.
3.1 Diagnosis
La diagnosis es una parte fundamental del análisis que, en muchos casos, no se menciona
hasta tener definido un modelo de estudio. Para facilitar la comprensión del desarrollo,
adelantaremos este paso, señalando los cambios que fueron necesarios para cumplir las hipótesis del
modelo sin entrar en la discusión del mismo.
5
Para poder realizar los contrastes necesarios, es preciso que nuestros datos cumplan ciertos
requisitos: han de ser normales (ajustados a una distribución normal), homocedásticos (han de tener
la misma varianza) e independientes. Para ello, realizaremos las pruebas con los residuos generados
a partir de los datos.
Como primer paso, analizaremos la homocedasticidad. Al generar el análisis factorial con
Statgraphics, obtenemos un gráfico que representa los residuos frente a predicho:
Gráfico de Residuos para Cons_mem
residuo
4800
2800
800
-1200
-3200
0
1
2
3
4
5
Cons_mem predicho
6
(X 1000)
Gráfica 3.1-1: Residuos frente a predicho para el consumo de memoria.
Podemos observar una clara heterocedasticidad, que requerirá de una transformación de los
datos. Elegiremos la transformación logarítmica (logaritmo neperiano), con lo que obtenemos el
siguiente gráfico de residuos frente a predicho o valores previstos (que corresponden a la media del
tratamiento):
Gráfico de Residuos para log[cons]
residuo
2,4
1,4
0,4
-0,6
-1,6
4,4
5,4
6,4
7,4
8,4
9,4
log[cons] predicho
Gráfica 3.1-2: Residuos frente a predicho para el logaritmo del consumo de memoria.
Vemos que los datos ahora pueden perfectamente considerarse homocedásticos. Además
debemos estudiar los gráficos de residuos por tratamientos, verificando que el ancho máximo entre
el mínimo sea menor que tres. En nuestro caso, se cumple perfectamente, por lo que no será
necesario realizar un contraste formal (como el contraste de Bartlett):
6
Gráfico de Residuos para log[cons]
2,4
2,4
1,4
1,4
residuo
residuo
Gráfico de Residuos para log[cons]
0,4
-0,6
0,4
-0,6
-1,6
med
-1,6
new
Linux
Antiguedad
Gráfico de Residuos para log[cons]
2,4
2,4
1,4
1,4
residuo
residuo
Gráfico de Residuos para log[cons]
0,4
0,4
-0,6
-0,6
-1,6
Windows
SO
-1,6
1
1
2
2
SWAP
RAM
Gráfica 3.1-3: Residuos por tratamiento.
El gráfico de residuos frente a número de fila, debido al carácter completamente aleatorio de
recogida de datos en nuestra muestra, no es significativo en nuestro estudio y no presenta ningún
inconveniente (consideraremos independiente la muestra):
Gráfico de Residuos para log[cons]
residuo
2,4
1,4
0,4
-0,6
-1,6
0
200
400
600
800
1000
1200
número de fila
Gráfica 3.1-4: Residuos frente a número de fila.
Debemos comprobar por último la normalidad de los residuos. Para ello, intentamos realizar
un ajuste de los residuos a una normal. El resultado gráfico que obtenemos es el siguiente:
7
Histograma para RESIDUALS
frecuencia
300
250
200
150
100
50
0
-2
-1
0
1
2
RESIDUALS
Gráfica 3.1-5: Ajuste de los residuos a una distribución normal.
Aunque aparentemente se ajuste bastante bien a una distribución normal, nos vemos
obligados a escoger el contraste de Kolmogorov Smirnoff, con el que obtenemos un p_valor de
0'0514667 (mayor que los niveles de significación normales: α <= 0,05), lo que nos lleva a aceptar
la hipótesis nula de normalidad. El contraste de la chi-cuadrado (más “exigente” que el de
Kolmogorov) proporciona un p_valor más bajo debido al ajuste imperfecto de los residuos, como
podemos observar en el gráfico cuantil-cuantil:
Gráfico Cuantil-Cuantil
RESIDUALS
2,4
1,4
0,4
-0,6
-1,6
-1,6
-0,6
0,4
1,4
2,4
Normal distribución
Gráfica 3.1-6: Gráfico cuantil-cuantil (Q-Q).
Tras realizar esta diagnosis, llegamos a la conclusión de que podremos considerar nuestros
residuos como normales, independientes y homocedásticos, lo que nos lleva a dar el siguiente paso
en nuestro estudio.
3.2 Modelo de estudio
Con lo realizado hasta ahora, podemos comenzar a analizar nuestra muestra y someterla a
análisis de la varianza para ver qué factores podemos considerar significativos y, en su caso,
estudiar sus correspondientes intervalos de diferencia de medias, etc.
8
Definimos un modelo en el que la variable respuesta, logaritmo del consumo de la memoria, se ve
afectada por los cuatro factores:
log yijkl  = i   j  k  l   ij   ik   il  ...    ijk  ...   ijkl  U ijkl
Uijkl representa la parte aleatoria de los datos que seguirá una distribución normal de
probabilidad con media 0 (cero) y desviación típica σ constante.  ,  ,  y 
representan los efectos de cada factor sobre el logaritmo del consumo. También aparecen
representados los efectos de las interacciones de segundo, tercer y cuarto orden. La estimación de
estos parámetros del modelo se realizará utilizando la técnica de máxima verosimilitud para una
distribución normal de datos.
Statgraphics realiza los cálculos correspondientes y nos proporciona la siguiente salida para
el análisis de la varianza (recordamos que el análisis es sobre el logaritmo del consumo de memoria,
porque sin esta transformación, no se cumple la diagnosis).
Análisis de la Varianza paralog[cons] - Sumas de Cuadrados de Tipo III
-------------------------------------------------------------------------------Fuente
Suma de cuadrados
GL Cuadrado Medio Cociente-F
P-Valor
-------------------------------------------------------------------------------EFECTOS PRINCIPALES
A:SO
83,3952
1
83,3952
556,22
0,0000
B:Antiguedad
10,444
1
10,444
69,66
0,0000
C:RAM
9,40861
1
9,40861
62,75
0,0000
D:SWAP
0,235689
1
0,235689
1,57
0,2099
INTERACCIONES
AB
AC
AD
BC
BD
CD
ABC
ABD
ACD
BCD
ABCD
9,46728
2,28094
0,532683
1,24968
0,533737
0,432332
1,315
0,000893377
0,0455596
0,0400639
0,0152064
1
1
1
1
1
1
1
1
1
1
1
9,46728
2,28094
0,532683
1,24968
0,533737
0,432332
1,315
0,000893377
0,0455596
0,0400639
0,0152064
63,14
15,21
3,55
8,34
3,56
2,88
8,77
0,01
0,30
0,27
0,10
0,0000
0,0001
0,0594
0,0039
0,0592
0,0895
0,0031
0,9385
0,5815
0,6052
0,7501
RESIDUOS
162,825
1086
0,149931
-------------------------------------------------------------------------------TOTAL (CORREGIDO)
490,555
1101
--------------------------------------------------------------------------------
Tabla 3.2-1: Análisis de la varianza con cuatro factores.
Vemos que todos los datos señalados en negrita poseen un p_valor mayor que los niveles de
significación usuales, lo que nos lleva a no poder rechazar la hipótesis nula de igualdad de medias.
Con esto podemos sacar una primera conclusión: la SWAP (o memoria virtual) no es significativa
ni como factor principal ni como interacción. Gracias a esto podemos eliminar este factor de nuestro
estudio, al no influir significativamente en los resultados.
9
3.3 Definición de un nuevo modelo; análisis de resultados
Con lo realizado hasta ahora, nos encontramos con que estamos estudiando un modelo con
tres factores (S.O., antigüedad y RAM) y que la variable respuesta es el logaritmo de la memoria
consumida por el ordenador>
l o g y ijk  = i   j  k   ij   i k    j k    ijk  U ijk
El resumen del procedimiento y la tabla de análisis de la varianza quedan ahora de la siguiente
forma:
Resumen del Procedimiento
Variable dependiente: log[cons]
Factores:
SO
Antiguedad
RAM
Número de casos completos: 1102
Análisis de la Varianza para log[cons] - Sumas de Cuadrados de Tipo III
-------------------------------------------------------------------------------Fuente
Suma de cuadrados
GL Cuadrado Medio Cociente-F
P-Valor
-------------------------------------------------------------------------------EFECTOS PRINCIPALES
A:SO
114,705
1
114,705
750,46
0,0000
B:Antiguedad
14,7867
1
14,7867
96,74
0,0000
C:RAM
13,429
1
13,429
87,86
0,0000
INTERACCIONES
AB
AC
BC
ABC
12,1185
2,06192
0,872607
1,5139
1
1
1
1
12,1185
2,06192
0,872607
1,5139
79,29
13,49
5,71
9,90
0,0000
0,0002
0,0169
0,0016
RESIDUOS
167,213
1094
0,152846
-------------------------------------------------------------------------------TOTAL (CORREGIDO)
490,555
1101
--------------------------------------------------------------------------------
Tabla 3.3-1: Análisis de la varianza con tres factores.
Con esta nueva tabla, casi todos los factores son significativos para cualquiera de los niveles
de significación más utilizados. Nosotros consideraremos α = 0'05, así que tomaremos todos los
factores e interacciones como significativos.
La primera gráfica que nos llama la atención es la que representa el consumo de memoria
(aplicándole la transformación logarítmica) frente al sistema operativo:
10
Medias y 95,0 Porcentajes Intervalos LSD
log[cons]
7,4
7,1
6,8
6,5
6,2
5,9
Linux
Windows
SO
Gráfica 3.3-1: Intervalos de confianza para el logaritmo del consumo según el sistema operativo.
con su correspondiente análisis formal:
Contraste Múltiple de Rangos para log[cons] según SO
-------------------------------------------------------------------------------Método: 95,0 porcentaje LSD
SO
Recuento Media LS
Sigma LS
Grupos Homogéneos
-------------------------------------------------------------------------------Linux
670
5,96343
0,023359
X
Windows
432
7,19806
0,0385424
X
-------------------------------------------------------------------------------Contraste
Diferencias
+/- Límites
-------------------------------------------------------------------------------Linux - Windows
*-1,23463
0,0883325
-------------------------------------------------------------------------------•
indica una diferencia significativa.
** De ahora en adelante entenderemos siempre (tanto en los gráficos como en los análisis
formales) que estamos tratando con intervalos LSD para un intervalo de confianza del 95%.
Tabla 3.3-2: Contraste múltiple de rangos según el sistema operativo.
Con este gráfico podemos asegurar que el sistema operativo Windows consume más
memoria (con una diferencia más que significativa) que Linux. El recuento representa el número de
datos de que disponemos en cada factor. Debemos tener en cuenta que para calcular el consumo
medio real de memoria no podemos simplemente tomar la exponencial de las medias:
log y 1   ...  log y n 
= media logarítmica
n
1
Tomando exponenciales : e
De donde :
n y 1⋅...⋅y n
= e
log  y 1⋅... ⋅y n  n
media logarítmica
= e media logarítmica
= media geométrica
11
Vemos que de esta forma obtenemos la media geométrica de los datos y no la aritmética,
que será siempre igual o superior (estaríamos calculando una media de consumo inferior a la real).
Para alcanzar el verdadero valor de la media, analizaremos la muestra sin transformaciones
(mostraremos la tabla de medias con los verdaderos valores más adelante).
Podemos ver también las diferencias de medias que existen para los otros dos factores. Los
interpretaremos sin recurrir a un análisis formal:
Medias y 95,0 Porcentajes Intervalos LSD
6,9
6,9
6,8
6,8
log[cons]
log[cons]
Medias y 95,0 Porcentajes Intervalos LSD
6,7
6,6
6,5
6,4
6,7
6,6
6,5
6,4
6,3
6,3
med
new
1
Antiguedad
2
RAM
Gráfica 3.3-2: Intervalos para el logaritmo del consumo según antigüedad y RAM.
Vemos que un sistema operativo tiende a consumir más memoria si dispone de ella (gráfico
de la derecha) y que los nuevos sistemas operativos consumen más memoria que los antiguos
(gráfico de la izquierda). Sin embargo estas conclusiones son un tanto imprecisas y poco resolutivas
teniendo en cuenta el tema que nos atañe, que es la diferenciación de los dos sistemas operativos.
Por ello pasaremos a la interpretación de los gráficos de interacción (que representan los resultados
del análisis en función de dos de los factores). La siguiente imagen representa el consumo de
memoria en función de la antigüedad del sistema operativo y de la memoria RAM de la que
dispongamos:
Interacciones y 95,0 Porcentajes Intervalos LSD
log[cons]
7,3
RAM
1
2
7,1
6,9
6,7
6,5
6,3
6,1
med
new
Antiguedad
Gráfica 3.3-3: Efecto de la interacción entre los factores “RAM” y “Antigüedad”.
Con este gráfico podemos sacar las siguientes conclusiones: un sistema operativo consume
menos memoria si es anterior al 2007 y dispone de menos de 1025 MB de RAM; en cambio, el
12
máximo consumo se alcanza para aquellos sistemas operativos más actuales y que dispongan de
más memoria. Observamos también que, por producirse un solapamiento en los intervalos LSD, no
podemos afirmar que exista una diferencia significativa entre el consumo de memoria de los
sistemas operativos con más memoria y más antiguos y los más modernos y con menos memoria
RAM.
A continuación analizaremos un gráfico que quizás resulte más representativo, pues en él ya
se ven reflejadas las diferencias entre los dos sistemas operativos que analizamos. Se trata de la
comparación del consumo de memoria en función del sistema operativo y la memoria RAM del
equipo:
Interacciones y 95,0 Porcentajes Intervalos LSD
log[cons]
7,7
RAM
1
2
7,3
6,9
6,5
6,1
5,7
Linux
Windows
SO
Gráfica 3.3-4: Efecto de la interacción entre los factores “RAM” y “SO”.
Como se puede observar a primera vista, sea cual sea el tamaño de la memoria RAM, Linux
optimiza mejor los recursos del sistema. Aún así observamos una tendencia común a aumentar el
consumo de recursos al disponer de más memoria; eso sí, este aumento resulta ser más exagerado
para el caso del sistema operativo Windows (recordemos que estamos representando el logaritmo
del consumo de la memoria y, por tanto, las diferencias que observamos en el gráfico son más
notorias cuanto mayor sea el logaritmo del consumo). Es posible que veamos más clara esta
diferencia en el siguiente gráfico (que representa también el logaritmo de la variable respuesta):
13
Interacciones y 95,0 Porcentajes Intervalos LSD
log[cons]
7,7
SO
Linux
Windows
7,3
6,9
6,5
6,1
5,7
1
2
RAM
Gráfica 3.3-5: Efecto de la interacción entre los factores “SO” y “RAM”.
A continuación examinaremos el gráfico más relevante o llamativo, en el que se representa
el logaritmo del consumo en función del sistema operativo y su antigüedad:
Interacciones y 95,0 Porcentajes Intervalos LSD
log[cons]
7,8
Antiguedad
med
new
7,4
7
6,6
6,2
5,8
Linux
Windows
SO
Gráfica 3.3-6: Efecto de la interacción entre los factores “Antigüedad” y “SO”.
Vemos claramente como, de nuevo, Linux consume menos recursos, esta vez para cualquier
antigüedad del sistema operativo. Además, no existen diferencias significativas entre el consumo de
memoria de sistemas Linux para ambas clasificaciones de antigüedad, lo que nos muestra la
tendencia de estos sistemas operativos a ofrecer cada día más mejoras y prestaciones sin renunciar a
la eficiencia. En cambio para el sistema operativo Windows vemos un gran salto entre las versiones
anteriores al 2007 y su última versión (Vista), lo que nos indica una tendencia, como vemos muy
fuerte, a consumir más recursos del sistema en sus nuevos lanzamientos. Recordemos de nuevo que
la diferencia real entre los consumos de memoria en la gráfica se haría más aguda al eliminar la
transformación logarítmica.
14
Llegados a este punto nos encontramos con un obstáculo. Statgraphics posee una importante
limitación: no analiza interacciones de orden mayor que dos; ni gráfica ni formalmente. Para una
correcta interpretación de los resultados, uniremos dos factores principales en uno: “Antigüedad” +
“RAM” → “Ant. RAM”. Este nuevo factor principal queda dividido entonces en cuatro niveles,
correspondientes a los cuatro cruces entre los niveles de RAM y Antigüedad. Al hacerlo, obtenemos
la siguiente tabla de análisis de la varianza:
Variable dependiente: log[cons]
Factores:
Ant RAM
SO
Número de casos completos: 1102
Análisis de la Varianza paralog[cons] - Sumas de Cuadrados de Tipo III
-------------------------------------------------------------------------------Fuente
Suma de cuadrados
GL Cuadrado Medio Cociente-F
P-Valor
-------------------------------------------------------------------------------EFECTOS PRINCIPALES
A:Ant RAM
65,4387
3
21,8129
142,71
0,0000
B:SO
114,705
1
114,705
750,46
0,0000
INTERACCIONES
AB
33,3546
3
11,1182
72,74
0,0000
RESIDUOS
167,213
1094
0,152846
-------------------------------------------------------------------------------TOTAL (CORREGIDO)
490,555
1101
--------------------------------------------------------------------------------
Tabla 3.3-3: Análisis de la varianza con el nuevo factor “Ant RAM” ≡ (“Antigüedad” + “RAM”).
Lo primero que observamos es que los dos factores y la interacción son muy significativos
(p_valor cercano a cero). Vemos también que no cambia, respecto a nuestro anterior modelo, la
variabilidad no explicada (suma de cuadrados) ni los grados de libertad de los residuos y del efecto
principal “SO”.
Statgraphics ahora sí nos puede proporcionar el gráfico adecuado de interacción entre los
factores. En él se muestran también los intervalos de confianza LSD con un 95% de confianza:
15
Interacciones y 95,0 Porcentajes Intervalos LSD
log[cons]
8,2
SO
Linux
Windows
7,7
7,2
6,7
6,2
5,7
11
12
21
22
Ant RAM
Gráfica 3.3-7: Efecto de las interacciones entre los tres factores.
En el factor “Ant RAM” el valor de las decenas representa el nivel del factor Antigüedad (1
para antiguo; 2 para nuevo) y las unidades representan los niveles del factor RAM (1 para menos de
1024 MB; 2 para más de 1024 MB). Ejemplo: “12” se corresponde con un sistema antiguo con más
de 1024 MB de memoria.
Es inmediato ver que existe una diferencia significativa entre el consumo de los dos sistemas
operativos (recordemos que esta diferencia se agudiza al deshacer la transformación logarítmica).
Además, aunque no de forma tan clara, se puede apreciar un solapamiento en los intervalos
correspondientes a Linux: entre el 11 y 21 y entre el 12 y 22. Esto significa que la antigüedad no
influye significativamente en el consumo de memoria en sistemas Linux. Son conclusiones que ya
fuimos capaces de deducir con las gráficas anteriores.
A continuación se muestra la tabla de medias resultante del análisis formal de los datos. Las
dos columnas de la derecha muestran los intervalos de confianza (del 95%) para cada una de las
medias. Las dos columnas de la derecha muestran los intervalos de confianza (del 95%) para cada
una de las medias. También representa el error estándar de cada media (medida de su variabilidad
en la muestra).
Tabla de Medias por mínimos cuadrados para log[cons]
con 95,0 Intervalos de confianza
-------------------------------------------------------------------------------Error
Límite
Límite
Nivel
Frecuencia
Media
Estándar
Inferior
Superior
-------------------------------------------------------------------------------Media Total
1102
6,58074
Ant RAM
11
276
6,20172
0,03055
6,14185
6,2616
16
12
179
6,51648
0,0376782
6,44263
6,59033
21
298
6,53732
0,0700585
6,40001
6,67463
22
349
7,06745
0,0293852
7,00985
7,12504
SO
Linux
670
5,96343
0,023359
5,91765
6,00921
Windows
432
7,19806
0,0385424
7,12251
7,2736
Ant RAM según SO
11 - Linux
50
5,79691
0,0552894
5,68854
5,90527
11 - Windows
226
6,60654
0,0260059
6,55557
6,65751
12 - Linux
33
6,08797
0,0680565
5,95458
6,22136
12 - Windows
146
6,94499
0,0323556
6,88157
7,0084
21 - Linux
290
5,87304
0,0229577
5,82805
5,91804
21 - Windows
8
7,2016
0,138223
6,93069
7,47251
22 - Linux
297
6,0958
0,0226855
6,05134
6,14026
22 - Windows
52
8,0391
0,0542157
7,93284
8,14536
--------------------------------------------------------------------------------
Tabla 3.3-4: Tabla de medias con intervalos de confianza del 95%.
Para interpretar mejor los datos, mostramos a continuación la tabla de medias real (sin la
transformación logarítmica). Las medias reales no han sido calculadas con la exponencial de la
media logarítmica, ya que con eso obtenemos la media geométrica de los datos (siempre igual o,
como en nuestro caso, inferior a la media real). En cambio, para calcular los intervalos de
confianza, sí hemos podido realizar esta transformación directa asegurando que, con un 95% de
probabilidad, el consumo de memoria de un ordenador con ciertas características de sistema
operativo, antigüedad y memoria RAM estará entre los límites superior e inferior establecidos.
----------------------------------------------------------------Límite
Límite
Nivel
Frecuencia
Media
Inferior
Superior
----------------------------------------------------------------Media Total
1102
1045,02
Ant RAM
11
276
576,185
464,913
524,057
12
179
805,246
628,056
728,021
21
298
890,163
601,851
792,054
22
349
1908,47
1107,488
1242,69
SO
Linux
670
424,362
371,538
407,162
Windows
432
665,67
1239,558
1441,73
Ant RAM según SO
11 - Linux
50
365,934
295,462
336,966
11 - Windows
226
786,437
703,150
778,610
12 - Linux
33
469,985
385,515
503,387
12 - Windows
146
1140,51
974,155
1105,88
21 - Linux
290
383,913
339,696
371,683
21 - Windows
8
1396,41
1023,200
1759,01
22 - Linux
297
477,615
424,682
464,174
22 - Windows
52
3339,32
2787,332
3447,34
-----------------------------------------------------------------
Tabla 3.3-5: Tabla de medias real con intervalos de confianza del 95%.
17
Las medidas más representativas son las correspondientes a las ocho últimas filas, ya que en
ellas estamos teniendo en cuenta la influencia de los tres factores.
Debemos recordar, para aquellos que se extrañen por los resultados del estudio, que la
variable analizada es el consumo base de memoria del sistema (y que la memoria consumida es la
suma de la RAM y memoria virtual consumidas), pero que las aplicaciones que corren por defecto
en el sistema (antivirus, firewall, algunos efectos de escritorio, etc...) no las hemos tenido en cuenta
y las hemos incluido dentro de este consumo base, suponiendo que el usuario medio no cambia esta
configuración para obtener un mayor rendimiento y que, por tanto, forman parte de ese consumo
base o permanente de memoria. Por supuesto puede haber errores en los datos achacables a la mala
interpretación de las instrucciones de la encuesta o a errores cometidos por el usuario al
completarla, pero hemos supuesto que estos errores se habrán cometido de forma parecida tanto
para usuarios de Linux como de Windows.
4. CONCLUSIÓN
El objetivo central de nuestro estudio era determinar qué sistema operativo optimiza mejor
el consumo de memoria del sistema. Después de hacer un análisis detallado de los datos, podemos
afirmar que Linux es claramente superior a Windows en ese aspecto, sin importar si se trata de
versiones actuales o antiguas. Además, podemos observar el gran aumento de consumo de memoria
que experimentó el sistema de Windows con la introducción de su última versión, algo que ha sido
objeto de muchas críticas.
Linux, en cambio, presenta una tendencia radicalmente diferente. No pudimos apreciar una
diferencia significativa en el uso de memoria entre las versiones más actuales y las versiones más
antiguas. Es un importante hecho que nos hace pensar que este sistema operativo puede ser el más
adecuado para entornos académicos, públicos o incluso empresariales, donde el coste de hardware
y software puede ser un factor determinante. Linux tiene grandes ventajas como su disponibilidad y
fácil acceso e instalación de software gratuito y su recién estudiado alto rendimiento en ordenadores
baratos o antiguos que tienen menos recursos disponibles. A esto, por supuesto, hay que añadir las
reivindicaciones del movimiento del software libre, que hemos explicado en la introducción de este
estudio.
Al analizar la importancia de los diferentes factores: sistema operativo, antigüedad, memoria
RAM total y SWAP, hemos determinado que el tamaño de la memoria virtual (SWAP o archivo
de paginación) no tiene una influencia significativa en el uso de memoria del sistema.
Común a ambos sistemas operativos es la tendencia a consumir más recursos al disponer de
ellos, hecho que se pone de manifiesto en la Gráfica 3.3-7. Vemos que al aumentar la memoria
RAM disponible, aumenta el consumo de memoria total y que este aumento es más agudo en
Windows.
18
19
ANEXO (Dónde encontrar el archivo de datos original y el utilizado en el estudio):
En principio tanto las encuestas como el archivo en el que se almacenarán los datos estarán
disponibles por un tiempo indefinido. De esta forma estarán accesibles los datos para el que quiera
utilizarlos para repetir el estudio o realizar otro cualquiera (recordamos que los datos de Linux
proporcionan información sobre el escritorio y la distribución, aunque no los hayamos utilizado en
nuestro estudio). Las direcciones de acceso son las siguientes:
http://wiki.dii.etsii.upm.es/etsii/windows.html (encuesta para usuarios de Windows)
http://wiki.dii.etsii.upm.es/etsii/linux.html (encuesta para usuarios de Linux)
http://wiki.dii.etsii.upm.es/etsii/form.xls (archivo de datos)
La estructura del archivo de datos es la siguiente:
•
•
Linux: Distribución; escritorio; antigüedad; tamaño de la RAM; tamaño de la SWAP;
memoria RAM en uso; memoria de intercambio en uso; consumo de memoria por el
navegador; consumo de memoria por la aplicación de monitorización de recursos del
sistema; deseo de recibir los resultados del estudio.
Windows: Antigüedad; tamaño de la RAM; tamaño del archivo de paginación; memoria
RAM disponible; uso del archivo de paginación; consumo de memoria por el navegador;
consumo de memoria por la aplicación de monitorización de recursos del sistema; deseo de
recibir los resultados del estudio.
Los primeros 74 datos corresponden a pruebas y respuestas al primer modelo de la encuesta,
por lo que es conveniente excluirlos; el 75 y 76 corresponden a las respectivas cabeceras de
Windows y Linux. Habría sido más correcto almacenar los datos en dos archivos, ya que los
resultados de cada encuesta no proporcionan la misma información; pero dado que se trata de una
hoja de cálculo no es difícil seleccionar los de un mismo tipo y extraerlos para realizar con ellos
cualquier estudio.
Además, estará disponible el archivo de datos “limpio” que utilizamos en nuestro estudio en
la dirección:
http://wiki.dii.etsii.upm.es/etsii/datosestudio.csv
Para cualquier comentario disponemos, en principio también por tiempo indefinido, de una
cuenta de correo electrónico que atenderemos: [email protected]. Debemos tener en
cuenta que éste es un trabajo realizado por dos estudiantes en su primera asignatura de estadística;
puede presentar imperfecciones, ambigüedades, etc.. Desconocemos las expectativas de éxito que
cada uno tuviera en nuestro análisis, para eso hemos facilitado el archivo de datos, quedando
accesible para todo aquel que no se sienta conforme con el estudio y prefiera comprobarlo, o
realizarlo de nuevo con el archivo de datos original.
20
AGRADECIMIENTOS
•
Ángel García y Beltrán (Profesor Titular en la División de Informática Industrial de la ETSI
Industriales de la Universidad Politécnica de Madrid) por su ayuda en la creación de la
encuesta HTML, la automatización de la ordenación de los datos (script apgForm 1.7) y por
brindarnos la oportunidad de utilizar los servidores de la escuela.
•
Jaime Carpio Huertas (Profesor Titular Interino en el Laboratorio de Estadística de la
E.T.S.I. Industriales de la Universidad Politécnica de Madrid) por su ayuda en la
representación de las interacciones de orden tres.
•
El equipo de http://www.ubuntu-es.org/, por acogernos con tanta amabilidad y en especial a
“slap” por poner nuestro anuncio en la página principal, haciendo que hayamos conseguido
una gran cantidad de datos de Linux.
•
A la revista UXi (Revista Cubana de Software Libre), por interesarse y publicar nuestro
estudio en la edición de febrero de 2009.
•
A todos los que habéis participado en la encuesta y los que habéis ayudado a promoverla o
difundirla por cualquier medio.
REFERENCIAS
‒
Daniel Peña. Regresión y diseño de experimentos. Madrid, Alianza Editorial, 2002.
21