Taller para estudiantes secundarios FCEyN (2004)
Anuncio

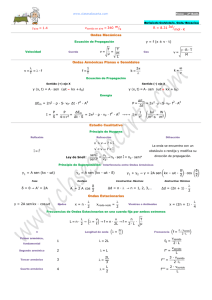
Taller 2004 Ondas: de la música a las imágenes Clase 1 Evaluar qué expectativas tienen del curso, qué carreras piensan seguir y porqué. Hablar sobre el método científico, la falsa antinomia física experimental vs. física teórica, el método aristotélico, etc. Contar cómo es la carrera y cómo trabaja un investigador. Describir cómo se va a desarrollar el taller, qué temas se van a ver y cuál va a ser la metodología de trabajo. Formar los grupos de trabajo. Comenzar con una introducción de ondas. Averiguar que es lo que saben al respecto. INTRODUCCIÓN A ONDAS MECÁNICAS Y ELECTROMAGNÉTICAS Una onda es una perturbación que avanza o que se propaga en un medio material o incluso en el vacío. A pesar de la naturaleza diversa de los fenómenos que pueden originarlas, todas las ondas tienen un comportamiento semejante. Algunas clases de ondas precisan para propagarse de la existencia de un medio material que haga el papel de soporte de la perturbación; estas se denominan genéricamente ondas mecánicas. El sonido, las ondas que se forman en la superficie del agua, las ondas en cuerdas, son algunos ejemplos de ondas mecánicas y corresponden a compresiones, deformaciones y, en general, a perturbaciones que se propagan a través del medio. Sin embargo, existen ondas que pueden propagarse aún en ausencia de medio material, es decir, en el vacío. Son las ondas electromagnéticas o campos electromagnéticos viajeros; a esta segunda categoría pertenecen las ondas luminosas. Independientemente de esta diferenciación, existen ciertas características que son comunes a todas las ondas, cualquiera que sea su naturaleza, y que en conjunto definen el llamado comportamiento ondulatorio, esto es, una serie de fenómenos típicos que diferencian dicho comportamiento del comportamiento propio de los corpúsculos o partículas. Vamos a tratar de comprobar que el sonido y la luz son ondas. Para ello comencemos analizando algunas experiencias en las cuales puedan observarse ondas mecánicas, por ejemplo la cuba de ondas y una cuerda vibrante. Llegado a este punto conviene mostrar que: i) No existe transporte de materia sino que es la perturbación la que se propaga en el medio material. ii) Son ondas transversales. Para demostrar que el sonido es una onda analicemos la experiencia del osciloscopio láser. Observando cómo el espejito es empujado por el parlante puede entenderse que es una onda mecánica pero del tipo longitudinal. Es decir que el parlante, al moverse hacia atrás y adelante, genera un cambio de presión en el aire que es transmitido a través del choque de las moléculas hasta llegar a mi oído, donde ese cambio de presión es detectado. A continuación, mediante el espejo rotante puede mostrarse que la deflexión que sufre el espejo es también un movimiento armónico. Luego se van a estudiar las expresiones matemáticas que describen ese tipo de perturbación. Veamos ahora que la difracción es otra característica de los fenómenos ondulatorios. Para ello volvamos a la cuba de ondas y estudiemos que sucede cuando ponemos obstáculos que perturban al frente de ondas. Depende éste de la longitud de onda y del tamaño del obstáculo? Analicemos qué pasa si ponemos dos ranuras. Vemos que de acuerdo a como se superpongan las perturbaciones provenientes de las dos ranuras, el valor de la amplitud resultante en un punto dado puede ser mayor o menor que para una perturbación individual o incluso pueden anularse entre sí. Sin embargo después de superponerse las ondas individuales se separan y continúan completamente inafectadas por su encuentro previo. A este fenómeno se lo llama interferencia. Si en vez de dos ranuras ponemos dos varillas que perturben la superficie del agua, originamos dos fuentes puntuales. Como varía la interfranja de la figura de interferencia en función de la separación de las fuentes puntuales? Piensen que pasaría si estas fuentes no emitieran en forma sincronizada. Se vería una figura de interferencia estable? Volveremos sobre el tema más adelante cuando tratemos interferencia de ondas electromagnéticas. Ahora estamos en condiciones de analizar si la luz es también un fenómeno ondulatorio. Veamos que sucede cuando un haz láser pasa a través de una ranura. Es similar el resultado que se obtiene al encontrado para la cuba de ondas? Podemos tener alguna idea sobre el tamaño de la longitud de onda de la luz? Que porción del espectro electromagnético vemos? Hace falta un medio material para que se propaguen este tipo de ondas? Son ondas transversales o longitudinales? (después lo veremos). En el siguiente gráfico se muestra la variedad de radiaciones que abarca el espectro electromagnético y los tamaños característicos de longitudes de onda representativas. estadio 103 102 persona pelota 101 1 10-1 mosca 10-2 célula 10-3 10-4 proteína bacteria 10-5 10-6 10-7 10-8 10-9 molécula 10-10 10-11 10-12 Longitud de onda (en metros) Infrarrojo Ondas de radio Micro-ondas Rayos X blandos Visible Radio AM TV, FM Horno Microondas Radar Rayos X duros Ultravioleta Objetos calientes Rayos Gama Sol Lámparas Sincrotrón Equipo de Elementos Rayos X radiactivos EL MOVIMIENTO ONDULATORIO Tipos de ondas De acuerdo a lo que vimos la clase pasada, junto a una primera clasificación de las ondas en mecánicas y electromagnéticas, es posible distinguir diferentes tipos de ondas atendiendo a criterios distintos. En relación con su ámbito de propagación las ondas pueden clasificarse en: Unidimensionales: Son aquellas que, como las ondas en las cuerdas, se propagan a lo largo de una sola dirección del espacio. Bidimensionales: Se propagan en cualquiera de las direcciones de un plano de una superficie. Se denominan también ondas superficiales y a este grupo pertenecen las ondas que se producen en la superficie de un lago cuando se deja caer una piedra sobre él. Tridimensionales: Son aquellas que se propagan hacia diferentes direcciones en un volumen. Por ejemplo una fuente puntual que emite ondas esféricas en el espacio. Atendiendo a la periodicidad de la perturbación local que las origina, las ondas se clasifican en: Periódicas: Corresponden a la propagación de perturbaciones de características periódicas, como vibraciones u oscilaciones que suponen variaciones repetitivas de alguna propiedad. Así, en una cuerda unida por uno de sus extremos a un vibrador se propagará una onda periódica. No periódicas: La perturbación que las origina se da aisladamente y en el caso de que se repita, las perturbaciones sucesivas tienen características diferentes. Las ondas aisladas se denominan también pulsos. Según que la dirección de propagación coincida o no con la dirección en la que se produce la perturbación, las ondas pueden ser: Longitudinales: El movimiento local del medio alcanzado por la perturbación se efectúa en la dirección de avance de la onda. Un resorte que se comprime, al igual que el sonido, dan lugar a ondas longitudinales. Transversales: La perturbación del medio se lleva a cabo en dirección perpendicular a la de propagación. En las ondas producidas en la superficie del agua las partículas vibran de arriba a abajo y viceversa, mientras que el movimiento ondulatorio progresa en el plano perpendicular. Lo mismo sucede en el caso de una cuerda; cada punto vibra en vertical, pero la perturbación avanza según la dirección de la línea horizontal. Ambas son ondas transversales. Las ondas electromagnéticas, como veremos, también son transversales. Descripción matemática de una onda armónica La clase pasada vimos, a través de experiencias, que una onda armónica tenía un perfil sinusoidal, ahora vamos a buscar una expresión matemática que la describa. Para ello es preciso partir de la ecuación que define la oscilación del origen de la perturbación. Si la onda es armónica simple su ecuación correspondiente será: = A · sen t donde A es la amplitud de la perturbación y = 2 / T, siendo T el período temporal. También podemos expresar esta ecuación en función de la frecuencia temporal f = 1 / T = A · sen (2ft) puede representar la alteración, con el tiempo, de propiedades físicas tan diversas como una densidad, una presión, un campo eléctrico o un campo magnético. Dado que la perturbación avanza a una velocidad v, en recorrer una distancia r invertirá un tiempo t’= r / v. Eso significa que el estado de perturbación de cualquier punto P situado a una distancia r del origen O coincidirá con el que tenía el origen t' segundos antes. Por tanto, si en la ecuación de la perturbación que describe la situación del origen, se cambia t por t - t' se obtiene una ecuación que describe el estado de la perturbación del punto P: = A · sen (t – t’) = A · sen (t – r/v) Evidentemente esta perturbación no sólo se repite a intervalos regulares en el tiempo sino también en el espacio. Se denomina longitud de onda a la distancia que separa dos puntos sucesivos del espacio que se encuentran en el mismo estado de perturbación. Es decir que coincide con el espacio que recorre la perturbación en un tiempo igual al período, esto es = v · T. Así el argumento de la función seno correspondiente puede expresarse también en la forma dado que = 2/T y v = /T; lo cual permite escribir la ecuación de ondas en función de sus parámetros o constantes características, tales como la amplitud A, el periodo T y la longitud y las variables t y r que indican el instante de tiempo considerado y la distancia al origen del punto en el que se desea estudiar la perturbación. Veamos un ejemplo La ecuación de una onda transversal que se propaga a lo largo de una cuerda viene dada por la expresión = 0,1 · sen (2t - 4r) Se trata de determinar a) la amplitud A de la onda, b) su periodo T, c) su longitud de onda, d) la velocidad de avance de la perturbación, e) la magnitud de la perturbación en un punto que dista 0,2 m del origen al cabo de 0,5 segundos de iniciarse el movimiento. Para resolver las cuestiones a, b, c basta con identificar la ecuación general con la que corresponde al movimiento ondulatorio concreto que se pretende analizar. Por tanto: a) Comparando el factor que multiplica en ambas a la función seno resulta A = 0,1 m. b) Comparando el argumento o ángulo de la función seno, también llamado fase de la onda correspondiente, resulta: En lo que respecta a los coeficientes respectivos de la variable t se tiene: c) En lo que respecta a los coeficientes de la variable r : d) La velocidad v es el cociente entre y T: e) Sustituyendo los valores de t = 0,5 s y r = 0,2 m en la expresión de resulta: = 0,1 · sen (2 · 0,5 - 4 · 0,2) = 0,02 m Es decir, en ese punto y en ese instante la magnitud de la perturbación, medida por la altura que alcanza la cuerda, es de 0,02 m, la quinta parte de la máxima altura o elongación dada por la amplitud A = 0,1 m. Clase 2 LA NATURALEZA DEL SONIDO Las ondas sonoras constituyen un tipo de ondas mecánicas que tienen la virtud de estimular el oído humano y generar la sensación sonora. En el estudio del sonido se deben distinguir los aspectos físicos de los aspectos fisiológicos relacionados con la audición. Desde un punto de vista físico el sonido comparte todas las propiedades características del comportamiento ondulatorio, por lo que puede ser descrito utilizando los conceptos sobre ondas. Desde un punto de vista fisiológico sólo existe sonido cuando un oído es capaz de percibirlo. El sonido y su propagación Las ondas que se propagan a lo largo de un resorte como consecuencia de una compresión longitudinal del mismo constituyen un modelo de ondas mecánicas que se asemeja bastante a la forma en la que el sonido se genera y se propaga. Las ondas sonoras se producen también como consecuencia de una compresión del medio a lo largo de la dirección de propagación. Son, por tanto, ondas longitudinales. La clase pasada vimos cómo un parlante genera sonido efectuando desplazamientos hacia delante y hacia atrás. Si un objeto se mueve en un medio produce una perturbación que se traduce en un cambio de presión. La campana de un timbre vibra al ser golpeada por su correspondiente martillo, lo que da lugar a compresiones sucesivas del medio que la rodea, las cuales se propagan en forma de ondas . Un diapasón, la cuerda de una guitarra o la de un violín o las cuerdas vocales producen sonido según un mecanismo análogo. En todo tipo de ondas mecánicas el medio juega un papel esencial en la propagación de la perturbación; en ausencia de medio material la vibración no puede propagarse. La velocidad de propagación del sonido depende de las características del medio. En el caso de medios gaseosos, como el aire, las vibraciones son transmitidas de un punto a otro a través de choques entre las partículas que constituyen el gas, de ahí que cuanto mayor sea la densidad de éste, mayor será la velocidad de la onda sonora correspondiente. En los medios sólidos son las fuerzas que unen entre sí las partículas constitutivas del cuerpo las que se encargan de propagar la perturbación de un punto a otro. Este procedimiento más directo explica que la velocidad del sonido sea mayor en los sólidos que en los gases. Sonido físico y sensación sonora No todas las ondas sonoras pueden ser percibidas por el oído humano, el cual es sensible únicamente a aquellas cuya frecuencia está comprendida entre los 20 y los 20000 Hz. En el aire dichos valores extremos corresponden a longitudes de onda que van desde 16 metros hasta 1,6 centímetros respectivamente. En general se trata de ondas de pequeña amplitud. Cuando una onda sonora de tales características alcanza la membrana sensible del tímpano, produce en él vibraciones que son transmitidas por la cadena de huesecillos hasta la base de otra membrana, llamada ventana oval, que se halla localizada en la cóclea o caracol. El hecho de que la ventana oval sea de 20 a 30 veces más pequeña que el tímpano da lugar a una amplificación que llega a aumentar entre 40 y 90 veces la presión de la onda que alcanza al tímpano. Esta onda de presión se propaga dentro del caracol a través de un líquido viscoso hasta alcanzar otra membrana conectada a un sistema de fibras fijas por sus extremos a modo de cuerdas de arpa, cuyas deformaciones elásticas estimulan las terminaciones de los nervios auditivos. Las señales de naturaleza eléctrica generadas de este modo son enviadas al cerebro y se convierten en sensación sonora. Mediante este proceso el sonido físico es convertido en sonido fisiológico. El oído es capaz de distinguir unos sonidos de otros porque es sensible a las diferencias que puedan existir entre ellos en lo que concierne a alguna de las tres cualidades que caracterizan todo sonido y que son la intensidad, el tono y el timbre. Aun cuando todas ellas se refieren al sonido fisiológico, están relacionadas con diferentes propiedades de las ondas sonoras. Intensidad La intensidad del sonido percibido, o propiedad que hace que éste se capte como fuerte o como débil, está relacionada con la intensidad de la onda sonora correspondiente, también llamada intensidad acústica. La intensidad acústica es una magnitud que da idea de la cantidad de energía que está fluyendo por el medio como consecuencia de la propagación de la onda. Se define como la energía que atraviesa por segundo una superficie unidad dispuesta perpendicularmente a la dirección de propagación. La intensidad de una onda sonora es proporcional al cuadrado de su frecuencia y al cuadrado de su amplitud y disminuye con la distancia al origen de la perturbación. La magnitud de la sensación sonora depende de la intensidad acústica, pero también depende de la sensibilidad del oído. El intervalo de intensidades acústicas que va desde el umbral de audibilidad, o valor mínimo perceptible, hasta el umbral del dolor es muy 14 amplio, estando ambos valores límite en una relación del orden de 10 Otro de los factores de los que depende la intensidad del sonido percibido es la frecuencia. Ello significa que para una frecuencia dada un aumento de intensidad acústica da lugar a un aumento del nivel de sensación sonora, pero intensidades acústicas iguales a diferentes frecuencias pueden dar lugar a sensaciones distintas. Tono El tono es la cualidad del sonido mediante la cual el oído le asigna un lugar en la escala musical, permitiendo, por tanto, distinguir entre los graves y los agudos. La magnitud física que está asociada al tono es la frecuencia. Los sonidos percibidos como graves corresponden a frecuencias bajas, mientras que los agudos son debidos a frecuencias altas. Junto con la frecuencia, en la percepción sonora del tono intervienen otros factores de carácter psicológico. Así sucede por lo general que al elevar la intensidad se eleva el tono percibido para frecuencias altas y se baja para las frecuencias bajas. Entre frecuencias comprendidas entre 1000 y 3000 Hz el tono es relativamente independiente de la intensidad. Timbre El timbre es la cualidad del sonido que permite distinguir sonidos procedentes de diferentes instrumentos, aun cuando posean igual tono e intensidad. Debido a esta misma cualidad es posible reconocer a una persona por su voz, que resulta característica de cada individuo. El timbre está relacionado con la complejidad de las ondas sonoras que llegan al oído. Pocas veces las ondas sonoras corresponden a sonidos puros, sólo los diapasones generan este tipo de sonidos, que son debidos a una sola frecuencia y representados por una onda armónica. Los instrumentos musicales, por el contrario, dan lugar a un sonido más rico que resulta de vibraciones complejas. Cada vibración compleja puede considerarse compuesta por una serie de vibraciones armónico simples de una frecuencia y de una amplitud determinadas, cada una de las cuales, si se considerara separadamente, daría lugar a un sonido puro. Esta mezcla de tonos parciales es característica de cada instrumento y define su timbre. Debido a la analogía existente entre el mundo de la luz y el del sonido, al timbre se le denomina también color del tono. Experiencia para medir la velocidad del sonido Se utiliza el montaje experimental esquematizado en la siguiente figura Emisor Generador de ondas Detector Osciloscopio Un emisor de ultrasonido es alimentado mediante un generador de funciones con una onda senoidal de aproximadamente 40 KHz. Se mide el período T de la misma en el osciloscopio para conocer exactamente el valor de la frecuencia f = 1 / T. Sabemos que la velocidad de propagación viene dada por v = f . con lo cual nos hace falta conocer el valor de la longitud de onda para poder determinar v. Para ello debemos utilizar la opción trigger externo del osciloscopio. Si ahora desplazamos el detector, con respecto al emisor, veremos que en la pantalla del osciloscopio la función registrada también se desplaza, pasando por determinado punto de la pantalla un cierto número de máximos y mínimos. Si la distancia que desplazamos el detector es conocida, dividiendo esta por el número de máximos que atravesaron el punto de la pantalla obtendremos la longitud de onda de la perturbación. Debemos recordar que la perturbación es espacial y temporalmente periódica; el osciloscopio nos permite medir directamente la periodicidad temporal para el punto fijo del espacio en el que se encuentra el detector. Para observar la periodicidad espacial debemos desplazar el detector y fijarnos que sucede ahora en un punto fijo de la pantalla. Podemos aprovechar esta experiencia para medir también el decaimiento de la amplitud con la distancia. Clase 3 Experiencias para analizar la composición espectral de distintos sonidos Estas tres experiencias están orientadas al estudio del contenido de frecuencias (espectro) de distintas perturbaciones periódicas. La primera de ellas permite realizar una introducción al análisis de Fourier. Joseph Fourier (1768-1830) fue un matemático y físico francés que, entre otras cosas, demostró que toda función periódica no senoidal puede expresarse como la suma de funciones senoidales de distintas amplitudes, frecuencias y fases. A la frecuencia más baja se la denomina fundamental y las demás son armónicas superiores. Para poder observar esta composición de funciones es conveniente utilizar un sintetizador de señales y un osciloscopio. Puede mostrarse como ejemplo la síntesis de una onda cuadrada y una triangular. En la segunda experiencia se estudia el contenido de frecuencias (espectro) de distintas señales sonoras. Para ello se utiliza una tarjeta digitalizadora (Multipurpose Lab Interface MPLI) con su correspondiente programa de adquisición, un micrófono, un diapasón y un sintetizador musical electrónico. Antes de comenzar la medición es conveniente introducir los conceptos de velocidad de muestreo y tiempo de medición. En primera instancia se muestra que un diapasón produce un sonido puro ya que la perturbación resultante es una onda sinusoidal y en consecuencia posee una sola frecuencia. A continuación se pasa a estudiar señales de contenido espectral más complejo generadas a partir del sintetizador. Se compara la forma de la onda y su contenido espectral (FFT). Unos buenos ejemplos para analizar son la flauta de pan, que produce un sonido casi puro cuando se toca una sola tecla, y el mismo instrumento cuando se tocan tres octavas juntas. Puede mencionarse al ecualizador de un equipo de audio como un dispositivo en el cual el contenido espectral de una señal es modificado intencionalmente. Por último, en la tercera experiencia, se muestra el fenómeno de batidos Qué sucede cuando tenemos dos fuentes que emiten con frecuencias muy cercanas? Supongamos que las ondas son del tipo = A · sen t = A · sen t Vamos a llamar = ( 1 + 2 ) / 2 = ( 1 - 2 ) / 2 Ahora bien, podemos escribir 1 = 1 /2 + 2 /2 + 1 /2 - 2 /2 = + 2 = 1 /2 + 2 /2 - 1 /2 + 2 /2 = - Luego sen t = sen t . cos t + sen t . cos t sen t = sen t . cos t - sen t . cos t Con lo cual 2 A cos t . sen t Vemos que obtenemos una función que oscila con la frecuencia promedio (sen t) pero modulada por una función de período mayor (2 A cos t) Para observar este fenómeno se realiza la siguiente experiencia Osciloscopio Generador dual Parlante El generador dual permite obtener dos señales, cuyas frecuencias pueden controlarse separadamente y también posibilita realizar la suma de las mismas. La perturbación resultante (batido) es graficada en un osciloscopio y al mismo tiempo enviada a un parlante que permite escuchar la señal. Variando la frecuencia de una de las ondas obtendremos batidos cuya frecuencia irá disminuyendo a medida que las frecuencias individuales sean tanto más parecidas. Se muestra el mismo efecto mediante la excitación de dos diapasones. ONDAS ESTACIONARIAS Hasta ahora hemos considerado el problema de propagación de ondas en el cual la perturbación puede viajar libremente en el medio. Sin embargo, un problema de interés práctico ocurre, por ejemplo, cuando una onda se refleja hacia atrás por algún tipo de “pared”. Cuando se dispone de un arreglo físico determinado, como en el caso anterior la pared, las soluciones de la ecuación de ondas deben ajustarse a las condiciones que el arreglo impone. Estas condiciones se conocen como condiciones de contorno, y restringen las posibles soluciones a un problema dado. Dos casos de particular interés lo constituyen las ondas estacionarias de presión en tubos y ondas estacionarias en cuerdas ya que son la base de los instrumentos musicales de viento y cuerda. Vamos a ver por ejemplo los modos normales de una cuerda 0 L r En este caso tendremos una combinación de dos perturbaciones: una viajando hacia la derecha y otra hacia la izquierda. Luego la perturbación resultante será: = A sen [2 (t/T – r/)] + B sen [2 (t/T + r/)] Desarrollando los senos y agrupando tenemos que = (A+B) sen [2t/T] cos [2 r/] + (-A+B) sen [2 r/] cos [2t/T] En r = 0 0 para todo t por lo tanto, y dado que sen [2 r/] = 0 debe cumplirse que A = - B , luego = 2B sen [2 r/] cos [2t/T] pero en r = L también debe ser 0 para todo t por lo tanto 2 L/ = n O sea que no todas las longitudes de onda estarán permitidas sino sólo aquellas que cumplan con esa relación Experiencia para estudiar modos normales en una cuerda y en superficies Estas dos experiencias permiten observar la existencia de modos normales unidimensionales (en una cuerda) y bidimensionales (placas de Chadny). En este último caso es sólo cualitativa ya que es matemáticamente muy complicado modelizar el sistema. En el caso de la cuerda puede realizarse el siguiente montaje: cuerda polea Wave driver generador osciloscopio pesas Se le aplica una tensión T o a la cuerda, mediante pesas y cuidando que no se estire. Los puntos fijos de la misma estarán determinados por la posición del wave-driver y del soporte indicado en línea de puntos en el gráfico. Variando la frecuencia de la señal entregada por el generador al wave-driver es posible excitar distintos armónicos en la cuerda. La frecuencia f puede obtenerse a partir de la medición realizada con el osciloscopio y la longitud de onda midiendo directamente la posición de los nodos sobre la cuerda. Luego sabemos que: .f =v pero a su vez, en el caso de la cuerda, v = (T o / )1/2 donde es la densidad de la cuerda. Así tenemos todos los elementos como para calcular el valor de pudiendo el mismo contrastarse con el obtenido a partir de la medición del largo de la cuerda y de su peso. Clase 4 LA NATURALEZA DE LA LUZ En este curso nos limitaremos a estudiar algunos aspectos del carácter ondulatorio de la luz y dejaremos de lado su carácter corpuscular. En la primera clase vimos que lo que comúnmente denominamos luz es la porción visible del espectro electromagnético. Dijimos también que este tipo de ondas eran transversales y que no necesitaban de un medio material para propagarse. Podemos hacer la analogía entre una onda electromagnética y la que se propaga en una cuerda (no olvidando que esta última es mecánica y por lo tanto necesita de un medio material para propagarse) ya que la amplitud del campo eléctrico es equivalente a la amplitud de la oscilación en la cuerda y en ambas la vibración es perpendicular a la dirección de avance de la perturbación. Sin embargo debemos considerar que una fuente de luz ordinaria consiste en un número muy grande de emisores atómicos orientados al azar. Cada átomo excitado emite un tren de onda de aproximadamente 10-8 s en el cual la orientación del campo eléctrico, si bien es siempre perpendicular a la dirección de propagación, varía de un emisor al otro. Se denomina a este tipo de radiación luz natural. Si por el contrario se tiene una radiación en la cual la dirección del campo eléctrico no fluctúa al azar a esa se la denomina luz polarizada. Esquemáticamente las podríamos representar como en la figura Luz polarizada Luz natural Vamos a ver mediante una sencilla experiencia que son ondas transversales. Para ello tomemos dos hojas polaroid y veamos que sucede cuando rotamos una con respecto a la otra. Qué está pasando acá? El filtro Polaroid está formado por moléculas alargadas conductoras que pueden pensarse como hilos de alambre alineados en una dirección determinada. Cuando el campo eléctrico tiene una orientación que es paralela al alambre hace que los electrones circulen por el mismo generando así una corriente. Los electrones a la vez tienen colisiones con los átomos de la red impartiéndoles energía y calentando los alambres. Así la energía que tenía el campo eléctrico es transferida a los alambres. Por el contrario cuando el campo eléctrico es perpendicular a los alambres, los electrones no disponen de lugar para moverse y en consecuencia la energía del campo eléctrico no es absorbida y la onda permanece inalterada. En general la orientación que tenga el campo eléctrico de una radiación lo podremos descomponer en una orientación paralela y otra perpendicular al eje de transmisión del polaroid. Dado que el ojo no distingue polarizaciones, es necesario dos polarizadores para efectuar la experiencia, uno para polarizar la luz natural y otro para analizarla. Cabe destacar que hay muchos procesos mediante los cuales puede obtenerse luz parcialmente polarizada. Analizar por ejemplo con un polarizador la luz reflejada por una superficie. Podemos preguntarnos ahora qué es el color y que analogía puede hacerse con lo visto para sonido. Habíamos visto que el espectro electromagnético está constituido por ondas con una gran variedad de frecuencias. Vimos también que la luz blanca está constituida por radiaciones cuyas longitudes de onda se hallan distribuidas en forma continua entre los 700 nm y los 400 nm, cada una asociada con determinado color. Sin embargo la percepción del color es un fenómeno complejo en donde no sólo interviene el aspecto físico de la radiación (frecuencia) sino también aspectos fisiológicos y psicológicos. Veamos por ejemplo si es necesario sumar radiaciones cuyas frecuencias estén distribuidas en un continuo para percibir “luz blanca”. Experiencias para la formación de colores Para ello montemos tres reflectores que emitan en el rojo (R), verde (G) y azul (B). Si hacemos superposición de los haces luminosos obtendremos algo como lo esquematizado en la figura Donde las combinaciones vienen dadas por R+G=Y R+B=M G+B=C En general obtendremos una extensa gama de colores combinando con los pesos adecuados radiación RGB ya que constituye una terna de colores primarios. Ahora bien, porqué esto es así? El ojo posee receptores (conos) que responden a un gran ancho de banda pero cuyas sensibilidades están centradas alrededor de longitudes de onda de 425 nm, 525 nm y 625 nm. Si graficamos sensibilidad vs. longitud de onda las respuestas serían algo como lo representado en la siguiente figura. Obsérvese que son campanas que se superponen. Cada tipo de cono no es capaz de distinguir cuál es la longitud de onda que lo está excitando sólo responde al estímulo de determinada forma y envía al cerebro una señal proporcional al estímulo recibido. Cómo hace el cerebro para interpretar que por ejemplo esta recibiendo radiación amarilla y no roja (las dos son detectadas por los conos rojos)? Porque en un caso también están excitados de forma adecuada los conos verdes. El cerebro “conoce” la curva de sensibilidades de cada tipo de cono y cómo ellas se superponen, luego pondera los estímulos recibidos. Surge ahora como duda porqué la obtención de los diferentes colores mediante pigmentos es distinta? Debemos pensar que los pigmentos absorben determinadas longitudes de onda y en realidad el color que vemos es debido a la luz reflejada. Por ejemplo si algo iluminado bajo radiación RGB se ve amarillo (Y), es porque en realidad está absorbiendo la radiación azul (B) y reflejando la roja y la verde (R+G = Y) Si en cambio se ve cyan (C) es porque está absorbiendo el rojo (R) y reflejando el azul y el verde (B+G = C). Si combinamos pigmentos cyan y amarillo, dado que uno absorbe el rojo y otro el azul, la radiación reflejada será la verde. Así para sustracción de colores la terna de colores primarios es cyan (C), amarillo (Y) y magenta (M) ya que a partir de ellos pueden formarse los restantes. Claramente una pantalla de TV no funciona absorbiendo radiación sino emitiendo luz por lo tanto los colores deberán formarse a partir de la mezcla (RGB). Es muy ilustrativo mirar una pantalla de TV con un microscopio, se verá algo así INTERFERENCIA Y DIFRACCIÓN DE ONDAS La primer clase vimos, en las experiencias realizadas con la cuba de ondas, que bajo determinadas circunstancias es posible hacer que las ondas se difracten e interfieran. Estos fenómenos son característicos de los procesos ondulatorios y si bien es más fácil generarlos empleando por ejemplo una fuente sonora, resulta más interesante verlos a partir de fuentes de luz. Ya habíamos observado difracción de un láser por una ranura pero ahora estudiaremos estos dos fenómenos con más detenimiento. Interferencia Vamos a realizar una experiencia en la cual podamos observar diferentes figuras de interferencia. Para ello montemos un interferómetro de Michelson ya que nos permitirá clarificar algunos conceptos. Por ejemplo, cuando trabajamos con la cuba de ondas dijimos que si las dos varillas que actuaban como fuentes puntuales generando las ondas no vibraban en forma sincronizada, entonces no era posible generar una figura de interferencia que permaneciese estable en el tiempo. Cuando trabajamos con luz, una forma de crear fuentes que se comporten de esa manera (fuentes coherentes) es, por ejemplo, generando dos imágenes de una fuente mediante espejos. Sin embargo esto no basta. Analicemos la siguiente figura: M1 M1’ SE M2 L Luz proveniente de una fuente luminosa llega a un semi-espejo (SE) que refleja parte de la misma hacia el espejo M 1 y parte la trasmite hacia el espejo M 2 . Luego ambos haces son reflejados y se recombinan luego de volver a reflejarse parcialmente en el semiespejo. Consideremos que si M 2 estuviese ubicado en la línea punteada M 1 ’ la diferencia de caminos entre los dos brazos sería nula. Si en cambio uno está más alejado que el otro la diferencia de distancias recorridas será 2 L. Una onda tiene una frecuencia tanto mejor definida cuanto más largo es el tren de ondas. Por ejemplo para tener una onda monocromática ésta debería tener un tren de ondas infinito y por lo tanto debería haber comenzado a emitirse en t = - . En la práctica las fuentes luminosas que se usan normalmente tienen trenes de onda muy cortos ya que cada átomo emite sólo un instante. Por lo tanto si la diferencia de caminos en el interferómetro (2 L) es mayor que la longitud del tren de ondas, cuando la luz proveniente de los dos brazos se recombine, en realidad se superpondrán trenes de ondas emitidos a distintos tiempos y por lo tanto la fase inicial de cada uno de ellos no variará en forma sincronizada. Así no tendremos una figura de interferencia estable. Se debe usar entonces una fuente de luz cuyos trenes de onda sean lo suficientemente largos, por ejemplo un láser. Ahora variando la orientación de los espejos es posible desplazar las dos imágenes de la fuente, así como en la cuba de ondas lo hacíamos juntando o separando los alambres que agitaban la superficie del agua. En este interferómetro tenemos más libertad de movimientos por lo que es posible no sólo variar el espaciado de la franjas sino también desplazar una fuente hacia atrás de la otra con lo que se obtiene figuras de interferencia más complicadas. Pensemos que entre un máximo de luz y un mínimo hay media longitud de onda de diferencia de camino óptico. Dado que la longitud de onda de la luz es muy pequeña (en este caso 633 nm) estamos en condiciones de medir cambios de camino óptico muy chicos. Resulta así que un interferómetro es una herramienta de medición muy precisa. Veamos por ejemplo que sucede si calentamos con un soldador el aire que rodea uno de los brazos cuando inicialmente el interferómetro estaba ajustado para que la diferencia de camino entre ambos brazos fuese casi cero............. Clase 5 Difracción En esta clase veremos el fenómeno de difracción que sufre un haz láser al atravesar una ranura y lo compararemos con el que produce un alambre muy fino. La geometría de la difracción por una ranura se esquematiza en la siguiente figura x d L La posición de los mínimos viene dada por: x mín = n L / d n = 1, 2, 3..... donde es la longitud de onda de la luz empleada, L la distancia de la ranura a la pantalla y d es el ancho de la ranura. Si bien esta relación surge de una formulación que aquí no desarrollaremos, analicen, al montar la experiencia, que sucede si se varían las magnitudes L y d. Qué esperan que suceda si se cambia la longitud de onda? Cuál es la figura de difracción que obtenemos si ahora cambiamos la ranura por un alambre delgado? Es similar o no al de la ranura? Si es similar, estimen a partir de la posición de los mínimos y de la ecuación dada para ellos, el grosor del alambre (tengan en cuenta que la longitud de onda empleada es = 633 nm y que 1 nm = 10-6 mm). Para verificar este valor se sugiere medir el alambre en forma directa con un microscopio. El microscopio tiene una escala grabada en el ocular que debe graduarse según el aumento empleado. Como lo harían? Clase 6 Procesado de imágenes Cuando analizamos señales sonoras vimos que en general estaban compuestas por numerosas frecuencias. También dijimos que a través de un ecualizador de audio lo que hacíamos era modificar intencionalmente el contenido espectral de la señal. Esto lo hacíamos incrementando o disminuyendo la amplitud de determinadas frecuencias. Podrá hacerse lo mismo con imágenes? Con anterioridad vimos que una función no senoidal podía sintetizarse como suma de funciones sinusoidales de distintas amplitudes, frecuencias y fases. Así generamos, por ejemplo, ondas cuadradas y triangulares. Ahora bien, podemos pensar una imagen como una función bidimensional que está constituida por muchas funciones sinusoidales con distintas frecuencias, amplitudes, fases y orientaciones (ya que ahora la función resultante ocupa un plano). Por ejemplo una onda cuadrada unidimensional en imágenes se vería así T (x) x y podría componerse sumando estas funciones T (x) + x T (x) x + T (x) x Para estar en condiciones de modificar el contenido de frecuencias de una imagen tenemos que ver que le sucede a un haz de luz cuando atraviesa una transparencia que tiene una sola frecuencia, esto es, cuando atraviesa un objeto cuya transmisión es sinusoidal. En ese caso la luz se difracta en tres órdenes, cuya separación y orientación depende de la frecuencia espacial del objeto y de su orientación. Así para un objeto complejo constituido por muchas frecuencias espaciales tendremos una multitud de órdenes difractados. Uno central, común para todos los elementos constitutivos y dos laterales dependientes del valor de la frecuencia y de la orientación de la periodicidad. Para modificar el contenido de frecuencias espaciales de un objeto complejo deberíamos primero, obtener todos los haces difractados, luego bloquear o retardar alguno de ellos y por último rearmar la imagen modificada. A esta operación se la denomina filtrado espacial y puede llevarse a cabo en un procesador óptico. En la siguiente figura se esquematiza un procesador óptico. Imagen del objeto Imagen de S La luz proveniente de un láser se expande y se colima (se obtiene nuevamente un haz paralelo) mediante la lente L 1 . Con ese haz se ilumina una transparencia (imagen de entrada) ubicada en el plano P 1 . La lente L 2 permite obtener en el plano P 2 los órdenes difractados que anteriormente mencionamos. En ese plano se realiza el filtrado espacial, luego la lente L 3 permite reobtener en el plano P 3 la imagen modificada. Veamos un ejemplo La imagen de entrada (izquierda) tiene un ruido que sería deseable eliminar, la imagen central muestra el espectro de una porción de esa imagen. Dado que el ruido es periódico estará caracterizado por frecuencias bien definidas que originan los puntos brillantes sobre el plano transformado. Si esas frecuencias son eliminadas, obstruyendo el pasaje de la luz por esas zonas, y se vuelve a componer la imagen, se logra eliminar el ruido en la zona filtrada (derecha).