matemáticas octavo - instituto san ignacio de loyola

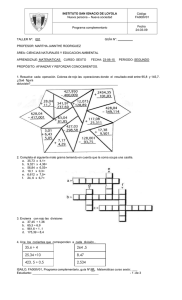
INSTITUTO SAN IGNACIO DE LOYOLA
Código
Nueva persona – Nueva sociedad
FA008V01
Programa complementario
Fecha
24-03-09
TALLER Nº: 3
GUÍA N°: _________
PROFESOR: LUIS HERNANDO BURGOS CONTRERAS
ÁREA: CIENCIAS NATURALES
CURSO: _8ª – 8C_
APRENDIZAJE: MATEMATICAS
FECHA: _23-06-15 PERIODO: SEGUNDO
PROPÓSITO: REFORZAR LOS TEMAS VISTOS EN CLASE
1) Indica las expresiones algebraicas correspondientes a los siguientes enunciados, utilizando una sola letra (x):
a) El siguiente de un número, más tres unidades.
b) El anterior de un número, menos doce unidades.
c) El doble de un número más su mitad.
d) El triple de un número, menos su cuarta parte.
e) La tercera parte de un número, más el doble de dicho número.
2) El número x es un número entero. Escribe frases equivalentes a las siguientes expresiones algebraicas:
a) x + 1
b) x - 1
c) 2 ·x + x : 2
d) x : 3 + 2 ·x
e) (x + 1) : 2
f) (3 ·x) : 5
3) Rellena la siguiente tabla:
Expresión
algebraica
3x + 2y + z
x
y
z
5
12’5
2
52 +7 – 9 = 23
x2 + y - z
x · (y2 – z)
Expresión numérica
4
3
7
2’5
3
7
x:2+ y:3–z
4 · 32 – 7 = 29
11 : 2 + 12 : 3 – 9 = 0’5
5
10
3
52 + 102 = 125
5) Calcula el valor numérico de la expresión:
a) 2x + 1, para x = 1
b) 2x2 – 3x + 2, para x = –1
c) x3 + x2 + x + 2, para x = –2
d) 2x2 – 5x + 1, para x = ½
6) Realiza las siguientes operaciones entre monomios:
ISAILO, FA008V01, Programa complementario, guía Nº:____, MATEMÁTICAS, curso: OCTAVO
Estudiante: ________________________________________
- 1 -de 3
a) –x2 + x + x2 + x3 + x
b) 8xy2 – 5x2y + x2y - xy2
c) 8x2 – x + 9x + x2
d) 2x2 · 4x3 · 5x6
e) –3x2 · xyz · 6y3 · x2
f) 15x3 : 5 x2
g) –8x3y2 : 2x2y
h) 10x4yz2 : 5xyz
i)  3x  (2x )  7 x
4
7) Realiza las siguientes operaciones con polinomios, dando el resultado lo más reducido posible.
a) (2x  3)  ( 4 x  2)
b) (3x  1)  (2x 2  8x  3)
c) (x  1)  (x 2  5x  3)
d) (18x 5  8x 4  6x 2 ) : (2x )
e) (24x 6  9x 4  6x 2 ) : (3x 2 )
8) Sabiendo que P(x) = 2x4 + x2 – 4x –1 y Q= 4x4 – 2x. Calcula:
a) P(x) + Q(x)
b) P(x) - Q(x)
c) 3x2 · P(x)
d) (-2x3) · Q(x)
e) Q(x) : (2x)
9) Expresa el desarrollo de los siguientes cuadrados.
Aplica la regla: (𝑎 + 𝑏)2 = 𝑎2 + 2𝑎𝑏 + 𝑏 2
a) (2𝑤 + 𝑎)2
b) (4𝑡 + 3ℎ)2
c) (𝑥𝑦 3 + 2𝑦)2
d) (4𝑑2 + 9𝑘 2 )2
10)
a.
b.
c.
Expresa el desarrollo de los siguientes cuadrados. Aplica la regla: (𝑎 − 𝑏)2 = 𝑎2 − 2𝑎𝑏 + 𝑏 2
(𝑥 2 − 3𝑝)2
(2𝑥 + 3𝑦 2 )2
(5𝑦 − 3𝑥 2 )2
1
2
1
d. (3 𝑥 3 − 2 𝑦 2 )
1
2
e) (2 𝑥 − 6)
11)
a)
b)
c)
Expresa el desarrollo de los siguientes productos. Aplicando la regla (𝑎 + 𝑏)(𝑎 − 𝑏) = 𝑎2 − 𝑏 2
(2x-3)(2x+3)
(a2b3-4) (a2b3+4)
(3x3y4+4xy5) (3x3y4+4xy5)
1
1
2
3
d) (2 − 𝑏 2 ) (2 + 𝑏 2 )
2
3
e) (3 𝑎3 𝑏 2 − 5 𝑎5 ) (3 𝑎3 𝑏 2 − 5 𝑎5 )
12) Halla el cubo de cada expresión. Aplicando la regla: (𝑎 + 𝑏)3 = 𝑎3 + 3𝑎2 𝑏 + 3𝑎𝑏 2 + 𝑏 3
a)
b)
c)
d)
e)
f)
(2𝑥 + 𝑦)3
(𝑚 + 3𝑡)3
(4𝑎 + 5𝑑)3
(𝑥 2 + 2𝑎3 )3
(3𝑥𝑦 + 2𝑥 2 )3
(5 + 𝑥 3 )3
ISAILO, FA008V01, Programa complementario, guía Nº:____, MATEMÁTICAS, curso: OCTAVO
Estudiante: ________________________________________
- 2 -de 3
g) (𝑧 + 6𝑥 4 )3
13) Halla el cubo de cada expresión. Aplicando la regla: (𝑎 − 𝑏)3 = 𝑎3 − 3𝑎2 𝑏 + 3𝑎𝑏 2 − 𝑏 3
a)
b)
c)
d)
e)
f)
(𝑏 − 5)3
(𝑦 − 2𝑥 2 )3
(2𝑥 − 𝑏 2 )3
(2𝑧 2 − 𝑥 2 )3
(2𝑎 − 3𝑐)3
𝑎
𝑥
( − )3
𝑏
2𝑥
2
𝑥
g) ( 𝑦 − 2)3
CRITERIOS DE EVALUACIÓN:

El trabajo debe ser realizado durante las vacaciones y se debe entregar la primera clase de
matemáticas después de las vacaciones.

Entregar en hojas cuadriculados tamaño carta, marcado y bien presentado

Recuerde que en la guía deben estar todos los procedimientos necesarios para el desarrollo de la
misma
ISAILO, FA008V01, Programa complementario, guía Nº:____, MATEMÁTICAS, curso: OCTAVO
Estudiante: ________________________________________
- 3 -de 3