1 FUNCIONES -geometria estadistica

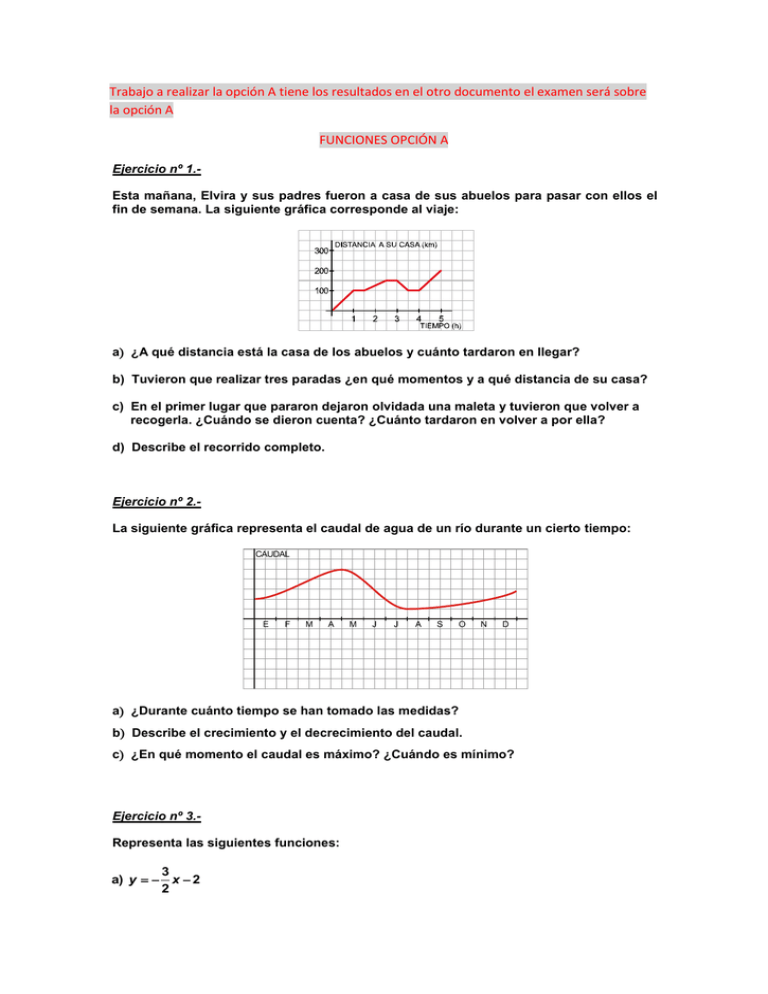
Trabajo a realizar la opción A tiene los resultados en el otro documento el examen será sobre
la opción A
FUNCIONES OPCIÓN A
Ejercicio nº 1.Esta mañana, Elvira y sus padres fueron a casa de sus abuelos para pasar con ellos el
fin de semana. La siguiente gráfica corresponde al viaje:
a ¿A qué distancia está la casa de los abuelos y cuánto tardaron en llegar?
b) Tuvieron que realizar tres paradas ¿en qué momentos y a qué distancia de su casa?
c) En el primer lugar que pararon dejaron olvidada una maleta y tuvieron que volver a
recogerla. ¿Cuándo se dieron cuenta? ¿Cuánto tardaron en volver a por ella?
d) Describe el recorrido completo.
Ejercicio nº 2.La siguiente gráfica representa el caudal de agua de un río durante un cierto tiempo:
a ¿Durante cuánto tiempo se han tomado las medidas?
b Describe el crecimiento y el decrecimiento del caudal.
c ¿En qué momento el caudal es máximo? ¿Cuándo es mínimo?
Ejercicio nº 3.Representa las siguientes funciones:
3
a) y   x  2
2
b 3x  2y  1
c y  2
Ejercicio nº 4.Halla la ecuación de cada una de estas rectas:
a Pasa por los puntos P1, 2 y Q1, 8.
b Es paralela a 4x  2y  1 y pasa por el punto A0, 4.
Ejercicio nº 5.Un depósito contenía inicialmente 20 litros de agua cuando abrimos un grifo que arroja
un caudal de 10 litros por minuto dejamos el grifo abierto durante 6 minutos.
a Halla la ecuación de la recta que nos da el contenido de agua del depósito en función
del tiempo, desde que abrimos el grifo hasta que lo cerramos.
b Represéntala gráficamente.
c ¿Cuánta agua había en el depósito al cabo de los 5 minutos?
Ejercicio nº 6.Un ciclista sale a hacer ejercicio y pedalea a 15 km/h. Media hora más tarde sale en su
busca un motorista a 60 km/h.
a) Representa las funciones que dan el espacio recorrido por cada uno en función del
tiempo y escribe sus expresiones analíticas.
b) ¿Cuánto tardará el motorista en alcanzar al ciclista?
FUNCIONES OPCIÓN B
Ejercicio nº 1.Pablo salió de su casa a las 8 de la mañana para ir al instituto. En el recreo, tuvo que
volver a su casa para ir con su padre al médico. La siguiente gráfica refleja la situación:
a ¿A qué hora comienzan las clases y a qué hora empieza el recreo?
b ¿A qué distancia de su casa está el instituto? ¿Y el consultorio médico?
c ¿Cuánto tiempo ha estado en clase? ¿Y en el consultorio médico?
d Haz una interpretación completa de la gráfica.
Ejercicio nº 2.Esta gráfica muestra en cuántos minutos se adelanta o se atrasa un reloj de sol en el
transcurso de un año:
a ¿En qué fecha el reloj de sol tiene el máximo adelanto? ¿Cuándo el máximo atraso?
b ¿En qué fechas es exacto?
c ¿Es una función continua?
d ¿Es una función periódica? En caso afirmativo, ¿cuál es su periodo?
e Describe el crecimiento y el decrecimiento de la función.
Ejercicio nº 3.Representa gráficamente las funciones:
2
a) y   x  1
3
b x  3y  1
c y  2
Ejercicio nº 4.Halla la ecuación de cada una de las siguientes rectas:
a Es paralela a y  5x y pasa por el punto P2, 8.
b Pasa por los puntos A2, 5 y B2, 7.
Ejercicio nº 5.Por 6 litros de leche hemos pagado 4,8 €; y 14 litros nos habrían costado 11,2 €.
a Halla la ecuación de la recta que nos da el precio, y, en función de los litros de leche
que compremos, x.
b Represéntala gráficamente.
c ¿Cuánto nos habrían costado 45 litros de leche?
Ejercicio nº 6.La siguiente gráfica recoge la evolución de la temperatura de una vivienda familiar, a lo
largo de un día de invierno:
a) ¿Cuál es el dominio de definición?
b) ¿A qué horas del día la temperatura es mínima? ¿Y máxima? Indica en cada caso la
temperatura que se llega a alcanzar.
c) ¿En qué intervalos crece la función? ¿Cuándo decrece?
d) Indica en qué momento del día la temperatura permanece constante. ¿A qué crees
que se debe?
GEOMETRÍA OPCIÓN A
Ejercicio nº 1.Indica el valor de los ángulos que faltan en las siguientes figuras:
Ejercicio nº 2.Observa la figura y dibuja el lugar geométrico de los puntos del plano que están a la
misma distancia de ambas rectas.
Ejercicio nº 3.Indica si son verdaderas o falsas las siguientes afirmaciones. En las que sean falsas,
explica por qué:
a En un poliedro simple, la suma del número de caras, el de vértices y el de aristas es
siempre igual a 2.
b El cubo y el dodecaedro son poliedros duales.
c El tetraedro es dual de sí mismo.
d La siguiente figura es un poliedro regular pues todas sus caras son triángulos
equiláteros:
Ejercicio nº 4.a La siguiente figura es un ortoedro con dos dimensiones iguales. ¿Cuáles son sus
planos de simetría?
b Dibuja una semiesfera e identifica sus ejes de simetría.
Ejercicio nº 5.Halla la longitud de la apotema de un hexágono regular de 8 cm de lado.
Ejercicio nº 6.Halla la generatriz de un tronco de cono de 15 cm de altura en el que la longitud de la
base mayor es de 50,24 cm, y la de la base menor, 18,84 cm.
Ejercicio nº 7.Halla el área de la parte coloreada:
AB  10 cm
CD  16 cm
AC  BD  5 cm
Ejercicio nº 8.Halla el área total de un tronco de pirámide de 9 cm de altura cuyas bases son
cuadrados de lados 15 cm y 12 cm, respectivamente.
Ejercicio nº 9.Halla el volumen de cada uno de los siguientes cuerpos geométricos:
a El mayor cilindro inscrito en este prisma:
b
diámetro  7 m
Ejercicio nº 10.Dibuja la figura, F, de vértices A3, 1, B1, 1, C1, 3 y D4, 3.
a) Obtén la figura, F , que resulta al aplicarle a F una traslación de vector t  7, 3 .
b Aplica a F ' una simetría cuyo eje sea el eje X.
Ejercicio nº 11.a Describe un movimiento que transforme el triángulo F1 en el triángulo F2.
b Describe otro movimiento que transforme el triángulo F1 en el triángulo F3.
Ejercicio nº 12.a Completa el siguiente friso e indica cuál es el motivo mínimo:
¿Cuál es la translación que transforma la figura en sí misma?
b Completa el siguiente rosetón e indica cuál es su orden de giro:
GEOMETRÍA OPCIÓN B
Ejercicio nº 1.Halla el valor de los ángulos señalados en cada figura:
Ejercicio nº 2.La siguiente figura es una esfera de centro C y radio 3 unidades. ¿Cómo definirías
dicha esfera como lugar geométrico?
Ejercicio nº 3.Dibuja cada una de las siguientes figuras y su desarrollo plano:
a Un prisma de base hexagonal.
b Una pirámide de base cuadrada.
c Un cono recto.
d Un tronco de cono.
Ejercicio nº 4.Identifica los planos de simetría y ejes de giro de un prisma heptagonal regular.
Ejercicio nº 5.Calcula la longitud de la diagonal de un ortoedro cuyas dimensiones son 7 dm, 6 dm
y 9 dm.
Ejercicio nº 6.a Desde un punto P se traza una tangente a una circunferencia. La distancia de P al
centro de la circunferencia es de 25 cm, y la distancia de P al punto de tangencia es
de 24 cm. ¿Cuál es la longitud del radio?
b En una circunferencia de 7 cm de radio trazamos una recta a 4 cm de su centro. Halla
la longitud de la cuerda que determina esta recta en la circunferencia.
Ejercicio nº 7.Halla el área de la siguiente figura en la que el triángulo inferior es equilátero:
Ejercicio nº 8.Halla la superficie total de cada una de estas figuras:
Ejercicio nº 9.Halla el volumen de cada una de las siguientes figuras:
Perímetro de la base  12,56 cm
Ejercicio nº 10.-
a Dibuja la figura que se obtiene al aplicarle a F una simetría de eje e:
b) Aplica a las siguientes figuras una traslación de vector t 1,  4  :
Ejercicio nº 11.a Describe un movimiento que transforme F1 en F2.
b Describe otro movimiento que transforme F1 en F3.
Ejercicio nº 12.La siguiente figura muestra el momento en que se encuentra una partida de billar. Indica
el recorrido que ha de hacer la bola B para dar a la bola N después de dar en las
bandas PS y PQ.
ESTADÍSTICA Y AZAR OPCIÓN A
Ejercicio nº 1.a Haz una tabla de frecuencias en la que se refleje el número de veces que aparece
repetida cada una de las vocales en esta frase:
"La felicidad no consiste en tener siempre lo que se quiere, sino en querer siempre lo
que se tiene".
b Representa gráficamente la distribución anterior.
Ejercicio nº 2.Una empresa de publicidad hace una encuesta entre los lectores de una revista para
saber su edad aproximada y estudiar si deben anunciarse o no en esa revista. Las
respuestas obtenidas se reflejan en esta tabla:
EDAD
10 - 13
13 - 16
16 - 19
19 - 22
22 - 25
25 - 28
N. DE LECTORES
110
248
115
20
4
3
a Calcula la media y la desviación típica.
b Calcula qué porcentaje de lectores tiene menos de 19 años. ¿Qué observas?

c En otra encuesta realizada, la edad media era de 30,4 años y la desviación típica, de
3,2. Halla el coeficiente de variación en los dos casos y compara las dispersiones.
Ejercicio nº 3.En una urna hay 5 bolas, cuatro rojas y una azul. Sacamos una bola y anotamos su color.
Escribe el espacio muestral y califica cada suceso según su probabilidad:
TIPO DE SUCESO
SUCESO
Seguro
Sacar bola roja o azul.
Sacar bola azul.
Sacar bola verde.
Sacar bola roja.
Ejercicio nº 4.En un bombo se introducen 100 bolas numeradas del 0 al 99. Se extrae una bola al azar.
Calcula la probabilidad de que:
a La bola extraída contenga un número de dos cifras.
b El número extraído sea menor que 10.
Ejercicio nº 5.Al lanzar 1 000 veces un dado se obtienen los resultados de la tabla:
a ¿Cuál es la frecuencia absoluta del 6?
b Calcula las frecuencias relativas de cada suceso.
c Estima la probabilidad de obtener par con ese dado.
Ejercicio nº 6.Hemos preguntado a 1 600 personas por el número de viajes que realizan anualmente
por motivos laborales y las respuestas fueron:
N. DE VIAJES
0
1
2
3
4 o más
N. DE PERSONAS
224
320
768
192
96
a Haz una taba de frecuencias.
b Expresa el número de personas en porcentaje y representa gráficamente la
distribución. ¿Qué porcentaje viaja como mínimo 2 veces al año?
ESTADÍSTICA Y AZAR OPCIÓN B
Ejercicio nº 1.Los huevos se clasifican según el peso máximo que tengan. Hemos pesado 30 huevos y
los resultados en gramos han sido los siguientes:
40,2 46 47,5 58 61
62,4 66 65,5 57,3 52
54 48,3 62,4 64 62
65,2 69 66,5 42 53,5
48 63,6 67,5 63 61
53
68 69,5 67 66
a Elabora una tabla de frecuencias repartiendo los datos en los siguientes intervalos:
40  45 45  50 50  55 55  60 60  65 65  70
b Representa la distribución con el gráfico adecuado.
Ejercicio nº 2.La edad de los asistentes a una determinada película en el cine viene dada en la
siguiente tabla:
EDAD
0 - 10
10 - 20
20 - 30
30 - 40
40 - 50
50 - 60
N. DE ASISTENTES
185
73
21
84
28
9
a Calcula la edad media de los asistentes y la desviación típica.
b En otra de las salas del mismo cine, la edad media de los asistentes es de 20,5 años y
la desviación típica, de 14,3. Calcula el coeficiente de variación en los dos casos y
compara la dispersión en ambos grupos.
Ejercicio nº 3.-
Al lanzar dos monedas al aire anotamos el número de caras obtenidas. Escribe el
espacio muestral y completa la tabla:
TIPO DE SUCESO
SUCESO
Suceso Seguro
Obtener una cara o una cruz.
Suceso posible
Suceso imposible
Suceso muy probable
Suceso poco probable
Ejercicio nº 4.Una urna contiene 12 bolas amarillas, 15 verdes y 23 azules. Calcula la probabilidad de
que al extraer una bola al azar:
a Sea de color amarillo.
b No sea de color verde.
Ejercicio nº 5.a Al lanzar 50 veces un dado hemos obtenido los siguientes resultados. Construye la
tabla de frecuencias absoluta y relativa de cada suceso.
CARA
1
2
3
4
5
6
FREC.
8
12
8
7
9
6
b Estima la probabilidad de obtener un 4 con ese dado.
Ejercicio nº 6.La siguiente tabla refleja el gusto o no por la lectura de un grupo de alumnos de 3 ESO:
CHICAS
CHICOS
LES GUSTA LEER
58
36
NO LES GUSTA LEER
28
28
Escogemos al azar a uno de esos alumnos. Calcula la probabilidad de que:
a Sea chica.
b No le guste la lectura.
c Sea chica que le guste leer.