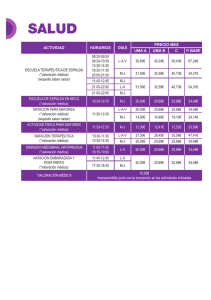
Problem Set 1 Solutions

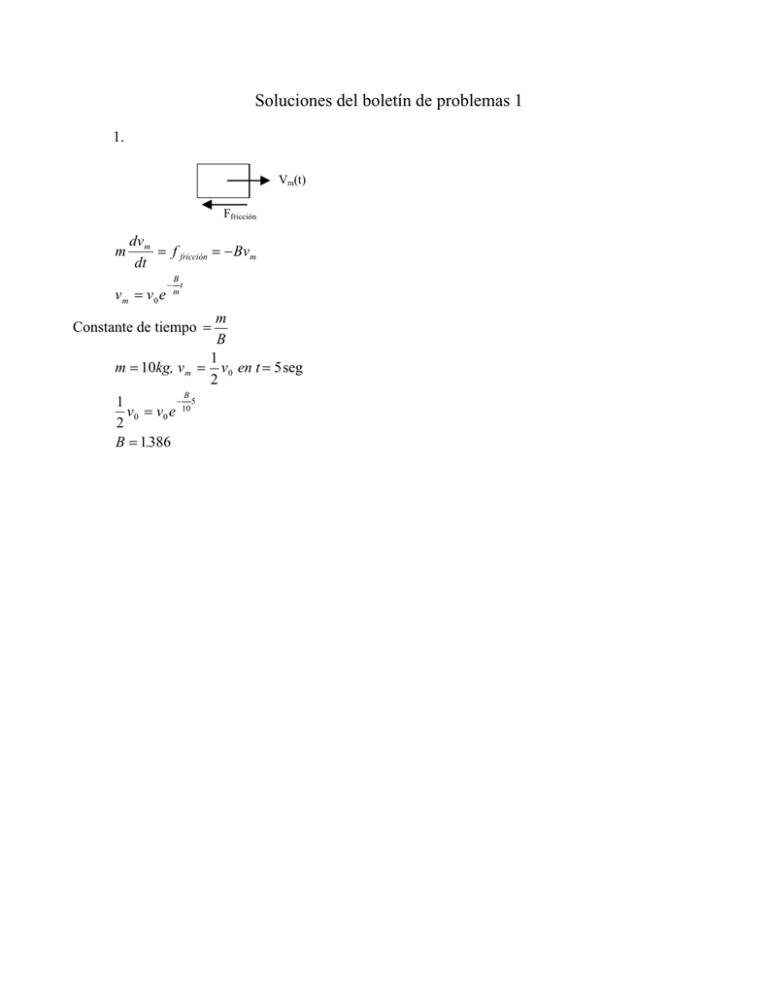
Soluciones del boletín de problemas 1
1.
Vm(t)
Ffricción
m
dv m
= f fricción = − Bv m
dt
vm = v0 e
B
− t
m
m
B
1
m = 10kg, v m = v0 en t = 5 seg
2
B
− 5
1
v 0 = v0 e 10
2
B = 1.386
Constante de tiempo =
2.
d
d d
d2
f fricción = B Ω = B
Ω = K B Ω, dondeK
2
2 2
4
Tentrada= K i I s (t), donde K i es constante
T fricción =
Tentrada− T fricción = J
B
=B
d2
4
dΩ
dt
dΩ
+ K B Ω = K i I s (t)
dt
La entrada I s se puede representar como:
J
Im
I
t − m (t − T )u (t − T )
T
T
Considere la transformada de Laplace , L[f(t − T)1(t − T)] = e −Ts F(s).
I s (t) =
Mediante la transformada de Laplace,
I 1
I s (s) = K i m 2 [1 − e −Ts ]
T s
I
1
Ω(s) = K i m 2
[1 − e −Ts ]
T s (Js + K B )
Utilizando la fracción parcial y la transformada inversa de Laplace, podemos obtener:
KI
J
J −
Ω(t) = i m [( −
e
+t +
TK B
KB
KB
KB
t
J
J
J −
)−( −
+ t −T +
e
KB
KB
KB
( t −T )
J
)u (t − T )]
J
.
KB
Basándonos en la ecuación anterior, podemos dibujar una gráfica con la constante de tiempo =0.5.
Constante de tiempo:
3.
d 2j dj
+
= K v v1
dt
dt 2
vj = kj j
τs
v1 = K(v - vj )
a) Sustituya una vez todas las ecuaciones
d 2j dj
+
+ K v Kkj j = K v Kv
dt
dt 2
b) En estado estacionario
τs
dj
d 2j
=0 y
=0
2
dt
dt
j
1
=
v kj
c)
K v Kkj /τ s
Kv K
j(s)
1
=
=
(
)
v(s) τ s s 2 + s + K v Kkj
kj s 2 + ( 1/τ s )s + (K v Kkj /τ s )
2
wn = K v Kkj /τ s , wn = K v Kkj /τ s : frecuencia natural no amortiguada
2ξwn = 1/τ s , ξ =
1
1
: relación de amortiguación
=
2 wn τ s 2 τ s K v Kkj /τ s
d)
En una amortiguación crítica no existe sobreexceso ni vía rápida. Por .tanto, ξ debería ser 1.
ξ=
K=
1
1
=
=1
2wn τ s 2τ s K v Kkj /τ s
1
4 K v kj τ s
j(t) =
1
[1 - e - wnt ( 1 + wn t)]
kj
wn = K v Kkj /τ s = 1/τ s , cuando K=
(j)t ®¥ =
1
4 K v kj τ s
1
kj
0.9 = 1 - e
- wnT
( 1 + wnT) = 1 - e
-
T
τs
(1 +
T
)
τs
A partir de la ecuación anterior, calculamos T. T/ts » 3.9