1613 - amontes

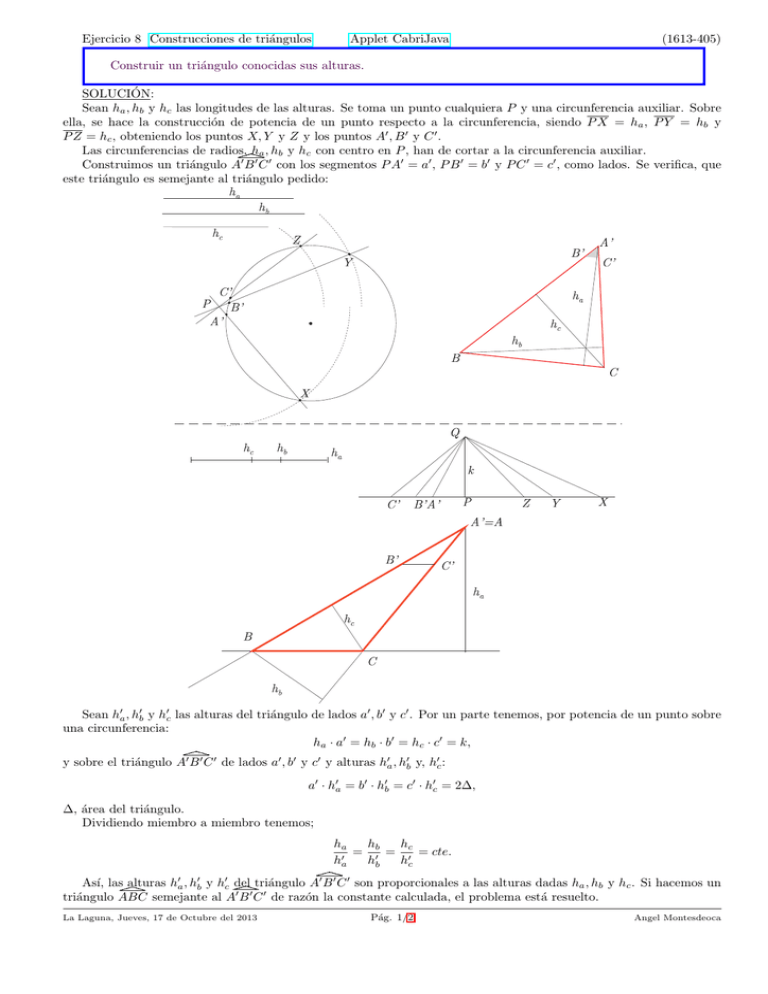
Ejercicio 8 Construcciones de triángulos
Applet CabriJava
(1613-405)
Construir un triángulo conocidas sus alturas.
SOLUCIÓN:
Sean ha , hb y hc las longitudes de las alturas. Se toma un punto cualquiera P y una circunferencia auxiliar. Sobre
ella, se hace la construcción de potencia de un punto respecto a la circunferencia, siendo P X = ha , P Y = hb y
P Z = hc , obteniendo los puntos X, Y y Z y los puntos A0 , B 0 y C 0 .
Las circunferencias de radios, ha , hb y hc con centro en P , han de cortar a la circunferencia auxiliar.
Construimos un triángulo A0 B 0 C 0 con los segmentos P A0 = a0 , P B 0 = b0 y P C 0 = c0 , como lados. Se verifica, que
este triángulo es semejante al triángulo pedido:
Sean h0a , h0b y h0c las alturas del triángulo de lados a0 , b0 y c0 . Por un parte tenemos, por potencia de un punto sobre
una circunferencia:
ha · a0 = hb · b0 = hc · c0 = k,
y sobre el triángulo A0 B 0 C 0 de lados a0 , b0 y c0 y alturas h0a , h0b y, h0c :
a0 · h0a = b0 · h0b = c0 · h0c = 2∆,
∆, área del triángulo.
Dividiendo miembro a miembro tenemos;
hc
ha
hb
= 0 = 0 = cte.
0
ha
hb
hc
Ası́, las alturas h0a , h0b y h0c del triángulo A0 B 0 C 0 son proporcionales a las alturas dadas ha , hb y hc . Si hacemos un
triángulo ABC semejante al A0 B 0 C 0 de razón la constante calculada, el problema está resuelto.
La Laguna, Jueves, 17 de Octubre del 2013
Pág. 1/2
Angel Montesdeoca
OTRA FORMA:
En el triángulo ABC a construir se verificará:
2∆ = aha = bhb = chc ,
a=
2∆
,
ha
b=
2∆
,
hb
c=
2∆
.
hc
Como desconocemos el área ∆, primero construimos un triángulo A0 B 0 C 0 , cuyos lados sean a0 = k 2 /ha , b0 = k 2 /hb ,
c = k 2 /hc , para k una constante arbitraria. Tal triángulo será semejante al pedido. Una vez construido A0 B 0 C 0 ,
para obtener ABC, hacemos coincidir los vértices A y A0 y los lados AB y A0 B 0 sobre la misma semirrecta (también
estarán sobre una misma semirrecta los lados AC y A0 C 0 ) y tomamos sobre la altura desde A0 , el segmento ha , y por
su extremo trazamos la paralela a B 0 C 0 que corta al los lados A0 B 0 y A0 C 0 en los vértice B y C del triángulo buscado.
0
Para construir los segmentos a0 , b0 y c0 , procedemos dela forma siguiente:
1) Sobre una recta arbitraria `, tomamos un punto P y sobre la perpendicular a ella por P y desde P , trazamos
un segmento de longitud k. Llamamos al otro extromo Q.
2) Llevamos sobre la recta `, desde P y en el mismo sentido, los segmentos de longitud ha , hb y hc , cuyos extremos
designamos, respectivamente, por X, Y y Z.
3) Las recta por Q, perpendiculares a QX, QY y QZ, determinan en la recta `, los puntos A0 , B 0 y C 0 . Entonces
QA0 = a0 , QB 0 = b0 y QC 0 = c0 , longitudes de los lados buscadas del triángulo A0 B 0 C 0 . Ya que, en los triángulos
rectángulo A0 QX, B 0 QY y C 0 QZ, la altura k es media proporcional ente los dos segmento en que divide a la hipotenusa,
se tiene
k 2 = P X · P A0 = ha a, k 2 = P Y · P B 0 = hb b, k 2 = P Z · P C 0 = hc c.
http://webpages.ull.es/users/amontes/pdf/trresolu.pdf
http://webpages.ull.es/users/amontes/pdf/ejct1613.pdf
La Laguna, Jueves, 17 de Octubre del 2013
Pág. 2/2
Angel Montesdeoca