3 horas - Universidad del Rosario

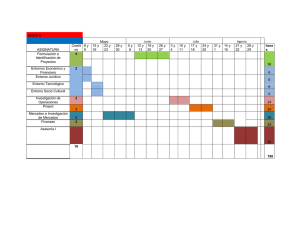
JUSTIFICACIÓN
En los últimos años, las sociedades han iniciado procesos de globalización e integración de los
mercados, procesos que merecen toda la rigurosidad por parte de la academia para analizarlos,
estudiarlos y proponer nuevos paradigmas que orienten las economías del futuro hacia los desafíos
mundiales. En este sentido, la Universidad del Rosario y la Facultad de Economía ofrecen un curso de
Introducción a las Finanzas Cuantitativas con el objetivo de formar cuantitativamente a aquellos
profesionales que deseen mejorar su comprensión de las áreas de matemática financiera y de
administración de riesgos.
¿Qué es finanzas cuantitativas?
Las finanzas cuantitativas es la disciplina que utiliza herramientas matemáticas y estadísticas aplicadas al
estudio de los mercados financieros y la economía financiera moderna. El área de finanzas cuantitativas
es uno de los campos que está demandando mayor recurso humano a nivel mundial (incluso después de
la crisis financiera de 2007 y 2008).
DIRIGIDO A
El curso esta dirigido para profesionales con experiencia en el área
financiera. El profesional deberá estar interesado en utilizar algunos
conceptos matemáticos en las áreas de Cálculo, Probabilidad y
Estadística, que son indispensables para entrar a abordar los temas
de matemática aplicada a finanzas y administración cuantitativa de
riesgos.
METODOLOGÍA
El curso está compuesto por 9 módulos. Cada módulo se cubrirá en un espacio de 3 a 6 horas. Casi todos
los módulos tienen un componente de clase magistral junto con otro componente aplicado donde se
hará énfasis en el uso de hojas de cálculo y paquetes estadísticos o matemáticos de libre distribución.
CONTENIDO ACADÉMICO
Módulos:
Matemáticas Financieras
Introducción a los instrumentos de renta fija (3 horas)
El objetivo de este módulo es presentar una introducción a los productos de renta fija y su aplicación
como herramienta de diversificación y cobertura en un portafolio de inversión, así como los riesgos
asociados a las inversiones en renta fija.
1.
2.
3.
4.
5.
6.
Bonos cupón cero y funciones de descuento
Tasas de interés de corto plazo
Tasas forward
Duración y Convexidad
Curvas de rendimiento
Estructura a plazos de las tasas de interés
Referencias:
Hull, J. Options, futures and other derivatives, Edicion 6, Prentice Hall, 2005.
Bodie, Z. Kane, A., Marcus, A. Investments, Edicion 7, McGraw Hill, 2008.
Modelos estocásticos en tiempo continuo (3 horas)
El objetivo de este módulo es presentar elementos básicos de análisis, probabilidad y procesos estocásticos
necesarios para la modelación de la dinámica en tiempo continuo de precios de activos, derivados y otros
instrumentos presentes en un mercado financiero.
1. Elementos de la teoría de la probabilidad para el estudio de los mercados financieros.
2. Introducción al cálculo estocástico y teoría del movimiento Browniano. Martingalas, Teorema
de Girsanov. Teorema de representación de martingalas.
3. Cambios de medida y valoración neutra en riesgo.
4. Procesos de difusión. Fórmula de Feynman-Kac.
Referencia:
T.W. Epps, Pricing derivative securities, Edición 2, World Scientific, 2007.
Instrumentos Derivados (6 horas)
El objetivo de este módulo es presentar una introducción a los derivados financieros y su uso como
herramienta de gestión de riesgo y especulación en los mercados financieros. Se hará énfasis en la
producción de fórmulas prácticas de valoración de instrumentos derivados y su implementación empírica.
1. Modelo de Black-Scholes-Merton.
2. Derivados “Plain Vanilla”.
a. Opciones.
b. Futuros.
c. Swaptions.
3. Opciones Exóticas.
a. Asiáticas.
b. Barrera.
c. Lookback.
4. Implementación: estimación, simulación y calibración
Referencia:
Epps T.W., Pricing derivative securities, Edición 2, World Scientific, 2007.
Modelos Estocásticos de Tasa de Interés (6 horas)
El objetivo principal de este curso es calcular analítica y numéricamente precios de derivados de tasas de
interés, y usar cambios de medida y otras técnicas avanzadas para simplificar expresiones matemáticas
originadas de los modelos de tasas de interés para los precios de derivados.
1. Teoría general de los modelos de tasas de corto plazo
2. Ecuación para los precios de bonos
3. Teoría de modelos afines. Modelos Gausianos: Vasicek, Hull-White
4. Modelo de Cox-Ingersoll-Ross (CIR) y extensiones
5. Modelo de Heath-Jarrow-Morton (HJM)
6. Estructuras de volatilidad en modelos de uno y dos factores
7. Valoración y cobertura de derivados de tasas de interés.
8. Implementación: estimación, simulación y calibración
Referencia:
Brigo, D. y Mercurio F., Interest rate models - theory and practice: With smile, inflation and credit,
Edición 2, Springer Finance, Springer-Verlag, Berlin (2006)
Administración cuantitativa de riesgos
Administración Cuantitativa de Riesgos (2 horas)
El objetivo de este módulo es orientar al estudiante en el estudio del campo de la administración
cuantitativa de los riesgos, mediante la presentación de diferentes conceptos que se encuentran en
cualquier ejercicio de cuantificación de riesgos independientemente de su naturaleza particular (mercado,
crédito, operacional, entre otros).
1.
2.
3.
4.
5.
6.
7.
¿Por qué administrar el riesgo?
Distribución de Pérdida.
Factores de Riesgo.
Mapas de Riesgo.
Medidas de Riesgo
Agregación de Riegos.
Distribución de las cargas de riesgo.
Referencia:
McNeil, A., Frey, R., Embrechts, P. Quantitative Risk Management: Concepts, Techniques, and Tools,
Princeton Series in Finance, (2005).
Riesgo de Mercado (2 horas)
El objetivo de este módulo es introducir los principales conceptos y métodos de cuantificación del riesgo de
mercado.
1. Valor en Riesgo.
a. Estimación no-paramétrica.
b. Estimación paramétrica.
2. Valor en Riesgo condicional o Expected Shortfall .
3. Backtesting.
4. Métodos de Colas y valores extremos.
Referencia:
Alexander, C. Value-at-Risk models, Market Risk Analysis, Vol. 4 (2008)
Análisis de Riesgo de Mercado (2 horas)
El objetivo de este módulo es ilustrar los principales métodos de cuantificación del riesgo de mercado
mediante la utilización de Excel y el paquete estadístico R.
1. Volatilidad.
2. Métodos de Estimación.
3. Medidas de Riesgo.
4. Backtesting
Referencia:
Danielsson, J. Financial Risk Forecasting, John Wiley & Sons Ltd (2011).
Riesgo de Crédito y de Contraparte (3 horas)
El objetivo de este módulo es orientar al estudiante a los conceptos y métodos utilizados en las principales
entidades financieras a nivel mundial para administrar el riesgo crediticio y de contraparte. Dentro de los
métodos que se van a resaltar quizás el más importante es el que permite cuantificar el capital de riesgo de
una entidad con exposiciones financieras.
1.
2.
3.
4.
5.
6.
Regulación (Basilea 1, 2 y 3).
Sistema de administración de riesgos crediticios.
Estimación delCapital Económico.
Modelos de riesgo de quiebra.
Modelos de riesgo del portafolio de Crédito, Credit VaR.
Introducción al riesgo de riesgo de Contraparte.
7.
Mitigación y cuantificación del Riesgo de Contraparte.
Referencias:
Servigny, A. Renault, O. Measuring and Managing Credit Risk, McGraw-Hill, (2004).
Gregory. J. Counterparty Credit Risk, Wiley Finance Series, (2009).
Análisis de Riesgo de Crédito (3 horas)
El objetivo de este módulo es ilustrar los principales métodos de cuantificación del riesgo de crédito y
contraparte mediante la utilización de Excel.
1. Matrices de Transición.
2. Probabilidad de incumplimiento.
3. Perdida dado un incumplimientos.
4. Merton, Vasicek, KMV.
5. Formula Basilea 2.
6. Credit Value Adjustment (CVA).
Referencia:
Loffler. G., Posch, P. Credit Risk Modelling using Excel and VBA, Wiley Finance Series, (2007).
DOCENTES
Carlos Alberto Castro Iragorri
Ph.D. en Economía, Université Libre de Bruxelles.
Maestría en Estadística, Université Libre de Bruxelles.
Producción académica publicada en: Financial Markets and Portfolio Management, Desarrollo y
Sociedad, Revista de Economía del Rosario.
Rafael Antonio Serrano Perdomo
Ph.D. en Matemáticas, University of York.
Maestría en Matemáticas (Matemática Financiera), Universität Kaiserslautern.
Producción académica publicada en: SIAM Journal of Control and Optimization, Proceedings of
the 2002 Colombian seminar on stochastic process.