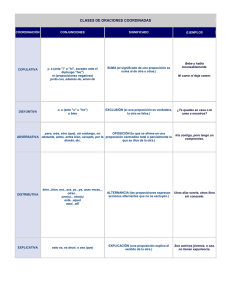
pdf Nuevos resultados sobre sistemas lineales y conjuntos

Universidad de Alicante
Nuevos resultados sobre sistemas lineales
y conjuntos convexos
Margarita Rodríguez Álvarez
Tesis de Doctorado
Facultad:
Ciencias
Directores: Dr. Miguel Ángel Goberna Torrent
Dr. Valentín Jornet Pla
2001
Universidad de Alicante
Depto. de Estadística e Investigación Operativa
1XHYRV UHVXOWDGRV VREUH VLVWHPDV
OLQHDOHV \ FRQMXQWRV FRQYH[RV
Memoria presentada por Margarita Rodríguez Álvarez para optar al grado
de Doctor en Ciencias Matemáticas, realizada bajo la dirección de los doctores
D. Miguel Ángel Goberna Torrent y D. Valentín Jornet Pla.
Alicante, Mayo de 2001
D. MIGUEL ÁNGEL GOBERNA TORRENT, Catedrático de Estadística e
Investigación Operativa de la Universidad de Alicante, y
D. VALENTÍN JORNET PLA, Catedrático E.U. de Estadística e Investigación Operativa de la Universidad de Alicante,
CERTIFICAN: Que la presente memoria 1XHYRV UHVXOWDGRV VREUH VLVWHPDV
OLQHDOHV \ FRQMXQWRV FRQYH[RV ha sido realizada bajo su dirección en el Departamento de Estadística e Investigación Operativa de la Universidad de Alicante por Dña. Margarita Rodríguez Álvarez, y constituye su tesis para optar al grado de
Doctor en Ciencias Matemáticas.
Y para que conste, en cumplimiento de la legislación vigente,
¿rman el presente certi¿cado en Alicante, a 10 de Mayo de dos
mil uno.
Fdo: Miguel A. Goberna
Fdo: Valentín Jornet
ËQGLFH
,QWURGXFFLyQ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . &DStWXOR 3UHOLPLQDUHV . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0.1. Conjuntos convexos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
0.2. Sistemas semi-in¿nitos lineales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
&DStWXOR 6LVWHPDV OLQHDOHV JHQHUDOHV HQ U? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
1.2. Existencia de soluciones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
1.3. Conjuntos linealizables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
1.4. Geometría . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
1.5. Optimización lineal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
&DStWXOR &RQItQ GH XQ FRQMXQWR FRQYH[R . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
2.2. Confín: Propiedades básicas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
2.3. Conexión del confín . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
2.4. El confín y la iluminación de los conjuntos convexos cerrados . . . . . . . . . . . 71
2.5. Algunas aplicaciones a los sistemas de desigualdades lineales . . . . . . . . . . . . 77
&DStWXOR &DUDFWHUL]DFLyQ GH IDPLOLDV GH FRQMXQWRV FHUUDGRV FRQYH[RV . . . . . . 3.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
3.2. Caracterización de las sumas de conjuntos convexos compactos con
subespacios vectoriales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
3.3. Caracterización de los símplices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
3.4. Caracterización de los sandwiches . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
3.5. Caracterización topológica de los &-sandwiches . . . . . . . . . . . . . . . . . . . . . . . 103
3.6. Caracterización de los paralelotopos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106
3.7. Caracterización de conjuntos continuos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
3.8. Caracterización de cuerpos convexos suaves . . . . . . . . . . . . . . . . . . . . . . . . . . 115
3.9. Caracterización de familias de cuerpos convexos mediante conceptos
de iluminación . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
%LEOLRJUDItD . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ,QWURGXFFLyQ
El conjunto de soluciones de cualquier sistema de desigualdades lineales de la forma
i@| % K| c | 5 A j, siendo A un conjunto arbitrario de índices (posiblemente in¿nito),
@| 5 U? y K| 5 U para todo | 5 A , es un conjunto convexo cerrado y, recíprocamente,
cualquier conjunto convexo cerrado se puede representar por medio de una in¿nidad
de sistemas lineales de este tipo. Existe, pues, una correspondencia entre sistemas
semi-in¿nitos lineales (SSIL) y conjuntos convexos cerrados.
Sin embargo, los sistemas anteriormente mencionados no son los sistemas lineales
más generales que podemos considerar. Un sistema en U? de la forma
j ' i@| % K| c | 5 (( @| % : K| c | 5 .j c
donde los conjuntos de índices, ( y ., son disjuntos y no simultáneamente vacíos,
@| 5 U? y K| 5 U para todo | 5 A G' ( ^ ., contiene un número arbitrario
(posiblemente in¿nito) de restricciones de desigualdad débil (dos de las cuales
reemplazan a una ecuación) y/o estricta. Se trata, pues, de un sistema semi-in¿nito
lineal general (SSILG) y su conjunto de soluciones es un conjunto convexo, por tratarse
de una intersección de semiespacios abiertos o cerrados.
En este punto, cabe preguntarse si, al igual que ocurre con los conjuntos convexos
cerrados (caso particular de los conjuntos convexos) y los SSIL (caso particular de
los SSILG), todo conjunto convexo se puede representar por medio de un SSILG. Al
ser negativa la respuesta, llamaremos conjuntos linealizables a la clase de conjuntos
convexos que sí cumplen esta propiedad. Estos conjuntos fueron introducidos por
Fenchel [14] (con la denominación de “evenly convex”) para extender la teoría de
la polaridad, pero sin analizar a fondo sus posibles caracterizaciones ni estudiar
1
2
Introducción
exhaustivamente sus propiedades. De la existencia de este trabajo tuvimos noticia
a través de una comunicación privada del Prof. Martínez Legaz, quien ha utilizado
estos conjuntos para de¿nir un tipo de funciones cuasiconvexas importante para la
generalización de la teoría de la conjugación (véanse [24], [30], [ 25] y [26]).
Aunque los SSIL han sido muy bien estudiados por su conexión con la
Programación Semi-In¿nita Lineal, no ocurre lo mismo con los SSILG, por lo
que dedicaremos el Capítulo 1 de la presente memoria al estudio de esta clase de
sistemas y de los conjuntos que admiten este tipo de representaciones lineales. En
él analizaremos la existencia de soluciones, caracterizaremos geométricamente los
conjuntos linealizables y probaremos que se pueden extender, a esta gran familia
de conjuntos convexos, la mayoría de las propiedades conocidas para la subfamilia
de los conjuntos convexos cerrados. También mostraremos que es posible obtener
información geométrica sobre estos conjuntos a partir de una representación lineal
dada y, ¿nalmente, discutiremos la teoría y los métodos para aquellos problemas de
optimización lineal que contienen restricciones de desigualdad estrictas.
Dentro de la correspondencia que existe entre SSIL y conjuntos convexos cerrados,
hay ciertos tipos de SSIL que se corresponden con determinadas familias de conjuntos
convexos cerrados. Así, por ejemplo, los llamados sistemas localmente poliédricos
(LOP), sistemas en los que la condición de Weyl (siempre su¿ciente para que un punto
sea extremo) es también necesaria, tienen conjuntos de soluciones cuasipoliédricos
(conjuntos convexos cerrados cuyas intersecciones con polítopos son polítopos) y,
viceversa, cualquier conjunto cuasipoliédrico admite una representación LOP. Por lo
tanto, podemos caracterizar los conjuntos cuasipoliédricos como aquellos conjuntos
convexos cerrados que admiten representaciones LOP.
La caracterización de familias de conjuntos convexos cerrados puede resultar
útil en diferentes campos de las matemáticas aplicadas.
Así, por ejemplo, una
condición necesaria para la convergencia de algoritmos de programación matemática
que progresan sobre la frontera del conjunto factible (como el método simplex en
programación lineal ordinaria y semi-in¿nita) es la conexión por arcos de la frontera,
por lo que sería útil caracterizar aquellos conjuntos convexos cerrados que poseen esta
Introducción
3
deseada propiedad. En el Capítulo 3 abordaremos la caracterización de determinadas
familias de conjuntos convexos cerrados (algunas de ellas con propiedades muy
interesantes de cara a las aplicaciones) desde diferentes puntos de vista, entre ellos
sus representaciones lineales.
En particular, para caracterizar la clase de los conjuntos convexos cerrados que
tienen la frontera relativa conexa por arcos será necesario el uso de un nuevo concepto,
el de confín de un conjunto convexo no vacío, que introduciremos en el Capítulo 2.
En este capítulo, además, analizaremos las propiedades del confín de los conjuntos
convexos en general y de los convexos cerrados en particular, así como sus relaciones
con ciertos conceptos de iluminación ya conocidos y sus aplicaciones a la teoría de los
sistemas lineales.
Por último, decir que los tres capítulos que constituyen el cuerpo de esta memoria
están precedidos por un capítulo de preliminares, el Capítulo 0, en el que se recoge la
notación, las de¿niciones y los enunciados de los resultados ya conocidos que se van
a utilizar en los demás capítulos. Buena parte de dichos resultados aparecen expuestos
en la reciente monografía de Goberna y López [19] de una manera ordenada y con una
notación uni¿cada que se ha mantenido en esta memoria. Hemos optado por referirnos
a [19], siempre que ha sido posible, en lugar de hacerlo a las fuentes originales (que el
lector puede encontrar en las notas ¿nales del correspondiente capítulo de [19]).
&DStWXOR 3UHOLPLQDUHV
&RQMXQWRV FRQYH[RV
En el espacio euclídeo, U? , denotaremos por nn, f? ,
? ' i% 5 U? m n%n j
y
7? ' i% 5 U? m n%n ' j c
la norma euclídea, el vector cero, la EROD XQLGDG DELHUWD y la HVIHUD XQLGDG,
respectivamente. La base canónica de U? la representaremos por e c c e? .
Un conjunto U? se dice que es FRQYH[R cuando, para todo par
%c + 5 , el segmento d%c +o G' iE b % n b+ m f b j está contenido en .
Consideraremos que el vacío es un conjunto convexo por convenio.
Un conjunto no vacío U? se dice que es un FRQR si contiene a todos los rayos
ib% m b : fj, con % 5 q if? j.
Dado > 9' U? , denotaremos por tT@? , @g , UL? , UL?i y z
al
VXEHVSDFLR YHFWRULDO GH U? JHQHUDGR por , la HQYROWXUD DItQ de , la HQYROWXUD
FRQYH[D de , el FRQR FRQYH[R JHQHUDGR por (de¿nido como la intersección de
todos los conos convexos que contienen al origen y al conjunto ) y el subespacio
5
6
0. Preliminares
de los vectores que son ortogonales a todos los elementos de , respectivamente. Si
' >, adoptaremos el convenio tT@? > ' @g > ' UL?i > ' if? j. Si es convexo
no vacío, denotaremos por _4 su GLPHQVLyQ (de¿nida como la dimensión de @g ).
Todas estas envolturas se pueden describir a través del espacio de VXFHVLRQHV ¿QLWDV
JHQHUDOL]DGDV, UEA , cuyos elementos son las funciones b G A $ U tales que b| 9' f
sólo en un subconjunto ¿nito de A . El cono convexo, en UEA , de las sucesiones ¿nitas
EA no negativas es Un .
Supuesto que es convexo, diremos que un conjunto convexo f es una
FDUD de si, para todo par  9' 2 de tal que f _ o  c 2 d 9' >, se tiene que
d  c 2 o f. El conjunto vacío también se considera una cara de por convenio.
Los SXQWRV H[WUHPRV, las DULVWDV y las IDFHWDV de son las caras de de dimensión f,
 y ? , respectivamente. Denotaremos por i |h el conjunto de todos los puntos
extremos de . Diremos que una cara es H[SXHVWD si se puede obtener como conjunto
de mínimos de una función afín sobre .
Para convexo no vacío de¿niremos el FRQR GH UHFHVLyQ de , n , que viene
dado por
n G' i 5 U? m % n > 5 para todo % 5 y para todo > fj
y el FRQR GH GLUHFFLRQHV IDFWLEOHV de en % 5 , (Ec %, dado por
(Ec % G' i 5 U? m % n > 5 para algún > : fj Si 9' > es un cono convexo, de¿niremos el FRQR SRODU SRVLWLYR de , J , dado por
J G' i 5 U? m % f para todo % 5 j Obsérvese que para todo % 5 , ( Ec % ' UL?i E %.
Al conjunto n _ En le llamaremos HVSDFLR GH OLQHDOLGDG de y se
denotará por *? .
Un cono convexo es DSXQWDGR cuando no contiene rectas, es decir, si su espacio de
linealidad se reduce al vector cero.
Un vector no nulo 5 n es una GLUHFFLyQ H[WUHPD del conjunto convexo no
vacío si, para todo par de vectores  , 2 5 n tales que ' >  n >2 2
0.1 Conjuntos convexos
7
(> y >2 números reales positivos), se tiene que
tT@? ' tT@? ij c
' c 2
Desde el punto de vista topológico, denotamos por ?| , U* y M_ los conjuntos
LQWHULRU, FODXVXUD y IURQWHUD de un subconjunto cualquiera de U? . Si el conjunto es
convexo, de¿nimos los conjuntos LQWHULRU UHODWLYR y IURQWHUD UHODWLYD de , denotados
por h?| y hM_ , como el interior y la frontera de cuando consideramos como
subconjunto de @g con la topología inducida.
Dado un conjunto convexo y un punto % 5 M_ , existe un vector @ 5 U? q if? j
tal que @ % @ % para todo % 5 a la frontera de este semiespacio le llamaremos
KLSHUSODQR GH VRSRUWH de en %.
Se utilizarán a menudo las siguientes familias de conjuntos convexos cerrados: los
SROLHGURV FRQYH[RV (de¿nidos como intersecciones ¿nitas de semiespacios cerrados),
los SROtWRSRV (poliedros convexos acotados) y los FRQMXQWRV FXDVLSROLpGULFRV (de¿nidos
por Klee como aquellos subconjuntos de U? cuyas intersecciones con polítopos son
polítopos).
Ciertas pruebas por inducción utilizan implícitamente la adaptación de los
conceptos anteriores a variedades: Las variedades a¿nes en  (variedad afín de U? )
son las variedades a¿nes de U? contenidas en , y son hiperplanos en  cuando
su dimensión es E_4  . Si u es un hiperplano en , cada una de las dos
componentes conexas de  qu es un semiespacio abierto en  determinado por u
su unión con u proporciona los dos semiespacios cerrados en  correspondientes a
u. La intersección de ¿nitos semiespacios cerrados de  es un poliedro convexo en
, pudiéndose probar que son exactamente los poliedros convexos de U? contenidos
en . Del mismo modo, los polítopos (cuasipoliedros) de  son los polítopos
(cuasipoliedros) de U? contenidos en . Las propiedades de los poliedros convexos,
polítopos y cuasipoliedros en una variedad afín de dimensión 6 ? son las
mismas que las de los objetos correspondientes en U6 (sustituyendo los operadores
topológicos, M_ e ?|, por los relativos correspondientes, hM_ y h?|).
Dado que será frecuente el uso de resultados de Análisis Convexo a lo largo de la
8
0. Preliminares
memoria, hacemos, a continuación, una recopilación de los mismos, dando, para cada
uno de ellos, la adecuada referencia bibliográ¿ca. En algunos casos aislados, daremos
el enunciado y su demostración, por tratarse de nuevas aportaciones.
352326,&,Ï1 >32 7K @ 6L g \ g2 VRQ FRQRV FRQYH[RV TXH FRQWLHQHQ DO
RULJHQ HQWRQFHV g n g2 ' UL? Eg ^ g2 352326,&,Ï1 6HD XQ FRQMXQWR FRQYH[R QR YDFtR HQ U? (QWRQFHV VH YHUL¿FDQ
ODV VLJXLHQWHV SURSRVLFLRQHV
(i) h?| HV XQ FRQMXQWR FRQYH[R QR YDFtR >32 7K @
(ii) h?| U* ' h?| \ U* h?| ' U* >32 7K @
(iii) VL % 5 h?| H + 5 U* HQWRQFHV d%c +d h?| /HPD GH $FFHVLELOLGDG >32 7K
@ \
(iv) 5 5 h?| VL \ VyOR VL SDUD WRGR % 5 H[LVWH > :  WDO TXH E > % n >5 5 >32 7K @
352326,&,Ï1 >32 7K @ 6HD U? XQ FRQMXQWR FRQYH[R \ VHD XQD
WUDQVIRUPDFLyQ OLQHDO GH U? HQ U6 (QWRQFHV
h?| E ' Eh?| 352326,&,Ï1 >32 &RU @ 3DUD FXDOTXLHU SDU GH FRQMXQWRV FRQYH[RV GH U?  \ 2 VH FXPSOH
h?| E n 2 ' h?|  n h?| 2 Como se ha señalado, el interior relativo de un conjunto convexo no vacío es no
vacío. Algo parecido ocurre con hM_ .
352326,&,Ï1 6HD XQ FRQMXQWR FRQYH[R QR YDFtR HQ U? (QWRQFHV VH YHUL¿FDQ
ODV VLJXLHQWHV SURSRVLFLRQHV
(i) hM_ HV QR YDFtR VL \ VyOR VL QR HV XQD YDULHGDG DItQ \
(ii) VL HV XQ VXEFRQMXQWR SURSLR GH U? HQWRQFHV WLHQH DO PHQRV XQ SXQWR IURQWHUD
'HPRVWUDFLyQ (i) Para demostrar la implicación no trivial, construiremos un par
de sucesiones i%? j e i+? j E@g q convergentes al mismo punto de @g .
Dicho punto estará en la frontera relativa de .
Por ser no vacío y no ser una variedad afín (E@g q 9' >), existe un
% n + 
punto % 5 y un punto +  5 E@g q. Si
(que pertenece a @g por
2
0.1 Conjuntos convexos
9
ser combinación convexa de elementos de dicho conjunto) pertenece a , entonces
tomamos
%2 '
% n + 
e +2 ' + 
2
En caso contrario, tomamos
% n + 
2
%2 ' % e + 2 '
En general, para construir los términos %?n e +?n , se toman
%?n '
%? n + ?
%? n +?
e +?n ' + ? c si
5 c
2
2
y
%?n ' %? e +?n '
%? n + ?
%? n + ?
c si
5 E@g q
2
2
De esta manera hemos construido una sucesión i%? j contenida en el conjunto y una sucesión i+ ? j contenida en el conjunto E@g q cuyos términos ?-ésimos
veri¿can que
n%? + ? n '
n%?

3
+?  n
2
3
La sucesión i%? j es de Cauchy en U? ya que, para todo ? 5 Q y R f, se tiene
que
?nR
n% +  n
%
%? n%? + ? n '
2? 
3
Del mismo modo, i+ ? j también es una sucesión de Cauchy en U? . Además, ambas
sucesiones son convergentes en U? a un mismo punto, el cual pertenece a @g por ser
éste un conjunto cerrado.
(ii) El argumento de la demostración es el mismo que en el caso anterior
sustituyendo @g por U? La siguiente proposición caracteriza los puntos del interior relativo de la envoltura
convexa (envoltura convexa cónica) de un conjunto no vacío de U? .
352326,&,Ï1 >19 7K $@ 6HD XQ FRQMXQWR QR YDFtR HQ U? \ 5 5 @g 5 5 tT@? (QWRQFHV ODV VLJXLHQWHV SURSRVLFLRQHV VRQ HTXLYDOHQWHV
10
0. Preliminares
(i) 5 5 h?| UL? 5 5 h?| UL?i UHVSHFWLYDPHQWH
(ii) H[LVWHQ SXQWRV % 5 ' c 2c c R FRQ @g i% c %2 c c %R j ' @g UHVSHFWL
YDPHQWH tT@? i% c %2 c c %R j ' tT@? , \ HVFDODUHV SRVLWLYRV k ' c 2c c R
R
R
R
S
S
S
WDOHV TXH 5 ' k % \
k '  UHVSHFWLYDPHQWH
k DUELWUDULD \
'
'
'
(iii) 5 n UL?i E 5 ' @g (Un dEUL?i 5o ' UL?i di5j ^ UL?i o ' tT@? ).
En la siguiente proposición demostramos algunas de las propiedades, claramente
intuitivas, que tienen los puntos del interior relativo de un convexo no vacío.
352326,&,Ï1 6HD XQ FRQMXQWR FRQYH[R QR YDFtR \ % 5 h?| (QWRQFHV VH
YHUL¿FDQ ODV VLJXLHQWHV SURSRVLFLRQHV
(i) tT@? E % ' UL?i E % ' E@g y
(ii) f? 5 h?|E %
'HPRVWUDFLyQ
(i) Para demostrar la primera igualdad es su¿ciente probar
que dada una base en tT@? E %, sus elementos y los opuestos pertenecen a
UL?i E %. Sea i+ %c ' c c 6j c con + 5 para todo ' c c 6c una
base de tT@? E % Puesto que % 5 h?| , existe 0 : fc tal que
E% n 0? _ E@g Para cada ' c c 6, el punto
%
0 E+ %
5 E% n 0? _ E@g c
2 n+ %n
de modo que
0 E% + 5 %
2 n+ %n
y, por lo tanto,
% + 5 UL?i E % Dado que también se veri¿ca que + % 5 UL?i E % para todo ' c c 6, se
0.1 Conjuntos convexos
11
obtiene que
UL?i E % ' tT@? E % Por otra parte, si % 5 h?| ,
E@g ' E@g %
(0.1)
En efecto, si + % 5 E@g , entonces
+ % ' + n % % % ' E+ n % % % 5 E@g %
La segunda igualdad en (i) se obtiene como consecuencia de (0.1) y de la
Proposición 0.6(iii).
(ii) Si % 5 h?| c entonces, por la Proposición 0.6, existen puntos % 5 ,
' c c R, con
@g ' @g % c %2 c c %R c
y escalares positivos k , ' c c R, tales que
R
[
%'
'
k % y
R
[
'
k ' 
Entonces
R
[
f? '
'
R
[
k % % '
con k : fc ' c c R,
R
[
'
'
k % R
[
'
R
[
k % '
k E% %
'
k '  y
@gE % ' @g % %c %2 %c c %R % c
y, por la Proposición 0.6,
f? 5 h?| UL?E % ' h?|E %
El siguiente resultado caracteriza la acotación de un conjunto convexo cerrado no
vacío a través de su cono de recesión.
352326,&,Ï1 >32 7K @ 8Q FRQMXQWR FRQYH[R FHUUDGR QR YDFtR U? HV
DFRWDGR VL \ VyOR VL n ' if? j
12
0. Preliminares
352326,&,Ï1 >32 &RU @ 6HDQ  c c 6 FRQMXQWRV FRQYH[RV QR YDFtRV
HQ U? TXH VDWLVIDFHQ OD VLJXLHQWH FRQGLFLyQ VL 5 c c 56 VRQ YHFWRUHV WDOHV TXH
5 5 n EU* \ 5 n n 56 ' f? HQWRQFHV 5 5 *? EU* SDUD ' c c 6
(QWRQFHV
U* E n n 6 ' U*  n n U* 6 c
n dU* E n n 6 o ' n EU*  n n n EU* 6 En las dos siguientes proposiciones se dan propiedades acerca de las caras de un
conjunto convexo.
352326,&,Ï1 >32 7K @ 6HD XQ FRQMXQWR FRQYH[R \ VHD XQD FDUD GH
6L ( HV XQ FRQMXQWR FRQYH[R HQ WDO TXH Eh?| ( _ 9' > HQWRQFHV ( 352326,&,Ï1 >32 &RU @ 6HD XQ FRQMXQWR FRQYH[R \ VHD XQD FDUD
SURSLD GH (QWRQFHV hM_ \ _4 _4 Se dice que un par de conjuntos no vacíos,  y 2 , son VHSDUDEOHV si existe un
hiperplano M G' i% 5 U? m @ % ' Kj tal que @ % K f @ + K para todo % 5  y
para todo + 5 2 . Si, además, E ^ 2 qM 9' >, entonces  y 2 están SURSLDPHQWH
VHSDUDGRV. En el caso de que las desigualdades sean estrictas, se dice que M separa a
 y 2 HVWULFWDPHQWH
Por otra parte, si se cumple la desigualdad
?u i@ % m % 5  j tT i@ + m + 5 2 j c
se dice que  y 2 están GpELOPHQWH VHSDUDGRV y si esta desigualdad es estricta, se
dice que M separa a  y 2 IXHUWHPHQWH.
352326,&,Ï1 >32 7K @ 6HD XQ FRQMXQWR FRQYH[R QR YDFtR UHODWLYDPHQWH
DELHUWR HQ U? \ VHD  XQD YDULHGDG DItQ QR YDFtD HQ U? TXH QR FRUWD D (QWRQFHV
H[LVWH XQ KLSHUSODQR M FRQWHQLHQGR D  WDO TXH XQR GH ORV VHPLHVSDFLRV DELHUWRV
DVRFLDGRV FRQ M FRQWLHQH D 352326,&,Ï1 >32 &RU @ 6HDQ  \ 2 FRQMXQWRV FHUUDGRV FRQYH[RV QR
YDFtRV GLVMXQWRV HQ U? TXH QR WLHQHQ GLUHFFLRQHV GH UHFHVLyQ HQ FRP~Q (QWRQFHV
H[LVWH XQ KLSHUSODQR VHSDUDQGR IXHUWHPHQWH D  \ 2 Dada una función s G U? $ U ^ i4j, se de¿nen el HSLJUDIR de s , iT s, y el
0.2 Sistemas semi-in¿nitos lineales
13
KLSRJUDIR de s , )TL s , como los conjuntos
%
?
n
iT s G'
5U
m s E% k
k
y
%
?
n
m s E% k )TL s G'
5U
k
Diremos que s es FRQYH[D o FyQFDYD según sea convexo el conjunto iT s o bien
)TL s .
Llamaremos GRPLQLR HIHFWLYR de s , _L4 s, al conjunto
_L4 s G' i% 5 U? m s E% n4j Una función convexa s se dice que es SURSLD si _L4 s 9' > y s E% : 4 para todo
% 5 U? .
Dada una función convexa propia, s , y un punto % 5 _L4 s , se dice que el vector
es un VXEJUDGLHQWH de s en % si, para todo + 5 U? ,
s E+ s E% n E+ % .
Se dice que s es VXEGLIHUHQFLDEOH en un punto % 5 _L4 s si existe algún subgradiente
de s en % y, en el caso de que éste sea único, se dice que s es GLIHUHQFLDEOH en %.
La subdiferenciabilidad de s en un punto % 5 _L4 ses equivalente
a la existencia
%
de un hiperplano no vertical que soporta a iT s en
y cada subgradiente
s E%
de s en %, , está asociado con exactamente
uno de estos hiperplanos de soporte
(el que tiene como vector normal a
). La existencia de tales hiperplanos de

soporte no verticales es una propiedad de los puntos de h?| E_L4 s , es decir, s es
subdiferenciable en todos los puntos de h?| E_L4 s [32, Th. 23.4].
6LVWHPDV VHPLLQ¿QLWRV OLQHDOHV
A lo largo de la memoria irán apareciendo repetidamente sistemas lineales de la
14
0. Preliminares
forma
j ' i@| % K| c | 5 A j c
(0.2)
donde A es un conjunto arbitrario de índices (posiblemente in¿nito), @| 5 U? y K| 5 U
para todo | 5 A . En esta sección haremos una recopilación de los principales conceptos
y resultados que se van a utilizar en relación con los sistemas semi-in¿nitos lineales
(SSIL).
Denotaremos por 8 el FRQMXQWR GH VROXFLRQHV de j y diremos que j es FRQVLVWHQWH
si 8 9' >. Cuando todos los coe¿cientes de una desigualdad lineal son cero, se dice
que esta GHVLJXDOGDG es WULYLDO. El VLVWHPD será WULYLDO cuando todas sus desigualdades
sean triviales.
Las caras de 8 son los conjuntos 8| ' i% 5 8 m @| % ' K| j, | 5 A , que, de hecho,
son caras expuestas de 8 . Si @| 9' f? entonces diremos que | 5 A es un tQGLFH
SURSLR. Se dice que | 5 A (@| % K| ) es un tQGLFH SRUWDGRU (GHVLJXDOGDG SRUWDGRUD)
de j cuando 8| ' 8 . El FRQMXQWR GH tQGLFHV SRUWDGRUHV lo denotaremos por AS .
Obviamente, si existe un cierto % 5 U? tal que @| % : K| para todo | 5 A entonces
AS ' >. Tales puntos reciben el nombre de SXQWRV GH 6ODWHU.
Asociados al sistema j se de¿nen los llamados SULPHU \ VHJXQGR FRQR GH
PRPHQWRV
 G' UL?i i@| c | 5 A j
y el FRQR FDUDFWHUtVWLFR
@|
y G' UL?i
c|5A ,
K|
f?
@|
c | 5 A(
g G' UL?i
K|

Cualquier conjunto convexo cerrado no vacío U? es la intersección de todos
los semiespacios de soporte de , de manera que es el conjunto solución de un cierto
sistema lineal j de la forma (0.2). Tal sistema j se llama UHSUHVHQWDFLyQ H[WHUQD de
. Llamaremos FRQR GH UHIHUHQFLD de , y lo denotaremos por g E, a la clausura
del cono característico de cualquier representación externa de . Esta de¿nición es
independiente de la representación considerada, ya que dos representaciones lineales
distintas del conjunto son sistemas lineales equivalentes, y por lo tanto, las clausuras
0.2 Sistemas semi-in¿nitos lineales
15
de sus correspondientes conos característicos son iguales [19, Th. 5.10].
En ocasiones, asociados al sistema j, de¿niremos un par de problemas
parametrizados, cuyo parámetro, S, recorre U? . El primero de ellos es de Programación
Semi-in¿nita Lineal (PSIL para abreviar), siendo el parámetro el gradiente del
funcional objetivo:
ES W?u S % r@ % 5 8
Denotaremos por 8 ES el FRQMXQWR ySWLPR de ES y por ES su YDORU ySWLPR, con
W
ES ' n4 si 8 ' >. Diremos que un punto % 5 8 es una VROXFLyQ IXHUWHPHQWH
W
~QLFD para ES si existe k : f tal que, para todo % 5 8 , S % S % n k n% % n.
W
W
Obviamente, en este caso, 8 ES ' i% j.
W
W
El segundo problema es el dual de ES (en el sentido de Haar), de modo que el
parámetro es el vector de la derecha en el sistema de restricciones,
[
[
EA ( ES 5T
b| K| r@
b| @| ' Sc b 5 Un |MA
|MA
EA Denotaremos por [ la función objetivo de ( ES, es decir, [ G Un $ U tal que
S
[ Eb G'
b| K| , por \ES su conjunto factible, por \ ES su conjunto óptimo y por
W
|M A
( ES su valor óptimo, acordando que ( ES ' 4 si \ES ' >. Llamaremos VDOWR
GH GXDOLGDG, B ES, a la diferencia entre el valor del problema primal y el del dual,
B ES G' ES ( ES c
que siempre es no negativo por el Teorema de Dualidad Débil.
Dado un sistema consistente j, se dice que @ % K es una FRQVHFXHQFLD de j si la
satisfacen todos los puntos de 8 , es decir, @ 5 K para todo 5 5 8 . En relación con
este concepto, el /HPD GH )DUNDV H[WHQGLGR [40] caracteriza las desigualdades lineales
@ % K que son consecuencia de un sistema consistente j como aquellas para las que
se satisface
@
5 U* g
K
Un caso particular es el /HPD GH )DUNDV H[WHQGLGR SDUD VLVWHPDV KRPRJpQHRV
[19, Cor. 3.1.3] que dice que la desigualdad @ % f es consecuencia del sistema
16
0. Preliminares
i@| % fc | 5 A j si, y sólo si, @ 5 U* 
En un sistema consistente, para cada % 5 8 , de¿nimos el FRQMXQWR GH tQGLFHV
DFWLYRV
A E% G' i| 5 A m @| % ' K| j
y el FRQR GH UHVWULFFLRQHV DFWLYDV
E% G' UL?i i@| c | 5 A E%j
en el punto %.
Los resultados más importantes sobre los sistemas ¿nitos de desigualdades lineales
sólo son válidos para ciertas clases de sistemas in¿nitos.
Consideremos, por ejemplo, el Teorema de Weyl [38] que caracteriza los puntos
extremos de 8 cuando mA m 4: % 5 8 es un punto extremo de 8 si, y
sólo si, _4 E% ' ?. En [1] se prueba que este resultado se cumple cuando
E%J ' ( E8c % para todo % 5 8 . Un sistema que satisface esta propiedad se
dice que es ORFDOPHQWH SROLpGULFR (LOP). Para aquellos problemas PSIL
E W?u S %
r@
@| % K| c | 5 Ac
cuyo sistema de restricciones es LOP, se han propuesto extensiones del método simplex
y del método del gradiente reducido [2].
El Teorema de Karush-Kuhn-Tucker para problemas PL establece que % 5 8 es
una solución óptima de (P) si, y sólo si, S 5 E%. En [31] se demuestra que esta
a¿rmación también es cierta cuando cualquier desigualdad que de¿na un semiespacio
soporte de 8 es también consecuencia de un subsistema ¿nito de j. Los sistemas que
satisfacen esta propiedad se llaman ORFDOPHQWH )DUNDV0LQNRZVNL (LFM).
Para los sistemas LOP se veri¿ca que 8 es cuasipoliédrico [19, Cor. 5.6.1] y,
recíprocamente, todo cuasipoliedro admite una representación LOP [19, Th. 5.11].
Cualquier sistema ¿nito es LOP y cualquier sistema LOP es LFM [19, Th. 5.7].
Un VLVWHPD j es FRQWLQXR cuando A es un espacio topológico compacto y
Hausdorff y todos los coe¿cientes, @ E c c @? E c K E, son continuos en A .
0.2 Sistemas semi-in¿nitos lineales
17
352326,&,Ï1 >19 /HP L@ 'DGR XQ VLVWHPD j VH YHUL¿FD OD VLJXLHQWH
UHODFLyQ
HQWUH ODV FODXVXUDV GH \g
f?
f?
5 U* VL \ VyOR VL
5 U* g


352326,&,Ï1 6L 8 9' > HV HO FRQMXQWR VROXFLyQ GH j ' i@| % K| c | 5 A j
HQWRQFHV VH FXPSOHQ ODV VLJXLHQWHV SURSRVLFLRQHV
(i) h?| 8 i% 5 U? m @| % : K| c | 5 A qAS ( @| % ' K| c | 5 AS j [19, Th. 5.1(i)] \
(ii) _4 8 ' ? _4 *? U* g [19, Th. 5.8].
352326,&,Ï1 >19 &RU @ 8Q VLVWHPD FRQVLVWHQWH j WLHQH DO PHQRV XQ
SXQWR GH 6ODWHU VL \ VyOR VL AS ' >
352326,&,Ï1 >19 7K @ &XDOTXLHU VLVWHPD /)0 QR WULYLDO j VDWLVIDFH ODV
VLJXLHQWHV SURSLHGDGHV
(i) _4 8 ' ? VL \ VyOR VL QLQJXQD FRPELQDFLyQ FRQYH[D GH GHVLJXDOGDGHV QR WULYLDOHV
GH j GD OXJDU D OD GHVLJXDOGDG WULYLDO
(ii)
_4 8 ' ? _4 tT@? i@| c | 5 AS j $GHPiV VL AS 9' > VH WLHQH
@g 8 ' i% 5 U? m @| % ' K| c | 5 AS j (iii) h?| 8 ' i% 5 U? m @| % : K| c | 5 A qAS ( @| % ' K| c | 5 AS j 352326,&,Ï1 >19 7K L@ 'DGR % 5 8 VL _4 E% ' ? HQWRQFHV % HV
SXQWR H[WUHPR GH 8 (VWD FRQGLFLyQ WDPELpQ HV QHFHVDULD FXDQGR j HV /23
352326,&,Ï1 >19 7K
@ 6L 8 9' > ODV VLJXLHQWHV D¿UPDFLRQHV VRQ
HTXLYDOHQWHV
(i) 8 HV DFRWDGR
f?
(ii)
5 ?| g

@
?
n
m @ % : K SDUD WRGR % 5 8 (iii) ?| g '
5U
K
(iv)  ' U? \
(v) H[LVWH XQ VXEVLVWHPD ¿QLWR GH j FX\R FRQMXQWR VROXFLyQ HV DFRWDGR.
352326,&,Ï1 >19 7K $@ 6HD XQ FRQMXQWR SROLpGULFR GH Pi[LPD
GLPHQVLyQ HQ U? \ FRQVLGHUHPRV XQD UHSUHVHQWDFLyQ OLQHDO GH i@ % K c ' c c Rj (0.3)
18
0. Preliminares
(QWRQFHV VH YHUL¿FDQ ODV VLJXLHQWHV SURSRVLFLRQHV
R
(i) M_ ' ^ M _ , donde M G' i% 5 U? m @ % ' K j (
'
(ii) si f es una faceta de , existe 5 ic c Rj tal que f ' M _ ( y
(iii) cada conjunto M _ es una faceta de si, y sólo si, (0.3) es una representación
minimal de (es decir un sistema sin restricciones redundantes).
&DStWXOR 6LVWHPDV OLQHDOHV JHQHUDOHV HQ U?
,QWURGXFFLyQ
Los sistemas lineales más generales en U? contienen un número arbitrario
(posiblemente in¿nito) de restricciones de desigualdad débil (dos de las cuales
reemplazan a una ecuación) y/o estricta, por lo que pueden escribirse en la forma
j ' i@| % K| c | 5 (( @| % : K| c | 5 .j c
(1.1)
donde los conjuntos de índices, ( y ., son disjuntos y no simultáneamente vacíos,
@| 5 U? y K| 5 U para todo | 5 A G' ( ^ .. Denotaremos por 8 el conjunto solución
de j.
Los sistemas ordinarios de desigualdades lineales (. ' > y m(m 4) han sido
ampliamente tratados en la literatura, debido a que están íntimamente relacionados
con la teoría y los métodos de la Programación Lineal. Por lo que se re¿ere a los
sistemas semi-in¿nitos lineales (. ' > y ( 9' > arbitrario), cuyo análisis da lugar a la
fundamentación teórica de la Programación Semi-In¿nita Lineal, son bien conocidos,
por ejemplo, los teoremas de existencia de Zhu [40] y Fan [12], así como los trabajos
de Eckhardt [11] y Goberna y López ([ 17] y [18]) acerca de la dimensión del conjunto
de soluciones o los estudios sobre su envoltura afín o su interior y frontera relativos
llevados a cabo por Goberna y López [17]. Más recientemente, han aparecido los
19
1. Sistemas lineales generales en U?
20
trabajos de Marchi et al. [23], Anderson et al. [1] y Goberna et al. [16] acerca de la
estructura facial de dicho conjunto.
Los sistemas lineales con desigualdades estrictas (. 9' >) surgen, de forma
natural, en problemas de separación, en optimización, en análisis de estabilidad y
en muchos otros campos. De hecho, una familia de 6 2 conjuntos no vacíos de
U? ,  c c 6 , se dice que es estrictamente separable [5] si existen 6 semiespacios
6
cerrados, P c c P6 , tales que ?| P , ' c c 6, y _ ?| P ' >, es decir,
'
si,
para
cada ' c c 6, existe una solución de j ' i@ % %?n : fc @ 5 j,
S
5 U?n , con S 9' f? , tal que el sistema jf ' ES % : _ c ' c c 6 es
_
6
inconsistente. Además, si _ & 9' >, ' c c 6, entonces la inconsistencia de jf
&'
&' 6
S
S
' f?n [5, Th. 2].
_
En particular, la búsqueda de un hiperplano que separe estrictamente a un par de
se puede sustituir por
'
conjuntos disjuntos de U? , t y ~, se puede formular como el sistema de desigualdades
estrictas
i+ % : %?n c + 5 t ( 5 % : %?n c 5 5 ~j c
%
donde la incógnita
5 U?n determina el vector de coe¿cientes del hiperplano
%?n
de separación.
Por otra parte, si f c  c c ? son matrices simétricas dadas y la construcción
del modelo de un cierto problema de optimización requiere que una combinación
?
S
lineal de ellas, digamos E% ' f n
% , sea de¿nida positiva, entonces
'
esta restricción se puede formular como ir E% r : fc r 5 7? j.
Finalmente, un sistema semi-in¿nito lineal continuo i@| % K| c | 5 A j es estable
(en los diferentes sentidos especi¿cados en [19, Th. 6.9]) si, y sólo si, existe solución
para el correspondiente sistema de desigualdades estrictas i@| % : K| c | 5 A j.
A pesar de la gran cantidad de aplicaciones que tienen, en potencia, los sistemas
lineales con desigualdades estrictas, hasta ahora sólo se han dado teoremas de
existencia para casos particulares. Así, son conocidos, el Teorema de Carver [10]
y el Teorema de Transposición de Motzkin [29], ambos para sistemas ¿nitos, y
1.1 Introducción
21
los Teoremas de Gordan y Motzkin extendidos [20] para sistemas semi-in¿nitos
homogéneos. Todos estos resultados son extendidos por el teorema de existencia que
probaremos en la Sección 1.2, donde también se discutirá el cálculo numérico de una
solución.
La Sección 1.3 muestra que los conjuntos de soluciones de los sistemas de
desigualdades lineales de la forma (1.1), poseen buenas propiedades geométricas.
En efecto, esta familia de conjuntos convexos (llamados “evenly convex” en [14])
captura la mayoría de las propiedades más notables de una subclase, los conjuntos
cerrados convexos, que juega un papel crucial en la teoría y en las aplicaciones de la
optimización.
La Sección 1.4 analiza las propiedades geométricas de 8 en términos de los
coe¿cientes de su representación lineal j.
Por último, en la Sección 1.5 demostramos que es posible tratar de modo efectivo
problemas de optimización lineal con restricciones estrictas, extendiendo a esta clase
de problemas PSIL resultados de optimalidad, unicidad fuerte y acotación del conjunto
óptimo.
En este capítulo explotaremos la relación entre j, como en (1.1), y su sistema
relajado j ' i@| % K| c | 5 A j (obtenido al sustituir @| % : K| por @| % K| para todo
| 5 .). Obviamente, la consistencia de j no implica la consistencia de j (considérese,
por ejemplo, el sistema j ' if % fj en U).
352326,&,Ï1 6HD j HO VLVWHPD UHODMDGR GH j \ VHD 8 HO FRQMXQWR VROXFLyQ GH j
(QWRQFHV VH YHUL¿FDQ ODV VLJXLHQWHV FRQGLFLRQHV
(i) 6L 8 9' > HQWRQFHV 8 ' U* 8 .
(ii) 6L 8 ' > \ j QR FRQWLHQH GHVLJXDOGDGHV WULYLDOHV HQWRQFHV R 8 ' > R _4 8 ?.
'HPRVWUDFLyQ (i) Sea % 5 8 . Si % 5 8 , entonces
E b % n b% 5 8c f b c
de modo que
% '*4 E b % n b% 5 U* 8 .
b<f
(1.2)
1. Sistemas lineales generales en U?
22
Por lo tanto, 8 U* 8 . La inclusión opuesta es trivial.
@|
9' f?n para todo | 5 A y 8 9' >.
(ii) Supongamos que 8 ' >,
K|
Puesto que j es consistente y i@| % : K| c | 5 A j no tiene solución (es decir, no
existe ningún punto de Slater para j), existe un | 5 A tal que @| % ' K| para todo % 5 8
(Proposición 0.16), con @| '
9 f? (en otro caso, tomando un % 5 8 arbitrario, se obtiene
@|
K| ' f? % ' f, de modo que
' f?n ). Por lo tanto, @| % ' K| de¿ne un hiperplano
K|
que contiene a 8 .
Obsérvese que, para j ' if? % : fj, 8 ' > y 8 ' U? . Por lo tanto, la a¿rmación
(ii) de la Proposición 1.1 podría fallar para sistemas que contengan desigualdades
triviales.
([LVWHQFLD GH VROXFLRQHV
352326,&,Ï1 6HD j HO VLVWHPD GH (i) 6L j HV FRQVLVWHQWH HQWRQFHV
f?
@|
5
* U* UL?i
c |5A 
K|
$GHPiV VL . 9' > HQWRQFHV WDPELpQ VH YHUL¿FD OD VLJXLHQWH FRQGLFLyQ
@|
@|
* UL?
c | 5 . n UL?i
c |5( f?n 5
K|
K|
(1.3)
(1.4)
(ii) &DGD XQD GH ODV VLJXLHQWHV FRQGLFLRQHV JDUDQWL]D OD FRQVLVWHQFLD GH j
(ii.a) . ' > \ VH YHUL¿FD (ii.b) . 9' > VH YHUL¿FDQ \ \ HO FRQMXQWR GH HV FHUUDGR
f?
HQ ORV FRQMXQWRV JHQHUDGRUHV GH ORV FRQRV GH
$GHPiV SXHGH DJUHJDUVH

\ 'HPRVWUDFLyQ (i) Supongamos que
f?
@|
5 U* UL?i
c |5A 
K|
1.2 Existencia de soluciones
o o _
f?
_
?
n
U
'
Entonces existe una sucesión
tal que *4
y
o
Bo
Bo

o [ _
@|
EA bo|
'
c bo 5 Un c o ' c 2c Bo
K|
| A
23
M
Puesto que j es consistente, podemos tomar %f 5 8 . Entonces, se tiene
o f [
_
%
bo| @| %f K| fc o ' c 2c c
'
Bo

| A
(1.5)
M
y, tomando límites en (1.5), se llega a la contradicción
f
f?
%
f


Así pues, se veri¿ca (1.3).
Supongamos ahora que . 9' >. Si
@|
@|
f?n 5 UL?
c | 5 . n UL?i
c |5( c
K|
K|
S
EA entonces existe b 5 Un tal que
b| '  y
|M .
[ @|
@|
n
f?n '
b|
b|
K|
K|
| .
| (
[
M
M
Tomando una solución arbitraria de j, %f , se tiene
f [
[ f
%
'
b| @| %f K| n
b| @| % K| : f
f ' f?n

| .
| (
M
M
Por lo tanto, se cumple (1.4).
(ii.a) Supongamos
que . ' > y se cumple(1.3).Por la Proposición 0.13,
existe
un
%
S
f
?
' , con S '
5 U? U, tal que S
'
hiperplano en U?n , S
S
%?n

?
n
@|
y S : para todo 5 U* UL?i
c | 5 ( . La última condición implica que
|
K
@|
S f : para todo 5 UL?i
c | 5 ( , en particular, @| S n K| S?n f para
K|
todo | 5 (.
Puesto que S?n ' f, de¿niendo % ' mS?n m  S, se tiene que @| % K| para
3
todo | 5 (, de manera que j es consistente
1. Sistemas lineales generales en U?
24
(ii.b) Supongamos ahora que . '
9 >, se veri¿can (1.3) y (1.4) y el conjunto
@|
@|
G' UL?
c | 5 . n UL?i
c |5(
K|
K|
es cerrado.
S
Puesto que f?n 5
5 U?n
* , por la Proposición 0.13, existe un vector
S
?n
S
@|
5 para todo | 5 ., por
tal que
@ : f para todo @ 5 . En particular,
S?n
K
|
@|
@r
lo que @| S n K| S?n : f, y
n>
5 para todo | 5 ., r 5 ( y > : f, de
K|
Kr
manera que
@r S n Kr S?n : @| S n K| S?n
>
Por lo tanto, @| S n K| S?n : f para todo | 5 . y @r S n Kr S?n f para todo r 5 (.
Sea % una solución de j (sistema que satisface (ii.a) y, por tanto, es consistente) y
consideremos el siguiente punto de U? :
;
S
A
c
si S?n f
A
A
mS
?n m
A
A
A
?
%
e G'
S n %c
si S?n ' f A
A
A
A
A
S
A
= 2% n
c si S?n : f
S?n
Realizando sencillos cálculos algebraicos, se demuestra que %
e 5 8 , por lo que j
es consistente.
@|
Finalmente, veremos que en (1.4) se puede sustituir UL?i
c | 5 ( por
K|
@|
f?
(el equivalente en (1.3) se obtiene directamente de la
UL?i
c | 5 ((
K|

Proposición 0.14).
En primer lugar, para probar (i), consideramos j consistente, . 9' > y
@|
f?
@|
f?n 5 UL?
c | 5 . n UL?i
c | 5 ((
K|
K|

Entonces,
[
f?n '
|MA
@|
f?
b|
n>
c
K|

(1.6)
1.2 Existencia de soluciones
EA para algún b 5 Un tal que
S
25
b| '  y > : f (ya que > ' f contradice (1.4)). De
|M .
(1.6) se deduce que
[ f?
b| @|
@|
'
5 UL?i
c |5A c

>
K
K
|
|
| A
M
lo que contradice (1.3). Por lo tanto, se veri¿ca
@|
f?
@|
c | 5 . n UL?i
c | 5 ((
f?n 5
* UL?
K|
K|

(1.7)
Por otro lado, si suponemos que . 9' > y se cumple (1.7), siendo cerrado el
conjunto del segundo miembro, aplicando (ii.b), se tiene que el sistema
i@| % : K| c | 5 .( @| % K| c | 5 (( f? % j
es consistente y, por lo tanto, j es consistente.
Obsérvese que si mA m 4, se cumple la hipótesis de clausura de la condición (ii.b)
y, a partir de esta versión de la Proposición 1.2, se prueba el Teorema de Transposición
de Motzkin [29], que fue utilizado por el propio Motzkin (1951) y por Slater (1951)
para probar el Teorema de Dualidad de la Programacion Lineal.
&252/$5,2 'DGDV ODV PDWULFHV E6 ? \ ER ? \ ORV YHFWRUHV K 5 U6 \
_ 5 UR HO VLVWHPD i% K( % _j HV FRQVLVWHQWH VL \ VyOR VL VH FXPSOHQ ODV GRV
FRQGLFLRQHV VLJXLHQWHV
(i) VL + n 5 ' f? + f6 \ 5 fR HQWRQFHV + K n 5 _ f
(ii) VL + n 5 ' f? + f6 + 9' f6 \ 5 fR HQWRQFHV + K n 5 _ : f
'HPRVWUDFLyQ La prueba del directo es trivial.
Supongamos ahora que i% K( % _j es inconsistente y probaremos que
falla (i) o (ii).
Denotemos las columnas de por @ c c @6 y las columnas de por
@6n c c @6nR . Denotemos también por K c c K6 las componentes de K y por
K6n c c K6nR las componentes de _. Entonces
i% K( % _j ' i@ % K c ' c c 6( @ % K c ' 6 n c c 6 n Rj 1. Sistemas lineales generales en U?
26
Si falla (1.3), podemos escribir
6
nR
[
@
f?
, b f, ' c c 6 n R.
'
b

K
'
De¿niendo + ' Eb c c b6 y 5 ' Eb6n c c b6nR , se tiene + f6 , 5 fR ,
+ n 5 ' f? e + K n 5 _ ' , por lo que falla (i).
Alternativamente, si falla (1.4), podemos escribir
6
[
nR
6
[
f?
@
b
b ' , b f, ' c c 6 n R.
,
'
f
K
'
'
De¿niendo + y 5 como antes, se tiene ahora + f6 , + 9' f6 , 5 fR , + n 5 ' f?
e + K n 5 _ ' f, por lo que falla (ii).
Si en el sistema (1.1) consideramos el caso particular . ' >, entonces la
Proposición 1.2 coincide con los teoremas de existencia de Zhu y Fan. En el caso
de que sea ( ' > (A ' .), (1.4) se convierte, simplemente, en
@|
f?n 5
* UL?
c |5A ,
K|
(1.8)
y este conjunto es cerrado si A es compacto y @| y K| son funciones continuas (en
particular si mA m 4). A partir de esta versión de la Proposición 1.2 se demuestra, de
forma análoga al Corolario 1.3, el Teorema de Carver [10].
&252/$5,2 'DGD OD PDWUL] E6 ? \ HO YHFWRU K 5 U6 HO VLVWHPD i% Kj
HV FRQVLVWHQWH VL \ VyOR VL OD ~QLFD VROXFLyQ GH i + ' f? c K + fc + f6 j HV OD
WULYLDO
Por
otra
parte, si j es un sistema semi-in¿nito lineal continuo, el conjunto
@|
UL?
c | 5 A es cerrado y la condición (1.8) caracteriza la estabilidad de este
K|
tipo de sistemas [21].
Otro caso particular que debemos considerar es que j en (1.1) sea homogéneo, en
cuyo caso, la Proposición 1.2 se convierte en el Teorema de Motzkin extendido [19,
Th. 3.5] si . 9' > y en el Teorema de Gordan extendido [19, Th. 3.2] si ( ' >.
El siguiente ejemplo muestra que la hipótesis de clausura de la condición (ii.b) de
la Proposición 1.2 no es superÀua.
1.2 Existencia de soluciones
27
(-(03/2 Considérese el sistema de desigualdades estrictas en U2
j ' |% n %2 : |2 c | 5 Uq ifj ( %2 : f E| ' f Se cumple (1.3) porque f2 es solución de j. Si fallase (1.4), entonces podríamos
escribir
3 4
3
4
3
4
f
f
|
[
C f D ' bf C  D n
b| C  D c
(1.9)
2
f
|
f
|'f
EU S b ' . Comparando las terceras componentes de ambos
donde b 5 Un y
|
|MU
miembros
de (1.9), se obtiene b| ' f para todo | 9' f, de manera que bf ' f y
S
b| ' f (contradicción). Así pues, también se cumple (1.4).
|M U
Supongamos ahora que % 5 U? satisface |% n%2 : |2 para todo | 9' f. Tomando
límites cuando | tiende a cero, se obtiene %2 f, de modo que j es inconsistente.
Por lo tanto, j satisface (1.3) y (1.4) a pesar de que carece de soluciones.
Se puede comprobar que, en este caso,
<
;3
4
4 3
f
|
@
?
@|
D
C
D
C
 (

UL?
c | 9' f
c | 5 . ' UL?
>
=
K|
f
|2
no es cerrado, ya que
pero
3
4
3
4
f
|
C  D ' *4 C  D
|< f
f
|2
;3
<
4
4 3
4
f
f
|
?
@
C  D5
C
D
C
D
 (

* UL?
c | 9' f =
>
f
f
|2
3
Diremos que el sistema j de (1.1) es un VLVWHPD JHQHUDO IXHUWHPHQWH LQFRQVLVWHQWH
si posee algún subsistema ¿nito inconsistente y es un VLVWHPD JHQHUDO DVLQWyWLFDPHQWH
LQFRQVLVWHQWH si es inconsistente y todos sus subsistemas ¿nitos son consistentes. Para
esta clasi¿cación de los sistemas generales inconsistentes se obtienen los siguientes
resultados como consecuencia de la Proposición 1.2.
1. Sistemas lineales generales en U?
28
&252/$5,2 6HD j HO VLVWHPD GH (i) 6L j HV IXHUWHPHQWH LQFRQVLVWHQWH HQWRQFHV
@|
f?
5 UL?i
c |5A

K|
R ELHQ
(1.10)
@|
@|
c | 5 . n UL?i
c |5( f?n 5 UL?
K|
K|
(1.11)
(Q SDUWLFXODU VL . ' > VH FXPSOH .
(ii) &DGD XQD GH ODV VLJXLHQWHV FRQGLFLRQHV JDUDQWL]D OD LQFRQVLVWHQFLD IXHUWH GH j
(ii.a) 6H YHUL¿FD .
(ii.b) . 9' > \ VH YHUL¿FD 'HPRVWUDFLyQ (i) Supongamos que j es fuertemente inconsistente. Entonces
existe 7 A ¿nito tal que
i@| % K| c | 5 7 _ (( @| % : K| c | 5 7 _ .j
es inconsistente.
Por el apartado (ii.a) de la Proposición 1.2, si . ' > se cumple
@|
f?
5 UL?i
c |57

K|
(1.12)
y, por lo tanto, se veri¿ca (1.10).
Si . 9' >, aplicando el apartado (ii.b) de la misma proposición, se obtiene (1.12)
(y, por lo tanto, (1.10)) o bien
@|
@|
c | 5 7 _ . n UL?i
c |57_(
f?n 5 UL?
K|
K|
y, por lo tanto, (1.11).
EA (ii.a) Supongamos que se cumple (1.10). Entonces existe b 5 Un tal que
[ f?
@|
'
b|
(1.13)

K|
|MA
Tomando el sistema
j
e ' i@| % K| c | 5 EtTT b _ (( @| % : K| c | 5 EtTT b _ .j
1.2 Existencia de soluciones
29
y aplicando a j
e el apartado (i) de la Proposición 1.2, (1.13) implica la inconsistencia
de j
e, por lo que j es fuertemente inconsistente.
EA (ii.b) Supongamos que . 9' > y que se cumple (1.11). Entonces existe b 5 Un
S
tal que
b| '  y
|M.
[ @|
@|
n
f?n '
b|
b|
K
K
|
|
|M .
|M (
[
(1.14)
Del mismo modo que en (ii.a), (1.14) implica que j
e es inconsistente y, por lo tanto,
j es fuertemente inconsistente.
&252/$5,2 6HD j HO VLVWHPD GH (i) 6L . ' >, j HV DVLQWyWLFDPHQWH LQFRQVLVWHQWH VL \ VyOR VL
f?
@|
@|
5 U* UL?i
c |5A
q UL?i
c |5A

K|
K|
(ii) 6L . 9' > VH FXPSOH \
@|
@|
* UL?
c | 5 . n UL?i
c |5( c
f?n 5
K|
K|
(1.15)
(1.16)
HQWRQFHV j HV DVLQWyWLFDPHQWH LQFRQVLVWHQWH
(O UHFtSURFR VH FXPSOH VL HO FRQMXQWR GH HV FHUUDGR
'HPRVWUDFLyQ (i) Es consecuencia de la Proposición 1.2 y del Corolario 1.6.
(ii) Supongamos que . 9' > y se cumplen (1.15) y (1.16).
La condición (1.15) implica que j es inconsistente (Proposición 1.2 (i)). Por otra
parte, si se cumplen (1.15) y (1.16), entonces no se cumplen ni (1.10) ni (1.11), por lo
que j no puede ser fuertemente inconsistente.
Para probar el recíproco, supongamos que j es asintóticamente inconsistente y que
el conjunto de (1.16) es cerrado. Dado que j no es fuertemente inconsistente, no se
cumplen ni (1.10) ni (1.11) (Corolario 1.6), lo que implica que se cumplen (1.15) y
(1.16). En efecto, si no se cumpliese (1.15), al no cumplirse tampoco (1.10), se tendría
@|
f?
5
* U* UL?i
c |5A

K|
y, por el apartado (ii.b) de la Proposición 1.2, j sería consistente.
1. Sistemas lineales generales en U?
30
Nótese que, al igual que en la Proposición 1.2, se puede añadir
f?

a los
generadores de los conos de (1.10), (1.11), (1.15) y (1.16).
La condición de clausura del Corolario 1.7 no es superÀua. Así, en el Ejemplo 1.5,
j es asintóticamente inconsistente, se cumple (1.16), pero no se cumple (1.15).
&252/$5,2 6HD j HO VLVWHPD GH 6L j HV LQFRQVLVWHQWH \ HO VLVWHPD
KRPRJpQHR DVRFLDGR D j j f ' i@| % fc | 5 (( @| % : fc | 5 .j WLHQH XQD VROXFLyQ
HVWULFWD HQWRQFHV j HV DVLQWyWLFDPHQWH LQFRQVLVWHQWH
'HPRVWUDFLyQ Si j fuese fuertemente inconsistente, entonces, por el Corolario
1.6, debería cumplirse (1.10) o bien (1.11).
EA Si se cumple (1.10), entonces existe b 5 Un tal que
[ f?
@|
'
b|

K|
|MA
Si % es una solución estricta de jf , multiplicando la igualdad anterior por
%
5 U?n , se obtiene
f
#
$
[
[
b| E@| % '
b| @| % ' f? % ' fc
(1.17)
|M A
|M A
y esto implica b| ' f para todo | 5 A , puesto que @| % es siempre estrictamente
S
positivo. Este hecho contradice la igualdad
b| K| ' .
|M A
Por otra parte, si no se cumple (1.10), deberá cumplirse (1.11), lo que implica que
S
EA b| '  y
existe b 5 Un tal que
|M .
f?n
[ @| '
b|
K
|
|MA
%
Multiplicando esta igualdad por
, se obtiene, de nuevo, (1.17) y b| ' f para todo
f
S
| 5 A , lo que se contradice con la igualdad
b| ' .
|M.
En [19] se realiza una clasi¿cación de los sistemas semi-in¿nitos lineales
inconsistentes según acepten o no soluciones extendidas. Se de¿nen dos tipos de
soluciones extendidas, las soluciones asintóticas y las soluciones polinomiales.
1.2 Existencia de soluciones
31
Se dice que una sucesión i%o j U? es una solución asintótica del sistema
j ' i@| % K| c | 5 A j si, para todo | 5 A ,
*4 ?u @| %o K| c
o
donde se permite n4 como límite.
Se dice que R ' ER c c R? 5 EU d+o? es una solución polinomial de j si, para
todo | 5 A ,
?
[
@ E| R K|
@| R G'
'
(con respecto del orden lexicográ¿co de U d+o).
En [19, Th. 4.3] se establece, para un sistema semi-in¿nito lineal j, la equivalencia
entre la existencia de ambos tipos de soluciones extendidas y la consistencia de todo
subsistema ¿nito de j. A los sistemas inconsistentes que cumplen estas condiciones
equivalentes se les da el nombre de asintóticamente inconsistentes y a los que no las
cumplen fuertemente inconsistentes.
Para sistemas con desigualdades estrictas, se pueden de¿nir, de forma análoga,
las soluciones asintóticas y polinomiales, aunque, en este caso, no se produce la
mencionada equivalencia (véase Ejemplo 1.9). Sin embargo, con las de¿niciones dadas
de sistemas generales asintótica y fuertemente inconsistentes, los Corolarios 1.6 y 1.7
subsumen las caracterizaciones de la inconsistencia fuerte y asintótica dadas en [19,
Th. 4.4] y el Corolario 1.8 extiende el resultado obtenido para sistemas semi-in¿nitos
lineales en [19, Cor. 4.4.1].
(-(03/2 Considérese el sistema j ' i%2 o 3 c o 5 Q( %2 : fj en U2 .
Toda solución de i%2 o3 c o 5 Qj cumple la restricción %2 f, por lo que j
es un sistema inconsistente. Además, cualquier subsistema ¿nito de j es consistente,
de modo que j es un sistema general asintóticamente inconsistente.
j no posee soluciones asintóticas ni polinomiales. En efecto, si
& Sin embargo,
2
% U fuese solución asintótica de j, se cumpliría
*4 ?u %&2 o 3 , para todo o 5 Q,
&
y
*4 ?u %&2 : f
&
(1.18)
1. Sistemas lineales generales en U?
32
Puesto que
*4 ?u %&2 ' *4 tT %&2 *4 ?u %&2 c
&
&
&
se tiene *4 ?u %&2 f, por lo que deberá existir un o 5 Q tal que
&
*4 ?u %&2 o 3 fc
&
lo que se contradice con (1.18).
Por otra parte, si R ' ER c R2 5 EU d+o2 fuese una solución polinomial de j,
entonces
R2 o 3 , para todo o 5 Q,
(1.19)
y
R2 : f
(con respecto del orden lexicográ¿co de U d+o).
El polinomio R2 debe tener grado mayor o igual que uno (ya que, en caso contrario,
j sería consistente) y coe¿ciente de mayor grado negativo (ya que R2 : f). Sin
embargo, en esas condiciones, no se cumple (1.19), por lo que R no puede ser solución
polinomial de j.
El siguiente resultado proporciona el método natural de decidir si j es consistente
o no, y de calcular una solución de j en el primer caso. Para ello, asociamos a j el
siguiente problema PSIL:
Ej W?u
%?n
s.a.
@| % n %?n K| , | 5 .
@| % K| , | 5 (
352326,&,Ï1 6HD j HO VLVWHPD GH (QWRQFHV VH YHUL¿FDQ ODV VLJXLHQWHV
FRQGLFLRQHV
(i) 6L Ej f HQWRQFHV j HV FRQVLVWHQWH
(ii) 6L Ej : f HQWRQFHV j HV LQFRQVLVWHQWH
(iii) 6L Ej ' f \ Ej HV QR UHVROXEOH HQWRQFHV j HV LQFRQVLVWHQWH
%
e
5 U?n tal que @| %
en%
e?n K| para todo | 5 .,
%
e?n
e K| para todo | 5 ( y %
e?n f. Entonces %
e es solución de j.
@| %
'HPRVWUDFLyQ (i) Sea
1.3 Conjuntos linealizables
33
%
(ii) Si % es una solución de j, entonces
es una solución factible de Ej , de
f
modo que Ej f. Por lo tanto, Ej : f implica la inconsistencia de j (y de j).
%
e
e es una solución de j, entonces
es una solución óptima
(iii) Si Ej ' f y %
f
de Ej .
Si Ej '
fy Ej es resoluble, existe una solución óptima de Ej que se puede
%
. Entonces % es solución de j. Sin embargo, j no es necesariamente
escribir como
f
consistente.
El sistema del Ejemplo 1.5 ilustra el caso dudoso: Ej ' f con Ej resoluble.
En efecto, tomando límites cuando | $ f en |% n %2 n % |2 , | 9' f, se obtiene
%2 n % f. La otra restricción es %2 n % f, de modo que % f para toda
solución factible de Ej . Puesto que f es solución factible, Ej ' f y f es una
solución óptima de Ej . En este caso j es inconsistente.
&RQMXQWRV OLQHDOL]DEOHV
Se dice que un conjunto U? es OLQHDOL]DEOH (“evenly convex set” en [14])
si es intersección de una cierta familia de semiespacios abiertos. Puesto que esta
familia puede ser vacía, U? y > son conjuntos linealizables. Por otra parte, puesto
que cualquier semiespacio cerrado es intersección de una in¿nidad de semiespacios
abiertos, es linealizable si, y sólo si, es el conjunto de soluciones de un cierto
sistema de desigualdades lineales de la forma (1.1). En particular, cualquier conjunto
convexo cerrado es linealizable.
De acuerdo con (1.2), si es un conjunto linealizable, % 5 y %2 5 U* ,
entonces o% c %2 d (compárese con la prueba de la a¿rmación 3.5 de [14]). El
siguiente resultado proporciona nuevas caracterizaciones de los conjuntos linealizables
que complementan las dadas en [14]. Las a¿rmaciones (ii), (iv) y (vi)-(ix) fueron
conjeturadas por el Prof. Martínez Legaz (comunicación privada).
352326,&,Ï1 'DGR XQ FRQMXQWR U? WDO TXH > 9' 9' U? ODV VLJXLHQWHV
FRQGLFLRQHV VRQ HTXLYDOHQWHV
1. Sistemas lineales generales en U?
34
(i) HV OLQHDOL]DEOH
(ii) HV OD LQWHUVHFFLyQ GH XQD FLHUWD IDPLOLD QR YDFtD GH FRQMXQWRV FRQYH[RV DELHUWRV
QR YDFtRV
(iii) HV XQ FRQMXQWR FRQYH[R \ SDUD FDGD % 5 U? q H[LVWH XQ KLSHUSODQR M WDO TXH
% 5 M \ M _ ' >
(iv) HV XQ FRQMXQWR FRQYH[R \ HV LQWHUVHFFLyQ GH XQD IDPLOLD GH FRPSOHPHQWRV GH
KLSHUSODQRV
(v) HV HO UHVXOWDGR GH HOLPLQDU GH XQ FLHUWR FRQMXQWR FHUUDGR FRQYH[R OD XQLyQ GH
XQD IDPLOLD SRVLEOHPHQWH YDFtD GH VXV FDUDV H[SXHVWDV
(vi) HV XQ FRQMXQWR FRQYH[R \ SDUD FXDOTXLHU FRQMXQWR FRQYH[R g EU* q, H[LVWH
XQ KLSHUSODQR TXH FRQWLHQH D g \ TXH QR FRUWD D (vii) HV XQ FRQMXQWR FRQYH[R \ SDUD FXDOTXLHU FRQMXQWR FRQYH[R g EU* q, OD
FDUD H[SXHVWD PLQLPDO HQ U* TXH FRQWLHQH D g QR FRUWD D (viii) HV XQ FRQMXQWR FRQYH[R \ SDUD FXDOTXLHU % 5 EU* q, OD FDUD H[SXHVWD PLQLPDO
HQ U* TXH FRQWLHQH D % QR FRUWD D \
(ix) HV XQ FRQMXQWR FRQYH[R \ SDUD FDGD % 5 EU* q H[LVWH XQ KLSHUSODQR M TXH
VRSRUWD D U* HQ % \ WDO TXH M _ ' >
$GHPiV FXDQGR HV OLQHDOL]DEOH ODV ~QLFDV FDUDV GH U* TXH SXHGHQ VHU FRPSR
QHQWHV FRQH[DV GH EU* q VRQ ODV H[SXHVWDV
'HPRVWUDFLyQ Probaremos que (i) , (ii) , (iii) , (iv) , (i) y (i) , (v) , (vi)
, (vii) , (viii) , (ix) , (i).
(i) , (ii) Es trivial.
(ii) , (iii) Sea ' _ | , con i| c | 5 A j una familia no vacía de conjuntos
|M A
convexos abiertos no vacíos. Entonces es un conjunto convexo y dado % 5 U? q,
existe | 5 A tal que % 5
* | .
Puesto que | es un conjunto convexo abierto no vacío y i%j es un conjunto afín
que no corta a | , podemos aplicar la Proposición 0.12 para obtener un hiperplano M
que contiene a % y que no corta a | y, por lo tanto, tampoco a .
(iii) , (iv) Por hipótesis, dado | 5 A G' U? q, existe un hiperplano M| tal que
| 5 M| y M| _ ' >. Por lo tanto,
_ EU? qM| |M A
(1.20)
1.3 Conjuntos linealizables
35
U? q ' A ^ M| (1.21)
y
|MA
De (1.21), y aplicando las Leyes de De Morgan, se obtiene la igualdad en (1.20).
(iv) , (i) Sea ' _ EU? qM| , con M| ' i% 5 U? m @| % ' K| j, @| 5 U? q if? j
|M A
y K| 5 U, para todo | 5 A . Puesto que es un conjunto convexo y, para cada | 5 A ,
U? qM| , estará contenido en uno de los semiespacios abiertos asociados con
M| . Así pues, podemos suponer, sin pérdida de generalidad,
_ i% 5 U? m @| % : K| j .
|MA
(1.22)
* , existe r 5 A tal que % 5
* U? qMr o, lo que es lo mismo,
Por otra parte, si % 5
@r % ' Kr . Por lo tanto, % 5
* i% 5 U? m @r % : Kr j y se obtiene la igualdad en (1.22).
(i) , (v) Sea el conjunto de soluciones de j ' i@| % : K| c | 5 A j y sea j su
correspondiente sistema relajado. El conjunto de soluciones de j es 8 ' U* (por
la Proposición 1.1). Dado | 5 A , el conjunto f| G' % 5 8 m @| % ' K| es una cara
expuesta de U* (posiblemente vacía). Además,
' 8 q ^ f| |MA
(v) , (vi) Sea f un conjunto convexo cerrado y sea if| c | 5 .j una familia de
caras expuestas de f tal que
' fq
^ f| |M .
Puesto que f| 9' f para todo | 5 . (en caso contrario ' >), por la Proposición
0.11, ^ f| hM_ f y se obtiene
|M .
h?| f ' fq EhM_ f f
(1.23)
Tomando clausuras en (1.23), se concluye que, en realidad, f ' U* , de manera
que
' EU* q
^ f| |M .
(1.24)
Sea g EU* q un conjunto convexo no vacío (si g ' >, cualquier hiperplano
1. Sistemas lineales generales en U?
36
que no corte a contiene a g) y sea % 5 h?| g. Entonces, existe | 5 . tal que
% 5 f| de manera que f| es una cara de U* que corta a h?| g y, por la Proposición
0.10, g f| . Dado que f| es una cara expuesta de U* , existe un hiperplano M tal
que f| ' M _ U* y, por lo tanto, g M y
M _ ' M _ dEU* _ o ' f| _ ' >
(1.25)
(vi) , (vii) Sea g EU* q un conjunto convexo y sea f la cara expuesta
minimal tal que g f.
Por hipótesis, existe un hiperplano M tal que g M y M _ ' >. Si tomamos
t ' M _ U* 9' > (ya que g t ), t es una cara expuesta que contiene a g, por lo
que f t y, dado que
t _ ' EM _ U* _ ' M _ ' >c
f _ ' >.
(vii) , (viii) Es trivial, ya que (viii) es un caso particular de (vii).
(viii) , (ix) Sea % 5 EU* q y sea f la cara expuesta minimal (en U* ) que
contiene a %.
Por ser f cara expuesta de U* , existe un hiperplano M tal que U* está contenido
en uno de los semiespacios cerrados asociados a M y f ' M _ U* , por lo que % 5 M
y M soporta a U* en %. Además, dado que, por hipótesis, f _ ' >, razonando
como en (1.25), se tiene
M _ ' >
(ix) , (i) Por ser un conjunto convexo, U* es un conjunto convexo cerrado
y, por lo tanto, es el conjunto solución de un cierto sistema semi-in¿nito lineal
i@| % K| c | 5 L j.
Por otra parte, dado | 5 . G' EU* q, por hipótesis, existe un hiperplano
M| ' i% 5 U? m @| % ' K| j, con @| 9' f? y K| 5 U, que soporta a U* en | y tal que
M| _ ' >, es decir, @| % K| para todo % 5 U* , @| % : K| para todo % 5 y @| | ' K| .
1.3 Conjuntos linealizables
37
De¿niendo A G' L ^ ., está claro que U* ' i% 5 U? m @| % K| c | 5 A j. Sea
( ' A q.. Probaremos que j, en (1.1), es una representación lineal de .
Si % 5 , @| % K| para todo | 5 A (puesto que % 5 U* ), con @| % : K| para todo
| 5 ., de manera que % es solución de j.
Recíprocamente, si % es solución de j, entonces % 5 U* (puesto que @| % K|
para todo | 5 A ). Supongamos % 5 EU* q ' .. Entonces, existe | 5 . tal que
| ' % y @| % ' @| | ' K| , lo que se contradice con el hecho de que % sea solución de j.
Así pues, % 5 .
Supongamos ahora que (1.1) es una representación lineal de y que f 9' > es una
cara de U* contenida en EU* q. Suponiendo que f no es expuesta, probaremos
que existe un arco contenido en EU* q que une un punto de f con otro punto no
perteneciente a f, por lo que f no podrá ser una componente conexa de EU* q.
Tomemos % 5 h?| f arbitrariamente. De acuerdo con la Proposición 0.6, existen
i% c c %R j f y escalares positivos k c c kR tales que
R
[
%'
'
k % c
R
[
'
k '  y @g % c c %R ' @g f
R
S
Si fuese @| % ' K| , con | 5 A , se tendría K| ' @| % '
'
k E@| % y, dado que
@| % K| , ' c c R (al ser % 5 f, ' c c R), esto sólo es posible si @| % ' K| ,
R
S
' c c R. Si % 5 @g f, también se puede escribir % ' q % para ciertos escalares
q  c c q R tales que
R
S
'
'
q ' , por lo que @| % ' K| para todo % 5 @g f, es decir,
@g f i% 5 U? m @| % ' K| j.
Estamos suponiendo % 5 h?| f f EU* q, de manera que % es solución
de j, pero no de j. Deberá cumplirse, por lo tanto, @| % ' K| para cierto | 5 ., con
f @g f i% 5 U? m @| % ' K| j Como estamos suponiendo que f es cara no
expuesta de U* , deberá existir un punto %| 5 EU* qf tal que @| %| ' K| . Entonces
cualquier % 5 d%c %| o U* satisface @| % ' K| , por lo que % no es solución de j y
%5
* . Así pues, d%c %| o EU* q. Este segmento es el arco buscado.
Como consecuencia de la Proposición 1.11 y de la Proposición 0.12, cualquier
conjunto convexo relativamente abierto es linealizable. Análogamente, cualquier
1. Sistemas lineales generales en U?
38
conjunto estrictamente convexo (es decir, un conjunto convexo tal que M_ U* no
contiene segmentos) es linealizable puesto que todas las caras expuestas propias de
son singulares. Obsérvese, además, que cualquier conjunto convexo f 9' > está
encajado entre dos conjuntos linealizables, h?| f y U* f, a distancia Hausdorff nula
de f.
&252/$5,2 6L HV XQ FRQMXQWR OLQHDOL]DEOH QR FHUUDGR HQWRQFHV EU* q QR
SXHGH VHU OD XQLyQ GH XQD IDPLOLD GH FDUDV QR H[SXHVWDV GH U* 'HPRVWUDFLyQ De acuerdo con la Proposición 1.11, bastará probar que ninguna
unión no vacía de caras no expuestas de U* es igual a una unión de caras expuestas
de U* . De hecho, probaremos que dos familias disjuntas de caras no vacías de un
conjunto convexo cerrado no pueden tener uniones iguales.
Sea f un conjunto convexo cerrado y sean if c 5 L j y if c 5 T j dos
familias disjuntas de caras no vacías de f.
Supongamos que ^ f ' ^ f .
ML
MT
Dado  5 L , existe % 5 h?| f ^ f , de manera que existe  5 T tal
MT
que % 5 f y Eh?| f _ f 9' >. Entonces, de acuerdo con la Proposición 0.10,
f f , inclusión que resulta ser estricta por ser if c 5 L j_if c 5 T j ' >.
Por lo tanto, _4 f _4 f . Razonando del mismo modo se tiene que, dado
 5 T , existe 2 5 L tal que _4 f _4 f2 .
Por inducción, se obtienen dos sucesiones i& j L y i& j T tales que
_4 f& _4 f& _4 f&n c & ' c 2c Por lo tanto, *4 _4 f& ' n4, contradiciendo que _4 f ? para todo
&
5 L.
(-(03/2 Consideremos el conjunto convexo cerrado
f ' % 5 U2 m |% n E |%2 | |2 c | 5 dfc o
(1.26)
representado en la Figura 1.1.
s
Las caras no triviales de f son f ' iEc  n 2 j, f ,
f2 ' ifj dc n4d y f ' dc n4d ifj. Todas estas caras son expuestas excepto
ff y f .
1.3 Conjuntos linealizables
39
;
)LJXUD Por lo tanto, ' fq
^ f
ML
es linealizable si, y sólo si, L ofc d ^ i2c j
(por la Proposición 1.11 y el Corolario 1.12).
Así pues, no es linealizable si > 9' L ifc j (por
Tampoco
el Corolario 1.12).
f
,
admiten representación lineal los conjuntos ' fq Edc n4d ifj ^

y ' fq Eo2c n4d ifj. En el primer caso, EU* q tiene una cara no expuesta
de U* como componente conexa, mientras que en el segundo, EU* q no es
unión de una familia de caras expuestas (es un trozo de una).
Obsérvese que, en el apartado (v) de la Proposición 1.11, no se puede sustituir
“caras expuestas” por “interiores relativos de caras expuestas”.
En efecto, si
consideramos el conjunto convexo cerrado f del Ejemplo 1.13 y la cara expuesta
f de f, el conjunto ' fq h?| f ' fq Eoc n4d ifj no es linealizable.
Los apartados (vi) y (vii) de la Proposición 1.11 pueden inducir a pensar que otra
condición equivalente a que un conjunto convexo no vacío sea linealizable es que,
para cualquier conjunto convexo
EU* q, E@g g _ ' >. Sin embargo, el
g conjunto convexo ' fq
^ f no es linealizable y veri¿ca esta condición
Mdfco
(ya que los únicos subconjuntos convexos de EU* q son los conjuntos singulares
f y @g f ' f ).
Los dos siguientes resultados comparan diferentes elementos de y U* cuando
es linealizable.
352326,&,Ï1 6L HV XQ FRQMXQWR OLQHDOL]DEOH QR YDFtR HQWRQFHV
(i) ( Ec % ' ( EU* c % SDUD WRGR % 5 \
1. Sistemas lineales generales en U?
40
(ii) ORV SXQWRV H[WUHPRV GH VRQ DTXHOORV SXQWRV H[WUHPRV GH U* TXH SHUWHQHFHQ D 'HPRVWUDFLyQ (i) Probaremos la inclusión no trivial ( EU* c % ( Ec % para
todo % 5 .
Supongamos lo contrario. Sea % 5 y 5 ( EU* c % q( Ec %. Sea 0 : f tal
0
* ( Ec %, % n 5 EU* q y existe una cara
que % n 0 5 U* . Puesto que 5
2
0
expuesta de U* , digamos f, tal que f _ ' > y % n 5 f (por el apartado (v)
2
de la Proposición 1.11).
Sea @ 9' f? y K 5 U tal que @ % K para todo % 5 U* y
f ' i% 5 U* m @ % ' Kj 0 % n ' K y @ % K, se tiene que @ f. Obtendremos una
2
contradicción en los dos casos posibles.
0 * U* Si @ f, entonces @ E% n 0 @ % n ' K, de manera que %n0 5
2
(contradicción).
0 Si @ ' f, entonces @ % ' @ % n ' K, de manera que % 5 f. Por lo tanto,
2
%5
* y esto es de nuevo una contradicción.
Puesto que @
(ii) Sea % 5 . Si % no es punto extremo de U* , entonces existe 9' f? tal que
5 ( EU* c % ' ( Ec %, de acuerdo con la parte (i), por lo que % no puede ser
punto extremo de .
El recíproco es trivial.
352326,&,Ï1 6L XQ FRQMXQWR OLQHDOL]DEOH QR YDFtR HQWRQFHV FRLQFLGHQ ORV
FRQRV GH UHFHVLyQ GH \ GH U* HV GHFLU n ' n EU* (Q FRQVHFXHQFLD HV
DFRWDGR VL \ VyOR VL n ' if? j
'HPRVWUDFLyQ Sea ' i% 5 U? m @| % : K| c | 5 A j. Entonces
n ' i+ 5 U? m @| + fc | 5 A j ' n EU* c
(1.27)
puesto que U* ' i% 5 U? m @| % K| c | 5 A j (Proposición 1.1).
Finalmente, es acotado si, y sólo si, U* es acotado o, lo que es lo mismo,
n EU* ' if? j (Proposición 0.8).
1.3 Conjuntos linealizables
41
Los dos últimos resultados pueden cumplirse o no para conjuntos convexos no
linealizables, como puede verse en el siguiente ejemplo.
(-(03/2 (revisitado). Ni  G' fq Ec f ni 2 G' fq Eo2c n4d ifj
son linealizables. Sin embargo,  satisface tanto la Proposición 1.14 como la 1.15,
mientras que 2 no satisface ninguna de las dos (considérese el punto E2c f en la
Figura 1.2).
&
)LJXUD 352326,&,Ï1 6HD XQ FRQMXQWR OLQHDOL]DEOH QR YDFtR \ VHD + 9' f? 6L H[LVWH
XQ % 5 WDO TXH i% n b+ m b fj HQWRQFHV + 5 n $GHPiV i% n b+ m b fj h?| SDUD WRGR % 5 h?| GH PRGR TXH
+ 5 n Eh?| 'HPRVWUDFLyQ Sea ' i% 5 U? m @| % : K| c | 5 A j y supongamos la existencia
de | 5 A tal que @| + f. Entonces @| E% n b+ K| para b su¿cientemente grande,
de modo que % n b+ 5
* . Por lo tanto, @| + f para todo | 5 A , y esto implica que
+ 5 n de acuerdo con (1.27).
Supongamos, ahora, % 5 h?| , entonces, para todo b f, d%c % n b+o es un
segmento en que corta a h?| y, por la Proposición 0.2 (iii), dicho segmento debe
tener su interior relativo en h?| . Por lo tanto,
i% n b+ m b fj h?| Aunque la Proposición 1.16 es consecuencia directa del Teorema 8.3 de [32]
(si se considera que, en este caso, n ' n EU* , por ser linealizable, y
1. Sistemas lineales generales en U?
42
h?| ' h?| EU* , por ser convexo), hemos preferido hacer la prueba directa
para subrayar que dicha proposición se puede considerar como una extensión, a los
conjuntos linealizables, del mencionado teorema. Así mismo, el siguiente resultado
extiende el Corolario 8.3.4 de [32].
352326,&,Ï1 6HD XQ FRQMXQWR OLQHDOL]DEOH QR YDFtR HQ U? \ VHD
G U6 $ U? XQD WUDQVIRUPDFLyQ OLQHDO WDO TXH 3 9' > (QWRQFHV 3 HV
OLQHDOL]DEOH \ n E3 ' 3 En 'HPRVWUDFLyQ Sea ' i% 5 U? m @| % : K| c | 5 A j.
Entonces, se puede
comprobar fácilmente que
3 ' 5 5 U6 m E @| 5 : K| c | 5 A c
de manera que 3 es linealizable.
3 En n E3 . En efecto, si + 5 3 En , tomando 5 5 3 cualquiera y puesto que + 5 n , se tiene para cada b f
E5 n b+ ' 5 n b+ 5 c
de manera que 5 n b+ 5 3 . Por lo tanto, + 5 n E3 .
Recíprocamente, supongamos que + 5 n E3 . Sea 5 5 3 elegido
arbitrariamente. Puesto que, para todo b f, 5 n b+ 5 3 , se tiene que
5 n b+ ' E5 n b+ 5 . Aplicando la Proposición 1.16, se concluye que
+ 5 n y, por lo tanto, + 5 3 En .
Probaremos que la imagen, , de un conjunto linealizable por una
transformación lineal no es necesariamente un conjunto linealizable. Pero antes,
debemos considerar el producto y la suma de dos conjuntos linealizables.
352326,&,Ï1 (O SURGXFWR FDUWHVLDQR GH GRV FRQMXQWRV OLQHDOL]DEOHV HV WDPELpQ
OLQHDOL]DEOH
'HPRVWUDFLyQ Si
 ' i% 5 U? m @ % : K c 5 Lj
1.3 Conjuntos linealizables
43
y
2 ' i% 5 U6 m S % : _ c 5 T j c
entonces
 2 '
% 5 U?n6 m
@
f6
f?
% : K c 5 L (
% : _ c 5 T .
S
Por lo tanto,  2 es linealizable.
Con relación a la suma de conjuntos convexos cerrados, sabemos que no es
necesariamente cerrada a menos que se cumpla cierta condición de recesión que
garantiza que el cono de recesión de la suma es la suma de los correspondientes conos
de recesión (véase [32, Cor. 9.1.2]). Seguidamente veremos que, esta última propiedad
se puede extender a los conjuntos linealizables, pero su suma no es necesariamente
linealizable (ni siquiera si uno de los dos conjuntos es acotado).
352326,&,Ï1 6HDQ  \ 2 FRQMXQWRV OLQHDOL]DEOHV QR YDFtRV HQ U? WDOHV TXH
En  _ En 2 ' if? j (QWRQFHV
n E n 2 ' n  n n 2 (1.28)
'HPRVWUDFLyQ De acuerdo con la Proposición 1.15,
n EU*  _ n EU* 2 ' if? j c
de manera que si 5 5 n EU* , ' c 2, y 5  n 5 2 ' f? , entonces
5  ' 5 2 ' f? 5 *? EU* c ' c 2c
que es la hipótesis de la Proposición 0.9. Por lo tanto, se cumple
n dU* E n 2 o ' n EU*  n n EU* 2 ' n  n n 2 Entonces, se tiene
n  n n 2 n E n 2 n dU* E n 2 o ' n  n n 2 c
de manera que se cumple (1.28).
(-(03/2 (revisitado). Consideremos el conjunto linealizable f de (1.26).
El conjunto compacto  G' i% 5 f m % n %2 j (véase Figura 1.3) y el conjunto
1. Sistemas lineales generales en U?
44
2 G' i% 5 U2 m % f( %2 f( % n %2 : fj (véase Figura 1.4) son obviamente
linealizables y satisfacen la condición de recesión de la Proposición 1.19. Sin embargo,
en la Figura 1.5 se puede ver que, aunque se veri¿ca
n E n 2 ' n 2 ' n  n n 2 c

f
el conjunto  n 2 no es linealizable, ya que los puntos
y
son puntos
f

extremos no expuestos de U* E n 2 .
Obsérvese también que  2 es un conjunto linealizable cuya imagen por la
transformación lineal G U2? $ U? tal que E%c 5 ' % n 5 es  n 2 , que
no es linealizable. Esto demuestra que la imagen por una transformación lineal de
un conjunto linealizable puede no ser linealizable (como ocurre con los conjuntos
convexos cerrados). En cambio, las transformaciones lineales convierten los conjuntos
relativamente abiertos en otros de la misma clase, como puede deducirse de la
Proposición 0.3.
Sabemos que la intersección de una familia arbitraria i m 5 Uj de conjuntos
convexos cerrados es un conjunto convexo cerrado y, aunque la intersección no es
una operación cerrada en la clase de los conjuntos relativamente abiertos, sí lo es
cuando consideramos la clase más general de los conjuntos linealizables. Acabaremos
esta sección con la extensión a los conjuntos linealizables de dos propiedades bien
conocidas de los conjuntos convexos cerrados (Cor. 8.3.3 y Cor. 8.4.1 de [32],
respectivamente).
352326,&,Ï1 6L i jMU HV XQD IDPLOLD DUELWUDULD GH FRQMXQWRV OLQHDOL]DEOHV
HQWRQFHV _ HV OLQHDOL]DEOH $GHPiV VL _ 9' > HQWRQFHV
M U
M U
n
_ M U
' _ n M U
'HPRVWUDFLyQ Denotemos por G' _ 9' >, que es trivialmente linealizable,
y sea % 5 .
M U
Si + 5 n para todo 5 U, entonces se tiene
i% n b+ m b fj 1.3 Conjuntos linealizables
&
)LJXUD &
)LJXUD &&
)LJXUD 45
1. Sistemas lineales generales en U?
46
para todo 5 U, de modo que
i% n b+ m b fj Por lo tanto, + 5 n y _ n n _ . La inclusión opuesta es
trivial.
MU
M U
Este resultado justi¿ca la de¿nición, dada por Fenchel [14], de la HQYROWXUD
OLQHDOL]DEOH de un conjunto no vacío f como el menor conjunto linealizable que
contiene a f (la intersección de todos los conjuntos linealizables conteniendo a f),
estando intercalado entre UL? f y U* UL? f. Si es un convexo no vacío, la
envoltura linealizable de se obtiene eliminando de U* todas sus caras expuestas
que no contienen puntos de .
&252/$5,2 6HD XQ FRQMXQWR OLQHDOL]DEOH \ VHD  XQD YDULHGDG DItQ WDO TXH
 _ HV QR YDFtR \ DFRWDGR (QWRQFHV  _ HV DFRWDGR SDUD WRGD YDULHGDG DItQ
 SDUDOHOD D 
'HPRVWUDFLyQ
Obviamente, puesto que toda variedad afín es un conjunto
convexo cerrado,  es linealizable. Además, puesto que estamos suponiendo que
 es paralela a  , n  ' n  (subespacio vectorial). Si  _ 9' >, por las
Proposiciones 1.20 y 1.15, se tiene
n E _ ' n  _ n ' n  _ n ' n E _ ' if? j c
de modo que  _ es acotado.
*HRPHWUtD
En esta sección probaremos que es posible obtener información geométrica acerca
del conjunto solución 8 de un sistema consistente
j ' i@| % K| c | 5 (( @| % : K| c | 5 .j Para ello apelaremos a las relaciones bien conocidas entre el correspondiente sistema
relajado j ' i@| % K| c | 5 A G' ( ^ .j y su conjunto solución 8 .
1.4 Geometría
47
352326,&,Ï1 6HD 8 9' > HO FRQMXQWR VROXFLyQ GH j \ VHD AS VX FRQMXQWR
GH tQGLFHV SRUWDGRUHV HV GHFLU AS ' i| 5 A m @| % ' K| SDUD WRGR % 5 8 j (
(QWRQFHV
h?| 8 i% 5 U? m @| % ' K| c | 5 AS ( @| % : K| c | 5 A qAS j (1.29)
$GHPiV VL j HV /)0 HQWRQFHV DPERV PLHPEURV GH VRQ LJXDOHV
_4 8 ' ? _4 tT@? i@| c | 5 AS j
\ VL AS 9' >
@g 8 ' i% 5 U? m @| % ' K| c | 5 AS j 'HPRVWUDFLyQ Obsérvese que los índices portadores de j son los mismos que
los de j, puesto que un hiperplano contiene a un conjunto convexo si, y sólo si,
contiene a su clausura y 8 ' U* 8 (Proposición 1.1). Por otra parte, h?| 8 ' h?| 8 ,
@g 8 ' @g 8 y _4 8 ' _4 8 , de manera que es su¿ciente probar todas las
a¿rmaciones para j y 8 en lugar de j y 8 . Así pues, la conclusión se sigue de las
Proposiciones 0.15 y 0.17.
352326,&,Ï1 6L HO FRQMXQWR VROXFLyQ GH j HV 8 9' > HQWRQFHV ODV VLJXLHQWHV
D¿UPDFLRQHV VRQ HTXLYDOHQWHV
(i) 8 HV DFRWDGR
f?
@|
f?
(ii)
5 ?| UL?i
c | 5 A(

K|

(iii) UL?i i@| c | 5 A j ' U? \
(iv) H[LVWH XQ VXEVLVWHPD ¿QLWR GH j FX\R FRQMXQWR VROXFLyQ HV DFRWDGR
'HPRVWUDFLyQ
Puesto que el conjunto solución de un sistema consistente
arbitrario es acotado si, y sólo si, el conjunto solución de su correspondiente sistema
relajado es acotado (por la Proposición 1.1), se cumple la equivalencia entre las
a¿rmaciones (i) a (iv) si, y sólo si, se cumple para j.
La conclusión es una
consecuencia directa de la Proposición 0.19.
Dado % 5 8 , el FRQR GH UHVWULFFLRQHV DFWLYDV en % (con respecto de j) es
E% ' UL?i i@| m @| % ' K| c | 5 (j 1. Sistemas lineales generales en U?
48
Denotaremos por E% el cono de restricciones activas en % 5 8 (con respecto de
j).
352326,&,Ï1 6HD % 5 8 6L _4 E% ' ? HQWRQFHV % HV SXQWR H[WUHPR GH 8 (O UHFtSURFR HV FLHUWR FXDQGR j HV /23
'HPRVWUDFLyQ Se puede ver fácilmente que E% ' E% para todo % 5 8 .
Además, % es un punto extremo de 8 si, y sólo si, % es un punto extremo de 8 (por
la Proposición 1.14). La conclusión se sigue de la Proposición 0.18.
El siguiente ejemplo muestra que las condiciones adicionales para los recíprocos
de las Proposiciones 1.22 y 1.24 no son supérÀuas.
(-(03/2 (revisitado) Sea j ' i|% n E |%2 : | |2 c | 5 ofc dj cuyo
conjunto solución, 8 , está representado en la Figura 1.6.
)
)LJXUD Aquí AS ' >, de modo que (1.29) se convierte en h?| 8 8 . Sin embargo,
h?| 8 9' 8 ya que j no es LFM (obsérvese que % f y %2 f no son consecuencia
de ningún subsistema ¿nito de j). Por otra parte,
|
UL?i i@| c | 5 A j ' UL?i
c | 5 ofc d 9' U2 ,
|
de modo que 8 es no acotado. Finalmente, obsérvese que E% ' if2 j para todo
% 5 8 , incluso en los puntos extremos de 8 , Ec f y Efc  (de hecho, cualquier
sistema LOP es LFM).
1.5 Optimización lineal
49
2SWLPL]DFLyQ OLQHDO
Asociamos al problema de optimización lineal con desigualdades estrictas
E W?u
S%
s.a.
@| % K| , | 5 (
@| % : K| , | 5 . 9' >c
donde S 9' f? , el problema PSIL
W?u
S%
s.a. @| % K| , | 5 A ' ( ^ .
Obviamente, los valores de ambos problemas están relaciones por E (la desigualdad puede ser estricta: por ejemplo, para E ? % s.a. f % f,
E ' n4 y ' f), con E ' si E es consistente (por la
Proposición 1.1). Por lo tanto, cualquier método de aproximación exterior para (como los métodos de discretización por planos de corte y por rejillas) es un método
de aproximación exterior para E . Por otra parte, cualquier método de direcciones
factibles para (como los métodos cuasi-simplex) da lugar a una sucesión de
soluciones factibles para E que aproximan E . De hecho, si i%o j 8 satisface
*4 S %o ' , tomando %
e 5 8 y una sucesión ibo j dfc o tal que *4 bo ' f, se
o
o
tiene iE bo %o n bo %
ej 8 y *4 S dE bo %o n bo %
eo ' E .
o
Aunque E será habitualmente irresoluble (incluso si 8 es acotado), podemos
establecer una condición KKT que da lugar a una regla exacta de parada para cualquier
método LSIP adaptado a E .
352326,&,Ï1 6HD %
e 5 8
6L S 5 Ee
% S 5 ?| Ee
% HQWRQFHV %
e
HV XQD VROXFLyQ ySWLPD GH E XQD VROXFLyQ ySWLPD IXHUWHPHQWH ~QLFD GH E UHVSHFWLYDPHQWH /RV UHFtSURFRV VH FXPSOHQ VL j HV /)0
'HPRVWUDFLyQ Si S 5 Ee
%, con %
e 5 8 , entonces se tiene que %
e 5 8 y S 5 Ee
%,
de manera que %
e es una solución óptima de [19, Th. 7.1].
1. Sistemas lineales generales en U?
50
Del mismo modo, si S 5 ?| Ee
%, entonces S 5 ?| Ee
% y %
e es una solución
óptima fuertemente única de [19, Th. 10.6].
Recíprocamente, si %
e es una solución óptima de E , entonces también es una
solución óptima de (puesto que ' E ). Entonces se aplica de nuevo [19,
Th. 7.1] para concluir que S 5 Ee
% ' Ee
% bajo la hipótesis de que j es LFM. El
argumento es similar para el otro recíproco, teniendo en cuenta [ 19, Th. 10.6].
El último resultado trata sobre la acotación del conjunto óptimo de E , que
denotamos por 8 W (la acotación de 8 W puede verse como una condición de buen
condicionamiento para E ).
352326,&,Ï1 6L E HV UHVROXEOH ODV VLJXLHQWHV FRQGLFLRQHV VRQ HTXLYDOHQWHV
(i) 8 W HV XQ FRQMXQWR DFRWDGR
(ii) WRGRV ORV FRQMXQWRV GH VXEQLYHO QR YDFtRV GH E (o i% 5 8 m S % kj o i% 5 8 m S % kj , con k 5 U)
VRQ DFRWDGRV
(iii) H[LVWH XQ VXESUREOHPD ¿QLWR GH E FX\RV FRQMXQWRV GH VXEQLYHO QR YDFtRV VRQ DFR
WDGRV \
(iv) S 5 ?| UL?i i@| c | 5 A j
'HPRVWUDFLyQ En primer lugar, obsérvese que los conjuntos de subnivel de E (en particular, 8 W ) son linealizables.
Sea k 5 U tal que i% 5 8 m S % kj 9' > (para conjuntos de subnivel estrictos se
utiliza el mismo argumento). De acuerdo con la Proposición 1.20, se tiene
n 8 W ' n E8 _ i% 5 U? m S % E j ' n 8 _ i+ 5 U? m S + fj '
' n E8 _ i% 5 U? m S % kj ' n Ei% 5 8 m S % kj Por lo tanto, puesto que n 8 W ' if? j si, y sólo si, n Ei% 5 8 m S % kj '
if? j, (por la Proposición 1.15) 8 W es acotado si, y sólo si, i% 5 8 m S % kj es
acotado.
Probaremos ahora que todos los conjuntos de subnivel no vacíos de E son
1.5 Optimización lineal
51
acotados si, y sólo si, todos los conjuntos de subnivel no vacíos de son acotados.
Esto es consecuencia de la doble inclusión
i% 5 8 m S % kj % 5 8 m S % k U* i% 5 8 m S % k n 0j
para todo k 5 U y para todo 0 : f (si % ' *4 %o , con i%o j 8 y
o
S % k, entonces S % k n 0 para o su¿cientemente grande, de manera que
o
% 5 U* i% 5 8 m S % k n 0j).
Se aplica el mismo argumento para los conjuntos de subnivel no vacíos de los
subproblemas obtenidos al sustituir ( y . por los conjuntos ¿nitos ( ( y . .
en E y . Por lo tanto, concluimos que (ii) / (iii) / (iv) por aplicación directa
de [19, Cor. 9.3.1].
&DStWXOR &RQItQ GH XQ FRQMXQWR FRQYH[R
,QWURGXFFLyQ
Informalmente hablando, el confín de un conjunto convexo en una dirección
dada es el conjunto de puntos de que se pueden ver desde el in¿nito en esa dirección.
En realidad, el confín de es el conjunto de puntos g-extremos de (en el sentido
de Yu [39]) para un cierto cono g y está conectado con dos conceptos de iluminación
que han sido introducidos para abordar problemas de combinatoria geométrica sobre
cuerpos convexos (véase el reciente artículo de Martini y Soltan [28]). En este capítulo
se analizan las propiedades del confín de los conjuntos convexos en general y de los
conjuntos convexos cerrados en particular (para los cuales los con¿nes no vacíos son
conexos por arcos), así como las relaciones entre el confín y ciertos conceptos de
iluminación sobre conjuntos convexos. Además, se pretende demostrar que el confín
puede ser una herramienta muy útil en análisis convexo y en temas relacionados (como
los sistemas lineales o la optimización lineal).
En la Sección 2.2, se de¿ne el confín de un conjunto convexo , se recupera
la de¿nición dada por Yu [39, Def. 4.1] de conjunto de puntos g-extremos, donde
g es un cono, y se establecen relaciones entre estos dos conceptos. De hecho, se
demuestra que el confín de en una dirección dada, 9' f? , es el conjunto de puntos
53
54
2. Confín de un conjunto convexo
g-extremos de para el cono g ' UL?i ij. También se dan, en esta sección, las
propiedades básicas del confín de un conjunto convexo, estableciéndose relaciones con
su estructura facial y su dimensión, con su frontera y frontera relativa, con su conjunto
de puntos extremos, etc.
Los con¿nes pueden no ser cerrados (incluso para los conjuntos convexos
compactos), pero siempre son conexos por arcos cuando el conjunto es convexo
cerrado. Este es el principal resultado de la Sección 2.3, donde también se obtiene,
como consecuencia, la conexión por arcos de la frontera relativa de los conjuntos
convexos compactos de dimensión mayor que 1.
En la Sección 2.4, se extienden las de¿niciones de iluminación por direcciones y
visibilidad en una dirección (dadas para cuerpos convexos por Boltyanski [8] y Soltan
[34], respectivamente) a los conjuntos convexos cerrados y se discuten las relaciones
entre el confín y estos dos conceptos de iluminación.
La última sección de este capítulo muestra algunas aplicaciones del confín a la
teoría de los sistemas lineales.
&RQItQ 3URSLHGDGHV EiVLFDV
El FRQItQ de un conjunto convexo no vacío en la dirección de un vector no nulo
es el conjunto
i?_E( ' i% 5 m 5
* (Ec %j Obviamente, i?_E( ' > tanto si es abierto como si 5 n y i?_E( ' ,
para todo 9' f? , cuando es singular. Por otra parte, dado un cono g U? , el
FRQMXQWR GH SXQWRV gH[WUHPRV de se de¿ne [39] como
, | d m go ' i% 5 m % 5
* + n g para todo + 5 q i%jj .
Obsérvese que si es singular, , | d m go ' cualquiera que sea el cono g.
Además, es obvio que , | d m if? jo ' y, para no singular, , | d m U? o ' >.
Las dos siguientes proposiciones establecen relaciones entre estos dos conceptos.
2.2 Confín: Propiedades básicas
55
352326,&,Ï1 6L HV XQ FRQMXQWR FRQYH[R QR YDFtR \ 5 U? q if? j HQWRQFHV
i?_E( ' , | d m UL?i ijo
'HPRVWUDFLyQ El caso singular es trivial, por lo que podemos suponer, sin
pérdida de generalidad, que es no singular.
Si % 5 q , | d m UL?i ijo, entonces existen + 5 q i%j y b : f tales que
% ' + b o, lo que es lo mismo, % n b ' + 5 . Esta última igualdad implica que
5 ( Ec % y, por lo tanto, % 5
* i?_E( .
Recíprocamente, si % 5 q i?_E( , entonces existe b : f tal que % n b 5 .
Tomando + G' % n b 5 q i%j, se tiene que % 5 + n UL?i ij y, por lo tanto,
%5
* , | d m UL?i ijo.
352326,&,Ï1 6L HV XQ FRQMXQWR FRQYH[R QR YDFtR \ g U? g 9' if? j HV XQ
FRQR HQWRQFHV
, | d m go '
_
+Mg .tf? i?_E( +
'HPRVWUDFLyQ Supongamos que es no singular.
Si % 5 q i?_E( + para algún + 5 gq if? j, entonces existe b : f tal que
% b+ 5 . Tomando 5 G' % b+, se tiene que 5 5 q i%j y % ' 5 n b+ 5 5 n g,
por lo que % 5
* , | d m go.
Recíprocamente, si % 5 q , | d m go, entonces existen 5 5 q i%j e
* i?_E( +. En
+ 5 gq if? j tales que % ' 5 n +, por lo que % + ' 5 5 y % 5
consecuencia, % 5
*
_
+Mg .tf? i?_E( +.
Podría pensarse que en el caso particular de que g ' UL?i ~, > 9' ~ 9' if? j,
debería cumplirse que , | d m go '
_
+ M~ .tf? i?_E( + y, por lo tanto, la
Proposición 2.1 se obtendría como consecuencia, tomando g ' UL?i ij. Sin
embargo, este resultado no es cierto ni siquiera cuando ~ es ¿nito.
(-(03/2 Sea ' i% 5 U2 m % ' %2 c % fc %2 j y sea g ' UL?i ~,
con ~ ' ie c e2 j. En
este
caso, i?_ E( + ' para todo + 5 ~q if? j y, sin

embargo, , | d m go '
.

56
2. Confín de un conjunto convexo
Las siguientes proposiciones proporcionan dos formas diferentes de describir el
conjunto i?_ E( .
352326,&,Ï1 6HD XQ FRQMXQWR FRQYH[R % 5 \ 5 U? q if? j 6L H[LVWH
+ 5 U? VDWLVIDFLHQGR
i + f( E% % + fc % 5 j c
(2.1)
HQWRQFHV % 5 i?_E( (O UHFtSURFR HV YiOLGR HQ % 5 SDUD WRGR 9' f? VL \ VyOR
VL (E( % HV FHUUDGR
'HPRVWUDFLyQ Sea S 5 U? tal que S f y S E% % f para todo % 5 . Si
% n k 5 para cierto k 5 U, entonces f S E% n k % ' kS y esto implica
que k f. Así pues, 5
* ( Ec % y % 5 i?_E( El recíproco es cierto en % 5 si % 5 i?_E( , con 9' f? , implica la existencia
de S 5 U? tal que S f y S E% % f para todo % 5 . Asumamos esta hipótesis
y sea 9' f? tal que 5 U* (Ec %. Entonces, se tiene
5 U* (Ec % ' U* UL?i i% % m % 5 j c
de modo que, por el Lema de Farkas Homogéneo, + f es una consecuencia del
sistema lineal homogéneo
iE% % + fc % 5 j
y no existe ningún S 5 U? tal que S f y S E% % f para todo % 5 . Por lo
* i?_E( , es decir, 5 (Ec %. En consecuencia, (Ec % es cerrado.
tanto, % 5
Recíprocamente, sea (Ec % cerrado y % 5 i?_E( . Si (2.1) no tuviese
solución, entonces + f sería consecuencia del sistema homogéneo
iE% % + fc % 5 jc
de manera que
5 U* UL?i i% % m % 5 j ' (Ec %c
en contradicción con % 5 i?_E( .
La interpretación de la proposición anterior es que, si está contenido en un
semiespacio cuyo hiperplano de frontera, M, soporta a en un punto, entonces dicho
2.2 Confín: Propiedades básicas
57
punto está en el confín de para toda dirección que forme ángulo agudo con la
dirección normal a M dirigida hacia el exterior del semiespacio. El recíproco no se
veri¿ca en general, como puede verse en el siguiente ejemplo.

f
(-(03/2 Sea ' U* 2 . Si consideramos % '
y'
c se tiene que
f

5
* (Ec %c por lo que % 5 i?_E( (véase Figura 2.1). Sin embargo,
el único

vector, S 5 U? , que veri¿ca que S E% % f para todo % 5 es S '
, para el
f
cual se cumple que S ' f (obsérvese que (Ec % no es un conjunto cerrado).
X
1
0.5
[
c
-1
-0.5
0
0.5
1
-0.5
-1
)LJXUD &252/$5,2 8Q FRQMXQWR FRQYH[R FHUUDGR 9' > HV FXDVLSROLpGULFR VL \ VyOR VL
i?_ E( ' i% 5 m HV FRQVLVWHQWHj SDUD WRGR 9' f? 'HPRVWUDFLyQ
Se sigue de la Proposición 2.4, ya que los conjuntos
cuasipoliédricos son aquellos conjuntos convexos cerrados tales que el cono de
direcciones factibles es cerrado en todos los puntos (véanse [1, Lem. 3.2] y [6, VII,
1.6]).
Es bien conocido que el interior relativo de las caras de un conjunto convexo no
vacío forman una partición de [32, Th. 18.2]. El siguiente resultado establece
que un determinado subconjunto de dicha partición de es, a su vez, una partición de
, | d m go y, en particular, de i?_ E( .
352326,&,Ï1 6HD f XQD FDUD GHO FRQMXQWR FRQYH[R 9' > \ VHD g XQ FRQR 6L
Eh?| f _ , | d m go 9' >c
HQWRQFHV f , | d m go $GHPiV , | d m go HV OD XQLyQ GH FLHUWD IDPLOLD GH FDUDV
GH \ ORV FRUUHVSRQGLHQWHV LQWHULRUHV UHODWLYRV IRUPDQ XQD SDUWLFLyQ GH , | d m go
58
2. Confín de un conjunto convexo
'HPRVWUDFLyQ Si es singular o g ' if? j, entonces , | d m go ' y
la proposición se cumple trivialmente. Supongamos, pues, que es no singular y
g 9' if? j.
Sea % 5 Eh?| f _ , | d m go y supongamos que % 5 fq , | d m go.
Entonces, existen +  5 q i% j y & 5 gq if? j tal que % ' + n &  .
Por ser % 5 h?| f, la Proposición 0.2(iv) nos asegura la existencia de > :  tal
que
%2 G' E > % n >% 5 f .
Tomando b ' E>  *>, se tiene f b  y
% ' E b %2 n b% ' E b %2 n b+ n b& 5 E b %2 n b+  n gc
con E b %2 nb+ 5 q i%j, de modo que % 5
* , | d m go en contra de la hipótesis.
Consideremos ahora la familia de todas las caras de cuyo interior relativo
contiene, al menos, un punto de , | d m go y denotémosla como if c 5 Uj. Puesto
que para cualquier 5 U, f es una cara de tal que
Eh?| f _ , | d m go 9' >c
acabamos de probar que
^ f , | d m go M U
(2.2)
Por otra parte, si % 5 , | d m go , existe una única cara de , digamos f, tal
que % 5 h?| f. Puesto que Eh?| f _ , | d m go 9' >, existe 5 U tal que f ' f .
Por lo tanto,
, | d m go ^ h?| f M U
(2.3)
La combinación de (2.2) y (2.3) da lugar a
, | d m go ' ^ h?| f ' ^ f M U
M U
Finalmente, ih?| f c 5 Uj es una familia de conjuntos disjuntos dos a dos de
acuerdo con [32, Th. 18.2].
2.2 Confín: Propiedades básicas
59
&252/$5,2 6HD f XQD FDUD GHO FRQMXQWR FRQYH[R 9' > 6L
Eh?| f _ i?_E( 9' >c
FRQ 9' f? HQWRQFHV f i?_E( $GHPiV i?_E( HV OD XQLyQ GH FLHUWD
IDPLOLD GH FDUDV GH \ ORV FRUUHVSRQGLHQWHV LQWHULRUHV UHODWLYRV IRUPDQ XQD SDUWLFLyQ
GH i?_E( Nótese que i?_ dfc o2 ( e contiene 3 caras del cuadrado ( Ec f , Ec  y
ij dfc o) e intersecta (pero no contiene) otras dos caras propias (dfc o ifj y
dfc o ij). Por otra parte, M_ dfc o2 se puede escribir, de diferentes maneras, como
unión de con¿nes por ejemplo, M_ dfc o2 ' i?_ E( e n e2 ^ i?_ E( e e2 .
Veremos que esto se cumple para cualquier conjunto convexo cerrado.
352326,&,Ï1 'DGR XQ FRQMXQWR FRQYH[R QR YDFtR VH FXPSOHQ ODV VLJXLHQWHV
SURSRVLFLRQHV
(i) EM_ _ ' ^ i?_E( \
M7?
(ii) EhM_ _ ' ^ ii?_E( c 5 7? _ dE@g oj 'HPRVWUDFLyQ (i) Si % 5 EM_ _ , existe un semiespacio soporte, % K,
para en % Entonces % 5 i?_ E( * nn, por lo que
EM_ _ ^ i?_E( M7?
Recíprocamente, si % 5 i?_E( para algún 5 7? , entonces % 5 y
% n 0 5
* para cualquier 0 : fc de modo que % 5 q E?| M_ .
(ii) Podemos asumir, sin pérdida de generalidad, que _4 ?, es decir, que
h G' n ` .
` G' dE@g oz 9' if? j. Sea Sea % 5 EhM_ _ . Entonces, existe una sucesión i%o j E@g q tal que
*4 %o ' %
o
h se puede descomponer como %o ' + o n o , con + o 5 y o 5 ` .
Si %o 5 ,
Entonces %o + o ' o 5 dE@g o _ ` ' if? j y llegamos a la contradicción de
h concluimos que % 5 M_ h y existe
que %o ' + o 5 . Puesto que % 5 ,
h en %, por lo que % 5 i?_ E( * nn.
un semiespacio soporte % K para h deberá ser ' f para todo 5 ` , es decir,
Además, puesto que ` n ,
5 ` z ' E@g y * nn 5 7? _ dE@g o.
60
2. Confín de un conjunto convexo
Recíprocamente, si % 5 i?_E( , con 5 7? _ dE@g o, entonces


% n 5 E@g q, para todo o 5 Q, y % '*4 % n 5 hM_ o
o
o
De la Proposición 2.9 se deducen las siguientes caracterizaciones de los conjuntos
convexos cerrados.
&252/$5,2 6HD XQ FRQMXQWR FRQYH[R QR YDFtR (QWRQFHV ODV VLJXLHQWHV
D¿UPDFLRQHV VRQ HTXLYDOHQWHV
(i) HV FHUUDGR
(ii) M_ ' ^ i?_E( y
M7?
(iii) hM_ ' ^ ii?_E( c 5 7? _ dE@g oj
'HPRVWUDFLyQ (i) , (ii) y (i) , (iii) son consecuencias directas de la Proposición
2.9.
(ii) , (i) Puesto que i?_E( para todo 9' f? , se tiene que M_ y
es cerrado.
(iii) , (i) Análogamente, hM_ y, por lo tanto, es cerrado en el conjunto
cerrado @g . Así pues, también es cerrado.
Realmente, como consecuencia de un resultado de combinatoria geométrica que
se mencionará más adelante, para cubrir M_ y hM_ son su¿cientes dos con¿nes,
aunque su unión puede no ser conexa (considérese dkc qo U?3 , con k q).
El siguiente ejemplo muestra que aunque el conjunto convexo sea cerrado o
compacto, i?_E( no tiene por qué serlo. Sin embargo, probaremos que los con¿nes
de los conjuntos cuasipoliédricos son cerrados y, por lo tanto, los con¿nes de los
polítopos son compactos.
(-(03/2 Consideremos el conjunto convexo compacto
;3
4
3 4 3 4<
f
f @
? ULt |
' UL? C f D c | 5 dfc Z*2o( C  D c C f D
= ti? |

f >
3
4
2.2 Confín: Propiedades básicas
61
f
y la dirección ' C  D. En la Figura 2.2 se puede comprobar que
f
;3 4 3 4 3 4<
f
f @
? 
i?_E( ' UL? C f D c C  D c C f D ^
= f

f >
;
?
4 3 46<
ULt |
f
@
^
^ 7C f D c C  D8 =|MofcZ*2d
>
ti? |

53
u
)LJXUD Obviamente,
3
3
4 3 4
ULt |
f
C
D
C
f
f D 5 U*Ei?_E( c
*4
'
|@ Z2
ti? |

4
f
C
f D5
mientras que
* i?_E( 
Por lo tanto, i?_E( no es cerrado.
352326,&,Ï1 6L HV XQ FRQMXQWR FXDVLSROLpGULFR HQWRQFHV i?_ E( HV
FHUUDGR SDUD WRGR 9' f? 62
2. Confín de un conjunto convexo
'HPRVWUDFLyQ Sea if , 5 Uj la familia (numerable) de todas las caras de tales que
Eh?| f _ i?_E( 9' >
En primer lugar, probaremos que i?_E( es cerrado cuando es un conjunto
poliédrico. En efecto, cualquier conjunto poliédrico tiene un número ¿nito de caras
[9, Cor. 8.5], todas ellas cerradas como consecuencia de que es cerrado [9, Th.
5.1]. Entonces, puesto que U es ¿nito y i?_E( ' ^ f (Corolario 2.8), i?_E( M U
resulta ser la unión ¿nita de una familia de conjuntos cerrados, de modo que también
es cerrado.
Asumamos ahora que es cuasipoliédrico y sea % '*4 %o , con %o 5 i?_E( ,
o
o ' c 2c . Consideremos un polítopo tal que % 5 ?| . Podemos asumir, sin
pérdida de generalidad, que %o 5 ?| , o ' c 2c .
Puesto que 5
* ( Ec %o ' ( E _ c %o , %o 5 i?_E _ ( para todo o 5 Q,
siendo _ un conjunto poliédrico (un polítopo). Puesto que hemos demostrado
que i?_E _ ( es cerrado, obtenemos que % 5 i?_E _ ( y, por lo tanto,
% 5 i?_E( . Esto prueba que i?_E( es cerrado.
Las dos proposiciones siguientes proporcionan caracterizaciones de los puntos
extremos y de la dimensión completa de los conjuntos convexos no vacíos en términos
de los con¿nes.
352326,&,Ï1 % HV XQ SXQWR H[WUHPR GHO FRQMXQWR FRQYH[R QR YDFtR VL \ VyOR
VL
% 5 i?_E( ^ i?_E( (2.4)
SDUD WRGR 9' f? 'HPRVWUDFLyQ
Probaremos la equivalencia entre ambas negaciones para
cualquier % 5 .
Si no se veri¿ca (2.4) para cierto 9' f? , entonces 5 ( Ec %, por lo que
deben existir 0 : f y 02 : f tales que % n 0 5 y % 02 5 . Entonces
% 5 o% 02 c % n 0 d y % no es un punto extremo de .
2.2 Confín: Propiedades básicas
63
Recíprocamente, si % no es un punto extremo de , entonces existe 9' f? c tal
que % 5 , en cuyo caso 5 ( Ec % y no se veri¿ca (2.4).
352326,&,Ï1 'DGR XQ FRQMXQWR FRQYH[R QR YDFtR VH YHUL¿FDQ ODV VLJXLHQWHV
SURSRVLFLRQHV
* E@g (i) i?_E( ' FRQ 9' f? VL \ VyOR VL 5
(ii) _4 ? VL \ VyOR VL H[LVWH 9' f? WDO TXH i?_E( ' 'HPRVWUDFLyQ (i) Si i?_E( 9' podemos tomar % 5 q i?_E( . Sea
0 : f tal que % n 0 5 Entonces 0 5 E@g y, por lo tanto, 5 E@g .
Recíprocamente, asumamos que 9' f? satisface 5 E@g . Tomando un
punto arbitrario % 5 h?| , por la Proposición 0.7, E@g ' tT@? E % y
f? 5 h?| E %. Por lo tanto, existe 0 : f tal que 0 5 % y 5 ( Ec %.
Entonces, % 5 q i?_E( .
(ii) Puesto que E@g ' tT@? E % cualquiera que sea % 5 h?| ,
* tT@? E % ' E@g _4 ? si, y sólo si, existe 9' f? tal que 5
o, equivalentemente (por la parte (i)), i?_E( ' La siguiente proposición establece condiciones su¿cientes para que un punto de sea punto extremo o punto extremo expuesto.
352326,&,Ï1 6HD XQ FRQMXQWR FRQYH[R QR YDFtR 6L i%j ' i?_E( SDUD
FLHUWR 9' f? HQWRQFHV % 5 i |h 6L DGHPiV HV FHUUDGR HQWRQFHV % HV SXQWR
H[WUHPR H[SXHVWR GH \ _4 
'HPRVWUDFLyQ Si % 5
* i |h , entonces existen dos puntos +, 5 5 y un escalar
f b  tales que
% ' b+ n E b5
Dado que +c 5 5
* i?_ E( (pues i?_E( ' i%j), existen 0 : f y 02 : f tales
que + n 0 5 y 5 n 02 5 . Por lo tanto,
% n db0 n E b02 o ' bE+ n 0 n E bE5 n 02 5 c
lo cual contradice que % 5 i?_E( 64
2. Confín de un conjunto convexo
Supongamos ahora que es cerrado y i%j ' i?_E( . Si ' i%j c es evidente
que % es punto extremo expuesto de y _4 ' f.
Sea, pues, un conjunto no singular. Probaremos, por reducción al absurdo, que
% tT@? ij * tT@? ij, se tiene que % 5
* i?_E( y
En efecto, si % 5 es tal que % % 5
existe 0 : f tal que % n 0 5 Consideremos el conjunto no vacío
u G' ik 5 U m % n k 5 j Dado que la aplicación ) G U $ U? de¿nida como ) Ek ' % n k es continua
y u ' )3 E, se tiene que u es cerrado. Entonces, se puede dar una de las dos
situaciones siguientes:
(i) tT u ' 4@ u ' k : f, con lo que % n k 5 y
% n Ek n k ' E% n k n k 5
* c
para todo k : f. Por lo tanto, % n k 5 i?_E( y % n k 9' % ( si fueran iguales,
% % 5 tT@? ij), lo cual contradice la hipótesis i?_E( ' i%j
(ii) tT u ' n4, con lo que % n 0 5 para todo 0 : f. Por lo tanto, 5 n y i?_E( ' >, lo cual contradice de nuevo la hipótesis.
Concluimos, pues, que % tT@? ij y, por lo tanto, _4  Es más,
puesto que no es singular, _4 ' 
Por otro lado, puesto que es un conjunto convexo cerrado unidimensional
contenido en % n tT@? ij y % 5
i?_E( , deberá ser la semirrecta
i% b( b fj o un segmento d%c +o con + ' % b, para cierto b : f. En ambos
casos
_ i% 5 U? m E% % ' fj ' i%jc
por lo que % es punto extremo expuesto de .
La hipótesis i?_E( ' i%j no implica que % sea punto extremo expuesto de .
En otras palabras, la condición de clausura (referida a ), en la segunda parte de la
2.2 Confín: Propiedades básicas
65
Proposición 2.15, no es superÀua. El siguiente ejemplo justi¿ca esta a¿rmación.
(-(03/2 Consideremos el conjunto de soluciones del sistema
|% n E |%2 : | |2 c | 5 ofc d ( % : f c
representado en la Figura 2.3.
1.2
1
0.8
0.6
&
0.4
0.2
[
X
0
0.5
1
1.5
2
)LJXUD 

Si consideramos el punto % '
y la dirección '
c i?_E( ' i%j
f
f
y % es punto extremo de , pero no es punto extremo expuesto. En efecto, el único
hiperplano que soporta a en el punto % es i% 5 U2 m %2 ' fj y también contiene a
todos los puntos del conjunto oc n4d ifj .
El recíproco de la primera parte de la Proposición 2.15 no se veri¿ca en general,
como veremos en el siguiente ejemplo. Sin embargo, probaremos que sí se veri¿ca
para _4 .
(-(03/2 Sea el conjunto de soluciones del sistema
|% n E |%2 : | |2 c | 5 ofc d c
representado en la Figura 2.4.
Los puntos % , %2 5 son puntos extremos y, sin embargo, no existe ninguna
dirección en la que el confín sea igual a uno de esos puntos. En efecto, cualquier vector
no nulo, , del primer cuadrante (incluidos los ejes) es una dirección de recesión, por
lo que i?_ E( ' >. Las restantes elecciones del vector 9' f? dan lugar a los
siguientes con¿nes:
Si 5 o4c fd ofc n4d, i?_ E( ' ifj dc n4d 
Si ' b
, con b : f, i?_ E( ' i% j ^ Eifj dc n4d f
66
2. Confín de un conjunto convexo
[
&
[
)LJXUD Si 5 o4c fd o4c fd, i?_ E( ' Eifj dc n4d ^ Edc n4d ifj f
Si ' b
, con b : f, i?_ E( ' i%2 j ^ Edc n4d ifj 
Si 5 ofc n4d o4c fd, i?_ E( ' dc n4d ifj &252/$5,2 6HD XQ FRQMXQWR FRQYH[R QR YDFtR WDO TXH _4  (QWRQFHV
% HV XQ SXQWR H[WUHPR GH VL \ VyOR VL H[LVWH 9' f? WDO TXH i%j ' i?_E( 'HPRVWUDFLyQ Si _4 ' fc entonces ' i%j para cierto % 5 U? y
i?_E( ' i%j, cualquiera que sea 9' f? .
Si _4 ' c entonces % tT@? ij para cierto 9' f? , es decir,
i% n k m k 5 Uj. Puesto que % 5 i |h , aplicando la Proposición 2.13, se
tiene que % 5 i?_E( ^ i?_E( y se puede dar una de las dos situaciones
siguientes:
* ( Ec %.
(i) % 5 i?_E( o, lo que es lo mismo, 5
En este caso,
4@ ik 5 U m % n k 5 j ' f y i%j ' i?_E( (ii) % 5
* i?_E( , en cuyo caso % 5 i?_E( .
Del mismo modo,
4@ ik 5 U m % k 5 j ' f y i%j ' i?_E( El recíproco es un caso particular de la Proposición 2.15
352326,&,Ï1 6L HV XQ FRQMXQWR FRQYH[R QR YDFtR WDO TXH _4 c HQWRQFHV
H[LVWH 9' f? WDO TXH i?_E( HV YDFtR R VLQJXODU
'HPRVWUDFLyQ Si _4 ' fc entonces ' i%j para cierto % 5 U? y
i?_E( ' i%j, cualquiera que sea 9' f? .
2.3 Conexión del confín
67
Si _4 ' c tomando % 5 c se tiene que % tT@? ij para cierto
9' f? Por lo tanto, i% n k m k 5 Uj y se puede dar una de las dos situaciones
siguientes:
(i) Existe un número real k ' tT ik 5 U m % n k 5 j. Si % n k 5 ,
entonces
i% n kj ' i?_E( y i?_E( es singular. De lo contrario, i?_E( ' >.
(ii) tT ik 5 U m % n k 5 j ' n4c con lo que 5 n y i?_E( es
vacío.
&RQH[LyQ GHO FRQItQ

Retomando el Ejemplo 2.17, podemos ver que si '
, entonces
f
i?_E( ' % ^ Eifj dc n4d c
que es la unión de dos cerrados disjuntos y, por lo tanto, no es un conjunto conexo.
Así pues, los con¿nes de los conjuntos convexos no son necesariamente conexos.
En el siguiente ejemplo veremos que también pueden ser conexos pero no conexos por
arcos.
2
(-(03/2 Sea f un subconjunto conexo de dc o que no sea conexo por arcos.
Consideremos la proyección estereográ¿ca ) G 7 q ie j $ U c que asocia a % 9' e c
la intersección de la semirrecta que sale de e y pasa por % con el plano % ' f, es
decir
%2
%
)E% '
c
cf  %  %
Es bien sabido que ) establece un homeomor¿smo entre 7 q ie j y el plano
i% 5 U m % ' fj c siendo fácil comprobar que la imagen mediante ) del hemisferio
inferior, i% 5 7 m % fj, es el círculo EU* 2 ifj s
Puesto que n%n"  para cualquier % 5 fc se tiene que f 2 U* 2 c es decir,

s f U* 2 2
68
2. Confín de un conjunto convexo

s f ifj es un conjunto convexo (al ser el resultado de
G'
2
agregar a una bola abierta un subconjunto de la esfera correspondiente) para el cual

3

s f ifj c
i?_ ( e ' )
2
^ )3
que es homeomorfo a f y, por lo tanto, conexo, aunque no conexo por arcos.
Una posible elección para f es el conjunto

2
f G' % 5 U m %2 ' ti? c % 5 dc o q ifj ^ Eifj dc o c
%
representado en la Figura 2.5.
1
0.5
-0.1
-0.05
0
0.05
0.1
-0.5
-1
)LJXUD En cambio, para los conjuntos convexos cerrados, todo confín es conexo por arcos
(y por lo tanto conexo), según veremos a continuación.
352326,&,Ï1 6HD XQ FRQMXQWR FRQYH[R FHUUDGR QR YDFtR \ 9' f? WDO TXH
i?_ E( 9' > (QWRQFHV i?_ E( HV FRQH[R SRU DUFRV
'HPRVWUDFLyQ Podemos asumir, sin pérdida de generalidad, que i?_ E( contiene dos puntos distintos, % e +. Probaremos la existencia de un arco contenido en
i?_ E( que une % e +
Consideremos s G $ Un tal que, para % 5 ,
s E% G' 4@ ib 5 U m % n b 5 j Puesto que no es dirección de recesión (en caso contrario i?_ E( ' >) y es
cerrado, s está bien de¿nida. Obviamente, s E% ' s E+ ' f.
2.3 Conexión del confín
69
Para probar que s es cóncava, consideremos % 5 , + 5 y 4 5 dfc o. Entonces,
puesto que % n s E% 5 e + n s E+ 5 , se tiene
E 4 % n 4+ n dE 4 s E% n 4s E+o '
' E 4 d% n s E% o n 4 d+ n s E+ o 5 c
de modo que
s EE 4 % n 4+ E 4 s E% n 4s E+ En consecuencia, la restricción de s al segmento d%c +o es cóncava y, por lo tanto,
continua en el interior de su dominio, es decir, en o%c +d. Probaremos, a continuación,
su continuidad en % (la prueba es la misma en +).
Supongamos que *4 s E% 9' s E% ' f. En tal caso, existe 0 : f y una sucesión
<
% %
i%o joMQ o%c +d tal que *4 %o ' % y s E%o 0 para todo o 5 Q.
o
Para cada o 5 Q se tiene que %o n s E%o 5 , de modo que
%o n 0 5 d%o c %o n s E%o o y, puesto que es cerrado, se obtiene % n 0 '*4 E%o n 0 5 , lo cual contradice
o
que % 5 i?_ E( .
Por lo tanto, la función ) G d%c +o $ i?_ E( de¿nida como ) E% G' %n s E% es continua y satisface ) E% ' % y ) E+ ' +. Se concluye que i) E% m % 5 d%c +oj es
la curva buscada.
Como consecuencia de la conexión por arcos de los con¿nes no vacíos de los
conjuntos convexos cerrados, se obtiene la conexión de la frontera de ciertos conjuntos
convexos compactos. Dicha propiedad es trivial cuando la dimensión es menor que ?
(ya que cualquier conjunto convexo es conexo por arcos). Por lo tanto, analizaremos
la conexión de la frontera relativa. Para ello necesitamos el siguiente lema.
/(0$ 6HD XQ FRQMXQWR FRQYH[R QR YDFtR t U? \ 5 UL?i t 9' f? 6L
% 5 i?_E( HQWRQFHV % 5 i?_E( + SDUD XQ FLHUWR + 5 t q if? j
'HPRVWUDFLyQ Supongamos que % 5
* i?_Ec + para todo + 5 t q if? j y sea
70
2. Confín de un conjunto convexo
'
R
S
'
b + , con b : f e + 5 t q if? j, ' c c R.
0 : f tal que % n 0 + 5 , ' c c R.
Puesto que % 5
* i?_Ec
+ , existe 0
De¿niendo > G' 4?
c ' c c R : f, se tiene
b
% n >b + 5 %c % n 0 + c ' c c Rc
y, por lo tanto, su media aritmética % n
contradice la hipótesis % 5 i?_E( .
>
5 . Por lo tanto, 5 ( Ec %, lo cual
R
352326,&,Ï1 6HD XQ FRQMXQWR FRQYH[R FRPSDFWR QR YDFtR (QWRQFHV hM_ HV FRQH[D SRU DUFRV FRQH[D VL \ VyOR VL _4 9' 
'HPRVWUDFLyQ Si _4 ' , entonces ' d%c +o para dos puntos %c + 5 U? , de
modo que hM_ ' i%c +j ni siquiera es conexa.
Para demostrar el recíproco podemos asumir, sin pérdida de generalidad, que
_4 2. Probaremos que
hM_ ' ^ ii?_ E( c 5 7? _ dE@g oj
(2.5)
(véase Corolario 2.10) es conexo por arcos. Sea  c c _ una base ortonormal de
_
s
S
E@g y sea _n G' * _ 5 7? _ dE@g o. Puesto que
'
7? _ dE@g o tT@?  c c _ ' UL?i  c c _n c
se obtiene, de (2.5) y del Lema 2.22,
_n
hM_ ' ^ i?_ ( '
Por lo tanto, hM_ es unión de _ n  conjuntos que son conexos por arcos
(Proposición 2.21), por lo que bastará probar que
i?_ ( _ i?_ ( n 9' >c ' c c _
Si 5 ic c _ j, consideremos una solución óptima, % , del problema
W?u n n % s.a % 5 c
(dicha solución existe por ser continua la función objetivo y ser compacto el conjunto
factible). Dicho punto satisface E n n E% % f para todo % 5 , mientras
2.4 El confín y la iluminación de los conjuntos convexos cerrados
71
que E n n ' , ' c n . Por lo tanto % 5 i?_ E( , ' c n ,
de acuerdo con la Proposición 2.4. En consecuencia,
i?_ ( _ i?_ ( n 9' >c ' c c _ 
Finalmente, sea %_ una solución óptima del problema
# _3
$
_
[
W?u
% s.a % 5 2
'
Puesto que
# _3
[
_
2
'
para todo % 5 y
# _3
[
_
2
'
$
% %_ f
$
fc ' _c _ n c
se obtiene, de nuevo por la Proposición 2.4,
i?_ ( _ _ i?_ ( _n 9' >
La demostración que acabamos de realizar se puede considerar como una mera
aplicación del confín al análisis convexo, ya que existen demostraciones alternativas
más cortas. Por ejemplo, se puede demostrar considerando que es un cuerpo
convexo compacto en U? , con ? : , eligiendo un punto cualquiera @ 5 ?| y
%@
de¿niendo la transformación A G U? $ U? tal que A E% '
si % 5 M_ y
n% @n
A E@ n b E% @ ' bA E% si b 5 dfc o. Dado que A es un homeomor¿smo de U?
que lleva la frontera de en la esfera 7? (que es conexa por arcos), resulta que M_ también es conexo por arcos.
(O FRQItQ \ OD LOXPLQDFLyQ GH ORV FRQMXQWRV FRQYH[RV
FHUUDGRV
Los siguientes conceptos son extensiones naturales para conjuntos convexos
72
2. Confín de un conjunto convexo
cerrados de los dados por Boltyanski [8] y por Soltan [34] para cuerpos convexos
compactos y cuerpos convexos, respectivamente.
Sea un conjunto convexo cerrado no vacío y 5 U? , 9' f? . Dado % 5 hM_ ,
se dice que % HVWi LOXPLQDGR SRU si i% n b m b : fj_h?| 9' >. Del mismo modo,
diremos que % 5 hM_ HV YLVLEOH HQ OD GLUHFFLyQ si i% b m b : fj _ ' >.
Denotaremos por ** E( (por t E( ) el conjunto de puntos de la frontera
relativa de que están iluminados por 9' f? (visibles en la dirección 9' f? ,
respectivamente).
La siguiente proposición establece relaciones entre los conjuntos que acabamos de
de¿nir y los con¿nes.
352326,&,Ï1 6HD XQ FRQMXQWR FRQYH[R FHUUDGR QR YDFtR \ 5 U? 9' f? (QWRQFHV VH YHUL¿FDQ ODV VLJXLHQWHV SURSRVLFLRQHV
(i) ** E( t E( i?_ E( (ii) ** E( 9' > VL \ VyOR VL 5 dE@g o q En y
(iii) t E( ' i?_ E( VL \ VyOR VL 5 E@g 'HPRVWUDFLyQ (i) Si % 5 ** E( q t E( , entonces existen b : f tal que
% n b 5 h?| y b2 : f tal que % b2 5 . Como consecuencia del Lema de
Accesibilidad (Proposición 0.2(iii)), se tiene
% 5 o% n b c % b2 d h?| c
lo que contradice la hipótesis.
La inclusión t E( i?_ E( es consecuencia directa de las de¿niciones
de ambos conjuntos.
(ii) Si ** E( es no vacío, entonces existen % 5 hM_ y > : f tales que

% G' % n > 5 h?| . Por lo tanto, ' E% % 5 E@g .
>
Por otra parte, si 5 n , entonces % > 5 y, por el Lema de
Accesibilidad, se tiene
% 5 o% n >c % >d h?| c
en contra de la hipótesis. Por lo tanto, 5 dE@g o q En 2.4 El confín y la iluminación de los conjuntos convexos cerrados
73
Recíprocamente, si 5 dE@g o q En y tomamos un punto arbitrario
% 5 h?| , entonces existe > : f tal que % > 5 . Sea
0 ' 4@ ib 5 Un m % b 5 j : f
(dicho máximo se alcanza por ser 5
* n y cerrado y es positivo por ser
0 >) y sea % G' % 0 5 . De nuevo por el Lema de Accesibilidad, se tiene
que o%c %d h?| y, por lo tanto,
> 9' o%c %d i% n b m b : fj _ h?| (2.6)
Dado que 5
* ( Ec %, se cumple que % 5 i?_ E( hM_ (véase Corolario
2.10 (iii)) y esto, junto con (2.6), implica que % 5 ** E( .
(iii) Si 5
* E@g , entonces 5
* E@g y, por la Proposición 2.14,
i?_ E( ' . Entonces, se tiene
t E( hM_ # ' i?_ E( c
lo que contradice la hipótesis.
Probaremos el recíproco viendo que i?_ E( t E( para cualquier
vector no nulo 5 E@g En efecto, si % 5 i?_ E( , por ser 5 E@g y por el Corolario 2.10,
se tiene que % 5 hM_ . Además, 5
* ( Ec % por lo que i% b m b : fj_ ' >
y % 5 t E( .
Nótese que t E( 9' > es conexo por arcos cuando 5 E@g (ya que t E( ' i?_ E( , conexo por arcos por la Proposición 2.21). Si
5
* E@g , entonces t E( ' hM_ que, como veremos en el Capítulo 3, es
conexo por arcos siempre que no sea un sandwich.
La primera inclusión en la Proposición 2.24 (i) puede ser estricta. Por ejemplo,
si ' dfc o2 , ** E( e ' ifj ofc d mientras que t E( e ' ifj dfc o. Sin
embargo, como veremos en la siguiente proposición, ambos conjuntos están bastante
próximos.
74
2. Confín de un conjunto convexo
352326,&,Ï1 6HD XQ FRQMXQWR FRQYH[R FHUUDGR QR YDFtR \ FRQVLGHUHPRV
hM_ GRWDGR GH OD WRSRORJtD LQGXFLGD SRU OD QRUPD (XFOtGHD GH U? 6L ** E( 9' >
HQWRQFHV ** E( HV DELHUWR FRQH[R SRU DUFRV \ GHQVR HQ t E( 'HPRVWUDFLyQ Sea % 5 ** E( y sea b : f tal que % n b 5 h?| . Sea 4 : f
tal que E% n b n 4? _ @g h?| . Dado % 5 hM_ tal que n% %n 4, se
puede ver fácilmente que % n b 5 E% n b n 4? _ @g h?| , de modo que
% 5 ** E( . Por lo tanto, ** E( es abierto en hM_ .
Sea, ahora, % 5 ** E( , ' c 2. La función [ G d% c %2 o $ Un tal que
[ E% ' 4@ ib 5 U m % b 5 j
está bien de¿nida porque 5 dE@g o q En (en otro caso ** E( ' >) y
es cerrado. Además, [ es continua (retomemos la demostración de la Proposición
2.21), [ E% ' [ E%2 ' f y % [ E% 5 i?_ E( hM_ para todo
% 5 d% c %2 o, por el Corolario 2.10. Tenemos que demostrar que %[ E% 5 ** E( para todo % 5 o% c %2 d. De hecho, si % ' E > % n >%2 , con f > , y
% n b 5 h?| , con b : f, ' c 2, entonces
d% [ E% o n dE > b n >b2 n [ E%o '
' E > % n b n > %2 n b2 5 h?| c
con E > b n >b2 n [ E% : f, de modo que % [ E% 5 ** E( . Por lo tanto,
i% [ E% m % 5 d% c %2 oj es un arco contenido en ** E( que conecta % y %2 .
Finalmente, dado % 5 t E( , tomemos un %2 5 ** E( arbitrario, %2 9' % ,
y consideremos de nuevo la función [. Probaremos que, para todo % 5 o% c %2 d,
% [ E% 5 ** E( .
Sea %2 n b2 5 h?| , con b2 : f. Entonces, si % ' E > % n >%2 , con
f > , el lema de accesibilidad establece que
d% [ E% o n d>b2 n [ E%o ' E > % n > %2 n b2 5 h?| c
con >b2 n [ E% : f.
Por lo tanto, % ' *4 E% [ E% 5 U* ** E( .
%<%
2.4 El confín y la iluminación de los conjuntos convexos cerrados
75
Nótese que, en la demostración de la conexión por arcos de ** E( y de su
densidad en t E( , hemos considerado ** E( no singular. Si fuese un conjunto
singular, hM_ ' ** E( ' t E( y se cumpliría trivialmente la proposición.
De la Proposición 2.25, ** E( ?| t E( mientras que la inclusión inversa
también es cierta cuando ** E( 9' >.
352326,&,Ï1 6HD XQ FRQMXQWR FRQYH[R FHUUDGR QR YDFtR \ FRQVLGHUHPRV
hM_ GRWDGR GH OD WRSRORJtD LQGXFLGD SRU OD QRUPD (XFOtGHD GH U? 6L ** E( 9' >
HQWRQFHV ** E( ' ?| t E( 'HPRVWUDFLyQ Sea % 5 ?| t E( q ** E( y sea 0 : f tal que
E% n 0? _ hM_ t E( (2.7)
0
, se tiene que % n b 5 E% n 0? , para todo f b b, y, si
nn
suponemos que % n b 5 hM_ , entonces, de acuerdo con (2.7), % n b 5 t E( ,
lo cual se contradice con % 5 . Por lo tanto, % n b 5
* hM_ para todo b 5 fc b .
Tomando b G'
* h?| (pues % 5
* ** E( ), se concluye que
Como, por otra parte, % n b 5
% n b 5
* para todo b 5 fc b y, como consecuencia, % 5 i?_ E( y 5
* n .
Sea + 5 ** E( . Puesto que no es dirección de recesión y es cerrado,
podemos considerar la restricción, al segmento d+c %o, de la aplicación de la Proposición
2.21, es decir, s
ƒd
+c%o
G d+c %o $ U tal que, para % 5 d+c %o,
n
s E% G' 4@ ib 5 U m % n b 5 j Dado que s E% ' f y s es continua en % (véase la demostración de la Proposición
2.21), se cumple que *4 E% n s E% ' % por lo que, para % su¿cientemente
%<%
próximo a %, se tiene % n s E% 5 E% n 0? . Además, por la propia de¿nición
de s , se tiene que % n s E% 5 i?_ E( hM_ , de modo que
% n s E% 5 E% n 0? _ hM_ y, sin embargo, % n s E% 5
* t E( , lo que se contradice con (2.7).
&252/$5,2 6L HV XQ FXHUSR FRQYH[R \ 5
* n HQWRQFHV i?_ E( '
t E( \ ?| i?_ E( ' ** E( $GHPiV i?_ E( HV FHUUDGR VL \ VyOR
VL i?_ E( ' U* ** E( 76
2. Confín de un conjunto convexo
'HPRVWUDFLyQ Al ser un cuerpo convexo, E@g ' U? , por lo que la
hipótesis 5
* n implica que 5 dE@g o q En o, lo que es lo mismo,
** E( 9' > (Proposición 2.24 (ii)) y t E( ' i?_ E( (Proposición 2.24
(iii)). Partiendo de estos dos resultados y aplicando la Proposición 2.26, se obtiene
** E( ' ?| t E( ' ?| i?_ E( Por otra parte, por la Proposición 2.25, ** E( es denso en t E( '
i?_ E( , por lo que
i?_ E( U* ** E( U* i?_ E( c
de donde se deduce la última parte de la proposición.
Acabaremos esta sección con algunos comentarios acerca de combinatoria
geométrica en conjuntos convexos cerrados.
Dado % 5 hM_ , si + 5 h?| , entonces % 5 ** E( + %. Por lo tanto,
i** E( m 9' f? j es un recubrimiento abierto de hM_ .
Denotemos por K E el mínimo número de direcciones que iluminan (es decir,
todos los puntos de hM_ ) y por E el mínimo número de direcciones en las que
es visible . Si e E es el mínimo número de con¿nes que cubren M_ , entonces
e E '  si _4 ? (véase Proposición 2.14 (ii)) y e E E K E para
todo conjunto convexo cerrado (consecuencia de la Proposición 2.24 (i)).
Por lo que respecta a K E, obsérvese que sólo las direcciones de E@g iluminan al menos un punto de hM_ y que
i** E( m 5 E@g c 9' f? j
es una familia de conjuntos abiertos en hM_ . Si es compacto, hM_ es compacto
también, de modo que K E 4. Puesto que K E ? n  para cuerpos convexos
compactos [8], se obtiene _4 n  K E 4.
Alternativamente, si es no acotado, es posible que K E ' 4 incluso para
cuerpos convexos. Si K E 4, la conjetura de Soltan sobre la iluminación de
cuerpos convexos no acotados [34] se puede reformular como K E 2_4 3 .
2.5 Algunas aplicaciones a los sistemas de desigualdades lineales
77
Por otra parte, E 2 si es un cuerpo convexo [34] (obsérvese que E ' 
si es el epigrafo de una función cuadrática estrictamente convexa). En consecuencia,
e E E 2 para todo conjunto convexo cerrado , es decir, bastan dos con¿nes
para cubrir la frontera o la frontera relativa de un conjunto convexo cerrado.
$OJXQDV DSOLFDFLRQHV D ORV VLVWHPDV GH GHVLJXDOGDGHV
OLQHDOHV
En esta sección, consideraremos sistemas en U? de la forma
j ' i@| % K| c | 5 A j c
donde A es un conjunto arbitrario de índices (posiblemente in¿nito), @| 5 U? y K| 5 U
para todo | 5 A . Al conjunto de soluciones de j, que es un conjunto convexo cerrado,
lo denotaremos por 8 .
A continuación, daremos dos propiedades geométricas de 8 (una de ellas para
sistemas LFM) y una caracterización de los sistemas LOP, a través de los con¿nes.
352326,&,Ï1 6HDQ 8
9' > \ g HO FRQMXQWR GH VROXFLRQHV \ HO FRQR
FDUDFWHUtVWLFR GH j ' i@| % K| c | 5 A j UHVSHFWLYDPHQWH 6L @r % Kr FRQ r 5 A GH¿QH XQ VHPLHVSDFLR VRSRUWH GH 8 HQWRQFHV
@r
f?
(2.8)
5 i?_ g(
Kr

(O UHFtSURFR HV FLHUWR FXDQGR 8 HV FRPSDFWR
'HPRVWUDFLyQ Supongamos que @r 9' f? , @r % Kr para todo % 5 8 y @r % ' Kr
para cierto % 5 8 .
%
@|
%
f?
Puesto que
f para todo | 5 A ,
' y

K|


%
@r
%
%
' f, la desigualdad
f de¿ne un semiespacio

Kr

%?n
@r
soporte de g en
.
Kr
Asumiendo que no se veri¿ca (2.8), podemos escribir
f?
@r
@r
n
'
5g
Kr

Kr n 78
2. Confín de un conjunto convexo
%
@r
f, es decir, @r % Kr '
para cierto : f. Por lo tanto,

Kr n f, y se obtiene la contradicción deseada.
Asumamos, ahora, que se veri¿ca (2.8). La compacidad de 8 implica (por la
Proposición 0.19) que
@
?
n
m @ % : K para todo % 5 8 ?| g '
5U
K
Si @r % Kr no de¿niese
un semiespacio soporte de 8 , entonces @r % : Kr para todo
@r
5 ?| g, lo que se contradice con (2.8).
% 5 8 , de modo que
Kr
El recíproco de la proposición anterior puede fallar si 8 no es compacto.
(-(03/2 Consideremos el sistema
q
r
s
j ' % n |%2 |c | 5 dfc o c
cuyo conjunto de soluciones está representado en la Figura 2.6, y tomemos el índice
r ' f, que no de¿ne un semiespacio soporte de 8 .
)
)LJXUD El cono característico del sistema es
;3
4
3
4<

f
?
@
C
D
C
D
|
f
g ' UL?i
c | 5 dfc o (
= s
 >
|
Veremos que,
@r
Kr
3
4

f
?
' C f D 5 i?_ g(

f
2.5 Algunas aplicaciones a los sistemas de desigualdades lineales
79
En efecto, si tomamos cualquier 0 : fc
3 4
3 4 3 4

f

C f D n 0C f D ' C f D 5
*g
f

0
pues, de lo contrario,
3
4
3
4
3
4


f
[
C f D'
b| C s| D n C f D

0
|
|Mdfco
(2.9)
EA para algún b 5 Un y 5 Un . De (2.9) se obtiene
[
[ s
[
b| ' c
b| | ' f y
b| | ' 0c
|Mdfco
|Mdfco
|Mdfco
de donde se deduce que
b| '
 si | ' f
f si | 9' f
y ' 0c
con lo que resulta ser negativo.
352326,&,Ï1 6HD 8
9' > HO FRQMXQWR GH VROXFLRQHV GH XQ VLVWHPD j '
i@| % K| c | 5 A j WDO TXH @| 9' f? SDUD WRGR | 5 A 6H FXPSOH
(i) 6L AS 9' > HQWRQFHV 8 ' i?_E8 ( ' i?_E8 ( SDUD FLHUWR 9' f? (ii) 6L 8 ' i?_E8 ( ' i?_E8 ( SDUD DOJ~Q 9' f? \ j HV /)0 HQWRQFHV AS 9' >
'HPRVWUDFLyQ (i) Sea r 5 AS y tomemos % 5 8 arbitrariamente Dado que
@r E% % ' f para todo % 5 8 , se tiene que @r 5 dE@g 8 8 oz , @r 9' f? , de
modo que @r 5
* E@g 8 8 y i?_E8 ( @r ' i?_E8 ( @r ' 8 de acuerdo con la
Proposición 2.14 (i).
(ii) Sea 8 ' i?_E8 ( ' i?_E8 ( c 9' f? . Puesto que _4 8 ? (por la
a¿rmación (ii) de la Proposición 2.14), existe 9' f? tal que E% % ' f para
todo % 5 8 , siendo % un punto arbitrario de 8 . Entonces E% % f son
semiespacios soporte de 8 en %, y existe un conjunto ¿nito de índices 7 A tal
que ambas desigualdades son consecuencia de i@| % K| m | 5 7j. De acuerdo con el
Lema de Farkas no homogéneo, podemos escribir
[ @|
f?
'
b|
n>
c
%
K|

|M 7
(2.10)
80
2. Confín de un conjunto convexo
y
%
[ @| f?
'
nB
c
|
K|

|M7
(2.11)
con > f, B f, b| f para todo | 5 7 y | f para todo | 5 7, no todos nulos
De (2.10) y (2.11) se sigue que
[
@|
f?
'
Eb| n | 5 gc
(2.12)
E> n B

K|
|M 7
f?
5 g si > n B : f. Aplicando, de nuevo, el Lema de Farkas, se
de modo que

obtiene, para todo % 5 8 , la relación absurda f? % .
Por lo tanto, > ' B ' f y (2.12) se convierte en
[
@|
Eb| n | ' f?n K|
|M7
Si br n r : f, entonces,
[ b| n @ @r
| 5 gc
|
'
Kr
K
b n r
|
|M7 .tr r
de modo que @r % Kr es consecuencia de j (de nuevo por el Lema de Farkas no
homogéneo). Por lo tanto, @r % ' Kr para todo % 5 8 y r 5 AS .
La condición de que j es LFM en (ii) no es supérÀua. Podemos verlo en el
siguiente ejemplo:
(-(03/2 Consideremos el sistema


j ' %2 c o 5 Q( %2 c o 5 Q( % %2 f c
o
o
cuyo conjunto factible está representado en la Figura 2.7.
Se trata de un sistema que no es LFM, pues la restricción % f de¿ne un
hiperplano soporte de 8 , pero
no es
consecuencia de ningún subsistema ¿nito de j

Si consideramos @r '
, se veri¿ca que i?_ E8 ( @r ' i?_ E8 ( @r ' 8 ,

pero no hay índices portadores.
352326,&,Ï1 6HD 8
9' > HO FRQMXQWR GH VROXFLRQHV GH XQ VLVWHPD j '
i@| % K| c | 5 A j (QWRQFHV VH YHUL¿FD
(i) 6L % 5 8 \ 5
* E%J HQWRQFHV % 5 i?_ E8 ( 2.5 Algunas aplicaciones a los sistemas de desigualdades lineales
81
)
)LJXUD (ii) j HV /23 VL \ VyOR VL 5
* E%J SDUD WRGR SDU E%c WDO TXH % 5 i?_ E8 ( (Q
RWUDV SDODEUDV j HV /23 VL \ VyOR VL HO UHFtSURFR GH L VH YHUL¿FD HQ WRGRV ORV
SXQWRV GH 8 'HPRVWUDFLyQ (i) Sean % 5 8 y 5
* E%J . Entonces, existe un vector
S
+ '
b| @| , con b| ' f para todo | 5
* A E% y b| f para todo | 5 A E%,
|MA
satisfaciendo + f. Puesto que, para cualquier % 5 8c
[
[
+ E% % '
b| @| E% % '
b| E@| % K| fc
|M A
|MA
se concluye que + satisface (2.1) y, por tanto, % 5 i?_ E8 ( de acuerdo con la
Proposición 2.4.
(ii) Sea % 5 8 y 9' f? tal que % 5 i?_ E8 ( . Si j es LOP, se veri¿ca que
* ( E8c % c se tiene que 5
* E%J .
E%J ' ( E8c % y, puesto que 5
Recíprocamente, dado 5 E%J , la hipótesis implica que % 5
* i?_ E8 ( , de
modo que 5 ( E8c %. Por lo tanto, E%J ( E8c % mientras que la inclusión
opuesta siempre es cierta. Se obtiene, pues, E%J ' ( E8c % para todo % 5 8 , por
lo que j es LOP.
&DStWXOR &DUDFWHUL]DFLyQ GH IDPLOLDV GH
FRQMXQWRV FHUUDGRV FRQYH[RV
,QWURGXFFLyQ
La caracterización de familias de conjuntos convexos cerrados puede ser útil
desde diferentes puntos de vista. Un problema PSIL consiste en la minimización
de un funcional lineal sobre un conjunto convexo cerrado de U? que se describe por
medio de in¿nitas desigualdades lineales. Si el conjunto factible es la suma de un
conjunto convexo compacto con un subespacio vectorial, veremos que la acotación
del problema PSIL implica su resolubilidad. Por otra parte, asumiendo las hipótesis
necesarias sobre el sistema de restricciones, es posible obtener un punto extremo del
conjunto factible desde cualquier solución factible sin pérdida del objetivo (se pueden
encontrar algoritmos de puri¿cación en [3] y [19]) y después, comenzando en este
punto extremo inicial, es posible construir una poligonal de aristas conectadas a lo
largo de las cuales el funcional óptimo decrece (se ha propuesto un método simplex
PSIL en [ 2]). Obviamente, la viabilidad de un algoritmo progresando sobre la frontera
de la región factible requiere su conexión por arcos. En este capítulo caracterizaremos
la clase de conjuntos convexos cerrados cuya frontera relativa es no vacía y conexa por
83
84
3. Caracterización de familias de conjuntos cerrados convexos
arcos (Sección 3.5).
Por otra parte, son problemas típicos de combinatoria geométrica, la
caracterización de aquellos cuerpos convexos (conjuntos convexos cerrados de
dimensión completa) para los cuales el mínimo número de puntos (o direcciones) que
los iluminan en un cierto sentido tienen una expresión dada (véanse [27] y [28]).
Este capítulo trata sobre los diferentes modos de caracterizar familias de conjuntos
convexos cerrados.
Cualquier conjunto convexo cerrado U? admite diferentes representaciones.
En primer lugar, se puede descomponer como la suma de su espacio de linealidad,
*? , con _ E*? z (este es el cono apuntado de , si es un cono convexo). Este
último conjunto es, a su vez, la suma de la envoltura convexa de su conjunto de puntos
extremos, . E 9' >, con la envoltura convexa cónica de su conjunto de direcciones
extremas, ( E [32, Th. 18.5], de modo que ' *? n . E n ( E. El triplete
E*? c . E c ( E constituye la UHSUHVHQWDFLyQ LQWHUQD de .
Por otra parte, es el conjunto de soluciones de un cierto sistema semi-in¿nito
lineal j ' i@| % K| c | 5 A j, con @| 5 U? y K| 5 U para todo | 5 A , el cual constituye
una representación externa de . Dicha representación no es única, pero el cono
@|
f?
g E ' U* UL?i
c | 5 A(
c
K|

es el mismo para todas las representaciones externas de 9' >, de modo que, el
cono de referencia, g E, se puede considerar como una UHSUHVHQWDFLyQ FyQLFD de
. A partir de
obtener diferentes representaciones externas de g E sepueden
@
5 U , donde el conjunto de índices U es un subconjunto
(por ejemplo, @ % Kc
K
denso arbitrario de g E). Sin embargo, existe una correspondencia biyectiva entre
los conjuntos convexoscerrados
no vacíos de U? y los
conos convexos cerrados de
f
f
?
?
U?n que contienen a
pero no contienen a
(sus correspondientes conos


de referencia).
El interés de la representación cónica deriva del hecho de que g E captura toda
la información relevante sobre . Por ejemplo, _4 ' ? _4 *? dg Eo [19,
Th. 5.8]) y el valor del problema de optimización ES G ? S % r@ % 5 ,
3.1 Introducción
85
S
?
donde S 5 U , es tT k 5 U m
5 g E [19, Th. 8.1(ii)], de modo que las
k
propiedades de g E y ES están íntimamente relacionadas unas con otras. Además,
dos conjuntos convexos cerrados,  y 2 , se pueden separar mediante un hiperplano
si, y sólo si, g E _ dg E2 o contiene al menos un rayo.
La unicidad, tanto de la representación interna como de la cónica, es una
característica útil, de modo que grandes familias de conjuntos convexos cerrados no
vacíos se pueden caracterizar por medio de las propiedades de sus correspondientes
representaciones interna y cónica. Así, por ejemplo, resulta sencillo caracterizar la
familia de los semiespacios cerrados.
352326,&,Ï1 'DGR XQ FRQMXQWR FRQYH[R FHUUDGR 9' > ODV VLJXLHQWHV
FRQGLFLRQHV VRQ HTXLYDOHQWHV
(i) HV XQ VHPLHVSDFLR
(ii) . E HV VLQJXODU _4 ( E '  \ _4 E*? ' ?  \
f?
(iii) g E HV XQ FRQR FRQYH[R FHUUDGR \ DSXQWDGR _4 g E ' 2 \

5 hM_ g E
'HPRVWUDFLyQ (i) , (ii) Supongamos
' i% 5 U? m @ % Kj c
con @ 5 U? q if? j y K 5 U. Entonces, *? ' i% 5 U? m @ % ' fj, por lo que
_4 E*? ' ?  y E*? z ' tT@? i@j.
K
z
Tomando % G'
2 @, resulta evidente que % 5 _ E*? y
n@n
i% n b@c b fj _ E*? z Para demostrar la inclusión contraria, tomamos % 5 _ E*? z .
Al ser
% % 5 E*? z , existe b 5 U tal que % ' % n b@, pero, dado que % 5 , debe
cumplirse
@ E% n b@ ' K n b n@n2 Kc
por lo que b f.
86
3. Caracterización de familias de conjuntos cerrados convexos
Así pues
. E n ( E ' _ E*? z ' i% n b@c b fj c
de donde se obtiene . E ' i%j y ( E ' UL?i i@j.
(ii) , (iii) Supongamos que . E ' i%j, ( E ' UL?i i@j, @ 9' f? , y
_4 E*? ' ? . Como
% n UL?i i@j ' _ E*? z E*? z
y _4 E*? z ' , se tiene
E*? z ' tT@? i@j
y
*? ' i% 5 U? m @ % ' fj .
Entonces, dado cualquier % 5 , % ' % n b@ n 5 con b f y @ 5 ' f. Tomando
K G' @ %, se obtiene
@ % ' @ E% n b@ n 5 ' K n b n@n2 Kc
@
por lo que, aplicando el Lema de Farkas,
5 g E.
K
Probaremos que
@
f?
g E ' UL?i
c
(3.1)
K

S
En efecto, si
5 g E, entonces, de nuevo por el Lema de Farkas, S % _
_
para todo % 5 y, en particular, S + _ para todo + 5 _ E*? z . Tomando
+ 5 _ E*? z ¿jo y 5 5 *? arbitrario, se tiene
S E+ n k5 ' S + n kS 5 _
para todo k 5 U, de donde obtenemos que S 5 ' f para todo 5 5 *? . Así pues,
S 5 E*? z y existe > 5 U tal que S ' >@. En realidad, > no puede ser negativo ya
_ S %
que, si lo fuese, S @ ' > n@n2 f y, tomando b :
f, se tendría
> n@n2
S E% n b@ _c
3.1 Introducción
87
con % n b@ 5 , contradiciéndose el hecho de que S % _ para todo % 5 . Así pues,
> f.
Por otra parte, puesto que >K ' S % _, podemos escribir
@
f?
S
@
f?
'>
n E>K _
5 UL?i
c

K

_
K
@
f?
Por lo tanto, se cumple (3.1) y, dado que
c
son linealmente
K

independientes, concluimos
que g E es un cono convexo cerrado apuntado
f?
bidimensional y
5 hM_ g E

(iii) , (i) Supongamos que
@
S
g E ' UL?i
c
c
K
_
@
S
con
c
un conjunto linealmente independiente en U?n .
K
_
f?
5 g E, podemos escribir

@
S
f?
'k
nq
c

K
_
Puesto que
k
f y q f. Si fuesen k : f y q : f, por la Proposición 0.6, tendríamos
f?
5 h?| g E, lo que contradice la hipótesis.

S
f?
'q
con q : f y
Por lo tanto, podemos suponer

_
@
f?
g E ' UL?i
c
,
K

de modo que ' i% 5 U? m @ % Kj es un semiespacio.
En la Tabla 3.1 se resume la información obtenida, en la proposición anterior,
para los semiespacios cerrados y se recogen las caracterizaciones, ya conocidas [19,
Ths. 5.8 y 5.13], de otras familias de conjuntos convexos cerrados. Dicha tabla podrá ir
completándose con los resultados obtenidos, en las distintas secciones de este capítulo,
para familias como la de las sumas de conjuntos convexos compactos con subespacios
vectoriales (Sección 3.2), la de los símplices (Sección 3.3), sandwiches (Sección 3.4)
o paralelotopos (Sección 3.6) (las tres subfamilias de la anterior), la de los conjuntos
88
3. Caracterización de familias de conjuntos cerrados convexos
continuos (Sección 3.7) o la de los cuerpos convexos suaves (Sección 3.8).
5HSUHVHQWDFLyQ LQWHUQD
semiespacio cerrado
. E singular,
_4 ( E ' c
_4 E*? ' ? 
variedad afín
. E singularc
( E ' if? j
conjunto convexo
poliédrico
conjunto singular
cuerpo convexo
. E polítopo,
( E poliédrico
. E singular,
( E ' if? j c
*? ' if? j
_4 E*? n
n _4 d. E n ( Eo ' ?
5HSUHVHQWDFLyQ FyQLFD
g E apuntado,
g E ' 2c
_4
f?
5 hM_ g E

El cono apuntado
de
f?
g E es UL?i

g E poliédrico
g E semiespacio
g E apuntado
7DEOD En la última sección caracterizaremos algunas familias de cuerpos convexos
utilizando ciertos conceptos de iluminación.
&DUDFWHUL]DFLyQ GH ODV VXPDV GH FRQMXQWRV FRQYH[RV
FRPSDFWRV FRQ VXEHVSDFLRV YHFWRULDOHV
352326,&,Ï1 'DGR XQ FRQMXQWR FRQYH[R FHUUDGR FRQGLFLRQHV VRQ HTXLYDOHQWHV
9' > ODV VLJXLHQWHV
(i) HV OD VXPD GH XQ FRQMXQWR FRQYH[R FRPSDFWR FRQ XQ VXEHVSDFLR YHFWRULDO
(ii) . E HV FRPSDFWR \ ( E ' if? j (
f?
(iii)
5 h?| g E \

(iv) E*? z ' Eg E GRQGH GHQRWD OD SUR\HFFLyQ YHUWLFDO
E% c c %?n ' E% c c %? 3.2 Caracterización de las sumas de conjuntos convexos compactos con subespacios vectoriales
89
'HPRVWUDFLyQ (i) , (ii) Si ' . n u, con . conjunto convexo compacto y u
subespacio vectorial, entonces *? ' u y _ uz ' E. n u _ uz es la proyección
ortogonal de . sobre uz , de modo que _uz es compacto por ser la imagen continua
de un conjunto compacto. Por lo tanto, ( E ' if? j y . E ' _uz es compacto.
(ii) , (iii) Asumamos que ' . E n *? , con
. E compacto, . E f
?
, de modo que se veri¿ca
E*? z . Si *? ' U? , ' U? y g E ' UL?i

(iii).
Sea i c c R j una base ortonormal de E*? z 9' if? j y sea 4 : f tal que
n+n 4 para todo + 5 . E.
Dado % 5 , podemos escribir % ' + n 5, + 5 .E y5 5 *? , de modo que
5 g E, ' c c R
m% m ' m+ m 4 y % 4. Por lo tanto,
4
(por el Lema
de
Farkas).
@
Dado
5 g E, @ % K para todo % 5 . Si 5 5 *? , tomando
K
un punto arbitrario % 5 . E, se tiene que % n k5 5 para todo k 5 U, de
modo que @ E% n k5 K para todo k 5 U, y esto implica que @ 5 ' f. Por lo
R
S
k para ciertos escalares k 5 U,
tanto, @ 5 E*? z y podemos escribir @ '
'
' c c R.
Puesto que
f?

R n
c
4
4
'
[
' E2R43
se tiene
$ [
#
R
R
[
@
f?
'
k
k
Kn4
5 tT@?
c ' c c R c
K
4

4
'
'
y el último conjunto resulta sertT@?g E. Por lo tanto, podemos aplicar la
f?
Proposición 0.6 para concluir que
5 h?| g E.

f?
?
n
?
(iii) , (iv) Puesto que G U
$ U es lineal y
5 h?| g E c se

tiene que f? 5 h?| dg Eo (Proposición 0.3), siendo dg Eo un cono convexo.
Entonces dg Eo es subespacio vectorial.
Si dg Eo ' if? j, entonces g E ' UL?i
f?

y ' U? , de modo que
90
3. Caracterización de familias de conjuntos cerrados convexos
*? ' U? y E*? z ' dg Eo. Podemos asumir, sin pérdida de generalidad, que
dg Eo 9' if? j.
Sea i  c c ^ j una base ortonormal del subespacio vectorial dg Eo. Dado
& 5 ic c ^j, existen escalares k& y q & tales que
&
&
5 g E y
5 g E c
k&
q &
de manera que k& % & q & para todo % 5 .
Probaremos que *? ' d dg Eooz .
En efecto, si 5 5 *? , tomando % 5 arbitrario, se tiene, para & 5 ic c ^j,
k& E% n k5 & q & para todo k 5 U, y esto implica 5 & ' f. Por lo tanto,
z
*? i  c c ^ j ' d dg Eooz .
z
?
Recíprocamente, si 5 5 d dg Eoo , entonces @ 5 ' f para todo @ 5 U tal que
@
5 g E para cierto K 5 U. Puesto que
K
@
@%Km
5 g E
K
es una representación lineal de , 5 es una solución del correspondiente sistema
homogéneo, de manera que 5 5 n y 5 5 *? .
Por lo tanto, d dg Eooz ' *? y se veri¿ca (iv).
(iv) , (i) Si dg Eo ' if? j, ' U? y se veri¿ca (i). Asumamos, pues, que
_4 dg Eo ' ^,  ^ ?.
Sea i  c c ^ j una base ortonormal de dg Eo y sean k c c k^ ( q  c c q ^
escalares tales que k& % & q & , para todo % 5 , & ' c c ^.
Si ^ ' ?, es compacto y se veri¿ca (i).
En otro caso E*? z ' dg Eo 9' U? y podemos seleccionar vectores
& 5 *? , & ' ^ n c c ?, tales que i  c c ? j es una base ortonormal de U? .
Dado % 5 _E*? z , se tiene que k& % & q & , & ' c c ^ (puesto que % 5 )
y % & ' f, & ' ^ n c c ? (puesto que % 5 E*? z ). Por lo tanto _ E*? z es
k
l
compacto y ' _ E*? z n *? es la descomposición buscada.
El siguiente resultado justi¿ca el interés de esta clase de conjuntos convexos
3.2 Caracterización de las sumas de conjuntos convexos compactos con subespacios vectoriales
91
cerrados en PSIL.
&252/$5,2 6HD OD VXPD GH XQ FRQMXQWR FRQYH[R FRPSDFWR FRQ XQ VXEHVSDFLR
YHFWRULDO \ VHD ES W?u S % VD % 5 6L ES HV DFRWDGR HQWRQFHV HV UHVROXEOH
GLVFUHWL]DEOH \ WLHQH VDOWR GH GXDOLGDG QXOR
'HPRVWUDFLyQ Asumamos que es la suma de un conjunto convexo compacto
con un subespacio vectorial. De acuerdo con la Proposición 3.2, podemos escribir
' . E n *? , con . E compacto y dg Eo ' E*? z .
Sea j ' i@| % K| c | 5 A j cualquier representación externa de y sea  el
primer cono de momentos de j. Dado | 5 A , se tiene que @| ' E@| c K| 5 dg Eo,
de manera que  dg Eo. Por otra parte, si 5 5 dg Eo, existe una sucesión
f?
@|
o
i5 j UL?i
c | 5 A(
K|

EA tal que 5 '*4 5o , ' c c ?. Para cada 5 o existen bo 5 Un y >o f tales que
o
S o
S o @|
f?
5o '
n >o
. Puesto que
b|
b| @| 5 , o ' c 2c c se tiene
K|

|M A
|MA
[
5 '*4 E5o c c 5?o '*4
bo| @| 5 U*  .
o
o
|MA
Hemos demostrado que  E*? z U* , de modo que U*  ' E*? z .
Por lo tanto,
E*? z ' h?| E*? z ' h?| U*  ' h?|   E*? z c
y esto implica h?|  ' E*? z .
Si ES tiene valor ¿nito, ES, entonces S 5 E*? z (en otro caso, existiría
+ 5 *? ' En _ En tal que o S + f e + 5 n o S E+ f y
+ 5 n , de modo que ES ' 4 en ambos casos). Por lo tanto, S 5 h?|  y
esto implica la resolubilidad de ES, su discretización (una solución óptima se puede
obtener como límite de soluciones óptimas de una sucesión de subproblemas ¿nitos) y
el salto de dualidad nulo [19, Ths. 8.1(v) y 8.2].
Aunque bajo las hipótesis del Corolario 3.3, ES es resoluble y el salto de
dualidad es nulo, ( ES puede no ser resoluble, como veremos en el siguiente ejemplo.
92
3. Caracterización de familias de conjuntos cerrados convexos
(-(03/2 Consideremos el problema PSIL
E W?u
%
r@ % *|c | ' c 2c c
%  E| ' f
f
cuyo conjunto factible es ' Edfc o ifj n tT@?
, suma de un conjunto

convexo compacto con un subespacio vectorial.
Se puede ver fácilmente que E ' Ef ' f, por lo que, como era de esperar,
E es resoluble.
Consideremos ahora el problema dual de E " b|
S
bf
|' |
" 
S

 r@
b|
n bf
'
f
f
f
|'
E( 5T b| fc | ' fc c Desde luego, [ Eb f, para todo b 5 \, por lo que E( f. Veremos que, en
realidad, E( ' f. En efecto, si ibo j"
o' \ es tal que
c | ' o
o
c
b| '
fc | 9' o

al ser [ Ebo ' , *4 [ Ebo ' f E(. Por lo tanto, E( ' f.
o o
Sin embargo, E( no es resoluble ya que, si lo fuese, existiría b 5 \ tal que
" b|
" b|
S
S
bf ' f. Como b| f para todo | ' fc c , bf f si algún
|' |
|' |
"
S
b| 9' f. Por lo tanto, b| ' f para todo | ' fc c , en cuyo caso
b| bf 9' , lo
|'
que se contradice con que b 5 \.
&252/$5,2 'DGR XQ FRQMXQWR FRQYH[R FHUUDGR D¿UPDFLRQHV VRQ HTXLYDOHQWHV
(i) HV XQ FRQMXQWR FRPSDFWR
(ii) . E HV FRPSDFWR \ *? ' ( E ' if? j (
f?
(iii)
5 ?| g E

(iv) Eg E ' U? \
9' > ODV VLJXLHQWHV
3.3 Caracterización de los símplices
93
(v) ES HV UHVROXEOH SDUD WRGR S 5 U? 'HPRVWUDFLyQ
La equivalencia entre las cuatro primeras a¿rmaciones es
consecuencia directa de la Proposición 3.2. Puesto que (i) , (v) es trivial, acabaremos
la demostración probando que (v) , (i). En efecto, si no se veri¿ca (i), entonces existe
+ 5 n , + 9' f? , y E+ no es ni siquiera acotado. Por lo tanto, tampoco se veri¿ca
(v).
&DUDFWHUL]DFLyQ GH ORV VtPSOLFHV
es a &VtPSOLFH si es la envoltura convexa de & n  puntos afínmente
independientes. Obviamente, cualquier &-símplice es compacto.
352326,&,Ï1 'DGR XQ FRQMXQWR FRQYH[R FHUUDGR D¿UPDFLRQHV VRQ HTXLYDOHQWHV
9' > ODV VLJXLHQWHV
(i) HV XQ &VtPSOLFH
(ii) . E WLHQH & n  SXQWRV H[WUHPRV _4 . E ' & \ *? ' ( E ' if? j \
f?
(iii)
5 ?| g E _4 *? dg Eo ' ? & \ HO FRQR DSXQWDGR GH g E WLHQH

& n  UD\RV H[WUHPRV
'HPRVWUDFLyQ (i) , (ii) Dado que es un conjunto convexo compacto, por el
Corolario 3.5, se tiene que *? ' ( E ' if? j y, por tanto, . E ' .
Si ' UL? % c c %&n , con % c c %&n afínmente independientes, es
obvio que % c c %&n contiene a todos los puntos extremos de . Por otra parte, si
&S
n
% , 5 ic c & n j, no fuese punto extremo de , podríamos escribir % '
b % ,
'
'
&S
n
&S
n
b ' . Entonces
b E% % ' f?n , de
b f, ' c c & n , 9' ,
'
'
'
'
modo que i% % c ' c c & n j son linealmente dependientes, lo que resulta
ser una contradicción. Así pues, los puntos extremos de son % c c %&n .
Por lo tanto, . E ' ' UL? % c c %&n tiene exactamente & n  puntos
extremos y _4 . E ' _4 ' &.
94
3. Caracterización de familias de conjuntos cerrados convexos
(ii) , (i) *? ' ( E ' if? j implica que ' . E. Si % c c %&n
es el conjunto de puntos extremos de . E ' , entonces, por el teorema de
representación, ' UL? % c c %&n . Si % c c %&n fuesen afínmente
dependientes, entonces _4 . E ' _4 @g % c c %&n & , lo que
contradice la hipótesis.
(i)
,(iii) Puesto que todo &-símplice es compacto, por el Corolario 3.5, se tiene
f?
que
5 ?| g E. Por otra parte, de acuerdo con la fórmula dimensional,

_4 *? dg Eo ' ? _4 ' ? &
(3.2)
Puesto que es un símplice de dimensión completa en la variedad afín T G' @g ,
con _4 T ' &, existen vectores no nulos
i@ , ' c c & n j T T
y correspondientes escalares
iK , ' c c & n j c
tales que i% 5 U? m @ % ' K j es un hiperplano soporte en los puntos del interior
relativo de la -ésima faceta, ' c c & n . Podemos asumir, sin pérdida de
generalidad, que @ % K para todo % 5 , ' c c & n , de modo que
' i% 5 T m @ % K c ' c c & n j Además, puesto que _4 T ' &, podemos escribir
T ' i% 5 U? m @ % ' K c ' & n 2c c ? n j c
con
@
c ' & n 2c c ? n 
K
linealmente independientes (si es un ?-símplice, entonces T ' U? y esta parte de la
prueba se puede simpli¿car).
Entonces,
@
f?
g E ' UL?i
c ' c c & n (
n
K

3.3 Caracterización de los símplices
95
@
c ' & n 2c c ? n  c
n tT@?
K
f?
y demostraremos que
se puede eliminar en esta expresión. Para ello,

apelaremos a la conocida caracterización de los puntos interiores de un cono convexo
dada en la Proposición 0.6.
f?
Puesto que
5 ?| g E, podemos escribir

[ @
f?
f?
'
b
c b : f si & n c > fc
n>

K

M U
(3.3)
para un cierto conjunto U ic c ? n j, con
@
tT@?
c 5 U ' U?n si > ' f
K
y
f?
@
c 5 U(
' U?n si > : f
tT@?
K

Si f > , de (3.3) se sigue
@
f?
@
c ' c c & n  n tT@?
c ' & n 2c c ? n  5 UL?i

K
K
(3.4)
Probaremos que el caso >  no sepuede
lo que
dar, por (3.4) se cumple siempre.
S
f?
@
b
En efecto, si > : , entonces E> 
'
5 g E y esto implica

K
MU
S
@
b
' f?n
' >. Por otra parte, si > ' , entonces de (3.3) se sigue que
K
M U
y existirá
que b : f (en otro caso U i& n 2c c ? n j y
un & n  tal @
c ' & n 2c c ? n  son linealmente dependientes). Entonces,
K
[
@
@
3

'
b b
5 g E c
K
K
MU .t
de modo que @ % ' K para todo % 5 . Por lo tanto,
@ 5 ET T _ ET T z ' if? j c
es decir, @ ' f? y esto es una contradicción.
96
3. Caracterización de familias de conjuntos cerrados convexos
De (3.4) se sigue
@
@
g E ' UL?i
c ' c c & n  n tT@?
c ' & n 2c c ? n  K
K
@
c ' & n 2c c ? n  ' ? & con (3.2), concluimos
Comparando _4 tT@?
K
que el cono apuntado de g E es
@
e
c ' c c & n  g E G' UL?i
K
@
e E, entonces
, 5 ic c & n j, no es un rayo extremo de g
Si UL?i
K
podemos escribir
[
&n @
@
'
c fc ' c c & n c 9' c
K
K
'
'
@
e E &.
e E ' UL?i
c ' c c & n c 9' y _4 g
de modo que g
K
e E n _4 *? dg Eo ? y esto contradice el hecho
Entonces _4 g E ' _4 g
de que ?| g E 9' >. Así pues,
@
UL?i
c ' c c & n 
K
e E.
es el conjunto de rayos extremos de g
f?
5 ?| g E y _4 *? dg Eo ' ? & garantizan
(iii) , (i) Las hipótesis

que es compacto y _4 ' &, respectivamente. Sea
@
UL?i
c ' c c & n 
K
e E. De acuerdo con el teorema de representación,
el conjunto de rayos extremos de g
@
e E ' UL?i
c ' c c & n  g
K
Sea
@
c ' & n 2c c ? n 
K
una base de *? dg Eo. Entonces ' i% 5 T m @ % K c ' c c & n j, donde
T ' i% 5 U? m @ % ' K c ' & n 2c c ? n j.
3.4 Caracterización de los sandwiches
97
&n
Así pues, el número de puntos extremos de es R ' &n. Asumamos
&
que R & n  y sea i% c c %R j el conjunto de puntos extremos de . El teorema de
representación establece que ' UL? i% c c %R j, de modo que _4 R &.
Por lo tanto, R ' & n  y % c c %&n es afínmente independiente (en otro caso,
_4 &). Esto completa la prueba.
&DUDFWHUL]DFLyQ GH ORV VDQGZLFKHV
Dos variedades a¿nes de la misma dimensión en U? , L y L2 , son paralelas si
L L ' L2 L2 y L _ L2 ' >. Diremos que un conjunto es un &-VDQGZLFK cuando
es la envoltura convexa de la unión de dos variedades a¿nes paralelas de dimensión
& . El siguiente resultado establece algunas propiedades elementales de los &sandwiches que se usarán más adelante.
352326,&,Ï1 6HD ' UL? EL ^ L2 GRQGH L \ L2 VRQ YDULHGDGHV D¿QHV
SDUDOHODV FRQ _4 L ' &  ' c 2 6HD T ' L L ' L2 L2 L _T z ' i% j
' c 2 \ ' %2 % (QWRQFHV VH FXPSOHQ ODV VLJXLHQWHV D¿UPDFLRQHV
(i) ' T n d% c %2 o \ SRU WDQWR HV OD VXPD GH XQ FRQMXQWR FRQYH[R FRPSDFWR FRQ
XQ VXEHVSDFLR YHFWRULDO
(ii) _4 ' &
(iii) @g ' L n tT@? ij c ' c 2
(iv) L ' i% 5 @g m E% % ' fj ' c 2 \
(v) hM_ ' L ^ L2 \ h?| ' T n o% c %2 d
'HPRVWUDFLyQ Por ser L una variedad afín paralela a T , L _ T z se reduce a un
sólo punto, por lo que % está bien de¿nido, ' c 2.
Como L ' % n T , ' c 2, y L _ L2 ' >, necesariamente % 9' %2 , es decir,
G' %2 % 9' f? .
Procedemos a la prueba:
(i) Si % 5 , podemos escribir % ' E b E% n  n b E%2 n 2 , donde
98
3. Caracterización de familias de conjuntos cerrados convexos
b 5 dfc o y  c 2 5 T . Entonces
% ' E b % n b%2 n E b  n b 2 5 % c %2 n T .
Recíprocamente, si 5 T y b 5 dfc o,
n E b % n b%2 ' E b % n n b %2 n 5 UL? EL ^ L2 ' (ii) Obviamente, para ic j ' ic 2j, se tiene
L n tT@? ij ' % n T n tT@? ij ' T n % n tT@? ij ' T n @g % c %2 c
variedad afín que contiene a L y a L2 . Así pues, si ic j ' ic 2j c
UL? L ^ % L n tT@? ij .
(3.5)
Puesto que % 5
* L y 5 T z , se sigue de (3.5)
& _4 UL? L ^ % _4 _4 dL n tT@? ijo '
' _4 dT n tT@? ijo ' &
Por lo tanto, se veri¿ca (ii).
(iii) Es consecuencia de la segunda inclusión en (3.5) y de la ecuación _4 '
_4 dL n tT@? ijo que hemos probado antes.
(iv) Dado % 5 L ' % n T , E% % ' f debido a que 5 T z .
Recíprocamente, si % 5 @g satisface que E% % ' f, entonces podemos
escribir (en virtud de (iii)) % ' % n n k, 5 T y k 5 U, con E n k '
k nn2 ' f. Esto implica que k ' f, es decir, % ' % n 5 L .
(v) Es consecuencia directa de la Proposición 0.4 aplicada a (i).
A continuación, damos tres caracterizaciones diferentes de los sandwiches basadas
en las representaciones interna, externa y cónica de los mismos. En la Sección 3.5 se
dará una caracterización topológica.
352326,&,Ï1 6HD XQ FRQMXQWR FRQYH[R FHUUDGR QR YDFtR \ VHD g E VX FRQR
GH UHIHUHQFLD /DV VLJXLHQWHV D¿UPDFLRQHV VRQ HTXLYDOHQWHV
3.4 Caracterización de los sandwiches
99
(i) HV XQ &VDQGZLFK
(ii) ( E ' if? j . E HV XQ VHJPHQWR FHUUDGR SURSLR \ _4 E*? ' & 
(iii) H[LVWH VXEHVSDFLR YHFWRULDO T E@g FRQ _4 T ' &  XQ YHFWRU QR QXOR
5 T z q dE@g oz \ GRV Q~PHURV UHDOHV k \ k2 WDOHV TXH k k2 \
' i% 5 @g m k % k2 j (iv) g E ' g n ` GRQGH g HV XQ FRQR FRQYH[R FHUUDGR \DSXQWDGR
\ ` HV XQ
f?
VXEHVSDFLR YHFWRULDO WDOHV TXH _4 g ' 2 _4 ` ' ? &
5 h?| g \

f?
f?
g _ ` n tT@?
' UL?i
(3.6)


'HPRVWUDFLyQ Probaremos (ii) / (i) , (iii) , (iv) , (i).
(ii) , (i) Si . E n ( E ' d% c %2 o, con % 9' %2 , de¿niendo L ' % n *? ,
es fácil probar que ' UL? EL ^ L2 , siendo L y L2 variedades paralelas, tales que
_4 L ' & , ' c 2.
(i) , (ii) Es consecuencia directa de la a¿rmación (i) de la Proposición 3.7.
(i) , (iii) Sea ' UL? EL ^ L2 , donde L y L2 son variedades a¿nes paralelas.
Sean T , % , %2 y de¿nidos como en la Proposición 3.7, cuyas a¿rmaciones (ii) y
(iii) demuestran que _4 T ' _4  y T T n tT@? ij ' E@g ,
respectivamente. Retomando la de¿nición de , se tiene que 5 T z q if? j y
5 E@g , por lo que 5 T z q dE@g oz .
Sean k ' % , ' c 2. Obviamente, k2 k ' nn2 : f.
Puesto que L ' i% 5 @g m % ' k j, ' c 2, de acuerdo con la a¿rmación
(iv) de la Proposición 3.7, se obtiene
' UL? EL ^ L2 ' i% 5 @g m k % k2 j (iii) , (iv) Sea _ ' _4 . Distinguiremos los casos _ ' ? y _ ?.
Supongamos que _ ' ?. Puesto que ' i% 5 U? m k % k2 j, k k2 ,
se tiene
g E ' UL?i
f?
c
c
k
k2

100
3. Caracterización de familias de conjuntos cerrados convexos
Además,
f?

de modo que g E ' UL?i
f?
5 h?| g E.

n
c
k
k2

'
k2 k
c
y la Proposición 0.6 establece que
k
k2
Es más, puesto que k 9' k2 ,
y
son linealmente independientes y
k2
k
g E es un cono apuntado bidimensional.
Acabaremos esta parte de la demostración probando que g E ' g Enif?n j
es la descomposición deseada. En efecto, si
5 5 g E _ tT@?
se puede escribir
f?
c

f?
, 4 f, 42 f, 5 Uc
n 42
'

k
k2
5 ' 4
lo que implica que 4 ' 42 y ' 4 Ek2 k f, de modo que 5 5 UL?i
Esto prueba que
g E _ tT@?
f?

f?
.

UL?i
f?
c

mientras que la inclusión opuesta se cumple trivialmente. Por lo tanto, se veri¿ca (3.6).
Supongamos ahora que _ ?. Sea
@g ' i% 5 U? m @ % ' K , ' c c ? _j c
con i@ , ' c c ? _j un subconjunto linealmente independiente de U? y K 5 U,
' c c ? _.
Puesto que ' i% 5 @g m k % k2 j, se tiene ahora
@
f?
g E ' UL?i c ' c c ? _(
c
c
'
K
k
k2

@
f?
' tT@?
c ' c c ? _ n UL?i
c
c
K
k
k2

3.4 Caracterización de los sandwiches
Sea
101
@
` G' tT@?
c ' c c ? _
K
y
f?
c
c
k2
k

g G' UL?i
` es un subespacio vectorial de U?n , con _4 ` ' ? _, y g (el mismo cono
que
en
el caso _ ' ?) es un cono convexo cerrado y apuntado, con _4 g ' 2 y
f?
5 h?| g. Además, es obvio que

f?
f?
f?
g _ tT@?
g _ ` n tT@?
(3.7)
UL?i



f?
Consideremos ahora 5 5 g _ ` n tT@?
arbitrario. Podemos

escribir
[
?3_ @
f?
5 ' 4
q
c
(3.8)
n 42
'
n
K

k
k2
'
con 4 f, 42 f, q 5 U, ' c c ? _, y 5 U. De (3.8), se deduce
E42 4 n
?3_
[
'
q @ ' f? c
siendo i( @ c ' c c ? _j un conjunto de vectores linealmente independientes,
debido a que 9' f? y
5
* dE@g oz ' tT@? i@ c ' c c ? _j Por lo tanto, 4 ' 42 y q ' f, ' c c ? _, de modo que (3.8) se convierte
en
f?
'
5 ' 4

f?
f?
y se llega a que ' 4 Ek2 k f. Así pues, 5 ' 5 UL?i
.


f?
k k2
Hemos probado que
f?
f?
g _ ` n tT@?
UL?i
c


102
3. Caracterización de familias de conjuntos cerrados convexos
que junto con (3.7) demuestra que se veri¿ca (3.6).
(iv) , (i) Cualquier cono convexo cerrado apuntado bidimensional es la envoltura
convexa cónica de dos
direcciones
extremas
(es
decir,
un ángulo agudo plano).
@
K
@
K
Sea g ' UL?i
c
, donde
c
es un conjunto linealmente
k
q
k
q
f?
?
n
independiente en U . Puesto que estamos asumiendo que
5 h?| g, podemos

escribir (por la Proposición 0.6),
@
K
f?
n 42
c 4 : fc 42 : fc
' 4
(3.9)

k
q
@
K
de modo que @ 9' f? (en otro caso @ ' K ' f? y
c
es linealmente
k
q
dependiente).
De¿niendo ' 4 @ 9' f? y ' 4 k, se obtiene de (3.9)
g ' UL?i
c

@
c ' c c ? _ una base de ` , con _ ' _4 .
Sea
k
Dado que estamos suponiendo que g E ' g n ` , se tiene
@
c ' c c ? _(
c
c
g E ' UL?i 
k
de modo que
' i% 5 U? m @ % ' k c ' c c ? _( % n j (3.10)
Sean  ' , 2 ' n  y
L ' % 5 U? m @ % ' k c ' c c ? _( % ' c ' c 2
Probaremos que L 9' >, ' c 2.
Si L ' >,
f?
@
5 g EL ' tT@?
c ' c c ? _(

k
y podemos escribir
[
?3_ f?
@
'
q
n qf
c q 5 Uc ' fc c ? _,

k
'
(3.11)
3.5 Caracterización topológica de los &-sandwiches
f?
5 ` n tT@?
de donde se deduce que q f
.

f?
5 ` n tT@?
Si q f : f, entonces
. Si ' ,

f?
f?
5 g _ ` n tT@?
' UL?i
c



103
de acuerdo con (3.6), contradiciendo que 9' f? . Alternativamente, si ' 2, entonces
f?
f?
5 g _ ` n tT@?
' UL?i
c
2


y obtenemos otra vez que ' f? .
Si q f f, se obtiene ' f? del mismo modo.
Finalmente, si q f ' f, (3.11) implica que i@ % ' k c ' c c ? _j es
inconsistente, en contradicción con (3.10) (ya que 9' >).
Se concluye que L y L2 son variedades a¿nes paralelas y se puede demostrar
fácilmente que ' UL? EL ^ L2 .
Esto completa la demostración.
&DUDFWHUL]DFLyQ WRSROyJLFD GH ORV &VDQGZLFKHV
Por la a¿rmación (v) de la Proposición 3.7, está claro que la frontera relativa
de cualquier &-sandwich no es ni siquiera conexa.
En la siguiente proposición
demostraremos que la no conexión de la frontera relativa es, en realidad, una propiedad
que caracteriza a los &-sandwiches.
352326,&,Ï1 6HD XQ FRQMXQWR FRQYH[R FHUUDGR QR YDFtR GH U? TXH QR HV XQD
YDULHGDG DItQ FRQ _4 ' & (QWRQFHV ODV VLJXLHQWHV D¿UPDFLRQHV VRQ HTXLYDOHQWHV
(i) hM_ HV QR FRQH[D
(ii) hM_ HV QR FRQH[D SRU DUFRV \
(iii) HV XQ &VDQGZLFK
'HPRVWUDFLyQ (i) , (ii) Es trivial.
104
3. Caracterización de familias de conjuntos cerrados convexos
(ii) , (iii) Supongamos, en primer lugar, que tiene dimensión completa. Así
pues, la hipótesis será que M_ no es conexa por arcos.
Si ? ' , puesto que _4 '  y 9' U, será o una semirrecta cerrada (lo cual
es imposible porque cualquier conjunto singular es conexo por arcos) o un segmento
cerrado propio de U. Por lo tanto, es un sandwich unidimensional.
Así pues, podemos suponer sin pérdida de generalidad que ? 2.
Sean % 5 M_ , ' c 2, puntos que no se pueden conectar por medio de ninguna
curva enteramente contenida en M_ .
Sean S 9' f? , tales que
S % % f para todo % 5 c ' c 2
(3.12)
Denotaremos por
M G' % 5 U? m S % % ' f c ' c 2c
los correspondientes hiperplanos soporte de . Probaremos que M _ M2 ' > por
reducción al absurdo. Así pues, sea 5 5 M _ M2 .
Para ic j ' ic 2j, puesto que 5 5 M y % 5 , se tiene
S 5 % ' S 5 % n % % ' S % % f
Si S E5 % ' f entonces % 5 M (ya que 5 5 M ), de modo que
% c % _ M M_ (ya que M es hiperplano soporte de ), y esto contradice la hipótesis acerca de % y
%2 . Por lo tanto,
S 5 % f si ic j ' ic 2j (3.13)
Consideremos ahora el vector ' 25 E% n %2 . De (3.13), se obtiene
S ' S 5 % n S 5 % f, si ic j ' ic 2j De (3.12) y (3.14) se deduce que, para ' c 2, S es solución del sistema
+ f( + % % fc % 5 (3.14)
3.5 Caracterización topológica de los &-sandwiches
105
y, por la Proposición 2.4, esto implica que % 5 i?_ E( , ' c 2. Entonces,
podemos aplicar la Proposición 2.21 para obtener la deseada contradicción.
Así pues, hemos probado que M _ M2 ' >, de modo que tT@? iS j ' tT@? iS2 j.
Probaremos, a continuación, que ' UL? EM ^ M2 .
* M2 y %2 5
* M (en caso contrario M _ M2 9' >), S2 E% %2 : f
Puesto que % 5
y S E% %2 f, de modo que S2 es un múltiplo negativo de S y podemos escribir
M ' i% 5 U? m S % ' k j, ' c 2, donde S 9' f? , S % ' k , ' c 2, y k k2 .
Puesto que M es un hiperplano soporte de en % , ' c 2, se tiene
i% 5 U? m k S % k2 j ' UL? EM ^ M2 (3.15)
Para probar la inclusión opuesta, consideremos un vector arbitrario
5 T G' M M ' M2 M2 Si 5
* n , existen números reales no negativos
b G' 4@
| 5 U m % n | 5 c ' c 2c
y % n b 5 i?_ E( , ' c 2.
Entonces, por una parte, d% c % n b o _ M M_ , ' c 2, y por otra,
existe un arco conectando % n b con %2 n b2 que está completamente contenido
en M_ (de nuevo por la Proposición 2.21), y esto signi¿ca que % se puede conectar
con %2 por medio de un arco contenido en M_ , compuesto por tres arcos conectados.
Esto es una contradicción, de modo que T n .
Así pues, M ' % n T n n ' , ' c 2, y se obtiene
UL? EM ^ M2 (3.16)
De (3.15) y (3.16), se concluye que ' UL? EM ^ M2 es un sandwich de
dimensión completa.
Supongamos ahora que & ?. Entonces es un conjunto convexo cerrado de
dimensión completa, en @g , tal que su frontera, en la topología de @g , no es
conexa por arcos. Aplicando el argumento previo, es de nuevo un sandwich de
dimensión completa en @g , es decir, un &-sandwich.
106
3. Caracterización de familias de conjuntos cerrados convexos
(iii) , (i) Es consecuencia directa de la a¿rmación (v) de la Proposición
3.7.
En la Proposición 2.23, se estableció como condición su¿ciente para la conexión
por arcos de la frontera relativa de un conjunto convexo no vacío de dimensión mayor
o igual que 2, la compacidad de dicho conjunto. Sin embargo, sólo hay que considerar
el caso en el que sea un semiespacio para ver que no es una condición necesaria.
Quedaba pendiente, por tanto, el estudio de la conexión por arcos de la frontera relativa
de los conjuntos convexos cerrados no vacíos de dimensión 1 y los de dimensión mayor
o igual que 2 no acotados, cuestión que queda resuelta en la Proposición 3.9.
&DUDFWHUL]DFLyQ GH ORV SDUDOHORWRSRV
Un SDUDOHORWRSR se puede de¿nir como la intersección de una familia de ? ??
sandwiches ”independientes”, es decir, un conjunto de la forma ' _ , con
'
' i% 5 U? m k @ % q j, k q para ' c c ?, y i@ c ' c c ?j
linealmente independientes. En la siguiente proposición se caracteriza esta familia de
conjuntos en términos de sus representaciones interna y cónica.
352326,&,Ï1 6HD XQ FRQMXQWR FRQYH[R FHUUDGR QR YDFtR GH U? (QWRQFHV
ODV VLJXLHQWHV D¿UPDFLRQHV VRQ HTXLYDOHQWHV
(i) HV XQ SDUDOHORWRSR
(ii) . E HV XQ SROtWRSR GH GLPHQVLyQ ? FRQ 2? IDFHWDV SDUDOHODV GRV D GRV \
*? ' ( E ' if? j \
(iii) H[LVWH XQD EDVH GH U? i@ c ' c c ?j \ GRV FRQMXQWRV GH HVFDODUHV
ik c ' c c ?j \ iq c ' c c ?j FRQ k q SDUD WRGR ' c c ? WDOHV TXH
@
@
f?
g E ' UL?i
c ' c c ?( c ' c c ?(
k
q

'HPRVWUDFLyQ (i) , (ii) Sea un paralelotopo, es decir,
' i% 5 U? m k @ % q c ' c c ?j c
3.6 Caracterización de los paralelotopos
107
con k q para ' c c ? y i@ c ' c c ?j linealmente independientes.
Entonces, denotando por j el sistema ¿nito ik @ % q c ' c c ?j que
representa a , el primer cono de momentos de j resulta ser
 ' UL?i i@ c ' c c ?j ' tT@? i@ c ' c c ?j ' U?
y, por la Proposición 0.19, es acotado.
Así pues, es un conjunto convexo compacto por lo que, aplicando el Corolario
3.5, se tiene
*? ' ( E ' if? j
y, en consecuencia,
. E ' ' i% 5 U? m k @ % q c ' c c ?j c
que es un polítopo por ser intersección de un número ¿nito de semiespacios cerrados
y ser acotado.
Por otra parte, como j es un sistema LFM no trivial, de acuerdo con la Proposición
0.17, _4 ' ? si, y sólo si, ninguna combinación convexa de desigualdades no
triviales de j da lugar a la desigualdad trivial. Por reducción al absurdo, supongamos
que
[
?
@
@
f?n '
b
>
c
k
q
'
'
?
S
con b c > 5 dfc o para todo ' c c ? y
Eb n > ' . Entonces, podemos
?
[
escribir
'
?
[
f? '
Eb > @
'
(3.17)
y
f'
?
[
'
b k > q (3.18)
Puesto que i@ c ' c c ?j son linealmente independientes, de (3.17) se deduce
108
3. Caracterización de familias de conjuntos cerrados convexos
que b ' > para todo ' c c ? y, sustituyendo en (3.18), obtenemos
f'
?
[
'
b Ek q Al ser k q f para todo ' c c ?, se tiene que b ' > ' f para todo
?
S
Eb n > ' .
' c c ?, lo cual se contradice con
'
Así pues, . E es un polítopo de dimensión ? representado linealmente por el
sistema j. De acuerdo con la Proposición 0.20 (ii), las facetas de deben ser de
la forma i% 5 m @ % ' k j o i% 5 m @ % ' q j, con 5 ic c ?j. Por otra
parte, si demostramos que j es una representación minimal de (es decir no tiene
restricciones redundantes), por el apartado (iii) de la misma proposición, se obtiene
que ' i% 5 m @ % ' k j y ' i% 5 m @ % ' q j, ' c c ?, son las 2?
facetas, paralelas dos a dos, de .
Supongamos, pues, que @ % k , 5 ic c ?j, es redundante en j (se haría
del mismo modo para @ % q ). Entonces, por el Lema de Farkas,
@
@
@
f?
c
5 UL?i
c ' c c ?c 9' ( c ' c c ?(
k
k
q

es decir, existen escalares b f, '  c ?, 9' , > f, '  c ? y 4 f
tales que
[
[
?
?
@
@
f?
@
b
>
'
n4
c
k
k
q

'
'
'
de donde se obtiene
?
[
f? '
'
'
Eb > @ > n  @ Entonces, por ser i@ c ' c c ?j linealmente independientes, b > ' f,
'  c ?, 9' , y > n  ' f, lo que se contradice con > f.
(ii) , (i) Por hipótesis, ' . E es un polítopo de dimensión ? con 2? facetas
paralelas dos a dos. Sean i c c ? c  c c ? j las 2? facetas y supongamos que
y son paralelas para todo ' c c ?.
Por ser un polítopo, siempre podemos encontrar una representación lineal ¿nita
3.6 Caracterización de los paralelotopos
109
minimal para . Sea
j ' @ % K c ' c c R
dicha representación. Por la Proposición 0.20 (iii), los conjuntos % 5 m @ % ' K ,
' c c R, son las facetas de , por lo que R ' 2?.
Reordenando si es
preciso las inecuaciones de j, podemos suponer que ' i% 5 m @ % ' K j y
' % 5 m @n? % ' Kn? , ' c c ?. Dado 5 ic c ?j y puesto que
y son paralelos, se tiene @ n? ' b @ para algún b 9' f, en cuyo caso podemos
escribir
@ n?
K n?
f?
@
' b
n EK n? b K K

Por lo tanto, si fuese b : f, entonces @ n? % K n? es consecuencia de @ % K
si K n? b K f (Lema de Farkas) y @ % K es consecuencia de @ n? % K n? si
K n? b K f. En ambos casos j no es minimal.
K n?
si, y sólo si, % 5 . Si denotamos k G' K y
Así pues, b f y K @ % b
K n?
q G'
, se tiene k @ % q si, y sólo si, % 5 .
b
Así pues,
' i% 5 U? m k @ % q c ' c c ?j .
Desde luego, k q para todo ' c c ?, puesto que _4 ' ?.
Por otra parte, i@ c ' c c ?j son linealmente independientes ya que, en caso
contrario,
 ' UL?i i@ c ' c c ?j ' tT@? i@ c ' c c ?j 9' U?
y, por la Proposición 0.19, no sería acotado y, por lo tanto, no sería un polítopo.
(i) / (iii) Se obtiene de forma inmediata aplicando la de¿nición de cono de
referencia y teniendo en cuenta que los conos ¿nitamente generados son cerrados.
110
3. Caracterización de familias de conjuntos cerrados convexos
&DUDFWHUL]DFLyQ GH FRQMXQWRV FRQWLQXRV
Un conjunto convexo cerrado no vacío es FRQWLQXR cuando su correspondiente
función soporte, B E m de¿nida por
W
B E% m ' tT i% + m + 5 j ,
W
es continua en U? q if? j.
B E m es una función convexa y _L4 B E m ' U? si es compacto (véase
W
W
[32, Th. 5.5]). Por lo tanto, cualquier conjunto compacto es continuo (las funciones
convexas son continuas en el interior de su dominio).
Esta clase de conjuntos fue introducida por Gale y Klee en 1959 en un artículo [15]
en el que dan algunas caracterizaciones geométricas de estos conjuntos. En particular,
la primera de ellas establece que un conjunto convexo cerrado de U? es continuo si,
y sólo si, no tiene ni rayos frontera ni asíntotas. Esta caracterización muestra que el
epigrafo de una función cuadrática estrictamente convexa (por ejemplo, %2 ' %2 ) es
continuo, a pesar de no ser acotado. Por lo tanto, todo conjunto convexo compacto es
continuo, pero no todo conjunto continuo es compacto.
Los conjuntos convexos compactos tienen importantes propiedades que no
cumplen, en general, los conjuntos convexos cerrados no acotados. Por ejemplo, si
es un conjunto convexo compacto no vacío y ( es cualquier convexo cerrado no
vacío, se cumple que n ( es cerrado y que y ( pueden separarse fuertemente en
caso de ser y ( disjuntos. En [15] se demuestra que cada una de estas propiedades
caracteriza a la familia de los conjuntos continuos, por lo que ésta es la clase maximal
de conjuntos que poseen dichas propiedades.
Por otra parte, se demostró en el Corolario 3.5 que un conjunto convexo cerrado
no vacío es compacto si, y sólo si, el problema ES W?u S % s.a. % 5 es
resoluble para todo S 5 U? y, en ese caso, su conjunto óptimo también es compacto.
La condición análoga que caracteriza a la familia de los conjuntos continuos en general
es la que damos en la siguiente proposición.
352326,&,Ï1 >4 3UR
@ 6HD XQ FRQMXQWR FRQYH[R FHUUDGR QR YDFtR
(QWRQFHV HV FRQWLQXR VL \ VyOR VL HO FRQMXQWR ySWLPR GH FXDOTXLHU SUREOHPD DFRWDGR
3.7 Caracterización de conjuntos continuos
111
ES S 9' f? HV XQ FRPSDFWR QR YDFtR
La condición de la Proposición 3.11 garantiza la anulación del salto de dualidad
para todo S 5 U? (si S ' f? o ES ' 4 la a¿rmación es trivial, mientras que si
S 9' f? y ES : 4, la conclusión se obtiene de la Proposición 3.11 y de [19, Th.
8.1]). Sin embargo, aunque la proposición
“Si ES, S 9' f? , es acotado entonces ES es resoluble y B ES ' f”
se cumple tanto para la familia de los conjuntos continuos como para la de
las sumas de compactos con subespacios vectoriales (Corolario 3.3), ésta no
caracteriza a la unión de ambas familias (basta considerar el semiespacio cerrado
' i% 5 U2 m % n %2 fj y el único problema, con conjunto factible , que es
acotado: W?u E% n %2 s.a. % 5 ).
En esta sección, obtendremos una caracterización de los conjuntos continuos en
términos de su cono de referencia, pero para ello será necesario probar previamente
dos lemas.
/(0$ 'DGRV GRV FRQMXQWRV FRQYH[RV FHUUDGRV QR YDFtRV  \ 2 ODV VLJXLHQWHV
D¿UPDFLRQHV VRQ HTXLYDOHQWHV
(i)  _ 2 9' >
(ii) g E n g E2 HVWi FRQWHQLGR HQ HO KLSRJUDIR GH XQD IXQFLyQ OLQHDO \
f?
5
* U* ig E n g E2 j
(iii)

'HPRVWUDFLyQ (i) , (ii) Sea % 5  _ 2 arbitrario.
Dado que
@
5 g E @ % Kc
K
@
f para todo
K
%

es una representación lineal de , ' c 2, se cumple
@
%
5 g E ^ g E2 . Por lo tanto,
5 f para todo 5 5 g E n g E2 K

y g E n g E2 está contenido en el hipografo de la función lineal s E% ' % %.
(ii) , (iii) La hipótesis implica que U* ig E n g E2 j está contenido en
112
3. Caracterización de familias de conjuntos cerrados convexos
f?
el hipografo (cerrado) de una función lineal s E% ' @ %. Si fallase (iii),

pertenecería a dicho hipografo, por lo que  @ f? , lo cual es imposible.
(iii) , (i) Por la Proposición 1.2 (ii.a), la hipótesis implica la consistencia del
sistema
@
5 g E ^ g E2 c
@ % Kc
K
(3.19)
ya que su cono de referencia es
f?
U* UL?i g E ^ g E2 ^
' U* ig E n g E2 j c

de acuerdo con la Proposición 0.1. Se llega a la conclusión observando que (3.19) es
una representación lineal de  _ 2 .
/(0$ 6HDQ  \ 2 GRV FRQMXQWRV FRQYH[RV FHUUDGRV QR YDFtRV  \ 2 VRQ
?n
IXHUWHPHQWH
VHSDUDEOHV VL \ VyOR VL H[LVWH XQ VXEHVSDFLR YHFWRULDO GH U ` WDO
f?
TXH
5 ` _4 ` ' 2 \ U* i` q dg E ^ g E2 oj HV XQ FRQR DSXQWDGR

'HPRVWUDFLyQ Sean  y 2 fuertemente separables y sea @ 9' f? tal que
tT i@ % m % 5  j ?u i@ + m + 5 2 j.
Sean k G' tT i@ % m % 5  j y q G' ?u i@ + m + 5 2 j. Como @ % k para
todo % 5  y @ + q para todo + 5 2 , se tiene
@
@
5 g E +
5 g E2 k
q
f?
@
f?
Sea ` G' tT@?
c
. Obviamente,
5 ` \ _4 ` ' 2.


f
Probaremos que
@
f?
@
f?
c
^ UL?i c
` _ g E2 UL?i
q

k

@
En efecto, sea
5 ` _ g E2 , con c B 5 U. Se pueden dar los siguientes
B
casos:
@
(i) Si : f,
5 g E2 , por lo que @ +  B para todo + 5 2 y  B q.
B
Entonces
f?
@
@
@
f?
'
n q B
5 UL?i
c
B
q

q

3
3
3
(ii) Si ' f,
@
B
3.7 Caracterización de conjuntos continuos
113
f?
'
5 g E2 , debiendo ser B f puesto que 2 9' >.
B
Entonces,
@
f?
@
f?
' EB
5 UL?i
c

q

B
@
@
son
(iii) Si f y k B, al ser k q, q k B y, como
y mm
q
B
elementos de g E2 , tendríamos
 @
@
f?
n
' B q
5 g E2 c

B
q
3
en contradicción con 2 9' >. Por lo tanto, para f, se cumple k B f y
@
f?
@
@
f?
n Ek B
5 UL?i c
' mm

k

B
k
Se cumple, pues, la doble inclusión
f?
@
c
` _ g E2 UL?i
q

f?
@
f?
@
c
^ UL?i c
UL?i
q

k

(3.20)
De forma semejante, se demuestra que
@
f?
UL?i c
` _ g E k

@
f?
@
f?
UL?i
c
^ UL?i c
q

k

(3.21)
De (3.20) y (3.21) se deduce que
@
f?
@
f?
` _ dg E ^ g E2 o ' UL?i
c
^ UL?i c
c
q

k

de donde (véase Figura 3.1)
@
@
c
(3.22)
U* i` q dg E ^ g E2 oj ' UL?i
q
k
@
@
Si
c
fuesen linealmente dependientes, sería posible escribir
q k
@
@
' b
, con b 5 U. Entonces, b '  y q ' k, en contradicción con
q
k
k q. Como el cono convexo generado por dos vectores linealmente independientes
114
3. Caracterización de familias de conjuntos cerrados convexos
β
D
D
−α
:∩[.(&1)∪.(&2)]
)LJXUD es siempre apuntado, (3.22) es un cono apuntado.
f?
Recíprocamente, si ` es un subespacio vectorial de U n tal que
5 `

_4 ` ' 2 \ U* i` q dg E ^ g E2 oj es un cono apuntado, podemos escribir
?
(3.22) para un vector @ 9' f? y dos escalares k y q tales que k q.
@
@
Dado que y
pertenecen a la unión de g E y g E2 , deberán
k
q
@
@
5 g E2 . Si 5 g E2 ,
pertenecer a uno de dichos conos. Supongamos
q
k
entonces

@
@
f?
' qk
5 g E2 
q
k
@
contradiciendo 2 9' >. Supondremos, por lo tanto, 5 g E k
De acuerdo con el Teorema de Farkas, se tiene, para % 5  e + 5 2 cualesquiera,
3
@ % k y @ + q. Por lo tanto,
tT i@ % m % 5  j k q ?u i@ + m + 5 2 j c
estando  y 2 fuertemente separados.
352326,&,Ï1 6HD XQ FRQMXQWR FRQYH[R FHUUDGR QR YDFtR
HV FRQWLQXR VL
\ VyOR VL SDUD WRGR FRQR FRQYH[R FHUUDGR g TXH FRQWLHQH D
f?
QR FRQWLHQH D

3.8 Caracterización de cuerpos convexos suaves
115
f?
f?
\ WDO TXH
5 U* ig E n gj H[LVWH XQ VXEHVSDFLR YHFWRULDO GH U?n `  
f?
5 ` \ _4 ` ' 2 WDO TXH U* i` q dg E ^ goj HV XQ FRQR DSXQWDGR
FRQ

'HPRVWUDFLyQ Se sabe que los conos de referencia delos cerrados
convexos no
f?
vacíos son los conos cerrados convexos que contienen a
pero no contienen

f?
. También se sabe [15] que  ' es continuo si, y sólo si, cualquier
a

otro conjunto cerrado convexo no vacío, 2 , disjunto con  puede ser separado
fuertemente de  . Se llega a la conclusión combinando estos resultados con los Lemas
3.12 y 3.13.
&DUDFWHUL]DFLyQ GH FXHUSRV FRQYH[RV VXDYHV
Dado un conjunto convexo cerrado no vacío , se dice que un SXQWR de M_ es VXDYH en cuando existe un único hiperplano soporte de en dicho punto. Un
FRQMXQWR convexo cerrado 9' U? es VXDYH cuando todos sus puntos frontera son
suaves en .
Si _4 ? y no es una variedad afín, entonces hM_ 9' > y no hay puntos de
hM_ que sean suaves. Si es variedad afín, es suave si, y sólo si, _4 ' ? .
Así pues, los conjuntos suaves son cuerpos convexos o hiperplanos. Dado que
estos últimos carecen de interés, se re¿eren a FXHUSRV FRQYH[RV VXDYHV Felcyn [13] y
Bezdek [7] en artículos sobre combinatoria geométrica. El concepto de punto suave
aparece en Valentine [36] para cuerpos convexos. La de¿nición de otros autores es más
exigente, imponiendo, por ejemplo, que M_ sea una variedad diferenciable de orden
R  (véase, por ejemplo, [22]).
Como se apunta en [36], la diferenciabilidad de las funciones convexas está
conectada con la suavidad de su epigrafo. En efecto, si s G U? $ U^ in4j es
una función convexa y iT s es suave (en cuyo caso es cuerpo convexo, porque los
únicos hiperplanos que pueden ser epigrafo son los verticales y entonces la imagen
de cierta recta de U? debería ser 4), entonces, para cada % 5 _L4 s , existe un
116
3. Caracterización de familias de conjuntos cerrados convexos
%
único hiperplano que soporta a iT s en
y, si dicho hiperplano es no vertical,
s E%
entonces tiene asociado un subgradiente de s en %. Por lo tanto, si iT s es suave,
la diferenciabilidad y la subdiferenciabilidad de s en un punto de _L4 s resultan ser
conceptos equivalentes y, en particular, s es diferenciable en h?| E_L4 s [32, Th.
23.4].
La siguiente proposición caracteriza los puntos suaves de un conjunto convexo
cerrado en función de su cono de referencia.
352326,&,Ï1 6HD XQ FRQMXQWR FRQYH[R FHUUDGR (QWRQFHV % 5 M_ HV XQ
SXQWR VXDYH GH VL \ VyOR VL HO FRQR FRQYH[R
@
?
@5U m
5 g E
(3.23)
@%
WLHQH GLPHQVLyQ (Q SDUWLFXODU VL HV XQ FXHUSR FRQYH[R % HV VXDYH VL \ VyOR VL HO
FRQMXQWR GH HV XQ UD\R
'HPRVWUDFLyQ Sea % 5 M_ un punto suavede y sea h
@ 9' f? tal que h
@%h
@%
h
@
para todo % 5 . Por el Lema de Farkas,
5 g E, es decir, h
@ pertenece al
h
@%
conjunto (3.23),
cuya dimensión es al menos 1.
@
Dado
5 g E, tenemos @ % @ % para todo % 5 (de nuevo por el Lema
@%
de Farkas) y se cumple
i% 5 U? m @ E% % ' fj ' i% 5 U? m h
@ E% % ' fj c
de donde @ ' kh
@ para cierto k 9' f. Entonces
@
?
5 g E tT@? ih
@j c
@5U m
@%
y
@
?
_4 @ 5 U m
5 g E ' 
@%
(3.24)
Supongamos ahora que % 5 M_ satisface (3.24), y sea h
@ '
9 f? un
elemento
@
de (3.23). Si @ % @ % para todo % 5 , con @ 9' f? , entonces
5 g E
@%
y, por la hipótesis, puede escribirse @ ' kh
@ para cierto k 9' f, en cuyo caso
i% 5 U? m @ E% % ' fj ' i% 5 U? m h
@ E% % ' fj. Por lo tanto, % es punto
suave de .
3.8 Caracterización de cuerpos convexos suaves
117
Supongamos ahora que es un cuerpo convexo y % 5 M_ es un punto suave o,
lo que es lo mismo, satisface (3.24).
% 5 ?| arbitrariamente,
Sea h
@ 9' f? un elemento de (3.23). Entonces,
tomando
@
se tiene h
@ E% % : f y @ E% % : f si
5 g E, lo que implica, junto
@%
con (3.24), que @ ' kh
@ para cierto k : f. Así pues,
@
?
UL?i ih
@j @ 5 U m
5 g E UL?i ih
@j @%
@
?
Por lo tanto, @ 5 U m
5 g E ' UL?i ih
@j es un rayo.
@%
Obsérvese que, si es un hiperplano, entonces el conjunto de (3.23) es una recta
por el origen f? .
&252/$5,2 8Q FRQMXQWR FRQYH[R FHUUDGR QR YDFtR FXHUSR FRQYH[R HV
VXDYH VL \ VyOR VL HO FRQMXQWR GH WLHQH GLPHQVLyQ HV XQ UD\R UHVSHFWLYDPHQWH
HQ WRGRV ORV SXQWRV GH M_ Este resultado caracteriza a los cerrados convexos suaves (cuerpos convexos
suaves) en función de su representación cónica.
Por otra parte, si j ' i@| % K| c | 5 A j es una representación LFM de (cuya
existencia garantiza [19, Th. 5.11]), el conjunto de (3.23) coincide con E% para
todo % 5 (por [19, (5.18)]) y, por lo tanto, % 5 M_ es suave si, y sólo si,
_4 E% ' . Obviamente, como consecuencia de esta a¿rmación, se puede obtener
una caracterización de los cerrados convexos suaves (cuerpos convexos suaves) en
relación con cualquier representación externa que sea LFM.
A continuación, nos proponemos caracterizar estos conjuntos en función de su
representación interna. Con tal ¿n relajaremos el concepto de conjunto suave para que
no implique dimensión máxima.
Si es un conjunto convexo cerrado que no es variedad afín y _ ' _4 , se
dice que un punto % 5 hM_ es UHODWLYDPHQWH VXDYH en si existe una única variedad
afín T @g , _4 T ' _ , tal que % 5 T y está contenido en una de las dos
componentes conexas de E@g qT . Decimos que es UHODWLYDPHQWH VXDYH cuando
todos los puntos de hM_ son relativamente suaves en .
118
3. Caracterización de familias de conjuntos cerrados convexos
352326,&,Ï1 6HD XQ FRQMXQWR FRQYH[R FHUUDGR TXH QR HV YDULHGDG DItQ
% 5 hM_ HV UHODWLYDPHQWH VXDYH HQ VL \ VyOR VL HO FRQR FRQYH[R
@
@ 5 E@g m
5 g E
@%
HV XQ UD\R
(3.25)
'HPRVWUDFLyQ Si _ ' ?, entonces es un cuerpo convexo, hM_ ' M_ y
E@g ' U? , por lo que los conjuntos de (3.25) y de (3.23) coinciden.
h G' n `
Suponemos, pues, _ ?. Sean ` G' dE@g o 9' if? j y z
(cuerpo convexo). Entonces, como se vió en la demostración de la Proposición 2.9(ii),
h Probaremos que % 5 hM_ es relativamente suave en si, y sólo si,
hM_ M_ .
h es suave en .
h
% 5 M_ En efecto, si T @g , con _4 T ' _ , es la única variedad afín tal que
% 5 T y está contenido en una de las dos componentes conexas de E@g qT ,
considerando M G' T n ` , se tiene _4 M ' _4 T n _4 ` ' ? , % 5 M y
h está contenido en uno de los semiespacios determinados por M (aquel que contenga
a la componente conexa de E@g qT que contiene a ), por lo que M es el único
h en % 5 M_ .
h Recíprocamente, si M es el único hiperplano
hiperplano que soporta a h en % 5 hM_ M_ ,
h tomando la variedad afín T G' M _ @g ,
que soporta a resulta que T @g , % 5 T , _4 T ' _  (ya que M ' T n ` ), está contenido
en una de las dos componentes conexas de E@g qT y además T es la única variedad
afín que cumple todas estas propiedades.
Sea @ 9' f? la dirección del hiperplano M y supongamos que @ E% % f
h Entonces, tomando % ' % n b, 5 ` ¿jo y b 5 U, debe
para todo % 5 .
cumplirse b E@ f para todo b 5 U, y esto sólo es posible si @ ' f. Por lo tanto,
@ 5 ` ' E@g .
z
Así pues, % es relativamente suave en si, y sólo si, existe un único vector (salvo
factor multiplicativo positivo) @ 5 E@g , @ 9' f? , tal que
@ E% % f para
@
todo % 5 , pudiendo sustituirse esta última condición por
5 g E como
@%
consecuencia de Lema de Farkas. Por lo tanto, (3.25) está formado por los múltiplos
positivos de dicho @ y por f? .
3.8 Caracterización de cuerpos convexos suaves
119
&252/$5,2 6HD XQ FRQMXQWR FRQYH[R FHUUDGR QR YDFtR TXH QR HV YDULHGDG
DItQ HV UHODWLYDPHQWH VXDYH VL \ VyOR VL HO FRQMXQWR GH HV XQ UD\R FXDOTXLHUD
TXH VHD % 5 hM_ 352326,&,Ï1 8Q FXHUSR FRQYH[R HV VXDYH VL \ VyOR VL . E n ( E HV
UHODWLYDPHQWH VXDYH
'HPRVWUDFLyQ Sea f G' . E n ( E, conjunto convexo cerrado no vacío.
Sabemos que ' f n *? . Repitiendo el argumento de la Proposición 3.17, con
` ' *? , es suave si, y sólo si, f es relativamente suave.
Obsérvese que si . E es relativamente suave y ( E ' if? j se cumple la
condición de la Proposición 3.19. Sin embargo, como se puede ver en el siguiente
ejemplo, el recíproco no es cierto.
(-(03/2 Sea ' i% 5 U m % %2 j el cilindro parabólico de la Figura 3.2.
25
20
15
10
5
0
-4
-4
-2
-2
0
0
2
2
4
4
)LJXUD ;3 4<
? f @
En este caso, *? ' tT@? C  D , . E '
= f >
;3 4<
? f @
( E ' UL?i C f D . Se observa que es suave,
=  >
es relativamente suave, pero ( E 9' if j.
;3
?
C
=
<
4
%
@
f D m % %2 y
>
%
. E n ( E ' . E
A pesar de lo visto anteriormente, no basta con que . E sea relativamente suave
para que el cuerpo convexo sea suave.
120
3. Caracterización de familias de conjuntos cerrados convexos
;3 4<
? f @
(-(03/2 Sea ' EU* 2 ifj n UL?i C f D el cono truncado de la
=  >
Figura 3.3.
&
(&
)LJXUD no es suave por no serlo los puntos de la circunferencia de
la base,
;3
4<a pesar de
? f @
que la base, . E, es relativamente suave. Aquí, ( E ' UL?i C f D .
=  >
Tampoco es cierto que suave implique que . E sea relativamente suave.
ULt |

(-(03/2 Sea ' UL?
c | 5 dZ*2c Z*2o n UL?i
el
ti? |
f
conjunto convexo cerrado de la Figura 3.4.
[
(&
&
[
)LJXUD En este caso, es suave, mientras que . E c que es la región sombreada de la
¿gura, no es relativamente suave por no serlo los puntos % y %2 .
3.9 Caracterización de familias de cuerpos convexos mediante conceptos de iluminación
121
&DUDFWHUL]DFLyQ GH IDPLOLDV GH FXHUSRV FRQYH[RV
PHGLDQWH FRQFHSWRV GH LOXPLQDFLyQ
Además de los conceptos de iluminación que ya hemos tratado en la Sección 2.4,
existen otros muchos (véase [28]). Entre ellos el siguiente, que fue introducido por
Valentine [37]: dado un cuerpo convexo y 5 5
* , se dice que % 5 M_ es YLVLEOH
desde 5 si o%c 5d _ ' >. Denotamos por t E( 5 el conjunto de puntos frontera
de visibles desde 5 5
* y por | E el mínimo número de puntos exteriores a necesarios para que sea visible toda la frontera de .
Soltan [34] demostró que, si es un cuerpo convexo compacto, entonces
2 | E ? n , por lo que t E( 5 9' M_ para cualquier 5 5
* .
En un reciente artículo de Martini y Soltan [27], se prueba que, dado un cuerpo
convexo compacto , es un ?-símplice si, y sólo si, para todo 5  5
* existe otro
punto 5 2 5
* tal que t E( 5  ^ t E( 5 2 ' M_ , es decir, todo el conjunto es
visible desde i5  c 5 2 j.
La compacidad de es esencial en esta caracterización, incluso reforzando la
anterior condición con t E( 5 9' M_ para todo 5 5
* . En efecto, dado un ?sandwich ' i% 5 U? m k @ % k2 j, con @ 9' f? y k k2 , y 5 5
* , se tiene
;
? i% 5 U? m @ % ' k j r @ 5 k
t E( 5 '
c
(3.26)
=
i% 5 U? m @ % ' k2 j r @ 5 : k2
de modo que los ?-sandwiches (que son cuerpos convexos no acotados) satisfacen
las condiciones anteriores. Desafortunadamente, no son los únicos cuerpos convexos
no acotados que satisfacen estas condiciones. Este es el caso de cualquier conjunto
convexo cerrado tal que . E es un E? -símplice, *? es una recta que pasa
por el origen y ( E ' if? j (por ejemplo, el producto cartesiano 7 U donde
7 es un E? -símplice de U?3 ). Sin embargo, los ?-sandwiches (la clase de
cuerpos convexos con frontera no vacía y no conexa) también se pueden caracterizar
en términos de visibilidades.
352326,&,Ï1 6HD XQ FXHUSR FRQYH[R (QWRQFHV HV XQ ?VDQGZLFK VL \ VyOR
VL t E( 5 HV XQ KLSHUSODQR \ t E( 5 9' M_ SDUD WRGR 5 5
* 122
3. Caracterización de familias de conjuntos cerrados convexos
'HPRVWUDFLyQ La implicación directa es consecuencia de (3.26).
Supongamos que t E( 5 es un hiperplano distinto de M_ para todo 5 5
* .
Puesto que it E( 5 c 5 5
* j es un recubrimiento de M_ , M_ resulta ser la
unión de al menos dos hiperplanos. Suponiendo que M_ contiene dos hiperplanos no
paralelos, obtendremos una contradicción. En efecto, sea M ' i% 5 U? m @ % ' K j,
con @ % K para todo % 5 , ' c 2, con tT@? i@ j 9' tT@? i@2 j. Puesto que M no
está contenido en i% 5 U? m @2 % K2 j, existe % 5 U? tal que @ % ' K y @2 % K2 .
Entonces % 5 M q, contradiciendo M M_ .
Puesto que M_ es la unión de al menos dos hiperplanos paralelos, M_ no es
conexa, y por tanto es un ?-sandwich por la Proposición 3.9.
Nótese que, en esta caracterización de los ?-sandwiches, se puede sustituir
t E( 5 por ** E( , t E( o i?_ E( , con 5 U? qn .
Al igual que los ?-símplices y los ?-sandwiches, los paralelotopos no sólo se
pueden caracterizar por medio de sus representaciones interna y cónica sino también
a través de sus propiedades de combinatoria geométrica. Un paralelotopo es una clase
particular de ?-zonotopo (cuerpo convexo que se puede expresar como la suma de un
número ¿nito de segmentos compactos). Un ?-zonotopo dado, , es un paralelotopo
si, y sólo si, el mínimo número de copias homotécicas más pequeñas de que cubren
(o direcciones iluminando ) es exactamente 2? [33].
También existen artículos ([34] y [35], por ejemplo) en los que se utilizan otros
conceptos de iluminación distintos para caracterizar familias de cuerpos convexos
como los semiespacios o los conos.
Así, a partir de la caracterización de los
semiespacios cerrados que se da en [34, Cor. 1], se puede demostrar fácilmente que un
cuerpo convexo es un semiespacio si, y sólo si, t E( 5 ' M_ para todo 5 5
* .
Los paralelotopos, ?-símplices y ?-sandwiches son sólo algunas de las familias
de cuerpos convexos que tienen buenas propiedades de combinatoria geométrica, de
optimalidad y de separabilidad (véase, por ejemplo, [28], [19] y [6], respectivamente).
La caracterización de todas estas familias en términos de sus representaciones interna
y cónica y sus propiedades de iluminación son desa¿antes problemas abiertos.
%LEOLRJUDItD
[1] E. J. ANDERSON, M. A. GOBERNA and M. A. LÓPEZ, Locally polyhedral linear
inequality systems, /LQHDU $OJHEUD DQG ,WV $SSOLFDWLRQV 270:231-253, 1998.
[2] E. J. ANDERSON, M. A. GOBERNA and M. A. LÓPEZ, Simplex-like trajectories on
quasi-polyhedral sets, 0DWKHPDWLFV RI 2SHUDWLRQV 5HVHDUFK, en prensa.
[3] E. J. ANDERSON and P. NASH, /LQHDU SURJUDPPLQJ LQ LQ¿QLWH GLPHQVLRQDO VSDFHV,
J. Wiley, New York, NY, 1987.
[4] A. AUSLENDER and P. COUTAT, On closed convex sets without boundary rays and
asymptotes, 6HW9DOXHG $QDO\VLV 2, NJ 1-2: 19-33, 1994.
[5] J. BAIR, Strict separation of several convex sets, %XOOHWLQ GH OD 6RFLpWp 0DWKpPDWLTXH
GH %HOJLTXH, Ser. B 32:135-148, 1980.
[6] J. BAIR and R. FOURNEAU, (WXGH JpRPHWULTXH GHV HVSDFHV YHFWRULHOV ,, SRO\qGUHV
HW SRO\WRSHV FRQYH[HV Springer-Verlag, Berlin, Germany, 1980.
[7] K. BEZDEK, On the illumination of smooth convex bodies, $UFKLY GHU 0DWKHPDWLN
58, NJ 6:611-614, 1992.
[8] V. BOLTYANSKI, A problem on illumination of the boundary of a convex body,
,]YHVWLMD 0ROGDYVNR )LOLDOD $NDGHPLL 1DXN 6665 10:77-84, 1960 (en ruso).
[9] A. BRØNDSTED, $Q LQWURGXFWLRQ WR FRQYH[ SRO\WRSHV, Springer-Verlag, New York,
123
124
Bibliografía
NY, 1983.
[10] W. B. CARVER, Systems of linear inequalities, $QQDOV RI 0DWKHPDWLFV 23:212-220,
1921-22.
[11] U. ECKHARDT, Theorems on the dimension of convex sets, /LQHDU $OJHEUD DQG LWV
$SSOLFDWLRQV 12:63-76, 1975.
[12] K. FAN, On in¿nite systems of linear inequalities, -RXUQDO RI 0DWKHPDWLFDO $QDO\VLV
DQG $SSOLFDWLRQV 21:475-478, 1968.
[13] P. FELCYN, Liminal number of a convex body with a smooth boundary, 'HPRQVWUDWLR
0DWKHPDWLFD 21, NJ 2:393-398, 1988.
[14] W. FENCHEL, A remark on convex sets and polarity, &RPPXQLFDWLRQV GX 6pPLQDLUH
0DWKpPDWLTXH GH O¶8QLYHUVLWp GH /XQG, Supplement 82-89, 1952.
[15] D. GALE and V. KLEE, Continuous convex sets, 0DWKHPDWLFD 6FDQGLQDYLFD 7:379391, 1959.
[16] M. A. GOBERNA, V. JORNET, R. PUENTE and M. I. TODOROV, Analytical linear
inequality systems and optimization, -RXUQDO RI 2SWLPL]DWLRQ 7KHRU\ DQG $SSOLFDWLRQV,
103:95-119, 1999.
[17] M. A. GOBERNA and M. A. LÓPEZ, A theory of linear inequality systems, /LQHDU
$OJHEUD DQG LWV $SSOLFDWLRQV 106:77-115, 1988.
[18] M. A. GOBERNA and M. A. LÓPEZ, Dimension and ¿nite reduction in linear semiin¿nite programming, 2SWLPL]DWLRQ 25:143-160, 1992.
[19] M. A. GOBERNA and M. A. LÓPEZ, /LQHDU VHPLLQ¿QLWH RSWLPL]DWLRQ, John Wiley
and Sons, Chichester, England, 1998.
[20] M. A. GOBERNA, M. A. LÓPEZ, J. T. PASTOR and E. VERCHER, Alternative
Bibliografía
125
theorems for in¿nite systems with applications to semi-in¿nite games, 1LHXZ $UFKLHI
YRRU :LVNXQGH IV, Ser. 2:218-234, 1984.
[21] M. A. GOBERNA, M. A. LÓPEZ and M. TODOROV, Stability theory for linear
inequality systems, 6,$0 -RXUQDO RQ 0DWUL[ $QDO\VLV DQG $SSOLFDWLRQV 17:730-743,
1996.
[22] C. O. KISELMAN, How smooth is the shadow of a smooth convex body?, 6HUGLFD
12:189-195, 1986.
[23] E. MARCHI, R. PUENTE and V. N. VERA DE SERIO, Quasi-polyhedral sets in semiin¿nite linear inequality systems, /LQHDU $OJHEUD DQG LWV $SSOLFDWLRQV, 225:157-169,
1997.
[24] J. E. MARTÍNEZ LEGAZ, A generalized concept of conjugation, 2SWLPL]DWLRQ
WKHRU\ DQG DOJRULWKPV, edited by A. Auslender, J. B. Hiriart-Urruty and W. Oettli,
Marcel Dekker, New York, NY, 45-59, 1983.
[25] J. E. MARTÍNEZ LEGAZ, Quasiconvex duality theory by generalized conjugation
methods, 2SWLPL]DWLRQ 19:603-652, 1988.
[26] J. E. MARTÍNEZ LEGAZ, Characterization of R-evenly quasiconvex functions,
-RXUQDO RI 2SWLPL]DWLRQ 7KHRU\ DQG $SSOLFDWLRQV 95, NJ 3:717-722, 1997.
[27] H. MARTINI and V. SOLTAN, A characterization of simplices in terms of visibility,
$UFKLY GHU 0DWKHPDWLN 72 NJ 6: 461-465, 1999.
[28] H. MARTINI and V. SOLTAN, Combinatorial problems on the illumination of convex
bodies, $HTXDWLRQHV 0DWKHPDWLFDH 57:121-152, 1999.
[29] T. S. MOTZKIN, %HLWUlJH ]XU WKHRULH GHU OLQHDUHQ XQJOHLFKXQJHQ, Azriel, Jerusalem,
1936 transl. in 7KHRGRUH 6 0RW]NLQ 6HOHFWHG SDSHUV (D. Cantor, B. Gordon and B.
Rothschild, eds.), Birkhäuser, Boston, 1-80, 1983.
126
Bibliografía
[30] U. PASSY and E. Z. PRISMAN, Conjugacy in quasiconvex programming,
0DWKHPDWLFDO 3URJUDPPLQJ 30:121-146, 1984.
[31] R. PUENTE and V. N. VERA DE SERIO, Locally Farkas-Minkowski linear inequality
systems, 7UDEDMRV ,QYHVWLJDFLyQ 2SHUDWLYD 7:103-121, 1999.
[32] R. T. ROCKAFELLAR, &RQYH[ DQDO\VLV, Princeton University Press, Princeton, New
Jersey, 1970.
[33] P. SOLTAN, On the covering of polyhedra by homothetic images, 6RYLHW 0DWK 'RNO
13:155-159, 1972.
[34] V. SOLTAN, External illumination according to L. Fejes Tóth, 6WXGLD 6FLHQWLDUXP
0DWKHPDWLFDUXP +XQJDULFD 28:473-483, 1993.
[35] P. SOLTAN, An illumination problem, 6WXGLD 6FLHQWLDUXP 0DWKHPDWLFDUXP
+XQJDULFD 29, NJ 1-2:25-32, 1994.
[36] F. A. VALENTINE, &RQYH[ VHWV, McGraw-Hill Series in Higher Mathematics, IX,
1964.
[37] F. A. VALENTINE, Visible shorelines, 7KH $PHULFDQ 0DWKHPDWLFDO 0RQWKO\ 77:146152, 1970.
[38] H. WEYL, Elementare theorie der konvexen polyeder, &RPPHQWDULL 0DWKHPDWLFL
+HOYHWLFL 7:290-306, 1935.
[39] P. L. YU, Cone convexity, cone extreme points, and nondominated solutions
in decision problems with multiobjectives, -RXUQDO RI 2SWLPL]DWLRQ 7KHRU\ DQG
$SSOLFDWLRQV 14:319-377, 1974.
[40] Y. J. ZHU, Generalizations of some fundamental theorems on linear inequalities, $FWD
0DWKHPDWLFD 6LQLFD 16, NJ 1:25-39, 1966.