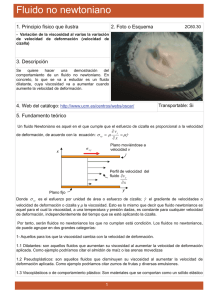
Ductos y Tuberías para Bioprocesos

Ductos y Tuberías para Bioprocesos:
Reología y Análisis
ii
iii
Ductos y Tuberías para Bioprocesos:
Reología y Análisis
James F. Steffe, Ph. D., P.E.
&
Christopher R. Daubert, Ph.D.
Traducido del original en inglés por:
Eduardo Castro Montero
Departamento de Ciencia de los Alimentos y
Tecnología Química
Universidad de Chile
[email protected]; [email protected]
Luis Puente Díaz
Departamento de Ciencia de los Alimentos y
Tecnología Química
Universidad de Chile
[email protected]
Título Original:
Bioprocessing Pipelines:
Rheology and Analysis
iv
James F. Steffe, Ph.D., P.E.
Dept. of Biosystems and Agricultural Engineering
Dept. of Food Sciences and Human Nutrition
Michigan State University
East Lansing, MI 48824-1323
[email protected]
&
Christopher R. Daubert, Ph.D.
Dept of Food Science
North Carolina State University
Raleigh, NC 27695-7624
[email protected]
Derechos reservados © 2006 James F. Steffe y Christopher R. Daubert. Ninguna parte de este
trabajo puede ser reproducida, almacenada o transmitida en cualquier medio tanto electrónico,
mecánico, fotocopia, grabado u otro dispositivo sin el permiso de los autores de la obra impresa.
Library of Congress Control Number 2005905876
ISBN 10: 0-9632036-2-2
ISBN 13: 978-0.9632036-2-5
Freeman Press
2807 Still Valley Drive
East Lansing, MI 48823
USA
v
Ductos y Tuberías para Bioprocesos:
Reología y Análisis
James F. Steffe, Ph. D. P.E.
y
Christopher R. Daubert, Ph.D.
Freeman Press
2807 Still Valley Drive
East Lansing, MI 48 823-2351
USA
vi
Prefacio
Este libro nace de la experiencia profesional de los autores y recomendaciones de colegas
en la industria. Nuestra revisión de la literatura comercial disponible ha revelado la escasa
información sobre fluidos no Newtonianos, así como también descripciones incorrectas del
comportamiento reológico relativo a los cálculos para el diseño de tuberías. Además, hay una
gran cantidad de investigaciones publicadas (algunas de las cuales tienen nuestros nombres)
relacionadas con la reología de biofluidos y el análisis de procesos en tuberías, sin embargo, esta
información no ha sido depurada y sintetizada de forma que resulte útil para abordar problemas
prácticos en bioprocesos. Nosotros esperamos que nuestro trabajo muestre nuevas luces en el área
y provea valiosas herramientas para el día a día práctico. El público objetivo para este libro son
estudiantes, tecnólogos e ingenieros interesados en el procesamiento de fluidos biológicos,
básicamente en las industrias alimentaria y farmacéutica. Estos materiales están sujetos a una
variedad de fuerzas mecánicas y tratamientos térmicos durante su procesamiento.
Nuestro trabajo está diseñado para el autoaprendizaje y después de un esfuerzo suficiente,
nosotros esperamos que los lectores sean capaces de: 1) Explicar los principios básicos de la
reología de fluidos necesarios para examinar problemas relacionados con tuberías y ductos; 2)
Determinar (mediante los instrumentos adecuados) las propiedades reológicas de fluidos
biológicos necesarios para calcular los parámetros de diseño de tuberías y ductos; 3) Resolver
problemas de bombeo (para fluidos Newtonianos y no Newtonianos) usando las ecuaciones de
balance de energía mecánica como estructura de análisis; 4) Caracterizar los tratamientos de
cizalla y térmicos aplicados a materiales biológicos en los sistemas de procesamiento.
vii
En el siglo XIV William de Occam dijo “Pluralis non est ponenda sine necessita”, lo
cual en términos actuales podría ser interpretado como “mantener las cosas simples”. Nosotros
hemos adoptado este principio. La Reología es un tema complejo, pero nosotros la hemos
simplificado utilizando el bisturí de Occam para quitar algunos supuestos, las teorías y modelos
que no son necesarias para caracterizar los fluidos con el propósito de analizar un
comportamiento en tuberías y ductos. Además hemos eliminado derivaciones y desarrollo de las
ecuaciones para solo presentar los resultados útiles. Afortunadamente, este enfoque permitirá
rápidamente a los lectores encontrar las soluciones apropiadas para los problemas prácticos de
diseño de tuberías. Información mas detallada sobre técnicas reológicas e interpretación de datos
puede ser encontrada en el libro “Rheological Methods in Food Processing”, Segunda Edición
(1996, Freeman Press), del autor J.F. Steffe. Obra que se encuentra disponible sin costo en
www.egr.edu/~steffe/freebok/offer.html
Nosotros -en nuestro rol múltiple de autores, ingenieros y académicos- estamos de
acuerdo en la protección del medioambiente y en el uso responsable de los recursos naturales.
Desde el momento en que nuestro trabajo es producido en hojas de papel, estamos preocupados
respecto del futuro de los bosques que están en peligro de extinción en el mundo y el impacto
ambiental de la producción de papel, y estamos comprometidos con las políticas que apoyen la
preservación de los recursos forestales en peligro y recomendamos adoptar las mejores prácticas
dentro de las industrias editoriales y productoras de papel. Además llamamos a las editoriales,
impresores y a nuestros colegas autores a adherirse a las recomendaciones sobre el uso del papel
de la iniciativa Green Press (greenpressinitiative.org). El papel usado en este libro cumple con las
mencionadas recomendaciones.
J.F. Steffe
C.R. Daubert
viii
Prólogo a la edición en español
La traducción del libro de Steffe & Daubert, señores de la reología, y en especial de
reología de alimentos ha sido un alto honor para mí estimado colega Luis Puente y para mí.
Esperamos que esta labor sea fructífera al ser aprovechada por los Ingenieros en
Alimentos y por los profesionales que tratan fluidos biológicos y que están batallando para que
Chile sea realmente una potencia alimentaria.
Dedico este trabajo a Patricia Bravo Rivera
Eduardo Castro Montero
A mi María Isabel, gracias por tu paciencia y
apoyo incondicional
Luis Puente Díaz
ix
Tabla de Contenidos
Prefacio
Prólogo a la edición en español
Nomenclatura
vi
viii
xii
1. Propiedades Reológicas de Fluidos Biológicos
1
1.1
1.2
1.3
1.4
1.5
1.6
Viscosidad y Parámetros Empíricos de Fluidos
Modelos de Fluidos Útiles
Fluidos Independientes del Tiempo vs Tiempo Dependientes
Esfuerzo de Cizalla y Velocidad de Deformación en Tubería
Comportamiento de Fluidos Adelgazantes en una Tubería
Selección de Velocidad de Deformación para la Recolección de
Datos Reológicos
1.7 Influencia de la Temperatura en el Comportamiento Reológico
2. Reología de Tuberías
2.1 Caracterización de Fluidos para el Diseño de Tuberías
2.2 Viscosimetría de Cilindros Coaxiales
2.3 Viscosimetría de Mezcla
2.3.1 Caracterización de Viscosímetro de Mezcla
2.3.2 Evaluando las Propiedades de Fluidos Tipo Ley de Potencia
2.3.3 Viscosímetro de Brookfield con Aguja de Disco
2.4 Viscosímetros Cono y Placa y Placas Paralelas
3. Cálculos de Pérdida de Energía y Carga
3.1
3.2
3.3
3.4
3.5
Ecuaciones de Balance de Energía Mecánica
Curvas del Sistema (Requerimientos de Proceso)
Determinando Trabajo y Altura
Curvas de Bomba (Bombas Centrífugas)
Altura de Succión Neta Positiva (Disponible y Requerida)
4. Factores de Roce de Fanning
4.1
4.2
4.3
4.4
Factores de Roce
Fluidos Newtonianos
Fluidos Tipo Ley de la Potencia
Perfiles de Velocidad del Fluido en una Tubería
1
2
5
6
7
8
10
13
13
13
17
18
27
27
31
33
33
36
37
43
44
47
47
47
47
55
x
5. Coeficientes de Pérdida por Fricción
5.1 Pérdidas en Válvulas y Accesorios estándar
5.2 Pérdidas en Equipamiento Basado en Datos para el Agua
6. Manejo de Fluidos Sensibles a la Cizalla
59
59
61
71
Fluidos Sensibles a la Cizalla
Trabajo de Cizalla (Ws)
Intensidad de la Potencia de Cizalla (S)
Valores Críticos para Ws y S
Partículas Sensibles al Cizalle
Cálculos de Escalamiento
71
72
74
75
78
79
7. Procesado Térmico de Fluidos Biológicos
83
6.1
6.2
6.3
6.4
6.5
6.6
7.1 Cinética de Muerte de Microorganismos
7.2 Método General
8. Problemas de Ejemplo
8.1 Comparación de Fluidos Newtonianos y Adelgazantes por Cizalla
8.2 Equivalencia de la Ley de Potencia de las ecuaciones de
Herschel Bulkley y Casson
8.3 Datos de Cilindros Coaxiales para Mix de Helados
8.4 Determinación del Coeficiente de Mezcla
8.5 Viscosimetría de Mezcla para Salsa para Pastas
8.6 Calculando la Caída de Presión con la Viscosidad Efectiva
8.7 Generando una Curva del Sistema para Bombear Crema
8.8 Bomba de Desplazamiento Positivo para Jugos de Fruta Pulposos
8.9 Bombeando un Fluido Sensible al Cizalle (Crema)
8.10Intensidad de Potencia de Cizalla en una Bomba Centrifuga
8.11Letalidad de un Proceso de Pasterización
9. Apéndices
9.1
9.2
9.3
9.4
9.5
9.6
9.7
9.8
9.9
Factores de Conversión y Alfabeto Griego
Propiedades Reológicas de Fluidos Biológicos
Diámetros de Tubos de Acero Inoxidable y Tuberías
Acero Inoxidable (304 y 316)
Propiedades del Agua Saturada
Entalpía de Vapor Saturado
Viscosidad (mPa s ó cP) del Agua
Galones de Agua por 100 pies de Tubo
Leyes de Afinidad para Bombas Centrífugas
83
87
95
95
98
103
108
109
112
114
121
128
133
134
137
137
139
141
142
144
146
148
149
150
xi
9.10 Ecuaciones para Fluidos Plásticos de Bingham en Flujo en Tuberías
9.11 Factores de Fricción de Fanning para Fluidos Tipo de La Ley de Potencia
9.12 Coeficientes de Pérdida por Fricción: Ecuación 3-k
Índice
151
153
157
xii
Nomenclatura
Este libro utiliza una combinación de unidades de los Sistemas Inglés e Internacional. Pese a que
los autores prefieren el Sistema Internacional, la mezcla de unidades presentadas en el presente
texto corresponde a una práctica actual en las industrias de alimentos y farmacéuticas en EE.UU.
A
constante, Pa s
A
área, m2
A
constante, adimensional
B
constante, adimensional
C
constante, adimensional
d
diámetro del rotor, m
D
tiempo de reducción decimal, min
D
diámetro, m
Dpulg
diámetro, pulgadas
D0
tiempo de reducción decimal a 250 ºF, min
Dh
diámetro hidráulico, m
Ea
energía de activación para fluir, cal / (g-mol)
f
factor de fricción de Fanning, adimensional
F
tiempo de destrucción térmica, min ó s
F
pérdida de energía viscosa (pérdida por fricción) por unidad de masa, J kg-1
F
fuerza, N
F0
tiempo de destrucción térmica a 250 ºF, min
g
aceleración de gravedad, 9,81 m s-2
h
altura del sensor separación entre placas paralelas, m
h0
altura agregada al sensor para corrección de punta, m
h´
altura definida por la figura 2.1, m
h´´
altura definida por la figura 2.1, m
xiii
Hp
altura total de elevación de la bomba, m
Hs
carga hidráulica del sistema, m
k
constante de inactivación microbiana, min-1
k´
constante de mezcla viscosímetro, rad-1
k´´
constante de mezclado, rad m-3
k1
constante, adimensional
kf
coeficiente de pérdida por fricción, adimensional
݇ఊሶ
factor de conversión velocidad de deformación en cizalla, min rev-1 s-1
ks
factor de conversión de esfuerzo de cizalla, Pa
k¶
constante, adimensional
K
coeficiente de consistencia, Pa sn
L
longitud, m
Le
longitud equivalente, m
LR
tasa de letalidad, adimensional
M
torque, N m
m
masa, kg
݉ሶ
caudal másico, kg s-1
n
índice de flujo, adimensional
N
velocidad angular, rev min-1
N
número de microorganismos
NHe
número de Headstrom, adimensional
N0
número inicial de microorganismos
NPo
número de potencia, adimensional
NRe
número de Reynolds (para fluidos Newtonianos), adimensional
NRe,B
número de Reynolds para fluidos de Bingham, adimensional
NRe,I
número de Reynolds para Rotor, adimensional
NRe,PL número de Reynolds para fluidos, Ley de la Potencia, adimensional
NRe,PL,I número de Reynolds del Rotor para fluidos, Ley de la Potencia, adimensional
(NPSH)A
Altura de succión neta disponible, m
(NPSH)R
Altura de succión neta requerida, m
xiv
P
presión, Pa
Pv
presión de vapor, Pa
r
radio (variable) o radio de curvatura, m
R
radio, m
R´
constante universal de los gases, 1,987 cal / (g-mol K)
Rb
radio del sensor, m
Rc
radio de la copa, m
Rs
radio del eje, m
Ro
radio crítico, m
RKT
tiempo relativo de destrucción, adimensional
S
intensidad de la potencia de cizalla, adimensional
SV
valor esterilizante, adimensional
t
tiempo, min o seg
T
temperatura ºC, ºF o K
Tr
temperatura de referencia, ºC, ºF o K
Q
caudal volumétrico, m3 s-1
u
velocidad, ms-1
‫ݑ‬ത
velocidad volumétrica promedio (o media), ms-1
umáx
velocidad máxima, m s-1
u+
velocidad adimensional
V
volumen, m3
W
trabajo del eje por unidad de masa, J kg-1
Ws
trabajo de cizalla por unidad de masa, J kg-1
z
elevación, m
z
cambio de temperatura para reducir un ciclo logarítmico en D, ºF o ºC
a
Rc/Rb, adimensional
a
factor de corrección de la energía cinética, adimencional
a
constante, adimensional
ߛሶ
esfuerzo de cizalla, s-1
ߛሶ a
esfuerzo de cizalla promedio, s-1
xv
ߛሶ b
esfuerzo de cizalla en el sensor, s-1
ߛሶ máx
esfuerzo de cizalla máximo, s-1
ߛሶ mín
esfuerzo de cizalla mínimo, s-1
ߛሶ rim
esfuerzo de cizalla en el borde de un sensor de placas paralelas, s-1
∆
constante, adimensional
∆P
pérdida de presión o cambio en la presión, Pa
ε
rugosidad de la superficie, m
η
viscosidad aparente, Pa s
η
eficiencia de la bomba, adimensional
ηr
viscosidad aparente de referencia, Pa s
θ
ángulo, grados
µ
viscosidad absoluta o viscosidad de un fluido Newtoniano, Pa s
µ pl
viscosidad plástica, Pa s
µr
viscosidad Newtoniana de referencia, Pa s
ν
viscosidad cinemática, cSt ó mm2 s-1
ρ
densidad, g cm-3 ó kg m-3
σ
esfuerzo de cizalla, Pa
σa
esfuerzo de cizalla promedio o promedio representativo, Pa
σb
esfuerzo de cizalla en el sensor, Pa
σ0
umbral de fluencia, Pa
σ max
esfuerzo de cizalla máximo, Pa
σR
esfuerzo de cizalla en el borde de un sensor de placas paralelas, Pa
Φ
potencia, W o J s-1
Ω
velocidad angular, rad s-1
1. Propiedades Reológicas de Fluidos Biológicos
1.1
Viscosidad y Parámetros Empíricos de los Fluidos
La reología es la ciencia que estudia la deformación y el flujo de la materia. Las propiedades
reológicas de los fluidos biológicos pueden variar considerablemente, incluso dentro de categorías de un
mismo producto como puré de manzana, kétchup o chocolate, por lo tanto, es importante que el
comportamiento reológico sea cuidadosamente evaluado para todos los nuevos productos. El
comportamiento de flujo puede ser ampliamente caracterizado en términos de dos medidas: medición de
las propiedades absolutas (necesario para el diseño de líneas de tuberías) que son independientes del
instrumento de medida, y mediciones empíricas (a menudo usadas en aplicaciones de control de calidad),
las cuales resultan ser completamente dependientes de las características del aparato de medición. Sin
datos reológicos apropiados existe poca exactitud en los cálculos para el diseño de tuberías.
Errores y equivocaciones pueden ser encontradas en los datos de propiedades reológicas y
descripciones provistas por varias compañías. Algunas cosas que deben ser aclaradas inmediatamente son:
•
La palabra “viscosidad” se utiliza para describir varias propiedades reológicas distintas y la
mayoría de ellas no tienen aplicaciones en el análisis de tuberías para bioprocesos. Ejemplos
(y esta no es una lista completa) incluyen los siguientes términos: viscosidad extensional,
viscosidad inherente,
viscosidad intrínseca, viscosidad reducida, viscosidad específica,
viscosidad compleja, y viscosidad dinámica. Claramente, uno debe ser cuidadoso cuando
emplea la palabra viscosidad para caracterizar propiedades de los fluidos.
•
Describir materiales utilizando la palabra “viscosidad” implica que el fluido en cuestión es
Newtoniano. La viscosidad cinemática es también común y también implica un
comportamiento Newtoniano.
•
Los fluidos no Newtonianos no pueden ser caracterizados correctamente con una única
medida de viscosidad en centipoise, o cualquier otra escala de unidades. Algunos ejemplos de
unidades empíricas que no deben ser usados (pero que han sido sugeridos o se usan
actualmente) para caracterizar fluidos no Newtonianos en los cálculos para el diseño de
tuberías incluyen los siguientes: Segundos Universales Saybolt, Grados Engler,
DuPont
Parlin, Krebs, viscosidad Redwood, MacMichael, viscosidad RVA (Rapid Visco Analyser) y
viscosidad Brabender.
2
Ductos y Tuberías para Bioprocesos
También existe una larga lista de instrumentos empíricos que son inapropiados para
determinar las características de diseño de tuberías para fluidos no Newtonianos incluyendo
copas de inmersión (por ejemplo copa Parlin, copa Ford, copa Zahn), burbujas ascendentes,
bolas descendentes, bolas rodantes, y algunos instrumentos específicos para la industria de
alimentos como el Viscoamilógrafo Brabender, Mixógrafo, Farinógrafo, consistómetro
Adams, y el consistómetro Bostwick.
1.2
Modelos de Fluidos Útiles
Un modelo para fluidos es una ecuación matemática que describe el comportamiento de flujo del
material y los modelos correctos son los que se determinan a través de ajustes estadísticos de curvas
(habitualmente análisis de regresión lineal) de datos experimentales. Un fluido es Newtoniano si el
comportamiento observado para la sustancia es una respuesta independiente del tiempo, corresponde a una
relación lineal entre el esfuerzo de cizalla y la velocidad de deformación y no tiene esfuerzo de fluencia.
Todos los otros escenarios de fluido son considerados como no Newtonianos. Esta sección se concentrará
en los fluidos que son independientes del tiempo, lo que significa que no tienen memoria. El
comportamiento tiempo-dependiente será discutido en una sección siguiente.
El comportamiento de flujo de los líquidos es caracterizado mediante la relación
experimentalmente determinada entre el esfuerzo de cizalla y la velocidad de deformación. Estos
parámetros pueden ser explicados considerando el comportamiento estacionario simple de corte de un
liquido fluyendo entre dos placas paralelas (Fig 1.1) con un área de superficie (A) en contacto con el
fluido, y las placas separadas por una distancia, h. La placa inferior esta inmóvil (velocidad igual a cero, u
= 0), y la placa superior se mueve a una velocidad máxima igual a u. Una fuerza (F) se requiere para
mantener la velocidad de la placa superior. Utilizando estas variables, el esfuerzo de corte (s) se define
como fuerza dividida por área:
σ=
(1.1)
F
A
con unidades de presión, comúnmente definidas como Newton por metro cuadrado ó Pascal. Velocidad de
deformación en cizalla
, correspondiente al esfuerzo de cizallamiento, es la velocidad del plato
superior dividido por la distancia que separa los platos:
Propiedades Reológicas de Fluidos Biológicos
3
(1.2)
Dado que la velocidad se presenta en unidades de metros por segundo y la altura tiene unidades de
metros, las unidades de velocidad de deformación son los recíprocos de los segundos, s-1. Los
viscosímetros son instrumentos que registran datos experimentales para determinar los esfuerzos de cizalla
y las velocidades de deformación bajo diferentes condiciones.
Para describir el comportamiento de un material, el esfuerzo de cizalla debe relacionarse con la
velocidad de deformación. Varios líquidos pueden ser descritos como Newtonianos debido a que los datos
reológicos muestran la relación entre el esfuerzo de cizalla y la velocidad de deformación es lineal:
(1.3)
Donde µ es la viscosidad absoluta del líquido. Los líquidos biológicos que caen dentro de esta categoría
incluyen agua, jugos de fruta clarificados, miel, bebidas alcohólicas, refrescos y aceites líquidos (oliva,
maíz, etc.). Las unidades típicas de la viscosidad absoluta son Pascal segundo ó centipoise (1 Pa s = 1000
cP). Los factores de conversión de viscosidad se presentan en el Anexo 9.1.
Perfil de
Velocidad
Figura 1.1 Flujo de un líquido entre placas paralelas.
El comportamiento de los fluidos Newtonianos a veces puede ser descrito en términos de la
viscosidad cinemática, definida como la viscosidad absoluta dividida por la densidad:
4
Ductos y Tuberías para Bioprocesos
(1.4)
La unidad habitual para la viscosidad cinemática es centistokes. Utilizando agua a 20ºC, por ejemplo,
1
1
1
(1.5)
Para líquidos que no cumplen con el modelo Newtoniano dado en la Ec. (1.3), que son, por
definición no-Newtonianos. Para el análisis de tuberías, la mayoría de los fluidos no Newtonianos pueden
ser descritos adecuadamente con el modelo de la ley de potencia:
(1.6)
Donde K es el coeficiente de consistencia (unidades Pa sn) y n es el índice del comportamiento de flujo
adimensional. El modelo Newtoniano es una caso especial de la ley de potencia donde: n = 1,0, la
ecuación colapsa en el modelo Newtoniano y K = µ. Los valores 0 < n < 1 indican un comportamiento
adelgazante (muy común), y n >1 indica un comportamiento espesante (poco común). Sinónimos para
adelgazante y espesante son pseudoplástico y dilatante, respectivamente. Adelgazante y espesante son los
términos habituales dado que estos son mas descriptivos respecto del comportamiento del fluido que está
siendo descrito. Además notar que no hay nada “pseudo” respecto a los fluidos adelgazantes y los fluidos
espesantes no se “dilatan”. Ejemplos de líquidos adelgazantes incluyen concentrados o pulpas de frutas,
pastas o purés, flanes, y geles débiles. Los valores típicos del coeficiente de consistencia y el índice de
comportamiento de flujo para líquidos biológicos están contenidos en el Anexo 9.2.
El modelo de ley de potencia puede ser descrito en términos de la viscosidad aparente (h) definida
como el esfuerzo de cizalla dividido por la velocidad de deformación:
(1.7)
La viscosidad aparente varía con la velocidad de deformación y depende de los valores numéricos de K y
n. Si un fluido es Newtoniano, la viscosidad aparente y la viscosidad Newtoniana son iguales, la Ec. (1.6)
y (1.7) son aplicadas para el relleno usado en pie de arándano y la miel en el problema ejemplo 8.1. La
Propiedades Reológicas de Fluidos Biológicos
5
viscosidad aparente no debe confundirse con la viscosidad efectiva – estos dos conceptos serán
comparados en el problema de ejemplo 8.6.
La gran mayoría de los problemas de bombeo de líquidos pueden ser resueltos utilizando los
modelos Newtoniano y la ley de potencia. Esto es beneficioso dado que las ecuaciones necesarias para el
análisis de tuberías de este tipo de materiales están bien desarrolladas. El modelo de la ley de potencia es
bastante apropiado para la mayoría de los fluidos no newtonianos y generalmente incluye materiales que
pueden ser descritos como untables o fácilmente puestos en una cuchara. Además, la ecuación de ley de
potencia a menudo es una buena aproximación del comportamiento de líquidos que presentan un esfuerzo
de fluencia importante (el esfuerzo mínimo requerido para iniciar el flujo) como por ejemplo la pulpa de
tomate. Pastas muy espesas, tienen un gran esfuerzo de fluencia, pueden requerir modelos reológicos mas
complejos, como por ejemplo el de la ecuación para plásticos de Bingham (ver Anexo 9.10). A veces, sin
embargo, ecuaciones más complejas son aplicadas a fluidos para mejorar la precisión del ajuste a pesar de
que el modelo de la ley de potencia es aceptable para los propósitos de diseño de tuberías. El problema
ejemplo 8.2 ilustra un caso en donde las ecuaciones de Herschel-Bulkley y Casson se aplican para
alimento de bebes, son convertidas al modelo de ley de potencia para proporcionar propiedades de diseño
de tuberías más útiles.
1.3
Fluidos Independientes del Tiempo vs. Tiempo-Dependientes
Los fluidos Newtonianos y los que se ajustan a la Ley de potencia son considerados como
independientes del tiempo debido a que no presentan memoria. Las propiedades reológicas de estos
materiales no se ven afectadas por efectos mecánicos introducidos en operaciones como la mezcla y el
bombeo. Midiendo la viscosidad de agua o aceite de oliva por ejemplo puede ser la misma sin importar
cuanto tiempo estén mezclándose o permanezcan separadas. Por otra parte, un gel débil (postre o loción)
puede presentar una consistencia muy reducida con la mezcla debido a la destrucción de estructuras
débiles dentro del material.
Los fluidos tiempo-dependientes se pueden dividir en dos categorías: fluidos tixotrópicos que se
adelgazan con el tiempo, y reopécticos (también llamados anti-tixotrópicos) que son fluidos que se
engrosan con el tiempo. Estos términos pueden ser explicados utilizando ketchup como ejemplo de fluido.
Los tomates son sometidos a varias operaciones (lavado, pelado, molienda y pulpado) antes que el
producto en forma de pulpa sea colocado en un recipiente para su distribución comercial.
6
Ductos y Tuberías para Bioprocesos
Cuando se bombea el fluido hasta el punto de manufactura, el producto se destroza completamente y el
kétchup se comporta como un fluido adelgazante (independiente del tiempo). Si el kétchup embotellado
permanece estático por un periodo de semanas, el fluido se espesa debido a la formación de una estructura
gelificada débil (causado fundamentalmente por la presencia de pectina en los tomates) al interior del
producto. Sometiendo el kétchup reposado a un esfuerzo de corte - debido a la agitación mecánica
inducida por revolver y agitar el envase, se produce una ruptura de la estructura débil y esto hace que el
producto sea más untable. El tiempo y la cantidad de energía de la energía mecánica aplicada determinan
el grado de adelgazamiento dependiente del tiempo. Entregando kétchup con un nivel suficiente de
degradación mecánica provoca que el fluido restablezca un comportamiento tiempo-dependiente similar al
que poseía en el momento de ser elaborado. Si el proceso de degradación fue controlado dentro de los
confines de un viscosímetro, el comportamiento del Kétchup podría ser cualitativamente evaluado. Un
especialista en reología podría realizar estas mediciones para estudiar la sensibilidad de corte, la
estabilidad, o la aceptabilidad por parte del consumidor del kétchup. Cuando se selecciona bombas para
una línea de proceso, el kétchup puede ser tratado como un fluido tiempo-independiente y sería necesario
considerar el comportamiento según la ley de potencia de fluidos.
1.4
Esfuerzo de Cizalla y Velocidad de Deformación en Tubería
Para determinar las propiedades reológicas de un fluido es necesario contar con datos
experimentales de esfuerzo de cizalla y velocidad de deformación. Un rango apropiado para estos
parámetros debe ser seleccionado para que los datos tengan utilidad. Cuando un fluido que se rige por la
ley de potencia fluye a través de una tubería bajo condiciones de flujo laminar (el criterio para establecer
un flujo laminar será discutido en la sección 4.3), la siguiente ecuación describe la relación entre la caída
de presión que induce el flujo (∆P) y el caudal resultante (Q):
3
Δ
2
1
4
(1.8)
4
Comparando la Ec. 1.8 con la Ec. 1.6, se pueden escribir expresiones para el esfuerzo de cizalla máximo y
la velocidad de deformación máxima presentes en el ducto:
Δ
2
(1.9)
Propiedades Reológicas de Fluidos Biológicos
3
4
1
7
(1.10)
4
La ecuación 1.10 es utilizada en el problema 8.1 para calcular la velocidad de deformación máxima
encontrada en el bombeo del relleno para pastel de arándanos.
Los valores máximos presentados arriba ocurren en la pared interna de la tubería, donde el valor del radio
variable (r) es igual a R, el radio interior de la tubería. El valor mínimo del esfuerzo de cizalla se presenta
en el centro del ducto (r = 0) y varía linealmente de acuerdo al radio según:
Δ
2
(1.11)
El valor mínimo de la velocidad de deformación en la tubería es cero y también sucede en el centro del
ducto (r = 0), pero varía de manera no lineal (a menos que el fluido sea Newtoniano, entonces n = 1) con
el radio según:
3
1
4
(1.12)
4
Las ecuaciones anteriores son válidas solamente para un régimen de flujo laminar debido a que la
velocidad de deformación en la tubería no puede ser definida fácilmente para flujos turbulentos.
1.5
Comportamiento de Fluidos Adelgazantes en una Tubería
Para un mejor entendimiento del significado físico de adelgazante (0< n <1), es necesario
considerar la relación existente entre la caída de presión y el caudal volumétrico durante el bombeo. El
descenso de presión en un tubo para el flujo laminar de un fluido Newtoniano puede ser descrito
empleando la ecuación de Hagen-Poiseuille:
Δ
8
(1.13)
De igual manera, la caída de presión en un tubo para un flujo laminar de un fluido, la ley de potencia es:
8
Δ
Ductos y Tuberías para Bioprocesos
3
2
1
4
(1.14)
4
Para el caso de un fluido Newtoniano, la ecuación (1.13) muestra que la caída de presión es directamente
proporcional al caudal, duplicando el caudal (Q) resulta en una duplicación de la caída de presión sobre un
largo de tubo igual a L. En el caso de los fluidos adelgazantes (ecuación 1.14), la caída de presión es
proporcional al caudal elevado a la potencia n; al duplicar el caudal, se incrementa la caída de presión en
un factor de 2n. Si n = 0,5, por ejemplo, la caída de presión se incrementará en un factor de 1,41.
Ahora reconsiderando el concepto de adelgazante. Duplicando Q con el fluido Newtoniano se
duplica ∆P, sin embargo duplicando Q con el fluido adelgazante teniendo un índice de flujo de 0,5 solo se
produce un incremento en el descenso de presión a 1,41 ∆P. Desde que se duplica el Q no se duplica el
∆P, parece que el incremento de la velocidad de deformación (una consecuencia de incrementar Q) causa
que el fluido no Newtoniano aparezca como menos viscoso, es decir, diluyente. Este fenómeno es el
resultado del comportamiento de la ley de potencia: las propiedades reológicas del material (K y n) no han
cambiado.
1.6
Selección de Velocidad de Deformación para la Recolección de Datos Reológicos
Datos experimentales obtenidos para determinar las propiedades reológicas necesarias para el
diseño de tuberías deben contemplar aproximadamente los mismos rangos de velocidad de deformación
encontrados en la tubería. Teóricamente, es posible utilizar esfuerzos de cizalla en vez de velocidades de
deformación dado que pueden coincidir, pero esto comúnmente es impracticable debido al conocimiento
limitado que existe respecto de la caída de presión. En la práctica, la estimación del rango de velocidad de
deformación para regímenes de flujo laminar o turbulento se basa en ecuaciones de tuberías para flujo
laminar. Uno debe además advertir que las velocidades reales de deformación pueden variar mucho en
diferentes partes del equipamiento que constituye en sistema completo de tuberías. Las velocidades
máximas de deformación encontradas en filtros y en válvulas neumáticas parcialmente abiertas, por
ejemplo, pueden ser mucho mas altas que la velocidad de deformación máxima encontrada en un tubo.
Además, a un caudal constante, las tuberías de diferentes diámetros tendrán velocidades de deformación
máximas diferentes.
Propiedades Reológicas de Fluidos Biológicos
9
Un límite superior de velocidad de deformación puede ser estimado a partir de la Ecuación 1.10, dados
los valores de tasa de caudal volumétrico máximo, radio del tubo e índice del comportamiento de flujo.
Para un fluido Newtoniano, la velocidad de deformación máxima se calcula como 4Q/(πR3).
Para calcular la velocidad de deformación máxima para fluidos no Newtonianos, este valor debe ser
multiplicado por el factor corrección de la velocidad de deformación:
Factor de corrección para velocidad de
(1.15)
deformación =
Es importante contar con una buena estimación del índice del comportamiento de flujo debido a
que el valor numérico del factor de corrección está fuertemente influenciado por esta propiedad reológica.
Un valor de n de 0,2 por ejemplo, conduce a un factor de corrección de velocidad de deformación de 2, lo
que duplica la velocidad de deformación máxima calculada mediante la aproximación Newtoniana simple.
Si un valor del índice del comportamiento de flujo es desconocido, lo cual puede ser el caso dado que se
necesita un rango de velocidad de deformación para el propósito de evaluar las propiedades reológicas –
uno puede ser capaz de obtener una buena estimación de n basándose en las propiedades de un producto
similar (ver apéndice 9.2). El mejor procedimiento, sin embargo, es recolectar datos reológicos
preliminares para determinar n antes de que sea establecido la velocidad de deformación final.
Aunque la velocidad de deformación mínima en un tubo es cero, no es necesario obtener datos a
velocidades de deformación tan bajos excepto en caso donde el flujo volumétrico sea extremadamente
bajo. Los datos reológicos obtenidos de velocidades de deformación menores que 1 s-1 generalmente no
son necesarios para el trabajo de diseño de tuberías. Un límite inferior razonable para el valor de velocidad
de deformación es de aproximadamente 1/10 del valor máximo de la velocidad de deformación predicha
con la ecuación 1.10. Esta idea se aplica en el ejemplo del problema 8.1. Velocidades de deformación
máximas para algunos procesos de plantas lácteas están dadas en la tabla 1.1.
10
Ductos y Tuberías para Bioprocesos
Tabla 1.1 Velocidades de deformación máximas en sistemas de bombeo típicos
D+(pulg)
Producto
n
Caudal
Caudal
(proceso)
-
(lbm/h)
(gal/min)
907
8
2
53
Mezcla
Helado
(planta 0,7
(1/s)
piloto)
Leche (planta piloto)
1,0
1.481
13
2
86
Mezcla Helado (comercial)
0,7
22.665
200
4
154
Proceso Queso (comercial)
0,3
27.000
50
3
136
Leche (comercial)
1,0
130.000
252
4
175
D+ = diámetro nominal del tubo, ver apéndice 9.3 para los diámetros reales.
1.7
Influencia de la Temperatura en el Comportamiento Reológico
El comportamiento reológico está fuertemente influenciado por la temperatura, y el cambio en la
viscosidad Newtoniana (µ) puede ser modelado con la ecuación de Arrhenius:
(1.16)
´
Donde Ea es la energía de activación para el flujo, R´ es la constante universal de los gases, y T es la
temperatura absoluta. La ecuación (1.16) también puede ser expresada en términos de una viscosidad de
referencia (µr) dada a una temperatura específica de referencia (Tr):
1
1
(1.17)
´
Evaluando la ley de potencia para fluidos, la viscosidad aparente a una velocidad de deformación
constante puede también ser modelado utilizando la ecuación de Arrhenius:
1
´
1
(1.18)
Propiedades Reológicas de Fluidos Biológicos
11
Esta relación es útil desde el momento en que el índice de comportamiento de flujo (n) generalmente no
es fuertemente dependiente de la temperatura. Si n no es dependiente de la temperatura, el coeficiente de
consistencia (K) puede también ser modelado con la ecuación de Arrhenius. Es importante notar que la
temperatura utilizada en la ecuación de Arrhenius esta dada en grados Kelvin, por lo tanto la razón Ea/R´
debe presentarse en grados Kelvin.
Utilizar las ecuaciones anteriores para resumir la influencia de la temperatura sobre el
comportamiento de flujo puede ser valiosa cuando un rango de temperaturas debe ser considerado. Por
ejemplo, datos para miel presentan un comportamiento Newtoniano con viscosidades entre los 76,9 Pa s a
6,5 ºC, mientras que 0,50 Pa s a 48,0 ºC. Recolectando datos a valores entre estos números y ajustándolos
a la ecuación 1.16, permite modelar la viscosidad (en Pa s) en función de la temperatura:
5,58 10
´
10.972
(1.19)
Donde Ea/R´ = 10.972 K. El comportamiento también puede ser modelado reordenando la ecuación 1.18
1
1
(1.20)
´
ó con la sustitución de una viscosidad de referencia (3,77 Pa s) a 300 K, como:
3,77
10.972
1
1
300
(1.21)
Las ecuaciones 1.19 y 1.21 permiten calcular la viscosidad de la miel a cualquier temperatura entre 6,5 ºC
y 48,0 ºC (278,7 K a 321,2 K). La ecuación 1.19 es utilizada para determinar el comportamiento de flujo
de miel a 24ºC en el problema ejemplo 8.1.
En un segundo caso, se estudió jugo de naranja concentrado a temperaturas de -18,8ºC, -5,4ºC y
9,5 ºC y 29,2ºC (254,4 K, 267,8 K, 282,7 K y 302,4 K respectivamente).
12
Ductos y Tuberías para Bioprocesos
El fluido presentó un comportamiento de la ley de potencia a cada temperatura con una pequeña variación
en el índice de comportamiento de flujo (promedio n = 0,77) pero con cambios importantes en el
coeficiente de consistencia. Modelando el coeficiente de consistencia con la ecuación de Arrhenius se
obtiene el siguiente resultado:
4,646 10
5.668
(1.22)
La ecuación 1.22 hace que el valor de K sea de fácil acceso a cualquier temperatura entre -18,8ºC
y 29,2ºC (254,4 K a 302,4 K). Este ejemplo es también útil puesto que muestra las causas por las cuales la
ecuación de Arrhenius se expresa utilizando temperaturas absolutas en vez de grados Celsius: cuando T =
0, la ecuación (1.16) se torna indefinida.
2. Reología de Tuberías
2.1
Caracterización de Fluidos para el Diseño de Tuberías.
La caracterización de fluidos para el diseño de tuberías y la selección de la bomba, caen
en el campo de los ensayos estacionarios del esfuerzo de la cizalla dentro del vasto mundo de la
reología. Para determinar las propiedades del fluido útiles para el diseño de tuberías, se utiliza el
viscosímetro rotacional, que es el instrumento más común y útil para obtener el esfuerzo de corte
en estado estacionario, en esta categoría de instrumentos, los más utilizados son los sistemas de
cilindros coaxiales que son
los instrumentos importantes en un laboratorio de reología de
tuberías, también son muy útiles los de cono y placa y placas paralelas, para este tipo de sensores
el tamaño de las partículas del fluido es la desventaja que tiene importancia y es limitante, este
efecto cobra más importancia para los sensores de cono y placa. Los viscosímetros de mezclas
(analizados en el capítulo 2.3), pueden ser utilizados para establecer el comportamiento de flujo
cuando las partículas son bastante grandes para obstaculizar el flujo de fluidos sometidos a cizalla
en los instrumentos rotacionales convencionales.
2.2.
Viscosimetría de Cilindros Coaxiales.
El viscosímetro de cilindros coaxiales, puede ser descrito como un cilindro (sensor),
colocado en el interior de un segundo cilindro (copa) y el fluido a ensayar se coloca en el espacio
anular que dejan los dos cilindros. Una geometría muy utilizada es la que se basa en los
estándares alemanes del Deutsches Institut für Normung DIN) (Instituto Alemán
de
Normalización), y es la que se presenta en la Fig. 2.1. Para obtener resultados seguros y por ende
sus cálculos, se recomienda las relaciones siguientes, entre las variables de cilindros coaxiales
que están especificados en la Norma DIN 53019.
1,0847;
3;
´
1;
´´
1;
0,3;
120°
1°
14
Ductos y Tuberías para Bioprocesos
Figura 2.1. Sistema de cilindros coaxiales basado en la Norma DIN 53019.
Donde θ es el ángulo del vértice cónico del extremo inferior del cilindro interior del sistema. Al
realizar un ensayo, el fluido es cargado hasta el nivel h” (Fig. 2.1). Otro diseño muy utilizado es
el que cumple las especificaciones de la Norma DIN 53018 y se presenta en la Fig. (2.2). Esta
geometría es de tal forma que el cilindro sensor tiene extremos rebajados para minimizar los
errores que producen los efectos de punta.
Al realizar un ensayo de un viscosímetro de cilindros coaxiales el operador elije una
velocidad de rotación (Ω) para el sensor y mide el torque resistente (M), al efecto de rotación. Se
toman datos a diferentes velocidades dentro del rango de esfuerzo de cizalla apropiado para el
problema en estudio.
Reología de Tuberías
15
Figura 2.2. Sistema de cilindros coaxiales que cumplen con la Norma DIN 53018.
Las propiedades reológicas, se obtienen al hacer el diagrama de esfuerzo de cizalla versus la
velocidad de deformación en cizalla a partir de los datos experimentales obtenidos, este gráfico es
el reograma del fluido en estudio. El esfuerzo de cizalla es directamente proporcional al torque y
a la velocidad de deformación en cizalla, es directamente proporcional a la velocidad de rotación
(velocidad angular). El esfuerzo de cizalla y la velocidad de deformación en cizalla en la
superficie del sensor (
1
2
Y,
y
respectivamente) pueden ser calculados aplicando:
(2.1)
16
Ductos y Tuberías para Bioprocesos
Ω
2α
α
(2.2)
1
Donde,
.
La variable ho en el denominador de la Ec. (2.1), es una medida ficticia que se agrega a la altura
del sensor (h) para tomar en cuenta el efecto de punta del sensor, dicho efecto de punta es la
contribución al torque que hacen la cara superior e inferior del sensor. Para el sensor de la Fig.
2.1 (DIN 53019), la corrección por efecto de punta es aproximadamente un 10 % de la altura
medida en una paralela a la copa ho = 0,1 h. Al utilizar el diseño presentado en la Fig. 2.2 y
manteniendo la distancia entre el fondo de la copa y en extremo superior del sensor en tres veces
la magnitud del espacio entre el sensor y la copa, la corrección por efecto de punta es muy
pequeña. Cumpliendo esta restricción por efecto de punta es aproximadamente 0,5 por ciento de
la altura del sensor: ho = 0,005 h.
También pueden utilizarse valores y promedios del esfuerzo de cizalla y de la velocidad de
deformación en cizalla dentro del área anular. La norma DIN establece que la velocidad de
deformación en cizalla (llamado el esfuerzo de cizalla representativo), puede calcularse
aplicando:
1
(2.3)
4
La velocidad en cizalla correspondiente (llamada la velocidad de deformación en cizalla
representativa), se calcula con:
Ω
α
α
1
1
(2.4)
Reología de Tuberías
17
Las constantes de proporcionalidad de las Ec. (2.1) hasta Ec. (2.4), están con paréntesis cuadrado.
Estas ecuaciones son válidas cuando el espacio anular es pequeño 1< α ≤ 1,10. Al tener
espaciamientos mayores, se producen errores significativos en las propiedades reológicas del mix
de helado de crema a partir de los datos obtenidos en el viscosímetro de cilindros coaxiales.
En el ejemplo resuelto en el problema 8.3, se analiza la problemática de encontrar las propiedades
reológicas del mix de helado de crema a partir de los datos obtenidos en el viscosímetro de
cilindros coaxiales.
2.3
Viscosimetría de Mezcla
Los viscosímetros de cilindros coaxiales son excelentes para caracterizar el
comportamiento reológico de fluidos, con el objetivo del diseño de tuberías y la selección de
bombas. Sin embargo, algunos fluidos no pueden ser probados en forma adecuada en los
viscosímetros de espacio anular pequeño o de separación pequeña de placas (viscosímetro de
placas paralelas y de cono y placa) debido a que presentan una o más de las características
siguientes:
•
Partículas demasiado grandes para la separación de los sensores, ya que se agrega un
torque. Para evitar los errores, la sección máxima de las partículas más grandes, debe ser
menor a un tercio del espacio anular (cilindros coaxiales) o de separación de placas (Rc –
Rb)/3, ya que las medidas de los espacios anulares están entre 1 a 6 mm, los diámetros de
las partículas están limitadas al rango de 0,33 a 2 mm en el caso de los viscosímetros de
cilindros coaxiales.
•
Materiales que presentan separación de fases (fenómeno llamado slip) durante los ensayos
provocan una migración de partículas durante la rotación que se traduce en que se forma
una capa más fluida en las superficies del sistema del ensayo.
•
La gravedad provoca decantación de las partículas transformando la muestra de
homogénea en una heterogénea.
Los viscosímetros de mezclas son la solución adecuada al presentarse los problemas indicados
que hacen inapropiados los viscosímetros rotacionales.
18
Ductos y Tuberías para Bioprocesos
Los
párrafos siguientes, presentan información práctica sobre la utilización del
viscosímetro de mezcla basada en la metodología k” (llamada también el método de la curva de
torque). En la sección 2.3.1, titulada Caracterización del Viscosímetro de Mezcla, se presenta
el procedimiento que está basado en la determinación del coeficiente de mezcla (k”) y de la
constante del viscosímetro de mezcla (k´). Estas técnicas requieren utilizar varios fluidos
estándares que son imprescindibles si una geometría de mezcla no probada va a ser utilizada para
obtener los datos reológicos.
En la sección, titulada: Encontrando las Propiedades Reológicas de Fluidos Tipo Ley de la
Potencia, se presenta la metodología para calcular la viscosidad aparente como función de k” y
se da una velocidad de deformación en cizalla definido por el valor k´. Esta aproximación da una
metodología consistente para obtener un reograma de un fluido con un viscosímetro de mezcla
que ha sido caracterizado reológicamente utilizando los métodos presentados en el punto 2.3.1.
2.3.1
Caracterización del Viscosímetro de Mezcla
El viscosímetro de mezcla, puede ser caracterizado en forma adecuada antes de ser
utilizado para obtener datos para el diseño de tuberías. El análisis se lleva a cabo utilizando
números adimensionales y fluidos estándares de propiedades reológicas conocidas. El análisis
dimensional de agitación de fluidos Newtonianos en régimen laminar, establecen las relaciones
empíricas entre el número de la potencia (NPo) y el número de Reynolds (NRe,I) del rotor.
(2.5)
,
Donde:
Φ
Ω
(2.6)
Reología de Tuberías
19
Ω
(2.7)
,
Donde A, es una constante adimensional. Las variables Φ, d y Ω representan la potencia
requerida para hacer girar el rotor, el diámetro del rotor y la velocidad angular del rotor,
respectivamente. Cuando las unidades de la velocidad angular son rad s-1, el flujo es considerado
laminar si NRe, I < 63.
La Ec. (2.5) es utilizada como la base para determinar las propiedades reológicas de los fluidos.
Reemplazando la Ec. (2.6) y (2.7) en la Ec. (2.5) resulta:
(2.8)
Ω
Ω
La potencia (Φ) es definida como el producto entre el torque (M) y la velocidad angular (Ω):
Ω
(2.9)
Reemplazando la Ec. (2.9) en la Ec. (2.8) y simplificando el resultado, se obtiene una ecuación
para la viscosidad de un fluido Newtoniano:
Ω
"
Ω
Donde k”, es una constante definida como el coeficiente de mezcla: "
(2.10)
. Los fluidos
Newtonianos con viscosidad conocidas son utilizados para obtener k”. Esta constante integra la
relación dinámica entre el sistema físico (mezclador, rotor, grado de llenado), el torque, la
velocidad angular del rotor y la viscosidad.
Para evaluar fluidos tipo ley de la potencia en un viscosímetro de mezcla, la viscosidad aparente
(η) se define como función de la velocidad de deformación promedio:
20
Ductos y Tuberías para Bioprocesos
(2.11)
La velocidad de deformación en cizalla promedio
es definida como el producto entre la
constante del viscosímetro de mezcla (k´) y la velocidad angular:
´Ω
(2.12)
Para determinar la velocidad de deformación en cizalla promedio, se debe aplicar la suposición
clave, que la viscosidad newtoniana y la viscosidad aparente son iguales a igual esfuerzo de
cizalle. De lo anterior la Ec. (2.10) se iguala a la Ec. (2.11):
"
Ω
(2.13)
Resolviendo la Ec. (2.13) para la velocidad de deformación en cizalla, resulta:
"
Ω
(2.14)
El coeficiente de mezcla (k”) y la constante del viscosímetro de mezcla (k´) pueden ser
encontrados, ejecutando los siguientes pasos:
1) Obtener fluidos newtonianos y medir la viscosidad a las temperaturas de ensayo
seleccionadas usando un viscosímetro rotacional con accesorios convencionales como el
cilindro coaxial. Los fluidos propuestos incluyen: miel, jarabe de maíz, aceite de silicona
y glicerina.
2) Usando los fluidos newtonianos estándar, evaluados en el Paso 1, recolectar los datos
experimentales de torque versus la velocidad angular en el sistema del viscosímetro de
mezcla. Usando la Ec. (2.10), escrita como:
Reología de Tuberías
Ω
"
21
(2.15)
Graficar el producto de la viscosidad y la velocidad angular (eje y) versus el torque (eje
x). Luego por regresión lineal, determinar k” como la pendiente de la Ec. (2.15). si la
relación es no linear, la suposición inicial, que hay una relación linear entre el número de
potencia y el número de Reynolds del rotor (establecido matemáticamente por la Ec. (2.5)
es invalida, y k” no puede ser determinada usando éste método. Los datos experimentales
tomados para el jarabe de maíz y la miel, fueron usados para establecer k” para un rotor
helicoidal tipo tornillo en el Problema Ejemplo 8.4.
3) Evaluar fluidos tipo ley de la potencia, que pueden ser ensayados en un viscosímetro de
cilindro coaxial, y determinar el coeficiente de consistencia y el índice de comportamiento
de flujo de éstos materiales a las temperaturas apropiadas. Los fluidos propuestos,
incluyen materiales como soluciones acuosas de goma guar (1%) y metilcelulosa (1,0;
2,0; y 2,5%).
4) Usando como estándar fluidos tipo ley de la potencia, evaluados en el Paso 3, recolectar
los datos experimentales de torque versus la velocidad angular en el viscosímetro de
mezcla. Usando éstos datos, k” encontrado en el Paso 2, y Ec. (2.14), determinar la
velocidad de deformación en cizalla para cada velocidad angular.
5) Tomando el conjunto de datos de la velocidad de deformación en cizalla versus la
velocidad angular generada en el Paso 4, determinar la constante del viscosímetro de
mezcla (usando además análisis de regresión) como la pendiente de la Ec. (2.12).
Si bien los principios del viscosímetro de mezcla están bien establecidos, las compañías de
instrumentos comerciales, no se han aplicado para establecer línea de producción para
viscosímetro para línea de producción. Algunas discusiones de los datos publicados, problemas
comunes y oportunidades en viscosímetros de mezcla son garantizadas.
22
Ductos y Tuberías para Bioprocesos
Tabla 2.1 Valores Típicos de k’’ y k’ para Rotores Escala de Laboratorio.
d*
Rotor
D#
Gap+
k´
k”
(cm)
(cm)
(cm)
(rad m )
(rad-1)
3,30
4,20
0,45
1.632
1,4
5,30
9,30
2,00
3.047
1,6
De paleta inclinada Haake
4,14
4,20
0,03
2.215
4,5
4
3,28
3,66
0,19
12.570
3,2
1,50
1,90
0,20
61.220
2,9
Helicoidal para gomas1
De tornillo helicoidal cortado2
3
De paleta inclinada RVA
Rotor tipo bandera de Brookfield5
*
#
-3
+
d= diámetro del rotor; D= diámetro de copa; gap=(D-d)/2
Nota: gap es la separación entre el sensor y la copa
1
Steffe, J.F., E. Agrawal y K.D. Dolan. J. Texture Stud. (2003) 34: 41-52;
2
Omura, A.P. y J.F. Steffe. J. Food Proc. Engr. (2003) 26: 435-445;
3
Steffe, J.F. y E.W. Ford. J. Texture Stud. (1985) 16:179-192;
4
Lai, K.P., J.F. Steffe y P.K.W. Ng. Cereal Chem. (2000) 77: 714-716;
5
Briggs, J.L. y J.F. Steffe. J. Texture Stud. (1996) 27: 671-677.
Los valores típicos de la constante del coeficiente de mezcla y de la constante del viscosímetro de
mezcla, determinados de acuerdo al procedimiento dado anteriormente se entregan en la Tabla
2.1. Éstas constantes son solo empíricas y se pueden relacionar exclusivamente con la geometría
(rotor y copa) con las que se han testeado. Otros factores como los niveles de fluido durante el
ensayo y el espacio entre el rotor y la copa, también deben ser mantenidos. Una limitación de la
viscosimetría de mezcla es que valores bajos de k´, restringen los instrumentos a valores
moderados del esfuerzo de cizalla, los que pueden estar por debajo del esfuerzo de cizalla
máximo encontrado en las líneas de tuberías. Además, la capacidad de torque del instrumento
puede limitar el análisis a bajos esfuerzos de cizalla cuando se trata de materiales espesos.
Todos los mezcladores son útiles para evitar el desfase (separación de fases) durante los
ensayos. Como guía general, el tamaño máximo de partícula debe ser de un tercio de la distancia
de separación entre el borde externo del rotor y la pared del contenedor:
Reología de Tuberías
ñ
23
(2.16)
á
6
En algunas ocasiones, los fluidos que exceden el tamaño de partícula recomendado, pueden ser
ensayados a velocidades angulares bajas de manera exitosa. Además, cuando se examinan los
fluidos tipo ley de la potencia, con un viscosímetro de mezcla, se deben mantener las condiciones
de flujo laminar para generar datos experimentales aceptables. Se asume un flujo laminar cuando
la ley de la potencia del número de Reynolds del rotor es menos que 63:
Ω
,
,
Ω
´Ω
63
(2.17)
Con la velocidad angular (Ω) en rad/s.
Los sensores identificados en la Tabla 2.1 se muestran en las Fig. 2.3 a 2.7. Cada sistema
de sensor es único.
•
Rotor Helicoidal para Gomas (Fig. 2.3). Este rotor (fabricado en el Laboratorio de
Reología de Alimentos de la Universidad Estatal de Michigan, East Lansing, MI), fue
diseñado para estudiar emulsiones tales como mayonesa. Durante la rotación del sensor,
el fluido en forma simultánea es agitado y elevado en el helicoide antes de caer a lo largo
del eje central, hacia el fondo de la copa.
•
Rotor de Tornillo Helicoidal Cortado (Fig. 2.4). Este rotor (fabricado en el Laboratorio
de Reología de Alimentos de la Universidad Estatal de Michigan, East Lansing, MI), fue
construido en escala 1/3, como réplica de un sistema exitoso de ensayo de hormigón. El
diseño ayuda en el movimiento de las partículas grandes. Los fluidos que han sido
ensayados en forma exitosa con este sensor son: crema de choclo, salsa espesa (picada),
salsa de tomates picados.
24
Ductos y Tuberías para Bioprocesos
Figura 2.3. Rotor helicoidal para gomas (diámetro= 3,30 cm).
Figura 2.4. Rotor de tornillo helicoidal cortado (diámetro 5,30 cm).
Reología de Tuberías
•
25
Rotor de Paletas Inclinadas Haake (Fig. 2.5). El agitador (fabricado por Thermo
Electron Corporation, Walthman, MA), tiene dos paletas verticales inclinadas en un
ángulo de 15 grados con una perforación de 9 mm de diámetro en cada una de las paletas.
Ésta geometría mantiene las partículas en suspensión, lo que permitió estudiar la
gelatinización de soluciones acuosas de almidón. También ha sido utilizado con diferentes
purés de fruta.
•
Paletas Inclinadas RVA (Fig. 2.6). El agitador RVA (Rapid Visco Analyser, Newport
Scientific, Warriewood, Australia), es utilizado para estudiar “las propiedades viscosas
del almidón cocido, granos, harinas y alimentos”, sirve para caracterizar el
comportamiento pastoso de soluciones acuosas del almidón durante el calentamiento y el
enfriamiento. Las paletas inclinadas y curvas mantienen las partículas en suspensión
durante la rotación.
•
Rotor tipo Bandera de Brookfield (Fig. 2.7). El agitador de bandera de Brookfield
(Brookfield Engineering Laboratories, Middleboro, MA), está diseñado para usar el
“adaptador para muestras pequeñas Brookfield” (copa de 13 cc). Este diseño ha sido
utilizado exitosamente en muchos productos alimenticios.
Figura 2.5. Paletas inclinadas (ángulo de 15 grados) Haake (diámetro 4,41 cm).
26
Ductos y Tuberías para Bioprocesos
Figura 2.6. Paletas inclinadas RVA (diámetro 3,28 cm).
Figura 2.7. Agitador de bandera de Brookfield (diámetro 1,5 cm).
Reología de Tuberías
27
2.3.2 Evaluando las Propiedades de Fluidos Tipo Ley de la Potencia
Una vez que se ha caracterizado el sistema de viscosímetro de mezcla al determinar k” y
k´, las propiedades del fluido tipo ley de la potencia, pueden ser calculadas a partir de los datos
experimentales. La velocidad rotacional del sistema debe ser seleccionada para que esté dentro
del rango de velocidades de deformación en la tubería.
Esto se cumple utilizando k´: ya que
⁄ ´ y
á
á
⁄ ´; se puede
establecer que el mejor rango para Ω es:
á
´
(2.18)
´
Una vez que se fija el rango de velocidad rotacional, se pueden obtener una serie de datos
de torque (M) versus la velocidad angular ( ). La suposición de la viscosidad, se aplica
utilizando k”, de modo que la viscosidad aparente puede ser calculada a cada velocidad.
"
Ω
(2.19)
La velocidad de deformación en cizalla correspondiente definida por la Ec. (2.13), puede
ser calculada a cada velocidad. Los valores obtenidos de viscosidad aparente versus la velocidad
de deformación en cizalla promedio se grafican; y aplicando un análisis de regresión a los datos,
utilizando la Ec. (2.11), se pueden obtener el índice de comportamiento de flujo y el coeficiente
de consistencia. Este procedimiento se aplica a salsa para pastas con trozos de tomate y callampas
que es tratado en el Problema Ejemplo 8.5.
2.3.3 Viscosímetro de Brookfield con Aguja de Disco
Los viscosímetros de Brookfield (Brookfield Engineering Laboratories, Middleboro,
MA), equipados con un rotor de aguja con disco (Fig. 2.8), se utilizan a menudo para estudiar
fluidos reológicos. Desgraciadamente sucede que la velocidad de deformación en cizalla sobre un
disco delgado no es uniforme y es muy difícil de modelar matemáticamente.
28
Ductos y Tuberías para Bioprocesos
Sin embargo se puede realizar una aproximación con la viscosimetría de mezcla y se pueden
definir un esfuerzo de cizalla promedio y una velocidad de deformación en cizalla promedio; con
esto, estos sensores pueden utilizarse para determinar propiedades de fluidos no newtonianos. El
procedimiento que se presenta a continuación fue desarrollado por Mitschka [Rheol. Acta (1982)
12:207-209] y complementado por Briggs y Steffe [J. Textures Studies (1997) 28: 517-522].
El primer paso es calcular el índice de comportamiento de flujo (n) que se obtiene
de:
(2.20)
ó en forma logarítmica:
ln
ln
ln
(2.21)
(rad/s) puede ser utilizado en lugar de N (revoluciones/min) en la Ec. (2.20) y Ec. (2.21) y no
se producen cambios en el valor calculado de n. N es utilizado por conveniencia porque los
operadores de Brookfield, seleccionan la velocidad en revoluciones por minuto cuando operan el
instrumento. Hay que destacar que el porcentaje de torque, el parámetro típico del instrumento de
Brookfield, puede ser sustituido por M en las ecuaciones descritas, sin afectar los cálculos para
encontrar el índice de comportamiento de flujo.
Reología de Tuberías
29
Figura 2.8. Viscosímetro de Brookfield con aguja de disco (diámetro de 3,5 cm).
El esfuerzo de cizalla promedio se calcula de acuerdo a:
(2.22)
Donde
, es conocido como el factor de corrección del esfuerzo de cizalla, que cambia con el
número del sensor (Tabla 2.2). El valor C (constante adimensional), depende del torque máximo
que soporta cada instrumento (Tabla 2.3).
Tabla 2.2. Factores de corrección de esfuerzo de cizalla (
rotor Brookfield.
Número de aguja, Brookfield
, Pa
1
0,035
2
0,119
3
0,279
4
0,539
5
1,05
6
2,35
7
8,40
) para rotores Brookfield. Número del
30
Ductos y Tuberías para Bioprocesos
Tabla 2.3. Valores de C para viscosímetros típicos de Brookfield.
Modelo de viscosímetro
Torque máximo, dina cm
C, adimensional
½ RV
3,584
0,5
RV
7,187
1,0
HAT
14,374
2,0
HBT
57,496
8,0
El porcentaje de torque, es el porcentaje de torque máximo obtenido durante los ensayos de
velocidad constante. La velocidad de deformación en cizalla promedio es:
(2.23)
Donde
, conocido como el factor de conversión de la velocidad de deformación de cizalla,
depende del calor numérico del índice de comportamiento de flujo:
0,263
1
,
(2.24)
La metodología estándar de Brookfield, se aplica a las muestras para obtener los datos reológicos.
Se colocan muestras en el vaso de Griffin de 600 ml de forma baja y un rotor se conecta a la
mordaza del eje. A continuación se registran la serie de datos de torque versus la velocidad
angular (rpm) y el cálculo de las propiedades reológicas, se realizan según el procedimiento
siguiente:
El índice de comportamiento de flujo (n), se calcula aplicando la Ec. (2.21). Los valores
promedios del esfuerzo de cizalla y de la velocidad de deformación en cizalla, se calculan
utilizando las Ec. (2.22) y (2.23), respectivamente. Las propiedades reológicas de fluidos tipo ley
de la potencia, se obtienen de los análisis de regresión de los resultados experimentales. El índice
de comportamiento de flujo calculado en este paso es idéntico al valor obtenido de aplicar la Ec.
(2.21).
Reología de Tuberías
2.4
31
Viscosímetros de Cono y Placa y Placas Paralelas
Los sensores cono y placa son muy comunes en los viscosímetros rotacionales. El ángulo
del cono (Fig. 2.9), es muy pequeño, comúnmente entre 2 y 4 grados. La ventaja que representa
la geometría como y placa, es que el esfuerzo de cizalla y la velocidad de deformación en cizalla
son uniformes en toda la zona que cubre el cono y puede ser calculada en forma sencilla como la
velocidad angular dividida por la tangente del ángulo del cono (θ):
(2.25)
tan
La velocidad de deformación en cizalla correspondiente, es directamente proporcional al
torque e inversamente proporcional al cubo del radio:
3
2
(2.26)
En los sistemas de placas paralelas (Fig. 2.9), la velocidad de deformación en cizalla, se
calcula en el borde exterior de la placa, en función de la velocidad angular, el radio y la distancia
que separa las placas (h):
(2.27)
Los valores típicos de h, estarían entre 0,5 y 2,0 mm. Al calcular el esfuerzo de cizalla en el
borde, puede requerir una corrección debido a fenómenos no newtonianos. Suponiendo que se
cumple la Ley de la Potencia, este puede ser determinado aplicando:
3
2
Donde:
(2.28)
32
Ductos y Tuberías para Bioprocesos
ln
ln
ln
ln
Figura 2.9. Sensores de cono y placa (izquierdos) y placas paralelas (derecha).
(2.29)
3. Cálculos de Pérdida de Carga y Energía
3.1
Ecuaciones de Balance de Energía Mecánica
La selección de bombas requiere una evaluación de la energía y potencia necesarias para mover un
líquido al interior de una tubería. Este transporte es evaluado mediante la ecuación general de balance de
energía mecánica (a veces llamada ecuación de Bernoulli), que puede ser escrito de la siguiente manera:
(3.1)
ó cuando es resuelta para W (el trabajo aportado por la bomba, J/kg) como:
(3.2)
Cada término en la ecuación (3.2) representa el balance de energía (el cual puede ser negativo o positivo)
por unidad de masa:
é
(3.3)
ó
é
é
í
(3.4)
é
í
(3.5)
é
, /
(3.6)
Los subíndices uno y dos se refieren a dos ubicaciones de control de volumen a lo largo del sistema de
bombeo. La ecuación de balance de energía mecánica aplicada a cambios en el diseño de tuberías se aplica
en los problemas ejemplos 8.7 y 8.8.
Ductos y Tuberías para Bioprocesos
34
Los valores del factor de corrección de energía cinética (a) pueden ser determinados como sigue: a = 2,0
para flujo turbulento o cualquier fluido; a = 1 para flujo laminar de fluidos Newtonianos y, para flujo
laminar de fluidos de ley de potencia, a es función de índice de comportamiento de fluido:
2 2
1 5
3 3
1
3
(3.7)
La sumatoria de las pérdidas por fricción descrita por la ecuación 3.6 incluye todos los siguientes casos:
1) Pérdidas en una tubería recta con un término separado para cada diámetro:
2
(3.8)
Donde f es el factor de fricción de Fanning. Los procedimientos para la determinación de f serán
presentados en el capítulo 4. Para secciones transversales no circulares, el diámetro hidráulico (Dh) puede
ser utilizado en lugar del diámetro interno del tubo:
4 á
ó
(3.9)
í
En el caso de un flujo a través de un anillo, una configuración común que involucra el flujo entre dos
tubos concéntricos, el diámetro hidráulico es:
(3.10)
Donde Dexterior y Dinterior son, respectivamente los diámetros exterior e interior definiendo un área de flujo
anular.
2) Pérdidas en válvulas y accesorios calculados utilizando el método de la altura de velocidad (el
método preferido en este texto)
Cálculos de Pérdida de Carga y Energía
35
(3.11)
2
O el método de la longitud equivalente (Le):
2
(3.12)
Los procedimientos para la determinación de kf serán presentados en el capítulo 5.
3) Pérdidas en otro equipamiento, como por ejemplo medidores de flujo y válvulas neumáticas, son
adicionados agregando datos entregados por el fabricante como caída de presión a lo largo del
equipamiento (cuando es operado al caudal requerido para agua) dividido por la densidad:
∆
(3.13)
Un método para cuantificar las pérdidas de energía para otros fluidos, basados en datos a partir del agua,
se discute en la sección 5.2. El método es aplicado para un fluido Newtoniano (crema) en el problema
ejemplo 8.7, y para un fluido no Newtoniano (jugo de pulpa de fruta) en el problema ejemplo 8.8.
La potencia hidráulica Φ se define como el trabajo multiplicado por el caudal másico.
Φ
(3.14)
Y la eficiencia de la bomba (no confundir con la viscosidad aparente, la cual es definida con el mismo
símbolo, η ) es:
á
(3.15)
Ductos y Tuberías para Bioprocesos
36
La potencia requerida, también es conocida como potencia al freno, representa la potencia aplicada
necesaria en el eje de la bomba. Esta incluye la potencia necesaria para transportar el fluido a través del
sistema (la potencia hidráulica), y la potencia requerida para superar las pérdidas por fricción en la misma
bomba.
3.2
Curvas del Sistema (Requerimientos de Proceso)
Las curvas del sistema describen la energía necesaria para alcanzar objetivos específicos de
procesamiento. Estas son obtenidas resolviendo las ecuaciones de balance de energía en términos de altura
(expresado en metros). Trabajo del eje (W) que puede ser definido utilizando la altura total del sistema
(Hs):
(3.16)
Hs es la altura total de la descarga menos la altura total de succión. Combinando la definición de trabajo
del eje definida por la ecuación 3.2 y la ecuación 3.16 da un Hs en términos de la presión, velocidad,
elevación y pérdida por fricción:
∑
(3.17)
Donde cada grupo de términos de la ecuación 3.17 representa un cambio (negativo o positivo) en la altura:
é
é
,
é
∑
é
(3.18)
ó ,
ó ,
ó ,
(3.19)
(3.20)
(3.21)
Cálculos de Pérdida de Carga y Energía
37
Aunque la altura se expresa en metros, realmente representa energía por unidad de peso. Dividiendo los
cambios de energía por unidad de masa expresados en la ecuación (3.3) a la ecuación 3.6, por g se
obtienen unidades de Joules por Newton. En el Sistema Internacional un Joule por Newton tiene unidades
de longitud: metro.
Hs es función del caudal volumétrico expresada en unidades de m3s-1 o gpm. Si se grafica la carga total del
sistema versus el caudal volumétrico se obtiene la curva del sistema requerida para el proceso. La altura
de velocidad (perfil de velocidad) (considerando la diferencia de energía cinética), es generalmente
pequeña y usualmente despreciada para los cálculos de carga. Las curvas del sistema son necesarias para
evaluar bombas centrífugas para aplicaciones específicas. No son necesarios para dimensionar bombas de
desplazamiento positivo debido a que el caudal es fuertemente independiente de las pérdidas por fricción
que se puedan encontrar en el proceso. Una curva de sistema para helados se presenta en el problema
ejemplo 8.7 y los cálculos para una bomba de desplazamiento positivo se muestran en el problemaejemplo 8.8.
3.3
Determinando Trabajo y Altura
Investigar algunas aplicaciones típicas es una manera útil para determinar ecuaciones de balance
de energía mecánica. Un problema muy habitual contempla el bombeo de un fluido desde un camióntanque hacia un tanque de almacenamiento. Tuberías flexibles (mangueras) que salen desde el camión
para unirse a tuberías rígidas cerca de la bomba. Asumiendo que los depósitos tienen las escotillas
abiertas, por lo tanto, la presión en la parte superior de cada tanque es de una atmósfera. La figura 3.1
ilustra una situación de descarga, donde la presión en los puntos uno y dos es igual: P1=P2. Dado que el
movimiento del liquido en la superficie es muy bajo, se puede asumir que las velocidades a los puntos
uno y dos son esencialmente cero:
0. La pérdida de energía en el filtro se calcula en términos
de la caída de presión a lo largo del filtro (a una tasa especifica de flujo) dividido por la densidad del
fluido: Δ / . Esta información está basada en datos experimentales del agua entregados por una empresa
manufacturera de filtros. Puede ser ajustada para fluidos no-Newtonianos utilizando el método dado en la
sección 5.2.
Ductos y Tuberías para Bioprocesos
B
38
Figura 3.1
3 Línea dee proceso enntre un camiión cisterna y un tanquee de almacennamiento coon control dee
volumenn ubicado enttre los nivelees de liquido.
Las pérddidas de enerrgía en ambaas secciones, rígida y flexxible en las zonas
z
ligeram
mente curvass, del sistemaa
de tuberíías (figura 3..1) se calculaa mediante el factor de frricción de Faanning. Las ppérdidas son en la entradaa
desde el camión cisteerna hacia laa cañería, doss codos, la válvula
v
y la salida desde lla cañería haacia el tanquee
de almaacenamiento son evaluaddas utilizanddo coeficienntes de pérddida de friccción. Adicio
onalmente see
requierenn otros térmiinos si tuboss de diferentees tamaños see usan en la línea de proccesamiento, debido a quee
este cam
mbio afecta ell parámetro
y f. Ademáás es importaante notar quue la mayor ddemanda de energía de laa
bomba sucede
s
cuanndo el camióón cisterna esta
e
cerca de
d vaciarse y el tanque de almacenamiento estaa
próximoo a completaarse debido a que en esee momento la bomba essta trabajanddo en contraa de la cargaa
máximo de elevaciónn (z2-z1). Ressultados anallíticos (Tablaa 3.1) deben ser evaluadoos en términoos del trabajoo
(W) ó dee la altura tottal del sistem
ma (Hs=W/g)..
E problema ilustrado enn la figura 3.2
El
2 es muy sim
milar al problema que se muestra en la figura 3.1,
excepto por que el ppunto dos se ubica justo antes
a
de la zzona de descaarga de la caañería. En essta aplicaciónn
de la ecuuación de balance de eneergía mecánicca es necesarrio introduciir algunas nuuevas considderaciones: laa
velocidaad a la salidaa del controll de volumenn es diferennte de cero debido
d
a quee el fluido essta aún en laa
cañería; P1 = 1 atm
m (presión abbsoluta) perro P2 > 1 attm (presión absoluta) y debe ser reetenido en laa
soluciónn; la pérdida por
debido a quee se encuentrra más allá el
p fricción en la salida del
d tubo es despreciable
d
e
control de
d volumen;; las pérdidaas por friccióón incluyen los tres coddos. Otros eelementos dee la ecuaciónn
permaneecen intactos y la soluciónn para el traabajo en el eje esta presenntado en la taabla 3.1
Cálculos de Pérdida de Carga y Energía
39
Tabla 3.1 Aplicación de las ecuaciones de balance de energía mecánica a las figuras 3.1 a 3.6
Trabajo del eje y carga total para el problema de la figura 3.1
2
2
,
2
2
2
,
,
º
, á
Δ
,
2
,
º
, á
Δ
,
Trabajo del eje para el problema de la figura 3.2
2
3
,
2
,
º
Δ
, á
Trabajo del eje para el problema de la figura 3.3
2
2
3
,
,
º
, á
Δ
,
Presión de bombeo diferencial para el problema de la figura 3.4
Presión a la salida de la bomba (P1) para el problema de la figura 3.5
2
2
2
,
º
, á
,
Presión en la entrada de la bomba (P2) para el problema de la figura 3.6
2
2
,
Δ
40
Ductos y Tuberías para Bioprocesos
Figura 3.2 Línea de proceso entre un camión cisterna y un tanque de almacenamiento con control de
volumen ubicado entre el nivel del fluido en el camión en un punto dentro del tubo de salida.
Un problema relacionado se presenta en la figura 3.3. En este caso, sin embargo, el control de volumen se
encuentra en un punto fuera de la tubería, donde la superficie del fluido alcanza la presión de una
atmósfera y la energía cinética ha sido mayormente disipada. Esta situación requiere que la pérdida por
fricción en la salida deba ser incluida en los cálculos, pero permite la eliminación de la energía de presión
debido a que P1 = P2. Las partes de la solución representadas para la solución de la figura 3.1 permanecen
inalteradas (Tabla 3.1). La ecuación de balance de energía mecánica [ecuación 3.2] también puede ser
aplicada a lo largo de la misma bomba (Fig. 3.4). Esto es útil en la predicción de la presión diferencial a lo
largo de la bomba dado un valor conocido de W
Cálculos de Pérdida de Carga y Energía
41
Figura 3.3 Línea de proceso entre un camión cisterna y un tanque de almacenamiento con control de
volumen ubicado entre el nivel del fluido en el camión en un punto justo en la salida del tubo.
Figura 3.4 Línea de proceso entre un camión cisterna y un tanque de almacenamiento con control de
volumen ubicado entre la entrada y la salida de la bomba.
Otro problema práctico se muestra en la Figura 3.5, donde el control de volumen se define entre la salida
de la bomba y la descarga al tanque. En este caso W = 0 (no hay bomba en el control de volumen),
0
(bombeo hacia un gran tanque), y las pérdidas por fricción suceden en la válvula, la rejilla, dos codos, la
salida y la tubería recta. Dadas estas condiciones, la presión real en la salida de la bomba puede ser
calculada (Tabla 3.1). La información puede ser necesaria para evaluar la integridad de los sellos de una
bomba. La figura 3.6 muestra el problema análogo de encontrar la presión en la entrada de la bomba.
42
Ductos y Tuberías para Bioprocesos
La solución está dada en la Tabla 3.1. Este problema debe ser resuelto para determinar la altura de succión
neta positiva disponible en un sistema de bombeo, más detalle podrá encontrar en la sección 3.5.
Figura 3.5 Línea de proceso entre un camión cisterna y un tanque de almacenamiento con control de
volumen ubicado entre la salida de la bomba y la salida del sistema.
Figura 3.6 Línea de proceso entre un camión cisterna y un tanque de almacenamiento con control de
volumen ubicado entre el camión cisterna y la entrada de la bomba.
Cálculos de Pérdida de Carga y Energía
3.4
43
Curvas de Bomba (Bombas Centrífugas)
Las curvas del sistema deben ser comparadas con las curvas de la bomba para determinar las
condiciones reales de operación para bombas centrífugas. Estas curvas son determinadas para una bomba
en particular, operando a una velocidad constante (habitualmente 1.750 o 3.500 rpm), midiendo la presión
en la entrada (P1) y la salida (P2) mientras se mueven diferentes volúmenes de agua (m3s-1 o gpm) a través
del equipamiento. Los datos resultantes pueden ser usados para determinar la carga generada por la
bomba, llamada carga total de bombeo (Hp):
(3.22)
La intersección de los dos gráficos (Hs vs caudal, y Hp vs caudal) dan el caudal operacional de una bomba
centrífuga (Figura 3.7). Las curvas de bomba no son utilizadas para evaluar el desempeño de bombas de
desplazamiento positivo (PD) debido a que el caudal en una bomba de desplazamiento positivo (PD) es
más o menos constante en relación a la presión.
Figura 3.7 Intersección de las curvas de bomba (Hp) y el sistema (Hs) mostrando la tasa de flujo a través
de una bomba centrifuga.
Ductos y Tuberías para Bioprocesos
44
3.5
Altura de Succión Neta Positiva (Disponible y Requerida)
Para evitar problemas de cavitación, la altura de succión positiva neta disponible debe ser mayor
que la altura neta de succión de carga necesaria: (NPSH)A > (NPSH)R. El valor de (NPSH)R es tomado
desde los datos experimentales para una bomba en particular. Para determinar el valor de (NPSH)A se debe
resolver la ecuación de balance de energía mecánica para la presión de entrada en la bomba [Ecuación
(3.1)]. Este problema se muestra en la figura 3.6 donde el punto 1 se encuentra al nivel del fluido del
tanque de entrada y el punto 2 esta ubicado en la entrada de la bomba. Evaluando la ecuación de balance
de energía mecánica lleva a la siguiente solución general para la presión de entrada en la bomba:
(3.23)
Si la presión de entrada a la bomba es menor que la presión de vapor del liquido, se pueden formar
burbujas de vapor provocando un fenómeno conocido como cavitación. La ecuación (3.23) provee un
resumen matemático de las circunstancias que pueden dar lugar a fenómenos de cavitación: 1) bombeando
desde una cámara vacía haciendo P1 muy baja. 2) Incrementos significativos de la velocidad del fluido
durante el bombeo hacen que la velocidad al punto uno sea más grande que la velocidad en el punto dos;
3) requiriendo que la bomba eleve sustancialmente el líquido haciendo z2 más grande que z1; 4) habiendo
una gran pérdida por fricción en la línea de entrada de la bomba causado por un largo de tubería excesivo,
o demasiadas válvulas y accesorios, u otras obstrucciones al flujo como intercambiadores de calor o
medidores de flujo.
Para evaluar (NPSH)A, la presión absoluta en la bomba (P2) y la presión de vapor (Pv) del fluido
deben ser consideradas. Esto se logra restando la presión de vapor desde la presión total (para asegurarse
de que la presión sea la adecuada para evitar la cavitación), y dividiendo por gρ para obtener resultados en
unidades de altura, m. Entonces, la altura de succión positiva neta disponible es calculada como sigue:
(3.24)
Valores de la presión de vapor de agua, que es el solvente habitual para fluidos biológicos se presentan en
el Apéndice 9.5.
Cálculos de Pérdida de Carga y Energía
45
Sustituyendo la solución para P2, dada en la ecuación (3.23), en la ecuación (3.24) se obtiene una
ecuación para la altura de succión positiva neta disponible en términos de los componentes reconocidos
del balance de energía mecánica:
∑
(3.25)
Donde:
Altura de presión en la superficie de suministro del líquido, m.
P1 es igual a la presión atmosférica si el suministro de fluido es desde un tanque
abierto.
Altura de velocidad, m.
tanque grande, y
se asume como cero si el bombeo se realiza desde un
es la velocidad promedio en la entrada a la bomba.
Altura de elevación sobre la línea media del tanque m. La situación física puede
ser descrita como levantamiento de succión si z2 es más grande que z1, o
succión positiva (inundado) si z1 es mayor que z2. La figura 3.6 muestra un
ejemplo de succión positiva.
∑
Altura de pérdida de succión debido a la fricción en tuberías, válvulas,
accesorios, m.
Altura de presión de vapor del fluido que está siendo bombeado, m. La presión
de vapor del agua, y la mayoría de los biofluídos que contienen cantidades de
agua importantes, puede ser obtenida de las propiedades del agua dadas en
tablas de vapor saturado.
Todas las presiones utilizadas anteriormente son absolutas. Recordar que la presión absoluta es la presión
manométrica mas la presión atmosférica.
46
Ductos y Tuberías para Bioprocesos
4. Factores de Roce de Fanning
4.1
Factores de Roce
Los factores de roce son números adimensionales necesarios para determinar las pérdidas de
energía en tuberías. Corrientemente se encuentran en la bibliografía dos factores de roce, que son: el de
Fanning y el de Darcy. El factor de Darcy es igual a cuatro veces el de Fanning. Sin embargo, los dos
factores dan los mismos resultados en los cálculos aproximados de ingeniería. En este capítulo se
presentan métodos de cálculo del factor de roce de Fanning para fluidos Newtonianos y fluidos de tipo
Ley de la Potencia.
La rugosidad superficial (ε) caracteriza las condiciones en que está la superficie del tubo. El Estándar
Sanitario 3-A (3-A Sanitary Standards, Inc., McLean, Virginia, USA) establece el grado de pulido del
metal que esté en contacto con leche o productos lácteos.
La norma (3-A Standard Number 33-01) especifica que el acabado superficial del acero inoxidable
equivale a 150 grit para leche y que produce una rugosidad máxima de 32 micro pulgadas (0,8 µm). Para
los productos farmacéuticos la tubería debe tener un acabado superficial de 180 grit. La rugosidad
superficial de los tubos de acero inoxidable con acabado comercial tiene valores pequeños (Tabla 4.1).
Los tubos de acero inoxidable pulidos pueden ser considerados lisos para los fines de calcular el factor de
roce de Fanning para números de Reynolds bajos. Pequeñas diferencias pueden ser observadas en números
de Reynolds mayores.
4.2
Fluidos Newtonianos
Por definición los fluidos newtonianos son los materiales que tienen una relación lineal entre el
esfuerzo de cizalla y la velocidad de deformación en cizalla
. El número de Reynolds que describe
el comportamiento en este material al fluir en el tubo es:
4.1
Donde la velocidad promedio (
del tubo.
se calcula como el caudal volumétrico dividido por el área transversal
48
Ductos y Tuberías para Bioprocesos
4
4.2
Tabla 4.1. Rugosidad superficial (ε) de tubos de distintos materiales.
Material
ε, micro-pulgadas
ε, µm
Acero comercial
1.970
50
Extruido cobre, bronce
59
1,5
Acero inoxidable: 120 grit acabado
43 - 48
1,09 – 1,22
Acero inoxidable: 150 grit acabado
30 - 35
0,76 – 0,89
Acero inoxidable: 180 grit acabado
23 - 28
0,58 – 0,71
Acero inoxidable: 240 grit acabado
15 - 20
0,38 – 0,51
Acero inoxidable: 320 grit acabado
9 - 13
0,23 – 0,33
Tubo suave
0
0
El factor de Fanning en flujo laminar (definido por NRe < 2.100) se calcula con:
16
4.3
La ecuación de Blasius puede utilizarse para predecir el factor de roce de Fanning en tubos lisos en flujo
turbulento con números de Reynolds (NRe) entre 5.000 y 100.000.
0,0791
4.4
,
Haaland (J. Fluids Eng. March, 1983, pág. 89-90) desarrolló una ecuación para predecir el factor de roce
en flujo turbulento (NRe > 4.100) que incluye el factor de roce relativo (ε/D).
1
4
0,782 ln
,
6,9
4.5
3,7
La ecuación siguiente publicada por Churchill (Chem, Engr., Nov 7, 1977, pág. 91) cubre todos los tipos
de regímenes (laminar, transición y turbulento) e incluye el efecto de rugosidad.
Factores de Roce de Fanning
8
2
49
/
1
4.6
/
Donde,
2,457 ln
4.7
1
,
7
0,27
4.8
37.530
El factor de roce de Fanning para un Fluido Newtoniano (crema) se calcula en el Problema Ejemplo 8.7.
4.3
Fluidos Tipo Ley de la Potencia
Los fluidos tipo Ley de la Potencia tienen una relación no lineal entre el esfuerzo de cizalla y la
velocidad de deformación en cizalla:
. Los fluidos tipo Ley de la Potencia están caracterizados
por el valor numérico del índice de comportamiento de flujo que vale: 0 < n < 1 para los fluidos
adelgazantes (muy comunes), n = 1 para el caso especial del fluido Newtoniano y n > 1 para los fluidos
espesantes (no muy comunes). El número de Reynolds para fluidos tipo Ley de la Potencia que fluyen por
un tubo es:
4.9
4
,
3
8
1
Otra forma en que es encontrada comúnmente en la literatura es:
4.10
2
,
3
1
50
Ductos y Tuberías para Bioprocesos
El término “Número de Reynolds generalizado” es un sinónimo de Número de Reynolds de ley de la
potencia. Utilizar la Ec. (4.9) o (4.10) es asunto de preferencia personal ya que ambas ecuaciones dan los
mismos valores numéricos.
El flujo laminar para un fluido tipo Ley de la Potencia se presenta en una tubería cuando se
cumple:
,
,
4.11
í
El valor crítico del Número de Reynolds de fluido tipo Ley de la Potencia depende del valor numérico del
índice de comportamiento de flujo (Darby, R. 2001. Chemical Engineering, March, pág. 66-73)
,
2.100
í
875 1
4.12
Los valores del Número crítico de Reynolds (Tabla 4.2) varían desde 2.888 con n = 0,1 hasta el valor
conocido de 2.100 para fluidos Newtonianos que se logra con n = 1,0.
En la zona de flujo laminar, el factor de Fanning se calcula con una ecuación análoga a la Ec. (4.3):
16
4.13
,
Los datos experimentales indican que los factores de roce de alimentos en flujo laminar pueden ser algo
bajos. Rozema y Beverloo [LebensmWiss u. Technol. (1974) 7: 222-228] encontraron que en fluidos
biológicos (mayoritariamente alimentos) se cumplía la relación siguiente:
4.14
Donde el valor medio de C fue 14,3 (desviación estándar= 3,1). En el estudio de Steffe et al. [Trans.
ASAE (1984) 27: 616-619] se encontraron valores similares de C para fluidos tipo Ley de la Potencia.
Factores de Roce de Fanning
51
Tabla 4.2. Valores críticos del Número de Reynolds de fluidos tipo Ley de la Potencia a diferentes valores
del índice de comportamiento de flujo.
Índices de comportamiento
n
,
0,1
2.888
0,2
2.800
0,3
2.713
0,4
2.625
0,5
2.538
0,6
2.450
0,7
2.363
0,8
2.275
0,9
2.188
1
2.100
í
El factor de roce de Fanning para régimen turbulento (
4.100 para tubos lisos puede ser
,
calculado con la ecuación de Dodge y Metzner [AIChE J. (1959) 5:189-204]:
4
1
/
,
log
,
/
0,4
4.15
,
La influencia de la rugosidad de la superficie en el valor del factor de fricción para fluidos tipo Ley de la
Potencia no se conoce, por eso está omitida en la ecuación. Favorablemente esta situación no es un
problema en los sistemas de procesos donde se utilizan preferentemente tubos de acero inoxidable que
presentan muy baja rugosidad superficial. La solución de la Ec. (4.15) para
cuando el
,
se conoce,
es engorrosa porque la ecuación es implícita en .
Una alternativa para la Ec. (4.15) que es explicita en , es la relación siguiente [Darby, R., Mun, R.,
Boger, V.B. 1992. Chemical Engineering, september, pág. 116-119]. Se puede utilizar para predecir el
factor de roce de Fanning para fluidos tipo Ley de la Potencia en tubos lisos y en todo el rango del número
de Reynolds para fluidos tipo Ley de la Potencia.
52
Ductos y Tuberías para Bioprocesos
1
4.16
/
ó
Donde,
1
1 4
∆
4.17
0ó1
∆
,
,
4.18
í
16
4.19
,
4.20
0,0682
,
ó
1,79
/
10
,
,
exp
5,24
,
,
,
4.21
Al construir un gráfico con las ecuaciones anteriores se nota claramente que el índice de comportamiento
de flujo tiene una incidencia significativa en el factor de roce. Las representaciones gráficas de los factores
de Fanning basadas en las ecuaciones (4.16) a la (4.21) están en las Figuras 4.1 y 4.2 y los valores
tabulados están en el apéndice 9.11. Las curvas se superponen a valores bajos de
,
(Fig. 4.1) el factor
de roce de Fanning para un fluido tipo ley de la Potencia (jugo de pulpa de fruta) es calculado en el
Problema Ejemplo 8.8.
Factores de Roce de Fanning
53
Figura 4.1. Factores de roce de Fanning para diferentes valores del índice de comportamiento de flujo basado en la Ec. (4.16) hasta la Ec. (4.21)
para números de Reynolds para fluidos tipo Ley de la Potencia hasta 10.000 (n = 1,0 para fluidos Newtonianos).
54
Ductos y Tuberías para Bioprocesos
Figura 4.2. Factores de roce de Fanning para diferentes valores del índice de comportamiento de flujo basado en la Ec. (4.16) hasta la Ec. (4.21)
para números de Reynolds para fluidos tipo Ley de la Potencia de 10.000 hasta 100.000 (n = 1,0 para fluidos Newtonianos).
Factores de Roce de Fanning
4.4
55
Perfiles de Velocidad del Fluido en Una Tubería
Los sistemas de procesos térmicos continuos para fluidos biológicos, incluyen un intercambiador
de calor (para calentar el fluido); cierta longitud de la tubería, conocida como “tubo de mantención” donde
el tiempo de residencia del fluido es suficiente para obtener un adecuado tratamiento térmico; y
generalmente incluyen un segundo intercambiador (para enfriar el fluido). Debido a que el tubo de
mantención es un componente crítico del sistema, entender el perfil de velocidad del fluido en el tubo es
muy importante para caracterizar numéricamente el proceso térmico.
Los perfiles de velocidad en un flujo turbulento están dados como función del factor de Fanning; por lo
que son presentados en éste capítulo.
En los párrafos siguientes se presentan ecuaciones de velocidades de fluidos completamente desarrollados,
sin perturbaciones de flujo en tubos horizontales rectos. En sistemas de procesamientos reales se
encuentran muchos elementos (válvulas, tees, codos, etc.) que producen mezclas del fluido durante su
trayectoria. Además están las trayectorias de la tubería que son producidas por la energía que
proporcionan las bombas y homogenizadores que contribuyen a la mezcla del fluido. Considerando estos
factores, las ecuaciones que se presentan a continuación pueden ser utilizadas como guía general al
analizar los perfiles de velocidad y para calcular la velocidad máxima que se presenta al circular el fluido
por la tubería.
Fluidos Newtonianos. En el caso del fluido Newtoniano en régimen de flujo laminar (NRe < 2.100) la
velocidad del fluido en función del radio de la tubería es:
∆
4
2
1
4.22
La velocidad máxima, que se encuentra en el centro del tubo es el doble de la velocidad media:
á
2
4.23
La velocidad en el centro del flujo turbulento (NRe >4.100) es descrita con el perfil universal de velocidad
[Brodkey, R.S. and H.C. Hershey. 1988. Transport Phenomena. McGraw-Hill Book Company, New
York]:
Ductos y Tuberías para Bioprocesos
56
5,5
5,756 log
30
4.24
Donde:
4.25
4.26
4.27
2
4.28
En que
es la velocidad en r y
es el factor de roce de Fanning. Una ecuación de correlación simple que
da la velocidad máxima en flujo turbulento [Edgerton and Jones, 1970. J. Dairy Science 53: 1353-1357] es
la siguiente:
4.29
á
0,0336 log
0,662
La Ec. (4.29) se utiliza en la solución del Problema Ejemplo 8.11 para determinar la velocidad máxima del
fluido de mantención de manera que se logre el tiempo de residencia y se establezca la historia térmica de
la partícula más rápida del fluido durante su pasteurización.
Fluidos Tipo Ley de la Potencia. Para un fluido tipo Ley de la Potencia en flujo laminar
2.100 875 1
∆
2
, la velocidad es una función del radio (r):
/
4.30
1
O, en términos de la velocidad promedio es:
,
Factores de Roce de Fanning
3
1
1
57
4.31
1
La velocidad máxima se encuentra en el centro del tubo donde r = 0; y depende del valor que tenga el
índice de comportamiento de flujo:
3
á
1
1
4.32
La velocidad en el centro del régimen turbulento [Skelland, A.H.P. 1967. Non Newtonian Flow and Heat
Transfer, John Wiley and Sons, NY] se puede evaluar utilizando el perfil de velocidad universal.
5,66
,
log
0,566
3,475
,
,
1,960
0,815
1,628 log
3
1
4.33
Donde,
4.34
4.35
y
4.36
2
4.37
en la Ec. (4.34) es la velocidad en r y
es el factor de roce de Fanning. Una relación simplificada para
el perfil de velocidad universal de fluidos adelgazantes, presentada a continuación, fue publicada por
Clapp [Clapp, R.M. 1996. International Developments in Heat Transfer, ASME, Part III, Sec. A., pág.
652-661]:
Ductos y Tuberías para Bioprocesos
58
2,78
2,303 log
3,80
Esta ecuación es válida cuando se cumple 0,698 < n < 0,813; y 5.480 < NRe < 42.800
4.38
5. Coeficientes de Pérdida por Fricción
5.1
Pérdidas en Válvulas y Accesorios Estándar
En la discusión de los cálculos de pérdida de energía para tuberías, se observó que las pérdidas por
fricción en válvulas y accesorios pueden ser calculadas usando el método de altura de velocidad basado en
los coeficientes de pérdida por fricción (kf):
(5.1)
2
Ó por el método de longitud equivalente (Le)
2
(5.2)
Igualando las ecuaciones 5.1 y 5.2, y resolviendo para el largo equivalente da:
(5.3)
4
Los largos equivalentes generalmente son calculados a partir de los valores numéricos de coeficientes de
pérdida por fricción, determinados por datos experimentales. Dado que el factor de fricción de Fanning
depende del número de Reynolds, el valor de Le es generalmente expresado como función del número de
Reynolds. Dado esto, y el hecho de que los valores de Le generalmente no son expresados como función
del número de Reynolds, se recomienda para los cálculos de perdida por fricción utilizar los valores de kf y
la ecuación 5.1. Coeficientes de perdida por fricción son calculados en los problemas ejemplos 8.7 y 8.8.
Coeficientes de pérdida por fricción para válvulas y accesorios estandards pueden ser estimados
utilizando la ecuación siguiente [Hooper, W.B. 1981 (Agosto 24). Chemical Engineering, 96-100]:
¶
1
1
(5.4)
Ductos y Tuberías para Bioprocesos
60
Donde Dinch = diámetro interno de la tubería en unidades de pulgada. Los valores k1 y k∞ fueron
determinados a partir de datos experimentales y son resumidos en la tabla 5.1. NRe,PL, debería ser utilizado
en lugar de NRe para fluidos de ley de potencia. La ecuación (5.4) es aceptable para diámetros de tubería de
uso habitual en aplicaciones alimentarias y farmacéuticas. Si se trata de tuberías de diámetros grandes
(mayor a 6 pulgadas), el método publicado por R. Darby [2001, Marzo. Chemical Engineering, 66-73]
debería ser considerado. La ecuación y las constantes para este procedimiento, conocido como el método
3-k, son presentados en el Apéndice 9.12.
Datos limitados han sido publicados describiendo las pérdidas de presión en válvulas y accesorios durante
el flujo laminar de fluidos biológicos No Newtonianos. Utilizando puré de manzana en varias diluciones,
Steffe y col. [1984, Trans ASAE 27: 616-619] entregó tres ecuaciones (Tabla 5.2) para componentes
sanitarios para 20<NRe,PL<700 en tuberías de acero inoxidable de 1,5 pulgadas (D1=1,50 pulgadas).
Calculando los coeficientes de pérdida por fricción utilizando el método propuesto por Hooper [Ec. (5.4)]
produjo valores de kf muy conservadores: números de dos a tres veces mayores que los encontrados
usando las ecuaciones de la tabla 5.2.
Los coeficientes de pérdida por fricción a la salida y entrada de tanques pueden ser predichos
como:
(5.5)
Los valores de k1 y k∞ están resumidos en la Tabla 5.3 y 5.4 para diferentes escenarios de salida. Los
coeficientes de pérdida por fricción para tuberías cónicas y cuadradas, con expansiones y contracciones
pueden ser encontradas en la Tabla 5.5 a 5.8, respectivamente; y las dimensiones de reductores ó
expansores típicos usados en tuberías sanitarias están dados en la Tabla 5.9.
Coeficientes de Pérdida por Fricción
5.2
61
Pérdidas en Equipamiento Basado en Datos para el Agua.
Los fabricantes a menudo proveen de datos experimentales describiendo la pérdida de presión
ocurrida cuando un fluido pasa a través del equipamiento. Estos datos habitualmente son obtenidos para el
agua, y graficados como pérdidas de presión (psi o pulgadas de agua) versus caudales volumétricos (gpm).
Considerando los factores de pérdida por fricción para cada fluido, es posible hacer una aproximación de
la pérdida por fricción que ocurre con otros fluidos Newtonianos (más o menos viscosos que el agua),
asimismo con los fluidos No-Newtonianos.
Asumiendo que la pérdida de energía por unidad de masa (∆P/ρ) puede ser expresada en términos del
factor de fricción de Fanning (f) y el largo equivalente del equipo (Le). Entonces la ecuación para la
aplicación del fluido es:
2
∆
(5.6)
ó
ó
y la ecuación para el agua es
2
∆
(5.7)
Asumiendo que la longitud equivalente es la misma en cada caso (los otros factores son claramente los
mismos); y dividiendo la ecuación 5.6 por la 5.7 tenemos:
∆
(5.8)
ó
í
ó
∆
Donde los factores de fricción son los correspondientes a las tuberías de conexión. Por lo tanto, pérdidas
para fluidos no Newtonianos pueden ser estimadas a partir de datos experimentales para el agua
incluyendo la razón de factores de fricción para los dos fluidos como sigue:
Ductos y Tuberías para Bioprocesos
62
∆
∆
í
í
ó
(5.9)
ó
Para el caso especial de fluidos Newtonianos en un flujo laminar, tenemos:
∆
∆
í
í
ó
(5.10)
ó
La ecuación (5.9) es aplicada a una válvula neumática, y a un filtro, para fluido Newtoniano y un fluido no
Newtoniano en los problemas ejemplo 8.7 y 8.8 respectivamente.
Coeficientes de Pérdida por Fricción
63
Tabla 5.1 Valores de k1 y k∞ para válvulas y accesorios estandard
Válvula ó accesorio#
k1
k∞
Codo 90º: standard (R/D = 1), con rosca
800
0,40
Codo 90º: standard (R/D = 1), con brida o soldados
800
0,25
Codo 90º: radio largo (R/D = 1,5), todos los tipos
800
0,20
Codo 45º: standard (R/D = 1), todos los tipos
500
0,20
Codo 45º: radio largo (R/D = 1,5), todos los tipos
500
0,15
Codo 180º: standard (R/D = 1), con rosca
1.000 0,60
Codo 180º: standard (R/D = 1), con brida o soldados
1.000 0,35
Codo 180º: radio largo (R/D = 1,5), todos los tipos
1.000 0,30
T usada como codo: standard, con rosca
500
0,70
T usada como codo: radio largo, con rosca
800
0,40
T usada como codo: standard, con brida o soldada
800
0,80
T (pasando a través de ella): con rosca
200
0,10
T (pasando a través de ella): con brida o soldada
150
0,50
Válvula de compuerta (abierta)
300
0,10
Válvula de globo, standard (abierta)
1.500 4,00
Válvula de globo, en ángulo o tipo Y (abierta)
1.000 2,00
Válvula de diafragma, tipo presa (abierta)
1.000 2,00
Mariposa
800
Válvula de retención (tipo elevador)
2.000 10,00
Válvula de retención (tipo swing)
1.500 1,50
Válvula de retención (con disco de inclinación)
1.000 0,50
#
0,25
Excepto para algunas aplicaciones de alta presión, superficies de contacto enroscadas no están permitidas
en los sistemas sanitarios (3A Standard número 63-10). Acero estándar con hilo es aceptable para sistemas
de suministro de agua.
Ductos y Tuberías para Bioprocesos
64
Tabla 5.2 Coeficientes de pérdida por fricción para puré de manzana en flujo laminar
Válvula o accesorio
Coeficiente de pérdida por fricción (-)
Válvula de cono, flujo cruzado
kf = 30,3 (NRe,PL)-0,5
T flujo cruzado de ella (como codo)
kf = 29,4 (NRe,PL)-0,5
Codo 90º, y brida
kf = 191 (NRe,PL)-0,9
Tabla 5.3 k1 y k∞ para entrada o salida cuadrada desde un tanque a la cañería
Tipo de entrada
k1
k∞
Entrada del tubo, cuadrada.
160
0,5
160
1,0
0
1,0
Estanque
Tubo
Flujo
Entrada del tubo, proyectado hacia el
estanque.
Estanque
Tubo
Flujo
Salida del tubo (todas las geometrías)
Fuente: Hooper, W.B. 1981. Chemical Engr. Ago. 24, 96-99
Coeficientess de Pérdida por Fricción
655
Tabla 5.44 Valores dee k1 y k∞ paraa salidas redoondeadas dessde un tanquue a la cañeríaa
Tipo de salida
r/D
k1
k∞
0,0 (filosso)
0,5
0,02
0,28
0,04
0,24
0,06
160 paraa todos r/D
0,15
0,10
0,09
0,15 (y más)
m
0,04
Fuente: Darby,
D
R. 20001. Chemicaal Engineerinng Fluid Mecchanics (Seggunda Edicióón). Marcel Dekker,
D
New
w
York, p. 213.
Ductos y Tuberías para Bioprocesos
66
Tabla 5.5 Coeficiente de pérdida por roce para expansión gradual de tubos
Expansión cónica de tubos
Entrada NRe
kf basado en la velocidad de entrada
0º < q < 45º
1
2 1
y
4
2,6 sen
2
2
NRe ≤ 4.000
o
ó
NRe > 4.000
1
45º < q < 180º
3,2
1
1
1
1
2 2
2,6
2
2
2 1
y
NRe ≤ 4.000
ó
ó
1
NRe > 4.000
3,2
2 2
2
Fuente: Hooper, W.B. 1988. Chemical Engr. Nov. 7, 89-92.
NRe es el valor aguas arriba de Reynolds; f = factor de fricción de Fanning calculado usando el número de
Reynolds aguas arriba; usar NRe, PL en lugar de NRe para fluidos de la ley de potencia; q = ángulo, grados.
Nota: q para expansiones sanitarias está entre 0 y 45 grados.
Coeficientes de Pérdida por Fricción
67
Tabla 5.6 Coeficientes de pérdida por fricción para expansiones de tuberías cuadradas
Expansión cuadrada
Entrada NRe
kf basado en la velocidad de entrada
NRe ≤ 4.000
2 1
ó
ó
NRe > 4.000
1
3,2
1
1
2 2
2
Fuente: Hooper, W.B. 1988. Chemical Engr. Nov. 7, 89-92
NRe es el número de Reynolds aguas arriba; f = factor de fricción de Fanning calculado con el número de
Reynolds aguas arriba, usar NRe, PL en lugar de NRe para fluidos de la Ley de Potencia.
Ductos y Tuberías para Bioprocesos
68
Tabla 5.7 Coeficientes de pérdida por fricción para contracciones cónicas de tubería
Contracciones cónicas
NRe entrada
kf basado en la velocidad de entrada
0º <q < 45º
1,2
y
160
1
4
1 1,6
2
2
NRe ≤ 2.500
ó
ó
NRe > 2.500
0,6
45º < q <180º
1,2
y
1,92
160
1
2
1
2
1
1 1,6
2
4
1
1
2
2
2
2
NRe ≤ 2.500
ó
NRe > 2.500
ó
0,2
1,92
1
2
2
1
2
2
1
1
2
2
Fuente: Hooper, W.B. 1988. Chemical Engr. Nov 7, 89-92.
NRe es el número de Reynolds aguas arriba; f = factor de fricción de Fanning calculado con el número de
Reynolds aguas arriba, usar NRe,PL en lugar de NRe para fluidos de la ley de potencia, q = ángulo, grados.
Nota q para expansiones sanitarias está entre 0 y 45 grados.
Coeficientes de Pérdida por Fricción
69
Tabla 5.8 Coeficientes de pérdida de fricción para contracciones cuadradas de tubo
Contracción cuadrada de tubo
NRe entrada
kf basado en la velocidad de entrada
NRe ≤ 2.500
1,2
ó
160
1
4
1
2
ó
NRe > 2.500
0,6
1,92
1
2
2
1
2
2
1
Fuente: Hooper, W.B. 1988. Chemical Engr. Nov. 7, 89-92.
NRe es el valor de Reynolds aguas arriba; f = factor de fricción de Fanning calculado con el número de
Reynolds aguas arriba; usar NRe,PL en lugar de NRe para fluidos de la ley de potencia.
Ductos y Tuberías para Bioprocesos
70
Tabla 5.9 Dimensiones de reductores o expansores típicos para tuberías sanitarias
Tamaño
A, pulgadas
B, pulgadas
C, pulgadas
q, grados
¾” x ½”
2
0,75
0,5
7,1
1” x ½”
2,5
1
0,5
11,4
1” x ¾”
2
1
0,75
7,1
1½” x ½”
3,5
1,5
0,5
16,2
1 ½” x ¾”
4
1,5
0,75
10,7
1 ½” x 1”
3
1,5
1
9,5
2” x ¾”
4,25
2
0,75
16,7
2” x 1”
5
2
1
11,4
2” x 1½”
3
2
1,5
9,5
2 ½” x 1½”
5
2,5
1,5
11,4
2 ½” x 2”
3
2,5
2
9,5
3” x 1 ½”
7
3
1,5
12,2
3” x 2”
5
3
2
11,4
3” x 2½”
3
3
2,5
9,5
4“ x 2”
9,125
4
2
12,5
4” x 2½”
7,125
4
2,5
12,0
4” x 3”
5,125
4
3
11,1
Nota q = 180º para entrada o salida de borde afilado
6. Manejo de Fluidos Sensibles a la Cizalla
6.1
Fluidos Sensibles a la Cizalla
Muchos fluidos biológicos son sensibles a la cizalla (frágiles) y son dañados fácilmente durante su
procesamiento. Los problemas típicos son la ruptura de las emulsiones, la destrucción de las colonias
microbianas en los sistemas de fermentación y el daño que sufren las partículas durante su manejo. La
sensibilidad frente a la cizalla que presenta un fluido puede contribuir en mejorar con objetivos
beneficiosos el procesamiento creando emulsiones, o ayudando en la floculación de coloides o
microorganismos. En ambos casos, las técnicas presentadas en este capítulo permiten cuantificar
características de los componentes mecánicos del proceso. Estos métodos son herramientas valiosas para
el escalamiento positivo o negativo de los sistemas de procesamiento, para analizar procesos alternativos y
para controlar los factores de calidad que se presentan en el procesamiento de fluidos sensibles a la cizalla.
La disipación viscosa de la energía se produce cuando el fluido está en movimiento y cada
componente de la tubería del sistema de procesos produce alteraciones en la corriente del fluido o su
mezcla. La mezcla es producida cuando se utilizan estanques agitados o mezcladores estáticos
(mezcladores en la tubería) en el proceso. La cizalla que a menudo es intensa es producida por fittings,
válvulas, intercambiadores de calor, filtros y cualquier otro componente de una red de tubería típica. Las
bombas también hacen un aporte significativo en el mezclado. En el caso de las bombas centrifugas, éstas
utilizan rotores de alta velocidad de giro para acelerar el fluido dentro de la carcasa de la bomba, lo que
genera una fuerte agitación del fluido y por tanto un daño en los materiales sensibles a la cizalla.
En este capítulo se presentan métodos para estimar el trabajo de cizalla, intensidad de la potencia
de cizalla y la velocidad de deformación en cizalla promedio que soportan las partículas que son
transportadas por un fluido. Estas técnicas son necesarias para cuantificar la cizalla que producen los
componentes mecánicos de una línea de procesos y permite investigar cuánto influye la sensibilidad que
presenta un material a la cizalla en su línea de procesamiento y en la calidad del producto.
Ductos y Tuberías para Bioprocesos
72
6.2
Trabajo de Cizalla (Ws)
El trabajo de cizalla (Ws) tiene que ver con los cambios de energía que se producen en un sistema
mecánico que somete el fluido a esfuerzos de cizalla. El término “trabajo de cizalla” se utiliza para
distinguirlo del trabajo mecánico, tal como los trabajos que contribuyen a cambiar la energía potencial sin
producir cizalla en el producto. Las contribuciones de todos los elementos participantes en el movimiento
del fluido deben ser tomados en cuenta para evaluar el trabajo de cizalla (Ws) en una línea de procesos.
El trabajo de cizalla (Ws) en un estanque con agitación depende si su operación es por lote o
continua, según se verá a continuación: 1) Operación por lote, Ws es el producto de la potencia consumida
por el agitador (Ф) multiplicada por el tiempo de mezcla (t) dividido por la masa (m) del fluido en el
estanque; 2) Operación continua, Ws es la potencia consumida, dividida por el flujo másico ( ) del fluido
en el estanque (Tabla 6.1). Los cálculos para los componentes típicos de una línea de proceso que son los
involucrados en un balance mecánico de energía (Ec. 3.2) se presentan resumidos en la Tabla 6.1.
Estos valores pueden ser predichos si se conoce la pérdida de carga en cualquier componente de la
tubería (incluidas válvulas, fittings y tubo recto), Ws puede ser calculado como ∆ / . Al considerar todos
los elementos mecánicos de un proceso en contacto con el fluido, el trabajo de cizalla total del sistema es:
Ф
,
2
∆
6.1
2
La Ec. (6.1) incluye la probabilidad de tener (en el caso de proceso continuo) múltiples componentes
como estanques, válvulas y fittings, tuberías de distintos diámetros y otros componentes incluyendo la
bomba.
Manejo de Fluídos Sensibles a la Cizalla
73
Tabla 6.1. Trabajo de cizalla para diferentes componentes de una tubería donde circula un fluido.
Componentes del sistema
Trabajo de cizalla (Ws )
Estanque: operación por lote
Ф
Estanque: operación continua
Ф
Válvulas y fittings estándar
2
Tubería recta
Equipamiento: válvulas neumáticas, intercambiadores de
2
∆
calor, filtros, bombas centrífugas, etc.
Ws tiene unidades de J/kg y representa el cambio de energía por unidad de masa del producto que
se desplaza a través de todos los componentes del sistema. El aumento o diminución de presión debido a
los diferentes componentes mecánicos del circuito es directamente proporcional al trabajo de cizalla. La
presión disminuye a medida que el fluido pierde energía, como cuando pasa a través de una válvula. En
forma inversa, la presión del fluido aumenta a medida que el fluido gana energía, como cuando el fluido
pasa a través de una bomba. En cada uno de estos casos, se produce una agitación mecánica significativa;
de aquí es que el diferencial de presión debe ser siempre positivo cuando se evalúa el trabajo de cizalla de
entrada, debido a que representa un cambio de energía que está ayudando en el cizalle del producto. El
diferencial (∆ ) de presión que produce la unidad en cuestión se puede medir antes y después del equipo
crítico. Si no se determina el trabajo en cizalla a partir de diferencias de presión, se puede evaluar
ocupando la Tabla 6.1 utilizando el factor de roce de Fanning ( ) ó el coeficiente de pérdida por roce
.
Al analizar un proceso se tiene que calcular el trabajo en cizalla para cada componente individual
y el trabajo en cizalla total del sistema en cuestión. Es necesario y es de mucha importancia realizar un
análisis cuidadoso de la bomba antes de incluirla como un factor relevante. Las bombas centrífugas
generan grandes pérdidas por roce porque trabajan convirtiendo energía cinética en energía de presión.
Sin embargo, hay bombas de bajo cizalle (bombas de lóbulo rotatorio y de engranaje) y de muy bajo
cizalle (bombas de diafragma y de cavidad progresiva) que pueden generar diferencias de presión muy
grandes por compresión del fluido pero agregan muy poco trabajo en cizalla.
Ductos y Tuberías para Bioprocesos
74
Solamente las bombas que producen pérdidas por roce significativas en el fluido, podrían incluirse en el
cálculo del trabajo de cizalla total.
6.3
Intensidad de la Potencia de Cizalla (S)
Fuera del trabajo en cizalla, se debe considerar la intensidad de la potencia en cizalla (S) para cada
componente del sistema. Este parámetro está definido para cada componente del sistema como el producto
del trabajo en cizalla por el flujo másico del producto dividido por el volumen fluido:
6.2
Donde
es la capacidad volumétrica del componente bajo condiciones estáticas. La intensidad de la
potencia en cizalla para un estanque es igual a la potencia dividida por el volumen del fluido en el
estanque (Ф/ ) tanto para condiciones de trabajo continuo o por lotes.
La intensidad de la potencia por cizalla tiene las dimensiones de Js-1m-3 o Wm-3 y representa el
cambio de potencia por unidad de volumen (velocidad de cambio de energía por unidad de volumen) dado
al fluido cuando se desplaza a través de los componentes de la tubería. Da una medida de la velocidad de
cambio de energía por unidad de volumen en los diferentes componentes mecánicos del sistema que
pueden aportar altos trabajos en cizalla pero bajas intensidades de cizalla. Esto es importante para
distinguir entre áreas que pueden tener entradas altas de trabajo en cizalla y baja intensidad de cizalla (por
ejemplo largas secciones del tubo recto) pero pueden contribuir muy poco en la degradación del producto
si la intensidad de la potencia de cizalla es baja. El Problema Ejemplo 8.9 aclara este concepto. La
intensidad de la potencia en cizalla generada por una bomba centrífuga es calculada en el Problema
Ejemplo 8.10.
El volumen estático,
en la Ec. (6.2) está definido claramente para la mayor parte del
equipamiento: sencillamente es el volumen vacío del objeto que normalmente es ocupado por el fluido.
Obviamente no hay volumen estático para el cálculo de S para la convergencia de la entrada a un tubo, en
la divergencia a la salida o para el flujo a través de un orificio, aunque la teoría de mezcla longitudinal
(con el apoyo de datos experimentales) podría ser utilizada para desarrollar una definición racional de
y
se requieren varías suposiciones que lo hacen impracticable desde el punto de vista de la ingeniería. Una
investigación engorrosa de la salida de un tubo es aún más complicada.
Manejo de Fluídos Sensibles a la Cizalla
75
Para facilitar el análisis, el término volumen para la entrada de una tubería, para la salida y para el orificio
se supone que es el espacio ocupado por una tubería de una longitud igual a dos veces su diámetro:
/2. En el caso de convergencia o divergencia que involucre dos tubos, se utiliza el diámetro del
tubo más pequeño para calcular .
6.4
Valores Críticos para
yS
La combinación de los ingredientes y del equipo de procesamiento utilizados para fabricar un
producto es única. Los valores críticos de la potencia de trabajo de cizalla
y de la intensidad de la
potencia de cizalla (S) son también únicos para cada producto y cada sistema de fabricación. Los valores
críticos pueden ser los valores máximos o mínimos necesarios para una operación exitosa. Para aclarar y
entender la discusión presentada en los párrafos anteriores se va a analizar el caso de la descarga y
almacenamiento de un fluido sensible a la cizalla, presentado en la figura 6.1. La operación de descarga
consta de los elementos siguientes: entrada del tubo donde el fluido sale del camión estanque, bomba,
válvula, filtro, salida del fluido por el tubo donde entra al estanque, tres codos y la longitud total de la
tubería necesaria para el transporte del fluido; y en las condiciones de almacenamiento debe tomarse en
cuenta el agitador del estanque.
Figura 6.1. Sistema mecánico para un sistema de fluido sensible a la cizalla.
Los componentes del sistema (Fig. 6.1) y las variables que deben ser tomadas en cuenta al evaluar
un fluido sensible a la cizalla se resumen en la tabla 6.2. La caída de presión en la bomba es determinada a
partir de medidas directas o por la aplicación de la ecuación de balance mecánico de energía a todo el
sistema.
Ductos y Tuberías para Bioprocesos
76
La Fig. 6.1 es análoga a la Fig. 3.3 y los resultados del trabajo necesario (W) para que la bomba (Tabla
3.1) aumente su presión, puede ser calculado con ∆
. Este cálculo está incluido en el problema
ejemplo 8.7. El valor de la caída de presión del filtro puede obtenerse del fabricante aunque estos datos
están dados para el transporte de agua, pueden ser utilizados para otros fluidos realizando los cálculos de
la Ec. (5.9) ó de la Ec. (5.10). El
para la válvula puede ser calculado utilizando los datos de pérdida de
carga para agua (común para las válvulas neumáticas) ó con la Ec. (5.4) utilizando los coeficientes
adecuados de pérdida por roce.
Los coeficientes de pérdida por roce son necesarios para encontrar el trabajo en cizalla y la
intensidad del trabajo en cizalla para los tres codos, la entrada del estanque y la salida de él. Los cálculos
de Ws y S para el tubo, necesitan el factor de roce de Fanning y L, que es la longitud total del tubo del
sistema en estudio. La capacidad volumétrica de llenado específica (V) de un componente puede ser dada
ó medida en galones (ó litros) de agua. Esta información es convertida en volumen espacial utilizando la
densidad del agua.
El fluido es bombeado desde el camión estanque hasta el estanque de almacenamiento que está
provisto con un agitador de hélice marina (Fig. 6.1). El estanque de almacenamiento debe ser tratado
como un sistema independiente. El trabajo de cizalla entregado al fluido que se produce durante la
agitación depende de la potencia aplicada (provista por el motor del agitador) y del tiempo total de mezcla
(t). la intensidad del trabajo en cizalla es simplemente la potencia total dividido por el volumen del fluido
en el estanque (Tabla 6.2).
Manejo de Fluídos Sensibles a la Cizalla
77
Tabla 6.2. Trabajo de cizalla (Ws), intensidad de trabajo en cizalla (S) y volumen (V), requeridos para el
cálculo de la intensidad de la potencia de cizalla para el sistema de la Fig. 6.1.
Parte del sistema
S
Ws
V
Descargando
,
entrada tubería
2
2
volumen de llenado de
∆
bomba
la bomba
volumen de llenado de
, á
válvula
2
la válvula
volumen de llenado
∆
filtro
del filtro
3
codos (3)
3 x el volumen de
3
,
2
llenado del codo
,
salida tubería
2
2
2
4
2
tubo recto
Almacenamiento
estanque
de
volumen del fluido en
Ф
Ф
el estanque
almacenamiento
debe ser calculado para cada componente individual del sistema (Tabla 6.2) y como el trabajo
es acumulativo, tiene que ser calculado para el sistema en su totalidad.
∆
,
3
∆
, á
,
2
Aunque es posible calcular un valor S total (
caracterizar un efecto acumulativo.
2
,
/
2
,
2
Ф
6.3
2
), este parámetro tiene un valor limitado para
Ductos y Tuberías para Bioprocesos
78
Ya que cada producto es diferente, se deben correlacionar medidas objetivas de la calidad del
producto con los valores críticos del trabajo de cizalla aplicado y la intensidad de la potencia de cizalla. El
efecto del transporte de fluido en una emulsión (por ejemplo: mayonesa) puede ser estudiado extrayendo
muestras en diferentes puntos cero para revisar la estabilidad de la emulsión o controlar la distribución del
tamaño de las partículas. Una aplicación de energía excesiva, por ejemplo, puede hacer que las gotas de
aceite se agrupen provocando la ruptura de la emulsión. El criterio de rotura puede establecerse por
análisis reológico, microscópico o colorimétrico. Estos criterios de calidad pueden correlacionarse con el
trabajo de cizalla y la intensidad de la potencia en cizalla encontradas en los diferentes componentes del
sistema de procesamiento para determinar los valores críticos, o como en este ejemplo, los niveles
máximos permisibles. El sistema mecánico puede ser diseñado de modo que cumpla estas limitaciones.
Una situación similar se puede presentar en el caso de agregados en el sistema coloidal que pueden ser
producidos por efectos de cizalla, la destrucción de colonias microbianas en los caldos de fermentación o
rotura estructural de los yogures.
Hay un gran número de factores que afectan a Ws y S durante un proceso.
El caudal es
obviamente el factor más importante ya que los niveles de trabajo y potencia aplicada aumentan con los
incrementos del caudal. La temperatura del fluido durante el procesamiento es también importante ya que
las propiedades reológicas dependen fuertemente de la temperatura y esta dependencia puede alterar la
influencia del trabajo y del trabajo en cizalla en la calidad del fluido. Como se ha establecido previamente
cada producto y proceso es único y hay que considerar cuidadosamente las características individuales de
cualquier sistema sometido a análisis.
6.5
Partículas sensibles al cizalle
Además del trabajo de cizalla y la intensidad de potencia de cizalla puede ser necesario tomar en
cuenta la velocidad de deformación en cizalla promedio que soportan las partículas al pasar por los
diferentes componentes del sistema. Partículas grandes tales como vegetales picados y trozos de pastas
pueden ser dañadas al pasar por espacios reducidos a velocidades altas. La velocidad promedio de
deformación en cizalla, a través del sistema, puede ser utilizada como factor preponderante del sistema. Se
puede estimar como dos veces la velocidad media dividida por la dimensión (d) característica del
componente del sistema.
2
6.4
Manejo de Fluídos Sensibles a la Cizalla
79
La dimensión característica es la longitud mínima libre en el área sometida al flujo. En el caso
sencillo de un tubo, la dimensión característica es el diámetro interno. Un valor razonable para una bomba
centrífuga sería la distancia entre el borde exterior del rotor y la carcasa de la bomba. Valores altos de
velocidad de deformación en cizalla en un sistema donde circula fluido pueden producir daños en las
partículas de mayor tamaño.
La velocidad promedio de deformación en cizalla definida por la Ec. (6.4) es un elemento valioso
para prever daños potenciales a las partículas durante su transporte. Tiene un significado diferente que el
de la velocidad de deformación en cizalla media (definida por la Ec. 2.12) utilizada en la viscosimetría de
mezcla. En un estanque de mezcla grande la velocidad de deformación en cizalla sería el mejor indicador
del daño de las partículas. Esto podría, por ejemplo, ser calculado en un estanque con un agitador tipo
ancla, como la velocidad en el borde de ataque del agitador dividido por la distancia mínima entre el borde
de ataque del agitador y el estanque.
6.6
Cálculos de Escalamiento
Escalamiento de Tuberías. El escalamiento de tuberías es un problema común en la ingeniería de
bioprocesos. En el análisis que se presenta a continuación se asume que la tubería se utiliza en el
transporte de un fluido sensible a la cizalla; y al examinar el proceso se tiene que un conjunto de
parámetros de flujo (Caso 1) produce un producto aceptable. Además, se supone que un nuevo proceso
(Caso 2) fue diseñado para un incremento de flujo másico en un factor C, definido como la razón de dos
flujos másicos.
6.5
Al mantener constante la potencia de cizalla, se debe mantener S constante para ambos casos, de aquí se
puede plantear la siguiente relación utilizando la Ec. (6.2),
6.6
Si las pérdidas en la bomba son despreciables, la intensidad de cizalla sólo incluye los tubos rectos y la Ec.
(6.6) queda como sigue:
Ductos y Tuberías para Bioprocesos
80
6.7
2
2
2
2
Suponiendo que la longitud es constante y el flujo es laminar, se tiene
debe recordar que
/
16 /
. También se
; y asumir que las propiedades del fluido (µ y ρ) no cambian con el caudal.
Al utilizar lo planteado y simplificar algebraicamente la Ec. (6.7) se llega a:
6.8
Sustituyendo el caudal para el caso 2
en la Ec. (6.8) y resolviéndola para el nuevo
diámetro, da el siguiente resultado:
6.9
/
Este resultado indica que la intensidad de cizalla puede ser mantenida en el tubo si el diámetro aumenta en
/
. Si se considera, por ejemplo, el caso donde el objetivo es duplicar el flujo másico (es decir, C = 2)
manteniéndolo los valores de intensidad de potencia al cizalle, se tiene:
2
/
1,32
6.10
La Ec. (6.10) muestra que es posible duplicar el caudal másico mientras se mantiene el aporte de energía
constante si el diámetro se incrementa 1,32 veces. En los sistemas de procesos reales en que las pérdidas
significativas de energía se producen en los fittings y en el equipamiento (que incluye válvulas, filtros,
bombas, intercambiadores de calor y otros), el análisis es más complejo, pero los principios son los
mismos. El escalamiento de un fluido sensible a la cizalla (crema) se analiza y resuelve en el Problema
Ejemplo 8.9.
Manejo de Fluídos Sensibles a la Cizalla
81
Escalamiento de Componentes Basado en la Intensidad Máxima de Cizalle. La intensidad máxima de
potencia de cizalle en un sistema de procesamiento ocurre en un componente particular del sistema, como
es el caso de una válvula. Podría ser importante mantener el valor sin excederlo. Supóngase, por ejemplo,
/
. Para mantener constante la intensidad de la potencia de cizalle, se debe mantener
constante S para ambos casos:
. Se sustituye el término de trabajo de cizalla adecuado que
en este caso es la pérdida de carga dividida por la densidad de la Ec. (6.6) dando
∆
∆
6.11
Para poder cumplir esta ecuación, es necesario aumentar el volumen estático del componente. Esto puede
lograrse con una válvula, por ejemplo, se utiliza una válvula con mayor cuerpo para soportar el flujo más
alto del proceso.
Escalando Diámetros de Tubería Utilizando el Número de Reynolds. En el caso de escalamiento de
tuberías discutido en el párrafo anterior (fluido Newtoniano en flujo laminar en tubo recto), manteniendo
el número de Reynolds constante, es decir,
6.12
ó,
6.13
Sustituyendo
4 /
en la Ec. (6.13) y recordando que
, da
6.14
Ductos y Tuberías para Bioprocesos
82
El resultado es totalmente diferente que el de la Ec. (6.8). Lo anterior demuestra que al utilizar la
constancia en el número de Reynolds como criterio de escalamiento para mantener constante el nivel de
entrada de cizalle, resulta en un fuerte incremento del diámetro de la tubería:
de
/
, en vez
. Por lo tanto, hay que tener cautela al utilizar el número de Reynolds como
criterio de escalamiento para evaluar la degradación que produce el esfuerzo de cizalla.
7. Procesamiento Térmico de Fluidos Biológicos
Los tratamientos térmicos son comúnmente empleados para la eliminación de microorganismos
patógenos en los fluidos biológicos como alimentos y productos farmacéuticos; sin embargo, una
evaluación cualitativa de estos sistemas puede jugar un papel importante en el análisis de tuberías para
bioprocesos. En este capítulo examinaremos que tan rápido mueren los microorganismos (cinética de
muerte) a una temperatura dada; y como un tratamiento a temperatura variable puede ser igualado a un
tiempo equivalente a una temperatura constante para determinar la letalidad total de un proceso mediante
el método general. Las técnicas presentadas proveen una manera simple de caracterizar la destrucción de
microorganismos durante un tratamiento térmico de un fluido biológico. Estas técnicas pueden también
ser utilizadas para caracterizar tratamientos térmicos para la inactivación enzimática (pectinasa en jugo de
naranja por ejemplo) y para examinar la destrucción de nutrientes (tiamina en leche) y varios cambios en
la calidad de los alimentos como textura y color.
7.1
Cinética de Muerte de Microorganismos
Es una práctica habitual el describir la muerte de microorganismos a una temperatura como una
reacción irreversible de primer orden involucrando el número de microorganismos (N), el tiempo (t) y una
tasa de inactivación de microorganismos constante (k):
(7.1)
Resolviendo la ecuación (7.1) usando la condición inicial donde existe un número de microorganismos
conocido al comienzo del proceso (N = N0 a t = 0), tenemos:
(7.2)
De acuerdo a la convención de la industria de alimentos, la ecuación (7.2) se expresa en términos de
logaritmos comunes (en base 10) en vez de los logaritmos naturales (en base e):
(7.3)
2,303
Ductos y Tuberías para Bioprocesos
84
Luego de introducir en valor D (tiempo de reducción decimal, minutos) esta ecuación queda:
(7.4)
ó
10
(7.5)
Donde D = 2,303/k
El valor z es utilizado para describir la relación existente entre dos valores D en función de la
temperatura:
10
(7.6)
Donde z es una constante igual a la diferencia de temperatura requerida para alcanzar un cambio de un
ciclo logarítmico en los valores D. DT1 y DT2 son los tiempos de reducción decimal (en minutos) a T1 y T2
respectivamente. Los valores D disminuyen conforme se incrementan las temperaturas debido a que los
microorganismos mueren más rápido a altas temperaturas. Valores pequeños de z significan que la muerte
del microorganismo es muy sensible a las temperaturas. Notar que cuando el subíndice 0 es utilizado, se
refiere a una temperatura de referencia de 250 ºF, por lo tanto D0 = D250 ºF.
Un enfoque alternativo para evaluar la cinética de muerte térmica de microorganismos es usar la
ecuación de Arrhenius para describir la influencia de la temperatura en k. El enfoque “valor z” representa
la práctica más común en la industria alimentaria. Desde un punto de vista práctico, ambos métodos
producen resultados similares cuando el procesamiento no cubre un rango amplio de temperaturas.
Valores típicos para algunos microorganismos importantes son:
Procesamiento Térmico de Fluídos Biológicos
85
Clostridium botulinum:
D250ºF = 0,21 min,
z = 18 ºF
Coxiellia burnettii:
D152ºF = 0,32 min,
z = 10,8 ºF
P.A. 3679:
D250ºF = 0,80 min,
z = 19,1 ºF
Salmonella:
D140ºF = 0,30 min,
z = 10 ºF
Diversos factores afectan los valores z y D, entonces se deben identificar números apropiados para
cualquier producto en particular y microorganismo objetivo bajo análisis.
El valor esterilizante (VE) en un proceso se define en términos de un número de reducciones
decimales en una población microbiana:
ú
(7.7)
log
EL VE alcanzado para una temperatura de referencia en particular (Tref) puede ser calculado a partir del
tiempo de proceso a la Tref dividido por el valor D apropiado:
(7.8)
log
Para asegurar la salud pública, los procesos térmicos para alimentos de baja acidez (pH mayor que 4,6)
son diseñados para alcanzar un mínimo de reducciones igual a 12D (VE = 12) en esporas de Clostridium
botulinum.
El microorganismo objetivo para la pasterización de leche es Coxiellia burnetti. Asumiendo z = 10,8 ºF
10,8°
0,30
, entonces el valor D para este microorganismo, a la temperatura de
(6,0 ºC) y
152,6°
pasterización (161 ºF = 71,7 ºC), es:
10,8°
161°
0,30 10
152,6 161
10,8
0,005
3,0
(7.9)
La ordenanza para leche pasteurizada grado A (US. Food and Drug Administration) especifica un
procesado mínimo de 15 s a 161 ºF para leche, entonces dado esto, el valor esterilizante requerido para el
proceso es:
Ductos y Tuberías para Bioprocesos
86
15
3
log
(7.10)
5
Reordenando la ecuación (7.8), es posible determinar el tiempo necesario para alcanzar un valor
esterilizante en particular a diferentes temperaturas de referencia:
(7.11)
log
Utilizando los parámetros de primer orden anteriores para Coxiella burnettii, y asumiendo una reducción
logarítmica de 5 ciclos como valor esterilizante objetivo, resulta una ecuación que entrega el tiempo de
proceso equivalente (en segundos) a una temperatura particular:
0,30 60
10
,
,
(7.12)
5
Los resultados están resumidos en la Tabla 7.1.
Tabla 7.1 Tiempo para alcanzar una reducción de 5 ciclos logarítmicos en Coxiellia burnettii a diferentes
temperaturas asumiendo
t,s
T,ºF
157
150
53,9
155
18,6
160
6,4
165
2,2
170
10,8°
152,6°
0,32
18
Requerimientos típicos de pasterización para varios fluidos biológicos están presentados en la tabla 7.2.
Una reducción de 5 ciclos logarítmicos en la población microbiana puede ser esperada en un proceso de
pasterización típico como la que se emplea para productos lácteos o sidra de manzana. Los requerimientos
mínimos de pasterización para algunos productos, como el jugo de naranja están basados en la
inactivación enzimática.
Procesamiento Térmico de Fluídos Biológicos
87
Las regulaciones federales para la inactivación de Salmonella (Federal Register, Febrero 27, 2001: 1258912636) requieren una reducción de 6,5 log en carne molida de vacuno y una reducción de 7 ciclos
logarítmicos en productos avícolas.
7.2
Método General
El método general es una técnica numérica que considera la influencia de diferentes
combinaciones tiempo-temperatura sobre la destrucción de microorganismos. El tiempo de muerte térmica
de un proceso (el valor F), es como los valores D, una función de z:
10
(7.13)
Donde FT1 es el tiempo de muerte térmica a T1, y FT2 , es el tiempo de muerte térmica a T2. Los valores F
a diferentes temperaturas producen una destrucción equivalente de los microorganismos objetivos.
Ductos y Tuberías para Bioprocesos
88
Tabla 7.2 Requerimientos para una pasterización típica para fluidos biológicos
Producto
T (ºF/ºC)
Tiempo
Sidra de Manzana
154,6/68,1
14 s
Sidra de Manzana
160/71,1
6s
Leche
145/62,8
30 min
Leche
161/71,7
15 s
Leche
191/88,3
1,0 s
Crema, y Leche Chocolatada
150/65,6
30 min
Crema
166/74,4
25 s
Mezcla para Helado
155/68,3
30 min
Mezcla para Helado
175/79,4
25 s
Mezcla para Helado
180/82,2
15 s
Jugo de Naranja
194/90
60 s
Jugo de Naranja
197,6/92
30 s
Jugo de Naranja
208,4/98
6s
Huevo entero
140/60
3,5 min
Ultra pasteurizados
280/137,8
2s
(todos los productos lácteos)
Productos de Baja Acidez. Alimentos de baja acidez (pH mayor que 4,6) procesados asépticamente son
transportados y procesados térmicamente en equipos para el manejo de fluidos. Una practica común para
caracterizar el tratamiento térmico de estos materiales es calcular el tiempo de muerte térmica a una
temperatura de referencia de 250 ºF (121,1 ºC) para un microorganismo (Clostridium botulinum) con un
valor z de 18 ºF (10 ºC). El valor F a esta temperatura es definido, por convención, como F0 = F250ºF.
Utilizando la ecuación anterior, un tiempo relativo de destrucción (TRD) puede calcularse [Pflug, I.J.
1997. J. Food Protection 60(10): 1215-1223]:
º
10
min
min 250º
(7.14)
La ecuación (7.14) establece (para alimentos líquidos de baja acidez) un minuto a 250 ºF como unidad de
letalidad. Si, por ejemplo, la temperatura del producto es 230 ºF, entonces el TRD es:
Procesamiento Térmico de Fluídos Biológicos
°
10
°
12,9
min 230
min 250
89
(7.15)
Lo que significa: manteniendo el producto a 230 ºF durante 12,9 minutos tiene el efecto letal equivalente
que mantener el producto a 250 ºF durante 1 minuto. Es conveniente introducir la tasa letal (TL) definida
como el valor recíproco del tiempo relativo de destrucción:
1
10
min 250º
min
(7.16)
En el ejemplo anterior,
1
1
12,9
0,077
min 250
min 230
(7.17)
Significando que el calentamiento durante 1 minuto a 230ºF es equivalente a calentar 0,077 minutos a
250ºF. En otras palabras, calentando durante un minuto a 230 ºF adicionaría 0,077 min de letalidad a un
proceso. Utilizando el concepto de tasa, la letalidad total de un proceso puede ser calculada sumando la
letalidad acumulativa producida mientras la temperatura del producto cambia durante el procesado. Las
tasas letales, basadas en z = 18 y una temperatura de referencia de 250 ºF, están dadas en la Tabla 7.3.
Ductos y Tuberías para Bioprocesos
90
Tabla 7.3 Tasas letales a 250 ºF con z = 18 ºF
T, ºF
Minutos a 250 ºF por minutos a T
210
0,006
215
0,011
220
0,022
225
0,041
230
0,077
235
0,147
240
0,278
245
0,527
250
1,000
255
1,896
260
3,594
265
6,813
Desde un punto de vista de salud pública, un proceso térmico para alimentos de baja acidez debe tener un
valor esterilizante de 12 (por ejemplo un procedo 12D significa VE = log( N 0 / N ) = 12) con Clostridium
botulinum como microorganismo objetivo (D250ºF = 0,21 min y z =18 ºF). Sabido esto, el tiempo de muerte
térmica a una temperatura de referencia de 250 ºF puede ser calculado: F0 = 12D = 12(0,21) = 2,52 min.
Cualquier proceso con F0 mayor que 2,52 min es considerado como seguro, y a veces se habla de “Cuello
de Botella”. Valores de F0 de 5 minutos a 12 minutos son los mas usados debido a que varios
microorganismos que causan alteraciones son mas resistentes a la destrucción térmica que el Clostridium
botulinum.
Pasterización de Productos Lácteos. Una temperatura de referencia de 250 ºF (121,1 ºC) es demasiado
elevada cuando se usa el método general para investigar la pasterización de un fluido. Teniendo en cuenta
la ordenanza para Leche Pasterizada, las temperaturas de referencia de 161 ºF (71,7 ºC) para leche y 175
ºF (79,4 ºC) para mezcla de helados, son mas prácticas. En este trabajo, las siguientes unidades de
letalidad serán establecidas para pasterización: 1 s a 161 ºF para leche y 1 s a 175 ºF para mezcla de
helados. Estos nos da los siguientes tiempos de muerte relativos para leche y la mezcla:
Procesamiento Térmico de Fluídos Biológicos
(7.18)
10
º
º
91
161º
(7.19)
10
175º
El valor z depende del microorganismo objetivo para el proceso. Para la pasterización de productos
lácteos donde el microorganismo objetivo es Coxiellia burnettii, el microorganismo responsable de la
enfermedad conocida como “Fiebre Q”, asumiendo z = 10,8 ºF (6,0 ºC) es razonable. Con este valor z, las
ecuaciones de tasa letal para leche y mezcla de helados pueden ser establecidas como sigue:
1
10
1
161º
,
10
,
175º
(7.20)
(7.21)
Las tasas letales a 161 ºF y 175 ºF están resumidas en la tabla 7.4. Tablas alternativas pueden ser
construidas, a varias temperaturas de referencia, usando diferentes valores z. Las tasas letales son menos
exactas mientras la temperatura se desvía de la temperatura de proceso (Tref).
Ductos y Tuberías para Bioprocesos
92
Tabla 7.4 Tasas letales a 161 ºF y 175 ºF con z = 10,8 ºF.
Temperatura de Proceso, T (ºF)
seg a 161 ºF/ seg a T
seg a 175 ºF/ seg a T
144
0,027
----
146
0,041
----
148
0,063
----
150
0,096
----
152
0,147
----
154
0,225
----
156
0,344
----
158
0,527
0,027
160
0,808
0,041
162
1,24
0,063
164
1,90
0,096
166
2,90
0,147
168
4,45
0,225
170
6,81
0,344
172
10,4
0,527
174
16,0
0,808
176
24,5
1,24
178
----
1,90
180
----
2,90
182
----
4,45
184
----
6,81
186
----
10,4
188
----
16,0
190
----
24,5
Letalidad del Proceso. El valor F de un proceso puede ser evaluado combinando la tasa letal TL y el
historial tiempo temperatura:
10
(7.22)
Procesamiento Térmico de Fluídos Biológicos
93
Para la pasterización de leche el valor F (en este caso, segundos a 161 ºF) del proceso es calculado como
sigue:
10,8
161
10
161
10,8
(7.23)
Donde tinicio representa el tiempo cuando la temperatura es lo suficientemente alta como para tener un
efecto letal significativo. El superíndice sobre F es usado para indicar claramente el valor z utilizado en el
análisis, y Tref corresponde a la temperatura de referencia para el proceso. Dado que la tasa letal es una
función fácilmente definida en función del tiempo (t), la ecuación (7.23) puede ser integrada
analíticamente. Por otra parte, la ecuación puede ser resuelta numéricamente dividiendo el proceso en
unidades de tiempo discretas (∆t) y adicionando la muerte térmica ocurrida en cada parte del proceso:
(7.24)
∆
Calculando el valor F de un proceso utilizando la ecuación anterior es conocido como el “método
general”. La letalidad de un proceso es la razón entre el valor F del proceso dividido por el valor F
requerido para una esterilidad comercial:
(7.25)
La letalidad del proceso debe ser mayor que uno para tener un proceso aceptable.
Este concepto es aplicado a la pasterización de leche en el ejemplo 8.11.
94
Ductos y Tuberías para Bioprocesos
8. Problemas de Ejemplo
8.1
Comparación de Fluidos Newtonianos y Adelgazantes por Cizalla
La miel es un fluido Newtoniano y la dependencia de la viscosidad de la temperatura puede ser
descrita por una ecuación tipo Arrhenius (1.16) utilizando las constantes apropiadas en:
exp
5,58 10
´
exp
10.972
8.1
El relleno de pie de arándanos a 20°C en un fluido tipo ley de la potencia con los valores siguientes de las
6,0
propiedades:
,
0,43. Analice el índice de comportamiento de flujo de la miel a 24°C y
relleno para pie de arándano a 20 ºC , por medio de la comparación del esfuerzo de cizalla versus la
velocidad de deformación en cizalla y la viscosidad aparente versus la velocidad de deformación en
cizalla. Dibuje los resultados en el rango de velocidad de deformación en cizalla apropiado para bombear
estos fluidos con un caudal de 60 gpm por una tubería de 3 pulgadas (diámetro nominal).
Solución. El diámetro interno del tubo de 3 pulgadas es 2,834 pulg = 0,07198 m (apéndice 9.3) y el caudal
de 60 gpm = 0,003785 m3s-1. La velocidad de deformación en cizalla máxima (Ec. 1.10) para el relleno de
pie de arándano se calcula con:
3
1
4
4
3 0,43
1
4 0,43
4 0,003785
0,07198/2
137,6
8.2
Suponiendo que la velocidad de la deformación en cizalla mínima es aproximadamente del 10% de la
máxima, entonces es aconsejable realizar el análisis desde 10 hasta 140 s-1. Ya que para la miel n = 1; el
factor de corrección es igual a 1,0 y la velocidad de deformación en cizalla máxima es 103,4 s-1.
La viscosidad de la miel se calcula a 24°C con la Ec. (8.1) y da:
96
Ductos y Tuberías para Bioprocesos
5,58 10
exp
10.972
24 273,15
6,06
8.3
Y como el comportamiento de la miel es Newtoniano,
6,06
8.4
Y si se cumple que la viscosidad es igual a la viscosidad aparente:
6,06
8.5
Las ecuaciones que se pueden comparar para el caso del pie de arándanos, son las siguientes:
6,0
,
8.6
Y
6,0
,
8.7
Figura 8.1. La viscosidad aparente y el esfuerzo de cizalla del relleno de pie de arándanos a 20°C (K = 6,0
Pa sn, n = 0,43) y miel a 24°C (µ = 6,06 Pa s) en el rango de velocidad de deformación en cizalla de 10 a
140 s-1.
Problemas de Ejemplo
97
La representación de los resultados (Fig. 8.1) ilustra el comportamiento característico de los fluidos
Newtonianos y adelgazantes. La curva de esfuerzo de cizalla versus la velocidad de deformación en
cizalla para la miel es una línea recta (a la izquierda de la figura) que aumenta rápidamente a partir del
origen. Debido al rápido incremento del esfuerzo de cizalla versus la velocidad de deformación en cizalla
se muestran solo dos puntos; y como el esfuerzo de cizalla aumenta fuertemente, solo se muestra en el
dibujo hasta valores de 20 s-1. Ya que la miel es un fluido Newtoniano, la viscosidad aparente es constante
y se presenta como una línea horizontal a η= 6,06 Pa s. el relleno de pie de arándanos es un fluido
adelgazante típico con una curva de esfuerzo de cizalla elevándose en forma gradual y una curva
descendente de la viscosidad aparente.
Figura 8.2. Viscosidad aparente y esfuerzo de cizalla del relleno de pie de arándanos a 20°C (K = 6,0 Pa
sn, n = 0,43) y miel a 24°C (µ = 6,06 Pa s) en el rango de velocidad de deformación en cizalla de 0,2 a 4,0
s-1.
Es muy instructivo analizar el comportamiento del flujo de estos materiales a velocidad de
deformación en cizalla baja (Fig. 8.2). Si se extienden hasta el valor cero las velocidades de deformación
en cizalla, sucede que ambas curvas pasan por el origen de las coordenadas. También sucede que ambas
curvas se cortan en 0,98 s-1, esto indica que las viscosidades aparentes son iguales a la velocidad de
deformación en cizalla.
98
Ductos y Tuberías para Bioprocesos
Es interesante destacar que se puede asumir de manera errónea que el relleno de pie de arándanos es un
fluido Newtoniano si se realiza solo una medida a 1 s-1, lo que llevaría a concluir que las propiedades
reológicas de la miel y el relleno de pie de arándanos son las mismas. Esta mala interpretación del
comportamiento reológico, puede producir errores garrafales en el análisis en tuberías de bioprocesos.
8.2
Equivalencia de la Ley de la Potencia de las Ecuaciones de Herschel Bulkley y Casson
Los datos reológicos de alimentos para bebés de durazno, fueron obtenidos a 25°C en el rango de
velocidad de deformación de 10 a 300 s-1. Los datos se ajustaron a la Ec. de Herschel Bulkley.
8.8
Donde
13
1,4
;
0,6. Esta ecuación es básicamente una expresión de la ley de la
;y
potencia donde el umbral de fluencia (σ0) representa el intercepto con el eje al ser la velocidad de
deformación en cizalla cero. Teóricamente, el umbral de fluencia representa el esfuerzo de cizalla mínimo
necesario para que el fluido se ponga en movimiento. Debido a la presencia del término umbral de
fluencia en la ecuación de Herschel Bulkley, K dado en esa ecuación, no es el mismo que para la
expresión de la ley de la potencia:
El mismo alimento para bebés de durazno fue ajustado al modelo de Casson:
,
Donde K1 = 3,7 Pa
,
0,5
8.9
y K2 = 0,22 Pa
0,5
s
0,5
. Esta ecuación se utiliza frecuentemente para modelar el
comportamiento reológico del chocolate líquido. El umbral de fluencia de Casson es el cuadrado del
intercepto: (K1)2. En este caso en particular, el umbral de fluencia de Casson es 13,7 Pa.
Para obtener los parámetros (K y n) de diseño de tuberías, convierta las anteriores ecuaciones al modelo
estándar de la ley de la potencia y compare los valores resultantes dibujando la viscosidad aparente (tanto
para la ecuación original como para la convertida) versus la velocidad de deformación en cizalla.
Problemas de Ejemplo
99
Solución. Para resolver este problema, se utilizan las ecuaciones dadas de Herschel Bulkley y Casson para
generar la nueva tabla de datos del esfuerzo de cizalla versus la velocidad de deformación en cizalla
(Tabla 8.1). Después de realizar la conversión logarítmica de los datos, se obtienen los parámetros de la
ley de la potencia por medio de una regresión lineal de estos datos. Al seguir este procedimiento se
convierte la curva de Herschel Bulkley en una de la potencia, tal como:
7,36
,
8.10
Y la curva de Casson a:
7,59
,
8.11
Las ecuaciones correspondientes de la viscosidad aparente son respectivamente:
7,36
,
8.12
7,59
,
8.14
Y
Al analizar las curvas de viscosidad aparente para el caso de Casson, se observa una concordancia muy
buena entre la ecuación original y la convertida (Fig. 8.3). El caso Herschel Bulkley da resultados
análogos. Desde el punto de vista práctico, las ecuaciones (8.10) y (8.11) son equivalentes. Además, los
problemas de diseño de tuberías pueden resolverse utilizando n = 0,34 y el valor medio del coeficiente de
consistencia K = 7,48 Pa sn.
100
Ductos y Tuberías para Bioprocesos
Figura 8.3. Viscosidad aparente calculada a partir de la ecuación de Casson original y de la ley de la
potencia.
101
Problemas de Ejemplo
Tabla 8.1. Datos de esfuerzo de cizalla versus velocidad de deformación en cizalla generados a partir de
las ecuaciones de Herschel Bulkley y Casson en el rango de velocidad de deformación en cizalla de 10 a
300 s-1.
13
1,4
,
3,7
(1/s)
(Pa)
(Pa)
10
18,6
19,3
20
21,4
21,9
30
23,8
24,1
40
25,8
25,9
50
27,6
27,6
60
29,3
29,2
70
30,9
30,7
80
32,4
32,1
90
33,8
33,5
100
35,2
34,8
110
36,5
36,1
120
37,8
37,3
130
39,0
38,5
140
40,2
39,7
150
41,3
40,9
160
42,4
42,0
170
43,5
43,1
180
44,6
44,2
190
45,6
45,3
200
46,6
46,4
210
47,6
47,4
220
48,6
48,5
230
49,6
49,5
240
50,5
50,5
250
51,4
51,5
260
52,4
52,5
270
53,3
53,5
0,22
,
102
Ductos y Tuberías para Bioprocesos
280
54,2
54,5
300
55,0
55,4
300
55,9
56,4
Problemas de Ejemplo
8.3
103
Datos de Cilindros Coaxiales para Mix de Helados
Los datos para el mix de helado de crema a dos temperaturas, una a condiciones de pasteurización
y la otra de vida útil, fueron obtenidos utilizando un viscosímetro de cilindros coaxiales (presentado en la
Fig. 2.2) con las siguientes condiciones: Rc = 21,00 mm; Rb = 20,04 mm; h = 60,00 mm; h0 = 0,32mm.
Calcular las propiedades de este material a ambas temperaturas. Comparar los reogramas obtenidos al
utilizar las ecuaciones para el esfuerzo de cizalla y la velocidad de deformación en cizalla del sensor (Ec.
2.1 y Ec. 2.4) con aquellos obtenidos de los valores medios (Ec. 2.3 y Ec. 2.4).
104
Ductos y Tuberías para Bioprocesos
Tabla 8.2. Datos experimentales del mix de helado de crema a 2°C y a 23°C obtenidos con un
viscosímetro de cilindros coaxiales: Rb = 20,04 mm; h = 60,00 mm; h0 = 0,32 mm.
T = 2°C
T = 83°C
Ω (rad/s)
M (N m)
Ω (rad/s)
M (N m)
2,08
0,01519
209
0,0019
2,61
0,01606
2,61
0,0021
3,13
0,01697
3,13
0,0022
3,64
0,01771
3,65
0,0024
4,15
0,01840
4,17
0,0025
4,70
0,01923
4,70
0,0026
5,23
0,02028
5,23
0,0026
6,26
0,02155
6,27
0,0030
7,30
0,02297
7,32
0,0031
8,36
0,02443
8,36
0,0033
9,40
0,02561
9,41
0,0036
10,44
0,02670
10,49
0,0038
11,49
0,02780
11,53
0,0040
12,54
0,02889
12,58
0,0042
13,62
0,03007
13,64
0,0045
14,68
0,03096
14,68
0,0047
15,71
0,03177
15,73
0,0048
16,76
0,03262
16,78
0,0050
17,81
0,03345
17,82
0,0053
18,86
0,03433
18,87
0,0055
19,91
0,03507
19,92
0,0055
20,97
0,03591
20,95
0,0057
22,01
0,03651
22,01
0,0059
Solución. Se utilizan los datos a 83°C para una velocidad angular de 10,49 rad s-1 en la Tabla 8.2. Los
ejemplos de cálculo para el esfuerzo de cizalla (Ec. 2.1) y la velocidad de deformación en cizalla en el
sensor (Ec. 2.2) son:
105
Problemas de Ejemplo
1
0,0038
2
1
0,02004 0,06032
2
25
8.14
Y con α= Rc/Rb= 21,00/ 20,02= 1,048,
2
1
10,49
2 1,048
1
1,048
8.15
234,8
Los valores medios del esfuerzo de cizalla (Ec. 2.3) y velocidad de deformación en cizalla (Ec. 2.4) son:
1
0,0038
4
1
1,048
0,021 0,06032
4
23,9
8.16
Y
1
1
10.49
1,048
1,048
1
1
224,3
8.17
Estos valores junto con los otros obtenidos en forma análoga se encuentran en la Tabla 8.3 y en la figura
8.4. Los análisis de regresión de las curvas resultantes da las siguientes propiedades reológicas:
•
Ecuación del sensor a T = 2°C, K = 21,10 Pa sn y n = 0,39;
•
Ecuación promedio a T = 2°C, K = 20,52 Pa sn y n = 0,39;
•
Ecuación del sensor y promedio (las curvas son casi idénticas) a T = 83°C, K = 1,76 Pa sn y n =
0,49.
106
Ductos y Tuberías para Bioprocesos
Las diferencias totales en los cálculos basados en los valores del sensor y promedio son despreciables.
Figura 8.4. Reograma para el mix de helado de crema a 2°C y 83°C determinados a partir de valores
calculados en la superficie del sensor (◊) y valores promedio (□).
107
Problemas de Ejemplo
Tabla 8.3. Valores del esfuerzo de cizalla para el mix de helado de crema a 83°C utilizando ecuaciones
,
que representan el comportamiento de superficie del sensor y la copa (
sensor y la copa (
,
) y valores promedio entre el
).
Ω (rad/s)
M (N m)
2,09
0,0019
46,8
12,5
44,7
11,9
2,61
0,0021
58,4
13,8
55,8
13,2
3,13
0,0022
70,1
14,5
66,9
13,8
3,65
0,0024
81,7
15,8
78,1
15,1
4,17
0,0025
93,4
16,4
89,2
15,7
4,70
0,0026
105,2
17,1
100,5
16,3
5,23
0,0026
117,1
17,1
111,9
16,3
6,27
0,0030
140,4
19,7
134,1
18,8
7,32
0,0031
163,9
20,4
156,6
19,5
8,36
0,0033
187,2
21,7
178,8
20,7
9,41
0,0036
210,7
23,7
201,2
22,6
10,49
0,0038
234,8
25,0
224,3
23,9
11,53
0,0040
258,1
26,3
246,6
25,1
12,58
0,0042
281,6
27,6
269,0
26,4
13,64
0,0045
305,4
29,6
291,7
28,2
14,68
0,0047
328,6
30,9
314,0
29,5
15,73
0,0048
352,1
31,5
336,4
30,1
16,78
0,0050
375,6
32,8
358,9
31,4
17,82
0,0053
398,9
34,8
381,1
33,3
18,87
0,0055
422,4
36,1
403,6
34,5
19,92
0,0055
445,9
36,1
426,0
34,5
20,95
0,0057
469,0
37,4
448,1
35,8
22,01
0,0059
492,7
38,8
470,7
37,0
(1/s)
(Pa)
(1/s)
(Pa)
108
Ductos y Tuberías para Bioprocesos
8.4
Determinación del Coeficiente de Mezcla
Se obtuvieron datos de jarabe de maíz (µ = 2,3 Pa s) y de miel a 25°C (µ = 7,5 Pa s) con un
viscosímetro de mezcla que tiene un rotor helicoidal cortado tipo tornillo (presentado en la Fig. 2.4).
Utilizando los datos obtenidos para el jarabe de maíz y la miel (Tabla 8.4) determinar el coeficiente de
mezcla (k”) para este sistema.
Solución. El producto de la viscosidad y de la velocidad angular (µΩ) versus el torque (M) se presenta en
la Fig. 8.5. La pendiente de la curva (k”) es calculada a partir de la regresión lineal y da 3070,8 ra. m-3.
109
Problemas de Ejemplo
Tabla 8.4. Datos para dos fluidos newtonianos obtenidos con un viscosímetro de mezcla.
Jarabe de Maíz a 23°C
Miel a 23°C
Ω (rad/s)
M (µN m)
Ω (rad/s)
M (µN m)
722
1,04
1.068
0,42
1.454
2,07
3.180
1,25
2.930
4,14
4.236
1,65
3.660
5,17
6.314
2,48
5.146
7,24
7.390
2,90
5.860
8,26
9.466
3,73
7.310
10,4
10.480
4,14
8.030
11,4
12.560
4,96
9.510
13,4
13.600
5,38
10.260
14,5
15.650
6,21
11.760
16,6
16.640
6,62
12.510
17,6
18.620
7,43
14.060
19,7
19.660
7,86
18.840
20,7
21.720
8,70
16.390
22,8
22.650
9,09
17.220
23,8
24.680
9,94
18.870
25,9
25.680
10,4
19.660
26,9
27.580
11,2
21.250
29,0
28.660
11,6
8.5
Viscosimetría de Mezcla para Salsa para Pastas
Utilizando el rotor helicoidal cortado tipo tornillo presentado en la figura 2.4 se obtuvieron los
datos para Pasta de Callampas Frescas Prego (Campbell Soup Co., Camden, NJ). Dados k´´= 3.047,4 rad
m-3 y k´= 1,6 rad-1 para este agitador, dibujar la viscosidad aparente versus la velocidad de deformación en
cizalla y determinar las propiedades (K y n) de ley de la potencia de la salsa para pasta.
Este fluido no puede ser evaluado en un viscosímetro de cilindros coaxiales convencional debido a
las partículas grandes que presenta el material a ensayar: pedazos de tomate y callampas con tamaños de
1,48 y 0,81 cm, respectivamente y medidos de forma experimental.
110
Ductos y Tuberías para Bioprocesos
Figura 8.5. Gráfico de µ Ω versus M para el jarabe de maíz y miel a 83°C para encontrar k´´: la pendiente
de la curva es igual a k´´= 3.070,8 rad m-3.
Tabla 8.5. Datos de viscosímetro de mezcla obtenidos con el rotor helicoidal de Salsa para Pasta Prego
(con callampas) a 80°C.
Ω (rad/s)
M (µN m)
Ω (rad/s)
M (µN m)
2,99
5.420
11,8
8.080
4,17
5.870
13,0
7.900
4,75
6.020
13,6
7.890
5,93
6.290
14,7
8.030
6,51
6.290
15,3
8.160
7,70
6.920
16,5
8.290
8,26
7.170
17,1
8.350
9,44
7.400
18,3
8.440
10,0
7.590
18,8
8.580
11,2
7.610
20,0
8.940
111
Problemas de Ejemplo
Solución. Para resolver este problema se realizarán los cálculos detallados para un punto. A la velocidad
angular de 10 rad s-1, la viscosidad aparente (Ec, 2.19) se calcula con:
"
7.590 10 3.047,4
10
2,31
8.18
Y la velocidad de deformación en cizalla (Ec. 2.12) es:
´
1,6 10
16
8.19
Aplicando esta metodología a los valores dados en la Tabla 8.4, se obtienen los puntos del gráfico (Fig.
8.6), lo que demuestra que no hay una relación lineal entre las variables. Las propiedades del fluido
adelgazante se encuentran localizando la línea de tendencia de la curva siguiente:
K = 17,5 Pa sn, y n = 0,26.
Figura8.6. Viscosidad aparente versus velocidad de deformación en cizalla para la salsa para pasta a 80°C
con un análisis de regresión mostrando K = 17,50 Pa sn, y n-1 = - 0,74.
112
Ductos y Tuberías para Bioprocesos
8.6
Calculando la Caída de Presión con la Viscosidad Efectiva
Se está bombeando un fluido espeso, salsa de tomate, que es adelgazante (K = 30 Pa sn, n = 0,2,
ρ = 1010 kg m-3) con un caudal de 40 gpm por una tubería de 50 m de largo y 3 pulgadas de diámetro
nominal (diámetro interno = 0,072 m). Calcular la razón de la caída de presión real en la tubería, calculada
utilizando los estándares de la mecánica de fluido con la caída de presión predicha utilizando la técnica de
la viscosidad efectiva. ¿Cuál es el error que se produce al ocupar la viscosidad efectiva?
Solución. El caudal volumétrico y la velocidad media (Ec. 4.2) son calculados utilizando los parámetros
siguientes.
40
60 264,17
40
8.20
0,00252
0,00252
/4 0,072
8.21
0,619
El número de Reynolds de la Ley de la potencia (Ec. 4.9) y el factor de roce de Fanning (que se encuentra
utilizando la Ec. 4.13 para flujo laminar) se calculan a partir de:
4
,
3
8
16
,
16
38,5
0,072
1
.
0,619
8 ,
30
,
1.010
4 0,2
3 0,2
1
38,5
8.22
8.23
0,415
No existe un método estándar para calcular la viscosidad efectiva; ella es comúnmente calculada como el
valor de la viscosidad aparente evaluada a la velocidad de deformación con cizalla máxima en la tubería y
suponiendo que el fluido es newtoniano (Ec. 1.10 con n = 1):
4
á
4 0,00252
0,072
2
68,9
8.24
113
Problemas de Ejemplo
Utilizando esta velocidad de deformación en cizalla y la definición de viscosidad aparente se puede
calcular la viscosidad efectiva.
30 68,9
,
1,02
8.25
A continuación se pueden obtener los valores del número de Reynolds y del factor de roce de Fanning
efectivo, suponiendo comportamiento newtoniano:
1.010 0,072 0,619
1,02
16
16
44,1
44,1
8.26
8.27
0,362
La pérdida de carga en la tubería se calcula aplicando la ecuación de balance de energía mecánica (Ec.
3.2).
8.28
2
∆
Al colocar los valores numéricos, la pérdida de carga predicha (utilizando la viscosidad efectiva) con la
pérdida de carga real es:
∆
∆
0,362
0,415
0,87
8.30
El resultado obtenido en la Ec. (8.30) indica que el valor predicho es el 87% del real; esto significa que en
este caso, hay un 13% de error al utilizar el método de la viscosidad efectiva para predecir la pérdida de
carga. Dependiendo del valor del índice de comportamiento de flujo y del valor de la velocidad de
deformación en cizalla se traduce en que la pérdida de carga predicha, utilizando la viscosidad efectiva,
puede ser significativamente diferente de la pérdida de carga real.
114
Ductos y Tuberías para Bioprocesos
Es didáctico realizar una comparación entre la viscosidad efectiva y la aparente. La velocidad de
deformación en cizalla en el tubo va desde valor cero en el centro del tubo hasta un valor máximo en la
pared del tubo que se debe calcular (Ec. 1.10) tomando en cuenta el índice de comportamiento de flujo.
3
á
1
4
4
3 0,2
1
4 0,2
4 0,00252
0,072
2
8.31
137,8
A esta velocidad de deformación en cizalla, la viscosidad aparente tiene un valor mínimo debido a
que hay una distribución de la viscosidad dado un caudal:
30 137,8
í
,
0,538
8.32
A la velocidad de deformación en cizalla 1,0 s-1, la viscosidad aparente es 30 Pa s. si el índice de
comportamiento de flujo fuera 1,0; esta sería la viscosidad newtoniana.
Ya que la viscosidad aparente en una función de la velocidad de deformación en cizalla y ésta es
una función del radio, η puede ser expresada en función del radio:
3
1
4
8.33
4
Como el radio tiende a cero en el centro del tubo, la viscosidad aparente tiende a infinito. De este
Problema Ejemplo, uno puede encontrar que la viscosidad aparente en el tubo va desde infinito hasta
0,583 Pa s. Este ejemplo ilustra que relacionar la viscosidad efectiva con la aparente puede llevar a errores
significativos en la predicción de la pérdida de carga en tuberías. Hay que resaltar que un único parámetro
es inadecuado para describir el comportamiento reológico del fluido no-newtoniano, para describirlo en
forma adecuada se requieren al menos dos parámetros (en este caso K y n).
8.7
Generando una Curva del Sistema para Bombear Crema
Suponiendo que el sistema de descarga de un fluido (desde el camión estanque hasta el estanque
de almacenamiento) fue diseñado tomando en cuenta los siguientes requerimientos:
115
Problemas de Ejemplo
1) El cambio de altura cuando el camión está casi vacío y el estanque de almacenamiento (con la
tubería de carga en el fondo del estanque) está casi lleno (máximo de diferencia de energía
potencial) es 3,5 m.
2) El fluido que se está bombeando es crema a 5°C: ρ = 985 kg m-3 y µ = 45 cP. Ambos
estanques son venteados a presión atmosférica durante la descarga.
3) El sistema de descarga incluye los siguientes componentes estándar de tubería en la línea de
succión:
4)
•
Entrada al tubo de 3”
•
2,5 m de tubo de 3” (del apéndice 9.3, el diámetro es 2,83 pulg = 0,072 m)
•
Tres codos de 90° (estándar, soldado) en la línea de 3 pulg.
Y los siguientes componentes estándar en la línea de descarga:
•
19,0 m de tubería de 2,5 pulg (del apéndice 9.3, el diámetro interno es 2,37 pulg = 0,0602 m).
•
Siete codos de 90° (estándar, soldado) en la línea de 2,5 pulg.
•
Una T de 2,5 pulg (estándar, soldada) utilizada como codo.
•
Salida del tubo de 2,5 pulg.
5) El sistema tendría un filtro y dos válvulas neumáticas en la línea de descarga de 2,5 pulg. Los
datos experimentales de estos componentes, obtenidos con agua a temperatura ambiente (ρ =
998 kg m-3) son los siguientes, provistos por el fabricante:
Q (gpm)
∆P, filtro (Pa)
∆P, válvula (Pa)
30
500
483
40
1.000
966
50
1.500
1.449
60
2.000
1.933
70
2.500
2.416
116
Ductos y Tuberías para Bioprocesos
Calcular lo siguiente:
1) Plantear la ecuación (teórica) del trabajo de la bomba considerando que todos los elementos del
sistema son evaluados y el cálculo de la altura total del sistema.
2) Cálculo numérico detallado para un caudal de 50 gpm. Incluya el cálculo de los requerimientos de
potencia hidráulica.
3) La curva característica del sistema necesaria para seleccionar la bomba centrífuga del proceso,
suponga que el caudal se mueve entre 6,8 y 15,9 m-3h-1 (30-10 gpm). Resuma los valores en un
gráfico de altura total del sistema (m) versus caudal (m3/h).
Solución Parte I. Ya que los dos estanques están venteados a la atmosfera, esto significa que las presiones
son iguales, así que se cumple P2-P1 = 0; y la velocidad con que cambia el nivel del liquido es muy
0, se cumple. Teniendo en cuenta lo expuesto, el trabajo
pequeña, esto hace que la suposición
de la bomba puede ser calculado utilizando la ecuación de balance de energía (Ec. 3.2).
8.34
Donde,
2
8.35
∆
2
La sumatoria de las pérdidas por roce debe ser ampliada para que tome en cuenta todos los elementos del
sistema (utilizando las Ecs. 5.4 y 5.5 para encontrar los valores de kf).
2
2
8.36
3
,
,
í
2
,
7
,
,
í
,
117
Problemas de Ejemplo
160
,
800
800
8.38
1
0,80 1
1,0
,
1
0,25 1
,
,
8.37
0,50
8.39
5.3
2
2
8.40
8.41
2
í
í
,
∆
∆
∆
2
,
8.42
á
á
,
Después que se ha calculado la necesidad de trabajo (W), la altura total del sistema puede evaluarse
considerando la aceleración de gravedad.
8.43
Solución Parte II. Se plantea la información preliminar disponible. Propiedades de la crema:
45
0,045
0,072
;y
4
y
2,5
985
;
50
11,4
0,00315
;
; y:
4 0,00315
0,072
8.44
0,774
0,072 0,774 985
0,045
1220
8.45
118
Ductos y Tuberías para Bioprocesos
160
1.220
,
800
1.220
,
16
16
1.220
0,50
0,63
0,25 1
1
2,83
8.46
0,99
8.47
8.48
0,0131
En la sección de la tubería de 2,5 pulg se tiene D = 0,0602 m y L = 19,0 m; kf, salida = 1,0; y
4 0,00315
0,0602
4
8.49
1107
0,0602 1.107 985
0,045
,
800
1.459
0,80 1
800
1.459
,
16
16
1.459
1
2,37
0,25 1
0,0110
1
2,37
1459
1,69
0,90
8.50
8.51
8.52
8.53
119
Problemas de Ejemplo
Las propiedades del agua y del vapor (Apéndices 9.5 y 9.7) a temperatura ambiente, son
necesarias para calcular el número de Reynolds del caudal volumétrico dado, con los datos siguientes:
0,001
998
;
. Estos datos se necesitan para calcular el factor de roce para agua que
es necesario para las correcciones del factor de roce. El número de Reynolds para el agua en la tubería de
2,5 pulg es:
0,0602 1,107 998
0,001
8.54
66.508
Se calcula el factor de roce con la ecuación de Blasius (Ec. 4.4) dando:
0,0791
,
0,0791
66.508 ,
8.55
0,00493
Se encuentran diferencias pequeñas al calcular el factor de roce utilizando otras ecuaciones tales como: la
ecuación de Haaland (Ec. 4.5) resulta
0,00485 y la ecuación de Churchill (Ec. 4.6) da
0,00487.
De acuerdo a lo expuesto, las diferencias del factor de roce son despreciables.
A continuación, se puede evaluar la ecuación con los antecedentes expuestos. El factor de roce en
la tubería recta es:
2
2
í
2 0,0131 0,774
0,0720
8.56
2
í
2,5
2 0,0110 1,107
0,0602
,
19
Y las pérdidas que presentan los fittings y la salida son:
9,03
120
Ductos y Tuberías para Bioprocesos
2
0,774
2
3
,
2
,
2
í
0,63
1,107
2
3 0,99
1,69
,
7 0,90
7
,
,
í
1,0
6,59
,
8.57
Y las pérdidas en el filtro y las dos válvulas neumáticas son:
0,0110
0,00493
∆
1.500
998
2
0,0110
0,00493
1.459
998
9,83
8.58
La pérdida total por roce es la suma de todas las pérdidas:
9,03
6,59
9,83
25,45
8.59
El trabajo requerido por la bomba (Ec. 8.34) puede ser determinado al incluir la diferencia de
energía potencial.
9,81 3,5
25,45
59,79
8.60
Hay que destacar que no se utiliza más del 40% de la energía en superar las pérdidas por roce en
la tubería y el resto se utiliza para elevar el fluido. Utilizando los resultados de la Ec. (8.60) se puede
determinar la altura del sistema a 50 gpm (11,4 m3h-1) utilizando la Ec. (8.43).
59,79
9,81
6,09
8.61
También se puede calcular el incremento de presión en la bomba que se produce a un caudal de 50
gpm, utilizando el trabajo requerido:
121
Problemas de Ejemplo
∆
59,79 985
58,9
8,5
8.62
Y la potencia hidráulica (Ec. 3.14) a 50 gpm es:
59,79 0,00135 985
186
8.63
Figura 8.7. Curva del sistema para crema a 5°C.
Solución Parte III. Rehaciendo los cálculos anteriores y aplicando las Ec. (8.44) a Ec. (8.61) a diferentes
caudales y con dichos resultados, se construye la curva del sistema para el proceso (Fig. 8.7). la
intersección de la curva de la bomba (bomba centrífuga) con la curva del sistema daría el caudal de la
crema en el sistema establecido.
8.8
Bomba de Desplazamiento Positivo para Jugos de Fruta Pulposos
Supóngase los mismos elementos físicos del Problema Ejemplo 8.7, incluyendo una reducción de
3 pulg a 2,5 pulg. El sistema fue diseñado para transportar 110 gpm de jugo de fruta pulposo (fluido
adelgazante con K = 0,43 Pa sn; n = 0,6; ρ = 1.030 kg/m3) a 10°C, utilizando una bomba de
desplazamiento positivo rotatoria de lóbulo.
122
Ductos y Tuberías para Bioprocesos
Los elementos siguientes están instalados en la tubería aguas arriba de la bomba (línea de succión):
•
Conexión a la tubería de 3 pulg
•
Tubería de 3 pulg de 2,5 m de longitud (del apéndice 9.3 se tiene diámetro interno =2,83 pulg =
0,072 m)
•
Tres codos de 90° (estándar, soldados) en la tubería de 3 pulg
Los componentes restantes 8 cada uno en la línea de 2,5 pulg se encuentran después de la bomba (en la
línea de descarga)
•
3 reducciones de 2,5 pulg (θ = 9,5°)
•
19,9 m de tubería de 2,5 pulg (del apéndice 9.3; diámetro interno = 2,37 pulg = 0,062 m)
•
7 codos de 90° (estándar, soldados) en la línea de 2,5 pulg
•
T de 2,5 pulg ((estándar, soldados) utilizada como codo
•
Salida del tubo de 2,5 pulg
•
Un filtro y dos válvulas neumáticas
Se supone que la diferencia de elevación (3,5 m) se mantiene. También se conoce por medio de los
folletos del fabricante que las pérdidas de carga (para agua a 110 gpm) en el filtro y la válvula neumática
son 4.000 Pa y 3.030 Pa, respectivamente.
Desarrollar la solución simbólica (teórica) para:
1) Requerimiento de trabajo de la bomba explicando la diferencia entre los factores de la solución
que pueda existir con los utilizados en el fluido Newtoniano estudiado en el Problema Ejemplo
8.7.
2) Presión de entrada de la bomba y el (NPSH)A
3) Presión en la descarga de la bomba
Utilizando las soluciones teóricas anteriores, encontrar los valores numéricos de:
123
Problemas de Ejemplo
4) El consumo de energía (J/kg) del sistema, y la pérdida de carga total del sistema (m) para el
sistema propuesto.
5) La presión absoluta (kPa y psia) en la entrada de la bomba (suponga que la diferencia de altura es
nula, z1 = z2) y el (NPSH)A
6) La presión absoluta (kPa y psia) en la descarga de la bomba, suponiendo que se produce la
máxima diferencia de energía potencial: el nivel de descarga de la bomba está 3,5 m sobre la
bomba
7) La pérdida de descarga total (en kPa y psia) a que está sometida la bomba
8) Los requerimientos de potencia hidráulica para el sistema (Watts y hp).
Solución Teórica:
1) El trabajo W, es el mismo que se calculó en el caso de la crema, tratado en el Problema Ejemplo
8.7, con la excepción que hay valores numéricos diferentes para
la ley de la potencia (NRe,
PL)es
y ; el número de Reynolds de
utilizado en vez de NRe para el cálculo de los coeficientes de
pérdidas por roce para la reducción de 3 pulg a 2,5 pulg.
2) El cálculo de presión de entrada de la bomba (P2, presión absoluta), se realiza suponiendo que el
punto está al nivel de entrada del fluido y se aplica la ecuación de balance de energía (Ec. 3.1) y
0 y z1 = z2, se obtiene:
considerando que
8.64
Donde P1 = 1 atm, presión absoluta; y
8.65
2
2
Y
2
2
,
3
8.66
,
í
124
Ductos y Tuberías para Bioprocesos
8.67
2
2
í
2 2
1 5
3 3
1
3
8.68
Se usa el valor de la presión de entrada de la bomba calculada anteriormente y el valor de la presión de
vapor (Pv) para calcular la altura neta positiva de succión disponible (Ec. 3.24).
8.69
3) El cálculo de la presión de descarga de la bomba puede realizarse con los valores conocidos de la
presión de entrada de la bomba y el trabajo necesario para que la bomba funcione.
4)
8.70
ó
Solución Numérica: se empieza estableciendo la siguiente información adicional: las propiedades de la
pulpa de fruta a 10°C son: K = 0,43 Pa sn; n = 0,6; y ρ = 1.030 kg m-3; Q = 110 gpm = 0,00694 m3 s-1;
flujo másico = 7,15 Kg s-1; D = 0,072 m; L = 2,5 m;
= 1,70 m s-1; y las ecuaciones relevantes para la
entrada de la bomba son:
,
0,072
,
8
,
,
,
.
1,70
0,43
2.100
160
0,50
2.183
800
0,25 1
2.183
,
1.030
4 0,6
3 0,6
1
875 1
2.100
875 1
8.71
2.183
0,6
2.450
8.72
8.73
0,57
1
2,87
,
0,70
8.74
125
Problemas de Ejemplo
16
2.183
8.75
0,00733
En la tubería de 2,5 pulg, D = 0,0602 m y L = 19,0 m;
salida =
,
,
= 2,44 m s-1;NRe,PL = 3237 (zona de transición; kf,
1,0; y:
800
3.237
0,80 1
800
3.237
0,00732
1
2,37
8.76
1,38
0,25 1
1
2,37
é
9.11
8.77
0,60
8.78
El coeficiente de roce para la reducción, se calcula con la ecuación siguiente (Tabla 5.7) para 0° < θ < 45°
y NRe ≤ 2.500:
,
ó
1,2
160
2.183
72,0
60,2
1 1,6 sen
9,5
2
0,18
8.79
Las propiedades del agua (apéndice 9.5 y 9.7) a temperatura ambiente, son necesarias para calcular el
número de Reynolds al caudal volumétrico dado: µ = 0,001 Pa s; ρ = 998 kg m-3. Estos datos se utilizan
para encontrar el factor de roce para el agua necesario para la corrección del factor de roce en el
equipamiento. El número de Reynolds para el agua en el tubo de 2,5 pulg es:
0,0602 2,44 998,2
0,001
146.623
8.80
El cálculo del factor de roce para el agua por medio de la Ec. de Churchill (Ec. 4.6) da:
0,00413
8.81
126
Ductos y Tuberías para Bioprocesos
5) Calcular el trabajo de la bomba. Al utilizar la información anterior se puede evaluar la ecuación
total. La pérdida por roce en el tubo recto es:
2
2
8.82
2
í
2,5
2 0,00733 1,70
0,0720
í
,
2 0,00732 2,44
0,0602
19
29,0
Y la pérdida combinada en los fittings y la descarga es:
2
2
,
2
3
,
8.83
,
í
ó
,
7
,
,
í
1,70
2
0,57
3 0,70
2,44
2
0,18
1,38
,
7 0,60
1,0
24,1
Y las pérdidas en el filtro y en las dos válvulas neumáticas son:
0,00732
0,00413
∆
4.000
998
2
0,00732
0,00413
3.030
998
17,9
8.84
La pérdida total por roce es la suma de las pérdidas de todos los componentes determinados en los
cálculos anteriores.
29,0
24,1
17,95
71,0
8.85
127
Problemas de Ejemplo
El trabajo que necesita la bomba puede ser calculado agregando a la pérdida total por roce la diferencia de
energía potencial:
9,81 3,5
71,0
8.86
105,3
Conociendo el valor del W se puede calcular la altura total del sistema.
105,3
9,81
8.87
10,7
6) Presión de la succión de la bomba y el NPSH disponible. Las pérdidas por roce aguas arriba de la
bomba se calculan:
7)
8.88
2
2
1,70
2
,
,
í
0,57
í
2 0,00733 1,70
0,0720
3 0,70
2,5
5,33
Utilizando la presión absoluta, P1 = 1 atm = 101.420 Pa y α = 1,12 (de la Ec. (8.68)), puede calcularse la
presión de succión de la bomba:
8.89
ó
1.030
101.420
1.030
1,70
1,12
5,33
93,3
13,5
El NPSH disponible, se calcula utilizando la presión en la succión de la bomba encontrada al aplicar la Ec.
(8.89) y la presión de vapor del agua a la temperatura del proceso (del apéndice 9.5, Pv = 1228 Pa a 10°C).
128
Ductos y Tuberías para Bioprocesos
93.300 1.228
9,81 1.030
8.90
9,1
8) Presión en la descarga de la bomba.
105,3 1.030
ó
93.300
201,8
29,3
8.91
9) Pérdida de carga de la bomba o caída total de presión en el sistema de bombeo:
∆
105,3 1.030
,
108,5
15,7
8.92
10) Requerimientos de potencia hidráulica:
105,3 7,15
8.9
753
1
8.93
Bombeando un Fluido Sensible al Cizalle (Crema)
Crema fría (5°C), fluido sensible al cizalle, está siendo bombeada con un caudal de 50 gpm por una
tubería recta de 3 pulg (D =2,83 pulg = 0,072 m) utilizando una bomba de diafragma que produce un
efecto mínimo de cizalle de degradación del fluido, por esto, sólo se debe evaluar ka degradación
mecánica del fluido por efecto del cizalle en la tubería. Las propiedades del fluido y parámetros aplicados,
son:
45
0,045
;
50
0,00315
0,774
;
985
3,10
1.219; ya que el fluido es laminar,
20
129
Problemas de Ejemplo
1) Evaluar la intensidad de la potencia de cizalla en el sistema propuesto.
2) Evaluar la intensidad de la potencia de cizalla en un sistema nuevo de procesamiento de la crema
con una longitud que se ha triplicado (L = 60 m), manteniendo el caudal volumétrico en 50 gpm
0,00315
(
).
3) Evaluar la intensidad de la potencia de cizalla en un sistema de procesamiento de crema nuevo en
el cual el caudal se ha incrementado en 50% (
75
0,00473
), y la longitud de
la tubería se mantiene constante (L = 20 m). También se pide calcular el diámetro de la tubería
nueva que puede utilizarse para aumentar el caudal y mantener un nivel aceptable de intensidad
del cizalle, “suponiendo que el proceso original es útil”.
Solución
1) Evaluar primero el trabajo de cizalla necesario (Ec. 6.1) y en seguida calcular la intensidad de la
potencia en cizalla (Ec. 6.2):
2)
2
8.94
∆
2
8.95
Para simplificar la discusión de estos conceptos, suponga que el único factor influyente en Ws es el factor
de roce en la tubería recta. Con esto la Ec. (8.94) puede ser simplificada a:
2
2
16
1.219
0,774
20
0,072
8.96
4,37
Al usar este valor para el trabajo de cizalla, la intensidad de potencia de cizalla encontrada en la tubería de
3 pulg puede ser calculada:
4
4 4,37 3,10
0,072 20
166
8.97
130
Ductos y Tuberías para Bioprocesos
Donde V, es la capacidad volumétrica de la tubería de 3 pulg y 20 m de largo.
Se supone que el bombeo realizado bajo las consideraciones expuestas (se considera el “sistema en
funcionamiento”) produce un producto aceptable.
3) En el caso en que la longitud de la tubería se triplica (L = 60 m) y el caudal volumétrico
permanece constante (Q = 50 gpm = 0,00315 m3 s-1) los valores de Ws y S para la tubería son:
2
2
4
16
1.219
0,774
60
0,072
4 13,1 3,10
0,072 60
8.98
13,15
8.99
166
Al triplicar la longitud de la tubería se triplica Ws y el valor de S no cambia, ya que el daño de la crema
por la cizalla es la rotura de la membrana que rodea el glóbulo graso, esto explica el aumento de Ws y el
mantenimiento del valor de S indica que no hay efectos adversos en la crema debido a que el consumo de
energía por unidad de volumen (calculado para el sistema original) no excedió el valor anterior.
4) En el caso del aumento del caudal en 50% (Q = 75 gpm = 0,00473 m3 s-1,
4,66
) y la
longitud de la cañería permanece constante (L = 20 m), la velocidad media y el número de
Reynolds, son:
0,00473 4
0,072
8.100
1,16
985 0,072 1,16
0,045
1.828
Con estos resultados Ws y S pueden ser calculados para el nuevo flujo:
8.101
131
Problemas de Ejemplo
2
2
16
1,16
1.828
0,072
4
4 6,54 4,66
0,072 20
8.102
20
6,54
8.103
374
En este caso, Ws aumenta en 50% y S aumenta en 225% en base al valor original de 166 W m-3. El nivel
alto de S, lo hace inaceptable porque dañaría el producto. Para mantener el caudal en 75 gpm y un nivel
aceptable en intensidad, se debe aumentar el diámetro de la tubería. el valor de C y el diámetro de la
tubería nueva puede ser calculado utilizando los dos caudales en estudio y el criterio de escalamiento
estable por la Ec. (6.8):
75
50
8.104
1,5
/
1,5
72
8.105
84,7
Ya que el diámetro interno de la tubería es 84,7 mm es invariable (ver apéndice 9.3), el tamaño siguiente
(aumenta a un tubo de 4 pulg) que tiene un diámetro 97,4 mm (3,83 pulg) es el adecuado. Al utilizar este
diámetro se tienen los valores siguientes para ,
0,00473 4
0,0974
2
4
16
0,635
1.354
0,0974
4 1,96 4,66
0,0974 20
y S:
8.106
0,635
985 0,0974 0,635
0,045
2
,
8.107
1.354
20
61,3
8.108
1,96
8.109
132
Ductos y Tuberías para Bioprocesos
Donde V, es la capacidad volumétrica de una sección de 20 m y de 4 pulg de diámetro. Este valor de S en
la tubería de 4 pulg, es significativamente menor que el máximo tolerable de 166
. En realidad, con
el bajo valor de S encontrado para la tubería de 4 pulg, es posible aumentar el caudal sin dañar el
producto. Este resultado puede ser predicho si la ecuación para S, se amplía incluyendo la definición para
Ws.
8.110
2
Para calcular la velocidad, suponga flujo laminar (así
16/
), reemplace
y
,y
resuelva para , dando:
8.111
32
Al reemplazar las variables por los valores conocidos, da la velocidad promedio siguiente:
166 0,0974
32 0,045
32
8.112
/
1,05
Esta velocidad corresponde a un caudal volumétrico de 0,0078
124
y se debe comprobar
que el número de Reynolds da:
985 0,0974 1,05
0,045
2.238
8.113
Este valor del NRe, rompe el supuesto de flujo laminar por lo que hay que evaluar el factor de roce de
Fanning en la zona de transición, al usar la ecuación de Churchill da
0,00717. Con estos valores, se
pueden recalcular Ws y S.
2
2 0,00717 0,05
0,0974
4
20
4 3,25 7,68
0,0974 20
3,25
167
8.114
8.115
133
Problemas de Ejemplo
Al utilizar el tubo de 4 pulg con un caudal de 124 gpm, es improbable que dañe la crema, porque la
intensidad de la potencia de cizalla se mantiene en un nivel aceptable que es aproximadamente 166
, valor obtenido con la Ec. (8.99).
Es interesante destacar que el NRe aumenta desde 1.354 a 2.238, mientras S se mantiene constante, lo que
demuestra claramente que el número de Reynolds no es constante durante el escalamiento. También, hay
que destacar que el Problema Ejemplo 8.9, se desarrolló para ilustrar los principios técnicos involucrados
en el bombeo de fluidos sensibles al cizalle. No está enfocado a establecer técnicas de diseño ingenieriles
para manipular crema.
8.10
Intensidad de la Potencia de Cizalla en una Bomba Centrífuga
El Problema Ejemplo 8.7 trata del bombeo de crema desde un camión a un estanque de
almacenamiento. Suponga que la bomba que se utiliza es centrífuga. Calcular la pérdida de carga de la
bomba y la intensidad de la potencia de cizalle entregada al fluido por la bomba, cuando el caudal
volumétrico en el sistema es 50 gpm (
0,00315
).
En la solución del Problema 8.7, el trabajo de la bomba fue de 59,79
información, junto a la densidad de la crema (
985
, a un caudal de 50 gpm. Esta
) puede utilizarse para calcular la pérdida
de carga de la bomba:
∆
59,79 985
58,9
8,54
8.116
El trabajo de cizalla (Ws) realizado en el fluido cuando es bombeado, es igual al trabajo de la bomba de
59,79
. Conociendo el trabajo de cizalla, la intensidad de la potencia de cizalla generada por la
bomba puede ser calculada, aplicando la Ec.(6.2):
59,79 0,00315 985
0,0012
154,6
8.117
Donde V, es la capacidad volumétrica de la bomba, bajo condiciones estáticas, cuya medida dio 1,2 litros
ó 0,0012 m3.
134
Ductos y Tuberías para Bioprocesos
La intensidad total de potencia de cizalla para el sistema, incluye los otros componentes que generan una
disipación viscosa de la energía, tales como: succión, descarga, válvulas neumáticas, filtro, tubería, tee y
codos. La Ec. (8.59) indica que estos elementos del sistema generan un trabajo de cizalla adicional en la
succión de: 25,45
8.11
.
Letalidad de un Proceso de Pasterización
Un sistema de pasteurizar leche a escala piloto, trata 10 gpm (1,34 pie3 min-1) de leche caliente del
sistema,
la
leche
0,000269
caliente
(
1.110,2
63,05
;
0,000400
) que sale del intercambiador de placas a 166°F, en la sección pasa por el tubo de
mantenimiento de temperatura; enseguida vuelve al intercambiador, entrando a la zona de enfriamiento a
163°F. Esta parte del sistema es un tubo de acero inoxidable de 2 pulg (diámetro interior = 1,87 pulg) y
tiene las siguientes longitudes en cada una de las secciones: 3,17 pie desde el intercambiador a la zona de
mantenimiento de la temperatura; 27,25 pie en la zona de mantenimiento de la temperatura y 3,92 pie
desde el retorno del tubo de mantención al intercambiador de placas. Calcular la letalidad del proceso.
Para resolver este problema, es necesario calcular la velocidad media siguiente (Ec. 4.2), número
de Reynolds (Ec. 4.1), y la velocidad máxima (Ec. 4.29)
1,34/60
4
1,87
12
8.118
1,17
1,87⁄12 1,17 63,05
0,000269
á
0,0336 log
0,662
8.119
42.735
0,0336 log
1,17
42.375
0,662
1,43
8.120
El análisis del proceso térmico está basado en la velocidad máxima, que teóricamente representa el
comportamiento de la partícula de leche, que es la que se mueve más rápido a través del centro del tubo,
en el sistema. Las partículas más lentas reciben un mayor tratamiento térmico.
135
Problemas de Ejemplo
Suponga que la caída de temperatura es lineal durante el proceso. El tiempo total del tratamiento
de la leche a temperatura alta, es igual a la longitud total del trayecto, dividida por la velocidad máxima:
tproceso = (3,17+27,25+3,92)/1,43 = 24 s. la velocidad letal, es una función que depende de la temperatura:
10
8.121
,
Suponiendo que z =10,8°F. las velocidades letales y letalidades están resumidas en la Tabla 8.5.
El valor de F del proceso, se calcula utilizando la Ec. (7.24) y se presenta en la Tabla 8.5:
, °
°
50,2 . El requerimiento legal para pasteurizar leche, exige un tiempo mínimo de calentamiento
de 15 s a 161°F. Utilizando los datos anteriores, puede calcularse la letalidad del proceso ( Ec. 7.25) como
sigue:
, °
°
, °
°
50,2
15
8.122
3,35
Este valor implica que el proceso aplicado es 3,35 veces más letal que el necesario para eliminar
patógenos. Aunque el sobrecalentamiento puede ser indeseable para la leche, esto no es inusual, ya que el
proceso térmico puede impedir la actividad de organismos de deterioro que pueden ser más
termoresistentes que los patógenos, o que se da un sobrecalentamiento para lograr un sabor a cocido que
es muy agradable en el producto.
136
Ductos y Tuberías para Bioprocesos
Tabla 8.5. Temperaturas y velocidad letal a intervalos de 2 s durante el proceso de calentamiento
t, s
T, °F
LR, s/s *
s a 161°F
2
165,8
2,8
5,5
4
165,5
2,6
5,2
6
165,3
2,5
5,0
8
165,0
2,3
4,7
10
164,8
2,2
4,5
12
164,5
2,1
4,2
14
164,3
2,0
4,0
16
164,0
1,9
3,8
18
163,8
1,8
3,6
20
163,5
1,7
3,4
22
163,3
1,6
3,2
24
163,0
1,5
3,1
Total
*LR, s a 161°F/ s a T °F
50,2
9. Apéndices
9.1
Factores de conversión y Alfabeto Griego
Densidad
1 g cm-3 = 1.000 kg m-3 = 62,428 lbm pie-3 = 0,0361 lbm pulg-3
1 lbm pie-3 = 16,0185 kg m-3
Masa y Fuerza
1 lbm = 16 oz = 0,45359 kg = 453,593 g
1 kg = 1.000 g = 0,001 ton metric = 2,20462 lbm = 35,274 oz
1 N = 1 kg m s-2 = 105 dyna = 105 g cm s-2 = 0,22481 lbf
1 lbf = 4,448 N = 32,174 lbm pie s-2
Longitud
1 m = 100 cm = 1.000 mm = 106 µm = 3,2808 pie = 39,37 pulg = 1,0936 yarda
1 pulg = 2,54 cm = 25,40 mm = 0,0254 m = 0,0833 pie = 0,02778 yarda
Potencia, Torque y Energía
1 Btu = 1.055 J = 1,055 kJ = 252,16 cal
1 hp = 550 pie lbf s-1 = 745,70 W = 0,7457 kW = 0,7068 Btu s-1
1 W = 1 J s-1 = 0,23901 cal s-1 = 0,414 Btu h-1 = 1,341 (10-3) hp
1 Btu hr-1 = 0,2931 W = 0,2931 J s-1
1 Nm = 1 kg m2 s-2 = 107 dyna cm = 0,7376 pie lbf = 9,486 (10-4) Btu
1 pie lbf = 1,35582 Nm = 1,35582 J = 1,2851 (10-3) Btu
Presión y Esfuerzo
1 bar = 105 Pa = 14,5038 lbf pulg-2 = 0,987 atm = 33,48 pie H20 a 4 ºC
1 Pa = 1 Nm-2 = 10 dyna cm-2 = 9,8692 (10-6) atm = 7,5 (10-3) torr
1 lbf pulg-2 = 6.894,8 Pa = 6,804(10-2) atm = 6,895 kPa
1 lbf pulg-2 = 2,309 pie H2O = 2,0360 pulg Hg
1 dyna cm-2 = 0,10 Pa = 10-6 bar = 0,987 (10-6) atm
1 atm = 101,325 kPa = 14,696 psi = 1,013 bar = 29,921 pulg Hg @ 0ºC
1 atm = 760 mm Hg @ 0 ºC = 33,90 pie H2O a 4 ºC
Temperatura
TKelvin = TCelsius + 273,15
TKelvin = (TFarenheit + 459,67)/1,8
TFarenheit = 1,8 TCelsius + 32
TCelsius = (TFarenheit -32)/1,8
Viscosidad (Absoluta o Dinámica, seguida por la cinemática)
1P = 1 dyna s cm-2 = 0,1 Pa s = 100 cP = 100 m Pa s
1 Pa s = 1.000 cP = 10 P = 1 kg m-1 s-1 = 1 N s m-2 = 0,67197 lbm pie-1 s-1
1 cP = 1 mPa s = 0,001 Pa s = 0,01 P
1 lbm pie-1 s-1 = 1,4882 kg m-1 s-1 = 1488,2 cP
Viscosidad cinemática: (cSt) = viscosidad absoluta (cP) / densidad (g cm-3)
1 cSt = 0,000001 m2 s-1 = 1 mm2 s-1 = 5,58001 pulg2 hr-1 = 0,00155 pulg2 s-1
1 St = 100 cSt = 0,0001 m2 s-1
1 m2 s-1 = 10-5 cSt = 10,7639 pie2 s-1
Volumen o Caudal
1 m3 = 106 cm3 = 103 L (litros) = 264,17 gal (US) = 35,3145 pie3
1 pie3 = 0,028317 m3 = 7,4805 gal (US) = 28,317 L = 6,2288 gal (UK)
1 gal (US) = 128 oz (fluida) = 3,7854 L = 0,8327 gal (UK) = 0,003785 m3
Ductos y Tuberías para Bioprocesos
138
1 m3 s-1 = 15.850,2 US gal min-1 = 264,17 US gal s-1
1 US gal min-1 = 6,30902 (10-5) m3 s-1 = 3,7854 L min-1
1 lbm hr-1 = 0,453592 kg hr-1 = 1,25998 (10-4) kg s-1
Alfabeto Griego (mayúsculas y minúsculas)*
alfa
Un
Α
α
Ν
ν
Xi
Beta
Β
β
Ξ
ξ
Gamma
Omicron
Γ
γ
Ο
ο
Delta
Pi
∆
δ
Π
π
Épsilon
Rho
δ
ε
Ρ
ρ
Zeta
Sigma
Ζ
ζ
Σ
σ
Eta
Tau
Η
η
Τ
τ
Theta
Ípsilon
Θ
θ
Υ
υ
Iota
Fi
Ι
ι
Φ
φ
Kappa
Ji
Κ
κ
Χ
χ
Lambda
Psi
Λ
λ
Ψ
ψ
Mu
omega
Μ
µ
Ω
ω
* Dedicado a todos (como los autores) que alguna vez se refirieron a ξ o a ζ como garabato.
Apéndices
9.2
139
Propiedades reológicas de fluidos biológicos
Producto #
Crema (40% grasa)
Crema (40% grasa)
leche (cruda)
leche (cruda)
leche (cruda)
Miel
Miel
Miel
Aceite de oliva
Aceite de oliva
Aceite de oliva
Aceite de soya
Agua
Agua
Agua
Agua
Agua
Huevo entero
Puré de manzana
Papilla para bebe
Relleno de arándano
Salsa de caramelo para helado
Chocolate
Salsa de chocolate
Crema de maíz
Crema de maíz
Aceite emulsionado (cremoso)
Aceite emulsionado (cremoso)
Acondicionador de pelo
Acondicionador de pelo
Acondicionador de pelo
Gel para el cabello
Jabón de mano (líquido)
Jabón de mano (líquido)
T, ºC
40
60
5
25
40
6,5
21,5
48
10
40
70
20
0
25
50
75
100
30
30
25
20
40
40
22
23
80
25
35
25
35
45
25
35
45
K, Pa sn
0,0069
0,0051
0,00305
0,00170
0,00123
76,6
7,20
0,50
0,1380
0,0363
0,0124
0,0636
0,001787
0,000890
0,000547
0,000378
0,000281
0,0064
11,6
18,0
6,08
35,6
26,2
6,83
23,8
20,4
0,03
0,01
16,1
13,0
11,5
58,7
5,07
1,24
n*
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
0,34
0,31
0,43
0,57
0,62
0,51
0,35
0,26
0,95
0,99
0,19
0,19
0,14
0,22
0,64
0,71
Ductos y Tuberías para Bioprocesos
140
T, ºC
Producto #
40
Caramelo blando para helados
1
Mezcla helado
80
Mezcla helado
25
Crema humectante
35
Crema humectante
45
Crema humectante
25
Mostaza
30
Jugo de naranja
-18,8
Jugo de naranja concentrado
-5,4
Jugo de naranja concentrado
9,5
Jugo de naranja concentrado
29,2
Jugo de naranja concentrado
25
Pomada analgésica
23
Salsa para pastas (tomate)
80
Salsa para pastas (tomate)
25
Salsa para pizza
25
Queso procesado
82
Queso procesado
23
Salsa (con trozos)
80
Salsa (con trozos)
25
Lavado de estomago (subsalicilato bismuto)
25
Bloqueador solar (crema)
35
Bloqueador solar (crema)
45
Bloqueador solar (crema)
25
Ketchup de tomate
#
Propiedades determinadas a las tasas de bombeo típicas
*
Fluido Newtoniano si n = 1,0
K, Pa sn
78,0
0,34
0,11
18,6
9,61
7,85
4,2
0,14
24,4
6,45
2,25
0,69
7,31
40,3
21,8
61,7
320
240
30,8
10,9
0,43
32,6
24,3
19,0
6,1
n*
0,43
0,76
0,70
0,33
0,37
0,35
0,60
0,79
0,76
0,77
0,76
0,80
0,47
0,19
0,18
0,18
0,50
0,30
0,20
0,28
0,81
0,28
0,29
0,31
0,41
Apéndices
141
9.3
Diámetros para tubos y tuberías de acero inoxidable
Tamaño
Tuberías sanitarias
Tubo Schedule 40
Nominal
Pulgada
D.I.*
D.E.#
D.I.*
D.E.#
Pulgada
Pulgada
Pulgada
Pulgada
0,84
0,62
0,50
0,37
½
1,05
0,82
0,75
0,62
¾
1,32
1,05
1,00
0,87
1
1,90
1,61
1,50
1,37
1½
2,38
2,07
2,00
1,87
2
2,88
2,47
2,50
2,37
2½
3,50
3,07
3,00
2,83
3
4,50
4,03
4,00
3,83
4
6,63
6,07
6,00
5,78
6
8,63
7,98
8,00
7,78
8
D.I.*
mm
9,4
½
15,7
¾
22,1
1
34,8
1½
47,5
2
60,2
2½
72,0
3
97,4
4
146,9
6
197,7
8
*
D.I. = Diámetro interior
#
D.E. = Diámetro exterior
Pulgada
D.E.#
mm
12,7
19,1
25,4
38,1
50,8
63,5
76,2
101,6
152,4
203,2
D.I.*
mm
15,8
20,9
26,6
40,9
52,5
62,7
77,9
102,3
154,1
202,7
D.E.#
mm
21,3
26,7
33,4
48,3
60,3
73,0
88,9
114,3
168,3
219,1
Ductos y Tuberías para Bioprocesos
142
9.4
Acero Inoxidable (304 y 316)
El acero es cualquier aleación de hierro y carbono que contenga menos del 2% de carbono. Los
aceros inoxidables números 304 y 316 son comúnmente utilizados en tuberías para procesos alimentarios
y farmacéuticos. Estos son materiales no magnéticos (Acero inoxidable austenitico) con una composición
básica de 18% de Cromo y 8% de Nickel: el término “acero inoxidable 18/8” se refiere a esta
composición.
Agregando más cromo y Nickel se incrementa la resistencia a la corrosión. Pequeñas cantidades de
molibdeno incrementan grandemente la resistencia a la corrosión. Los números 304L y 316L son
aleaciones bajas en carbono desarrolladas para minimizar la precipitación de carburos durante la
soldadura, lo cual puede conducir a problemas de corrosión. Los tipos 304 y 316 son denominaciones del
Instituto Americano del Hierro y Acero (del Ingles AISI). Las propiedades físicas y térmicas de los aceros
inoxidables 304 y 306 incluyen las siguientes: densidad 8.000 kg m-3; conductividad térmica (a 100 ºC) =
16,3 W m-1 ºC-1; calor específico (0 º C a 100 ºC) = 0,46 kJ kg-1 ºC-1; coeficiente de expansión térmica (20
ºC a 500 ºC) = 17 x 10-6 m/m por ºC.
Las juntas de tope son una manera de conectar a dos miembros que descansan en el mismo plano.
Tubos de acero inoxidable (incluyendo accesorios, etc) pueden ser unidas con juntas de tope usando un
proceso conocido como soldadura de arco a gas-tungsteno (GTAC). También es conocido como soldadura
TIG (Gas Inerte y Tungsteno). El calentamiento es causado por un arco eléctrico entre la superficie del
acero y un electrodo de tungsteno. El electrodo no se consume durante el proceso y el metal de relleno
puede ser necesario dependiendo de la soldadura. Un gas inerte (como el Argon) es utilizado como un gas
protector para prevenir la contaminación atmosférica de la soldadura. La soldadura TIG requiere un alto
grado de habilidad. Esta soldadura produce soldaduras de alta calidad en varios materiales además del
acero inoxidable: aluminio, magnesio, acero al carbono, cobre, niquel y titanio.
Apéndices
Composición química de aceros inoxidables típicos (Fuente: ASTM A270)
Elemento
304
304L
316
*
Composición, %
0,08
0,035
0,08
Carbono, máx.
2,00
2,00
2,00
Manganeso, máx.
0,040
0,040
0,040
Fósforo, máx.
0,030
0,030
0,030
Azufre, máx.
0,030
0,75
0,75
Silicio, máx.
10,00-14,00
8,00-13,00
8,00-11,00
Níquel
16,00-18,00
18,00-20,00
18,00-20,00
Cromo
2,00-3,00
------Molibdeno
*
Balance de composición es hierro
143
316L
0,035
2,00
0,040
0,030
0,030
10,00-15,00
16,00-18,00
2,00-3,00
Ductos y Tuberías para Bioprocesos
144
9.5
Propiedades del agua saturada
T
ºC
0,01
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
115
120
T
ºF
32,018
41
50
59
68
77
86
95
104
113
122
131
140
149
158
167
176
185
194
203
212
221
230
239
248
abs P*
kPa
0,6117
0,8726
1,228
1,706
2,339
3,170
4,247
5,629
7,384
9,594
12,351
15,761
19,946
25,041
31,201
38,595
47,415
57,867
70,182
84,609
101,42
120,90
143,38
169,18
198,67
abs P*
psi
0,089
0,127
0,178
0,247
0,339
0,460
0,616
0,816
1,071
1,391
1,791
2,286
2,893
3,632
4,525
5,598
6,877
8,393
10,179
12,271
14,710
17,535
20,795
24,537
28,815
vacío
pulg Hg
29,74
29,66
29,56
29,42
29,23
29,98
28,67
28,26
27,74
27,09
26,27
25,27
24,03
22,53
20,71
18,52
15,92
12,83
9,20
4,94
0
0
0
0
0
densidad
kg/cm3
999,8
999,9
999,7
999,1
998,2
997,0
995,6
994,0
992,2
990,2
988,0
985,7
983,2
980,5
977,7
974,8
971,8
968,6
965,3
961,9
958,3
954,7
950,9
947,1
943,1
densidad
lbm/pie3
62,42
62,42
62,41
62,37
62,33
62,24
62,15
62,06
61,94
61,82
61,68
61,54
61,38
61,21
61,04
60,86
60,67
60,47
60,26
60,05
59,83
59,60
59,36
59,12
58,88
Apéndices
T
ºC
125
130
135
140
145
150
155
160
165
170
175
180
185
190
195
200
205
145
T
ºF
257
266
275
284
293
302
311
320
329
338
347
356
365
374
383
392
401
abs P*
kPa
232,22
270,26
313,20
361,50
415,63
476,10
543,57
618,14
700,99
792,05
892,65
1.000,3
1.123,5
1.255,0
1.398,9
1.554,7
1.724,4
abs P*
psi
33,681
39,198
45,426
52,431
60,282
68,052
78,838
89,653
101,67
114,88
129,47
145,08
162,95
182,02
202,89
225,49
250,10
vacío
pulg Hg
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
densidad
kg/cm3
939,1
934,8
930,5
926,1
921,7
917,0
912,2
907,4
902,5
897,4
892,3
887,0
881,6
876,1
870,4
864,7
858,7
densidad
lbm/pie3
58,62
58,36
58,09
57,81
57,54
57,25
56,95
56,65
56,34
56,02
55,70
55,37
55,04
54,69
54,34
53,98
53,61
* Presión absoluta
Fuente: ASME, 2000. ASME Tablas Internacionales de Vapor para uso Industrial. The American
Society of Mechanical Engineers, ASME Press, New York.
Ductos y Tuberías para Bioprocesos
146
9.6
T
ºC
0,01
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
115
120
125
Entalpía de vapor saturado
T
ºF
32,018
41
50
59
68
77
86
95
104
113
122
131
140
149
158
167
176
185
194
203
212
221
230
239
248
257
Abs P*
kPa
0,6117
0,8726
1,228
1,706
2,339
3,170
4,247
5,629
7,384
9,594
12,351
15,761
19,946
25,041
31,201
38,595
47,415
57,867
70,182
84,609
101,42
120,90
143,38
169,18
198,67
232,22
Abs P*
psi
0,09
0,13
0,18
0,25
0,34
0,46
0.62
0,82
1,07
1,39
1,79
2,29
2,89
3,63
4,53
5,60
6,88
8,39
10,18
12,27
14,71
17,54
20,80
24,54
28,81
33,68
Entalpía (kJ/kg)
hL
∆h
2.500,9
0,001
2.489,1
21,019
2.477,2
42,021
2.465,4
62,984
2.453,5
83,92
2.441,7
104,84
2.429,8
127,75
2.417,9
146,64
2.406,0
167,54
2.394,0
188,44
2.382,0
209,34
2.369,9
230,24
2.357,7
251,15
2.345,4
272,08
2.333,1
293,02
2.320,6
313,97
2.308,1
334,95
2.295,4
355,95
2.282,6
376,97
2.269,6
398,02
2.256,5
419,10
440,21
2.243,2
461,36
2.229,7
482,55
2.216,0
503,78
2.202,1
525,06
2.188,0
hv
2.500,9
2.510,1
2.519,2
2.528,4
2.537,5
2.546,5
2.555,6
2.564,6
2.573,5
2.582,5
2.591,3
2.600,0
2.608,8
2.617,5
2.626,1
2.634,6
2.643,0
2.651,3
2.659,5
2.667,6
2.675,6
2.683,4
2.691,1
2.698,6
2.705,9
2.713,1
Apéndices
T
ºC
130
135
140
145
150
155
160
165
170
175
180
185
190
195
200
205
147
T
ºF
266
275
284
293
302
311
320
329
338
347
356
365
374
383
392
401
Abs P*
kPa
270,26
313,20
361,50
415,63
476,10
543,57
618,14
700,99
792,05
892,65
1000,3
1123,5
1255,0
1398,9
1554,7
1724,4
Abs P*
psi
39,20
45,43
52,43
60,28
69,05
78,84
89,65
101,67
114,88
129,47
145,07
162,95
182,02
202,89
225,49
250,09
Entalpía (kJ/kg)
hL
∆h
2.173,7
546,39
2.159,1
567,77
2.144,2
589,20
2.129,1
610,69
2.113,7
632,25
2.097,9
653,88
2.081,9
675,57
2.065,5
697,35
2.048,7
719,21
2.031,6
741,15
2.014,0
763,19
1.996,1
785,33
1.977,7
807,57
1.958,9
829,92
1.939,7
852,39
1.919,9
874,88
hv
2.720,1
2.726,9
2.733,4
2.739,8
2.745,9
2.751,8
2.757,4
2.762,8
2.767,9
2.772,7
2.777,2
2.781,4
2.785,3
2.788,9
2.792,1
2.794,9
* presión absoluta
Fuente: ASME, 2000. ASME Tablas Internacionales de Vapor para Uso Industrial. The American Society
of Mechanical Engineers, ASME Press, New York.
Ductos y Tuberías para Bioprocesos
148
9.7
Viscosidad (mPa s o cP) del agua
TºC
0,01
1,792
1,306
1,002
0,890
0,797
0,653
0,02
1,792
1,306
1,002
0,890
0,797
0,653
0,547
0,466
0,05
1,792
1,306
1,002
0,890
0,797
0,653
0,547
0,466
0,404
0,354
Presión (MPa)
0,1
0,2
1,791
1,792
1,306
1,306
1,002
1,002
0,890
0,890
0,797
0,797
0,653
0,653
0,547
0,547
0,466
0,466
0,404
0,404
0,354
0,354
0,314
0,314
0,282
0,255
0,232
0,5
1,1791
1,305
1,001
0,890
0,797
0,653
0,547
0,467
0,404
0,355
0,315
0,282
0,255
0,232
0,213
0,197
0,183
1
0,1789
1,305
1,001
0,890
0,797
0,653
0,547
0,467
0,404
0,355
0,315
0,282
0,255
0,232
0,213
0,197
0,183
0,170
0,160
2
1,787
1,304
1,009
0,890
0,797
0,653
0,547
0,467
0,404
0,355
0,315
0,282
0,255
0,233
0,213
0,197
0,183
0,171
0,160
0,150
0,142
0,134
0
10
20
25
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
Nota: 1 atm = 0,101 MPa = 14,96 psi
Fuente: ASME, 2000. ASME Tablas Internacionales de Vapor para Uso Industrial. The American Society
of Mechanical Engineers, ASME Press, New York.
Apéndices
9.8
149
Galones de agua por 100 pies de tubos
Tamaño
pulg
½
¾
1
1½
2
2½
3
4
6
8
nominal, D.I
pulg
0,370
0,620
0,870
1,370
1,870
2,370
2,834
3,834
5,782
7,782
D.E.
pulg
0,500
0,750
1,000
1,500
2,000
2,500
3,000
4,000
6,000
8,000
Gal por 100 pies de
tubo
0,6
1,6
3,1
7,7
14,3
22,9
32,8
60,0
136,4
247,1
Ductos y Tuberías para Bioprocesos
150
9.9
Leyes de Afinidad para Bombas Centrífugas
Para variaciones pequeñas en el diámetro del impulsor (a velocidad constante)
/
(9.1)
/
(9,2)
Para variaciones pequeñas en la velocidad (a diámetro constante del impulsor)
/
(9.3)
/
(9.4)
Donde: D = diámetro del impulsor; H = altura; Q = capacidad volumétrica; N = velocidad angular; bhp =
caballos de fuerza al freno.
Apéndices
9.10
151
Ecuaciones para Fluidos Plásticos de Bingham en Flujo en Tubo.
Factores de fricción de Fanning. La ecuación de estado para un plástico de Bingham es:
(9.5)
Donde µpl = viscosidad plástica (Pa s); σ0 = umbral de fluencia (Pa). La presencia de un umbral de
fluencia hace que este modelo sea único.
El criterio para flujo laminar es:
,
,
,
í
(9.6)
í
1
8
4
3
(9.7)
3
(9.8)
16.800
1
(9.9)
Donde el Número de Hedstrom (NHe), el número de Reynolds Bingham (NRe,B) y los esfuerzos de cizalla
(σw) son:
(9.10)
(9.11)
,
y
(9.12)
∆
El factor de fricción de flujo laminar [de Heywood, N. 1991. Pipeline design for non-settling slurries. En
Brown, N.P. y N.I Heywood (editors). Slurry Handling: Design of Solid-Liquid Systems. Elsevier Applied
Science, NY] asumiendo (σ0/σw)4 << 1 es:
16 6
6
(9.13)
,
,
Ductos y Tuberías para Bioprocesos
152
El factor de fricción para flujos turbulentos [de Darby, R., Mun, R., Boger, V.B. 1992. Prediction friction
loss in slurry pipes. Chemical Engineering, Septiembre, pg 116-119] es:
10
,
(9.14)
0,193
Donde:
1,47 1
0,146
2,9
10
(9.15)
Perfiles de velocidad en flujo laminar en tubos. El perfil de velocidad en la porción cizallada (R0 ≤ r ≤
R) donde σ ≥ σ0) del fluido en el tubo es:
∆
4
2
1
1
(9.16)
Donde el radio crítico (R0) es calculado en términos del umbral de fluencia:
2
∆
(9.17)
La máxima velocidad (u = umax) está localizada en el extremo no compartido (0 ≤ r ≤ R0 donde σ ≤ σ0):
∆
4
(9.18)
1
ó
2 1
4
1
3
(9.19)
3
Apéndices
153
Tabla 9.11
NRe,PL
2.100
2.200
2.300
2.400
2.500
2.600
2.700
2.800
2.900
3.000
3.100
3.200
3.300
3.400
3.500
3.600
3.700
3.800
3.900
4.000
4.100
4.200
4.300
4.400
4.500
4.600
4.700
4.800
4.900
5.000
5.100
5.200
5.300
5.400
Factores de Fricción de Fanning para Fluidos Tipo de La Ley de Potencia
n = 0,2
0,00762
0,00727
0,00696
0,00667
0,00640
0,00615
0,00593
0,00571
0,00489
0,00487
0,00483
0,00480
0,00475
0,00471
0,00467
0,00462
0,00457
0,00453
0,00448
0,00444
0,00440
0,00435
0,00431
0,00427
0,00423
0,00420
0,00416
0,00412
0,00409
0,00405
0,00402
0,00398
0,00395
0,00392
n = 0,3
0,00762
0,00727
0,00696
0,00667
0,00640
0,00615
0,00593
0,00571
0,00541
0,00540
0,00538
0,00535
0,00532
0,00528
0,00524
0,00520
0,00515
0,00511
0,00506
0,00502
0,00498
0,00493
0,00489
0,00485
0,00481
0,00477
0,00473
0,00470
0,00466
0,00462
0,00459
0,00456
0,00452
0,00449
n = 0,4
0,00762
0,00727
0,00696
0,00667
0,00640
0,00615
0,00592
0,00596
0,00599
0,00601
0,00600
0,00599
0,00597
0,00594
0,00591
0,00587
0,00583
0,00578
0,00574
0,00570
0,00565
0,00561
0,00557
0,00553
0,00548
0,00544
0,00540
0,00537
0,00533
0,00529
0,00525
0,00522
0,00518
0,00515
n = 0,5
0,00762
0,00727
0,00696
0,00667
0,00640
0,00635
0,00645
0,00571
0,00659
0,00663
0,00665
0,00665
0,00664
0,00663
0,00660
0,00656
0,00653
0,00649
0,00645
0,00640
0,00636
0,00631
0,00627
0,00623
0,00619
0,00614
0,00610
0,00606
0,00602
0,00599
0,00595
0,00591
0,00587
0,00584
n = 0,6
0,00762
0,00727
0,00696
0,00667
0,00670
0,00686
0,00700
0,00711
0,00720
0,00726
0,00730
0,00732
0,00733
0,00731
0,00729
0,00726
0,00723
0,00719
0,00715
0,00711
0,00706
0,00702
0,00698
0,00693
0,00689
0,00684
0,00680
0,00676
0,00672
0,00668
0,00664
0,00660
0,00657
0,00653
n = 0,7
0,00762
0,00727
0,00696
0,00697
0,00719
0,00739
0,00756
0,00571
0,00782
0,00791
0,00796
0,00799
0,00800
0,00800
0,00798
0,00796
0,00792
0,00788
0,00784
0,00780
0,00775
0,00771
0,00766
0,00762
0,00757
0,00753
0,00749
0,00744
0,00740
0,00736
0,00732
0,00728
0,00724
0,00721
n = 0,8
0,00762
0,00727
0,00717
0,00745
0,00771
0,00794
0,00815
0,00832
0,00845
0,00855
0,00862
0,00866
0,00867
0,00867
0,00865
0,00863
0,00859
0,00855
0,00851
0,00847
0,00842
0,00837
0,00833
0,00828
0,00823
0,00819
0,00814
0,00810
0,00806
0,00802
0,00798
0,00793
0,00790
0,00786
n = 0,9
0,00762
0,00727
0,00763
0,00795
0,00825
0,00851
0,00875
0,00571
0,00909
0,00920
0,00927
0,00931
0,00933
0,00932
0,00930
0,00927
0,00924
0,00920
0,00915
0,00910
0,00906
0,00901
0,00896
0,00891
0,00886
0,00882
0,00877
0,00873
0,00868
0,00864
0,00860
0,00856
0,00852
0,00848
Ductos y Tuberías para Bioprocesos
154
NRe,PL
5.500
5.600
5.700
5.800
5.900
6.000
6.100
6.200
6.300
6.400
6.500
6.600
6.700
6.800
6.900
7.000
7.100
7.200
7.300
7.400
7.500
7.600
7.700
7.800
7.900
8.000
8.100
8.200
8.300
8.400
8.500
8.600
8.700
8.800
8.900
9.000
9.100
n = 0,2
0,00389
0,00386
0,00383
0,00380
0,00378
0,00375
0,00372
0,00370
0,00367
0,00365
0,00363
0,00360
0,00358
0,00356
0,00353
0,00351
0,00349
0,00347
0,00345
0,00343
0,00341
0,00339
0,00337
0,00335
0,00334
0,00332
0,00330
0,00328
0,00327
0,00325
0,00323
0,00322
0,00320
0,00319
0,00317
0,00316
0,00314
n = 0,3
0,00446
0,00443
0,00440
0,00437
0,00434
0,00431
0,00428
0,00426
0,00423
0,00421
0,00418
0,00416
0,00413
0,00411
0,00409
0,00406
0,00404
0,00402
0,00400
0,00398
0,00396
0,00394
0,00392
0,00390
0,00388
0,00386
0,00384
0,00382
0,00380
0,00379
0,00377
0,00375
0,00374
0,00372
0,00370
0,00369
0,00367
n = 0,4
0,00512
0,00508
0,00505
0,00502
0,00499
0,00496
0,00493
0,00491
0,00488
0,00485
0,00482
0,00480
0,00477
0,00475
0,00472
0,00470
0,00468
0,00465
0,00463
0,00461
0,00459
0,00457
0,00454
0,00452
0,00450
0,00448
0,00446
0,00444
0,00443
0,00441
0,00439
0,00437
0,00435
0,00433
0,00432
0,00430
0,00428
n = 0,5
0,00580
0,00577
0,00574
0,00571
0,00567
0,00564
0,00561
0,00558
0,00555
0,00553
0,00550
0,00547
0,00544
0,00542
0,00539
0,00537
0,00534
0,00532
0,00529
0,00527
0,00525
0,00523
0,00250
0,00518
0,00516
0,00514
0,00512
0,00510
0,00508
0,00506
0,00504
0,00502
0,00500
0,00498
0,00496
0,00495
0,00493
n = 0,6
0,00649
0,00646
0,00642
0,00639
0,00636
0,00633
0,00629
0,00626
0,00623
0,00620
0,00618
0,00615
0,00612
0,00609
0,00606
0,00604
0,00601
0,00599
0,00596
0,00594
0,00591
0,00589
0,00587
0,00584
0,00582
0,00580
0,00578
0,00576
0,00574
0,00571
0,00569
0,00567
0,00565
0,00563
0,00562
0,00560
0,00558
n = 0,7
0,00717
0,00713
0,00710
0,00706
0,00703
0,00700
0,00696
0,00693
0,00690
0,00687
0,00684
0,00681
0,00678
0,00675
0,00673
0,00670
0,00667
0,00665
0,00662
0,00659
0,00657
0,00654
0,00652
0,00650
0,00647
0,00645
0,00643
0,00641
0,00638
0,00636
0,00634
0,00632
0,00630
0,00628
0,00626
0,00624
0,00622
n = 0,8
0,00872
0,00778
0,00775
0,00771
0,00768
0,00764
0,00761
0,00758
0,00754
0,00751
0,00748
0,00745
0,00742
0,00739
0,00737
0,00734
0,00731
0,00728
0,00726
0,00723
0,00720
0,00718
0,00715
0,00713
0,00711
0,00708
0,00706
0,00704
0,00701
0,00699
0,00697
0,00695
0,00693
0,00691
0,00689
0,00687
0,00685
n = 0,9
0,00844
0,00840
0,00837
0,00833
0,00830
0,00826
0,00823
0,00819
0,00816
0,00813
0,00810
0,00807
0,00804
0,00801
0,00798
0,00795
0,00792
0,00790
0,00787
0,00784
0,00782
0,00779
0,00776
0,00774
0,00772
0,00769
0,00767
0,00764
0,00762
0,00760
0,00758
0,00755
0,00753
0,00751
0,00749
0,00747
0,00745
Apéndices
NRe,PL
9.200
9.300
9.400
9.500
9.600
9.700
9.800
9.900
10.000
12.000
14.000
16.000
18.000
20.000
22.000
24.000
26.000
28.000
30.000
32.000
34.000
36.000
38.000
40.000
42.000
44.000
46.000
48.000
50.000
52.000
54.000
56.000
58.000
60.000
62.000
64.000
66.000
155
n = 0,2
0,00313
0,00311
0,00310
0,00308
0,00307
0,00306
0,00304
0,00303
0,00302
0,00279
0,00261
0,00247
0,00235
0,00225
0,00216
0,00208
0,00201
0,00195
0,00189
0,00184
0,00179
0,00175
0,00171
0,00167
0,00164
0,00161
0,00158
0,00155
0,00152
0,00150
0,00147
0,00145
0,00143
0,00141
0,00139
0,00137
0,00135
n = 0,3
0,00366
0,00364
0,00363
0,00361
0,00360
0,00358
0,00357
0,00355
0,00354
0,00330
0,00311
0,00295
0,00282
0,00271
0,00261
0,00252
0,00245
0,00238
0,00232
0,00226
0,00221
0,00216
0,00211
0,00207
0,00203
0,00200
0,00196
0,00193
0,00190
0,00187
0,00184
0,00182
0,00179
0,00177
0,00175
0,00173
0,00171
n = 0,4
0,00427
0,00425
0,00423
0,00422
0,00420
0,00419
0,00417
0,00416
0,00414
0,00388
0,00368
0,00351
0,00337
0,00324
0,00313
0,00304
0,00295
0,00288
0,00281
0,00275
0,00269
0,00263
0,00258
0,00254
0,00249
0,00245
0,00241
0,00238
0,00234
0,00231
0,00228
0,00225
0,00222
0,00220
0,00217
0,00215
0,00212
n = 0,5
0,00491
0,00489
0,00488
0,00486
0,00484
0,00483
0,00481
0,00479
0,00478
0,00450
0,00428
0,00410
0,00394
0,00381
0,00369
0,00359
0,00350
0,00341
0,00334
0,00327
0,00321
0,00315
0,00309
0,00304
0,00299
0,00295
0,00290
0,00286
0,00283
0,00279
0,00276
0,00272
0,00269
0,00266
0,00263
0,00261
0,00258
n = 0,6
0,00556
0,00554
0,00552
0,00551
0,00549
0,00547
0,00545
0,00544
0,00542
0,00513
0,00490
0,00470
0,00454
0,00439
0,00427
0,00416
0,00406
0,00397
0,00389
0,00381
0,00374
0,00368
0,00362
0,00356
0,00351
0,00346
0,00342
0,00337
0,00333
0,00329
0,00325
0,00322
0,00318
0,00315
0,00312
0,00309
0,00306
n = 0,7
0,00620
0,00618
0,00616
0,00615
0,00613
0,00611
0,00609
0,00607
0,00606
0,00575
0,00551
0,00530
0,00513
0,00498
0,00485
0,00473
0,00463
0,00453
0,00444
0,00436
0,00429
0,00422
0,00416
0,00410
0,00404
0,00399
0,00394
0,00389
0,00385
0,00380
0,00376
0,00372
0,00369
0,00365
0,00362
0,00359
0,00356
n = 0,8
0,00683
0,00681
0,00679
0,00677
0,00675
0,00673
0,00671
0,00670
0,00668
0,00636
0,00611
0,00590
0,00572
0,00556
0,00542
0,00530
0,00519
0,00509
0,00499
0,00491
0,00483
0,00476
0,00469
0,00463
0,00457
0,00451
0,00446
0,00441
0,00436
0,00432
0,00428
0,00423
0,00420
0,00416
0,00412
0,00409
0,00405
n = 0,9
0,00743
0,00471
0,00739
0,00737
0,00735
0,00733
0,00731
0,00729
0,00728
0,00695
0,00559
0,00647
0,00629
0,00612
0,00598
0,00585
0,00574
0,00563
0,00554
0,00545
0,00537
0,00529
0,00522
0,00515
0,00509
0,00503
0,00498
0,00493
0,00488
0,00483
0,00478
0,00474
0,00470
0,00466
0,00462
0,00459
0,00455
Ductos y Tuberías para Bioprocesos
156
NRe,PL
68.000
70.000
72.000
74.000
76.000
78.000
80.000
82.000
84.000
86.000
88.000
90.000
92.000
94.000
96.000
98.000
n = 0,2
0,00133
0,00132
0,00130
0,00129
0,00127
0,00126
0,00124
0,00123
0,00122
0,00121
0,00120
0,00118
0,00117
0,00116
0,00115
0,00114
n = 0,3
0,00169
0,00167
0,00165
0,00163
0,00162
0,00160
0,00158
0,00157
0,00156
0,00154
0,00153
0,00151
0,00150
0,00149
0,00148
0,00147
n = 0,4
0,00210
0,00208
0,00206
0,00204
0,00202
0,00200
0,00199
0,00197
0,00195
0,00193
0,00192
0,00190
0,00189
0,00187
0,00186
0,00185
n = 0,5
0,00256
0,00253
0,00251
0,00249
0,00247
0,00244
0,00242
0,00240
0,00239
0,00237
0,00235
0,00233
0,00232
0,00230
0,00228
0,00227
n = 0,6
0,00303
0,00301
0,00298
0,00296
0,00293
0,00291
0,00289
0,00287
0,00285
0,00283
0,00281
0,00279
0,00277
0,00275
0,00273
0,00272
n = 0,7
0,00353
0,00350
0,00347
0,00344
0,00342
0,00339
0,00337
0,00334
0,00332
0,00330
0,00328
0,00326
0,00324
0,00322
0,00320
0,00318
n = 0,8
0,00402
0,00399
0,00396
0,00393
0,00391
0,00388
0,00385
0,00383
0,00380
0,00378
0,00376
0,00373
0,00371
0,00369
0,00367
0,00365
n = 0,9
0,00452
0,00448
0,00445
0,00442
0,00439
0,00437
0,00434
0,00431
0,00429
0,00426
0,00424
0,00421
0,00419
0,00417
0,00415
0,00412
Basado en ecuaciones (4.16) (4.21) Darby, R., Mun, R., Voger, V.B. 1992. Chemical Engineering,
September, pag. 116-119.
Apéndices
9.12
157
Coeficientes de pérdida por fricción: Ecuación 3-k
La ecuación 3-k es:
1
2
(9.20)
3
1
,
0,3
Donde Dn,pulg = diámetro nominal, pulgadas, y k3 tiene dimensiones de (pulgadas) elevado a 0,3. Usar
NRe,PL en lugar de NRe para los fluidos de la ley de potencia. Nota esta ecuación fue formulada para tubos
de acero estandard. Utilizando diámetros nominales para tuberías producirá valores ligeramente mayores
del coeficiente de pérdida por fricción.
Válvula o accesorio #
Codo 90º: con rosca, estándar
Codo 90º: con rosca, radio largo
Codo 90º: con brida, soldadura al tope
Codo 90º: con brida, soldadura al tope
Codo 90º: con brida, soldadura al tope
Codo 90º: con brida, soldadura al tope
Codo 45º: con rosca, estándar
Codo 45º: con rosca, radio largo
Codo 180º: con rosca, doblado cerca del final
Codo 180º: con brida, soldadura al tope
Codo 180º: todos
T: con rosca, a través de la rama (como codos)
T: con rosca, a través de la rama (como codos)
T: con brida/rosca, a través de la rama (como codos)
T: con rosca, a través
T: con brida/rosca, a través
r/D = 1
r/D = 1,5
r/D = 1
r/D = 2
r/D = 4
r/D = 6
r/D = 1
r/D = 1,5
r/D = 1
r/D = 1
r/D = 1,5
r/D = 1
r/D = 1.5
r/D = 1
r/D = 1
r/D = 1
k1
800
800
800
800
800
800
500
500
1.000
1.000
1.000
500
800
800
200
150
k2
0,14
0,071
0,091
0,056
0,066
0,0075
0,071
0,052
0,23
0,12
0,10
0,274
0,14
0,28
0,091
0,017
k3
4,0
4,2
4,0
3,9
3,9
4,2
4,2
4,0
4,0
4,0
4,0
4,0
4,0
4,0
4,0
4,0
Válvula ángulo 45º
950
0,25
4,0
β = 1*
*
1.000 0,69
4,0
Válvula ángulo 90º
β=1
1.500 1,70
3,6
Válvula de globo, estándar
β = 1*
Válvula de cono, flujo en rama
500
0,41
4,0
Válvula de cono, flujo a través
300
0,084
3,9
Válvula de cono, tres vías (flujo a través)
300
0,14
4,0
300
0,037
3,9
Válvula de compuerta, estándar
β = 1*
300
0,015
3,5
Válvula de bola, estándar
β = 1*
Diafragma, tipo presa
1.000 0,69
4,9
Fuente: Darby, R. 2001 (Marzo) Chemical Engineering, 66-73
# Excepto para algunas aplicaciones de alta presión, superficies con rosca en contacto con el producto no
se admiten en sistemas sanitarios (3A Número Standard 63-10). Acero estándar con rosca es aceptable
para sistemas de alimentación de agua.
*
β = diámetro de orificio/diámetro interior del tubo
158
Ductos y Tuberías para Bioprocesos
Índice
12D, proceso,90
3-A Estandares Sanitarios, 47
Acero inoxidable, 142
Alimento de baja acidez, 85
Altura de succión positiva neta, 44, 124
Altura de fricción, 38
Altura de elevación, 38,45
Altura, 36,37,38,39,45,127
Altura de presión, 36, 45
Altura de la bomba, 43
Adelgazante, 4, 95
Altura de velocidad 37,45
Altura del sistema, 120
Altura de succión, 44
Balance de energía mecánica, 33,113
Bomba Centrífuga, 43, 133
Bomba de desplazamiento positivo,
43,121
Clostridium botulinum, 85, 85,88
Coexiellia burnettii, 85,86,91
Cinética de muerte, 83
Coeficiente de pérdida por fricción, 59
Curva de la bomba, 43
Coeficiente de mezcla, 18, 19, 20,22, 108
Constante de mezcla viscosímetro, 13,
17,18, 20, 22,27,108, 109,110
Curva de sistema, 37, 114
Devolución de fluido, 17
DIN, 13
Diámetro hidráulico, 34
Ecuación de Arrhenius, 10, 95
Velocidad de deformación cizalla
promedio. Ver velocidad de deformación
cizalla
Ecuación de Bernoulli, 33
Escalamiento de tubería, 79,81
Ecuación de Hagen-Poiseuille, 7
Ecuación de Blasius, 48
Ecuación de Casson, 5,98
Ecuación de Churchill 48, 119, 125
Efecto de corrección de fin, 16
Ecuación de Haaland, 48,119
Esfuerzo de cizalla, 2
Promedio, 28, 78,29
En una tubería, 6
Eficiencia de la bomba, 35
Ecuación de Herschel-Bulkley, 5, 98
Esfuerzo de cizalla mínimo, 98
Espesante, 4,49
Fuerza de cizalla representativo. Ver
esfuerzo de cizalla
Fluido anti-tixotrópico, 5
Factor de fricción de Darcy, 47
Factor de fricción de Fanning, 34, 47, 49,
50, 51,52,55
Fluido reopéctico, 5
Factor de corrección de esfuerzo de
cizalla, 29
Fluido tixotrópico, 5
Fluido dependiente del tiempo, 5
Fluido independiente del tiempo, 5
Factor de corrección de energía cinética,
34
Fluido Newtoniano, 1,2,3,48,97
Fluido de la ley de potencia, 4, 48,96
Letalidad, 83,89,92,93,98, 131,132, 134,
135
Letalidad del proceso. Ver letalidad, 92
159
Método de longitud equivalente, 35,59
Método general, 83,87, 90,91, 93
Método k”, 18
Método altura de velocidad, 34, 45
Número de Hedstrom, 151
Número de Bingham Reynolds, 151
Número de potencia, 21
Número de Reynolds, 18,21,47, 50,115,
Número de Reynolds Impulsor, 21, 23
Número de Reynolds de impulsor de ley
de potencia, 23
Potencia al freno, 36
Pérdidas por fricción, 33
Pérdida de energía presión, 37, 59
Potencia hidráulica, 35, 116, 121, 123,
128
Propulsor
Disco Brookfield, 27
Bandera Brookfield, 25
Paleta Haake, 25
Cinta helicoidal, 23
Tornillo helicoidal interrumpido, 23,
108
Paleta RVA, 1, 25
Plástico de Bingham, 5, 151
Placas paralelas, 2
Pasterización, 85,86, 88,90,91,131,134
Procesamiento térmico, 83
Presión de vapor, 44
Perfiles de velocidad, 55, 152
Propiedades de vapor, 146
Propiedades del agua, 144
Vapor, 146
Viscosidad, 148
Reducciones decimales, 85
Rugosidad relativa, 48
Reograma, 15, 18,100, 103, 106
Reología, 1
Rugosidad, 47, 48, 51
Ductos y Tuberías para Bioprocesos
Salmonella, 85, 87
Tasa letal, 89, 91, 92, 93
Tiempo de muerte térmica, 87, 88,90,93
Tamaño de partícula, 23
Trabajo de cizalla, 71, 72, 73, 75,76, 77,
78, 129
Valor critico,
Total, 76
Viscosidad aparente, 4, 5, 10, 18,19,20,27
Viscosímetro Brookfield, 27
Viscosímetro de cilindros coaxiales, 13,
103
Viscosímetro de cono y placa, 13, 31
Valor D, 85, 84
Viscosidad efectiva, 112
Valor F, 87, 92
Volumen estático, 74, 81
Valor esterilizante, 85
Viscosidad, 1
Absoluta, 3
Aparente, 4, 19, 95,109
Cinemática, 4
Velocidad volumétrica promedio, 46
Valor z, 82
Viscosidad cinemática, 1,3,4,
Viscometría mezcla, 17, 105