Cátedra de Campos y Ondas - Universidad Nacional de La Plata

UNIVERSIDAD NACIONAL DE LA PLATA
FACULTAD DE INGENIERIA
Cátedra de Campos y Ondas
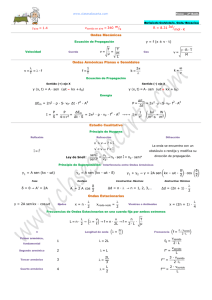
Resumen de Fórmulas sobre Ecuaciones de Maxwell, Notas
sobre Corrientes y Campos variables con el tiempo en los
conductores, Ecuación de Difusión y Propagación de Ondas
Planas1
Parte 2
1
Resumen de fórmulas de los apuntes de la Cátedra: “Notas sobre Corrientes y Campos variables con el tiempo en los conductores” y“Notas sobre
Ecuaciones de Maxwell, Propagación de Ondas Planas y Vector de Poynting”
CÁTEDRA CAMPOS Y ONDAS - UNLP
CASO DE PROPAGACIÓN EN EL ESPACIO LIBRE (VACÍO).
ONDAS ELECTROMAGNETICAS
Considerando un medio sin cargas (ρ=0) y sin pérdidas (σ=0), es decir el
vacío o dieléctrico ideal(σ=0), las ecuaciones de Maxwell se reducen a:
∂B
∂t
∂D
∇×H = J +
∂t
∇×E= −
∇⋅D=0
∇ ⋅B = 0
ó Expresando todo en función de E y H
∂H
∇ × E = −µ
∂t
∂E
∇×H = ε
∂t
∇⋅E = 0
∇⋅H = 0
Si se aplica el operador rotor a la ecuación que expresa el rotacional del
campo eléctrico E, se tiene que:

∂H 
∂
 = − µ (∇ × H )
∇ × (∇ × E ) = ∇ ×  − µ
∂t 
∂t

Si se usa la siguiente identidad vectorial:
∇ × (∇ × E ) = ∇ (∇ ⋅ E ) − ∇ 2 E
Se obtiene el siguiente resultado:
−∇ 2 E = − µ
∂
∂  ∂E 
µ
∇
×
H
=
−
(
)
ε
∂t
∂ t  ∂t 
2
∂
E
2
∇ E = µε
∂t2
idem para H
2
H
∂
2
∇ H = µε
∂t 2
ecuaciones de onda
1
CÁTEDRA CAMPOS Y ONDAS - UNLP
ONDAS PLANAS EN EL ESPACIO LIBRE
Los campos eléctrico y magnético dependen, además del tiempo, solamente
de una dirección espacial, y a su vez ambos campos no poseen componentes
según esa dirección (dirección de propagación de la onda electromagnética,
en este caso elegimos x como dirección de propagación):
Ex = 0
Hx = 0
Ey ≠ 0
Hy ≠ 0
Ez ≠ 0
Hz ≠ 0
∂ Ey
≠0 ;
∂x
∂ Ey
=0 ;
∂y
∂ Ez
≠0
∂x
∂E y
∂ Ez
=0
∂z
∂z
=0
;
∂ Hy
≠0 ;
∂x
∂ Hy
=0 ;
∂y
∂ Hy
=0 ;
∂z
∂ Ez
=0
∂y
∂ Hz
≠0
∂x
∂ Hz
=0
∂y
∂ Hz
=0
∂z
Por simplicidad supondremos el campo eléctrico E en una sola dirección por
ejemplo en “y”, propagándose en la dirección del eje x
E x = 0;
Ey ≠ 0
Ez = 0
∂ Ey
≠0
∂x
∂ Ey
∂ Ey
= 0;
= 0;
∂z
∂y
Por lo tanto el campo eléctrico de esta onda plana deberá satisfacer la
siguiente ecuación diferencial:
∂ 2Ey
∂x
2
= µε
∂ 2Ey
∂t2
La ecuación de onda es una ecuación diferencial de segundo orden, cuya
solución general es la siguiente:
2
CÁTEDRA CAMPOS Y ONDAS - UNLP
Ey
Donde:
1
v=
µε
= f1 (x − vt ) + f 2 ( x + vt )
v la velocidad de propagación en la direcciçon x.
f 1 ( x - v t 1)
x
f1 ( x - v t 2 )
x
v (t 2 - t 1 )
Figura. Onda propagándose en dirección de las x positivas, mostrada en los
instantes t1 y t2
Así la solución general de la ecuación de onda, está compuesta por dos
ondas que viajan en la misma dirección, pero en sentidos opuestos.
- onda incidente
- onda reflejada
3
CÁTEDRA CAMPOS Y ONDAS - UNLP
Ahora si no existe discontinuidad, tampoco existirá la onda reflejada y la
solución para la ecuación de onda consistirá en sólo la onda viajando en un
sentido:
Ey = f1 ( x − vt )
ONDAS PLANAS EN EL ESPACIO LIBRE. CASO ARMONICO.
Suponiendo la onda plana
E ( x, t ) = 0iˆ + Ey ( x, t ) ˆj + 0 kˆ
Ey ( x, t ) = E 0 ( x ) cos (ω t + φ ) = Re {E 0 ( x )e j φ ⋅ e j ω t }
x) ⋅ e j ω t }
Ey ( x, t ) = Re {E(
donde ω= 2πƒ, es la pulsación angular, siendo ƒ la frecuencia.
Usando fasores la ecuación diferencial espacio-temporal
∂ 2Ey
∂ x2
= µε
∂ 2Ey
∂t2
se reduce a una ecuación diferencial espacial
2
i
i
i
∂ Ey
2
2
= −ω µ ε E y = − β E y
2
∂x
Esta ecuación es conocida con el nombre de ecuación vectorial de
Helmholtz.
donde :
β = ω µε
es la denominada constante de fase y, como se verá más adelante,
es la parte imaginaria de otra constante compleja denominada
constante de propagación.
4
CÁTEDRA CAMPOS Y ONDAS - UNLP
2
i
i
∂ Ey
2
La solución general de la ecuación diferencial ∂ x 2 = − β E y será:
∗
i
∗
E y = C1 e − j β x + C2 e + j β x
∗
∗
En las que C1 y C2 son constantes complejas arbitrarias
∗
Considerando al medio infinito, C2 = 0
i
E y = E0 e j ( − β x +ϕ )
La solución en función del tiempo y del espacio será:
{
E y ( x, t ) = Re E0 e j ( − β x +ϕ ) e j (ω t )
}
E y ( x, t ) = E0 cos (ωt − β x + ϕ )
ó
E y ( x, t ) = E0 cos β ( vt − x + θ )
ϕ
llamando θ = β
ω
v
=
Siendo la velocidad de propagación:
Y la longitud de la onda λ:
λ = 2π β
5
β
CÁTEDRA CAMPOS Y ONDAS - UNLP
Volviendo a las ecuaciones de Maxwell puedo demostrar que la solución
para el campo magnético de esta onda plana que viaja por el espacio libre
resulta:
E0
H z ( x, t ) =
µ0
cos (ωt − β x + ϕ ) = H 0 cos (ωt − β x + ϕ )
ε0
Los campos eléctrico y magnético están en cuadratura espacial y en fase
temporal, siendo estas características correspondientes a una onda plana
progresiva.
y
Ey
0
λ
4
λ
3λ
4
2
λ
5λ
4
3λ x
2
z
Hz
Figura - Ubicación en cuadratura espacial, y en fase temporal,
de las ondas de campos eléctrico y magnético,
correspondientes a una onda plana progresiva
La velocidad de propagación de la onda puede ser obtenida si, observando
un punto particular de la onda, se realiza el cociente entre el desplazamiento
a lo largo del eje x, que sufre dicho punto y el tiempo transcurrido para que
dicho desplazamiento tenga lugar.
Para una onda que se desplace en la dirección de las x positivas, un punto
particular se identifica por:
ωt − β x = Cte .
6
CÁTEDRA CAMPOS Y ONDAS - UNLP
ν=
∂x ω
=
∂t β
Esta velocidad de un punto de una onda senoidal recibe el nombre de
velocidad de fase.
Recordando que
propagación será:
ν=
ω
=
β
β = ω µε
(constante de fase) la velocidad de
1
µε
Siendo para el espacio libre:
µ0 = 4π 10−7 [ H / m ]
ε 0 = 8,85 10 −12 [F/m]
c = v0 = 1
resulta:
µ 0ε 0
donde c es la velocidad de la luz.
7
3 × 108 [m/s]
CÁTEDRA CAMPOS Y ONDAS - UNLP
ECUACIONES DE MAXWELL, PARA EL CASO DE MEDIOS
LINEALES, ISOTROPICOS Y HOMOGENEOS, PARA
CAMPOS CON VARIACION ARMONICA.
Hipótesis
- medios homogéneos, isotrópicos y lineales
- medio no acotado espacialmente.
- ondas planas
- campos armónicos en el tiempo
Considerando que no hay cargas libres en el espacio
∇⋅E = 0
∂H
∇ × E = −µ
∂t
∇⋅H = 0
∇×H =σE +ε
∂E
∂t
Considerando fasores
i
i
i
∇ × E = − j µω H
∇⋅E = 0
i
i
i
i
∇ × H = σ E + jωε E
∇⋅H = 0
Si se aplica el operador rotor a la ecuación que expresa el rotacional del
campo eléctrico E, se tiene que:
i
i
i





∇ ×  ∇×E  = ∇ ×  − jωµ H  = − jωµ  ∇ × H  =




i
= − jωµ (σ + jωε ) E
Si se usa la siguiente identidad vectorial:
∇ × (∇ × E ) = ∇ (∇ ⋅ E ) − ∇ 2 E
Se obtiene el siguiente resultado:
8


CÁTEDRA CAMPOS Y ONDAS - UNLP
i
i
∇ E = jωµ (σ + jωε ) E
2
2
∗
i
2
i
∇ E=ϒ E
∗
Siendo
ϒ
la constante de propagación, un número complejo
∗
ϒ=
α =ω
β =ω
jωµ (σ + jωε ) = α + j β
µε 

σ2
 1 + 2 2 − 1
ωε
2 


σ2
 1 + 2 2 + 1
ωε
2 

coeficiente de atenuación
µε 
9
constante de fase
CÁTEDRA CAMPOS Y ONDAS - UNLP
Para ondas planas será:
i
2
∂ E y ( x)
∂x
∗
i
2
= ϒ E y ( x)
2
y la solución para el fasor será:
i
∗
i
E y ( x) = E 0 e − ϒ x = E0 e−α x − j β x + jϕ
La solución para la onda viajando por el medio infinito será:
E y ( x, t ) = E0 e −α x cos(ωt − β x + ϕ )
IMPEDANCIA INTRÍNSECA DEL MEDIO
Para conocer el campo magnético volvemos a la notación fasorial y a la
ecuación de Maxwell:
i
i
∇ × E = − jωµ H
iˆ
∂
kˆ
ˆj
∂
∂x
∂y
∂
i
∂z
= 0iˆ + 0 ˆj + ∂ E y ( x)
i
0
∗
E y ( x)
0
i
i
− ϒ E y kˆ = − jωµ H z kˆ
jωµ i ˆ
ˆ
Ey k = ∗ H z k
ϒ
i
De acá es posible obtener dos conclusiones:
10
i
∂x
kˆ = − jωµ H z kˆ
CÁTEDRA CAMPOS Y ONDAS - UNLP
Para una onda plana donde el campo eléctrico sólo tiene componente en
y (viajando en el sentido de x) se deduce que el campo magnético sólo
puede tener componente en z. En una onda plana E y H están en
cuadratura espacial y son perpendiculares a la dirección de
propagación.
La relación entre campo eléctrico y campo intensidad magnética (entre
los fasores), está impuesta y a esta relación se la denomina
∗
∗
impedancia intrínseca del medio η
η=
i
E
i
H
Volviendo al resultado de la ecuación de Maxwell:
jωµ i ˆ
ˆ
Ey k = ∗ H z k
ϒ
i
∗
la impedancia intrínseca del medio η será:
i
∗
η=
Ey
i
Hz
=
jωµ
∗
=
ϒ
jωµ
jωµ (σ + jωε )
En el caso general de la propagación en un medio cualquiera (LIH ) la
impedancia intrínseca será un número complejo.
∗
∗
η=η e
11
jθη
CÁTEDRA CAMPOS Y ONDAS - UNLP
∗
η
me da la relación de módulos entre los fasores E y H
θη me da el desfasaje temporal que hay entre ambas ondas.
Conocida la onda de campo eléctrico es posible obtener la de campo
magnético a través de la impedancia intrínseca.
E y ( x, t ) = E0 e −α x cos(ωt − β x + ϕ )
Es posible reconstruir la onda de campo magnético:
H z ( x, t ) =
E0
∗
e−α x cos(ωt − β x + ϕ − θη )
η
12
CÁTEDRA CAMPOS Y ONDAS - UNLP
CASO: MEDIO DIELECTRICO PERFECTO
Para un dieléctrico perfecto (σ=0), la impedancia intrínseca resulta ser un
número real igual a:
i
η=
E
i
jωµ
=
jωµ (0 + jωε )
=
H
µ
ε
Esto implica que en un un dieléctrico perfecto los campos eléctrico E y de
intensidad magnética H se encuentran en fase temporal.
Para el espacio libre (vacío, σ=0)
i
η=
E
=
i
H
µ0
ε0
µ0
η0 =
= 120 π = 377 [ Ω]
ε0
Para un dieléctrico perfecto la impedancia intrínseca puede expresarse en
función de la impedancia intrínseca del vacío como:
µ0 µr
µ
η=
=
= 377
ε
ε0 εr
µr
εr
[Ω]
∗
La constante de propagación
número imaginario puro:
∗
ϒ=
ϒ
para un dieléctrico perfecto, resulta ser un
jωµ ( 0 + jωε ) = jω µε = j β
Esto implica que en un un dieléctrico perfecto los campos eléctrico E y de
intensidad magnética H viajan sin atenuación α=0 (consecuencia de que no
hay pérdidas, no hay disipación).
13
CÁTEDRA CAMPOS Y ONDAS - UNLP
RESUMEN PARA EL CASO GENERAL (PARA TODO MEDIO LIH)
Recordando las hipótesis
- medios homogéneos, lineales e isotrópicos
- medio no acotado espacialmente.
- ondas planas
- campos armónicos en el tiempo
la ecuación diferencial será:
2
i
∂ E y ( x)
∂x
2
∗
2
i
= ϒ E y ( x)
siendo la constante de propagación:
∗
ϒ=
jωµ (σ + jωε ) = α + j β
y la solución será:
E y ( x, t ) = E0 e−α x cos(ωt − β x + ϕ E )
α =ω
β =ω
µε 

σ2
 1 + 2 2 − 1
2 
ωε
 coeficiente de atenuación
µε 

σ2
 1 + 2 2 + 1
ωε
2 

constante de fase
14
CÁTEDRA CAMPOS Y ONDAS - UNLP
Conocido el campo eléctrico puedo obtener el campo magnético a través de
la impedancia intrínseca:
i
∗
η=
Ey
i
=
η=η e
∗
=
ϒ
Hz
∗
jωµ
jωµ
jωµ (σ + jωε ) impedancia intrínseca
jφη
El campo magnético será:
H z ( x, t ) =
E0
η
e −α x cos(ωt − β x + ϕ E − φη )
15
CÁTEDRA CAMPOS Y ONDAS - UNLP
CLASIFICACION DE LOS MATERIALES SEGUN SU
COMPORTAMIENTO A LA FRECUENCIA DE INTERÉS
i
Recordando que
i
i
i
i
∇ × H = J c + J d = σ E+ jωε E
Volviendo a la definición del factor de pérdida fp que mide la relación entre
los módulos de la corriente de conducción y la corriente de despalzamiento
JC
σ
f
=
=
factor de pérdida P
J D ωε
Dependiendo del factor de pérdida podemos clasificar a los medios según su
comportamiento a una dada frecuencia en tres tipos, a saber:
•
•
•
fP =
Buenos conductores:
σ
> 100
ωε
Cuasiconductores:
0, 01 < f P =
Dieléctricos:
fP =
σ
< 100
ωε
σ
< 0, 01
ωε
En condiciones ideales podemos definir al conductor perfecto y al
dieléctrico perfecto (o vacío):
•
•
Conductor perfecto:
fP =
σ
=∞
ωε
Dieléctrico ideal (vacío):
fP =
σ
=0
ωε
16
CÁTEDRA CAMPOS Y ONDAS - UNLP
Sin importar la frecuencia se puede decir que los buenos conductores
(cobre, aluminio, etc.) siempre se comportan como buenos conductores.
Sin importar la frecuencia se puede decir que el aire y el vacío se comportan
casi como dieléctricos perfectos.
Sin embargo algunos materiales como la tierra, el agua dulce, el agua salada,
su comportamiento depende de la frecuencia, habrá un rango donde se
comporten como buenos conductores, otro como cuasi conductores y otro
como dieléctrico:
M= 6
σ/ωε = 10
M
5
Región
conductora
4
3
2
b
a
c
e
d
1
Región
cuasiconductora
0
-1
-2
-3
Región
dieléctrica
-4
Visible
-5
Frecuencias de radio
bajas, medias y altas
N= 1
2
3
(a) Agua dulce
(b) Terreno urbano
4
5
6
Microondas
7
8
(c) Terreno rural
(d) Agua de mar
9
Infrarrojo
Rayos X
Ultravioleta
10 11 12 13 14 15 16 17
(e) Cobre
N
Frecuencia = 10 Hz
Figura - Relación entre las densidades de corrientes de
conducción y de desplazamiento, para distintos materiales, en
función de la frecuencia.
17
CÁTEDRA CAMPOS Y ONDAS - UNLP
fP =
CASO BUENOS CONDUCTORES
σ
> 100
ωε
El factor de pérdida es muy alto entonces la corriente de desplazamiento
es despreciable frente a la de conducción. El fenómeno resultante es de
DIFUSIÓN
Puede demostrarse que resulta
α =β =
1
= πµσ f ═►efecto pelicular por difusión.
δ
Hay disipación (α≠0), yla impedancia intrínseca tal como se la definió para
un medio LIH coincide con la Impedancia unitaria definida para los buenos
conductores semi-infinitos:
i
∗
η=
Ey
i
=
jωµ
∗
=
ϒ
Hz
jωµ
1
1
+j
= Z INTu
σδ
jωµ (σ + jωε ) σδ
Hay desfasaje temporal entre E y H de (θη=π/4)
fP =
CASO CONDUCTOR IDEAL(σ=∞)
δ=
1
πµσ f
=
σ
=∞
ωε
1
∞
O sea δ = 0, por lo tanto el conductor ideal no deja penetrar a los campos
Dentro del conductor no podrá haber ningún tipo de campo (ojo en la
superficie del conductor para x = 0 no sé cuanto vale el campo
Para x > 0 es decir adentro del conductor ideal
E = 0 para x > 0; H = 0 para x > 0; J = 0 para x > 0
18
CÁTEDRA CAMPOS Y ONDAS - UNLP
0, 01 < f P =
CASO CUASICONDUCTORES:
α =ω
σ
< 100
ωε
µε 
β =ω

σ2
 1 + 2 2 − 1 coeficiente de atenuación
2 
ωε

µε 

σ2
 1 + 2 2 + 1
ωε
2 

constante de fase
fP =
CASO DIELÉCTRICOS
σ
< 0, 01
ωε
µε 

σ2
 1 + 2 2 − 1
2 
ωε

α =ω
Para buenos dieléctricos (bajas pérdidas), se cumple que:
σ
<< 1
ωε
y en tales casos es posible realizar la siguiente aproximación binómica:
σ2
σ2
1+ 2 2 ≅ 1+
ω ε
2 ω 2ε 2
α ≅ω
µ ε 
β ≅ω
µ ε 
σ2
1+

2  2ω 2 ε 2
σ2
1+
2  2ω 2 ε 2

 −1 = σ

2

µ
ε
2


 + 1 = ω µε 1 + σ

 8ω 2 ε 2


19




CÁTEDRA CAMPOS Y ONDAS - UNLP
σ
CASO DIELÉCTRICO PERFECTO (σ=0) f P = ωε = 0
No hay corriente de conducción es toda corriente de desplazamiento.
α =ω
β =ω
µε 

σ2
µε
(0) = 0
 1 + 2 2 − 1 = ω
2 
2
ωε

µε 

σ2
µε
1
+
+
1
=
ω
2 = ω µε


2 2
2 
ωε
2

o sea:
α = 0 y β = ω µε
No hay atenuación (pues no hay disipación por corriente de conducción)
Siendo la velocidad de propagación:
v =ω
β
1
v=
µε
20