Variables eléctricas

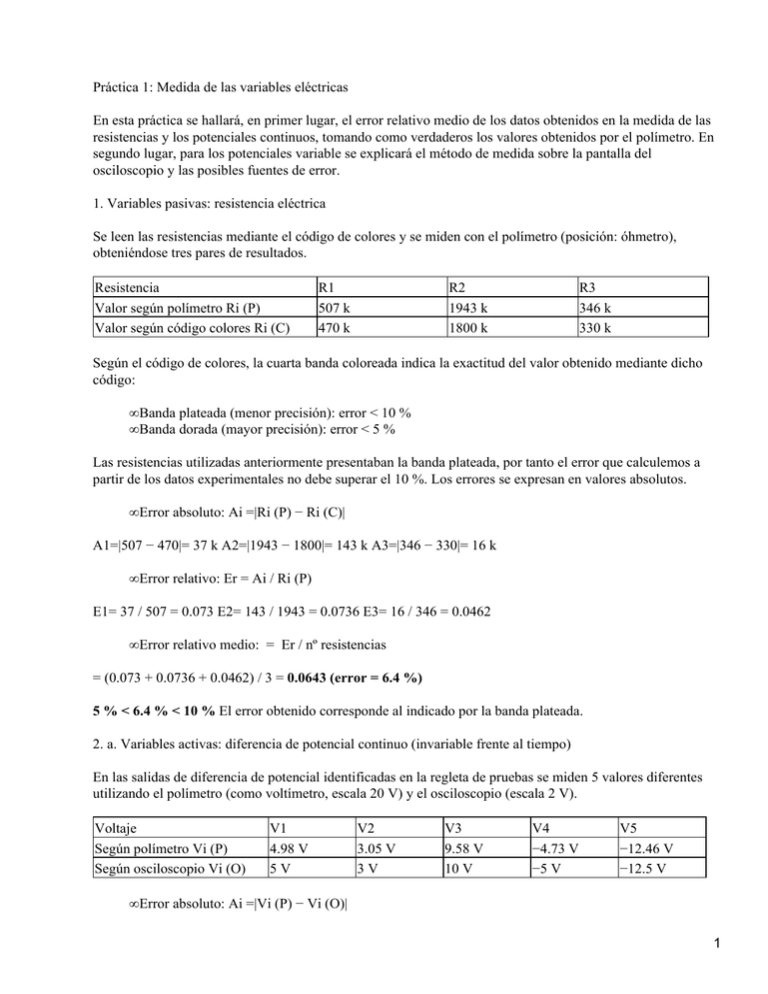
Práctica 1: Medida de las variables eléctricas
En esta práctica se hallará, en primer lugar, el error relativo medio de los datos obtenidos en la medida de las
resistencias y los potenciales continuos, tomando como verdaderos los valores obtenidos por el polímetro. En
segundo lugar, para los potenciales variable se explicará el método de medida sobre la pantalla del
osciloscopio y las posibles fuentes de error.
1. Variables pasivas: resistencia eléctrica
Se leen las resistencias mediante el código de colores y se miden con el polímetro (posición: óhmetro),
obteniéndose tres pares de resultados.
Resistencia
Valor según polímetro Ri (P)
Valor según código colores Ri (C)
R1
507 k
470 k
R2
1943 k
1800 k
R3
346 k
330 k
Según el código de colores, la cuarta banda coloreada indica la exactitud del valor obtenido mediante dicho
código:
• Banda plateada (menor precisión): error < 10 %
• Banda dorada (mayor precisión): error < 5 %
Las resistencias utilizadas anteriormente presentaban la banda plateada, por tanto el error que calculemos a
partir de los datos experimentales no debe superar el 10 %. Los errores se expresan en valores absolutos.
• Error absoluto: Ai =|Ri (P) − Ri (C)|
A1=|507 − 470|= 37 k A2=|1943 − 1800|= 143 k A3=|346 − 330|= 16 k
• Error relativo: Er = Ai / Ri (P)
E1= 37 / 507 = 0.073 E2= 143 / 1943 = 0.0736 E3= 16 / 346 = 0.0462
• Error relativo medio: = Er / nº resistencias
= (0.073 + 0.0736 + 0.0462) / 3 = 0.0643 (error = 6.4 %)
5 % < 6.4 % < 10 % El error obtenido corresponde al indicado por la banda plateada.
2. a. Variables activas: diferencia de potencial continuo (invariable frente al tiempo)
En las salidas de diferencia de potencial identificadas en la regleta de pruebas se miden 5 valores diferentes
utilizando el polímetro (como voltímetro, escala 20 V) y el osciloscopio (escala 2 V).
Voltaje
Según polímetro Vi (P)
Según osciloscopio Vi (O)
V1
4.98 V
5V
V2
3.05 V
3V
V3
9.58 V
10 V
V4
−4.73 V
−5 V
V5
−12.46 V
−12.5 V
• Error absoluto: Ai =|Vi (P) − Vi (O)|
1
A1=|4.98 − 5|= 0.02 V A2=|3.05 − 3|= 0.05 V A3=|9.58 − 10|= 0.42 V
A4=|−4.73 + 5|= 0.27 V A5=|−12.46 + 12.5|= 0.04 V
• Error relativo: Er = Ai / Vi (P)
E1 = 4· 10− 3 E2 = 1.64· 10− 3 E3 = 4.38· 10− 2 E4 = 5.71· 10− 2 E5 = 3.21· 10− 3
• Error relativo medio: = Er / nº voltajes
= 0.10977 /5 = 0.022 V (error = 2.2 %)
2. b. Variables activas: diferencia de potencial variable (variable frente al tiempo)
Para medir la diferencia de potencial variable se utiliza el osciloscopio, aparato de medida que representa una
magnitud, en este caso el voltaje, frente al tiempo (variable independiente).
El método de medida sobre la pantalla es sencillo: se elige la escala de medida más cómoda para los rangos de
diferencia de potencial y periodo utilizados, se ajustan los máximos y mínimos a valores definidos de los ejes
de coordenadas y, multiplicando la escala ya conocida por el numero de unidades obtenidas, se calculan los
datos correspondientes a tensión pico a pico, periodo y frecuencia.
Las posibles fuentes de error serían:
• El alumno, debido a la elección arbitraria de la escala, la interpretación de los datos obtenidos y a la
poca precisión al ajustar la onda a los ejes.
• El osciloscopio, debido al propio error del aparato y a las fluctuaciones de la corriente eléctrica.
Interpretación:
Comparando los métodos de medida, se observa que el más preciso de todos es el polímetro porque el alumno
no ha de interpretar ningún dato y porque ofrece valores con exactitud centesimal. Respecto al balance de las
fuentes de error, tanto el código de colores como el osciloscopio inducen más error que el polímetro.
Práctica 2: Circuitos y amplificación
1. Estudio de un circuito simple
Observando el circuito preparado en la regleta de pruebas, se distinguen tres resistencias (R1, R2 y R3) y dos
fuentes de alimentación continuas (V1 y V2). Se miden las resistencias por el código de colores y las
potenciales mediante el polímetro. También se medirán las diferencias de potencial entre los extremos de las
resistencias R1 y R2 (VR1 y VR2).
Se aplican las ecuaciones de Kirchoff para obtener las intensidades atraviesan el circuito (I1 e I2).
V1 = I1 · (R1 + R3) − I2· R3 V2 = − I1 · R3 + I2 · (R2 + R3)
Se resuelve el sistema de ecuaciones por sustitución:
I1 = (V1+ I2· R3 )/ (R1 + R3) I1 = [ − V2 + I2 · (R2 + R3)] / R3
2
(V1+ I2· R3 )/ (R1 + R3) = [ − V2 + I2 · (R2 + R3)] / R3
Se sustituyen las incógnitas por los datos en valores absolutos:
(10 + I2· 1500) / 5400 = (− 15 + I2· 40500) / 1500
I2 = 4.44· 10 − 4 I1 = 1.98· 10 − 3
Verificación: los datos obtenidos han de cumplir la Ley de Ohm
VR1= I1 · R1 I1= VR1 / R1 I1= 1.97 · 10 − 3
VR2= I2 · R2 I2= VR2 / R2 I2= 4.43 · 10 − 4
Se cumple la Ley de Ohm, los datos son válidos.
2. Amplificador diferencial
Este circuito representa a un paciente, en él se colocan dos electrodos (entradas VE1 y VE2) y la salida se
sitúa en el papel, como en un electrocardiograma (en nuestro caso, utilizaremos el osciloscopio).
El elemento principal del circuito es el amplificador operacional:
• Clavícula
Se coloca el primer electrodo en la pata 3 del amplificador operacional, que está a su vez conectar a dos
resistencias, una que va a la toma de tierra y otra que se enlaza con el generador de funciones.
• Tobillo
Se coloca el segundo electrodo en la pata 2, con la que están conectadas dos resistencias, una que va a la pata
6 (salida del amplificador) y otra que está conectada a un generador de corriente continua (+ 5V).
Restando las dos señales, se obtiene una resultante continua, pero no constante, que mantiene la diferencia de
potencial y el periodo de la primera (clavícula) y el máximo de la segunda (tobillo).
Práctica 3: Identificación de fuentes y estimación energética
Esta práctica consiste en reconocer diferentes tipos de emisiones radiactivas conociendo su comportamiento
ante distintas sustancias atenuantes.
Se miden cuatro fuentes radiactivas con el ratímetro, interponiendo los diferentes blindajes.
Blindaje
Am 241
Cs 137
Co 60
Sr 90
ninguno
15
25
20
500
papel
15
25
20
500
aluminio
7
25
20
20
Pb 2 mm
2
20
20
2
Pb 10 mm
2
9
10
2
Análisis:
3
• Am 241: se reconocen radiaciones y , de baja energía (poco penetrante) ya que es parcialmente
atenuada por el aluminio.
• Cs 137: solo se distinguen radiaciones , ni ni , de alta energía (el aluminio no las atenúa).
• Co 60: se reconocen radiaciones , aunque más energéticas que las anteriores.
• Sr 90: se distinguen radiaciones , ya que el aluminio reduce considerablemente su intensidad. Son
poco energéticas.
Una radiación muy energética es muy penetrante, mientras que las menos energéticas son absorbidas
rápidamente. Por tanto, a igual distancia, las radiaciones son más penetrantes y más perjudiciales que las
radiaciones o , que son rápidamente absorbidas por el medio.
Práctica 4: Variación de dosis por tiempo, distancia y blindaje
En esta práctica se determinará la disminución de la dosis de radiación con el tiempo, la distancia y los
blindajes.
1. Dependencia de la dosis con el tiempo
La relación dosis−tiempo es lineal (y = ax + b ! I= at + b). Se ajustan los datos por mínimos cuadrados:
a = [nxiyi − xiyi] / [nxi2 − (xi) 2] a = 17.8 (pendiente)
b = [xi2yi − xixiyi] / [nxi2 − (xi) 2] b = 14.7 (ordenada en el origen)
Se representa la recta correspondiente junto a los valores experimentales (papel milimetrado). Se calcula el
coeficiente de correlación lineal (r).
r = 0.9993
2. Dependencia de la dosis con la distancia
La ley del inverso cuadrado define que la dosis que llega al receptor disminuye conforme la distancia entre
ellos aumenta, según la siguiente ecuación:
Para comprobar que dicha ley se cumple, se utilizarán dos procedimientos:
2. a. Comparación de los datos experimentales con los datos teóricos
Se toma como referencia el valor 15 cm, a partir del cual se calcularán los valores de I esperados (Ei) para el
resto de las distancias. Comparando los siete valores de Ei y los experimentales Ii, se obtendrá el error relativo
medio.
Ei = I15· (152 / di 2) Er i = (Ei − Ii) / Ii = Er i / 7
E2 = 881.44 Er 2 = 0.040
E3 = 564.12 Er 3 = 0.002
E4 = 391.75 Er 4 = 0.031
E5 = 287.82 Er 5 = 0.133
4
E6 = 220.36 Er 6 = 0.075
E7 = 174.11 Er 7 = 0.054
E8 = 141.03 Er 8 = 0.102
2. b. Ajuste de ecuación correspondiente
I (d) = k· da Si la ley se cumple, teóricamente a = − 2. Teniendo en cuenta el error producido, el valor de a
será un número próximo a −2.
Se transforma la ecuación exponencial en la ecuación de una recta:
Log I = Log K + a· Log d
Se calcula a por mínimos cuadrados (se toman los para las variables x e y los logaritmos de los datos
experimentales):
a = − 1.98 (~ − 2)
Como el error obtenido es pequeño y el coeficiente a se aproxima mucho a −2, se comprueba la validez de la
ley del inverso cuadrado.
3. Variación de la dosis con el blindaje
La atenuación de la dosis debido al blindaje viene determinada por la siguiente ecuación:
I x = I0· e − x
3. a. Ajuste de ecuación de atenuación
Al igual que en el cálculo anterior, se transforma la ecuación exponencial para obtener otra lineal que ajustada
por mínimos cuadrados nos da el coeficiente de atenuación (se toman para la variable y los logaritmos
neperianos de los datos experimentales).
Ln I x = Ln I0 − · x
= − 0.516 cm −1 ! ||= 0.516* cm −1
* El signo negativo nos indica que la relación dosis−blindaje es indirecta.
Sustituyendo en la siguiente expresión se obtiene el valor de la capa hemirreductora:
CHR = Ln2 / CHR = 1.34 cm
3. b. Representación gráfica
Los datos experimentales se representan gráficamente (previa normalización a 100 de los valores de I)
definiendo la capa hemirreductora como el valor del eje de absisas que se corresponde con el valor 50 del eje
de ordenadas.
Despejando de la expresión anterior y sustituyendo el valor de CHR obtenido en la gráfica:
5
= Ln2 / CHR = 0.5
Los valores del coeficiente de atenuación obtenidos tanto por ajuste de la ecuación como por representación
gráfica prácticamente coinciden.
Escala 2 V // 50 s
Forma senoidal
Tensión pico a pico: 4· 2 = 8 V
Periodo: 2.5· 50 = 125 s
Frecuencia: 1 / T = 8 kHz
Escala 1 V // 0.1 ms
Forma triangular
Tensión pico a pico: 4· 1 = 4 V
Periodo: 1.5 · 0.1 = 0.15 ms
Frecuencia: 1 / T = 6.67 kHz
Escala 5 V // 0.1 ms
Forma rectangular
Tensión pico a pico: 2· 5 = 10 V
Periodo: 2 · 0.1 = 0.2 ms
Frecuencia: 1 / T = 5 kHz
V
V
t
t
t
V
t
R1 = 39· 10 2
R2 = 39· 10 3
6
R3 = 15· 102
V1 = − 10 V
V2 = 15 V
VR1 = 7.67 V
VR2 = 17.29 V
Este coeficiente nos indica que la relación entre la dosis y el tiempo es directa (r > 0) y además que los datos
se ajustan a la recta ideal (r ~ 1).
I (d) = k· d− 2
D2 = D1· (d1 2/d2 2)
d1
d2
Dosis 1
Dosis 2
Emisor
= 0.437 / 7 = 0.062 (error 6.2 %)
VE1
VE2
VS
VE2 = − 15
A
O
VE1 = + 15
1
2
3
4
5
7
6
7
8
t
V
Señal procedente de la clavícula
Forma senoidal
Tensión pico a pico: 10 V
Periodo: 100 s
T
t
V
Señal procedente del tobillo
La señal es continua (5 V)
5V
−5V
−5V
5V
t
V
5V
t
V
5V
Punto cero
t
8
V
Clavícula 0 V
Tobillo 5 V
Tobillo 5 V
Clavícula 5 V
Punto máx.
Tobillo 5 V
Clavícula − 5 V
Punto mín.
V=−5V
V=0V
V = − 10 V
VS = VD = VE2 − VE1
9