Material de apoyo de Matemáticas Trayecto Inicial Lcda. Ramona
Anuncio

REPÚBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL PODER POPULAR PARA LA EDUCACIÓN SUPERIOR
INSTITUTO UNIVERSITARIO DE TECNOLOGÍA
“JACINTO NAVARRO VALLENILLA”
CARÚPANO- ESTADO SUCRE
MATERIAL DE APOYO DE MATEMÁTICAS
TRAYECTO INICIAL
Elaborado por:
Lcda. Isbelia Lugo
Lcda. Ramona Salazar
LOS NÚMEROS REALES
Los números 1,2,3… se denominan números naturales. El conjunto de
los números naturales se representan con la letra N, así
N = {1,2,3}
Si se suman dos números naturales el resultado es otro natural, pero si
se resta el resultado no necesariamente es un número natural. Los números
enteros representados por Z y dados por
Z = { ,−3,−2,−1,0,1,2,3}
son cerrados bajo las operaciones de suma, resta y multiplicación, esto quiere
decir que si multiplicamos dos número enteros el resultado es otro número
entero. Sin embargo los números enteros no son cerrados bajo la división, es
decir que si dividimos dos números enteros el resultado no necesariamente es
un número entero.
Los números racionales, Q, expresados de la forma
n
, donde n, m son
m
números enteros con m distinto de cero, es cerrado bajo las cuatro
operaciones. Sin embargo no contempla todos los números que podemos
conseguir. Por ejemplo 2 π que es el perímetro de una circunferencia de radio
1, no es un número racional. Tampoco 2 ≈ 1.41 es un número racional, este
número representa una solución de la ecuación h 2 = 2 y es un número que está
en la naturaleza, pues él es la longitud de la hipotenusa de un triángulo
rectángulo con los dos catetos iguales a 1. Estos números que no son
racionales, pues no pueden ser expresados de la forma
n
se llaman números
m
irracionales y se representan con la letra І. Una diferencia entre los números
racionales y los irracionales está dada en su representación decimal. Los
números racionales pueden ser representados por números decimales que o
1
4
son exactos terminan ( = 0.25 ) o por números decimales que se repiten
1
6
indefinidamente ( = 0.16666 ,
1
= 0.09090 ). En cambio los números
11
irracionales son representados por números decimales que no terminan y que
no tienen ninguna periodicidad es decir que no tienen ninguna secuencia que
se repita.
Los números reales están formados por la unión de los números
racionales (Q) e irracionales (І). La expresión 2 es un número irracional y
por tanto real.
Ejemplo 1.- Diga cuales de los siguientes números son naturales, enteros,
irracionales, racionales y reales: a) -3; b)
−
4
;
3
c)
0. 2 ;
d) π + 1 ; e) 101.
Solución:
a) -3 es un número entero, también es racional pues puede ser escrito
como
b) −
4
3
−3
1
y es real.
es un número racional pues puede ser escrito como
−4
.
3
También es
2
.
10
También es
real.
c)
0 .2
es un número racional pues puede ser escrito como
real.
d) π + 1 es un número irracional. Observe que como π es irracional su
expansión decimal es infinita no periódica al sumarles 1 da como
resultado un número cuya expansión también es infinita no periódica,
también es un número real.
e) 101 es un número natural, entero, racional y es real.
Ejercicio de desarrollo.- Elabore una tabla que identifique cada conjunto
numérico y señale con una X el conjunto al cual pertenecen los siguientes
números:
a) 3π
b)
2+2
c) - 3.1
Los números reales pueden ser representados en la recta real. Para ello
se traza una línea recta y se escoge arbitrariamente un punto en ella, el cual
representará el número 0, luego se escoge una unidad patrón de medida y a
partir del 0 se hacen mediciones de una unidad tanto a la izquierda como a la
derecha, los puntos medidos representan los números enteros en el orden dado
en la figura. Los puntos a la derecha del 0 representarán los números
positivos y a la izquierda
los números negativos. Para representar
geométricamente a los números racionales podemos valernos de su forma
b
c
mixta: a bc con b<c, este número representa a a + , por ejemplo el número
13
5
3
5
13
3
= 2 está a 3/5
5
5
10
unidades de distancia a la derecha del 2. La representación del número − es
3
10
1
= 3 . Hay métodos precisos
simétrica con respecto al origen del número
3
3
puede ser escrito como 2 . Ahora es claro que el número
para representar los números irracionales a través de construcciones
geométricas, sin embargo en esta guía se harán representaciones no muy
exactas de estos números a través de los primeros dígitos de su representación
decimal.
Ejercicio de desarrollo: Represente aproximadamente los siguientes números
en la recta real.
a) 3π ; b)
2 + 2;
c) - 3.1 ; d)
−3
5
Algunas propiedades de los números reales
A continuación enunciamos las propiedades más importantes de los números
reales. Asuma en lo que queda de sección que a, b, c y d son números reales,
tenemos entonces:
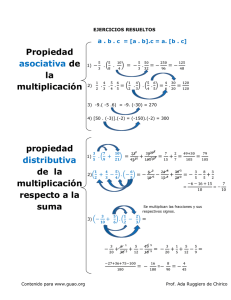
1.-
Propiedad conmutativa de Propiedad conmutativa
la suma
multiplicación
Ejemplo
a+b = b+a
3+ 4 = 4+3
2.-
de
la
a ⋅b = b⋅a
2⋅6 = 6⋅2
Propiedad asociativa de la Propiedad asociativa de la
suma
multiplicación
( a + b ) + c = a + (b + c )
( 2 + 13) + 7 = 2 + (13 + 7)
Ejemplo
Comentarios En ambos casos da 22
a ⋅ (b ⋅ c) = (a ⋅ b) ⋅ c
13 ⋅ (2 ⋅ 5) = (13 ⋅ 2) ⋅ 5
En ambos casos da 130, pero es
más
rápido el cálculo de la primera
El elemento neutro es el que con la operación que consideremos deja
inalterable el número.
3.- Elemento
suma: 0
neutro
de
a+0= a
la Elemento neutro de la multiplicación:
el 1
a ⋅1 = a
El inverso de un número es el que con la operación que consideremos
nos produce el elemento neutro de la operación.
4.-
Inverso de la suma: − a
a + (− a ) = 0
Inverso de la multiplicación:
a⋅
1
a
1
=1
a
El inverso de la multiplicación es denotado en ocasiones por a −1 . Esto es
a −1 =
1
.
a
El número 0 no tiene inverso para la multiplicación ya que no existe
ningún número que multiplicado por 0 de 1.
5.- Propiedad transitiva: Si a = b y b = c entonces a = c
Ejemplo: Si sabemos que x = y y y = 4 entonces x = 4
6.-
Propiedad distributiva a la Propiedad distributiva a la
izquierda
derecha
a ⋅ (b + c ) = a ⋅ b + a ⋅ b
3 ⋅ (2 + 5) = 3 ⋅ 2 + 3 ⋅ 5
(b + c) ⋅ a = b ⋅ a + c ⋅ a
(2 + 5) ⋅ 3 = 2 ⋅ 3 + 5 ⋅ 3
Ejemplo
Comentarios En todos los casos da 21
La resta se define como la operación inversa de la suma:
a − b = a + (−b)
Recuerde que (−b) es el inverso u opuesto de b .
Muchas veces usamos la definición al escribir una resta como una suma:
4 − 9 = 4 + (−9)
Para definir el producto a ⋅ b ⋅ c usamos la propiedad asociativa
A continuación listamos una serie de propiedades de los números negativos
de mucha utilidad:
Propiedades
− a = (−1)a
(− a)b = −(a ⋅ b) = a(−b)
(−a )(−b) = a ⋅ b
− ( a + b) = −a − b
a (b − c) = ab − ac
Ejemplos
Comentarios
Reescritura
− (4 + 7) = −4 − 7
2(4 − 5) = 2 ⋅ 4 − 2 ⋅ 5
El signo menos se distribuye
La
propiedad
distributiva
también se cumple con la
diferencia
− 4 = (−1)4
(−2)3 = −(2 ⋅ 3) = 2(−3)
Ejemplo 1.- Demostrar que 3 − 4 = −4 + 3
3 − 4 = 3 + (−4) . Ahora por la propiedad
Solución: Tenemos que
conmutativa 3 + (−4) = (−4) + 3 . Por la propiedad transitiva de la suma
resulta que 3 − 4 = (−4) + 3 , quitando los paréntesis en el lado derecho
tenemos la igualdad deseada.
En general tenemos que:
x − y = −y + x
Ejercicios de desarrollo: Demostrar
a) ( y − x) = −( x − y )
b) ( x + 3 ) − 4 = ( x − 4) + 3
Propiedades del cero
1.- a ⋅ 0 = 0
2.- Si a ⋅ b = 0 entonces a = 0 ó b = 0 .
La división, a ÷ b es definida a través de la multiplicación:
Si b ≠ 0 , entonces a ÷ b = a ⋅ b −1
Donde b −1 es el inverso por la multiplicación
Para la división también se emplea la notación
1
b
Recordando que b −1 = ,
a
=a ÷b
b
la división también puede ser definida con la
siguiente notación
a
1
= a( )
b
b
Con esta notación podemos interpretar por ejemplo que
veces
5
es cinco
7
1
7
La propiedad 1 del cero permite justificar porque la división entre 0,
a ÷ 0 , no está definida.
- Si a ÷ 0 = c y a ≠ 0 entonces a = c ⋅ 0 = 0 , pero a no es cero.
- 0 ÷ 0 tampoco está definida. Si 0 ÷ 0 = c entonces 0 = c ⋅ 0 es decir que 0 entre
0 pudiese dar cualquier valor lo cual no tiene sentido.
Para fracciones presentamos el siguiente recuadro de propiedades:
Propiedades
Ejemplos
Comentarios
a −a
a
3 −3
3
El signo menos se
− =
=
− =
=
b
b
−b
5
5
−5
puede
transferir
a
cualquier parte de la
fracción
a b a±b
1 4 1+ 4 5
Suma o diferencia con
± =
+ =
=
c c
c
3 3
3
3
igual denominador
a b a⋅d ± b⋅c
2 5 2 ⋅ 6 − 5 ⋅ 7 12 − 35
23 Suma
en
cruz,
± =
− =
=
=−
c d
c⋅d
7 6
7⋅6
42
42 recomendable
cuando
los denominadores no
tienen factores comunes
2 7 2 ⋅ 7 14
a c a ⋅c
Multiplicación
de
⋅ =
⋅ =
=
b d b⋅d
3 9 3 ⋅ 9 27
fracciones
a⋅c a
3⋅ 2 3
Fracciones equivalentes
=
= ;
b⋅c b
5⋅2 5
Ley de Cancelación: c
− 4 (−1)4 4
es un factor en el
=
=
− 7 (−1)7 7
numerador y en el
denominador
b a b a ⋅b
5 2 5 2⋅5
Multiplicación de un
a⋅ = ⋅ =
2⋅ = ⋅ =
c 1 c
c
3 1 3
3
número entero por una
fracción
a ⋅b a
b
3⋅5 3
5
Reescrituras
= ⋅b = a ⋅
= ⋅5 = 3⋅
c
c
c
a
a 1 1 a
= ⋅ = .
b⋅c b c b c
a
a b
a⋅d
÷ = c =
b
c d
b⋅c
d
a b a d a⋅d
÷ = ⋅ =
c d c b c ⋅b
a
a
a⋅d
= 1 =
b
b
b
d
d
2
2
2
2
2 1
= ⋅
3⋅5 3 5
2
2 7
2 ⋅ 5 10
÷ = 3 =
=
7
3 5
3 ⋅ 7 21
5
1 9 1 4 1⋅ 4
÷ = ⋅ =
3 4 3 9 3⋅9
3
3
3⋅ 2 6
= 1 =
=
5
5
5
5
2
2
Reescrituras
División
División a través de una
multiplicación
División
entre
un
número real cualquiera
y una fracción
a
c
b
a
= c
b
1
a
=
b⋅c
División entre una
fracción y un número.
1
1
3 = 3 = 1 = 1
5
5
3 ⋅ 5 15
1
Ejemplo 2.- Realice y simplifique las siguientes expresiones:
x
3
a) 3( + 1) ;
−x
3 1
1
÷ (−4) ; e) − + 3 ;
b) − (−2)(−3) ; c) − 3 ⋅ 4 ; d)
2
−2
5
5
Solución:
a) Se usa primero la propiedad distributiva
x
x
3 x
3( + 1) = 3 ⋅ + 3 ⋅ 1 = ⋅ + 3 Se realiza la multiplicación de fracciones
3
3
1 3
3⋅ x
=
+3
Se simplifica usando la ley de cancelación.
3
= x+3
Observe: en este tipo de situación se distribuye y luego se simplifica
b) Se usa primero la propiedad asociativa
− (−2)(−3) = (−1) ⋅ (−2)(−3) = (−1)( (−2)(−3) )
= (−1)(6) = −6
c) Podemos distribuir primero
1
1
− 3 ⋅ 4 = ⋅ 4 − 3 ⋅ 4 .
Se realiza la multiplicación de fracciones
2
2
1 4
4
= ⋅ − 3 ⋅ 4 = − 12 = 2 − 12 = −10
2 1
2
d) Para la división reescribimos la expresión como fracción
x(−1)
−x
2(−1) . Se usa la ley de cancelación
÷ (−4) =
−2
−4
x
x ⋅1
x
x
= 2 =
=
=−
− 4 2 ⋅ (−4) − 8
8
1
e) Usamos primero la propiedad asociativa de la suma
3 1
3 1
− + 3 = − + 3 Las fracciones tienen igual denominador
5 5
5 5
2 3 2 ⋅ 1 + 5 ⋅ 3 2 + 15 17
+ =
=
=
5 1
5 ⋅1
5
5
Para expresiones numéricas más complicadas se debe tomar en cuenta
que lo primero que se resuelve o elimina son los paréntesis más internos, o
bien haciendo la operación interna o bien aplicando alguna propiedad de los
números reales. Luego se procede a realizar las multiplicaciones o divisiones
planteadas de izquierda a derecha y finalmente las sumas y restas.
2−
Ejemplo 3.- Realice y simplifique las siguientes expresiones: a)
3
4
5 − 1 ; b)
1 2
3
2 + 5( − ) ; c) − 3 + 5( − 2)
2 3
5
Solución:
a) Resolvemos primero la diferencia dada en el numerador de
4
2 4
2 ⋅ 5 − 4 ⋅1
10 − 4
6
−
5 −1 = 1 5 −1 =
5
−1 = 5 −1 = 5 −1
3
3
3
3
3
1
2−
3
4
5 −1
2−
Aplicamos la doble C para resolver la división planteada, luego procedemos a
simplificar para finalmente realizar la diferencia planteada.
6
5 − 1 = 6 − 1 = 2 − 1 = 2 ⋅1 − 1⋅ 5 = − 3
3
5⋅3
5
5
5
1
Posteriormente en este texto se realizaran las sumas de fracciones
usando la técnica del mínimo común múltiplo de los denominadores.
1
2
2
3
b) Resolvemos primero el paréntesis 2 + 5( − ) = 2 + 5(
1⋅ 3 − 2 ⋅ 2
1
) = 2 + 5(− )
6
6
Pasamos a resolver la multiplicación planteada:
5 1
5
2 + (− ) = 2 −
1 6
6
y finalmente resolvemos la diferencia:
2−
5 2⋅6 −5
7
=
=−
6
6
6
c) En esta parte, preferimos eliminar los paréntesis usando la propiedad
distributiva, pues observamos que al aplicarla en este ejemplo desaparece el
denominador
3
3
− 3 + 5( − 2) = −3 + 5 ⋅ − 5 ⋅ 2 = −3 + 3 − 10 = −10
5
5
Ejercicio de desarrollo.- Realice y simplifique:
2 1
2−( − )
4 3
a)
1
1−
2
2
3
b) 3 − 5(1 − ) ⋅
1
5
Ejercicios
1) Diga cuales de los siguientes números son naturales, enteros, irracionales,
racionales y reales: 1.1) − 12 1.2) π − 4 ; 1.3) 3 5 ; 1.4) 0 1.5)– 6.4; 1.6) 31
2) Represente aproximadamente los siguientes números en la recta real.
π
1
2.1) -12; 2.2) − 2 + 2 ; 2.3) - 3 − 1 ; 2.4) 5 ; 2.5)
2
3) Realice y simplifique las siguientes expresiones:
3.1) (−3x) ⋅
1
;
9
−1
3.2) (−5)(−4)(−3) ; 3.3) ÷ 3 ⋅ (−4) ;
5
3.4) 3 ÷
−x
; 3.5)
2
1 5
3− −
3 2
1
3
1
1
0
÷ ( ) ; 3.10) 2 ⋅
3x 9
5
2 1
4
−
1−
5
1
1 3
4 1
3
4
3
1 − 2( − 1) ;
3.11) 2 ⋅ ; 3.12) ( − ) ÷ ( − ) ; 3.13) 3 4 ; 3.14)
;
3.15)
8
0
5 5
3 2
5
−
2−
2 3
3
1 2 5
2
4
1
3
3.16) 2 − 6( − + ) 3.17) ( − 1 + ) ÷ 2 ; 3.18) ( − 2 + )10 − 3 ; 3.19)
2 3 6
3
3
2
5
1
1
4 3
−3
3
−3
3 + 2 ⋅ ( − 3) ⋅ ; 3.20) 4 − 3( − ) ; 3.21) −
+ 1 ; 3.22)
+ 1 ; 3.23)
+1;
3 2
5
2
4
−4
−4
1
( − 3)
3.24) 1 − 3 3
2
.6) (−3)(− x + ) ; 3.7) 0 ⋅ (12)(−27) ; 3.8) (−3)(−3) + 2 ; 3.9)
4) Diga cuál de las siguientes proposiciones son verdaderas. Justifique
4.1) ( )La diferencia entre dos números racionales es un número racional
4.2) ( ) a − b = −b + a ;
4.3) ( ) 3( x ⋅ y ) = 3x ⋅ 3 y
4.4) ( )
4.6) ( )
x x x
+ = ;
2 3 5
3x
3
= ;
x+2 2
4.5) ( ) 1 −
x
−x
= 1+
2
2
;
4.7) ( ) La diferencia de dos números irracionales puede ser racional
Respuestas: 1.1) es un número entero, también es racional y es real. 1.2) es
un número irracional y es real; 1.3) es un número irracional y es real; 1.4) es
un número entero, también es racional y es real, 1.5) es un número entero,
también es racional y es real 1.6) es un número natural entero, también es
racional y es real
x
4
6
1
; 3.2) − 60) ; 3.3) ; 3.4) − ; 3.5) ; 3.6) 3 x − 1 ; 3.7) 0 ; 3.8)
3
15
x
6
3
12
5
1
11 ; 3.9) ; 3.10) 0 ; 3.11) No está definido; 3.12) −
; 3.13) ; 3.14) ;
x
25
2
2
1
13
3.15) ; 3.16)-2; 3-17) ;
5
2
1
9
7
7
1
3.18) -12; 3.19) ; 3.20) ; 3.21) ; 3.22) ; 3.23) ; 3.24) 5; 4)
4
5
2
4
4
3.1) −
Verdaderas: 4.1); 4.5) y 4.7)
Ejercicios adicionales
1) Realice y simplifique las expresiones siguientes:
1 5
3 3 2 5
1 (−2) 5
3
2⋅ ⋅ ⋅3
1
− 2 ; 1.4)
1.1) − 3 4 ; 1.2) − ⋅ − ⋅ 3 ; 1.3) 3 − −
4 5 3 4
2
3 2
2
3
5
1
3−
−2
−4
1
2
2 5
÷ 2 − 3(
− ) ; 1.6)
;
1.5)
2(− + )
3
−2 3
3 2
1 1 1 1
1 −1
−3 6 4
−3 6 4
(5 ⋅ 0 ⋅ 3 ⋅ 12) ÷ ( − + − + 4) − 9 +
( ⋅
) ; 1.8)
( +
)
; 1.7)
2 3 4 5
3 4
4 5 −3
4 5 −3
1
17
8
17
13
6
2
Respuestas: 1.1) − ; 1.2) − ; 1.3) ; 1.4) ; 1.5) ; 1.6) − ; 1.7) ;
3
6
5
11
6
4
5
1
1.8)
10
VUELVE
A EMPEZAR
Aunque sientas el cansancio,
Aunque el triunfo te abandone,
Aunque un error te lastime,
Aunque una traición te hiera,
Aunque una ilusión te apague,
Aunque el dolor queme tus ojos,
Aunque ignoren tus esfuerzos,
Aunque la ingratitud sea la paga,
Aunque la incomprensión corte tu risa,
Aunque todo parezca nada…….
VUELVE A EMPEZAR
EXPONENTES
La potenciación o notación exponencial es una notación para abreviar
una multiplicación:
Notación:
a n = a
⋅ a
a , para n un entero positivo y
n veces
a ≠ 0.
Se lee como a elevado a la n o más abreviado: a a la n.
a es llamada la base y n el exponente o potencia e indica el número de veces
que se repite el factor a.
Presentamos a continuación varios ejemplos ilustrativos
Ejemplo 1.a) 2 3 = 2 ⋅ 2 ⋅ 2 = 8 ;
5
c) = ⋅ ⋅ ⋅ ⋅ =
1
3
1 1 1 1 1
3 3 3 3 3
b) (−5) 3 = (−5) ⋅ (−5) ⋅ (−5) = −125
1
1
=
3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 243
4
1
1
1
1 1 1 1
=
d) − = − ⋅ − ⋅ − ⋅ − =
2
2 2 2 2 2 ⋅ 2 ⋅ 2 ⋅ 2 16
2
e) (a + b) = (a + b) ⋅ (a + b)
Observaciones:
1.- Si a negativo entonces a n es positivo si n es par y negativo si n es
impar, como podemos apreciar en el ejemplo anterior en b y d.
2.- Una expresión como 2 ⋅ x n o simplemente 2 x n es una escritura abreviada
de 2 ⋅ ( x n ) , donde se puede analizar que la convención es que primero se hace
la potencia y luego la multiplicación por 2. De manera similar − x n representa
a − ( x n ) y − 2 ⋅ x n quiere decir (−2) ⋅ ( x n )
3.- − x n ≠ (− x) n
Convención: La potencia es la primera operación que se ejecuta frente a
multiplicaciones, divisiones, sumas o restas o cambio de signo.
Ejemplo 2.- Evaluar a) 2 ⋅ 33 ; b) − 2 3 ; c) 3 ⋅ (−4) 3 ;
Solución:
a) 2 ⋅ 33 = 2 ⋅ 27 = 54
b) − 2 3 = −(2 3 ) = −8
c) 3 ⋅ (−4) 3 = 3 ⋅ (−4) ⋅ (−4) ⋅ (−4) = 3 ⋅ (−64) = −192
Aplicación
Ejemplo 1.- Una compañía pretende aumentar su producción en los próximos
4 años, duplicando la producción con respecto al año anterior. ¿Cuál será su
producción anual dentro de 4 años, si la actual es de 2500 artículos por año?
Solución:
Observe que después de un año la producción es 2 ⋅ 2500
A los dos años se tendrá el doble del primer año 2(2 ⋅ 2500)
A los tres años se tendrá el doble del segundo año 2(2 2 ⋅ 2500) = 2 3 ⋅ 2500
A los cuatro años se tendrá el doble del tercer año 2(2 3 ⋅ 2500) = 2 4 ⋅ 2500 = 40000
artículos.
Definición de Exponentes Negativos y Cero
Los casos exponentes negativos o cero se definen como:
Definición: Si a ≠ 0 se define
a0 = 1
y si n un entero positivo
a −n =
1
.
an
0 0 no está definido
Ejemplo 1.1 1
= ;
23 8
b) 2 0 = 1 ;
a) 2 −3 =
c) ( 3 ) 0 = 1 ;
1
−n
d) ( x + 2) = ( x + 2) n ;
e) (2 x 2 ) 0 = 1 .
Ejercicio de desarrollo.- Complete la igualdad
a) (3π ) 0 =
b)
(x 2 + 1) −2 =
PROPIEDADES DE LOS EXPONENTES
En la siguiente tabla se presentan las propiedades más importantes de
exponentes
Propiedad
Ejemplo
1 a n ⋅ a m = a n+ m
Justificación sólo para el caso n
natural
n+m
a n ⋅ a m = ( a ⋅ a a ) ⋅ ( a a ) = a ⋅
a
a
a ⋅
a = a
2 3 ⋅ 2 4 = 2 2+ 4 = 2 6
n veces
2 ( a n ) m = a n ⋅m
(2 2 ) 4 = 2 2⋅4 = 2 8
m veces
n + m veces
n
n + n +n
(a n ) m = a n
⋅an
= a n⋅ m
a ⋅ = a
m veces
3 ( a ⋅ b) = a ⋅ b
4 a n an
n
5
6
n
n
= n
b
b
n
a
1
= m−n
m
a
a
n
a
= a n−m
am
7 a −n b n
=
b
8
a
a
1
b −m
=
=
b m b m a −n a −n
n
( 2 ⋅ b)
3
= 2 ⋅ b = 8b
3
3
2
22
4
2
= 2 =
25
5
5
3
3
1
1
= 5 −3 =
5
9
3
3
5
3
= 3 5−3 = 9
33
−4
2
3
=
3
2
2 −3
5
= 3
−1
5
2
4
3
( a ⋅ b)
n
= (a ⋅ b) ⋅ (a ⋅ b) (a ⋅ b) = =a n ⋅ b n
n
a a a a ⋅ aa a n
a
=
= ⋅ =
b b b b ⋅ b b b n
b
a n a n ⋅ a −n
a0
1
= m − n = m− n = m −n
m
a
a .a
a
a
Ejercicio
a
b
−n
a −n 1/ a n b n b
= −n =
=
=
b
1/ b n a n a
Ejercicio
n
“
”
RAZÓN, PROPORCIÓN Y PORCENTAJE.
En estadística se trabaja intensamente con razones, proporciones y porcentajes como
también en química y en nuestra gastronomía, entre otras. Generalmente solemos decir: en
esa finca hay cinco (5) becerros por cada 20 vacas, en ese salón hay tres (3) hembras por
cada varón, tres (3) tazas de harina por cada una (1) de azúcar, se planta (siembra) una
mata de naranja por cada 4 metros cuadrados de tierra, etc.
Se darán algunas nociones generales de razón, proporción, porcentajes y regla de tres.
Razón
La razón es una relación de comparación entre dos magnitudes o cantidades. La razón es el
cociente indicado (pero no calculado) de dos cantidades o magnitudes.
Dos cantidades pueden compararse de dos maneras:
1- Hallando en cuanto excede una a la otra, es decir restándolas
2- Hallando cuantas veces contiene una a la otra, es decir dividiéndolas.
De esto, se divide en dos clases de razones:
a- Razón aritmética o por diferencia.
b- Razón geométrica o por cociente
La que se estudiará en este curso es la razón geométrica o por cociente que es la que
más se utilizará.
RAZÓN GEOMÉTRICA O POR COCIENTE.
Se llama razón geométrica entre dos números a y b (b ≠ 0) al cociente de la división
de “a” por “b”.
El número “a” recibe el nombre de antecedente de la razón y el número b de
consecuente de la razón.
Simbólicamente expresamos
es a
, se expresa:
, a ÷ b o también
a
b
Ejemplos:
1- La razón 5 es a 10 se escribe:
2- La razón entre los números
4
17 = 4 × 5 = 20 ;
3
17 × 3 51
5
5
, 5 ÷ 10, 5 :10
10
4
3
y
es :
17
5
4 3 20
÷ =
;
17 5 51
4 3 20
: =
17 5 51
3- En un salón de clase hay dos varones por cada siete hembras.
La razón de varones a hembra es: 2 es a 7, y se escribe:
2
, 2 ÷ 7 , 2:7
7
4- Supongamos que un automóvil recorre 185 Km. por cada 5 galones de gasolina.
¿Cuál es el rendimiento del automóvil por galón de gasolina?
Solución:
Llamaremos rendimiento del automóvil a la razón de los kilómetros recorridos entre los
galones consumidos.
Así, rendimiento del automóvil =
185 km
= 37 km
gl
5 gl
Es decir, el rendimiento del automóvil es 37 kilómetros por galón de gasolina.
RAZONES IGUALES.
Se llama serie de razones iguales a la igualdad de dos o más razones.
Simbólicamente:
a c c g
= = = = …. es una serie de razones iguales.
b d f
h
Nota: Dada una razón, existen infinitas razones iguales a ella.
Ejemplo:
3 6
9 12 15
= = =
=
5 10 15 20 25
PROPIEDAD FUNDAMENTAL DE UNA SERIE DE RAZONES IGUALES.
En toda serie de razones iguales, la razón entre la suma de los antecedentes y la
suma de los consecuentes es igual a una cualquiera de las razones de la serie
Simbólicamente:
Sea
a c e g i
= = = = , entonces
b d f h j
a+c+e+g+i
a c
i
= = = .......... =
b+d+f +h+ j
b d
j
Ejemplo:
3 6 9 12 15
3 + 6 + 9 + 12 + 15
45 3
= = =
=
=
=
=
5 10 15 20 25
5 + 10 + 15 + 20 + 25 75 5
La razón se simplificó por m.c.d (45, 75) = 15
Ejercicios
Dada la siguiente serie de razones iguales, aplicar la propiedad fundamental.
1. −
7 14 21 28 35 42
=
=
=
=
=
4 8 12 16 20 24
2. −
7
7
− 7 − 1 14
=
=
=
= 5
5
−5
5
− 10 − 1
7
3. −
3 6
9 12 15 18 21
=
=
=
=
=
=
8 16 24 32 40 48 56
Actividad
1.- En un salón de clase del I.U.T.J.N.V. hay 11 varones y 15 hembras. La razón de
varones a hembras es: ___________
2.- En un barco se necesitan 3 cocineros por cada 21 tripulantes. La razón de cocineros por
tripulantes es: __________
3.- En un terreno se planta una mata de naranja por cada 4 m 2 . La razón de mata de
naranja por m 2 es: _________
4.- En una finca se recogen 13 pimentones por cada 2 matas. La razón de pimentones por
matas es: ________
Ejercicios.
1.- Se venden 3 libretas por Bs. 11, ¿cuál es la razón de libretas a Bs.?
2.- 5 millas náuticas es lo mismo que 9300 metros. ¿Cuál es la razón de millas náuticas a
metros?
3.- Hay 5 cajas de naranjas, 2 de anones y 4 de mangos. Hallar la razón de cajas de
naranjas a cajas de frutas.
4.- Una fábrica de calzados produce 23 pares de zapatos de caballeros cada 4 horas. ¿Cuál
es la razón entre pares de zapatos y las horas?
5.- Para el cableado de 3 computadoras se utilizan 17 metros de cable. ¿Cuál es la razón
entre las computadoras y los metros de cable?
PROPORCIÓN.
Una proporción es la igualdad entre dos razones geométricas.
Simbólicamente.
a
c
= , es una proporción y se lee: “a” es a “b”
b
d
En la proporción
como “c” es a “d”
a c
= , a y d se llaman extremos; c y b se llaman medios.
b d
Ejemplo:
Las razones
7 14
7
14
y
=
son iguales, por tanto
es una proporción.
10 20
10
20
PROPIEDAD FUNDAMENTAL DE LAS PROPORCIONES
Teorema: En toda proporción el producto de los medios es igual al producto de los
extremos.
Simbólicamente:
Si
a c
= , entonces a x d = c x b
b d
Como por ejemplo:
Veamos si estas proporciones son verdaderas.
1.
18 63
=
, así (18) (7) = (63) (2)
2
7
126
2.
15 23
=
;
105 60
=
126, por tanto la proporción es verdadera.
(15) (60) = (23) (105)
900 ≠ 2415, por lo tanto la proporción es falsa.
3.- Determinar un término de una proporción, conocidos los otros tres.
a)
a 3
= , resolviendo:
32 4
a (4) = (3) (32)
4 a = 96 ⇒ a =
96
= 24
4
El termino de la proporción es a = 24
b)
4
c
84
⇒ (4) (21) = (c) (7) ⇒ 84 = c7 ⇒ 7c = 84 ⇒ c = =1 ⇒ c = 12, el
=
7 21
7
termino de la proporción es c = 12.
Ejercicios.
1. Verifique que las siguientes proporciones son verdaderas o falsas:
a) 14: 10 = 28: 20
b)
11 32
=
23 65
c) 15:21 = 40:56
2. Determinar un término de una proporción, conocidos los otros tres.
a)
3
c
=
5 22
b)
0.432
0.05
=
d
0.632
b) 3
1
1
: 2 13 = 3 : d
5
4
3. En un refugio de animales la razón de perros a gatos es de 5 : 7. Si hay 40 perros,
¿Cuántos son los gatos?
4.
La razón de millas a kilómetros es como 7 es a 11. Si recorro 28 millas, ¿Cuántos
kilómetros recorro?
5. Si cuatro libros cuestan Bs.200, ¿Cuánto costarán 5 docenas?
6. Cinco mandarinas cuestan BS. 1, ¿Cuánto costarán 15 mandarinas?
7. Los 2/3 de la capacidad de un estanque son 500 litros,¿Cuál será la capacidad de los
4/9 del mismo estanque?
PROPORCIONALIDAD DIRECTA
Supóngase que el precio de cada litro de leche es de Bs. 2,2; conocido el precio unitario
(precio por unidad) se puede calcular fácilmente el precio de cualquier cantidad de litros
de leche, multiplicando el número de litros por el precio unitario.
Lo anterior nos permite elaborar una tabla, donde “x” representa la cantidad de litros de
leche y “y” el precio correspondiente
LITROS DE LECHE
x
1
2
3
4
5
6
7
8
PRECIO(Bs.)
y
2,2
4,4
6,6
8,8
11
13,2
15,4
17,6
Observemos que si aumentamos el número de litros de leche, el precio aumenta en la
misma proporción, y si disminuye el número de litros de leche, el precio disminuye en la
misma proporción.
Cuando ocurre lo anterior, se dice que el precio varía de forma directamente proporcional a
la cantidad de litros de leche.
Es decir:
Si x es la medida de la magnitud P e y es la medida de la magnitud Q, entonces P y Q son
directamente proporcionales si
x
= k , donde k recibe el nombre de constante de
y
proporcionalidad.
En nuestro ejemplo, la razón entre el precio y la cantidad de leche (en litros) es Bs. 2,2.
Luego, la constante de proporcionalidad es k= Bs. 2,2 por litros. Nótese que k coincide
con el precio unitario.
Ejemplo 1
Los datos de la tabla siguiente, corresponden a número de obreros y piezas de cierto
artículo que producen diariamente
OBREROS PIEZAS
x
y
Determinar
la
constante
de
25
2250
proporcionalidad
5
450
10
900
Solución:
7
630
Observemos que el número de obreros y
30
2700
las piezas producidas diariamente son directamente proporcionales, ya que
2250 450 900 630 2700
=
=
=
=
= 90, luego la constante de proporcionalidad k es 90
25
5
10
7
30
piezas diarias por obrero.
En general,
Si O1 obreros hacen P1 piezas y O 2 obreros hacen P2 piezas, entonces
O1 P1
=
O 2 P2
La siguiente propiedad se deduce de lo anterior expuesto.
Propiedad
Si dos magnitudes son directamente proporcionales, la razón entre dos cantidades de una
magnitud es igual a la razón entre las cantidades correspondientes de la otra.
Ejemplo 2
Cinco lápices cuestan BS. 4,5. ¿Cuánto cuestan 12 lápices?
Solución 1.
Suponiendo que el costo C es directamente proporcional a la cantidad de lápices
comprados, tendremos una ecuación relacionando C y n, así:
C = kn
En nuestro caso n = 5, C = 4,5; luego k =
4,5
= 0,9. Por lo tanto, el costo de 12 lápices será
5
12*0,9 = 10,80 Bs.
Solución 2.
Como C es directamente proporcional a n, se tendrá que el cociente del costo de 12 lápices
entre 12, será igual al costo de 5 lápices entre 5. O sea,
C (12 ) C ( 5)
C (12 ) 4,5
12 ∗ 4,5
=
⇒
=
⇒ C(12) =
= 10,80
12
5
12
5
5
El costo de los 12 lápices es Bs. 10,80
Solución 3.
Como C es directamente proporcional a n, tendremos que si el costo de cinco lápices es 4,5
1
Bs. el costo de cada lápiz será igual a de 4,5; y, el costo de doce lápices será igual a
5
doce veces el costo de uno. O sea, C (12) =
1
∗ 4,5 ∗ 12 = 10,80.
5
LOS REPARTOS PROPORCIONALES
Se trata del tipo de situación en la que hay que repartir una cantidad de alguna magnitud
entre diversos sujetos de acuerdo con ciertas razones establecidas entre éstos. Se debe hacer
uso de la siguiente propiedad:
a c
a+b c+d
a+b c+d
= , entonces
=
y
=
.
b d
b
d
a
c
Ejemplo:
En la empresa MAZECA, la razón de T.S.U. en administración de Empresa a T.S.U.
Mercadeo Agrícola es de 7:11. Si hay 72 trabajadores en la empresa. ¿Cuántos son de
Administración y cuántos de Mercadeo?
Solución:
Sean A= el número de T.S.U. en Administración de Empresa
M= el número de T.S.U. en Mercadeo Agrícola, sabemos que A+M= 72 y
A
7
A + M 7 + 11
A + M 7 + 11
( aplicando la fórmula anterior )
= , entonces
=
y
=
M 11
M
11
A
7
.
72 18
72 18
72 * 11
72 * 7
=
y
=
⇒M =
y A=
M 11
A
7
18
18
Así , M = 4 * 11 = 44 y A = 4 * 7 = 28, lo que significa que en la empresa hay 28 T.S.U. en Administración
de Empresa y 44 en Mercadeo Agrícola
Ejercicio :
La razón de partidos ganados a partidos perdidos de mi equipo favorito es 8 : 6. Si en total jugaron 24 partidos,
¿Cuántos ganaron? ¿Cuántos perdieron?
Ejercicios variados.
1.- En una cierta fábrica, una operadora empaca en una hora 7 cajas, ¿Cuántas empacará
en 8 horas? ¿En 5 horas?
2.- Cinco lápices cuestan Bs. 0,8, ¿Cuánto cuestan 12 lápices?
3.- Si una media docena de huevos cuesta Bs. 3, ¿Cuánto cuestan siete docenas?
4.- Un metro tiene 100 cm, ¿Cuántos centímetros hay en 3/10 de un metro?
5.- Al cuestionar a una muestra de 50 personas, 35 de ellas indicaron que su refresco
favorito era Pepsi-Cola. Si la muestra era representativa, ¿A cuantos de de cada 100
personas le gusta la Pepsi-Cola?
6.- Dos amigos deben repartirse Bs. 27.000. Las cantidades respectivas están en la razón
5:4. ¿Cuánto dinero recibirá cada uno?
7.- Las edades de Carolina y Marcela están en la razón 3:2. ¿Que edad tiene cada una, si la
suma de sus edades es 80 años?
8.-
La suma de dos números es 91 y están en la razón 4:3. Calcula el valor de cada
número
9.- La diferencia entre los pesos de dos vehículos es 1.200 Kg. y están en la razón 7:4.
Calcular el peso de cada vehículo.
10.- El auto de Wilfredo tiene un estanque de gasolina con una capacidad de 40 L. Como
se va de paseo, llena el estanque, por lo que paga Bs. 5. Si el costo de la gasolina Bs. 2.46.
¿Qué parte del estanque estaba con gasolina?
PROPORCIONALIDAD INVERSA
Con mucha frecuencia se presenta este tipo de situación:
En una fábrica 6 máquinas de la misma clase (igual rendimiento) realizan un trabajo en 8
horas. Si se dedica la mitad de las máquinas a realizar el mismo trabajo, entonces necesitan
el doble del tiempo. Es decir, si 6 máquinas realizan el trabajo en 8 horas, 3 máquinas
harían igual trabajo en 16 horas.
De acuerdo con lo anterior, podemos elaborar la siguiente tabla, donde x representa el
número de máquinas y t el tiempo que necesitan para realizar el mismo trabajo, así:
NÚMERO DE MÁQUINAS
TIEMPO(horas)
x
6
3
12
16
t
8
16
4
3
48
2
1
1
24
48
Observemos que si se aumenta el número de máquinas, disminuye el tiempo en que se
realiza el trabajo y si se disminuye el número de máquinas, aumenta el tiempo.
Cuando ocurre lo anterior, se dice que el número de máquinas varía en forma inversamente
proporcional al tiempo.
Decimos que dos magnitudes varían en forma inversamente proporcional, cuando el
producto de las cantidades correspondientes, es una constante.
Es decir:
Si x es la medida de la magnitud P e y es la medida de la magnitud Q, entonces P y Q son
inversamente proporcionales, si x.y = k, donde k es la constante de proporcionalidad.
En nuestro ejemplo k = 48, representa el tiempo de duración total para efectuar la obra por
máquina o sea, k = 48 horas.
En general,
Si m1 máquinas efectúan un trabajo en t 1 horas y m 2 máquinas realizan igual trabajo en t 2 horas,
como la cantidad de máquinas y el tiempo son inversamente proporcionales, entonces :
m1 t 2
t
m
=
o 1 = 2
m 2 t1
t 2 m1
Ejemplo: El alquiler de una casa es de Bs. 500, si en ella viven cinco (5) estudiantes
pagarían Bs.100 c/u. Si en la misma casa por el mismo alquiler viven diez (10) estudiantes.
¿Cuánto pagarían?
Solución:
Observemos que a medida que aumenta el número de estudiantes, el precio a pagar
disminuye, por tanto se trata de un problema de proporcionalidad inversa, así: Planteando la
ecuación:
n1 p 2
p
5
=
, luego
= 2 ⇒ 10 p 2 = 100 ∗ 5 ⇒ p 2 = 50, luego cada estudiante
n2
p1
10 100
debe pagar Bs. 50
NOTA: Dos magnitudes son inversamente proporcionales cuando al aumentar el valor de
una variable la otra disminuye y viceversa.
Ejercicios.
1.- Entre 3 personas pintan una casa en 6 días. ¿Cuántas personas se necesitan para
realizar el mismo trabajo en 2 días?
2.- Un bus demora 6 horas entre Puerto La Cruz y Carúpano a una velocidad promedio de
80 Km/hr. ¿A que velocidad promedio se desplazó otro vehículo que hizo el mismo
recorrido en 8 horas?
PORCENTAJE COMO APLICACIÓN
El concepto de porcentaje, que tiene una gran importancia dentro de la economía, es una
aplicación de la proporcionalidad directa.
La razón de proporcionalidad para su uso en porcentajes tiene como base 100
Definición: El tanto por ciento es una proporcionalidad que se establece con base 100; para
expresar que la razón se establece con base 100 se usa el signo %.
Ejemplo: En una hectárea que se siembra 50 matas de lechosas, 7 son de lechosa pajarito; la
razón de proporcionalidad es
7
(7 de cada 50), si cambiamos la base, a base 100, se tiene
50
14
(14 por cada 100), lo que se puede expresa como 14%, si se escribe en forma decimal
100
0.14, es el tanto por uno; estas son dos formas equivalentes
14%(14 de cada 100) o 0.14(0.14 de cada unidad)
El tanto por ciento (%) es el número de unidades que se toma por cada ciento.
porcentaje
= tasa
base
En estadística se debe ser muy cuidadoso al escoger la base para expresar el tanto por
ciento
Ejemplo:
En un corral de ganado vacuno, se encontró 35 animales sanos y 18 enfermos; el técnico
informó lo siguiente: El 51% de los animales están enfermos.
Solución:
18
= 0.51(51%), es decir tomó como base los sanos y la información correcta es tomar
35
como base el número total de animales; 0 sea
18
= 0.33(33% enfermos) . Por tanto, la
53
información suministrada por el técnico es incorrecta.
Ejercicios:
1.- Los productores de leche, aumentan el precio del litro de leche de Bs. 2,2 a Bs. 2,45 y
sostienen que aumentaron el precio en 10 %, explique:
a.- Sobre que base calcularon
b.- ¿Cuál es el aumento real?
2.- En 8 fincas de una población venezolana, nacieron en un año 11432 hembras y 10841
machos de un ganado bovino; halle:
a.- El porcentaje de machos y el porcentaje de hembras sobre el total de nacidos
b.- Sobre la base del total de nacidos, el porcentaje en que las hembras superan a los
machos
c.- El porcentaje que representan los machos sobre la base del total de hembras nacidas.
3.- El agua de mar contiene 2,5g de sal por cada 100g de agua. ¿Cuántos gramos de sal
hay en 7kg de agua de mar?
4.- El sueldo de un obrero es Bs. 700 mensuales. Si se reajusta en un 35%, determine el
nuevo sueldo.
5.- En una finca de café que contiene 15.300 matas de café, el técnico de la finca, informó
que 27% de la plantación tiene Roya, ¿Qué cantidad de matas tiene Roya?
6.- La producción total de café en una finca fue de 12.400 kg. Al vender el café se
encontró que el 12% tenía Broca, ¿Cuántos kilogramos de la producción contiene Broca?
7.- Si el P.V.P de una pera es de Bs. 2 y la aumentaron a Bs. 3 ¿Cuál es el porcentaje de
aumento?
8.-
Un trabajador ahorra cada mes Bs. 60,775 que es el 15,75% se su sueldo. ¿Cuál es su
sueldo mensual?