facultad de ingeniería 1er - División de Ciencias Básicas

FACULTAD DE INGENIERÍA
1ER. EXAMEN FINAL DE TERMODINÁMICA
DIVISIÓN DE CIENCIAS BÁSICAS
MIÉRCOLES 6.12.2006., 10:00 (h), SEM 2007-1
COORDINACIÓN DE FÍSICA GENERAL Y QUÍMICA
DEPARTAMENTO DE TERMODINÁMICA
MAYER, JULIUS ROBERT VON (1814-1878)
Instrucciones: lea cuidadosamente los problemas que se ofrecen y resuelva cualesquiera
cuatro en dos horas. La consulta de cualquier documento propio es decisión del profesor.
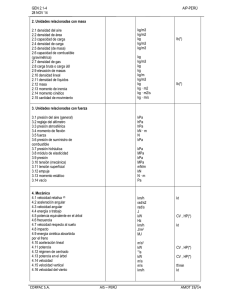
1. Un recipiente de paredes rígidas e inmóviles contiene agua a 4[MPa] y 280[ºC]. El recipiente
entrega 1.5717[kW] al entorno durante un lapso de 78[min]. Transcurrido dicho tiempo, el
recipiente llega a 900[kPa]. Determine la masa de agua que hay dentro del recipiente.
2. Se tiene una sustancia que se somete a un proceso cíclico durante el cual recibe 16.5[kJ]
de un depósito de alta temperatura y libera al entorno 8670[J]. También se presentan durante
el ciclo interacciones de trabajo: en la primera la sustancia recibe 1.8[kJ] y en la segunda no se
logra medir dicha energía. Determine el trabajo y la dirección de éste en la segunda
interacción.
3. En un arreglo de cilindro y pistón lubricado perfectamente, se tiene oxígeno (de masa
molar 32[kg/kgmol]) a 90[°C] y sometido a un vacío de 280[mm de Hg]. El gas se comprime
isotérmica y casiestáticamente hasta 9.8[bar] manométricos. ¿Cuánto trabajo por unidad de
masa se necesita para realizar dicho proceso? Considere que el entorno está a 77170[Pa],
9.78[m/s2] y que Ru = 8314[J/kgmol K].
4. Un ciclo ideal de refrigeración por compresión de vapor utiliza R-134a como sustancia de
trabajo y el flujo másico es 2.5[kg/min]. Se conoce la temperatura a la salida del evaporador, 5.37[°C], y la presión a la entrada de la válvula, 5[bar]. Determine el coeficiente de operación
del ciclo.
5. El pistón de la figura tiene de diámetro 13[cm] y pesa 48.9[N]. Cuando se encuentra a una
distancia x = 34[cm], la presión en el gas atrapado en el cilindro es 1.01325[bar]. Si la presión
es inversamente proporcional al volumen, calcule el trabajo que se requiere para situar el
pistón en x = 12.6[cm]. Considere que el pistón se mueve sin fricción.
D
x
6. Un tanque de acero con paredes adiabáticas contiene 150[dm3] de agua a 150[kPa] y
40.21[%] de calidad. El tanque cuenta con un eje que mueve una hélice con la ayuda de un
motor eléctrico externo. Calcule el trabajo que se debe suministrar para que el agua en el
interior del tanque alcance 700[kPa].
7. Calcule la entropía que se genera en el problema 6.
Resolución del primer examen final de Termodinámica. Semestre 2007-1
Miércoles 6 de diciembre de 2006. 10:00 (h)
MAYER, JULIUS ROBERT VON (1814-1878)
1.- H2O, V = cte., Po = 4 [MPa], To = 280 [ºC], Pamb = 77.17 [kPa], Tamb = 19 [ºC], t = 78 [min], P1= 900
[kPa], { Q& }= -1.5717 [kW];
m= ({ Q& }*t)/ (u1-u0), de tablas obtenemos uo=2680[kJ/kg],
3
vo=0.05546[m /kg] , vf =1.1212 x 10-3 [m3/kg], vg = 0.215 [m3/kg] , uf = 741.83 [kJ/kg] y
ug=2580.5[kJ/kg], x=0.254, u1=uf + x (ug-uf), u1=1208.85 [kJ/kg];
m = 5 [kg].
2.- {Q}entra = 16.5 [kJ], {Q}sale = 8670 [J], {W}entra = 1.8 [kJ] ; {W}2a = - Qentra + Qsale - Wentra ;
{W}2a = - 9.63 [kJ].
ˆ O =32[kg/kgmol], Pivacío =280[mmHg], Pf = 9.8[bar]; Pi = Pamb – ρHg g ZHg , Pf =
3.- O2, Ti =90[ºC], Μ
2
man
ˆ O , {W} = − (Ru Ti Μ
ˆ O )× Ln (Pi Pf ) ;
{W}=309.1199 [J/g].
Pamb - Pf , R= Ru / Μ
man
2
2
4.- R-134a, m& =2.5 [kg/min], T1 = -5.37 [ºC], P3 = 5 [bar]; β = (h1 − h4 ) (h2 − h1 ) , de tablas h1=244.09
[kJ/kg], S1= 0.9222 [kJ/kgJ], h2 = 259.12 [kJ/kg], h3= h4 = 71.33[kJ/kg] ; β = 11.49.
5. - D = 13 [cm], W = 48.9 [N], xi = 34 [cm], Pi = 1.01325 [bar]; V = πD 2 x 4
{W } = −(Pi πD 2 xi
)
4 × Ln(x f xi ) ; {W} = 453.9147 [J]
6.- V=150[dm3], Po=150[kPa], xo=0.4021, P1=700[kPa]; {W } = (V v )(u1 − u 0 ) , de tablas vf=1.0528x10-3
[m3/kg], vg =1.159 [m3/kg] , uf = 466.94[kJ/kg], ug= 2519.7[kJ/kg], vo=0.4667[m3/kg], uo=1292.35
{W}=557.3976 [kJ]
[kJ/kg] , u1=3026.6 [kJ/kg];
7.- V=150 [dm3], Po=150 [kPa], xo=0.4021, P1=700 [kPa], v =0.4667 [m3/kg]; S gen = m( s1 − s 0 ) , de tablas
sf = 1.4336 [kJ/kg K], sg=7.2233 [kJ/kg K], s0=3.7616 [kJ/kg K], s1=7.7571 [kJ/kg K];Sgen=1284.17 [J/K]