pau junio 2013 - IES LAS SALINAS

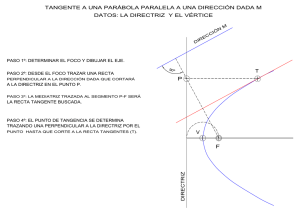
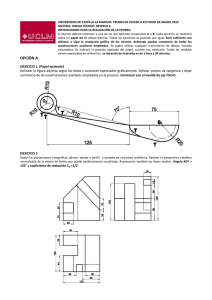
OPCIÓN A
Junio 2013
Calificación máxima: 3 puntos
BLOQUE I: GEOMETRÍA MÉTRICA
1.- Dibujad, dejando las construcciones necesarias, una circunferencia tangente a la
circunferencia de centro O y a la recta t en el punto P. Señalad también el punto de tangencia con la
circunferencia dada. (2 puntos)
2.- Determinad el segmento AB sabiendo que su punto medio es el punto M dado, el punto A
pertenece a la recta r y el B a la recta s. Dejad indicadas las construcciones. (1 punto)
Línea de centros
1.A2
FUNDAMENTO: Este es un problema de tangencias
que se puede resolver de varias maneras, la más
sencilla es aprovechando las inversiones, positiva y
negativa, existentes entre la recta y la circunferencia.
T1
t
Q1
O
Resolución del problema :
1.- Trazamos la perpendicular desde O a la recta y
obtenemos los puntos A1 y A2, centros de Inversión.
2.- Alineamos con P y obtenemos los inversos T1 y T2,
puntos de tg. en la circunferencia.
3.- Los centros de las soluciones estarán en la línea de
centros y alineados con O, puntos Q1 y Q2.
P
Q2
T2
A1
r
2.A
FUNDAMENTO: Este es un problema de segmentos
proporcionales, relacionados con el T. de Thales.
También está relacionado con la simetría central.
R
M
R’
s
B
Resolución del problema :
1.- Trazamos una recta, cualquiera, desde M que corta en el punto
R a la recta r y hallamos su simétrico R’.
2.- Desde el punto R’, trazamos una paralela a r que corta en B a la
recta s.
3.- Trazamos la recta que une B con M, que corta el A a la recta r,
este punto es el simétrico de B respecto a M, es el punto A buscado
sobre la recta r.
2º
Bach.
I.E.S. Las Salinas de Laguna de Duero
DIBUJO TÉCNICO
Paujun2013
OPCIÓN A
Junio 2013
Calificación máxima: 3 puntos
BLOQUE II: SISTEMA DIÉDRICO
Hallad el punto Q simétrico del punto P respecto al plano a.
FUNDAMENTO: El punto simétrico del P, respecto al
plano a, estará en una perpendicular desde P a este
plano, y a la misma distancia.
A la derecha se ha realizado un esquema del trazado a
realizar.
A
H’
P
A
PA=AQ
Q
a2
P”
r”-b2 -s”
A”
V”
Q”
H”
P’
r’
s’ V’
A’
b1
Q’
a1
Resolución del problema :
1.- Trazamos la recta r (r’-r”) perpendicular al plano desde el punto P. Las proyecciones son perpendiculares a las
trazas del plano.
2.- Hallamos la intersección de la recta r y el plano a, nos hemos servido del plano proyectante vertical b que se
corta con el a , en la recta s, la intersección de r y s nos da el punto A, intersección de r y a .
3.- En la proyección vertical hallamos Q”, simétrico de P” respecto de A” y en r’ su proyección horizontal Q’.
2º
Bach.
I.E.S. Las Salinas de Laguna de Duero
DIBUJO TÉCNICO
Paujun2013
OPCIÓN A
Junio 2013
BLOQUE III: REP. DE PERSPECTIVAS y NORMALIZACIÓN
Calificación máxima: 4 puntos
Ajustándose a los ejes del sistema que se facilitan dibujad, a escala 1/1, el Dibujo
Isométrico (sin coeficiente de reducción) de la pieza dada por sus proyecciones.
Tomad las medidas de las vistas. Dibujad las líneas ocultas.
Colocad la Perspectiva según la orientación de los ejes y del origen (O) que se facilita.
z
z
x
y
O
FUNDAMENTO: Pieza muy sencilla,
sin elementos curvos, se visualiza
rápidamente observando las zonas
que faltan en la planta y el alzado, del
prisma envolvente. El lateral nos
ayuda en la visualización.
Realizad un dibujo de la perspectiva, a
mano alzada.
O
x
O
z
y
O
Resolución del problema :
1.- En nuestro ejemplo hemos situado la
planta sobre el Plano Horizontal, y la hemos
colocado en perspectiva llevando las
medidas directamente. Una vez situada
trazamos segmentos perpendiculares a la
planta, paralelos al eje z y llevamos con el
compás las alturas correspondientes,
tomadas del alzado o el lateral. Unimos
puntos y se dibuja la pieza.
* Insisto es vital visualizarla, antes.
y
x
2º
Bach.
I.E.S. Las Salinas de Laguna de Duero
DIBUJO TÉCNICO
Paujun2013
OPCIÓN B
Junio 2013
Calificación máxima: 3 puntos
BLOQUE I GEOMETRÍA MÉTRICA
Definid por todos sus elementos (eje, foco, vértice y tangente en el vértice) la parábola dada por
dos puntos de paso P y Q y su directriz d. Trazad la parábola hallando al menos 9 puntos.
Tomad la solución más próxima a la directriz-
FUNDAMENTO: Este es un problema se puede resolver fácilmente si recordamos que
los puntos de la parábola equidistan del foco y de la Directriz. Si conocemos dos puntos y
la directriz el hallar el foco es inmediato. Puede haber dos soluciones, una o ninguna, en
nuestro caso hay dos y nos obligan a utilizar la más cercana a la directriz.
d
F5
Q5
D1
Q
F4
Q4
F3
F2
F1
D
Q3
M1
M1
M1
M1
M1
Q2
QD1
Q1
M1
A
F
P1
P2
P3
P4
P5
D2
P6 P
P7
P8
P9
Resolución del problema :
1.- Trazamos las perpendiculares desde P y Q a la directriz(distancias) y trazamos los arcos de centros P y Q y
radio estas distancias, se cortan en F, Foco de la parábola.
2.- Desde el foco F, trazamos la perpendicular a la directriz, eje de la parábola, y el punto A, equidistante de F y D
será su vértice, la paralela a la directriz en A es la tangente y a su vez es la C. Principal de la cónica.
3.- Hallados los elementos hemos dibujado la rama superior hallando tangentes y puntos de tangencia y la
inferior buscando puntos que equidistan del foco y la directriz.
2º
Bach.
I.E.S. Las Salinas de Laguna de Duero
DIBUJO TÉCNICO
Paujun2013
OPCIÓN B
Junio 2013
BLOQUE II: SISTEMA DIÉDRICO
Calificación máxima: 3 puntos
Hállense los puntos P y Q de la recta r que disten 20 mm del plano a.
Observación: se recomienda utilizar, como procedimiento idóneo, un cambio de plano.
FUNDAMENTO: Los puntos buscados estarán en planos paralelos al plano a , a 20 mm. Y
sobre la recta r, situación que en diédrico se visualiza fácilmente cuando los planos son
proyectantes.
d d
a2
V”
M”
P”
r”
A”
N” Q”
V’
N’
r’
Q’
20
Q”1
N”1
A’
P’
(a 2)1
V”1
M’
20
A”1
a1
H
r”1
P”1
V1
M”1
Resolución del problema :
1.- En el enunciado del problema nos recomiendan el cambio de plano como el mejor procedimiento, vamos a
realizar un cambio de plano vertical para que el plano a pase a ser proyectante.
2.- Trazamos la LT perpendicular a la traza horizontal del plano a, y hallamos la nueva traza vertical (a2)1, del
plano y de la recta r”1, nuevas proyecciones de dos puntos M y N.
3.- Trazamos paralelas a (a 2)1, a 20 mm. de distancia que cortan a r”1 en P”1 y Q”1.
4.- Deshacemos el cambio de plano y obtenemos las proyecciones de P y Q.
2º
Bach.
I.E.S. Las Salinas de Laguna de Duero
DIBUJO TÉCNICO
Paujun2013
OPCIÓN B
Junio 2013
Calificación máxima: 4 puntos
BLOQUE III: REP. DE PERSPECTIVAS y NORMALIZACIÓN
Dada la perspectiva isométrica de la pieza simétrica
que se adjunta, cuya acotación está efectuada en mm.,
dibujad a escala 1:1, alzado, planta y perfil izquierdo,
según el método del primer diedro de proyección. Las
dimensiones no acotadas serán deducidas de la
perspectiva. Dibujad todas las líneas ocultas.
10
50
30
10
15
R10
45
60
30
10
10
20
50
Alzado
30
Resolución del Problema: Calculamos la parte del papel
que nos va a ocupar, no es necesario dejar espacio para
la acotación, la planta debajo y el alzado alineando
verticalmente aristas, contornos, ejes, etc.y el lateral
izquierdo a la derecha de las vistas.
1.- En nuestro ejemplo hemos dibujado el alzado, de
acuerdo a las medidas que figuran en la perspectiva y
debajo la planta , alineando verticalmente los diversos
elementos, son importantes los ejes.
2.- A la derecha del alzado hemos dibujado la vista del
lateral izquierdo con una rotura para dejar con líneas
vistas el recorte de la base inferior.
2º
Bach.
I.E.S. Las Salinas de Laguna de Duero
DIBUJO TÉCNICO
Paujun2013