Primer examen final A - División de Ciencias Básicas

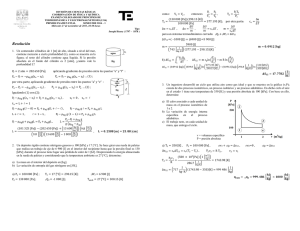
DIVISIÓN DE CIENCIAS BÁSICAS
COORDINACIÓN DE FÍSICA Y QUÍMICA
EXAMEN COLEGIADO DE PRINCIPIOS DE
TERMODINÁMICA Y ELECTROMAGNETISMO (1314)
PRIMER EXAMEN FINAL
SEMESTRE 2013 – 2
Jueves 30 de mayo de 2013, 10:30 horas
Tipo
Jozef Stefan (1835 – 1893)
Resolución
2. Una masa de 5 [g] de aire, como gas ideal, realiza el ciclo descrito
V1 = 4 V2
en el cuadro 1 y en la gráfica (V,P) mostrada. Con la información
de las propiedades mostradas, determine en el SI:
a) La presión y temperatura absolutas máximas en el ciclo.
b) El trabajo desarrollado en el proceso 34, explique el signo.
c) La variación de entropía del aire durante la compresión isotérmica.
d) El trabajo neto realizado por el ciclo.
e) La eficiencia porcentual del ciclo.
cuadro 2
cuadro 1
1. Un gas se encuentra en el interior de un cilindro vertical, el cual tiene un área transversal de 30 [cm2],
éste se cierra mediante un pistón cuya masa es de 150 [kg]. Dentro del gas se tiene un resistor en el que
circulan 8 [A] de corriente eléctrica de una pila externa de 6 [V], durante 3 [min]. El gas cede 5.8 [kJ] en
forma de calor y su energía interna aumenta en 2.4 [kJ]. Si el entorno se encuentra a una presión
ambiente de 78 [kPa], aceleración gravitatoria de 9.78 [m/s2] y el proceso es reversible, determine:
a)
b)
c)
d)
e)
La presión absoluta del gas.
El tipo de proceso que efectúa el gas. Argumente su respuesta.
La cantidad de energía, en forma de calor, que entrega el resistor al gas.
El trabajo de expansión efectuado por el gas. Indique si este último se expande o se comprime.
La distancia que se desplaza el émbolo.
a P
P
A
W
P A;P
78000 Pa
150 kg
P
W
A
9.78
567000 Pa ,
0.003 m
a m
V
estado
1
2
3
4
descripción
isotérmico
isométrico
isotérmico
isométrico
5g
0.005 kg ,V
1
1
V
5.55 10 m
4
4
b Conbaseenlaexpresión 1 delincisoanterior, seobservaquelapresión
c Q
P ∆t,Q
V i∆t
6 V
8 A
á
3 60 s
b W
.
8640 J ,
.
PdV
W
1.4333
c ∆S
1Q2=QR+Qced=(8.64kJ)+(5.8kJ)=2.84[kJ]
1W2=Wexp;1W2=∆U121Q2=(2.4kJ)–(2.84kJ)=–0.44[kJ]
e W
P dV
∆x
W
PA
P
dV
P V
V
440 J
567000 Pa 0.003 m
; comoW
P ∆V
∆S
0, entonces .
d W
W
P A∆x;
,∆
.
25 °C
10 m
T [K]
298.15
154 000
596.23
298.15 K V
.
.
mRT ln
Pam
K
V
V
,comoV
596.23 K ln 4
V yV
V ,
entonces
1184.6945 J , W
V
V
V
V
4
1.1847 kJ comoW<0elgasseexpande
T
V
V
V
mc ln
T ,∆S
mRln
mRln
,T
mRln
T
V
V
4V
1
Pam
1
mRln
1.4333
ln
,∆
.
4
4
K
1W2+2W3+3W4+4W1,2W3=4W1=0,W
1W2+3W4
V
1
mRT ln
mRT ln
4
V
Pam
1
1.4333
298.15 K ln
592.4168 J 4
K
592.4168 J
1184.6945 J ,
.
d)1Q2+1W2=∆U12
1.3875
V [m3]
5.55103
á
delgasesconstante, porlotantosetratadeun
4V ,T
P [Pa]
77 000
308 000
308000 Pa 1.3875 10 m
PV
Pam
PV
mRT ,mR
1.4333
298.15 K
T
K
mRT
PV T
mRT ,P
 ,comoV
V ,entonces
PV
V
T
V
PT
308000 Pa 596.23 K
P
,
.
á
298.15 K
T
m g
…….. 1 A
P
proceso
12
23
34
41
T1 = 25 [°C]
W
W
e η
,2Q3+2W3=∆U ,2W3=0,∆U
∆U
mc ∆T
∆U
1068.6168 J
3Q4 Q
η
0.005 kg
596.23
298.15 K ,∆U
0,3Q4=3W4
a) El vector campo magnético en el punto P debido al
solenoide únicamente. Exprese el resultado en [T].
b) El vector campo magnético total en el punto P. Exprese el
resultado en [T].
c) El flujo magnético en la sección transversal del solenoide
que contiene al punto P, debido exclusivamente a la
corriente en el solenoide.
d) La fuerza de origen magnético que experimenta una carga
puntual q =  8 [pC] que pasa por el punto P con una
velocidad de 500 ı̂ [m/s]
e) La inductancia del solenoide. Exprese el resultado en
[mH].
1184.6945 J 1068.6168 J
592.2777 J
2253.3113 J
J
kgK
2Q3,3Q4+3W4=∆U
1184.6945 J
2Q3+3Q4
717
4. En la figura se muestra un solenoide de 4500 vueltas, de núcleo de aire, cuyo eje coincide con el “x” y
un conductor recto largo, que es paralelo al eje “y” y que pasa por el punto B. Si por el solenoide circula
una corriente de 2.8 [mA], por el conductor recto 38 [A] y se sabe que el campo magnético en la sección
transversal del solenoide que contiene al punto P es uniforme, determine:
2Q3
1184.6945 J
2253.3113 J 0.2628,
.
%
3. Para el circuito eléctrico de corriente continua que se muestra en la figura: R1 = 5 [], R2 = 5 [],
R3 = 1 [], R4 = 4 [], R5 = 1 [] y dos baterías de 12 [V], obtenga:
a) El valor de la corriente eléctrica I.
b) La diferencia de potencial Vae.
c) La energía asociada a cada fuente de fuerza electromotriz en
un minuto de operación. Indique para cada caso si la fuente
entrega o recibe energía.
d) El total de energía que consumen los resistores en su
conjunto, en 5 minutos de operación.
e) El potencial en el nodo a.
a ConleydevoltajesdeKirchhoffenlamalla:R I
(R
R I
V
R I
R I
V
R I
0
R
R I V
V
V
12 12 V
V
I
,
R
R
R
R
R
5 5 1 4 1 Ω
b ConbaseenlasumadevoltajesdeKirchhoff:V
R I V
R I 0
V
R
N = 4500 vueltas ;
A = 3.14103 [m2] (área de la sección transversal del solenoide)
P (7.5, 0, 0) [cm]
B (17, 0, 0) [cm]
U
b B
B
4π
ı̂
R I,V
R
P ∆t
P ∆t
V I∆t
V I∆t
12 V
1.5 A
12 V
60 s
4Ω
1Ω
1.5 A ,
. .
ı̂ ,
4π
μ i
k
2πa
B ;B
10
38 A
∙
k 2π 0.095 m
Bds
B
ds
BA
105.5575
10
T
3.14
10
m
U
P
∆t
16 Ω
R
1.5 A
I ∆t;R
5 60 s
R
R
R
R
R d F
;
e L
. obien:
U
U ∆t
e V
V
V
V
2 1080 J
V ,V
R I
12 V
5
0;V
1Ω
10800 J V ;V
V
R I
0
1.5 A . ̂
.
16 Ω 10800 J ,
̂
q
B
8
10
m
C 500ı̂
s
105.5575ı̂
Nϕ
i
μ N A

4π
10
∙
4500 3.14
0.15 m
10
80k 10
m
lasdosfuentesentreganenergíaalrestodelcircuito.
d U
.
80k μT .
1080 J U ,
4500 0.0028 A
∙
c ϕ
.
10
0.15 m
R
V
c U
μ Ni

a B
T .
̂
.