Ejercicios de curva normal

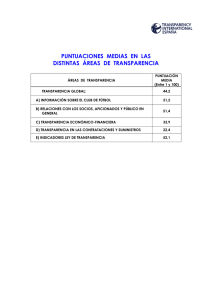
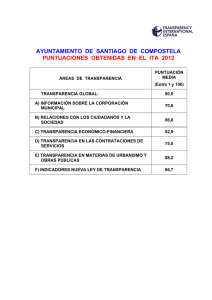
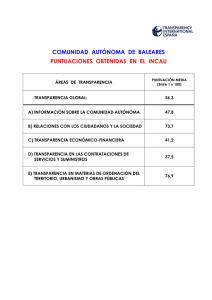
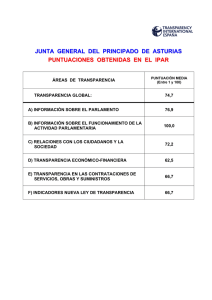
EJERCICIOS SOBRE CURVA NORMAL
Los recursos que encontrarás en esta página te serán útiles para comprender y manejar con
soltura los conceptos y los procedimientos relacionados con la distribución normal. Entra y
maneja las cuatro aplicaciones que hay desarrolladas para la distribución normal.
http://docentes.educacion.navarra.es/msadaall/geogebra/azar.htm
EJERCICIO 1
Sabiendo que la variable “Conocimientos previos” se obtuvo una media 4,269 y una desviación
típica de 0,918, y suponiendo que las puntuaciones se distribuyan normalmente, halla:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
La proporción de alumnos que hay entre zi=-1,57 y zi=+1,57.
La proporción de alumnos que hay por encima de la puntuación típica zi=+2,05.
La proporción de alumnos que hay por encima de la puntuación típica zi=-0,55.
La proporción de alumnos que hay por debajo de la puntuación típica zi=+0,70.
La proporción de alumnos que hay por debajo de la puntuación típica zi=-2,95.
La proporción de alumnos que hay entre las puntuaciones típicas zi=-2,02 y zi=+0,51.
La proporción de alumnos que hay entre las puntuaciones típicas zi=-1,77 y zi=-1,57.
Las puntuaciones típicas entre las que se encuentra el 97% central de la distribución.
La puntuación directa que deja por debajo de sí al 65% de la distribución.
La puntuación directa que deja por debajo de sí al 15% de la distribución.
La puntuación directa que deja por encima de sí al 70% de la distribución.
La puntuación directa que deja por encima de sí al 30% de la distribución.
Las puntuaciones directas entre las que se encuentra el 25% de alumnos cuyas
puntuaciones están por debajo de la media y el 35% de alumnos cuyas puntuaciones
están por encima de la media.
14. En cualquier distribución, la puntuación típica correspondiente a la media:
1. Es 0.
2. Se aproxima a 1.
3. Es -3 ó +3.
4. Depende de cada distribución.
15. Las distribuciones de puntuaciones típicas tienen como desviación típica un valor:
1. Igual a 0.
2. Igual a 1.
3. Que se encuentra entre -3 y +3.
4. Que depende de cada distribución.
16. Entre las siguientes afirmaciones en torno a la distribución normal, señala la que
carece de sentido:
1. Lo normal es lo frecuente.
2. Lo normal es lo común.
3. Lo normal está relacionado con la medida.
4. Lo normal lo reflejan los sucesos extremos.
EJERCICIO 2
La medida de altura de los alumnos de la Universidad Complutense es de 1,65 m. y la
desviación típica es de 0,05 m. Según datos de la propia universidad, el curso 2009-2010 el
número de alumnos era 85.5051. Suponiendo que esta variable tiene una distribución normal,
calcular:
1.
2.
3.
4.
5.
6.
7.
Número de alumnos que miden más de 1,80 m.
Número de alumnos que miden menos de 1,70 m.
Número de alumnos que miden más de 1,55 m.
Número de alumnos que miden menos de 1,50 m.
Número de alumnos que miden entre 1,60 m. y 1,75 m.
Número de alumnos que miden entre 1,50 m. y 1,55 m.
Número de alumnos que miden entre 1,70 m. y 1,75 m.
EJERCICIO 3 Interpretación de baremos publicados referidos a pruebas estandarizadas
A continuación se describen brevemente tres pruebas cuyos baremos se reproducen a
continuación. Lee cada una de las descripciones e inspecciona el baremo correspondiente. En
la sesión presencial de prácticas comentaremos los tres ejemplos y se formularán preguntas
específicas de interpretación.
Ejemplo 1. La Batería de Aptitudes para el Aprendizaje Escolar (BAPAE) es una prueba que se
aplica a niños de seis a siete años de edad y está formada por cinco subpruebas que son:
comprensión verbal (vocabulario), aptitud numérica (conceptos cuantitativos y manejo de
números), relaciones espaciales, constancia deforma y orientación espacial (estas tres últimas
subpruebas conforman la aptitud perceptiva). Es una prueba sencilla y fácil de aplicar, tanto a
nivel individual como colectiva, que evalúa las aptitudes básicas requeridas para el aprendizaje
en los primeros cursos escolares. De la Cruz (1989) parte del supuesto de que las subpruebas
que constituyen la BAPAE se han concebido como un instrumento que ayuda a detectar a los
niños que no alcanzan, en los aspectos evaluados, el nivel que se podría considerar «básico».
Además, considera que las aptitudes que aprecian estas subpruebas tienen un carácter de
«adquiridas», lo cual significa que son susceptibles de desarrollo. La prueba se entiende útil
para detectar a los niños con retrasos o problemas en determinados aspectos, lo que
permitiría ayudarles a alcanzar el nivel normal mediante actividades o programas de
desarrollo. En este estudio se trata de verificar si la prueba, construida y baremada
originalmente con población española puede ser usada con garantías en México, para lo cual
fue baremada con población infantil de la zona metropolitana de la Ciudad de México.
Ejemplo 2. El test Test de Pensamiento Creativo de Torrance (TTCT Torrance Thinking of
Creative Test) fue desarrollado por Torrance y sus colaboradores en 1966. Después ha sido
revisado en diferentes momentos. En este trabajo se ha utilizado el TTCT-Figurativo (forma A),
1
http://www.madrid.org/iestadis/fijas/estructu/general/anuario/ianucap05.htm
cuyo objetivo es evaluar las producciones creativas a través de dibujos y composiciones.
Consta de tres subtests: componer un dibujo, acabar un dibujo y líneas paralelas. En el
primero, componer un dibujo, se le pide al niño que realice un dibujo a partir de una forma
dada, consistente en un trozo de papel adhesivo de color. El papel, según el autor, podría
parecerse a una lágrima, un huevo o a una pera. Hay que destacar que si el niño no pone título
no se puede calificar. El objetivo es dar una finalidad a algo que previamente no tenía. Las
habilidades que se valoran con este primer subtest son: a) originalidad, consistente en
considerar las respuestas novedosas, no familiares e inusuales; y b) elaboración, se refiere a la
cantidad de detalles que el niño añade al dibujo con el objetivo de embellecerlo. El segundo
subtest, acabar un dibujo, consta de10 trazos, a partir de los cuales el niño tiene que utilizarlos
realizando diferentes dibujos y poniéndoles un título. Se evalúa la elaboración (número de
detalles añadidos al dibujo), la originalidad (respuestas inusuales y poco convencionales), la
flexibilidad (variedad de categorías en las respuestas) y en menor grado la fluidez (número de
dibujos con título realizados). El tercer y último subtest, las líneas paralelas, consta de 30 pares
de líneas paralelas. El objetivo es hacer tantos dibujos como se puedan a partir de las líneas. Se
mide la fluidez (aptitud para hacer asociaciones múltiples a partir de un estímulo único); la
flexibilidad (capacidad para cambiar el patrón o estructura de las composiciones), originalidad
(habilidad para realizar estructuras diferentes y poco familiares) y elaboración (habilidad para
añadir detalles a las estructuras realizadas con las líneas paralelas).
Ejemplo 3. El inventario de personalidad NEO revisado (NEO-PI-R) es probablemente la medida
más utilizada en la literatura reciente sobre el Modelo de los Cinco factores de personalidad, el
cual cuenta en la actualidad con un importante consenso entre los investigadores dada su
universalidad en distintas culturas así como con diversas medidas e instrumentos
desarrollados por distintos autores. En el momento de diseñar el estudio no existía ninguna
versión en lengua española del inventario. Por este motivo se adquirió a la editorial americana
la versión original en inglés para su uso en la investigación. Se realizó una traducción y
adaptación socio-cultural del cuestionario por los autores y se supervisó por un traductor
profesional bilingüe. El inventario se compone de 240 ítems y tiene un formato de respuesta
tipo Likert de 5 opciones. Consta de cinco dimensiones de personalidad: Neuroticismo (N),
Extraversión (E), Apertura (O), Afabilidad (A) y Responsabilidad (C).
Ejemplo del Baremo 1
Ejemplo del Baremo 2
Ejemplo del Baremo 3