VIBRACIÓNS E ONDAS O

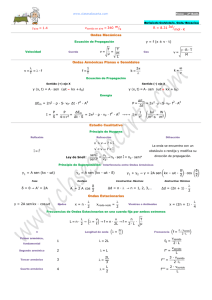
VIBRACIÓNS E ONDAS
OBXECTIVOS ESPECÍFICOS
•
•
•
•
•
•
Identifica-las características xerais do M.H.S. e aplicalas a resolución de problemas contemplando os aspectos cinemáticos,
dinámicos e enerxéticos.
Comprende-las características xerais do movemento ondulatorio e distinguir entre os diferentes tipos de ondas.
Identifica-las magnitudes que aparecen na ecuación dunha onda armónica, así como as relacións entre elas. Comprende-los
conceptos de intensidade e enerxía dunha onda e explica-lo fenómeno do amortiguamento.
Explicar de forma cualitativa os fenómenos de reflexión, refracción, difracción, polarización, interferencia e resonancia.
Comprobar experimentalmente o cumplimento da lei de Hooke, analizando as características do movemento oscilatorio dun
resorte e determinando a constante elástica polos métodos estático e dinámico.
Determinar experimentalmente os factores dos que depende o período dun péndulo simple e determina-lo valor da gravedade no
laboratorio, analizando e discutindo os valores obtidos.
CONTIDOS
1. Coñecementos previos. Movemento harmónico simple.
1.1. Características xerais e conceptos previos.
Un cuerpo describe un movimiento periódico cuando las variables posición r,velocidad v y a de su movimiento
toman los mismos valores después de un intervalo de tiempo constante llamado período. (MCU móvil con con
trayectoria circular y w cte.; también los movimientos oscilatorios o vibratorios lamina sujeta en base-muellepéndulo en ellos una partícula se desplaza a un lado y otro de su posición de equilibrio repitiendo a
intervalos regulares sus variables cinemáticas.). Observa el montaje de la figura desplazamos mediante una
fuerza el resorte hacia la derecha soltamos y se inicia un movimiento oscilatorio en torno
a un punto O, que se convierte en el centro de oscilación o equilibrio. Este movimiento
se produce porque sobre el cuerpo se ejerce una fuerza recuperadora F que lo
O
devuelve a la posición de equilibrio. Esta fuerza viene dada por la ley de Hooke:
F= -K.r = -K.x.i
El movimiento oscilatorio de un cuerpo sobre una trayectoria recta es armónico simple cuando está
sometido a una atracción proporcional al vector de posición, con origen en su punto de equilibrio, y de sentido
contrario. Características: Vibración-Distancia recorrida por la partícula en un mov. completo de vaivén.
Centro de oscilación-Punto medio que separa las 2 posiciones extremas de la partícula.
Elongación x: Distancia en un momento dado de la partícula al centro de oscilación.
Amplitud A: Valor máximo de la elongación.
Período T: Tiempo empleado por la partícula en una oscilación completa.
Frecuencia f: número de oscilaciones por segundo. F= 1/T Hz o s-1.
Pulsación w: numero de períodos comprendidos en 2Π unidades de tiempo;w= 2Πf
1.2. Estudio cinemático, dinámico e enerxético do M.H.S.
La ecuación fundamental del MHS describe como varía la elongación x a lo largo de una trayectoria
recta con el transcurso del tiempo. Esta variación varía con el seno del ángulo, que como sabes varía
periódicamente: x= Asen (ω
ωt+ϕ
ϕo) ángulo de fase: ωt+ϕo (rad) ; ϕo-fase inicial (rad)
Si ϕo=0 el movimiento se inicia en...______________________.Si ϕo= el movimiento se inicia en un
extremo (dcha.) es decir x=___. El valor de x se repite cada vez que wt+ϕo aumenta en 2Π radianes.
t(s)
0
T/4
T/2
3T/4
T
ωt(rad)
0
π/2
sen(ωt)
0
0
x(m)
0
-A
0
*Ej. Cierta partícula se mueve con MHS según x=0,05sen20πt S.I..Calcula:a)fase inicial.b)Amplitud.
C)pulsación. D)Período. E)frecuencia. F)elongación en t=0,02 s y t=0,025 segundos.
Aω
ω
Para obtener la ec. de la velocidad derivamos la ecuación de la posición:
v= dx/dt=d(Asen (ωt+ϕo) /dt= Awcos(ω
ωt+ϕ
ϕo)
⇒
T
v2= A2 w2 cos2 (ωt+ϕo) = A2 w2 (1- sen2 (ωt+ϕo))= w2(A2-x2)
Para obtener la ec. de la aceleración derivamos la ecuación de la veolocidad:
ωt+ϕ
ϕo)= - w2x
a= dv/dt= d(Awcos(ωt+ϕo) /dt= -Aw2sen(ω
Aω
ω2
Observa la aceleración de un MHS es directamente proporcional
a la elongación y de sentido contrario.
T
.Dinámica del MHS: A partir de la aceleración del MHS podemos deducir la F que debe actuar sobre una
partícula de masa m a fin de que oscile con ese movimiento: F= ma
F= -mω2x = -Kx
a= -ω2x
La expresión anterior nos indica que en un MHS la fuerza es proporcional al desplazamiento y opuesta a él., se
dirige hacia el punto de equilibrio siempre, punto en el que se anula. De la anterior ec. obtenemos:
mω2x = Kx ; ω= √ K/m como T=2Π/ω ⇒ T=2Π√ m/K Vemos que el período de un
oscilador sometido a una fuerza elástica depende de su constante recuperadora, y masa, pero no de la
amplitud del movimiento.
*Ej.Se conecta a un resorte de cte.elástica 5 N/m un cuerpo de 200 g que oscila sobre una superficie horizontal sin
rozamiento. Se estira el resorte y se separa el cuerpo 5 cm de la posición de equilibrio y se suelta. Halla:a)T del
movimiento.b)x,v,a en función del t.c)vmax y amax. D)F recuperadora si x=0,05 m.(a)5;0,4Π,b,c)±0,25; ±1,25d)-0,25)
ϕo
ωt
(proyección MCU sobre diam. es MHS)
x
.Energía de un oscilador armónico simple:
Energía cinética: La energía cinética de una masa con MHS será:
Ec fíjate función periódica del tiempo, y
proporcional a la cte. recuperadora K y al
cuadrado de la amplitud de la oscilación A.
.Energía potencial: La variación de Ep que experimenta una masa m al pasar del punto A al B coincide con el
trabajo realizado por la fuerza elástica F pero cambiado de signo: WA→B= - ∆Ep= EpA-EpB
=EpA - EpB
2
2
2
Es decir: Ep= ½.K.x = ½.K.A .sen (ωt+ϕo )
Energía mecánica total: E= Ec+Ep= ½.K.A2.cos2 (ωt+ϕo )+ ½.K.A2.sen2 (ωt+ϕo )= ½.K.A2
La energía mecánica total de un oscilador armónico es cte. y proporcional al cuadrado de la amplitud.
2
1.2. Aplicación dos conceptos teóricos ó análise experimental de movementos harmónicos
simples: o resorte elástico e o péndulo simple.
3
Sobre la esferita actúan solo 2 fuerzas: Tensión T y peso P=m.g.
Al descomponer el peso en F´y F, vemos que F= mgcosϕ se anula
con la tensión T, y F =mgsenϕ origina el movimiento oscilante de la bola:
F= -mgsenϕ= -mgϕ (rad) (ángulos <5º senϕ=ϕ
ϕ (rad);F- pues ϕ↓)
F= -mgϕ= - mgs/l = - K.s (ϕ (rad) = arco/radio= s/l; K= mg/l)
Esto nos indica que la fuerza del mov. pendular es variable,
atractiva hacia la posición de equilibrio, directamente proporcional a la
elongación y de sentido contrario a ella⇒ Oscilaciones <5º es un MHS.
Vimos: T=2Π√ m/K = 2Π√ m/(mg/l)= 2Π√ l/g
Leyes:1- El T es independiente de
la masa y amplitud.2-El T direct proporc a raíz cuadrada longitud e
inversamente proporcional a la raíz cuadrada de la gravedad en el
lugar de la experiencia.
2. Ondas armónicas unidimensionais.
2.1. Propagación de perturbacións en medios materiais elásticos.
La energía se puede transmitir de unos lugares a otros en forma de energía cinética,
por medio de la interacción de los cuerpos en movimiento. Pero también se puede llevar a
cabo por medio de ondas que se propagan sin transporte de materia. Las ondas se
originan en un foco vibrante que produce una perturbación (onda) que se propaga en el
medio que le rodea sin transporte neto de materia.
Fíjate en la cuerda producimos una perturbación inicial. Esta vibración se transmite a las
partículas más próximas: la energía que reciben les permite reproducir la vibración inicial
sin realizar mas que un desplazamiento vertical -suben y bajan al rededor de la posición
de equilibrio - pero sin desplazarse horizontalmente. Conforme pasa el tiempo la
vibración va alcanzando los puntos más alejados de la cuerda. Es decir no se propagan las
partículas vibrantes sino la energía que poseen.
Si a una cuerda le damos un golpe con la mano, se produce una perturbación inicial
llamada pulso, éste avanza, quedando los puntos por los que ha pasado de nuevo en
reposo. Si el extremo de la cuerda lo hacemos vibrar continuamente, suministro
continuo de energía, se obtiene un tren de ondas.El lugar geométrico de todos los
puntos que son alcanzados por una perturbación se llama frente de ondas. Aquí a la
izqda. puedes ver superficies esféricas (sonido), circunferencias (ondas superficiales del
agua), planos (a gran distancia del foco emisor)
2.2. Tipos de ondas: ondas lonxitudinais e transversais; ondas materiais e electromagnéticas
a)Según el tipo de Energía que transportan:
-Mecánicas o materiales- Transportan Energía mecánica.Necesitan de un medio material para su
propagación.Ej: sonido,ondas superficiales del agua,ondas en una cuerda tensa de guitarra,de un muelle..
-Electromagnéticas-Transportan energía electromagnética mediante la propagación de 2 campos
oscilatorios el eléctrico y el magnético, no requieren medio físico ya que son variaciones del estado eléctrico y
magnético del espacio, por eso se propagan en el vacío.(luz visible,ondas de radio,RX )
b)Según las direcciones de vibración y propagación:
-Ondas Transversales- Son aquellas en las que las partículas vibran perpendicularmente a la dirección de
propagación.Cuando un pulso o tren de ondas avanza en una cuerda las partic
vibran perpend. a la direcc avance. (Ej tren ond cuerda,electromagnet.,sísmicas S)
-Ondas Longitudinales-El extremo de la lámina vibra
horizontalmente estirando y comprimiendo las espiras del resorte.. Estas
compresiones y enrarecimientos producidas por la lámina se propagan a su
vez horizontalmente en el resorte. La piel del tambor al vibrar provoca
compresiones y dilataciones del aire circundante (sonido) que se propagan en
la misma dirección de vibración de la piel del tambor.
4
2.3. Magnitudes características: lonxitude de onda, frecuencia, amplitude e número de onda.
λ
A
Amplitud A- Valor máximo de la elongación , y, en su oscilación
Longitud de onda λ-Distancia mínima entre dos puntos en
igual estado
vibración. metros
Período T-Tiempo que emplea el mov. ondulatorio en avanzar una longitud de onda. Frecuencia fNúmero de ondas que pasan por un punto del medio por unidad de tiempo.Hz Número de ondas k es el
cociente 2π/λ es el nº de ondas contenidas en 2π.(rad/m)
2.4. Velocidade de propagación. Factores dos que depende.
La velocidad de propagación de las ondas es uniforme así: v= ∆x/∆t= λ/T= λf
Ondas electromagnéticas en el vacío y prácticamente en el aire es c=300000 km/s=λ/T= λf
Ondas mecánicas: la velocidad de propagación depende de las condiciones del medio. Así:
Ondas transversal cuerda: v=√F/µ donde F-Tensión de la cuerda; µ-masa/longitud cuerda
Onda longitudinal sonido: v=√1,4.R.T/M donde R=8,31 J/K.mol y M(mol aire )=28,8.10-3 Kg/mol
Ej.Calcula la velocidad de propagación de las ondas de una cuerda de 2 m y 40 g sometida a una tensión de30 N
3. Ecuación dunha onda armónica unidimensional.
3.1. Doble periodicidade espacial-temporal. 3.3. Distintas expresións da ecuación de ondas
Si la propagación que se propaga en la onda es un MHS, las
ondas se llaman ondas armónicas. Si la perturbación en el origen de coordenadas viene dada por el
armónico y= Asen wt, una partícula p.ej. de una cuerda que se encuentre que se halla a distanica x vibrará
según y= Asen wtv, siendo tv el tiempo que lleva ese punto vibrando. La relación
x
t a tv será: tv = t- x/vp sustituyendo en la ecuac. y= Asen wtv= Asenw ( tx/vp)= Asen (wt- wx/vp) pero vp= λf
y=Asen (wt-kx) ; sentido –X y=Asenwt+kx) ; wt-kx =fase de la onda
2π
2π
y= A.sen( t −
x) Ec. de la onda armónica en sentido creciente X
T
λ
Se observa la doble periodicidad respecto a la posición (x) y al tiempo (t). Se comprueba que
para un instante determinado se repite cada λ metros el estado vibratorio del medio; también para cada
punto concreto cada T segundos se repite su estado de vibración.
Ej. Una onda transversal se propaga por una cuerda tensa según: y=0,06 sen (4πt-2πx) S.I.
Deduce: a)La longitud onda.b)El período.c)velocidad propagación.d)sentido propagación.e)para t=2 s,
la coordenada Y, así como la velocidad, de un punto de la cuerda situado a 1,0 m origen (Sol 0; 0,75 m/s)
4. Enerxía e intensidade do movemento ondulatorio. Atenuación e absorción polo medio.
Cuando un punto es alcanzado por la perturbación empieza a vibrar y se convierte en un
oscilador armónico., y adquiere Ecinet. y Epot: las ondas al propagarse, transportan energía:
Como viste la Emec del oscilador armónico= Ep+Ec= ½.K.x2 + ½.m.v2= ½.KA2= (Cuando
La energía
pasa por la posición de eq Epot=0 Ecin=max) ½.mv2maxima= ½.m(Aw)2= 2mπ2.A2f2
que transmite una onda es proporcional al cuadrado de la amplitud y al cuadrado de la frecuencia.
La intensidad es la energía que se propaga por unidad de tiempo, a través de la unidad de
superficie normal o perpendicular a su dirección de propagación en dicho punto: I= E/t.SN W/m2
La energía que se propaga por unidad de tiempo en los frentes de ondas 1 y 2 si
suponemos que no es absorbida la energía (no roztos): E1= 4πR12I1 = 4πR22I2 = E2
De aquí vemos I1/I2 = R22 /R12 ⇒ La intensidad de las ondas esféricas
decrece con el cuadrado de la distancia por consideraciones geométricas: atenuación.
5
Ej:La sensación sonora en decibelios viene dada por β= 10.log I/Io siendo Io= 10-12 W/m2 umbral de audición
para el oído humano. Para un sonido de intensidad 2.10-7 W/m2 a 10 m del foco emisor suponiendo onda
armónica esférica, y que no hay absorción: a)su sonoridad.b)energía emitida por el foco en medio minuto.
(S:53dB;0,0075J)
Absorción : las ondas ceden energía al medio, que se calienta.La disminución de la intensidad de la
onda se traduce en disminución de la amplitud . La amplitud inicial Ao de una onda disminuye cuando
penetra una distancia x según: A = Aoe-αx α- coeficiente de absorción que depende del medio material.
αx
Como la intensidades son proporcionales al cuadrado de la amplitud I = Ioe-2
5. Principio de Huygens.
Dado un foco productor de ondas, se llama frente de ondas a la
superficie constituida por todas las ondas que en un momento dado vibran en
concordancia de fase. Las distintas superficies de onda alejadas por una distancia
igual a λ reúnen todos puntos del medio en igual estado de vibración. Rayos son
las rectas que indican la direccion de propagación del mov.ondulatorio, son
perpendiculares al frente de onda en cada uno de sus puntos. (ver dibujo)
El principio de Huygens enuncia una propiedad fundamental de cada uno de los
puntos del frente de onda que permite saber como será el nuevo frente más tarde.
Dice: Todo punto del frente de onda se convierte en centro productor de ondas
secundarias de igual velocidad y frecuencia que la onda inicial, cuya envolvente
constituye el nuevo frente de ondas. (Como ves dibujo es igual si el frente es esférico ,plano,..etc)
6. Propiedades das ondas:
6.1. Reflexión. El ángulo que el frente de onda incidente AB forma con la superficie de
separación al chocar con esta recibe el nombre de ángulo de incidencia î, éste es igual que
el que forma el rayo incidente con la normal a la superficie en el punto incidencia A.
Conforme la onda choca con la superficie de separación, cada punto se convierte en
centro emisor de ondas, mientras la onda recorre BC los puntos del frente de onda
empezaron a producir sucesivamente ondas secundarias, cuya envolvente es el frente de
ondas reflejado A´C y su dirección (rayo reflejado) es perpendicular a A´C. El ángulo de
reflexión r es el formado por A´C y la superficie de separación que es igual al ángulo
entre rayo reflejado y la normal. Así reflexión: Al llegar una onda a la superf.separación
de 2 medios es devuelta al primero con parte de la energía del mov.ondulatorio,
cambiando la dirección de propagación.
Dada la igualdad de los triángulos ABC y AA´C leyes reflexión: a) Rayo
incidente,normal y rayo reflejado en el mismo plano.b) angulo incidencia=ang reflexión.
6.2. Refracción. Cuando una onda plana incide sobre la superficie de separación de 2 medios
materiales, en el que la velocidad de propagación en el
segundo medio v2 es menor que en el primero v1. Al alcanzar
el frente de onda la superficie el radio de las ondas
secundarias formadas es menor que en el primer medio por
ser menor la velocidad de las ondas en ese medio (AA´<BC).
La envolvente de estas ondas secundarias A´C es el nuevo
frente de onda refractada. Como ves en la construcción
gráfica el rayo refractado se acerca a la normal,y:
BC ACseni seni v1t v1
= n21 Leyes
´=
=
=
=
AA′ ACsenr senr v 2t v 2
refracción: a) Rayo refractado,normal e incidente están en un mismo plano.b)Razón del seno
del ángulo incidencia y refracción es cte., es razón de las velocidades o n21 índice de refracción
relativo del 2º medio respecto 1º.Ley Snell
6.3. Difracción.Es la desviación en la
propagación rectilínea de las ondas cuando
en su propagación se encuentran con una
abertura o un obstáculo. Gracias a la
difracción las ondas pueden bordear
obstáculos. Como ves en la figura se puede
escuchar un sonido detrás de una esquina
(difracción del sonido). Puede explicarse a partir del principio de Huygens, los puntos del
frente de ondas al llegar al orificio se transforman en emisores de ondas elementales; la
relación entre la longitud de onda y el obstáculo determina la forma del nuevo frente envolvente
6.4. Interferencias.
6.4.1. Principio de superposición. Interferencia constructiva e destructiva: descrición cualitativa.
La superposición de 2 o más mov.ondulatorios en un punto del medio se
llama interferencia. Sea un punto P distante x1 y x2 de los focos emisores
respectivamente A y B. Si los mov. ondulatorios tienen igual frecuencia,
amplitud y velocidad de propagación de acuerdo con el Principio de
Superposición la perturbación en el punto P es la suma de las perturbaciones
que originan en ese punto las ondas: y= ya +yb= Asen (wt-kx1)+Asen(wt-kx2)
[sen a+senb= 2sen (a+b/2)cos(a+b/2)]
y= A2sen
k ( x 2 − x1 )
2wt − k ( x1 + x 2 )
=
. cos
2
2
A´=2 A interf.constructiva
A´= 0
interf.destructiva
2Acosk(x2-x1)/2. sen (wt-k(x1+x2)/2)= A´.sen( wt-kd) A´es amplitud en P
λ máxima interferencia
Se presenta máximo si cosk(x2-x1)/2= 1,es decir :k(x2-x1)/2 =nπ x2-x1=nλ
cuando la diferencia de caminos es un múltiplo de la longitud de onda.
λ/2 se presenta
Se presenta mínimo si cosk(x2-x1)/2=0 es decir: k(x2-x1)/2= (2n+1). π/2 x2-x1=(2n+1)λ
un mínimo cuando la diferencia de caminos es un número impar de semilongitudes de onda.
6.4.2. Ondas estacionarias.El extremo de una cuerda está unido a una lámina que vibra a 50 Hz el otro extremo
está sujeto por la mano. La vibración del extremo móvil se propaga por la cuerda en forma de onda transversal, al
llegar al otro extremo se refleja y se superponen dos ondas de igual frecuencia, velocidad de propagación y
amplitud pero que avanzan en sentidos opuestos,
el resultado una onda estacionaria. Al producirse
la onda estacionaria hay puntos del medio que no
vibran (nodos) y otros lo hacen con vibración
máxima (vientres o antinodos). Fíjate que la
vibración de los puntos depende de sus posición
respecto a los extremos de la cuerda. Como los
nodos se encuentran siempre en reposo, la onda
parece fija sobre la dirección de propagación, no
viaja y no transporta energía. (nodo-nodo=λ/2)
6.5. Polarización: descripción cualitativa. Una onda transversal puede vibrar en todos los planos perpendiculares
a la dirección de propagación (sacudir una cuerda de arriba hacia abajo; o de derecha a izquierda). Si a una onda,
por ej. luminosa que vibra en varios planos, la hago atravesar una rendija situada en una determinada dirección,
entonces sólo permito la transmisión de la vibración en ese plano, obtengo luz polarizada linealmente. Se suelen
utilizar materiales sintéticos como los polaroides
7. O son.
7.1. Propagación do son. Velocidade de propagación do son.
7.2. Cualidades do son: Tono, intensidade e timbre.
7.3. Percepción do son.
8. Resonancia: concepto e descripción cualitativa mediante exemplificacións.
CRITERIOS DE AVALIACIÓN
• Determinar e avalia-las características xerais do movemento harmónico simple.
Preténdese constatar se o alumnado é capaz de analiza-las consideracións cinemáticas, dinámicas e enerxéticas
que caracterizan un movemento harmónico simple, para aplicalas a resolución de problemas e cuestións relativos
ó resorte elástico e péndulo simple.
• Estima-las características do Movemento Ondulatorio e clasifica-los diferentes tipos de ondas en función dos
distintos criterios.
Trátase de verificar se o alumnado e quén de analiza-los factores que condicionan a existencia dun movemento
ondulatorio, para distinguir entre os diferentes tipos de ondas, valorando o por qué desa clasificación.
Asimesmo, deberá ser capaz de comparar distintos fenómenos ondulatorios da vida cotiá e clasificalos dacordo
con criterios antes reseñados.
• Analiza-las magnitudes que aparecen na ecuación da onda armónica, así como as relacións entre elas.
Este criterio pretende comprobar se o alumnado e capaz de analiza-la ecuación dunha onda armónica,
identificando as súas magnitudes e as relacións entre elas, para a súa aplicación na resolución de cuestións
teóricas e numéricas (obtención dos valores de amplitude, velocidadE, lonxitude de onda, e frecuencia, a partires
dunha ecuación de onda dada).
• Relaciona-los conceptos de intensidade e enerxía do movemento ondulatorio, e explicar o amortiguamento
das ondas.
Preténdese verificar se os alumnos son capaces de determina-la intensidade e enerxía do movemento ondulatorio,
e de xustificar cómo varían as mesmas en función da distancia e do medio.
• Xustificar, dun xeito cualitativo, os fenómenos de reflexión, refracción, difracción, polarización,
interferencia de ondas, resonancia.
Con este criterio pretendemos verificar se o alumnado e quén de discriminar entre os diferentes tipos de
fenómenos ondulatorios, analizando as leis que os regulan, e de xustificar en base as mesmas a resolución das
cuestións plantexadas. O analise destes fenómenos ondulatorios servirá de base para o achegamento ó estudio das
ondas sonoras e das características ondulatorias da luz.
• Contrastar experimentalmente o cumprimento da lei de Hooke, analizando as características do movemento
oscilatorio dun resorte e determinando a constante elástica polos métodos estático e dinámico.
Este criterio tenta de verificar si os alumnos son capaces de deseñar e realizar unha montaxe experimental que
permita analiza-las características cinemáticas e dinámicas do movemento harmónico simple dun resorte elástico,
tomando datos, plantexando hipóteses e establecendo conclusións sobre a realización da experiencia .
• Avaliar experimentalmente os factores de que depende o período dun péndulo simple e determina-lo valor da
gravedade no laboratorio, analizando os resultados obtidos.
Trátase de constatar se o alumnado pode analiza-lo movemento harmónico simple dun péndulo, xustificando as
desviacións experimentais do modelo teórico plantexado, e de aplica los datos obtidos ó cálculo da aceleración
da gravedade.
PROBLEMAS
1.- Un sistema cun resorte estirado 3 cm sóltase en t=0 deixándoo oscilar libremente, co
resultado dunha oscilación cada 0'2 s. Calcula:
a. A velocidade
b. A aceleración do extremo libre ó cabo de 19 s (Considérase que o amortecemento é
desprezable)
SOLUCIÓN
a) O resorte deixado libre describe un MHS, polo tanto correspóndelle unha
ecuación para a elongación: x =Asen(ωt+φ0)
No instante inicial, a elongación é máxima e sen(ωt+φ0)=1, e como t=0
φ0=(π/2)rad, quedando a ecuación : x =Asen(ωt+π/2)
do mesmo xeito podemos razoar para a velocidade, que resulta
v=Aωcos(ωt+π/2)
A=3 cm ; ω=2π/T=2π/0'2 =31'416rads-1
substituíndo os datos anteriores e o tempo transcorrido:
v = 3. 31'416.cos(31'416.19+π/2) = 0cms-1= 0ms-1
b) Os mesmos razoamentos son aplicables neste caso, quedando:
a=Aω2cos(ωt+π/2)
A=3 cm
ω=2π/T=2π/0'2 =31'416 rad s-1 ;
a = 3. 31'4162.sen(31'416.19+π/2) = 2961 = 29'61ms-2
A velocidade é mínima e a aceleración máxima, atopándonos na situación
inicial, xa que transcorreu un número enteiro de períodos. Por erros de
redondeo na calculadora ou ordenador, pode darse o caso de que o resultado da
velocidade non resulte 0 exactamente.