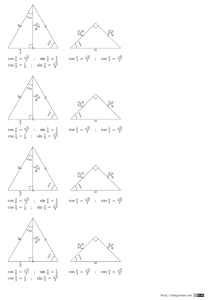
Formule des angles associés cos(-x)
Anuncio

Formule des angles associés Formule des angles associés Formule des angles associés cos(−x) = cos x cos(−x) = cos x cos(−x) = cos x sin(−x) = − sin x sin(−x) = − sin x sin(−x) = − sin x cos(π+x) = − cos x cos(π+x) = − cos x cos(π+x) = − cos x sin(π+x) = − sin x sin(π+x) = − sin x sin(π+x) = − sin x cos(π−x) = − cos x cos(π−x) = − cos x cos(π−x) = − cos x sin(π−x) = sin x (π ) cos +x = − sin x ( π2 ) sin +x = cos x 2 (π ) cos −x = sin x 2 (π ) sin −x = cos x 2 Identité remarquable sin(π−x) = sin x (π ) cos +x = − sin x ( π2 ) sin +x = cos x 2 (π ) cos −x = sin x 2 (π ) sin −x = cos x 2 Identité remarquable sin(π−x) = sin x (π ) cos +x = − sin x ( π2 ) sin +x = cos x 2 (π ) cos −x = sin x 2 (π ) sin −x = cos x 2 Identité remarquable cos2 a + sina = 1 cos2 a + sina = 1 cos2 a + sina = 1 Formule d’addition et de différence Formule d’addition et de différence Formule d’addition et de différence cos(a+b) = cos a· cos b − sin a· sin b cos(a+b) = cos a· cos b − sin a· sin b cos(a+b) = cos a· cos b − sin a· sin b cos(a−b) = cos a· cos b + sin a· sin b cos(a−b) = cos a· cos b + sin a· sin b cos(a−b) = cos a· cos b + sin a· sin b sin(a+b) = sin a· cos b + cos a· sin b sin(a+b) = sin a· cos b + cos a· sin b sin(a+b) = sin a· cos b + cos a· sin b sin(a−b) = sin a· cos b − cos a· sin b sin(a−b) = sin a· cos b − cos a· sin b sin(a−b) = sin a· cos b − cos a· sin b Formule de duplication ( )2 ( )2 cos(2a) = cos a − sin a ( )2 cos(2a) = 2· cos a − 1 ( )2 cos(2a) = 1 − 2· sin a sin(2a) = 2· sin a· cos a Formule de duplication ( )2 ( )2 cos(2a) = cos a − sin a ( )2 cos(2a) = 2· cos a − 1 ( )2 cos(2a) = 1 − 2· sin a sin(2a) = 2· sin a· cos a Formule de duplication ( )2 ( )2 cos(2a) = cos a − sin a ( )2 cos(2a) = 2· cos a − 1 ( )2 cos(2a) = 1 − 2· sin a sin(2a) = 2· sin a· cos a http://chingatome.net