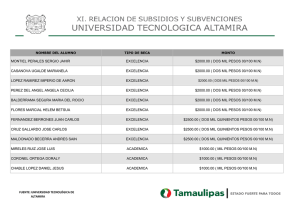
1. Conjunto
Anuncio

1.
Conjunto
TAD Conjunto(α)
observadores básicos
· ∈ · : α × conj(α) −→ bool
generadores
∅ : −→ conj(α)
Ag : α × conj(α) −→ conj(α)
axiomas
a∈∅
a ∈ Ag(b, c)
≡ false
≡ (a = b) ∨ (a ∈ c)
Fin TAD
1.1.
Interfaz
Pertenece(in c:conjnat, in e:nat) → res:bool
{true}
{res = e ∈ c}
Pre
Pos
Vacio() → res:conjnat
{true}
{res = ∅}
Pre
Pos
Ag(in/out c:conjnat, in e:nat)
Pre {c0 = c}
Pos {c = Ag(e, c0 )}
1.2.
Representación
conjnat se representa con puntero(estr), donde
estr es tupla helem: nat,
menores: puntero(estr),
mayores: puntero(estr)i
Rep : puntero(estr) → boolean
Rep(p) ≡ p = NULL ∨
Rep(p → menores) ∧ Rep(p → mayores) ∧
(p → menores = NULL ∨ máx(Abs(p → menores)) < p → elem) ∧ (p → mayores = NULL ∨ mı́n(Abs(p →
mayores)) > p → elem)
Abs : puntero(estr) → conj(nat)
{Rep(e)}
Abs(p) ≡ c:conj(nat) |
e ∈ c ⇔ p 6= NULL ∧
p → elem = e ∨ e ∈ (Abs(p → menores) ∪ Abs(p → mayores))
iPertenece(in c:puntero(estr), in e:nat) → res:bool
if c = NULL then
res ← false
else if c → elem = e then
res ← true
else if c → elem < e then
res ← iPertenece(c → mayores, e)
else
res ← iPertenece(c → menores, e)
end if
1
Vacio() → res:puntero(estr)
res ← NULL
iAg(in/out c:puntero(estr), in e:nat)
if c = NULL then
c ← &he,NULL,NULLi
else if c → elem < e then
iAg(c → mayores, e)
else if c → elem > e then
iAg(c → menores, e)
end if
2.
Conjunto con #MenoresQue
TAD Conjunto(α)
observadores básicos
· ∈ · : α × conj(α) −→ bool
generadores
∅ : −→ conj(α)
Ag : α × conj(α) −→ conj(α)
otras operaciones
#MenoresQue : α × conj(α) −→ nat
axiomas
a∈∅
a ∈ Ag(b, c)
#MenoresQue(e, ∅)
#MenoresQue(e, Ag(b, c))
≡
≡
≡
≡
false
(a = b) ∨ (a ∈ c)
0
if e < b then 1 else 0 fi + #MenoresQue(e, c)
Fin TAD
2.1.
Interfaz
Pertenece(in c:conjnat, in e:nat) → res:bool
{true}
{res = e ∈ c}
Pre
Pos
Vacio() → res:conjnat
{true}
{res = ∅}
Pre
Pos
Ag(in/out c:conjnat, in e:nat)
Pre {c0 = c}
Pos {c = Ag(e, c0 )}
MenoresQue(in c:conjnat, in e:nat) → res:nat
{true}
{res = #MenoresQue(c, e)}
Pre
Pos
2.2.
Representación
conjnat se representa con puntero(estr), donde
estr es tupla helem: nat,
menores: puntero(estr),
mayores: puntero(estr),
cardinal : nati
2
Rep : puntero(estr) → boolean
Rep(p) ≡ p = NULL ∨
Rep(p → menores) ∧ Rep(p → mayores) ∧
(p → menores = NULL ∨ máx(Abs(p → menores)) < p → elem) ∧ (p → mayores = NULL ∨ mı́n(Abs(p →
mayores)) > p → elem)
∧ p → cardinal = 1 + #(Abs(p → menores) ∪ Abs(p → mayores))
Abs : puntero(estr) → conj(nat)
{Rep(e)}
Abs(p) ≡ c:conj(nat) |
e ∈ c ⇔ p 6= NULL ∧
p → elem = e ∨ e ∈ (Abs(p → menores) ∪ Abs(p → mayores))
iPertenece(in c:puntero(estr), in e:nat) → res:bool
if c = NULL then
res ← false
else if c → elem = e then
res ← true
else if c → elem < e then
res ← iPertenece(c → mayores, e)
else
res ← iPertenece(c → menores, e)
end if
Vacio() → res:puntero(estr)
res ← NULL
iAg(in/out c:puntero(estr), in e:nat)
if c = NULL then
c ← &he,NULL,NULL,1i
else
if c → elem < e then
iAg(c → mayores, e)
else if c → elem > e then
iAg(c → menores, e)
end if
c → cardinal ← 1
if c → menores 6= NULL then
c → cardinal ← c → cardinal + (c → menores) → cardinal
end if
if c → mayores 6= NULL then
c → cardinal ← c → cardinal + (c → mayores) → cardinal
end if
end if
iMenoresQue(in c:puntero(estr), in e:nat) → res:nat
if c = NULL then
res ← 0
else if c → elem ≤ e then
res ← iMenoresQue(c → mayores, e)
if c → menores 6= NULL then
res ← res + (c → menores) → cardinal
end if
if c → elem < e then
res ← res + 1
end if
else
res ← iMenoresQue(c → menores, e)
end if
3