f - Campus Virtual - Universidad del Valle

Definiciones Básicas
Fuente de Información: Entidad que produce la
información que va a ser transmitida a través del
sistema.
Formateo de Fuentes Discretas y
Fuentes Continuas
Mensaje Textual: En transmisión digital un
mensaje es una secuencia de dígitos o símbolos de
un conjunto finito de símbolos (o alfabeto).
Comunicación Digital
Fabio G. Guerrero
Universidad del Valle
De forma general, un mensaje está compuesto de
una cadena de caracteres.
2
1
Símbolo: Grupo de k bits considerado como una
unidad o carácter, mi, en un conjunto de símbolos.
Carácter: Miembro de un alfabeto o conjunto de
símbolos. Existen muchos códigos estandarizados para
codificación de caracteres (ASCII, EBCDIC, etc.).
Tamaño del alfabeto M = 2k
Dígito Binario: La unidad fundamental de
información de todos los sistemas digitales. También
se utiliza como unidad de contenido de información.
k es el número de bits en un símbolo. En transmisión,
cada símbolo, mi, (i = 1,2...M) se representa por su
correspondiente onda s1(t), s2(t), ....sm(t). El símbolo
mi, es enviado transmitiendo si(t) durante T segundos.
Torrente de bits (bit stream): Secuencia de dígitos
binarios (unos y ceros). Frecuentemente referido como
señal banda base.
Onda Digital: Onda de voltaje, corriente, luz, etc.
que representa un símbolo digital.
3
4
Ejemplos
Rata de Datos (Data Rate)
k 1
R[bit /s ]= = log 2 M
T T
Mensajes Textuales:
Como estás?
Bien
Degradación y Regeneración de Pulsos
Caracteres:
C,O,M,E,T,B,..
Bit Stream:
1100001=C
1111001=O
1011001=M
5
Símbolos
1
10
101
6
Formateo de Información Textual
mi (i = 1, 2,.... , M) M=2k
símbolo binario (k =1, M=2)
símbolo cuaternario (k =2, M=4)
símbolo octario (k = 3, M=8)
Ondas Digitales
si(t) (i = 1, 2, 3......, M)
7
Fuente: Esta figura ha sido tomada del estándar ISO/IEC 8859-1:1997 (E)
8
Fuentes continuas
Mensajes, Caracteres y Símbolos
Para transmitir señales continuas como (voz, vídeo) por
medios digitales, la señal se debe convertir a forma digital.
Este proceso se conoce como conversión analógica- digital.
El proceso de muestreo es el primer paso en esta conversión,
el cual convierte una señal continua en el tiempo en una señal
de tiempo discreto o una secuencia de números.
La transmisión digital de señales continuas es posible en
virtud del teorema de muestreo.
10
9
Un sistema pasabanda
Sistemas Bandabase
Fuente
discreta
Fuente
análoga
Información
análoga
LPF
Modulador
bandabase
Demod
bandabase
Información
discreta
Tomado de: Carlos Salazar. SIMULACION DE LA CAPA FISICA PARA EL ESTANDAR
IEEE 802.15.3a PARA UWB –OFDM. Trabajo de grado. Universidad del Valle. 2009
11
12
Formateo de Información Análoga
Diagrama de bloques del transmisor
802.11a/g.
S IG N A L
D ATA
A le a to riz a d o r
C o d ific a d o r
C o n v o lu c io n a l
C o d ific a d o r
C o n v o lu c io n a l
P e rfo ra d o r
In te rc a la d o r
In te rc a la d o r
B PSK
M o d u la c ió n
E N T R E N A M IE N T O
LA R G O
IF F T
In s e rc ió n
In te r-G u a rd a
E N T R E N A M IE N T O
C O RTO
IF F T
In s e rc ió n
In te r-G u a rd a
In s e rc ió n
P ilo to s
In s e rc ió n
p ilo to s
IF F T
In s e rc ió n
In te r-G u a rd a
F u n c ió n
E n v e n ta n a d o
IF F T
In s e rc ió n
In te r-G u a rd a
F u n c ió n
E n v e n ta n a d o
El Teorema del Muestreo
Una señal limitada en banda que no tenga componentes
espectrales por encima de fm hertz puede determinarse
unívocamente por valores muestreados a intervalos
uniformes de:
T s
1
s
2fm
Esta restricción expresada en términos de la rata de muestreo
se conoce como criterio de Nyquist:
Tomado de: Winans Oliver Cardona. SIMULACIÓN DE LA CAPA FÍSICA PARA REDES
INALÁMBRICAS DE ÁREA LOCAL WLAN IEEE 802.11g. Trabajo de grado. Universidad
del Valle. 2007.
f s 2 f m Hz
13
14
Recordemos
Vladimir Kotelnikov
Función Delta Dirac (impulso unitario):
t dt =1
t =0, t0
Propiedad de muestreo (colador):
x t tt d dt=x t d Convolución
x t tt d =x tt d Otras propiedades
Traducción completa del artículo de 1933 «On the capacity of the 'ether' and cables
in electrical communication»: http://ict.open.ac.uk/classics
15
x t tt d = x t d tt d 16
Muestreo ideal
La transformada de Fourier de x(t) es
1
x f =
f nf s T s n=
Sea x(t) una señal análoga con espectro X f igual a cero
por fuera de (- fm f fm) muestreada por un tren de
impulsos
x t= tnT s T s= 2 1f s
La convolución con una función impulso desplaza a la
función original al valor donde existe el impulso:
m
n=
Por la propiedad de muestreo de la función delta
X f f nf s = X f nf s x t t t 0 = x t 0 t t 0 Por tanto:
la versión muestreada de x(t) es:
1
X s f =X f X f =X f Ts
x s t=x t x t= x t tnT s n=
n=
]
f nf s n=
1
=
X f nf s
T s n=
=
[
x nT s tnT s 17
18
Interpretación física del teorema del muestreo
X(f)
x(t)
f
t
k(f)
k(t)
t
f
x(n t/2W)
x(t)
LPD
ideal
t
19
t
20
Kotelnikov's theorem 1
Reconstrucción en el dominio t
Cualquier función f(t) consistiendo de frecuencias entre 0 y
f1 Hz puede ser representada por la serie
{ }
sin 1 t
f t= D k
k
2 f1
t
k
2 f1
donde k es un entero, ω1 = 2πf1, y Dk son constantes que
dependen de f(t).
21
22
Qué pasa si fs < 2fM
Muestreo ideal
23
24
Muestreo Natural
Efecto espectral de fs
En este caso la señal es multiplicada por un tren de pulsos
rectangulares de periodo T y amplitud 1/T.
x s t=x t x p t
x p t= c n e j 2 n f
s
t
1
=2 f m
Ts
f s=
n=
AT
T
Para un tren de pulsos rectangulares c n= T 0 sinc n T 0
por tanto:
c n=
1
T
sinc n
Ts
Ts
25
26
La transformada Xs(f) de la onda muestreada se encuentra
de la siguiente manera:
x s t=x t cn e j 2 n f
s
t
n=
{
X s f =F x t
cn e j 2 n f
s
t
n=
X s f = cn F { x t e j 2 n f
s
t
}
}
n=
X s f = cn X f nf s n=
27
28
Muestreo Sample-and-Hold
Se puede describir como la convolución del tren de pulsos
muestreados [x(t)x(t)] con un pulso rectangular de
amplitud unitaria p(t):
[
x s t= p t
{x t x t}= p t
x t
{
[
X s f =P f F x t {
n=
t nT s
n=
tnT s
]
}
]}
1
=P f X f f nf s T s n=
1
=P f X f nf s T s n =
29
30
Aliasing
Espectro Señal Continua
Espectro Señal Muestreada
31
32
Espectro Señal Continua
Remoción efecto
aliasing
Espectro Señal Continua
Espectro Señal Muestreada
Prefiltrado
Anti-aliasing
Espectro Señal Muestreada
33
Espectro Señal Continua
Postfiltrado antialiasing
34
Frecuencia Alias
Espectro Señal Muestreada
35
36
Compromisos de Diseño
Para qué sobre-muestrear?
Se necesita un balance entre el costo de un ancho de banda de
transición pequeño y el costo de una rata de muestreo más
alta.
Sin oversampling:
La señal pasa a través de un LPF análogo de alto
desempeño para limitar su ancho de banda.
En muchos sistemas la respuesta ha sido tomar el ancho de
banda de transición entre el 10 y el 20% del ancho de banda
de la señal.
La señal filtrada es muestreada a la rata de Nyquist a la
señal (aproximadamente) limitada en banda.
Las muestras son procesadas por un ADC que convierte las
muestras del dominio continuo al discreto.
Considerando un 20% de ancho de banda de transición para el
filtro antialising se tiene una versión de ingeniería de la rata
de Nyquist:
f s 2.2 f m
37
38
Muestreo señales pasabanda
Con oversampling:
La señal se filtra con un LPF análogo de bajo
desempeño (más económico) para limitar su BW.
Una señal real m(t) se llama pasabanda si su transformada
de Fourier M() cumple con la condición
La señal pre-filtrada se muestrea ahora a una mayor
rata de Nyquist.
M = 0 excepto por
Las muestras son procesadas por un ADC.
1 2
2 1
Las muestras digitales son procesadas por un filtro
digital de alto desempeño para reducir su BW.
donde 1 = 2πf1 y 2 = 2πf2
La rata de muestreo a la salida del filtro digital se
reduce en proporción a la reducción en BW obtenida
por este filtro digital.
39
Usando la definición básica sería necesario muestrear a
2f2. Sin embargo para señales del tipo de m(t), la mínima
velocidad de muestreo permitida depende de f1, f2 y el
ancho de banda fB = f2 - f1.
40
M Para evitar traslapamiento es necesario que
M M s 2 2 1 2
1
1
0
k 1 s 1 1
2
B
k s 2 2
y
M [ k 1 s ]
Ya que
M k s f 1= f 2 f B
1 k 1
0
k 1 s 1
2
f2
fB
k fs
2 fB
f2
k 1 fs
1
2 fB
fB
k s 2
41
min { f s }=
fs / fB
2f2
m
m=floor
42
Ejemplo
f2
fB
Sea una señal pasabanda con f1 = 1.5 kHz y f2 = 2.5 kHz.
k=1
k=2
fB = f2 - f1 = 1 kHz, y f2 / fB = 2.5
7
6
k=3
m= floor
5
2.5
1
min { f s }=
2 2.5
2
=2.5 kHz
Vemos que la tasa mínima de muestreo es 2.5 kHz, y rangos
admisibles de la rata de muestreo son 2.5 kHz ≤ fs ≤ 3 kHz y fs
4
3
≥ 5 kHz (= 2f2).
2
1
2
2,5
3
4
5
6
7
f2 / f B
43
44
PCM
El concepto de cuantización
M = 2n
Transmisor PCM
(conversión análoga-digital)
Señal de entrada
Análoga
señal análoga
limitada en banda
LPF
Bandwidth = B
sampling
and hold
instantáneo
Señal
Flat-top
PAM
Señal
PAM
cuantizada
voltaje
entrada
Señal
PCM
Cuantizador
No. de niveles = M
8
Codificador
6
M=8
4
Para que no haya aliasing se requiere que fs ≥ 2B.
R = nf S
2
0
-8
Teorema de la dimensionalidad: BPCM
1
1
R = nf S
2
2
-6
-4
-2
2
4
6
8
voltaje salida = x
-2
-V = -8
-4
V=8
-6
Fisrt-null bandwidth usando NRZ:
-8
NRZ BPCM =R=n f S Hz
PCM Bandwidth Lower bound: BPCM n B
Tipos de ruido que pueden existir (dependiendo del rango):
Overload noise, random noise (quantization noise),
granular noise, haunting noise.
46
45
Definición
Conjunto de niveles
Regla de cuantización
Uniform quantizer, cell width = ∆, N=8
C={yi ; i I }
q x = y i 1 s x Distorsión
i
i
{
}
1s x = 1 x S S={Si ; i I }
0 otherwise
i
Zona de
saturación o
sobrecarga
Zona granular
Dq =E [d X , q X ]
El MSE (Mean Squared Error) es la medida más común de distorsión:
2
d x , x =x x 47
48
Relación (S/N) para pulsos
cuantificados
Rate-distorsion function
La función r(D) determina la rata mínima de cualquier
cuantizador escalar de rata fija con distorsión D o menor. Es
la función inversa de δ(R) donde:
R= Inf
El paso entre intervalos de cuantificación se denomina
intervalo de cuantificación: q voltios.
Dq q : R q R
Considerar un cuantificador de L niveles para una señal
análoga con un rango Vpp = Vp- (-Vp) = 2Vp voltios.
En la práctica la función δ(R) más usada es el índice
subjetivo MOS (Mean Opinion Score).
Se asume que el error de cuantificación, e, se distribuye
uniformemente sobre un intervalo de cuantización de ancho
q.
SNR=10 log 10
Var X c6 R dB
2
E [q X X ]
49
+Vp
Vp-q/2
Vp-3q/2
La varianza del cuantificador corresponde a la potencia
promedio del ruido de cuantificación:
.
.
.
.
Quantizer rate:
q/2
R q=log N
2
q /2
3q/2
q/ 2
2
2
1
q
de=
q
12
Si asumimos una onda sinusoidal con amplitud A = Lq/2, la relación
señal a ruido debida a la cuantificación será:
q/2
Vpp
(L niveles)
-q/2
q/2
= e pe de= e
2
5q/2
-3q/2
2
2
2
A Lq /2 L q
S= =
=
2
2
8
-5q/2
.
.
.
.
2
2
2
S
L q /8 3 2 3 n 2
= L = 2 = 2
N q q /12 2
2
S
N
-Vp+3q/2
-Vp+q/2
-Vp
50
51
3 n2
dB=10 log 10 2 1.776.02 n
2
6-dB-per-bit rule
q
52
Arquitecturas y desempeño
Aplicación y desempeño
1G
Flash
Pipeline
100M
Sub-range
10M
Multi-bit
sigma-delta
1M
100k
10k
4
Conversion Rate (MSample/s)
Conversion frequency (S/s)
10G
Successive
approximation
Single-bit sigma-delta
1000
500
300
HDD/DVD
Graphics
Video/
Communication
100
50
30
DVC/DSC/Printer
10
5
Servo
Automobile
1
General
Purpose
0.5
(µ-Computer)
0.1
Audio
0.05
Integrating
Meter
6
8
10
12
14
16
18
20
6
Resolution (bit)
Fuente: VLSI Symposia, 2006. A. Matsuzawa, Tokio Tech.
8
10
12
14
16
Resolution (bits)
53
Fuente: VLSI Symposia, 2006. A. Matsuzawa, Tokio Tech.
54
Distribución estadística de una señal
de voz
Modulación por Pulsos Codificados
(PCM)
55
56
Cuantificación uniforme y no
uniforme
Muchos de los pasos de cuantización en un sistema de
cuantificación uniforme para señales de voz serían raramente
usados.
El ruido de cuantificación es igual para todas las magnitudes,
por lo tanto, la relación S/N es peor para señales de bajo nivel
que para señales de alto nivel.
Con cuantificación no uniforme se puede brindar una
cuantificación fina para las señales débiles y una cuantificación
gruesa para las señales fuertes.
El ruido de cuantificación se puede hacer proporcional al tamaño
de la señal.
57
58
Cuantificación
no uniforme
El efecto de la cuantificación no uniforme es mejorar la relación
S/N global reduciendo el ruido de las señales débiles
predominantes a expensas de un incremento en el ruido para las
señales fuertes que raramente ocurren.
Una forma práctica de obtener cuantificación no uniforme es
distorsionar primero la señal con una característica de compresión
logarítmica seguido de un cuantificador uniforme.
Un cambio de señal dado a pequeñas magnitudes llevará al
cuantificador uniforme a través de más pasos que el mismo
cambio a magnitudes grandes.
1
x =G [qG x]
2
f x
D q 2
dx
12 g x
g x=
d G x
dx
59
60
Características de Compansión
y= y max
log e [1my x/ x max ]
sgn x
log e 1my
{
sgn x= 1 para x0
1 para x0
}
{
Ax/ x max 1
x
sgn x 0
1log e A
x max A
y=
1log e [ Ax/ x max ]
1 x
sgn x
1
y max
1log e A
A x max
y max
Ley (Norte América)
}
Ley A
(Europa)
61
62
Ejemplos de códecs de audio y
video
Trade-offs fundamentales:
Bit-Rate
Quality
Complexity
Delay
Complexity:
consumption
memory,
instructions,
cost,
power
Aplicaciones: one-way, two-way (< 300 ms round-trip)
63
64
Códecs de audio
ITU-T G.711
Banda angosta: 300 Hz a 3400 Hz
Pulse Code
Frequencies.
Banda Ancha: 50 Hz a 7kHz
Modulation
(PCM)
of
Voice
Bit rate: 64 kbit/s
Fixed Networks (Historical PSTN Networks, etc.),
Intranets, Internet (Mandatory for H.323)
Fuente: G.719: The first ITU-T Standar for High-Quality Conversational Audio Coding.
IEEE Communications Magazine, October 2009.
Material basado en el anexo A de la norma ETSI TS 185 001 V.1.1.1 (2005-11).
65
ITU-T G.726
66
ITU-T G.727
Adaptive Differential Pulse Code Modulation
(ADPCM)
5 -, 4-, 3- and 2-bits Sample Embedded Adaptive
Differential Pulse Code Modulation (ADPCM)
A: uniform-quantized input and output
Annex A: uniform-quantized input and output
B: Packet format
Bit rate (kbit/s): 16 / 24 / 32 / 40
Bit rate (kbit/s): 16/24/32/40
Transmission applications (DCME)
DECT Telephony
67
68
ITU-T G.728
ITU-T G.723.1
Coding of Speech at 16 kbit/s using low-delay Code
Excited Linear Prediction (LD-CELP).
Dual rate speech coder for multimedia
communications transmitting at 5.3 and 6.3 kbit/s
Videophony
Mayo de 2006
Sensible a errores de transmisión
Videophony sobre Internet (H.324)
Bajo retardo (tramas de 5 ms)
H: Variable bit rate
I: packet concealment
69
ITU-T G.729
70
GSM
Coding of speech at 8 kbit/s using conjugatestructure algebraic-code-excited linear prediction
(CS-ACELP).
EFR. 12.2 kbit/s. Frame=20 ms. Más usado.
FR. 13 kbit/s. Frame=20 ms. Primera generación.
HR. 5.6 kbit/s. Frame=20 ms.
Telefonía sobre IP.
AMR. 12.2/10.2/7.95/7.40/6.70/5.90/5.15/4.75
kbit/s. GSM y redes 3G
Trama = 10 ms.
71
72
Redes CDMA (IS127)
IETF
EVRC: Estándar TIA y 3GPP2. USA, Asia.
iLBC. Voz sobre IP. Audio streaming.
8.55/4/0.8 kbit/s.
IEFC RFC 3951. Libre de patente.
SMV: Estándar 3GPP2. 8.55/4/2/0.8 kbit/s
13.33/15.2 kbit/s.
Telefonía sobre redes CDMA (IS127).
Ejemplos de uso: Gizmo5 (VoIP), Ekiga,
OpenWengo, Google Talk, Yahoo, Messenger and
Memo Recorder (on the Nokia N800/N810).
73
Códecs audio banda ancha
74
Audio banda ancha y angosta
G.722. 48/56/64 kbit/s. Teleconferencia.
CELP MPEG. Estándar ISO/IEC 14496 (audio).
G.722.1. 24/32/48 kbit/s. Teleconferencia. Frame=20 ms.
Tiene múltiples variantes.
Voz sobre IP. Digital Radio Broadcast.
AMRWB (G.722.2).
Narrowband (kbit/s): 3.85, 4.25, 4.65, 4.9, 5.2, 5.5,
5.7, 6.0, 6.2, 6.3, 6.6, 6.9, 7.1,....,12.2
23.85/23.05/19.85/18.25/15.85/14.25/12.65/8.85/6.6 kbit/s.
Frame=20 ms. Telefonía banda ancha para redes fijas y
móviles 3G.
Broadband (kbit/s): 10.9, 11.5, 12.1, 12.7, 13.3,
13.9, ..., 23.0, 23.8.
VMR-WB. Códec 3GPP2. Telefonía banda ancha para
redes cdma2000. 13.3/6.2/2.7/1 kbit/s. Frame=20 ms.
ITU-T G.729.1. 8-32 kbit/s scalable wideband
speech and audio coding.
75
76
Algunos códecs de video
Tipos de Ondas PCM
H.261. Videotelefonia H.320 (ISDN)/H.323
Cuando a un dígito binario se aplica modulación de
pulsos la onda resultante es una onda PCM binaria.
H.263. H.263+. 64 a 16384 kbit/s (720x576). Para
videotelefonia H.323/SIP. Usados en broadcast y
streaming en MMS en servicios 3GPP.
Cuando a un dígito no binario se aplica modulación
de pulsos la onda binaria resultante se denomina
onda PCM M-aria (e.g. PAM).
MPEG4 video.
H.264. Para videotelefonia H.323/SIP. Usados en
broadcast y streaming en MMS en servicios 3GPP.
Es una versión mejorada de H.263.
77
78
Bits por palabra PCM y bits por
símbolo
Ondas PCM M-arias
Es importante no confundir la idea de bits por palabra PCM
con el concepto de transmisión multinivel (M niveles) de k
bits por símbolo.
Para palabra PCM L = 2l, donde L es el número de niveles
de cuantificación, y l es el número de bits que se necesita
para representar cada nivel.
Transmisión multinivel M = 2k, donde M es el tamaño del
conjunto de símbolos, y k es el número de bits que se
necesita para representar cada símbolo.
79
80
Tamaño palabra PCM
Cuántos bits asignar a una muestra análoga?
V pp
V pp
q
emax = =
2 2 L1 2 L
e p V pp
V pp
p V pp
2L
l
2 = L
llog 2
Transmisión Banda Base
1
niveles
2p
Codificación de Línea
1
bits
2p
El número de niveles o de bits por muestra depende de cuánta
distorsión de cuantificación se va tolerar con el formato PCM
81
82
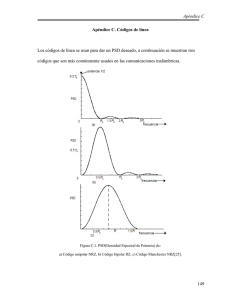
Clasificación códigos de línea
Representación de Dígitos Binarios
+V
1
0
1
1
0
0
0
1
1T
2T
3T
4T
5T
6T
7T
8T
1
1
0
0
Existen códigos de nivel y códigos por transición, códigos
con memoria y sin memoria. Se pueden identificar, entre
otras, las siguientes familias:
Polar NRZ
-V
9T 10T 11T 12T
No retorno a cero (NRZ)
NRZ-L (lógica digital)
El término line coding proviene de la era de la telefonía
clásica.
NRZ-M (grabación de cintas magnéticas)
NRZ-S
Retorno a cero (RZ): Ampliamente usados
transmisión de datos, y grabación magnética
en
RZ-Unipolar
RZ-Bipolar
RZ-AMI (sistemas telefónicos)
83
84
Fase Codificada: Estos esquemas se utilizan en sistemas
de grabación magnética, comunicaciones ópticas y
algunos enlaces de telemetría satelital.
bi--L
1
0
1
1
0
0
0
1
1
1
0
Unipolar NRZ
T
2T
3T
4T
5T
6T
7T
8T
9T
10T
11T
(a.k.a Manchester coding)
Unipolar RZ
bi--M
bi--S
Polar NRZ
Delay Modulation (DM) (a.k.a Miller Coding)
Bipolar (AMI)
Binaria Multinivel: tres niveles en vez de dos. Además
de RZ bipolar y RZ-AMI están:
Manchester (Bi-phase)
Dicode NRZ
Dicode RZ
Delay Modulation
Duobinary
85
1
0
1
1
0
0
0
1
1
1
86
0
Porqué tantas ondas PCM?
Split Phase (Mark)
Split Phase (Space)
Componente DC
Contenido de temporización (timing)
Uso del espectro (ancho de banda)
Sensibilidad a inversión de polaridad
(Codificación Diferencial)
Inmunidad al ruido (probabilidad de error)
Detección de errores
Transparencia a los datos
Bi- Phase (Mark)
Bi-Phase (Space)
Code Mark Inversion
T
2T
3T
4T
5T
6T
7T
8T
9T
10T
11T
NRZ (M)
NRZ (s)
87
88
Unipolar NRZ
1
0
T
11T
1
2T
1
3T
0
4T
0
5T
0
6T
2
1
7T
1
8T
1
9T
0
Pe =
10T
1
erfc
2
Eb
2N0
T = 1/R
First-null bandwidth: R Hertz
Desventajas: secuencias largas de 0s y 1s, componente
DC, Pe menor que sistemas polares, no permite
detección de errores.
0 .2 5
0 .1 0
0 .0 5
Si R = 64 kbps con la cadena 01010101.... existirá
componente frecuencial a 64 kHz?
4
2
2
2
1
1
0
0
0
1
4
90
2
V T sin f T / 2
S 2 f =
16
f T /2
Unipolar RZ
0
2
V
f 4
0 .1 5
89
1
2
0 .2 0
V T sin f T
S1 f =
4
fT
1
1
2
[
2
1
V
f 2 n1 R
f 2
2
4 4
n= 2n 1
0
]
0 .2 5
0 .2 0
T = 1/R. Presencia de componente discreta a 1/T.
First-null bandwidth: 2R Hertz.
Desventajas: secuencias largas de 0s y 1s, componente
DC, Pe peor en 3 dB que unipolar NRZ, no permite
detección de errores.
0 .1 5
0 .1 0
0 .0 5
Si R = 64 kbps con la cadena 01010101.... existirá
componente frecuencial a 64 kHz?
91
4
2
2
4
92
NRZ Polar
Señalización del tipo Pulso/No-pulso
1
0
1
1
0
0
0
1
1
1
0
En general para señalización del tipo Pulso/No-pulso:
2
S PNP f = p1 p RG f 2
p R
2
G nR2 f nR
Cuando P(1) = p, (p diferente de 0.5), existe componente DC
y la PSD está dada por
n=
sin f T
S 3 p f =4 V T p 1 p
fT
2
2
2
2
V 12 p f 93
Pe =
p = 1/2:
sin f T
S 3 f =V T
fT
2
2
1
erfc
2
94
RZ Polar (bipolar, AMI o
seudoternario)
Eb
N0
1
1 .0
0
1
1
0
0
0
1
1
1
0
0 .8
0 .6
0 .4
Este código es un código con memoria. Su PSD está dada por:
0 .2
4
2
1cos 2 f T
S 4 p f =2 p1 p RG f 2
12 p1 22 p1 cos 2 f T
2
2
2
4
95
96
Cuando p = 0.5, se usan pulsos cuadrados de amplitud ±V,
y duración T/2 segundos, la PSD se vuelve:
RZ (AMI) bipolar
2
V 2 T sin f T /2
2
S 4 f =
sin f T 4
f T /2
3
P e erfc
4
0 .2 0
0 .1 5
Eb
,
2N0
E b / N 02
0 .1 0
0 .0 5
3
2
1
1
2
3
97
98
Manchester
1
0
1
1
0
0
0
1
1
1
0
Cuando P(1) = p, (p diferente de 0.5), la amplitud de la
parte continua de la PSD se reduce y aparecen componentes
discretas a múltiplos enteros de la bit rate, R=1/T.
La transición negativa o positiva en la mitad del periodo
de bit indica un 1 ó 0 respectivamente.
Tiene este código memoria? Permite detectar errores?
Usado en 10 Mbps Ethernet.
PSD con símbolos fuente igualmente probables:
2
sin f T /2
2 f T
S 5 p f =V T 4 p 1 p
sin
2
f T /2
2
2
2
V 12 p
n=, n0
2
2
f nR
n
2
sin f T / 2
2
S 5 f =V T
sin f T / 2
f T /2
2
99
100
Manchester
PSD para esquemas antipodales
0 .5
g2(t)= -g1(t)
0 .4
Ejemplos: Manchester, NRZ Polar.
0 .3
2
S BP f =4 p 1 p RG f 0 .2
2
2 p1 R
0 .1
2
G nR2 f nR
n=
4
2
2
4
|G( f )| es la magnitud de la FT de g1(t) ó g2(t)
101
Delay modulation (código Miller)
1
0
1
1
0
0
0
1
1
1
102
PSD con símbolos fuente igualmente probables:
V2T
S 6 f =
2 f T 2 178 cos 2 f T 0
×( 232 cos f T 22 cos 2 f T
12 cos 3 f T 5cos 4 f T 12 cos 5 f T
2 cos 6 f T 8 cos 7 f T 2 cos 8 f T )
Un 1 se representa mediante una transición en la mitad
del periodo de un bit y un 0 por ausencia de transmisión.
Sin embargo, si un 0 es seguido de otro 0 existe
transición al final del periodo del bit.
103
104
Delay modulation PSD
B6ZS
2 .0
Si el último pulso fue positivo (+), el código especial es 0 + - 0 - +
Si el último pulso fue negativo (-), el código especial es 0 - + 0 + 1 .5
0
0
1 .0
0
0
0
+
0
-
0
0
0
-
0
+
1
-
1
+
0
0
1
-
0
0
0
-
0
+
0
0
0
+
0
-
1
+
1
-
Reglas de sustitución B3ZS
0 .5
2
2
Numero de Pulsos B
desde última violación
Polaridad del
último pulso B
Odd
Odd
Even
Even
Negative ( - )
Positive ( + )
Negative ( - )
Positive ( + )
Código de
sustitución
0000+
+0+
-0-
forma de
sustitución
00V
00V
B0V
B0V
4
105
106
Comparación BEP
0.30
(T/4)
2
0.25
Unipolar NRZ
Unipolar RZ
10-1
5
2
Unipolar NRZ
0.20
Bipolar (AMI)
10-2
PSD / V2T
Bit Error Probability, Pe
4
1
+
5
2
Atributos
espectrales
de algunas
ondas PCM
AMI (Bipolar)
0.15
10-3
Polar NRZ
Manchester
5
0.10
(T/16)
2
10-4
T /4 2 0.05
Unipolar RZ
5
2
0.00
10-5
0.0
0.5R
1.0R
1.5R
2.0R
Frequency, f (Hz)
5
2
10-6
0
2
4
6
8
10
SNR per bit, Eb/N0 (dB)
12
14
107
108
Algunas Fuentes de Corrupción
2.5
PSD / V2T
2.0
Efectos de cuantización y
muestreo
1.5
Ruido de cuantificación
Delay Modulation
Saturación del cuantificador
Polar NRZ
1.0
Inestabilidad Base de
Tiempo (timing jitter)
0.5
Efectos del Canal
Ruido del canal (efecto
umbral)
Interferencia Intersimbólica
(ISI)
Manchester
0.0
0.0
0.5R
1.0R
1.5R
2.0R
Frequency, f (Hz)
109
Bibliografía
Sklar, B. Digital Communications, Fundamentals and
Applications (2nd Edition). Prentice Hall, 2002.
J. D. Gibson (editor in chief), The Mobile
Communications Hanbook, Second Edition, CRC Press,
1999.
A. Bruce Carlson, Communication Systems: An
introduction to Signals and Noise in Electrical
Communications, McGraw-Hill, 1986.
111
110