2_InformeProctor. - U

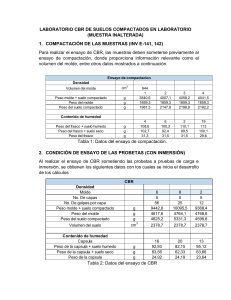
1. Ensayo Proctor Modificado
Procedimiento
Para realizar en este laboratorio el ensayo de proctor modificado se dividió el curso en 6 grupos
que trabajaron cada grupo con la misma muestra de suelo, pasada por el tamiz #4 para eliminar
las partículas grandes, pero a humedades distintas para ahorrar tiempo.
A nuestro grupo se le asignó trabajar con una humedad del suelo de un 8,5%. Para lograr esta
humedad se le vertió 595 mL de agua a los 7kg de suelo para lograr una muestra de 8,5% de
humedad. Luego se revolvió la mezcla con el propósito de lograr una muestra homogénea.
Ya con la muestra lista, se procedió a pasar el proceso de compactación, Este proceso consistía en
el uso de un martillo con dimensiones y pesos normados (peso de 44,5 kN) y se dejaba caer de una
altura de 45,7 cm. Además se utilizó un molde de medidas y peso conocidos y se llenó con 6 capas
de la muestra donde para cada capa se procedió a golpear con el proctor 56 veces.
Ya terminado con la compactación se enraso el molde con tal de que no quedara muestra que
sobresaliera del molde. Luego se fue a pesar el molde con la muestra de suelo y como ya se
conocía el peso del molde se puede calcular el peso del suelo.
Por último para calcular el valor real de la humedad del suelo, se sacó una muestra del molde que
se pesó y se pesaría después de secarlo en un horno para tener así con la diferencia el peso del
agua que tenía el suelo.
Resultados
Con los datos obtenidos tuvimos que calcular primero la humedad real para luego poder calcular
las densidades. Se utilizaron las siguientes formulas y se obtuvieron los siguientes resultados que
se muestran en las tablas de a continuación.
Humedad:
𝑤=
𝑊𝑎𝑔𝑢𝑎
𝑊𝑠𝑢𝑒𝑙𝑜 ℎ𝑢𝑚𝑒𝑑𝑜 − 𝑊𝑠𝑒𝑐𝑜
=
𝑊𝑠𝑢𝑒𝑙𝑜 𝑠𝑒𝑐𝑜
𝑊𝑠𝑢𝑒𝑙𝑜 𝑠𝑒𝑐𝑜
Densidad seca:
𝛾𝑑 =
𝛾𝑡
1+𝑤
(𝐈𝐈)
(𝐈)
Densidad total:
𝛾𝑡 =
#
1
2
3
4
5
6
capsula + suelo
capsula humedo
96,17
366,89
90
274
77,93
468,71
72
296,52
78
216
72
534
1
2
3
4
5
6
humedad
aparente
2,5
5
6,5
7
8,5
9,5
#
𝑃𝑒𝑠𝑜 𝑠𝑢𝑒𝑙𝑜 ℎú𝑚𝑒𝑑𝑜
𝑉𝑜𝑙𝑢𝑚𝑒𝑛
(𝐈𝐈𝐈)
peso
capsula +
suelo seco
agua
suelo seco
358,95
7,94
262,78
263,78
10,22
173,78
443,31
25,4
365,38
281,27
15,25
209,27
204,88
11,12
126,88
491,9
42,1
419,9
real
molde+suelo
3,02153893
7290
5,88099896
7794
6,95166676
7994
7,28723658
7982
8,76418663
7976
10,0261967
7950
humedad
3,02153893
5,88099896
6,95166676
7,28723658
8,76418663
10,0261967
pesos
volumen molde densidad
molde suelo
humeda
3032 4258
2105,56 2,02226486
3080 4714
2121,65 2,22185563
3058 4936
2126,96 2,32068304
3096 4886
2126,96 2,29717531
3124 4852
2123,2 2,28522984
3133 4817
2124,32 2,26754915
seca
1,96295346
2,09844604
2,1698428
2,14114501
2,10108668
2,0609175
Luego para obtener la densidad seca máxima, se ajusto a una curva polinomio de segundo orden
que nos da la siguiente curva con su siguiente ecuación.
2.2
2.15
y = -0.0103x2 + 0.1484x + 1.606
R² = 0.9352
2.1
Series1
2.05
Poly. (Series1)
2
1.95
1.9
0
5
10
15
Para obtener las curvas de saturación se utilizó la siguiente formula:
𝛾𝑑 =
𝐺 ∗ 𝛾𝑤
𝑤∗𝐺
1+ 𝑆
(𝐈𝐕)
Donde:
G:
Densidad específica
𝛾𝑤 :
Densidad del agua = 1 [g/cm^3]
𝑤:
Humedad
S:
Saturación
Para obtener la densidad especifica supusimos que la densidad seca saturada correspondiente a la
humedad optima es un 5% mayor que la densidad máxima seca dándonos la siguiente ecuación
𝑔
𝛾𝑑 𝑆𝑎𝑡 = 0,05 ∗ 𝛾𝑑 𝑚𝑎𝑥 + 𝛾𝑑 𝑚𝑎𝑥 = 0,05 ∗ 2,139 + 2,139 = 2,246 [ 3 ]
𝑐𝑚
Y de la ecuación (IV) se despeja para obtener la siguiente ecuación
𝐺=
𝛾𝑑
𝛾 ∗𝑤
𝛾𝑤 − 𝑑 𝑆
(𝐕)
Lo que nos dio un
G = 2.679
Luego, al graficar la curva de saturación, se observó que ésta queda sobre la curva obtenida del
ensayo Proctor, por lo que no fue necesario hacer cambios a G.
Conclusiones
2.1 Resultados ensayo Proctor modificado
De acuerdo a lo obtenido en el informe se observa que la curva que se obtiene cumple con la
teoría y lo único como fuera de lo esperado que se observa es uno de los puntos que se desvia
bastante de la curva calculada. Esto se podría deber a un mal procedimiento del proctor efectuado
por ese grupo.
Otro punto a destacar es que al imponer o suponer que la densidad saturada es un 5% mayor a la
densidad optima nos lleva a una aproximación de G, lo que lleva también a un error de las curvas
de saturación, por lo tanto no es una representación exacta.