Año 2004 - Seminario 18

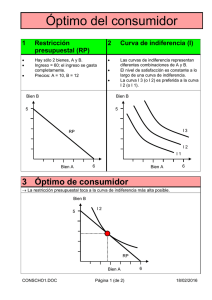
Seminario 18
Curso 2004.
Parte A
Se supone la existencia de un consumidor h cuyo ingreso es de 1000 unidades monetarias (Yh = $1000).
Dicho consumidor gasta totalmente su ingreso en la adquisición de dos bienes (1 y 2) cuyos precios
respectivos son p1 = $1 y p2 = $1, datos provenientes del mercado. Se supone además que la función de
utilidad del consumidor h responde a la siguiente expresión: Uh = X1 . X2, donde Uh representa los niveles
de utilidad y Xi las cantidades consumidas del bien i.
Teniendo en cuenta los datos arriba mencionados, se pide:
1) Determinar el punto que indica la posición de equilibrio del consumidor h.
2) Suponiendo que el nivel de ingreso del consumidor h pasa a ser de $2000, determine el nuevo
punto de equilibrio. Calcular para ambos bienes el efecto ingreso.
3) Suponiendo un cambio permanente en el nivel de ingresos del consumidor h, determine la curva
de ingreso – consumo y señale sus posibles formas en función del tipo de bien de que se trate.
4) Se supone que el conjunto de datos que determinaron la conducta del consumidor del ítem 1)
sufre algunos cambios. Siendo ahora Yh = 1000, Uh = X1 . X2, pero varían los precios relativos
de los bienes pasando a ser ahora p1 = $1 y p2 = $2. Determinar el punto que corresponde a la
nueva situación de equilibrio en la que se situará el consumidor h debido a la variación de p2.
Parte B
1) Obtener gráficamente la curva de precio – consumo y la curva de demanda del consumidor h por
el bien 2 en base a los puntos de equilibrio correspondientes a los siguientes precios para dicho
bien: p2 = $0,5; p2 = $1; p2 = $2.
2) Suponiendo que el mercado está integrado por mil consumidores cuyos comportamientos
respectivos son análogos al del consumidor h y además poseen el mismo ingreso ($1000),
determinar la curva de demanda agregada por el bien 2.
Parte C
C.1. Elasticidad – ingreso de la demanda.
Se supone que, ante diferentes ingresos, un consumidor k se comporta en relación a las compras de los
bienes A, B y C de acuerdo a lo que indica el siguiente cuadro:
Ingreso
$10
$20
$30
$40
$50
Cantidad demandada
del bien A
20
28
34
38
40
Cantidad demandada del
bien B
20
25
26
20
10
Cantidad demandada del
bien C
120
270
600
1400
3500
Se pide:
1) Calcular la elasticidad – ingreso de la demanda de cada uno de los bienes para los intervalos (10
– 20) y (40 – 50).
2) Indicar el tipo de elasticidad calculado en cada caso y asimismo indicar cómo se designan los
bienes cuyas demandas tienen tal tipo de elasticidad.
C.2. Elasticidad – precio de la demanda.
C.2.1. Cálculo de la elasticidad – precio cuando se conoce la función de demanda:
A partir de la función de demanda de la Parte B, calcule la elasticidad – precio de la
por el bien 2 (o por el bien genérico i).
demanda
C.2.2. Cálculo de la elasticidad – precio cuando se conocen solamente datos sobre
precio y cantidad demandada:
Se supone que un consumidor, ante variaciones en los precios del bien i tiene el comportamiento
indicado a continuación:
Precio
Cantidad demandada
Gasto
$1
500
$500
$2
250
$500
$4
125
$500
$5
100
$500
Se pide:
1) Calcular la elasticidad – precio de la demanda (en el punto y en el arco) de dicho bien para los
intervalos (1 – 2) y (5 – 4).
2) Indicar el tipo de elasticidad de que se trata en cada caso.
3) Analizar qué relación existe entre el valor de la elasticidad – precio y el gasto del consumidor.
C.2.3. Elasticidad – precio cruzada.
Sabiendo que la demanda del bien A aumenta un 10% cuando el precio del bien
B desciende en un 5% y que aumenta en la misma proporción cuando el precio
del bien C aumenta en un 2%:
Se pide:
1) Calcular la elasticidad – precio cruzada de los bienes A y B y de los bienes A y C.
2) Señalar en base al resultado obtenido, qué relación existe entre dichos bienes.
Solución al Seminario 18
Curso 2004.
Parte A
1) Datos: Yh = $1000
p1 = $1
p2 = $1
Uh = X 1 . X 2
De acuerdo a los datos que se poseen, podemos determinar la ecuación de la recta de
balance, instrumento gráfico que supone dados los precios de los bienes (p1 y p2), el
ingreso nominal del consumidor individual (Yh), bajo el supuesto del gasto total de
dicho ingreso en bienes de consumo.
De la función de utilidad se obtienen las curvas de indiferencia. Cada una de ellas
representa las diferentes combinaciones de ambos bienes que le brindan al individuo el
mismo grado de satisfacción o utilidad (U). De dichas curvas de indiferencia se obtiene
la relación o tasa marginal de sustitución TMS, la que indica las posibles sustituciones
en el consumo de ambos bienes de modo que el “ingreso real” o nivel de utilidad total
no cambie (lo que se representa al moverse a lo largo de una curva de indiferencia
dada).
La pendiente negativa de las curvas de indiferencia nos permite expresar que siempre
que se quiera aumentar el consumo de uno de los bienes tenga que reducirse el consumo
del otro, este “doble movimiento” provocará que a la par que uno de los bienes
“adiciona” bienestar, satisfacción o utilidad, el otro la “sustrae”. Esto se expresa tanto
en el caso de curvas de indiferencia lineales como en las convexas.
La convexidad, sin embargo, agrega otra concepción teórica más: ella expresa que la
teoría asume que las utilidades marginales respectivas de los dos bienes cambian (es
decir, no son constantes sino variables) al aumentar el consumo de uno y disminuir el
del otro de tal manera que las “ganancias” y “pérdidas” de utilidad total debidas a ese
movimiento contrapuesto en el consumo podrían compensarse. Dicho de otra manera,
una persona puede sentirse sistemáticamente no afectada por la reducción continua en el
consumo de un bien si es debidamente compensada por aumentos más que
proporcionales en el consumo de otro (aunque, se advertirá, la reducción continua
tolerable, en la generalidad de los casos, no llega a tanto como para admitir exista
compensación alguna a la posibilidad de la privación total o de la renuncia absoluta al
consumo de alguno de ellos: es decir, sin admitir la especialización o el consumo nulo
de uno de los dos bienes).
Las utilidades marginales respectivas las expresamos por medio de la derivada primera
de la utilidad total respecto al bien en cuestión (∂U/∂Xi). La TMS sustitución puede
expresarse como el cociente, ratio o relación de las utilidades marginales de ambos
bienes.
El punto de equilibrio del consumidor es aquel donde obtiene la máxima satisfacción
posible. Posible pues pertenece a su recta de balance y máxima pues corresponde a la
curva de indiferencia más alejada del origen que el consumidor puede alcanzar. Tal
punto se representa mediante el punto de tangencia entre la recta de balance y una curva
de indiferencia. Se trata, pues, de determinar el nivel de preferencia Uh, en el cual el
consumidor alcanza su equilibrio.
a) Uh = X1 . X2
es la curva de indiferencia
b) Yh = p1 X1 + p2 X2 ⇒ X1 = (Yh / p1) – (p2 / p1) . X2 es la recta de balance
c) La condición de primer orden para maximizar Uh condicionado o sujeto a Yh viene
dada por la igualación, en valores absolutos de la TMS y el cociente de precios o
precios relativos, la primera obtenida de la función de utilidad, el segundo de la
restricción presupuestaria, y es:
TMS = precios relativos
Donde
TMS = - ∂U/∂X2 / ∂U/∂X! = - ∂X1/∂X2
Precios relativos = – p2 / p1
Los que tomamos en valor absoluto, dado que los signos negativos se cancelan al
igualar y expresamos la condición de primer orden o punto de tangencia como
∂X1/∂X2 = p2 / p1
Alternativamente puede procederse como sigue.
Expresando las pendientes o ecuaciones marginales de (a) y (b), tenemos:
a’) Uh = X1 . X2
⇒
X1 = Uh / X2 (este arreglo es el que se toma para
graficar)
∂X1/∂X2 = – Uh / X22 = – X1 . X2 / X22 = – X1 / X2
tasa marginal de sustitución (TMS)
b’) ∂X1/∂X2 = – p2 / p1
precios relativos
Igualando la TMS (a’) con los precios relativos (b’):
– X1 / X2 = – p2 / p1 ⇒ X1 / X2 = p2 / p1
Que es la expresión analítica de la condición de equilibrio. Aquí, la TMS mide la
disposición del sujeto a cambiar o renunciar a consumir cierta cantidad de un bien a
cambio de adicionar a su consumo una unidad (o más precisamente un aumento
infinitesimal) del otro, de tal manera que se mantenga el nivel de utilidad o satisfacción
total. Por su parte, los precios relativos indican las posibilidades de sustitución
económica o de cambios entre dichos bienes que el mercado permite.
En definitiva, lo que el consumidor desea comprar debe ser igual a lo que puede
comprar en el mercado. En otras palabras, dentro de sus posibilidades económicas
(dadas por los precios relativos y su ingreso) elige la canasta de bienes que más le
satisface.
Finalmente, todo lo anterior se sintetiza en la función de demanda individual de cada
bien. Estas se obtienen de despejar, respectivamente, Xi en la condición de equilibrio
encontrada y sustituir en la ecuación de la recta de balance o restricción presupuestaria.
Así, para la función específica de utilizada con que venimos trabajando aquí, tenemos:
X1 = X2 p2 / p1
Yh = p1 (X2 p2 / p1) + p2 X2
o
X2 = X1 p1 / p2
Yh = p1 X1 + p2 (X1 p1 / p2)
Yh = 2 p1 X1
Yh = 2 p2 X2
De donde las respectivas funciones de demanda serán:
X1Dh = Yh / 2 p1
X2Dh = Yh / 2 p2
Con los datos del problema se obtiene la siguiente elección de consumo para el sujeto h:
X1E = 500
∴ Uh = 250 000
X2E = 500
2) Efecto ingreso: es el nombre técnico que usualmente se da al efecto que una
variación del ingreso tiene sobre la conducta del consumidor, considerados constantes
los precios de los bienes.
Con Yh = $2000 y sin cambios en los precios, la elección óptima del individuo h es:
X2E = 1000
X1E = 1000
∴ Uh = 1 000 000
3) Representación gráfica de la curva de ingreso – consumo
X1
2000
Curva de ingreso – consumo
1000
E’
500
E
0
500
1000
2000
X2
Se observa en el gráfico anterior que la curva de ingreso – consumo correspondiente al
consumidor h tiene inclinación positiva, indicando que el consumo de ambos bienes
aumenta al aumentar Y. Ambos bienes son de la misma categoría, en concreto, son
bienes cuya cantidad demandada varía en forma proporcional a las variaciones en el
ingreso (el ingreso se duplicó y lo mismo ocurrió con las cantidades demandadas).
También se pueden concebir curvas de ingreso – consumo del tipo de las que se
incluyen en el siguiente gráfico.
X1
Bien 2: inferior
Bien 1: inferior
0
X2
Las cuales indican que a partir de cierto punto, al aumentar el ingreso, el consumo de
uno de los bienes se reduce considerablemente. Se denomina bienes inferiores a los
bienes que se adquieren en menor cantidad cuando el ingreso aumenta.
4) Datos: Yh = $1000
p1 = $1
p2 = $2
Uh = X 1 . X 2
La elección óptima será ahora:
X1E = 500
X2E = 250
∴ Uh = 125 000
Parte B
1)
Determinación gráfica de la curva de demanda individual por el bien 2
X1
1000
E’’’
500
E’’
0
250
Curva de precio – consumo
E
500
1000
2000 X2
p2
$2
$1
X2Dh = 1000 / 2p2
$0,5
0
250
500
1000
X2
2) La demanda agregada correspondiente a 1000 consumidores idénticos al individuo h.
Demanda individual: X2Dh = 1000 / 2p2 = 500 / p2
Demanda agregada: X2DA = 1000 . 500 / p2 = 500 000 / p2
p2
$2
$1
X2Dh
$0,5
0
250
500
X2DA
1000
250 000
500 000
1 000 000
X2
Nota: las líneas cruzadas sobre el eje de abscisas indican el cambio de escala.
Parte C
C.1. Elasticidad – ingreso de la demanda
1) y 2)
εY = (∆Xi / Xi) / (∆Y / Y) = (∆Xi / ∆Y) · (Y / Xi)
Bien A:
Intervalo 10 – 20: εY = (8 / 10) . (10 / 20) = 0,40 (demanda parcialmente inelástica)
Intervalo 40 – 50: εY = (2 / 10) . (40 / 38) ≅ 0,21 (demanda parcialmente inelástica)
Bien B:
Intervalo 10 – 20: εY = (5 / 10) . (10 / 20) = 0,25 (demanda parcialmente inelástica)
Intervalo 40 – 50: εY = (-10 / 10) . (40 / 20) = -2 (demanda regresiva)
Bien C:
Intervalo 10 – 20: εY = (150 / 10) . (10 / 120) = 1,25 (demanda parcialmente elástica)
Intervalo 40 – 50: εY = (2100 / 10) . (40 / 1400) = 6 (demanda parcialmente elástica)
Donde los bienes se clasifican de la siguiente manera:
superiores o suntuarios: εY > 1
normales: 0 < εY < 1
inferiores: εY < 0
C.2. Elasticidad – precio de la demanda
∂X / X
∂X
η=– = ·
∂p / p
∂p
p
X
C.2.1. Cálculo de la elasticidad – precio para la función de demanda de la Parte B.
∂X1 /∂p1 = (– Yh / 2p1 ) ⇒
2
η=–
-Yh
p1
·
2p12
=
X1
2p12 X1
(2p1X1) · p1
=
2p12 X1
= 1
2p12 X1
La función de demanda de la Parte B –tanto la individual como la agregada– tiene
elasticidad unitaria en todo el recorrido de la misma, lo que implica que el gasto por el
bien en cuestión no varía ante cambios en su precio.
C.2.2. Cálculo de la elasticidad – precio cuando se conocen solamente datos sobre
precio y cantidad demandadas.
1) y 2)
Elasticidad en el punto:
η = – (∆X i / Xi) / (∆pi /pi) = – (∆Xi / ∆p i) · (pi / Xi)
Intervalo 1 – 2: η = – (–250 / 1) . (1 / 500) = 0,5 (demanda parcialmente inelástica)
Intervalo 5 – 4: η = – (25 / –1) . (5 / 100) = 1,25 (demanda parcialmente elástica)
Elasticidad en el arco:
η=–
∆Xi
·
∆pi
∆Xi
(piA + piB) / 2
=–
(XiA + XiB) / 2
(piA + piB)
·
∆pi
(XiA + XiB)
Donde los subíndices piA y piB representan, respectivamente, el precio del bien i antes y
después del cambio en el mismo.
Intervalo 1 – 2: η = – (–250 / 1) . [(1+2) / (500 + 250)] = 1
Intervalo 5 – 4: η = – (25 / –1) . [(4+5) / (100 + 125)] = 1
El cuadro presentado en esta sección C.2.2 muestra que el gasto del consumidor no
cambia ante cambios en el precio del bien; esto estaría indicando que la demanda del
consumidor por este bien es de elasticidad unitaria. Los cálculos anteriores muestran
que la elasticidad “en el arco” es una mejor aproximación a la elasticidad de la función
que la elasticidad “en el punto”.
3) Ver cuadro de relaciones entre elasticidad – precio y gasto del consumidor en el
repartido teórico.
C.2.3. Elasticidad – precio cruzada
εXi, pj = (∆Xi /Xi) / (∆pj/ pj)
con Xi = cantidad demandada del bien “i”
pj = precio del bien “j”
1)
Para los bienes A y B: εXA, pB = 0,1 / (–0,05) = – 2
Para los bienes A y C: εXA, pC = 0,1 / (0,02) = 5
2) Dado que la elasticidad – precio cruzada de los bienes A y B es negativa cabe pensar
que dichos bienes son complementarios; en cambio, es de esperar que los bienes A y C
sean sustitutivos.