V - Ipen.br

Sp ISSN 0081-3397
por
G. Vefarde
Toda correspondencia en relación con este trabajo debe dirigirse al Servicio de Documentación Biblioteca y
Publicaciones, Junta de Energía Nuclear, Ciudad Universitaria, Madrid-3, ESPAÑA.
Las solicitudes de ejemplares deben dirigirse a
este mismo Servicio.
Los descriptores se han seleccionado del Thesauro
del INIS para describir las materias que contiene este info£
me con vistas a su recuperación. Para más detalles cónsul
tese el informe IAEA-INIS-12 (INIS: Manual de Indización) y
IAEA-INIS-13 (INIS: Thesauro) publicado por el Organismo
Internacional de Energía Atómica.
Se autoriza la reproducción de los resúmenes analíticos que aparecen en esta publicación.
Este trabajo se ha recibido para su impresión en
Febrero de 1976
Depósito legal n2 M-14592-1976
I.S.B.N. 84-500-7555-6
JEN 334
ECUACIONES INTEGRODIFERENCIALES E INTEGRALES NORMALES
Y ADJUNTAS DEL TRANSPORTE DE NEUTRONES
PARTE I
Guillermo Velarde
ÍNDICE
i.
II.
III.
Hipótesis simplif icativas
,
1-1
Determinación de los parámetros nucleares
II-l
Ecuaciones Integrodiferenciales de Boltzmann del Transporte
de Neutrones . . , ,
,
III-l
I.- HIPÓTESIS SIMPLIFICATIVAS.
1.- PROBLEMA.
Vado un H.e.actoh. de. con{¡<¿guAac¿ón y compo¿Zc¿ón conodidaé
te. ÁJÚ.CÁ0JL, y dada Za di¿>thÁhuQÁ.ón de. La fuente.
te.,
ne.utn.ón¿ca e.n cada
¿e. pn.eX.znde. deXeJmJjiaA. La de.v\&¿dad {¡¿LóZca newtn.ón¿ca
¿Zco y en. cada
en eL Á.n¿tan_
¿notan-
e.n cada panto ¿ á -
instante,.
1.1.-El problema así planteado, dá lugar a un sistema de ecuaciones integrodiferenciales no lineales, con s i e t e variables independientes: tres de
la posición, tres de la velocidad, y una del tiempo. Estas ecuaciones se
obtienen al establecer el balance de los neutrones, de los núcleos precur
sores de neutrones retardados, de los núcleos obtenidos en el quemado, y
de las magnitudes termohidráulicas del medio.
Las ecuaciones de balance anteriores pueden ponerse en la forma gene
ral
" | | = Bf + Q
(1)
en la cual f es la densidad neutrónica, la densidad de núcleos precursores,
la densidad de núcleos del quemado, o la temperatura; y B el operador de
balance (ganancias menos pérdidas).
2.- DEFINICIONES.
Sea un neutrón incidente o primario de baja energía n', que al interaccionar con el núcleo blanco N ! a través del canal de entrada v', según
la reacción nuclear
n+N,
n'+N'
v=v', dispersión elástica
->• <¡ n+N, v^v1 , dispersión inelástica
b+B,
(2)
captura, fisión
dá lugar a la producción de una partícula b y de un núcleo residual B, a
través del canal de salida v. En particular, en la dispersión se produce un
neutrón secundario n y un núcleo residual N.
2.1.-VARIABLES INDEPENDIENTES.
Además de la variable temporal t, se consideran las siguientes varia-
(1)
Vélarde, G. - Física Nuclear, Vols. I y II - ETSII, Universidad Polite£
nica de Madrid. (1973 y 1975).
I -2-
bles independientes:
->r
_,
. vector posición del neutrón o del núcleo, que representa un punto
del espacio Euclídeo de tres dimensiones, llamado de configuración,
y perteneciente al subespacio constituido por el reactor considera_
do R, reí?.
v=vQ vector velocidad del neutrón o del núcleo, que representa un punto
del espacio Euclídeo de tres dimensiones, llamado de velocidades
1/xfi, vgl/, QeQ, siendo ü la superficie esférica de radio unidad.
De este modo (r,v) será un punto del espacio de las fases R
El superíndice ' se empleará para indicar la velocidad del neutrón
incidente o primario, y la del núcleo blanco; y sin prima para indicar
la velocidad del neutrón secundario, y la del núcleo residual.
Los subíndices n y N se emplearán para las magnitudes correspondientes al neutrón y al núcleo; y los L y C para las magnitudes referidas a los sistemas del laboratorio y del centro de masas. En particular,
con objeto de simplificar la notación, se suprimirán los subíndices Ln,
es decir, v=vT .
Ln
Según la clase de problema considerado, se empleará el módulo de la
velocidad v, la energía cinética E-U, o la letargía u del neutrón. Para
neutrones no relativistas, en una región de energía potencial nula
U=0,
tal como se establecerá en las Hipótesis I y II de los §3.1 y §3.2, las
magnitudes anteriores estarán relacionadas entre sí, por
E = i v2,
u = ln -£• = 2 ln —
1
2
siendo E_ = y v
(3)
„
una energía de referencia. La relación entre los elemen-
tos diferenciales será entonces
dv = v2dvdfi,
du = u2dvdfi,
dE = vdv,
du = - ^ dE = - — dv
O)
habiéndose tomado la masa del neutrón como unidad de masa.
2.2.-FUNCIONES DE DENSIDAD.
n(r,v,t)drdv
Numero probable de neutrones, que en un instante t están
situados dentro del elemento de volumen fásico drdv en el
punto fásico
n(r,v,t)
r,v ERxfxfi.
Densidad fásica neutrónica.
I -3-
-,v,t)=vn(r,v,t)
Densidad fásica de flujo neutrónico, o densidad de
flujo, o simplemente flujo.
Número probable de núcleos de la especie i (i_sótopos),
que en el instante t están situados dentro del delemen
to de volumen fásico drdv T W en el punto fásico r,vT
e
e R x v x n.
Densidad fásica de núcleos de la especie i, o simplemente densidad de núcleos i.
Número probable de núcleos precursores de neutrones
retardados (diferidos) producidos en la fisión induci
da por neutrones de velocidad v ! en núcleos i de velo
cidad v' , que en el instante t, están situados dentro
del elemento de volumen de configuración dr, en el pun
to r e R, multiplicado por la probabilidad de que el
precursor emita un neutrón.
C (r,v',v' ,t)
Densidad de núcleos precursores de neutrones retardados, o simplemente densidad de precursores.
X (v',t'->v,t ;v' .)dvdt
Probabilidad de que un neutrón incidente o primario
de velocidad v', habiendo producido en el instante
t' un proceso de la clase x con un núcleo de la especie i, de velocidad v' , dé lugar a la emisión de un
neutrón secundario en el intervalo de tiempo dt en t,
y situado dentro del elemento de volumen de velocidades dv en el punto v £ V x ü.
i ,->•
->
->•
X (v ,t'->v,t;v'^.)
Espectro de los 'neutrones secundarios.
El superíndice i indica el núcleo de la especie i, o simplemente núcleo
i, que sufre el proceso de la clase x.
El subíndice x representa la clase de proceso producido en la reacción
nuclear: el (elástico), in (jmelástico) , s (dispersión, scattering) -> el+in,
c (captura), f (fisión), a (absorción) -> c+f, t (total) -> a+s; o el proceso
de obtención de los neutrones secundarios: el (elástico), in (inelástico), p
(instantáneos de fisión, prompt) , d (retardados de fisión, diferidos).
2.2.1.- Si f = n, (j), N
es una de las funciones de densidad definidas anterior_
mente, se verifica
f(v)dv = f(u)du = f(v,fi)dvdfi = f(u,fi)dudft = f(E,fi)dEdP.
(5)
I -l+-
y según (M-), resulta
.3
2
f(u,ft) =u f(í) =-^~ f(v) = - J f(v) = - I f(v,ft) = - E f(E,Q)
(6)
Si 1/ c 1/ es un intervalo g de velocidades, se empleará la siguiente
notación
f(v,fi)dvdQ = f (ü)d
,
para todo
v e 1/
(7)
f(v,fi)dvdft = f(v)dv
,
para todo
Ü e ü
(8)
En el caso de que f sea isótropa, de (8) resulta
= UTT f(v,fi) = f(v) = > f(v,ü) = ^
f(v)
(9)
2.3.-FUNCIONES FINITAS Y PARÁMETROS.
X (.v1 ,v' )
Constante de desintegración de los núcleos precursores de'neu
trones retardados producidos en la fisión inducida por neutro
nes de velocidad v' en núcleos i de velocidad v' .
v (v',v' )
Número medio de neutrones secundarios producidos por colisión
en el proceso x, entre los neutrones incidentes o primarios de
velocidad v', y los núcleos i de velocidad v' .
a (v,v-w)
Sección eficaz microscópica del proceso x, entre los neutrones
incidentes de velocidad v, y los núcleos i de velocidad
V
TN-
Esta sección eficaz vendrá dada por (11), en función de magnitudes
bien definidas.
Se llama sección eficaz microscópica diferencial a
cT(v',t'-4,t;v¿N) = X^(v',v¿N) X^(v',t'+v5t; v¿ N )
(10)
2.4.-OTRAS FUNCIONES.
2.4.1.- VELOCIDAD DE REACCIÓN.
En el caso de que la interacción se produzca entre un solo neutrón y
un solo núcleo, mediante un proceso biunivoco bien definido, tal como se
establecerá en la Hipótesis III del §3.3, se obtiene que el número de
neutrones que en el-instante t producen en los núcleos i el proceso x,
por unidad de intervalo de las variables (unidades de tiempo, velocidades del neutrón y del núcleo, y de volumen de configuración), es igual
al número de núcleos i que sufren el proceso x por los neutrones, por
1-5-
unidad de intervalo de las variables, e igual al número de procesos x pro_
ducidos por los neutrones en los núcleos i, por unidad de intervalos de
las variables; cuya expresión, llamada velocidad de reacción, puede descom
(1)"
~
ponerse en la forma
[V
= V
[ r n ^ . v . t i p ^ v ^ t ) c^Cv,^)]
(11)
siendo
= V -
v
(12)
VT
LN
el módulo de la velocidad relativa entre el neutrón y el núcleo.
2.4.2.- FRACCIONES Y ABUNDANCIAS DE NEUTRONES.
El número medio de neutrones producidos por fisión, es
v 1 = vt = v 1 + Y vt
r
p
(13)
L d
definiéndose como fracciones de neutrones instantáneos, y de neutrones retardados d, a las razones
i
i
v_
_.
i d
D
V Vj
v3
_.
^ d
i
v
Vd
v
d
i
p
v
y como abundancias relativas de neutrones retardados d,
i _
V
d _ d
y Vj g1
d d
r i_
d
De e s t e modo, e l e s p e c t r o de l o s n e u t r o n e s de f i s i ó n
i _
i
i
r
i i _
i
f
i s
r
valdrá
i QÍ
3.- HIPÓTESIS SIMPLIFICATIVAS PARA LAS ECUACIONES DEL TRANSPORTE DE NEUTRONES.
El sistema de ecuaciones integrodiferenciales que resuelve el problema
considerado, puede simplificarse considerablemente, teniendo en cuenta la
naturaleza del problema físico.
De este modo se introducen una serie de hipótesis simplificativas que
(1)
Velarde, G. - Véase ref. 1, pag. 1.
I -6-
permiten linealizar las ecuaciones, reducir el número de términos de cada
ecuación, reducir el número de ecuaciones, eliminar variables, y obtener
una estructura más sencilla del operador de balance B.
En este párrafo se establecerán la mayoría de las hipótesis simplificativas apropiadas para las ecuaciones del balance neutrónico y de los
precursores de neutrones retardados, y en párrafos posteriores se completarán estas hipótesis, y se establecerán las correspondientes a las ecuaciones del balance de los núcleos del quemado, y de la temperatura.
3.1.-CLASE DE MECÁNICA A EMPLEAR.
En los reactores nucleares la energía media de los neutrones de fisión
es de unos 2 Mev, mientras que la masa del neutrón en reposo es de 939,5
Mev. Por otra parte, la energía media de los núcleos es del orden de la
fracción del ev, mientras que su masa en reposo es igual o superior a la
2
del protón 938,2 Mev. Por t a n t o , en ambos casos se v e r i f i c a que E << m e ,
por lo cual puede considerarse l a h i p ó t e s i s :
¿& 1. - En eJL cÁLcuLo de. hJLa.cXoh.zi, ¿e. apLíca. La mecánica, no hJi_
Lat¿v¿¿£a..
3.2.-TRAYECTORIA DE LOS NEUTRONES.
Como los neutrones no sufren interacción electromagnética, y la inte_
racción fuerte es de muy corto alcance, puede considerarse la hipótesis:
WJjpót<n,ÁÁ II.- EntAz. do¿ coLü>¿onzA ¿UCZAÍVOA
, oJL nz.vJih.on eó-tó ¿omz-
t¿do a. un potencial, nato, poh. Lo que. iu movÁynLznto ¿ZAÓL h.z.cXiLtnz.0 y un¿{¡ohmz..
Come resultado de las Hipótesis I y II se obtienen las ecuaciones (3).
3.3.-DENSIDAD NUCLEAR.
En los reactores nucleares, la razón entre la densidad neutrónica y
la nuclear, es inferior a 10
, por lo que las colisiones más probables
son entre núcleos y entre neutrones y núcleos, siendo despreciables las
colisiones entre neutrones.
Según la teoría cinética de los gases, las colisiones entre neutrones
y núcleos alteran las funciones de distribución, o sea las densidades fási_
cas neutrónica y nuclear, dando lugar a un sistema de dos ecuaciones de
Boltzmann, una para cada densidad. Sin embargo, considerando que el gas
neutrónico está enrarecido respecto al nuclear, las alteraciones sufridas
en el g£s nuclear debidas a las colisiones producidas por los neutrones,
son despreciables.
I -7-
A pesar de que la densidad de los núcleos es muy superior a la neutrón^
ca, las distancias entre núcleos son lo suficientemente grandes como para que
la interacción se produzca entre un único neutrón y un único núcleo, dando
lugar a un proceso biunívoco bien definido.
Debido a no considerar las colisiones entre neutrones, la ecuación del
balance neutrónico puede linealizarse, y debido a que la interacción se produce entre un solo neutrón y un solo núcleo puede establecerse el concepto
de sección eficaz dado en (11).
Excepto en el caso de medios constituidos por cristales distribuidos
anisótropamente, la densidad fásica nuclear es isótropa en L.
Teniendo en cuenta que el neutrón tiene spin y momento magnético, debido a la interacción neutrón-núcleo, pueden obtenerse neutrones secundarios
de dispersión polarizados. Sin embargo, estos efectos son despreciables en
el cálculo de reactores nucleares
En los reactores nucleares, excepto durante el arranque, las fluctuacio_
nes de la densidad fásica neutrónica relativas a su valor medio, son pequeñas,
por lo cual, puede emplearse la ecuación de Boltzmann del transporte de
(2)
neutrones para obtener la densidad probable de neutrones
Teniendo en cuenta lo anterior, se introducen las hipótesis siguientes:
. - LOÓ Ü.YIÍ&OUS
coLÁÁ¿oneÁ
c.oní,¿de.fiada&
tnisie. do¿
nácZ&o¿>
y e.ntxe. un ¿oLoI I Ine.uXM.on
y un ¿>oLo
ná.cLe.0, dando
Zagal a ¿on
un p/ioceio
b¿u.ní\joco
b¿&n d<¿yjhido, pon. eJL cuaL no ¿e, modX.{yíca La densidad ficUZca di Lo¿ YIÜ.CZZ.06.
LOA {¡Lactuac-íoneÁ d<¿ La d<¿Yii¿dad {¡cU)¿c.a nívutAónlca ¿on deJ>pn.e.c¿abL&>.
I i/.- La dzn&Zdad
{ióu>Á.cia
YIUCZZOA
QJ>
ÁÁÓtxopa
zn L, te.nle.ndo La
vaAÁxibLz veJLocÁ.dad Ae.paA.abLe..
Por tanto,
3.4.-REACCIÓN NUCLEAR.
En la reacción nuclear a baja energía (2), al penetrar la onda asociada
(3)
al neutrón incidente por el canal de entrada v1 puede sufrir dos procesos
':
(1)
B e l l , G . I . , y Goad, W.B. - N u c í . S c i . Eng. 2 3 , 380 ( 1 9 6 5 ) .
(2)
H a r r i s , D.R. - Naval R e a c t o r P h y s i c s Handbook, e d . p o r Radkowsky I . A . - USAEC (19614).
(3)
V e l a r d e , G. - Véase r e f - 1 , p á g . 1 .
I -8-
es reflejada a la entrada del canal, originando la dispersión elástica potencial, o bien penetra por el canal formando el núcleo compuesto, para sa
lir después por uno cualesquiera de los canales de salida v abiertos.
• En particular, si la onda sale por el canal de entrada, v 1 , se obtiene
la dispersión elástica a través del núcleo compuesto, la cual se compone co_
herentemente con la potencial para dar lugar a la dispersión elástica.
Si la onda sale por otros canales distintos del de entrada, se obtiene
la dispersión inelástica, la captura, y la fisión.
El núcleo compuesto está caracterizado por las siguientes propiedades:
i) La vida media del núcleo compuesto es del orden de 10
-14
seg.
ii) La formación y desintegración del núcleo compuesto son dos procesos
independientes entre sí, o sea el canal de desintegración es independiente del de formación.
iii) El modo de desintegración del núcleo compuesto solo depende de su
.energía de excitación, spín y paridad.
3.5.-DISPERSIÓN.
El proceso de dispersión de neutrones depende principalmente de la ener_
gía del neutrón incidente, de la especie de núcleo blanco, y de sí el núcleo
blanco es libre (medio formado por un gas monoatómico) o está ligado en una
molécula o en una red cristalina. Estos efectos de ligadura solo son aprecia
bles cuando la dispersión se produce con neutrones térmicos.
En la dispersión elástica se emite un solo neutrón secundario, y según
i) del §3.4. Se emitirá en el mismo lugar e instante de la dispersión.
En la dispersión inelástica de neutrones de baja energía, generalmente
se emite un solo neutrón. Sin embargo, cuando la energía del neutrón incideri
te es suficientemente grande, después de haberse emitido el primer neutrón,
el núcleo residual puede quedar en un estado excitado tal, que su energía de
excitación sea superior a la de separación de un neutrón, en cuyo caso se
emitirá un segundo neutrón, dando lugar a la reacción (n',2n) con la emisión
de dos neutrones secundarios. Aunque esta reacción es importante en el Be,
puede despreciarse en los materiales que componen los reactores nucleares.
Según i) del §3.4, el neutrón será emitido en el mismo lugar e instante de
la dispersión.
De lo anterior, puede introducirse la siguiente hipótesis:
WÁspótzÁÁA V.~ En la. cLú>p2A¿Zón &Mó¿cca. e Á.ntlÁ¿t£Á,ca. t>i emitz un ¿,olo
nzutnón en eJL mtirno lugaA e -¿notante. e.n que. ¿e. produce, la cotú-Cón.
I -9-
Por tanto,
(18)
= el, in
ó(t-t'),
3.5.1.- DISPERSIÓN ELÁSTICA CON NÚCLEOS LIBRES.
En la dispersión elástica, según (2) y el §3.4, el núcleo no pierde su
identidad, emitiéndose el neutrón por el canal de entrada, es decir, el núcleo residual queda en el mismo estado cuántico que el del núcleo blanco.
Como los núcleos están libres, la dispersión elástica es azimutalmente
simétrica en L, pero debido a la dispersión elástica potencial, no será coal_
turalmente simétrica en C ni en L. Si 8 p
sarrollar x
es el ángulo de dispersión, al de-
en serie de polinomios de Legendre, resulta
X~1
A&n ">= I
A
e l p o t Cn
, L_
1=0
(.20)
6n )
Cn
i, - AX~\
o. -, P-,
el pot
1 1
4TT
habiéndose omitido las restantes variables. Si se expresa la energía del ne\a
tron en Mev, se obtiene que cuando
(12)
' :
"
~
„„ ,2
A
2/3
A
el pot 1
(21)
0
habiéndose tabulado en la Tabla I.
TABLA I
10 I 2 A " 2 / 3
A
1
12
23
58
238
1
10
1.91
1.21+
0.67
0.26
2
40
7.63
4.95
2.67
1.04
3
90
17.17
11.13
6.01
2.34
4
160
30.52
19.78
10 .6 8
4.17
1
Aunque la expresión (21) es únicamente válida para la dispersión elásti
ca potencial, como la dispersión elástica a través del núcleo compuesto es
(1)
Velarde, G. - Véase ref. 1, pág. 1.
(2)
Davison, B. - Neutrón Tra.nsport Theory - n^-
(1957).
I -10-
pequeña frente a la potencial, la expresión (21) puede emplearse para la
dispersión elástica en general.
_ , „ , , , .
,
, _
r 10 Mev para núcleos ligeros
En la labia I se observa que cuando E < i n „_ .,
^ .,
, ,
^
0.26 Mev para núcleos pesados
la dispersión elástica es isótropa en C, y la reacción nuclear solo se produce con neutrones S. Teniendo en cuenta que la energía media de los neutro
nes de fisión es de unos 2 Mev, se obtiene que la dispersión elástica en
los núcleos ligeros es isótropa en C, produciéndose solo con neutrones S,
mientras que en los núcleos pesados es añisótropa en C, aunque solo basta
considerar dos o tres términos en el desarrollo del espectro en polinomios
de Legendre, pero en este caso los neutrones P, D, . . . intervienen en la reac
ción nuclear.
En el caso de los reactores nucleares térmicos, debido al empleo de ma
teriales moderadores de número másico pequeño, la población neutrónica tendrá una energía media del orden de los ev, por lo que la dispersión elástica sera prácticamente isótropa en C y solamente intervendrán los neutrones
S. En el caso de los reactores nucleares rápidos, al evitar en los posible
el empleo de materiales moderadores, y emplear en cambio materiales de ele
vado número másico, la población neutrónica tendrá una energía media algo
inferior a los 2 Mev, por lo que la dispersión elástica sera añisótropa en
C, interviniendo los neutrones P, D,...
Debido a lo anterior, se obtiene la siguiente hipótesis:
1/1,- La dí¿peA¿<¿ón ztcUtlca. e¿> az<muta£m&nte. ¿Ámí&L¿ca <¿n L.
En oZ
pon.
QJXMO
d<¿ núc£.eo¿ LígeAo¿
o¿> ÁAó&iopa
e n C, ptiodü.cÁ.indo&<¿
neiL&ione¿> S.
Por tanto,
^ f r
5
/
= ¿ x^CV - v, $> .fi; v¿/' N )
C22)
que para el caso de núcleos ligeros, se reduce a
4 ( v ¿ n ^ n *V c J W V¿N^N} = ¿ 4 C v ¿ n *VCn' V¿n)
(23)
3.5.2.- DISPERSIÓN INELASTICA CON NÚCLEOS LIBRES.
En la dispersión inelástica, el núcleo tampoco pierde su identidad, pe
ro el neutrón es emitido por un canal distinto del de entrada, es decir, el
núcleo residual queda en un estado cuántico distinto que el del núcleo blan
co. Por tanto, la dispersión inelástica solo puede producirse cuando la ener
I -li-
gia del neutrón incidente es superior a la del primer estado excitado del nú
cleo blanco. Para núcleos ligeros muy simétricos, como el C y el 0, la energía del primer estado excitado es del orden de los Mev, disminuyendo algo a
medida que se consideran núcleos ligeros menos simétricos. Para núcleos pesa
dos,
es prácticamente del orden de los 40 Kev. Por tanto, como la energía me
dia de los neutrones de fisión es de unos 2 Mev, la dispersión inelástica só
lo es apreciable en los núcleos pesados.
Como según el §3.4, la dispersión inelástica es un proceso a través del
núcleo compuesto, será isótropa en C, y como en el caso de núcleos libres,
solo es apreciable en los núcleos pesados, en los cuales los sistemas L y C
coinciden, se obtiene la siguiente hipótesis:
Á Vil.- La &Up2M<Lón
¿yieZcUstica. i,oto ó& donkJL&QJioJiá. en Zo¿> nú
&n L.
Por tanto,
4 C V ' ^ * ^ V¿N ^ N } = W xÍnCV-v; v¿N)
(24)
3.5.3.- DISPERSIÓN CON NÚCLEOS LIGADOS.
En la dispersión elástica, además de cumplirse las condiciones dadas en
el caso de núcleos libres, la molécula o el cristal residual quedan en el mis
mo estado cuántico vibracional y rotacional que la de la molécula o el cristal blanco.
Cuando la energía del neutrón incidente es inferior a la del primer nivel excitado del núcleo blanco,- no puede producirse la dispersión inelástica
en el sentido indicado en el §3.5.2, pero puede ser suficiente para modificar
el estado cuántico vibracional o rotacional de la molécula o del cristal, dan
do lugar a una dispersión inelástica.
En el caso de un reactor nuclear empleando los refrigerantes y moderado
res habituales, el estado de ligadura de los núcleos no afecta prácticamente
a la reactividad ni a los otros parámetros integrados que intervienen en su
operación, por lo cual puede considerarse que el medio está formado por núcleos libres, efectuando posteriormente determinadas correcciones para el ca
so frecuente de que el reactor tenga como refrigerante o moderador agua lige
ra o pesada.
3.6.-FISIÓN.
En la fisión
(1)
Velarde, G.
, el núcleo compuesto se desintegra en dos núcleos llama• Véase ref. 1, pág. 1.
I -12-
dos, uno ligero y otro pesado. Ambos tienen exceso de neutrones y se encuen
tran en sendos estados altamente excitados, tanto más excitados cuanta mayor
sea la energía del neutrón incidente. Para la fisión inducida por neutrones
térmicos, la energía de excitación media del núcleo ligero puede ser de unos
11 Mev, y la del pesado de unos 11 Mev.
Como la energía de separación de un neutrón para estos núcleos es del
orden de 5,5 Mev, se desexcitarán emitiendo sendos neutrones, los cuales soremitidos con una energía media de 1 Mev relativa al sistema solidario al frag
mentó. Después de haber emitido su primer neutrón, la energía de excitación
del núcleo ligero será de 14-(5,5+l) =7,5 Mev, suficiente para emitir un segundo neutrón, después de lo cual, tendrá una energía de excitación de 7,5 -(5,5+1) = 1 Mev, insuficiente para emitir un tercer neutrón. Después de emitir su primer neutrón, la energía de excitación del núcleo pesado será de
ll-(5,5+l) =4,5 Mev, insuficiente para emitir un segundo neutrón.
A partir de entonces continúan desexcitándose, emitiendo un total de
unos 6 fotones, de casi 1 Mev cada uno.
A todos estos núcleos se les llama fragmentos primarios de fisión, y a
los neutrones y fotones emitidos por los fragmentos primarios de fisión al
-14
ser producidos con una vida media del orden de 10
seg, se les llama neu-
trones y fotones instantáneos de fisión.
Una vez que los fragmentos primarios han emitido estos neutrones y fo_
tones instantáneos, se obtienen los dos núcleos precursores, el ligero y
el pesado, a cada uno de los cuales les sobra todavía un promedio de tres
neutrones, deshaciéndose de este exceso de neutrones mediante sucesivas emi
siones g , con vidas medias de hasta varios minutos. De esta forma, cada
uno de los precursores encabeza su correspondiente serie radiactiva, con
emisiones 3 , y, y en el caso poco frecuente de que uno de los núcleos de
la serie tenga una energía de excitación superior a la de separación de un
neutrón, emitirá el correspondiente neutrón. Este núcleo que emite el neutrón se le llama padre, y al precursor de la serie en la cual se emite un
neutrón, se le llama precursor de neutrones retardados.
A todos los núcleos de ambas series se les llama fragmentos secundarios de fisión. Aunque el padre emite el neutrón con una vida media de unos
-14
10
seg, este padre se ha formado a partir del precursor mediante transi_
ciones g
con vidas medias de hasta varios minutos, por lo que estos g , y,
n son emitidos con retardos medios de hasta algunos minutos, llamándoseles
retardados.
I -13-
Los precursores de neutrones retardados, y por tanto sus constantes de
desintegración, son prácticamente independientes de la especie del núcleo
que sufre la fisión, y de las velocidades del neutrón incidente y del núcleo
blanco. De este modo, los diversos precursores de neutrones retardados obtenidos en las fisiones, pueden clasificarse en un determinado número de grupos,
los cuales son prácticamente los mismos para todos los núcleos fisiona-
bles, cualesquiera que sean las velocidades del neutrón incidente y del núcleo blanco, obtenidas en los reactores nucleares.
Según lo anterior, teniendo en cuenta que la fisión solo se produce en
núcleos pesados, en los cuales los sistemas L y C coinciden, que el camino
recorrido por los fragmentos de fisión es despreciable, y de acuerdo con los
valores experimentales de las funciones y parámetros dados en las Tablas del
cap.
I I , se obtienen las siguientes hipótesis:
H¿pótzt>ii
VIH.- En La {¡Z&Zón? todoi
Loi ne.utA.onej, ÍZ enUtzn
mo LugaA. en oJL que. ÁZ pJiodu.ce. La coLÁJ,Á.6n. Loi nzutxonzi
tídoi
¿nitantánzamzntz.
Loi ne.vutA.on.ej> n.ztan.dadoi
en eZ nuj>-
¿nitantánzoi
¿>on zmitldoi
ion eme
con un n.etand.o
mzdío de. \~~.
a
H-LpóteAÁJ, I X . - EL númzno mzdto
Lo de.pe.nde, de. La. ziptciz
de. ne.u£A.oneJ> ¿.nitantánzoi
I de. nu.cLe.oi, que ¿e, pilonan,
de. fiZbZón, ¿o-
y de,L móduLo de. La ue_
LociAad fieJLoJJjoa. znt/te. e£ ne.uZn.5n Ln.QA.de.nte. y eX nácLzo que. ¿u{¡A.e. La {¡ZiZón.
EL núme.n.0 me.dio de, ne.utn.onej, n.eXa.n.dado¿> de. {¡¿¿¿ón, do.pe.nde, ademáj, deJL gnupo
dz ne.utn.onej, n.eXjxn.dadoi> con¿¿dtn.a.do.
Wi,póteJ,ÍÁ X . - EL eJ,pe.c£n.o de. Lo¿ ntutn.one.6 de. ii&ián
EL eApe.ctn.0 de. Lo¿ ne.uth.one.& ¿nétantánzoi
ej> ÁÁÓtXopo en L.
de. {¡¿¿¿ón, de.pe.nde, ¿oLo de. La eópe_
cLe, Á, de, núcLzo¿> que, ¿u^A-m La {¡ÁJ>¿ón y de.L móduLo de. La. veJLocX.da.d deZ ne.utxón
ie.cundaAÁ.0 emiti-do.
EL eApe.ctA.0 de. Lo¿ ne.utn.one,¿ A.etaxdadoi> de. {ÁÁÁJón,
de.pe.nde. ¿oLo deZ gn.upo de. ne.utn.onej, A.<itaA.dadoi con¿>¿de.n.ado y deJL móduLo de.
La \ieZocÁ.dad del. ne.utn.6n ¿e.cundaA¿o
WJjpóteÁÁJ, X I . - La inacción
cle. Á. de. núcLzoi
exnitZdo.
de, neutAonej,
n.etan.dado¿ de.pe.nde. de. La ej,pz-
que. ¿u{¡A.e.n La ^ij,Á,ón, ¿Á.e,ndo Znde.pe.ndÁ,e.nte. de. La¿>
vetocída-
deJ> deZ ne.utn.6n y deZ núcLzo.
U¿póteJ>-iA X I I . - Lo¿ pn.e,cuAÁon.eÁ dz Laj, AznÁ.z& na.dia.ctiuaÁ,
LOA. LO¿ dz Lo¿ nzutn.onz¿
netan.da.doi
¿z ¿uponzn
HZpótzAÁJ, X I I I . - Loi QA.upoi dz nzutn.onzi
¿¿dadej,
tzgnaclón,
dz Loi pn.zcunAon.zi dz nzutnonzi
ion ¿.ndzpzndizntzi
en
dz La zipzcíz
Kzpoio.
n.ztan.dadoi,
n.ztan.dadoi
y en paAt¿cu_
y pon. tanto
y ÍUÍ conitantzi
dzl núctzo
quz iu^nz
LOA dzn_
dz
dziin-
La ¡yóó-tón y
I -14-
de. la¿ vzLocA.dad.QA deJL ne.utn.6n Á.nc¿dznte. y d&l núcJLzo b¿anco, de.pe.ndie.ndo
ú.YÚ.came.nte. d&L gAupo de. ne.ath.oneA h.e£an.dado¿,.
Según las hipótesis anteriores, resulta
^'fr^LN^
= V (v }
^'^¿N^
=
(25)
p r
(26)
Í^V
xj(v'fi',t' +vfi,t; v¿ N n¿N) = ¿ X p ( v ) ó(t-t')
(27)
(28)
6
^''^N)
=B
Í '
X=
P' d
(29)
C^í.v'.^.t) = Cd(?,t)
XÍ
^'> ^ N }
(30)
= A
(31)
d
3.7.- SECCIONES EFICACES.
Respecto a la dependencia energética de las secciones eficaces no dife_
renciales definidas en (11), puede admitirse la hipótesis:
XIt/.- La& ¿eccxoneó z.^-ícaaej, m¿cAo¿cóp<Lca¿>, no
de.pznde.n cíe la e¿pzc¿& -i de. ndcle.o¿ que -óu^en la colisión,
c.on6<ídeAa.do, y doJL módulo de. la veJLoddad nilatíva.
dzl px.oc&>o x
zntnz eJL ne.atn.6n Á,ncÁ,de.Yi_
te. y el. nácJL&o blanco.
Por lo tanto,
O (V
Í ^ ' V LN "LN}
=
<(vr}
(32)
3.8.-CLASIFICACIÓN DE LAS HIPÓTESIS SIMPLIFICATIVAS.
Las hipótesis simplificativas anteriores pueden clasificarse en dos
grupos:
En el primer grupo se incluyen las Hipótesis I, II, III, V, VIII, XII
y XIII, las cuales son necesarias para formular las ecuaciones de Boltzmann
del transporte de neutrones, en la forma dada en los cap. III y cap. IV.
En el segundo grupo se incluyen las restantes hipótesis, las cuales
aunque están prácticamente de acuerdo con las medidas experimentales, no
son estrictamente necesarias para obtener las ecuaciones de Boltzmann mencionadas anteriormente.
II - 1 -
II.- DETERMINACIÓN DE LOS PARÁMETROS NUCLEARES.
1.- CONSIDERACIONES GENERALES.
Para poder resolver las ecuaciones del transporte de neutrones, es nece
sario conocer previamente las funciones empleadas como coeficientes en dichas
ecuaciones, llamadas impropiamente parámetros nucleares.
En el Cap. I se considero que estos parámetros cumplían ciertas hipóte
sis simplificativas, pero en realidad, o no las cumplen, o solo lo hacen en
determinados intervalos de las variables. Por tanto, es preciso efectuar un
análisis de los parámetros nucleares, y de sus intervalos de validez.
En este capítulo se han incluido diversas formulas empíricas y valores
numéricos de los parámetros "~ , con objeto de analizar las variables de que
dependen, y justificar algunas hipótesis simplificativas introducidas. Por
tanto, en la resolución de las ecuaciones del transporte de neutrones deben
emplearse los valores numéricos más apropiados.
En los párrafos siguientes se considerará solamente que el medio está
formado por núcleos libres (.gas monoatómico], dejando para otro informe el
caso de que los núcleos formen parte de una molécula o de una red cristalina .
2.- DENSIDAD FÁSICA NUCLEAR.
Según la Hipótesis IV, la densidad fásica nuclear es isótropa en L, te_
niendo la variable velocidad separable,
siendo N (r,t) la densidad nuclear, o sea el número de núcleos i que en el
instante t hay en la unidad de volumen en r, y N (VTW)
el espectro nuclear
de velocidades.
2.1.-DENSIDAD NUCLEAR.
En el arranque del reactor, la densidad nuclear N (r,t)
es función de
r debido a las heterogeneidades del medio, y durante la operación del reactor,
será función de t debido a las transiciones 3 y a las reacciones nuclea_
res inducidas por los neutrones en los núcleos del medio.. La densidad nuclear
(1)
Reactor Physics Constants - AWL 5800 (1963).
II - 2 -
en función del tiempo se obtendrá de las ecuaciones d e l quemado ( , V I ) .
En g e n e r a l , la densidad nuclear puede ponerse en función del número
de A v o g a d r o , de l a densidad másica y del peso atómico, p o r medio de
pl N
i
N
=
A
;
-3
, átomos i • cm
del medio
(2)
a
siendo
p
= densidad másica de los átomos i, o sea g de átomos i por cm
-3
del medio, g-crn
24- .,
-1
átomos» (_átomo-gramol
N
= numero de Avogadro = 0,6025*10
Aa
= *peso atómico del átomo i, g«(átomo-gramo)
En p a r t i c u l a r , pueden considerarse los siguientes casos:
2.1.1.- Si el medio es un gas m o n o a t ó m i c o , como a la temperatura y presión
normales un átomo-gramo ocupa 22400 cm , será A~/p = 2240.0, luego
ci
p
i
N
-
N
..
-3
-3
átomos
i
•
cm
átomos i • cm de gas monoatómico
A
22400 3
(.31
2.1.2.- Si el medio es un compuesto químico d e densidad p , peso molecular
A , y con un número de átomos i p o r molécula a , se tiene
a
a
}
átomos i • cm
de compuesto químico
•
.
(.4-1
A
a
2.1.3.- Si el medio es una mezcla de isótopos de densidad p, peso atómico
medio <A >, y con un enriquecimiento del isótopo i, o sea, con una razón
a
.
entre el número de átomos i al total dado por e , se obtiene
p N
i
A i
-3
N =
e , átomos i • cm
de mezcla
(.5)
<A >
a
2.1.4.- Si el medio es una aleación de densidad p, y con unas ppm de átomos
i, o sea g de i por T de aleación dado por p , resulta
N
=
p N
— (p
A1
a
'10
) , átomos i • cm
de aleación
(6)
2.2.-ESPECTRO NUCLEAR EN UN MEDIO CON NÚCLEOS LIBRES.
Según l a Hipótesis I I I , las colisiones neutrón-núcleo no modifican el
espectro nuclear, y si además de considerar que los núcleos están libres
(gas m o n o a t ó m i c o ) , se cumplen l a s condiciones siguientes:
II -3-
i) Medio homogéneo,
ii) Medio infinito,
iii) No "hay fuentes ni sumideros de núcleos,
los núcleos seguirán la distribución maxwelliana dada por la mecánica clásica para un sistema de partículas idénticas pero discernibles, en equilibrio
termodinamico con el medio,
Mi,
s
N (V
, M1
,
LN }= ^
(
,3/2
271<f )
V
2
M1
.
2
V
LN %
,_.
LN 6 X P ( - - ^ - }
(7)
la cual está normalizada a la unidad (1), siendo M
la razón entre la masa
del núcleo i y la del neutrón, K la constante de Boltzmann, y T(r,t) la tem
peratura local del medio, la cual se determinará a partir de las ecuaciones
termohidraulicas del reactor ( ,VI).
La velocidad más probable de los núcleos i, viene dada por
y
LN
M
a la cual corresponde una energía dada por
'LN'TJ = I M Í ( V L N ) 2 = K T
(9)
La velocidad media de los núcleos i, será
a la cual corresponde la energía
E
(<VLN>) ^ M ^ v ^
2
=ÍKT
(11)
2.2.1.- De todas las condiciones impuestas anteriormente para la obtención
del espectro nuclear, la más restrictiva es la de considerar los núcleos li
bres, de tal modo que si el medio es hetereogéneo, finito, y con fuentes y
sumideros de núcleos, pero formado por núcleos libres, puede suponerse que
el espectro nuclear sigue siendo maxwelliano.
3.-
NUMERO MEDIO DE NEUTRONES EMITIDOS POR FISIÓN.
El número medio de neutrones instantáneos y retardados emitidos por fi
sión puede ajustarse a los dos primeros términos del desarrollo en serie de
Taylor en E 1
vi(E) = v*(E)
+I
vj(E) = v W
) +
pv '
% dv '
' u'
d
üE
i
u
E~
(E-E*) + ...
u
.
(12)
siendo E 1 la energía umbral del neutrón, para la fisión del núcleo i.
II -M~
Si el núcleo es fisionable con neutrones térmicos se toma E
= 0 , mien
tras que en los restantes casos se toma para la energía umbral la que da lu
gar a una sección eficaz de fisión detectable.
*
*
•
A
En la Tabla I se dan los valores de E , v (E ) , -TTT i, para los prin
u
u
dE
cipales núcleos.
La ecuación (12), justifica la parte correspondiente de la Hipótesis IX.
TABLA I
Núcleo i
E 1 , Mev
vV)
dv 1
dE
u
u233
u235
u238
Pu239
Ei,
Mev
u
0
2.50
0.115
0
2.H3
0.135
1.1
2.Í+1
0.139
0
2.87
0.111
3.1.-El número medio de neutrones retardados d, emitidos por fisión v , en
unión de (t. / o ) , , A , a,, ¿ v j 5 vienen dados en la Tabla II, en función del
1/ ¿ a
a
a ^ a
grupo de neutrones retardados, para los principales núcleos fisionables.
Del examen de esta tabla, se pueden justificar las Hipótesis XIII y IX,
ya que prácticamente X
es independiente de la especie de núcleo fisiona-
ble i, y de la energía del neutrón incidente, por lo que pueden considerar^
se los mismos 6 grupos de neutrones retardados, para los divei-sos núcleos
fisionables con neutrones de cualquier energía.
También puede justificarse la Hipótesis XI , ya que 3
no varía apre_
ciablemente con la energía del neutrón incidente.
4.-
ESPECTRO DE LOS NEUTRONES DE FISIÓN.
4.1.-Entre las diversas fórmulas empíricas empleadas para representar el
espectro de los neutrones instantáneos de fisión, puede considerarse la si_
guíente
P
v^E1)
u
II
-5-
TABLA
K = fTv-
i
d
d
(t
G
II
l/2
}
ú
d
1
Q-
•
vm
0.0066 ± 0.0003
i
2
3
O
O
•H
4
5
6
u235
0.0158 ± 0.0005
P-
1
2
3
4
1
CO
&
5
0
6
£
pu2S9
0.0061 ± 0.0003
s
1
2
3
4
5
6
u233
0.0070 ± 0 .0004
1
2
3
4
5
6
u
235
0.0165 ± 0 .0005
CO
1
2
3
4
5
6
o
•H
a«Ti
K
0.0412 ± 0 .0017
Q)
1
2
3
4
+J
£_,
5
en
c
o
--i
O)
6
Pu
239
0.0063 ± 0 .0003
1
2
' 3
4
5
6
'
55.00 ±
20.57 ±
5.00 ±
2.13 ±
0.615 ±
0.277 ±
0.54
0.38
0.21
0.20
0.242
0.047
0.0126 ± 0.0002
0.0337 ± 0.0006
0.139 ± 0.006
0.325 ± 0.030
1.13 ± 0.40
2.50 ± 0.42
0.086 X 0.003
0.299 ± 0.004
0.252 ± 0.040
0.278 ± 0.020
0.051 ± 0.024
0.034 dt 0.014
0.057
0.197
0.166
0.184
0.034
0.022
± 0.003
± 0.009
± 0.027
± 0.016
±0.016
± 0.009
55.72 ±
22.72 ±
6.22 =
2.30 ¿
0.61 ±
0.23 ±
1.28
0.71
0.23
0.09
0.083
0.025
0.0124 ± 0.0003
0.0305 ± 0.0010
0.111 ± 0.004
0.301 ± 0.012
1.13 ± 0.15
3.00 ± 0.33
0.033 ± 0.003
0.219 ± 0.009
0.196 ± 0.022
0.395 ± 0.011
0.115 ± 0.009
0.042 x 0.008
0.052
0.346
0.310
0.624
0.182
0.066
± 0.005
± 0.018
± 0.036
±0.026
± 0.015
±0.008
54.28 ±
23.04 ±
5.60 ±
2.13 ±
0.618 ±
0.257 ±
2.34
1.67
0.40
0.24
0.213
0.045
0.0128 ± 0.0005
0.0301 ± 0.0022
0.124 ± 0.009
0.325 ± 0.036
1.12 ± 0.39
2.69 ± 0.47
0.035 X 0.009
0.298 ± 0.035
0.211 ± 0.048
0.326 ± 0.033
0.086 ± 0.029
0.044 ± 0.016
0.021 ± 0.006
0.182 ± 0.023
0.129 ± 0.030
0.199 ± 0.022
0.052 ±0.018
0.027 ± 0.010
55.11
20.74
5.30 ±
2.29 ±
0.546 ±
0.221
1.86
0.86
0.19
0.18
0.108
0.042
0.0126
0.0334 ±
0.131
0.302
1.27 ±
3.13 ±
0.0004
0.0014
0.005
0.024
0.266
0.675
0.086 ± 0.003
0.274 0.005
0.227 ± 0.035
0.317 ± 0.011
0.073 ± 0.014
0.023 ± 0.007
0.06 ± 0.003
0.192 ± 0.009
0.159 ± 0.025
0.222 ± 0.012
0.051 ± 0.010
0.016 ± 0.005
54.51 ±
21.84 ±
6.00 a.
2.23 ±
0.496 ±
0.179 ±
0.94
0.54
0.17
0.06
0.029
0.017
0.0127 ±
0.0317
0.115 ±
0.311 ±
1.40 ±
3.87
0.0002
0.0008
0.003
0.008
0.081
0.369
0.038
0.213
0.188
0.407
0.128
0.026
± 0.003
± 0.005
± 0.016
0.063 ± 0.005
0.351 ± 0.011
0.310 ± 0.028
0.672 ± 0.023
52.38 ±
21.58
5.00 ±
1.93
0.49 ±
0.172 ±
1.29
0.39
0.19
0.07
0.023
0.009
0.0132 ± 0.0003
0.0321 ± 0.0006
0.139 0.005
0.358 ± 0.014
1.41 0.067
4.02 ± 0.214
53.75 ±
22.29
5.19 ±
2.09 ±
0.549 ±
0.216 ±
0.95
0.36
0.12
0.08
0.049
0.017'
0.0129
0.0311 ±
0.134 X
0.331 ±
1.26
x
3.21
±
0.0002
0.0005
0.003
0.012
0.115
0.255
± 0.007
x 0.008
± 0.003
0.211 ± 0.015
0.043 ± 0.005
0.013 ± 0.001
0.137 ± 0.002
0.162 ± 0.020
0.388 ± 0.012
0.225 ± 0.013
0.075 ± 0.005
0.054 ± 0.005
0.564 ± 0.025
0.667 ± 0.087
0.038
0.280
0.216
0.328
0.103
0.035
0.024
0.176
0.136
0.207
0.065
0.022
X
±
±
±
±
X
0.003
0.004
0.018
0.010
0.009
0.005
1.599 ± 0.081
0.927 ± 0.060
0.309 ± 0.024
±
±
±
±
±
±
0.002
0.009.
0.013
0.012
0.007
0.003
II -6-
que al normalizarla a la unidad, se obtiene la relación entre a
y b ,
= i
v (E u )
La energía más probable de los neutrones instantáneos, viene dada por
(15)
dE
la cual vale unos 0.6 5 Mev.
La energía media de los neutrones instantáneos, se obtiene por
_ i
V
E ) d E
"
»
vi(Ei,
- 2
(16)
h
la cual tomará valores alrededor de los 2 Mev.
En la Tabla III, se dan los valores de a , b , E
P
y <E> 1 para los prin
*
~~
cipales núcleos fisionables.
Teniendo en cuenta que a~ y b , prácticamente no dependen de la ener_
gía del neutrón incidente, puede justificarse la parte correspondiente de
la Hipótesis X.
TABLA III
i
i
a
b ~ ,Mev
E 1 , Mev
P
<E> , Mev
u233
u235
1 .888
1 .306
0 .653
1 .957
1 .872
1 .290
0 .645
1 .936
Pu239
2 .121
1 .333
0 .667
2 .002
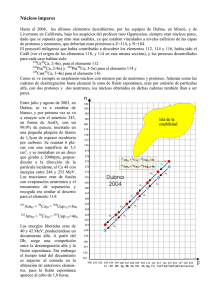
4.2.-El espectro de los neutrones retardados de fisión
( 1 2 ) .
tado
'
XJ(E),
se ha represen
~
en la fig. 1, para los cuatro primeros grupos de neutrones retar-
dados, indicando la energía media en cada grupo.
De este modo queda justificada el resto de la Hipótesis X.
(1)
Keepin, G.R. - Delayed Fission Neutrons - IAEA (1968).
(2)
Keepin, G.R. - Physics of Nuclear Kinetics - Addison Wesley (1965).
II - 7 -
5.- ESPECTRO DE LOS NEUTRONES DE DISPERSIÓN ELÁSTICA EN NÚCLEOS LIBRES.
Según la Hipótesis VI, la dispersión elástica en núcleos ligeros es Iso_
tropa en C, y en general, teniendo en cuenta la ecuación (.21,1), cuando se
verifica que
2
E(Mev) < - ;° "L = > X ^ -, ^ 0
(.17)
es decir, el termino l~simo del desarrollo en polinomios de Legendre del ángulo de dispersión en C, del espectro de los neutrones de dispersión elástica , es nulo.
Por tanto, la anisotropía en la dispersión elástica es tanto más importante cuanto mayor sea la masa del núcleo y la energía del neutrón incidente.
Por un lado, en los reactores rápidos han de tomarse dos o tres términos del
desarrollo, mientras que en los reactores térmicos basta con uno, es decir,
la dispersión elástica es isótropa en C. Por otro lado, en la moderación pue_
den influir los efectos de anisotropía, mientras que en la termalización la
dispersión elástica es Isótropa en C.
Como según (.17), puede limitarse el número de términos del desarrollo,
y especificar determinadas leyes de dispersión en C, mientras que la formula
ción de las ecuaciones del transporte de neutrones se efectuará en L, es necesario establecer las fórmulas de transformación del sistema C al L.
5.1.-FORMULAS DE TRANSFORMACIÓN DEL SISTEMA C AL L.
Las fórmulas de transformación del sistema C al L se obtienen partiendo
(1)
de las ecuaciones de conservación de la energía y del impulso
, dadas en
la Tabla IV, y teniendo en cuenta que
velocidad en L = velocidad en C + velocidad en L del centro de masas
(18)
El tercer miembro de (21) es debido a la definición de velocidad en L
del centro de masas, la cual toma los valores
íl)
Velarde, G. - Véase ref. 1, pág. 1.
II -8-
TABLA
^^\sistema
ley
\
^
Conservación
L
1
,2
de la energía
7T V T
cinética
2
1 ..i , 2
1
2
+ 7T M VJ . = -r- V_
Ln
2
LN
del impulso
2
l..i 2
1 .2 1 ..i ,2 1 2 1 ..i 2
— v
+— M v
= — v i— M v
2 Cn 2
CN 2 Cn 2
CN
+ 7T M V T „
Ln
2
LN
(20)
^¿n+M ^CN = \n + M ^CN = °
(22)
(21)
1 •+.
1+Mi
C
(19)
->
i->
->
í->
i -v
vi +M vi =vT +M v =(1+M )v_ „
Ln
LN Ln
LN
LnN
Conservación
LnN
IV
1
VJ
Ln
1+M
v'
i LN
M1
-y
— V
. ,,1
1+M
Ln
+
. .,i
1+M
-^
V
LN
-9",
~ V
—
Ln
M1
„ ,,i
1+M
•+.
V
Lr
->
— V
Ln
(23)
1+M1
VLr
La anulación del impulso en C, expresado en (22), es debida a que pa_
ra pasar del sistema C al L hay que efectuar una translación v
, es de-
cir
V
= V
—V
Cn
V
Ln
= V
Cn
™ V
LnN
LN
1+M
M
V
Lo" LnN
LnN
Lr '
v
1
V
c
LN
Lr
1+M"
-5-
V.
1+M 1
1
— V
v
V
LnN
1+M1
Lr
(24)
(25)
siendo
-y
->-
v' = v t
Lr
Ln
V
=
LN' ^Lr
-y
V
(26)
Ln "^LN
con lo cual, al sustituir (24- y 25) en (21), se obtiene (22).
Por tanto, vjl, y v'
tienen sentidos opuestos, y lo mismo v_
y v_ M ,
con lo cual puede construirse parte de la fig. 2.
Eliminando v'
CN
v
=v
Cn
Cn
1+M
i
y v
vJ
Lr
CN
entre las ecuaciones (20 y 22), se obtiene
Vi
Lr
= V
:
Lr
V
— V
CN
CN
1+M i
vJ
Lr
(27)
luego, el módulo de las velocidades enC ,y el módulo délas velocidades relativas
en L, son invariantes en la dispersión elástica, es decir, los lugares geo
métricos de las v
y v
\~* i i
son sendas circunferencias de radios v'
v^ 1N
y v'
V-* 11
\*-x s
II -9-
y centro en v
, con lo cual puede completarse la fig. 2.
De lo anterior resulta que dadas las velocidades en L antes de la dispersión v' y v' , por (23) se obtiene v
, por (24 y 25) se obtienen v' y
Ln
LIIN "
LnJN Ln
v' , y por (27) se obtienen los módulos v p = v' y v • = v' .
Sin embargo, queda indeterminada una de las siguientes magnitudes: 8. ,
6
J-JIN
, 6
, 6~,T, v
un
CN
Ln
,v
LÍN
, es decir, dada una cualesquiera de ellas, quedan de
~
—~
terminadas todas las restantes. A continuación se establecerán las relacio-:
nes entre las magnitudes correspondientes al neutrón.
5.1.1.-RELACIÓN ENTRE v L n y
Del triangulo de lados v , v
, v , en la fig. 2, se obtiene
Ln
LnM
Ln
v
2
2
2
= v n + v. ., + 2 v o vT
eos 6 n
Ln
Cn
LnN
Cn LnN
Cn
(28)
y como eos 8
puede tomar todos los valores entre -1 y +1, los valores extre_
2
„
mos de vT , serán
Ln
eos 6. = 1 = = > (vT )
= v- + vT „
Cn
Ln max
Cn
LnN
(29)
eos 6 n = -1 = 7 ' (vT ) . = v_ - vT M
Cn
Ln m m
Cn
LnN
(30)
en las cuales v
y v
se calculan por (24 y 23), ambas en función de v'
y V' . De (29 y 30), resulta
V
Cn ~ 2" _ Ln max +
Cn
LnN
Ln minj '
4 ¡ Ln max
V
LnN ~ ~2 [ Ln max ~
Ln minj '
Ln minj
Haciendo
(v
m + 1 =
• •
)
Ln max
.
, m - 1 =
(v )
Ln max
v
v
LnN
LnN
la ecuación (28) toma la forma
i r,
^2
, • .2 ~\
(v )
(v ) 2
„
" Ln m m
i
Ln m m
,m-lN2
2 =
•—, a =
r— =
v
\v J
LnN
Ln max
.
i r
v T 2 = ^ | ( v (v
) '
+ ( v . )) \ I ++ ~ | ( v (T
)"
- ( v . ) ' .
. L n = 22 •L
|_ T LLn
n )m
a x +(v Ln
L n minJ
minj
Ln max
L n min_
n.a
22 |_L '
X
COS
9
Cn
2
i
m +2m eos 8 +1
m
+2m eos 8 +1
= - (v )
(1+a1) t d - a 1 ) eos 9PP
=
= (v.
(v. TT
^=H-_
(33)
(1+m)2
2 ^ Ln max
Cnl
max
Ln max
1 2
o bien, representando por E = -^ v. , la energía cinética del neutrón en L,
II -10-
la ecuación anterior toma la forma
2
m + 2m eos Qn + 1
= -r (1+a1) + (1-a ) eos
E
Cn
Cn
2
(1 + m)
max
los cuales relacionan v_ ó E con eos 6_ .
Ln
Cn
5.1.2.- RELACIÓN ENTRE v,_n y 8 L n .
Considerando el mismo triángulo que en el párrafo anterior, resulta
v^ = v 2 +v^ ..-2 vT vT .. eos 6,
Cn
Ln
LnN
Ln LnN
Ln
(35)
y teniendo en cuenta (31), se obtiene
v
y = eos 8.
i ¡v
Ln
v — v
Cn
LnN
2 v
LnN
2 v
v
Ln LnN
=
m+1
Ln
_______
Ln max
=
v
Ln
2 v
LnN
(v)
( v ) .
Ln max
Ln min
————
=
? v v
Ln LnN
m-1
Ln max
_____
Ln
,~^
(3o)
la cual relaciona v. con y.
Ln
5.1.3.- RELACIÓN ENTRE 8 P n y 8, .
un
Ln
Puede obtenerse eliminando v
entre (33 y 36), o bien directamente
Ln
de la fig. 1, proyectando el triángulo considerado en los párrafos ante_
riores, sobre el eje v
y su perpendicular,
v
sen 8
=,
—
—
tg e
vT „ t v o eos 8 O
LnN
Cn
Cn
luego de (31 y 32), resulta
tg 8T
1 + m eos 8_
o
° Ln
Cn
y = eos eT =
=
;•Ln
- •"
VI + tg2 8.
/nr + 2m eos Q
+ 1
(37)
f„0s
(38)
que establece la relación entre y y eos 8 .
5.2.-LEY DE DISPERSIÓN ELÁSTICA.
Dada la ley de dispersión elástica en C, y conocidas las fórmulas de
transformación del sistema C en el L, obtenidas en el §5.1, puede calcular
se el espectro de los neutrones de dispersión elástica en L.
5.2.1.- CASO DE DISPERSIÓN ELÁSTICA ISÓTROPA EN C.
Al seT1 la dispersión elástica isótropa en C. la probabilidad de que un
II -11-
neutrón de velocidad vJ al chocar con un' núcleo i de velocidad v' , el neuLn
LN
trón dispersado tenga una dirección dentro de áüp en Q p , es
(39)
Cn
Tomando como dirección de referencia la de fiT .T, como dfi_ =d(cos Qn )dcj>.
LnN
Cn
Cn
siendo é el azimut y 0
la coaltura de Q
, y al ser la dispersión elástica
azimutalmente simétrica, al integrar (39) para todos los azimutes, resulta
X
el(cOS
9
¿n *
COS
9
Cn ;
COS 9
*Ln'
es decir, todos los valores de eos 6_
Cn = f d COS 6 Cn
(40)
son igualmente probables, pero no los
de y=eos 0 , ya que según (38) la relación entre eos 8^ y y no es lineal.
Ln
'
Ln
5.2.1.1.- Las probabilidades de que un neutrón incidente' de velocidad v'
al
chochar con un núcleo i de velocidad v' , de lugar a la emisión de un neutrón
d eos
dispersado elásticamente dentro de <
eos e
Cn
d v
Ln
, son iguales,
Ln
en <
d E
Cn
E
y
ya que el problema queda perfectamente determinado al fijar una cualesquiera
de las magnitudes anteriores.
Por tanto
Xel ( c o S 6¿n - COS 9 Cn ; ^Ln' \^
E; Phn,
\^)
dE
d cos
XÍ1^'
dv
Cn
y,
Ln»
LN
)
Ln
dy
Como el primer miembro se conoce por (40), y las relaciones entre cos 6- ,
v
, E, y vienen dadas en el §5-1, pueden obtenerse las restantes probabilidaLn
des .
De (33), resulta
,
d vL
d E
(v ) 2
(v ) 2
iN 1
Ln max 4 m
1 ,
Ln max
)
= _ 2 vT
<(1+m)'
- — - d c o s e Cn
2 v
Ln
Ln
- I d cos 8, = E
(1 - a1) ~ d cos 9P
= E
Cn
max
2
Cn
max (1+m) 2 2
De (38) se obtiene dy en función de dcos 0
sión complicada en y.
9
Cn
(43)
, dando lugar a una expre-
II -12-
Sustituyendo (40, 42 y.43) en (41), resulta
X
¡1(COS
(44)
COS
2 v
(1+m)'
Ln
(v. )
(v
Ln max
2 v
X , (v' -> vT ; v' , v' ) = <"
el Ln
Ln
Ln
LN
|
Ln
9
Ln max
O,
•
v,
Ln
X
) . < v < (v )
Ln min — Ln — Ln max
(45)
1-
)
(v
. ,
Ln min
Ln
v. )
Ln max
L ' V LN ) =
¡1 (E '
(46)
5 . 2 . 1 . 2 . - Dadas l a s v e l o c i d a d e s i n i c i a l e s , antes de l a d i s p e r s i ó n , vj y
Ln
v' , l a p r o b a b i l i d a d de que el n e u t r ó n d i s p e r s a d o e l á s t i c a m e n t e tenga la
v e l o c i d a d dentro de d v T en v T , viene dada en ( 4 5 ) . Pero u n a v e z filada
Ln
Ln
la v e l o c i d a d v , s u á n g u l o d e d i s p e r s i ó n 8. queda p e r f e c t a m e n t e determi
Ln
*
Ln ~
^
~~
nado p o r ( 3 6 ) , es d e c i r , fijada v. la p r o b a b i l i d a d de que el n e u t r ó n sea
Ln
dispersado elásticamente dentro de dy en y , vendrá dada por una delta de
Dirac, ó(y-
y) dy, siendo y uno cualesquiera de los valores de y dados en
(36).
Por tanto, la probabilidad de que un neutrón incidente de velocidad
v' til al chocar con un núcleo i de velocidad v' . £2' de lugar a un neu
Ln Ln
LN LN
°
—
trón dispersado elásticamente dentro de dv_ d£L en vT ÍL , será
Ln
Ln
Ln Ln
"Ln
Ln
LN
L
Ln
'Ln
2TT
Ln
Ln
<$(\i - y) dv_
dy dé
Ln
(47)
Sustituyendo (45) en la ecuación anterior, se obtiene el espectro
buscado de los neutrones de dispersión elástica isótropa en C,
II -13-
2
V
Ln
(v
)
Ln max
2 vr
Ln
X1-,(vT' Ü! ->vT ttT , v' i ! ' )=< 1
ó(y-y)
r
e l Ln Ln Ln Ln
LN LN ^ 2 1 1
(v. )
1 - a1
Ln max
O,
v
vT ) . ,
Ln min
Ln
(V
)
.
< (V T
<V
Ln min— Ln —
)
Ln max
(48)
T )
v Ln
max
vT
Ln
y análogamente para la energía
ó(p-p)
E
max
4m
E . < E <E
min —
— max
1
Xel
Ln
Ln
LN LN
1
271
E
1-a1
max
0,
E < E . ,
min
(49)
6(u-p)
E •• E
max
con
y =
m-1
Ln
m+1
(
Ln max
)
Ln max
T
m+1
(50)
Ln
5.2.1.3.-Es conveliente determinarlos valores propios de las siguientes magnitudes
empleando el espectro de los iieutior.es dispersados elásticamente.
; v' , v' ) d cos 9
i Ln
LN
Cn
max
max
-1
E
ii)
(1+a 1 ) + (1-a 1 ) cos 6P
Cn
> - <u
E
max
-u> =
m X
d cos 6. = i (1-a 1 )
Cn 2
(51)
+ (1-a ) cos
ln
~ J-l
• d cos f1Cn= 1 +
—2—_
.
i
1-a
x
ln
(52)
a
•1
Üi)
x
_1
2
el(c°S
9
Cn
8
Cn ;
d
cos
9
Cn
1 + m cos Qc
2m cos Bn + 1
Cn
d cos 0. = -r—
Cn
3m
(53)
5.2.2.-CASO DE DISPERSIÓN ELÁSTICA ANISOTROPA EN C.
Cuando la dispersión elástica es anisotropa en C, la ecuación (40) deja
ii
-14-
de cumplirse. Desarrollando el primer miembro de (40), en serie de polinomios de Legendre, resulta
4(COS
9
Cn •*C O S 9Cn' \n> ^LN}= A
x
el(^Ln' ^LN)P l ( c O S
^
W
1 - 0
(54)
De (54 y 4 1 ) , se o b t i e n e
i
X
, ,
-*,
(v
el Ln -
V
Ln
; V
~*~,
V
\
Ln
}=
Ln' LN
2
1
v-
21+1
T
^ ~ J
]jo ~ ~
*
i
el X
,-»-,
¿n
'
->, s
V¿N
Ln max
• P1(cos 9 Cn )
(55)
y de (47), resulta
X
el^VLn2Ln
V
i¿
Ln Ln'
Ln'VVLN
LNi¿
LN
L ;
,
,2
(v. )
Ln max
,
i
1 - a
n ¿n
1=0
4TT
X
e l V\n>
• P1(cos 6 C n ) ó(y - y)
V
LN J
(56)
Teniendo en cuenta la expresión de eos 6,, en función de vT dada en
Cn
Ln
(33)
v2
2
eos 9
= 1 - ilgL
Cn
(1
2m
í£~)
^.
(57)
^¿
Ln max
el espectro buscado, de los neutrones de dispersión elástica anisótropa en
C, valdrá
X
(
n
"
n
fi)
^ ^
i
vT )
1 - a
Ln max- y),
'
—
XX
(v
VV }
el
e l ll ( v¿n'
¿ n ' LN
LN '
^ n
1=0
(vT ) . < vT < (vT )
(58)
Ln mm — Ln — Ln max
2
Ln max
anulándose para vT
< (vT ) . y vT
> (v. )
Ln
Ln mm J
Ln
Ln max
Del mismo modo se o b t i e n e para l a e n e r g í a ,
Y
x - >
( E ' Q'
- > • - » • " * • •>
~** F Q
v 1 Q' ) =
1 _ (-1^m^
2m
2
1
i
E
1 - a1
max
n
[
2
r
\
21+1
i
y
1=0
-i
(l
— ) 5(y - y ) , E . < E < E
J
mm —
max
max
anulándose para E < E . y E > E
r
mm
max
En las ecuaciones anteriores y viene dada en (50).
(59)
II -15-
5.3.-ESPECTRO DE LOS NEUTRONES DE DISPERSIÓN ELÁSTICA EN LA TERMALIZACION.
En el caso de termalizacion, de (17) se obtiene que la dispersión elás.tica es isótropa en C, por lo cual los desarrollos en serie de polinomios de
Legendre del §5.2.2, quedan reducidos al primer término, o bien el espectro
de los neutrones de dispersión elástica viene dado en (.4-8 y 49).
5.4.-ESPECTRO DE LOS NEUTRONES DE DISPERSIÓN ELÁSTICA EN LA MODERACIÓN.
En el caso de moderación, de (17),la cual está tabulada en la Tabla 1,1,
se obtiene que la dispersión elástica puede ser anisotropa en C, aunque solo
basta considerar dos o tres términos del desarrollo en serie de polinomios
de Legendre.
Como entonces la velocidad de los núcleos es despreciable frente a la de
los neutrones, basta hacer en las ecuaciones de los §5.1 y §5.2 v' - 0 , luego
v' = vT' ,
Lr
Ln
i+M 1
V
Cn
= v
vT
= —i-r- vT'
LnN
. ,,i Ln
1+M
(60)
v' =
CN
(.61)
Ln
'
^ r v' = -vT „
„ . w i Ln
LnN
Cn = ~ T VLn' VCN = VCN = 7 7 T vLn
1+M
obteniéndose l a f i g . 3 , 1 1 .
5 . 4 . 1 . - RELACIÓN ENTRE v,
(62)
1+M
y er .
Del §5.1.1, se obtiene
i
(vT )
= v' , E
= E ! , (v_ ) . =—:
Ln max
Ln
max
" Ln m m M i
i
m = M , a
i
v' = /ai v' , E . = a E' (.63)
Ln
Ln
mm
n1-^ 9
= (iVi)
(64)
i2
M
v
= — v' (1+a ) + (1-a ) eos
Ln
2 Ln [_
eos 6Cn
J
+ 2M~ eos Q
n
:
M l 2 + 2M 1 eos 6
=
r~^
12
5.4.2.- RELACIÓN ENTRE v L p y
De (36), resulta
2
v
.
= eos 6
LXi
2 ¡
—v' 'ct-^-
Ln
=
vT
iv
i
M +1 Ln
—— =—
¿
vi (1 - 4 1 )
y'
Ln Ln
+ 1
Ln
Ln
v'
M -1 Ln
¿
vT
Ln
+ 1
(66)
II -16-
5.4.3.- RELACIÓN ENTRE 6 r n y e . .
un
Ln
De (38), se obtiene
1 + M 1 eos 8
U = eos 0
=
(68)
/ M i2 + 2M 1 eos 6 C n + 1
5.4.4.- CASO DE DISPERSIÓN ELÁSTICA ANISOTROPA EN C.
En este caso, de (58 y 59) se obtiene
^X
v'
1 - a
1=0
2
(69)
V
2M
T
Ln
anulándose para vT
< /a 1 v' , vr
> v'
Ln
Ln
Ln
Ln
1 - a
1=0
ó(y - y ) , a 1 E' < E < E'
P
1
(70)
i
2M
anulándose para E < a
E'
y
E>E'.
En (69 y 70) y viene dada en (.50).
Los valores medios (51 a 53) son en este caso
<£-> = ~ (1 - a 1 ),
L
<ln ^-> = 1 + —
,- ln a1, <y> = -\
¿
1 - a
3M
¿
(71)
5.5.-ESPECTRO DE LOS NEUTRONES DE DISPERSIÓN ELÁSTICA EN NÚCLEOS DE MASA
INFINITA.
Cuando se supone que M =°°, de los párrafos anteriores se obtiene
— V
V"'
LN
— V
LN
~ \r ^
LnN
CN
~ v
VT
— 0
CN
'
=
V
V
Ln
vi = v' ='vT
= vn
Ln
Cn
Ln
Cn
Cn'
— V
Ln
Cn'
(72)
y los sistemas L y C coinciden
(vT
)
= (vT ) .
Ln max
Ln m m
= v. ,
Ln
a
= 1
El espectro correspondiente, valdrá
(73)
II -17-
9' -*• vT nT , 0) = ~
1(vJ
l
Ln Ln
Ln Ln
M-TT
6.-
6(vJ
Ln
- vT )
Ln
ESPECTRO DE LOS NEUTRONES DE DISPERSIÓN INELASTICA CON NÚCLEOS LIBRES.
Al no tener en cuenta la modificación de los estados cuánticos vibracio-
nal o rotacional de la molécula o del cristal, la dispersión inelástica solo
se produce cuando el núcleo residual queda en un estado excitado.
En este caso de considerar los núcleos libres, según la Hipótesis VII,
la dispersión inelástica solo se aplicará
a los núcleos pesados, siendo isc^
tropa en L.
6.1.-Cuando el núcleo compuesto está altamente excitado, y por tanto, los niveles energéticos son tan densos que pueden considerarse como continuos, el
(1)
modelo de evaporación del núcleo compuesto
, da resultados aceptables. En
este modelo, la emisión de los neutrones de dispersión elástica puede asimilarse a la evaporación de las moléculas de una gota líquida, la cual se ajusta a una distribución maxwelliana, caracterizada por una temperatura nuclear
dada por
0 =
3.226
(75)
Mev
En estas condiciones, el espectro de los neutrones de dispersión inelás(2)
tica, viene dado por
>4(.E' - E, 0) = fCE)
~E/0
(76)
siendo
1,
f(.E) =
E > 0.5 Mev
Jl
15
,
E < 0.5 Mev
(77)
'O
0
el cual se ajusta a las medidas en reactores rápidos.
(1)
Velarde, G. - Véase ref. 1, pág. 1.
(2)
Okrent, D., Avery, R., Hummel, H.H. - Proc. Int. Conf. Ginebra 5, 357
(1955).
O
0.2
0.4
0.5
0.8
1.0
1.2
0
0.2
0.4
0.6
Fig.- 1,11
0.8
1.0
1.2
1.4 1.5
sistema L
sistema C
núcleo antes de
la dispersión
neutrón después
de la dispersión
núcleo ,después
de la/dispersión
neutrón antes de
la dispersión
FIG. 2,11
neutrón después
de la dispersión
ViLn
neutrón antes
de la dispersión
\
"'
\de la dispersión
\
\
\
núcleo después
de la dispersión
\
\
FIG. 3, II
III -1-
III.-ECUACIONES INTEGRODIFERENCIALES DE BOLTZMANN DEL TRANSPORTE DE NEUTRONES.
1.-
ECUACIÓN DEL BALANCE DE NEUTRONES.
La ecuación correspondiente a la densidad fásica neutrónica, se obtie-
ne al plantear el balance entre las pérdidas y las ganancias de neutrones.
Esta ecuación se establecerá para la densidad n(r,vfi,t), en vez de para
n(r,v,t), con objeto de evitar el factor v
en los espectros de neutrones
secundarios.
Sea R. un subespacio arbitrario de R y S Q S U superficie exterior, con
re R o c R.
Se considera una determinada clase de neutrones, caracterizados por
que en el instantet, tienen un modulo de velocidad dentro de dv en v y una
dirección dentro de dfi en ti.
1.1.'-PERDÍDAS POR FUGAS.
El número de neutrones de la clase considerada, perdidos por fugas a
través de la superficie exterior S_, durante dt, es
n(ro,v^,t)dvdí2
dt dS Q
= -dvd dt fi-Vv n(r,vn,t)dr
(1)
con la integración extendida para todo re R n , r.e5_.
1.2.-PERDIDAS POR COLISIONES.
Cualquier neutrón que sufra una colisión, deja de pertenecer a la clase de neutrones considerada, ya que es absorbido, o sufre una dispersión, en
la cual modifica el módulo de su velocidad, su dirección, o ambas cosas. El
número de neutrones de la clase considerada, perdidos por colisiones en R ,
ü
durante dt, es
-I
R^(í,vQ,v
^(í,ví,vLN
0LN
,t)d?dvdí2dvLNdnLNdt = -dvdíídt n(r s vft,t) I J ~ N 1 (r,t)
LN í
LN,t)d?c
. N^v
) a * ( v )v
LN
t
r
dv TM dP,
r
LN
T
dr"
(2)
LN
con la integración extendida para todo re Rfi; v tiT 6 Vxti.
1.3.-GANANCIAS POR DISPERSIONES Y FISIONES.
Un neutrón incidente o primario de velocidad v' al producir en el ins-
III - 2 -
t' un proceso de dispersión o fisión, con un núcleo i de velocidad v' ,
puede dar lugar a neutrones secundarios de la clase considerada. El núme_
ro de neutrones secundarios de la clase considerada, producidos por las
dispersiones y fisiones en R Q , durante dt, es
^ J
con la integración extendida para todo r e R
/
[^v'fr.f-vS, t;
; v'ü' , v' ü' e Vxíí ; t' > t ,
y siendo x = s,f; p,d.
1.3.1.- Para los neutrones de dispersión, teniendo en cuenta (17,1; 18,1;
19^1 y 32,1), el término anterior toma la forma
^(v,t) N X (v¿ N ) a¡CvM x^v'í'-.víj v<Jí'w) v¿ n(?,v'^',t).
dvdfldt i i ±
• dv dí2 dv
LN
ÚQJ
(4-)
dr
LN
1.3.2.- Para los neutrones instantáneos de fisión, teniendo en cuenta (25,1
y 27,1), el término (3) vale
dvdfidt Y ji- x 1 ( v )
T^T N 1 (r,t) N 1 (v' T ) v ^ v 1 ) a^(v' ) v1
h 4-ir p
J 4ÍT
LN
p r
f r
i
1.3.3.- Para los neutrones retardados de fisión, teniendo en cuenta (26,1
y 28, I ) , el término (3) se transforma en
dvdfidt I ¿ : X d
i,d
(
J
t-X'1) dv'dft'dv' Tdí2' dr
d
LN LÍN
(6)
El término anterior puede sustituirse por otro más apto para el estudio de la cinética neutrónica, teniendo en cuenta que
A,C,(r,t)drdt es el
número de precursores d desintegrados dentro de dr en r, en el intervalo dt
en t, y que según la definición de C,, dada en el §2.2, I, es igual al núme
ro de neutrones retardados d emitidos dentro de dr en r, en el intervalo dt
en t. El número de neutrones retardados d, pertenecientes a la clase de neu_
trones considerados en este balance, producidos en R , durante dt, serán eii
tonc.es
III -3-
A,C,(r,t)drdt
dd
7—
xJ(v)dvdí2
= dvdQdt I •— X x H ( v )
C ( r , t ) d r (7)
d
con la integración extendida para todo r e R .
1.4.-GANANCIAS POR FUENTES INDEPENDIENTES.
Sea Q(r,vO,t) la densidad fásica de fuente neutronica independiente,
o simplemente densidad de fuente. El número de neutrones de la clase considerada, emitidos por la fuente en R , durante dt, es
Q(r,vfi,t)drdvdQdt = dvdftdt
Q(r,v^,t) dr
(8)
1.5.-El balance neutrónico se establece al igualar la suma algebraica de
las pérdidas y las ganancias de neutrones, a la variación temporal de la
densidad fásica neutronica (1, I ) . Como R un subespacio arbitrario de R,
resulta,
^-n(r,vfi,t) =-n.Vvn(r,vn,t) -n(r,v«,t) \ N ^ r . t )
~ N ^ v ^ ) °Í(vr)•
o _ ( v ) v n ( i " . v ñ , t ) dv dü d v i dü
+ ) -,— y , v v ) A, C , ( . r , t ; +
f r
T>
'
'
JJN LN
T 4TT d
d d
d
Q(r,vfi,t)
(9)
Ecuaciones análogas a la anterior, pueden obtenerse para las densidades neutrónicas n(r,EÍ2,t), n(r,uíí,t), n(r,v,t), n(r,u,t), y para las de los
flujos correspondientes <j> =vn.
La ecuación anterior es una ecuación integrodiferencial lineal, llamada ecuación general de Boltzmann del transporte de neutrones, la cual debe
completarse con la correspondiente para la densidad de precursores de neutrones retardados, que se obtendrá en el párrafo siguiente.
1.5.1.- En vez de v~ y v,, se suelen emplear las fracciones de neutrones re_
tardados (14, I) y la v 1 ,
Vp(v;) = fsjj vi(v;)= (i-e1) v V ) , vj(v;) = ej vV;)
do)
III -1+-
2.-
ECUACIONES DEL BALANCE DE PRECURSORES.
La ecuación correspondiente a la densidad de precursores de neutrones
retardados, se obtiene, análogamente al caso anterior estableciendo el balance entre las pérdidas y ganancias de estos precursores.
Se consideran los precursores d, que en el instante t están situados
enRQ.
2.1.- PERDIDAS POR FUGAS.
De acuerdo con la Hipótesis XII, los precursores de neutrones retardados se consideran en reposo, por lo que las perdidas por fugas a través de
S. serán nulas.
2.2.-PERDIDAS POR DESINTEGRACIONES.
El número de precursores d, perdidos por desintegración en R , durante
dt, es
-|X d
C d (r,t) drdt = -dt
C d (r,t) dr
(11)
2.3.-GANANCIAS POR FISIONES.
El número de precursores d producidos por fisiones en R~ , durante dt,
es igual al número de fisiones originadas en R
durante dt, multiplicado
por la probabilidad de que en la fisión se emita un precursor d. Teniendo
en cuenta que en la definición de C-, dada en el §2.2,1, se incluía la pro_
babilidad de que el precursor d emitiese un neutrón, se obtiene que el número de precursores d es igual al número de neutrones retardados producidos por fisiones en R.., durante dt, o sea
.,t) vj(v') d?dv'díl'dv' d$i'
dfl^ dt=dt I
V
2.4.-
dv
'
El balance de precursores d, se obtiene, análogamente al caso de
los neutrones, igualando la suma algebraica de las pérdidas y ganancias,
a la variación temporal de la densidad de estos precursores (1,1). Al ser
R_ arbitrario, resulta
£ Cd(?,t) =-Ad Cd(?,t)
vhv,t) f ¿r
) vj(v') aj(v') v' n(r,v'3't)
(13)
III -5-
obteniéndose ecuaciones análogas para las restantes densidades de neutrones
y de flujo.
Las dos ecuaciones lineales anteriores (9 y 13) forman el sistema de ecua
ciones integrodiferenciales generales de Boltzmann del transporte de neutro^nes,
que en unión de las ecuaciones del quemado (
termohidráulicas (
,VI) y de las ecuaciones
,VI), constituyen las ecuaciones generales del reactor.
3.- CONDICIONES GENERALES, DE CONTINUIDAD, DE CONTORNO, E INICIALES.
Teniendo en cuenta la naturaleza física del problema, la densidad fásica neutrónica debe cumplir determinadas condiciones. Ademas, para poder
resolver el sistema de ecuaciones integrodiferenciales (9 y 13) debe especificarse las condiciones de contorno e iniciales.
3.1.-CONDICIONES GENERALES Y DE CONTINUIDAD.
Estas son:
i) n(r,vQ,t) debe ser real, finita, y no negativa, para todo v,vü
eRxl/xfi, t > t .
ii) n(r,vQ,t) debe ser función continua de r en la direcciónti,para
todo r,vti e R x 1/ xfi, t > t .
La condición ii) se aplica a todo el reactor cuando las fuentes neutrónicas son continuas. En particular, puede aplicarse a la superficie S~ ,
supuesta sin fuentes, que separa dos regiones del reactor con materiales
distintos, es decir, en la superficie de discontinuidad de las secciones
eficaces que intervienen en las ecuaciones del transporte de neutrones. En
R'
estas condiciones, el número de neutrones por unidad de tiempo en t
que
-
*
•
-
»
•
-
>
-
>
•
atraviesan la unidad de superficie normal a ü en r' = r. - R'íí, debe ser
igual al número de neutrones por unidad de tiempo en t + — que atraviesan
la unidad de superficie normal atien r = r +RS¿, cuando R,R' -»• 0, fig. 1.
0 de otro modo, las densidades fásicas de flujo o de neutrones, <Hr + Rfi,
vfi, t + —) = vn(rn+Rfi, vfi, t + —) deben ser funciones continuas de R para
R=0,
y para todo r eS Q , vti e V xü, t > t .
Nótese que n(r, víí, t) no necesita que sea función continua de v,fí,
ya que por ejemplo, en el caso de un haz colimado de neutrones en un medio
no dispersor ni fisionable y sin fuentes neutronicas, para valores detidi
ferentes de los de propagación del haz, n(r,vfi,t) se anula, presentando una
discontinuidad.
Cuando existen fuentes puntuales o superficiales, la densidad fásica
neutrónica es discontinua, pero el problema puede solucionarse expresando
III -6-
las fuentes mediante las correspondientes deltas de Dirac.
3.2.-CONDICIONES DE CONTORNO.
La superficie exterior S de R, es decir, la superficie exterior del
reactor considerado, debe cumplir las siguientes condiciones:
i) Ser una superficie bien definida, es decir, la densidad nuclear
en todo punto exterior a la superficie debe ser despreciable com
parada con la interior.
ii) No tener entrantes, es decir, todos los puntos de cualquier segmento que una dos puntos del reactor, pertenecen al reactor. Si
la superficie real del reactor tuviese entrantes, se consideraría
como superficie exterior del reactor a una superficie ficticia,
sin entrantes, en cuyo interior se encontraría todo el reactor y
parte de la región vacía incorporada al reactor original al suprimir los entrantes.
3.2.1.- Si se supone que no hay fuentes de neutrones fuera del reactor, o
sea exteriores a R, ni sobre S, a la superficie S se la llama superficie
libre, indicando con ello que se verifican las dos condiciones anteriores
i) y ii) y que no existen neutrones entrantes en el reactor.
La condición de contorno correspondiente a la superficie libre, es
n(r ,vfi,t) = 0,
para n • ü < 0, r e S
s
s
s
siendo n la normal exterior a S en r .
s
s
(14)
3.2.2.- Si el reactor se extiende al infinito, aunque en el existiesen
fuentes de neutrones, se supone que el número de neutrones que vienen directamente del infinito a la región considerada, sin sufrir colisión, es
nulo.
3.3.-CONDICIONES INICIALES.
En los problemas temporales, es necesario especificar las condiciones iniciales, o sea los valores de n(r,ví2,0) y C,(r,0).
3.4.-ESPACIO DE FUNCIONES.
El conjunto de funciones que cumplen las condiciones generales, de
continuidad, y de contorno anteriores, definen el espacio de funciones F.
Mientras que las que cumplen solamente las condiciones de continuidad y
contorno definen el F C F.
c
4.- FORMAS COMPACTAS DE LAS ECUACIONES GENERALES DE BOLTZMANN DEL TRANSPORTE DE NEUTRONES.
Con objeto de evitar la laboriosa formulación de las ecuaciones (9 y
III -7-
13), se suelen emplear en forma más compacta, tal como se hace a continuación.
4.1.-SECCIONES EFICACES EVALUADAS A LA VELOCIDAD DEL NEUTRÓN.
En las ecuaciones (9 y 13) se ha expresado explícitamente la dependencia
de las diversas magnitudes con la velocidad de los núcleos y con la velocidad
relativa del neutrón respecto del núcleo. Teniendo en cuenta que en estas ecua
ciones v. „ y Í2. „ son variables mudas, es conveniente efectuar el siguiente cam
bio de notación
•
dv
LN
díí
LN
R*(r,vfi,t)
o (v) - - ,
—
a
N (?)
^x
v
'
1
ua ( vv ' )
xv " '
(?vSt)
= V- U L N ^ V -LN
. . ) < T ( V ) v dvT.T díl T
X P r LN LN
N
(16)
= vvv1 s( V ) u a v1 s( V y) = -v!i! - \~U-IT NVa (vJI,N
) v 1 ( v t ) 1 ( v ' ) v ' dv \, do_'
x " ' x "
~ v IU-TT *' " L MN ' v x vw r 'r> u xa vx" r ' " r ^ " LTN "°°LN
a1(v')
.s
IxtCv'n1 -> vfi) dv dü = 1
• v^ d v ¿ N dpJ>T,
(18)
Las a (v) se llaman secciones eficaces microscópicas del proceso x en
los núcleos i, evaluadas a la velocidad del neutrón, las cuales dependen, a
través de N (V-N) de la temperatura del medio T(r,t), y demás parámetros que
intervienen en el espectro nuclear. En determinados casos particulares,
den simplificarse considerablemente
i) Fuera de las resonancias, las secciones eficaces microscópicas de
captura y fisión siguen la ley 1/v, luego
p
v
0
= 12. CTi(Vo), x = c,f
Q
ii) Fuera de las resonancias, como la sección eficaz microscópica de dis
t>ersión es una función suave de v , se tiene
r
i/- \
(3
n-
V
,
V >> V T „,
s r '
LN'
o~(v) =
V
^ V
r
(20)
f(T,v),
v % vLN
iii) Dentro de las resonancias, como entonces a (v ) no es una función sua
ve de v , aunque sea v
integrando, con lo cual
'v v, la sección eficaz no puede sacarse del
III - 8 -
a (v) = f(T, v, parámetros de la resonancia)
(21)
4.1.1.- Con objeto de simplificar la notación, se introducen las secciones
eficaces macroscópicas del proceso x en los núcleos i, por
lX(v,v,t)
X
= N X (r,t) a a ( v ) ,
X
x = s,c,f
(22)
y 1 (r,v'Q'-^vn. t ) = y (r,v',t) x"L(v'^'-> vü) ,
''S
'
S
S
J <-'S
-> vñ,t) ávdü = y1(r,v' t)
(23)
Además se suprimirán los superíndices i, indicativos de la especie del
núcleo blanco, mediante la notación
i
i
i
Por último se hará,
Pd(r\v,t) = x d (v) Cd(r,t) ,
P = I ?d
d
(25)
4.1.2.- Al sustituir las expresiones anteriores en (9 y 13) se obtienen las
ecuaciones generales de Boltzmann del transporte de neutrones, en forma coii
densada
1
v
3
-
>
-
v
3t * r ' V '
t —
# / • • *r • V* "
* '
'
1 Xá Pd(r,v,t) + Q(r,v^,t),
d
•^- P d (r,v s t) =-X
V
•*"
^ ^
¿tl-r5v5
<p(.r,v ,
í
v
j¿s(.r,v
4> e F
P (r,v,t) +x d (v) B d
^
(26)
v(v') ^ f (r,v',t) ^>(r,v'^',t) dv'dfi',
<j> e F
(27)
4.1.3.- Eliminando X,P,, y teniendo en cuenta (16, I ) , resulta
v 3t
'
'
4-TT
3t
' '
^ ^
-> v ,
'
'
^"t
' '
'
'
III -9-
v(v') If(r,v! ,t) •
1
( ? ' f i 1 ,t) dv'dfi' + Q(r,vft,t),
<}>(?,v'fi
<j) e F
(28)
en unión de la ecuación (28).
4.1.4.- Resolviendo la ecuación (27), según (14,IV), resulta
-í->
~Xñt i 1
-x,(t-t!)
(
P d (r,v,t) =P d (r,v,0) e
+
dt' e
x d (v) &á v(v') £f(r",v',t') •
• <Kr,v'n! ,t' ) dv'dn1
(29)
que sustituida en (26), dá
i ~
(?(?,vQ,t) =-n-V <f>(r,vfi,t) -lt(r,v,t)
<j)(?,v^,t) + I s ( r " , v ' f i ' •*• vfi,t) •
• « K r . v ' n ' , t ) dv'dfi 1 + ¡— X (v) (1-B) I v ( v ' ) ^ f ( r , v ' , t )
+ —
^
ó(?,v'fi' , t ) dv'dñ' +
rt
-A ( t - f )
(_^
I dt' e
Xd x d ( v ) e d v ( v ' ) y . f ( r , v ' , t ' )
^
^
^ ( r ^ ' Q 1 , t ! ) dv'da'+
- X , t "i
Q(r,v^,t) + —
I X¿ P d (r,v,0) e
|,
<j> e F
(30)
J
d
4.2.- OPERADORES DE EVOLUCIÓN.
Las ecuaciones del transporte de neutrones (26 y 27) o las (28 y 27) pue
den expresarse en forma más compacta, definiendo los siguientes operadores de
evolución:
L = -Ú V
R
operador diferencial lineal de fugas (losses), definido en R.
(31)
- - ¿ (r,v,t)
X
operador numérico de extracción (removal), con x = a 3 s,t.
~
(32)
X
S = dv'dfi' ¿
s (r,v'fi' ->ví2,t)* operador integral lineal de dispersión (scaJ
~
ttering), definido en V x
fi.
(33)
=
F
Jí
T^r X (v) B
4" t!
X
dv'dQ' v(v') ^ £ (r,v',t)*
X J
operador integral
J»
lineal de fisión, definido en V xfi,con x = p,d, y sin subíndice
para x = f.
(34)
M =L + R + S
B = M+F = L+R^ + S + F
(35)
operador de balance o de Boltzmann
habiéndose representado por
(36)
• la función sobre la que operan S y F^ .
Con objeto de indicar las variables indpendientes que intervienen, si 0
es uno cualesquiera de los operadores anteriores, se empleará la notación
0 <¡> 5 0 cj>(r,vf2,t) = (0 <f>) (r,vÓ,t), suprimiéndose el argumento cuando no dé
III -10-
lugar a confusión.
4.2.1.- Al sustituir estos operadores en (26 y 27), se obtienen las ecuaciones generales de Boltzmann del transporte de neutrones, en forma opera_
cional
v 1 4z ó = (L+R. +S+F )(j)+ 7 f-yx, P, + Q= (M+F )
dt '
D
T
=
d
p
- Í 7 Xd P d
4.2.2.- Eliminando X
47T ^
+ F
d *' *
Q
e
Q
P
(37)
(38)
F
P , o bien de (28 y 27), resulta
•¿r * + ¿r 4r P = (L+R.+S+F) 4> + Q =
= (M+F) <j> + Q =
eF
(39)
4.3.-MATRICES DE EVOLUCIÓN.
Las ecuaciones (37 y 38) pueden expresarse en forma matricial, definiendo las siguientes matrices de evolución, cuyos elementos son los operadores de evolución anteriores:
V=
V
0
0
1
o ;
0 j
0
0
1
0
0
i
;
0
0
0
o !
1
(40)
(M+F )
"• '
C=
F
l
F
2
X
P
dm
d
0
0
0
~X2
0
0
0
x
- !
m
y los vectores
Q
0
1
s =
Air
m
(42)
llamándose a C matriz cinética y a s vector fuente. Sustituyendo estas ma
trices en (37 y 38) se obtiene la ecuación general de Boltzmann del transporte de neutrones, en forma matricial
ot
5.-
ELIMINACIÓN DE VARIABLES Y FUNCIONES.
Los métodos de resolución de las ecuaciones generales de Boltzmann del
transporte de neutrones, se basan en un proceso sucesivo de promedio de se£
ciones eficaces. Para lo cual se parte de las ecuaciones anteriores aplicadas a casos particulares, después de haber eliminado algunas variables. De
este modo, su resolución es menos laboriosa.
En este párrafo se incluyen las eliminaciones directas de las variables
que intervienen en el problema, dejando para otros capítulos los desarrollos de las funciones de densidad (desarrollo de la dependencia angular, por
ejemplo, en armónicos esféricos; desarrollo de la dependencia espacial en s_e_
rie de Fourrier,...).
5.1.-ELIMINACIÓN DE LA POSICIÓN.
Cuando se verifica que:
i) Medio homogéneo, N (r,t) = N (t)
£ (r,v,t) =£ (v,t).
ii) Medio infinito.
iii) Fuentes uniformes, Q(r,v°, ,t) = Q(vQ,t) .
iv) Densidades iniciales de flujo y de precursores uniformes, <j>(r,vfi,0) =
= <j>(vñ,0), C,(r,0) = C,(0,0) = constante distinta para cada clase d.
no habrá en el medio ningún punto preferente o de referencia, con lo que el
flujo deberá ser uniforme.
En este caso las ecuaciones (28 y 27) se simplifican en
P(v,t) = - L ( v , t )
•dv'dQ' +~
x f (v)
v(v') lf (v1 ,t) cKv'fi'jt) dv'díí' + Q( vfl,t) , <f> e F
-^r P d (v,t) =-X d P d (v,t) +X d (v) B d ív(v')
(f> e F
y las (39 y 38), en
III -12-
v 1-|^(|)(vn,t) +~
¿ ^
j£ P(v,t) = ((Rt+S+F)(j)) (vfi,t) +Q(vfi,t),
M F
F d ( v ,t)=-¿-X d P d (v 5 t) + (F d «,) (v,t), * 6 F
(47)
5.2.-ELIMINACIÓN DE LA DIRECCIÓN DE LOS NEUTRONES.
Como las secciones eficaces no diferenciales, y las densidades de nú
cieos se han supuesto isótropas en L (32,1 y 1 7 , 1 ) , llamando a
J(r,v,t) = m
<j)(r,vfi,t) dtt
(.4-8)
densidad de corriente neutrónica, o simplemente corriente, y teniendo en
cuenta que
[ (r,v'ti1 -*• ví2,t) áti = I (r,v! -> v,t)
s
s
al integrar las ecuaciones (28 y 27) para todo ti e ti, resulta
- T - ^(r,v,t) + T - P(r,v,t) — ?
V Ot
J(r,v,t) - L(r,v,t) <¡>(r,v,t) +
01
L
^(r,vT •*• v,t) é(r,v',t) dv' +Xx:( v ) N í v ' ) ¿jr(r5v' »"t) <|>(r,v't) dv'
+ Q(r,v,t) ,
^
<j) 6 F
. (50)
P d (?,v,t) = - X d P d (r,v,t) + x d ( v ) 3 d (v(v') ^ f (?,v't) <ji(?,v' ,t) dv',
<f> £ F
(51)
y análogamente para las (39 y 3 8 ) ,
- -¿r <f>(r,v,t) + ~ P(r,v,t) =-V J(r,v s t) + ((R.+S+F)*) (r,v,t) +
V
OL
+ Q(?,v,t),
01
T-
(j) e F
(52)
¿••¿P d (?,v,t)=¿ r A d P d (?,v,t) + (Fd *) (í,v,t),
*e F
(í
5.2.1.-Cuando, según el problema considerado, no se precise conocer la de
pendencia angular del flujo, pudiera parecer a primera vista que la solución de las ecuaciones (50 y 51) es más fácil que la de las (28 y 27), ya
III -13-
que se han eliminado dos variables independientes. Sin embargo, está simpli_
ficación es solo aparente, ya que para poder resolver las ecuaciones (50 y
51) se precisaría conocer J(r,v,t), para lo cual habría que resolver prime_
ramente las ecuaciones (26 y 27), luego por (4-8), obtener J(r,v,t), y por fin
resolver las (50 y 51) ', cuando en realidad, una vez resueltas las (28 y 27)
se obtendría directamente <j>(r,v,t) = <j>(r,vfl,t) dti. No obstante, en la práctica, la simplificación puede ser importante, ya que en algunos casos partí
culares es posible sustituir aproximadamente J por una función sencilla de
<j>, tal como sucede en la aproximación de la difusión.
5.3.-ELIMINACIÓN DE LA VELOCIDAD NEUTRONICA. MULTIGRUPOS.
Al integrar las ecuaciones generales de Boltzmann para toda v e
siendo V
el segmento de extremos v
., v , con g = 1, 2, . . . , s
V C V,
indicando
el grupo energético de neutrones, y v. = c o , v_ +j_ = 0, se" obtienen expresiones
l
fem
f
CT
de l a forma
°
Jv
y
_i.
¿ ( r , v 5 t ) cj>(r 3 vn 5 t) d.v5 l a s c u a l e s pueden descomponerse en
g+i x
el producto de un flujo integrado en el grupo g
O"
<j>(r,vfi,t) d v
C5M-)
Vi
y de una sección eficaz macroscópica promediada en el grupo g
I (r,v,t) (j)(r,vO,t) dv
(55)
De este modo, el sistema de 1+d
y 27) se transforma en g +d
ecuaciones generales de Boltzmann (28
ecuaciones con <p , P,, g = l,2,..., g , d =
1,2,
X
dg
..., d incógnitas,
= — - P, .. Este nuevo sistema de ecuaciones,
&
y ya H que P,
m
dg
x d i dg'
se llama de multigrupos energéticos de neutrones.
5.3.1.- Lógicamente, para obtener los ¡j> (r,fi,t) habría que calcular previamente los <¡>,(r,vñ,t) resolviendo el sistema (28 y 27), luego se obtendrían
las \
xg
(r,u,t) por (55), y por último se resolverían las ecuaciones de mul-
tigrupos anteriores, siguiendo un proceso innecesario, ya que obtenidos los
<j>(r,vfi5 t ) , por (54) se calcularían los <j> (r,Q,t).
o
En la práctica, se sigue un proceso sucesivo de promedio de secciones
eficaces. Primeramente, se emplean las secciones eficaces microscópicas di-
III -11+-
rectamente obtenidas de las librerías primarias (con varios miles de grupos de neutrones), y con ellas se resuelven las ecuaciones (28 y 27) apljL
cadas a casos muy simplificados: régimen estacionario; medio homogéneo e
infinito o seminfinito; eliminación de la dependencia angular o desarrollo de la dependencia angular del flujo, por ejemplo en armónicos esféri
eos;
valores asintóticos del flujo,... Con los flujos obtenidos en estas
condiciones, se promedian las secciones eficaces microscópicas, condensar^
do el número de grupos a unos pocos ( l a unos 30)
rv
(v) dv
-X.
g+1
ó (v) dv
V
(56)
g+1
siendo <j> el 1-simo término del desarrollo angular del flujo, y g el orden del grupo en un sistema de pocos grupos. Partiendo de estas secciones
eficaces microscópicas se obtienen las macroscópicas, que son los coeficientes del sistema de ecuaciones (28 y 27). Por último, se resuelve este
sistema de ecuaciones aplicado a la configuración y composición real del
reactor.
5.3.2.- SECCIONES EFICACES FUNCIÓN ESCALERA DE LA VELOCIDAD NEUTRONICA.
En el
caso ficticio de que las secciones eficaces fuesen función es
calera de la velocidad del neutrón, las ecuaciones de multigrupos en régi
men estacionario, suponiendo que se verifica la Hipótesis VI, toman una
forma muy simplificada.
En este caso, se tiene
= v
. jv^-h =
(57)
x(v)
(r,v'-*-v, n 1 -ü) dv
(58)
e+1
y haciendo
•v
*(?,«) =
<}>(r,ví2)dv,
ñ+1
Q
g+1
con v'e 1/ ,, ve \¡ ==>
o
Xx(v)dv,
xg
o
v
! + 1 f. v ' ^ v 5 v
o '1
&
(59)
+117£
o -I-
V
» a l integrar la ecuación
g
(28) en régimen estacionario, en el grupo g, se obtiene
Q< = 1 '
Q(r,vQ)dv
III -15-
g
+
x
¿F fg f_ V ^fg'(?) K ' ( ? ^ M dü'+ Q g <^>=°. *geF
y para el caso de eliminar la dependencia angular, integrando (60) para to
do ü e ü, resulta
S
m
+x
fg L v W ( ? ) v ( í ) + Qg(?)= °' *g eF
En las ecuaciones anteriores cuando no hay dispersión con ganancia"de
energía, se verifica
W
= o
Ig,.g = 0
'
v-n-'g^8'<g
,
vg, < v g + 1 = = > g ' >g
(62)
(63)
5.3.2.1.- Aparte de las consideraciones sobre la densidad de corriente, dadas en el §5.2.1, el suponer que las secciones eficaces son función escalera de la velocidad del neutrón, supone una aproximación rudimentaria al método indicado en el §5.3.1. El suponer que se cumple la expresión (58), introduce otra aproximación más burda, ya que cuando el neutrón incidente tie
ne la velocidad v', el dispersado elásticamente tendrá la velocidad v, la
cual, según se demostró
<_ v <
en (.63,11)., estará situada en el intervalo va1 v'<
v' . Si por ejemplo, v' está comprendida en el grupo g-1, o sea v
<
O
< vT < v
, dividiendo este intervalo en dos subintervalos: v
— y — T % < v' < v
< vT <
, , resultará que cuando v' pertenezca al primero, v
estará situada en Va1 v < v < —==, y (58) tomará cierto valor: mientras que
g - /ax
cuando v1 pertenezca al segundo subintervalo, v estará situada en v
f_v
< v <
y (58) será nula. Por tanto, para dos valores de v' en el grupo g, le
corresponden dos valores diferentes de (58), en contra de lo supuesto.
5.4.-ELIMINACIÓN DE LA VELOCIDAD NUCLEAR. MODERACIÓN.
En los reactores nucleares, las energías medias de los núcleos, corres
pondientes a la temperatura del medio, son inferiores a 0.1 ev. Por otro la
do,
la probabilidad de que un neutrón de fisión tenga una energía inferior
a los 1.6 ev, es menor del 1% . Por tanto, puede establecerse una energía in
1 2
~
termedia E. = — v. , tal que para v < v., se desprecien los neutrones de fi1
A
X
"
—
2.
sión, y para v > v, se consideren los núcleos en reposo, salvo en la región
III -16-
de las resonancias, que se tratarán por separado.
El valor de E. es arbitrario, y según las librerias de secciones eficaces condensadas en pocos grupos, se suele tomar en E. =0,625 ev.
En estas condiciones, el flujo puede descomponerse en un flujo de mode
ración § , y otro de termali zacion o térmico <
j
> ,
(64)
v. £ v
=<
$_(r,vO,t) ,
0 < v < v.
i
—
—
(65)
i
empleándose en las ecuaciones de Boltzmann, con las condiciones
X (v) = 0 ,
X
v < v. ;
—
-i
v
=v ,
I
v > v.
—
(66)
1
5.4.1.- ECUACIONES DE BOLTZMANN PARA LA MODERACIÓN DE NEUTRONES.
Estas ecuaciones se obtienende las (28 y 27), teniendo en cuenta (6M- a
66),
- • g - <f>M(r,vfl9t) + ¿ -g- P(r,v,t)
¿ X-(V) v(v!
(r,v'íl' -> vñ,t)
F (67)
'dfi' +Q(r,vQ,t)
(?JvIn'st)dvIdnl
Pd(r\v,t) =-X d Pd(?,v,t) +x d (v) 3 d ív(v')
QdT(r",v,t),
i
;
(j)M,
(68)
<j)T e F
siendo Q^ la densidad de fuente de neutrones debida a las dispersiones y a
las fisiones producidas por neutrones incidentes de velocidad v' < v., y
Q,™ la debida a los neutrones retardados d producidos por neutrones incidentes de velocidad v' < v.,
.v'S1 ,t) dv' dfl1 +^
QT(r,vfi,t) =
í>T(?,v'Q',t) dv'díl1,
v >_v i 5 v 1 < v i ?
Q dT (r,v,t) =x d (v) B d v(v')
x f (v)
v(v')
(69)
<j>T 6 F
3v'Q'
,t)dv'dn' , v
III -17-
<I>T e F
(.70)
Análogamente, las ecuaciones de moderación en forma operacional (39 y
38),
son
V-1
7 F *M
+
P = B
W £
I5TWPd = - ¿
A
d
P
d
+F
*M+
Q + Q
T'
d*+WQdT'
V
V
1 V
>
V
V
' > V ' *M' ^T £
i ' V' ^ V * T 6 F
R71)
(72)
con
€ F
(73)
En el caso de que no se considere la dispersión con ganancia de energía,
el primer término de (69 y 73) sería nulo.
5.4.2.- ECUACIONES DE BOLTZMANN PARA LA TERMALIZACION DE NEUTRONES.
Partiendo de las ecuaciones (28 y 27), y teniendo en cuenta (64 a 66),
resulta
^ —
4>T(?,ví3,t) +~
P(r,v,t) =-fi-V(t)T(r,vn,t) - ^(r.v.t) í>T(r,vfi,t) +
'dQ1
+ Q(r ,vtt,t) + Q^ir ,vfi,t) , v
v.
siendo Q M la densidad de fuente de neutrones debida a las dispersiones producidas por neutrones incidentes de velocidad v1 > v.,
gCr.v'ft1 -»-vfl,t) ^(r.v'íí1 ,t) dv'dfl1 , v<_v i , v'>v., ^
^ 6F
(76)
Análogamente, la ecuación de termalización en forma operacional (39 y
38),
es
v,
con
<|)M, ^
e F
(77)
I I I -18-
QM
= S
^M
'
V
-
V
i'
V
'
> V
i'
^M
£ F
(78)
5.4.3.- Las ecuaciones de moderación (69 y 70) son de estructura más senci
lia que las generales (28 y 27), debido a que fuera de las resonancias se
suponen los núcleos en reposo. Las de termalización (75 y 76) carecen del
termino de fisión. En realidad, lo que se ha hecho es transformar un siste
ira de 1 + d
ecuaciones Íntegrodiferenciales (28 y 27), en un sistema de
2(1 + d ) ecuaciones Íntegrodiferenciales (69, 70, 75 y 76) más sencillas,
que pueden resolverse por un procedimiento iterativo.
En la práctica la simplificación es más importante, ya que en el cálculo de reactores es suficiente emplear valores asintóticos para los flujos
4>M y <j> que intervienen en las fuentes 0,,, Q™, Q,_.
5.5.-ELIMINACIÓN DE LOS NEUTRONES RETARDADOS.
En el caso de la cinética de reactores es importante la contribución
de los neutrones retardados, por lo que ha de tenerse en cuenta la ecuación
(27 ó 38).
Si no se consideran los neutrones retardados, la ecuación general (26),
se simplifica en:
^ TTT <j>(r9vft,t) = -fi'V <f>(r,v£2,t) - I (r,v,t) $(r,vü,t)
• (Kr.v'ft' ,t) dv'díí' + ~
+ Q(r,vQ,t),
X f (v)
v(v') ^ f (r,v',t) ^(r.v'n' ,t) dv'dfi'
tj) £ F
(79)
y l a e c u a c i ó n g e n e r a l o p e r a c i o n a l ( 3 7 ) , p r e s c i n d i e n d o de l o s a r g u m e n t o s , en
v ' 1 -— $ = (L+R.+S+F) <j) + Q = (M+F) <¡>+Q=B<j>+Q,
ot
§ e F
(80)
t
5.5.1.- En los casos particulares considerados en los §5.1 a §5.4, se obtie_
ne para la ecuación operacional:
i) Reactor homogéneo, infinito, con fuente uniforme C+6)
v" 1 ^(j)(vÍt) = ((R,+S+F)í)) (vü,t) +Q(vñ,t),
(f> £ F
ii) Caso de eliminar la dirección de los neutrones (52)
(81)
III
v
1
-19-
j£ <K?,v,t) =-V J(r,v,t) + ((Rt+S+F)(p) (r,v,t) +Q(í,v,t), <j>eF
(82)
iii) Moderación de neutrones (71 y 73)
(83)
Q T = (S+F) 4>T, v >_ v.., v' < v.., (J)T S F
(84)
iv) Termalización de neutrones (77 y 78)
v" 1 ~
«1>T = M <j)T + Q + Q M , v <_ v i S v» <_ v i , <j)T 6 F
Q M = S $M,
v1
V i
,V
(85)
> v ^ <j.M £ F
(86)
5.6.-ELIMINACIÓN DEL TIEMPO. REACTORES CRITICO Y ESTACIONARIO.
El análisis de la dependencia temporal del flujo comprende el estudio
de los reactores crítico y estacionario incluidos en este párrafo, de los
reactores virtualmente críticos dados en el §6, y de la cinética de reactores desarrollada en el cap. VI.
5.6.1.- REACTOR CRITICO.
Se dice que el reactor es crítico en el instante t , cuando se verifica que
~
$(v,vü,tQ) = 0,
^P(r,vQ,t0) = 0
(87)
en cuyo caso, las ecuaciones de Boltzmann del transporte de neutrones (28- y
27),
se reducen a
\.v'n' ,tQ)
^ (v) jv
1
.dv'dQ' + ^ Xf
Xf (v) jv(v') £ f (r\v',t Q ) (K?,v'Q',t 0 ) dv'dfi +Q(í,vfi,t0) = 0
cf> £ F
(88)
y l a s (39 y 38) a
(B ó) ( r , v f i , t 0 )
+ Q(r,vfi,t0)
=0,
(J) e F
(89)
III -20-
5.6.2.- REACTOR ESTACIONARIO.
Se dice que un reactor está en régimen estacionario, o es un reactor
estacionario, en el intervalo de tiempo (t 1 , t " ) , cuando es crítico en cada
instante t
de dicho intervalo.
Si para todo t , t' <_ t Q <_ t" se verifica:
i) Reactor con configuración y composición independientes del tiempo
en el intervalo considerado, o sea N~(r,t 0 ) =N~(r) =]> £ (r,v,t ) =
ii) Fuentes independientes del tiempo en el intervalo considerado, o
sea Q(r,vfi,t0) = Q(r,vQ).
iii) Reactor crítico en un instante cualquiera t. del intervalo, o sea
£*c?,vfi,t0) = o, ¿ p t M . y = o.
al derivar sucesivamente, respecto al tiempo, las ecuaciones (39 y 38), se
obtienen las derivadas sucesivas de <£ y P como funciones homogéneas de — c*>
3
Y TT Pj p°r lo que al anularse estas en t., se anularán todas las derivadas.
ot
0
Como una función que tiene en el instante t
todas sus derivadas nulas, de_
be ser independiente de t, se obtiene que si el reactor es crítico en un ins_
tante cualquiera t
del intervalo (t',t"), lo será en todo instante de dicho
intervalo, mientras perduren las condiciones i) y ii).
6.- REACTORES VIRTUALMENTE CRÍTICOS. ECUACIONES DE VALORES PROPIOS.
Sea un reactor real sin fuentes independientes, cuyo flujo evoluciona
con el tiempo según las ecuaciones del transporte de neutrones. Se considera un reactor ficticio, idéntico al real en un cierto instante, pero con un
parámetro determinado modificado por un sumando o factor constante, de modo
que el reactor así obtenido sea crítico en el instante considerado, por lo
cual se le llama reactor virtualmente crítico.
Procediendo de esta manera, se consigue transformar las ecuaciones tern
porales de Boltzmann, en una ecuación estacionaria de valores propios.
6.1.-REACTOR VIRTUALMENTE CRITICO CON K.
Se define como reactor virtualmente crítico conk, en el instante t-,
al reactor que tiene la misma configuración y composición que tiene el reac
tor real en el instante t , excepto que el número de neutrones emitidos por
fisión queda dividido por un factor constante k, de tal modo que el reactor
virtual así obtenido sea crítico, es decir, tenga un flujo que cumpla la
condición (87).
La ecuación integrodiferencial de Boltzmann del reactor virtualmente
III -21-
crítico, será entonces (28)
v(v') I f (í,v',t 0 ) $k(í,v'Q') dv'dJÍ' = 0 ,
<j>k 6 F c
(90)
o en forma operacional (39), prescindiendo de los argumentos,
s )
^FF*k
=M
\ 4
F
\
; 0
'
*ke Fc
'
(91)
Introduciendo la reactividad p definida por
(92)
la ecuación (91) se transforma en
B <j>k = p F (J)k, $ k e
Fc
(93)
6.1.1.- ECUACIÓN DE VALORES PROPIOS EN K.
Las ecuaciones (90, 91 y 9 3) son ecuaciones de valores propios generalizadas, las cuales pueden transformarse en ordinarias. Teniendo en cuenta
que el operador F puede ser singular, mientras que el M no lo es, admitirá
inverso M
, y la ecuación (91) toma la forma de una ecuación integral
K ¿ k = k <|>k, <j>ke F c
(94)
siendo K el operador de criticidad desarrollado en serie de Neumann en (66,
IV),
y dado por
K = -(L+F^+S)" 1 F = -M" 1 F
(95)
Por tanto, el problema queda reducido a determinar los valores propios
k. y las funciones propias <j>k. e F
del operador K.
6.1.2.- ANÁLISIS DE LA ECUACIÓN DE VALORES PROPIOS.
Es de gran importancia determinar en que condiciones los valores propios
son simples o múltiples, reales o complejos, discretos o continuos, y si exis
te uno de módulo predominante. También interesa determinar las condiciones de
existencia y unicidad de soluciones pertenecientes a F, es decir, cuando exis
te y es única una función propia, que además de satisfacer las condiciones
de continuidad y contorno que satisfacen todas las funciones propias cumpla
la condición de ser real, finita, y no negativa en todo el reactor. Por últi
mo,
es conveniente determinar en que casos las funciones propias forman un
conjunto completo respecto a las funciones pertenecientes a F .
III -22-
6.1.2.1.- Con respecto a los valores propios y a la existencia y unicidad
de soluciones en F, se han analizado las ecuaciones anteriores de valores
propios aplicadas a casos particulares: condiciones restrictivas sobre con_
tinuidad (Shikhov
vicz y Mika
, Vladimirov
y Ebersoldt
) , multigrupos (Borysie-
) , difusión en multigrupos (Habetler y Martino
,.. Mien-
tras no exista un análisis completo de las ecuaciones generales, se consi_
derará la siguiente hipótesis:
HÁ.pótQJ>ÁJ¡
Xl/. - Ex¿ó¿e un valoh. pfiopí.o k , pohÁJtivo y ¿Xmptz. tal
k >|k | , n^O, al cual cohXZÁpowLn una {¡uncÁón pftopia
vfi e R x [/ x ti. Ade/nU, cj>^
e¿> Za única
función
^
e F pana, todo
pnop¿a cíe ¿-¿gno
que.
r,
donhtan-
t<¿ en R x V x ti.
Por tanto, todas las «ji^.e F , y únicamente <j>^ £
F.
6.1.2.2.- Con respecto a las funciones propias, se han obtenido los siguien_
tes resultados:
i) La condición necesaria, pero no suficiente, para que las funciones
propias formen un conjunto completo
, es que se incluyan las in
finitas funciones propias correspondientes al valor propio infini_
tamente degenerado k = 0.
ii) En el caso de que los parámetros nucleares no dependan de la velo(2)
cidad del neutrón, y después de eliminar la dependencia angular
,
las <j>, (r) forman un conjunto completo de funciones propias respeck
to a las funciones pertenecientes a F .
iii) En el caso general existen serias dudas de que las funciones propias formen un conjunto completo.
Cuando se verifican las condiciones necesarias y suficientes para que
las 4>, formen un conjunto completo, cualquier función f e F , puede desarro
liarse en la forma
f = a, r<j>. +• S
a.
é,
+ S an
én
(96)
k n k.
,n ,
k ,m Y k ,m
0,m Y0,m
0
0
n;¿0,k
n n
n n mm n
'n
'n
m
n
habiendo separado los términos de L y k = 0, y representando el subíndice
mn las diversas funciones propias (ta m linealmente independientes, corresn' n
pondientes al mismo valor propio k .
(1)
(2)
(3)
(4)
(5)
(6)
Shikhov, S.B. - Zh. Vychisl. Mat. Mat. Fiz. 7_, 1, 113 (1967).
Vladimirov, V.S. - AECL 1661 (1963).
Ebersoldt, F. - Jul 711 MA (1970).
Borysievicz, M. Mika, J. - Tran. Theo. and Stat. Phy. 2, 3, 243 (1972).
Habetler, G.J. y Martino, M.A. - KAPL 1886 (1958).
Henry, A. - Nuclear Reactor Analysis - MIT Press (1975).
III -23-
6.1.3.- RELACIÓN ENTRE REACTOR CRITICO Y REACTOR VIRTUALMENTE CRITICO.
Si el reactor sin fuentes independientes, es crítico en el instante t , ten
drá por ecuación la (81) B<j>=0, que comparada con la (93), dará entonces el valor
propio P n =0, k =1, y el reactor virtual coincidirá con el real. Pero no recípro_
camente, ya que si p =0, k =1, como la ecuación B<}>-, =0 es distinta de la (39)
-13
1*9
°
v
-KI: 41 + Tt—"•^rP=^(íl> s e r á <j>, ¿$, no teniendo por que verificar <j> la condición
dt
H Tí ot
Kn
de criticidad (87). En resumen,
en un reactor sin
fuentes
si es
=
=
n o independientes,
es
crítico se verifica que Pn 0, k =1; pero s i Pn 05 ^ = 1 ,
según (
j> tiende
5VI)(
e s t i c o , aunque
asintoticamente a <j>, .
K
0
6.1.4.- SIGNIFICADO FÍSICO DE K Q .
Integrando (90) en todo el espacio fásico R x V x Q, y teniendo en cuenta
que según (23) después de la integración, el tercer término se anula con la componente de dispersión del segundo, resulta
fv(v') £f(r\v',tQ) *k (r.v'ft1) dv' dfl' dr
(97)
<j>k (r,vfi) dvdfidr + h ( r , v , t Q ) <f>k (r,vfi) dvdfidr
La ecuación anterior representa la razón entre el número de neutrones produ_
cidos por fisión en el reactor, por unidad de tiempo, y el número de neutrones
perdidos por fugas a través de la superficie libre del reactor y por absorción
en el reactor, en la unidad de tiempo. Debido a esto, K Q se llama factor efectivo
de multiplicación del reactor.
Nótese que en (97) los parámetros nucleares son los del reactor real, mientras que los flujos corresponden a los del reactor virtualmente crítico.
6.2.- REACTOR VIRTUALMENTE CRITICO CON a.
Cuando:
i ) La configuración del reactor es independiente del tiempo,
i i ) Las densidades nucleares son independientes del tiempo, o sea N ( r , t ) =
al efectuar la transformada de Laplace de ( 4 3 ) , resulta
= 0
(98)
que desarrollada y eliminando P,, o directamente hallando la transformada de L a
place de (28 y 27) y eliminando P,, resulta
'Q' ->-vfi)
• dv'dfi' + ± [xf(v) - I l ^ .
III
f
d
\* i /\ -.
-24-
K±
?
l
1
Ct
(99)
£ F
o en forma o p e r a c i o n a l , p a r t i e n d o de (39 y 38)
(B-
)
^
v
a i a+A,
d
d
siendo f
da
Q (r,vfi,a)+ — é(r,vQ,O)+ ;— > — r — P,(r,v,O) =o,
d
d
(100)
* eF
a
la transformada de Laplace de parámetro ex. La ecuación anterior es
de forma análoga a la ecuación del reactor crítico (88), con tal de sustituir
•(?,vft,t o w a (r,vn,co, lt -»• lt + ^,Xf •+ x f - I ^ - x d , Q(?,vn,t 0 ) -»•
d
-»• Qd(?,vn,a) + i (j)(?,v^,0) + ^
^ ~ r Pd(?,v,0)
d
d
' d
(101)
6.2.1.- ECUACIÓN DE VALORES PROPIOS EN a.
Para que la (98) sea una ecuación de valores propios, es necesario que .
i) <j)C?,v^,O) = Pd(r,vft,0) = 0
ii) Q(r,vfi,t) = 0
luego
C | = a V" 1 i>
a
a
(102)
Para que las (99 y 100) lo sean, ha de verificarse además que
iii) No se consideran los neutrones retardados,
con lo cual se obtiene
-ít-V <f>a(r,vfi,a) - I t ( r , v ) <
>
¡ (r,v£!,a) + I s ( r , v ' ü ' -»• vfi) ^ ( r j v ' ñ ' . a )
dv'dQ' +
+ I ~ X f (v) Jv(v') I f ( r , v ' ) <j> a (r,v'n',a) dv' «• = a i ^ ( r . v ^ a ) , ^ e F Q
(103)
o en forma
operacional
B <>
f = a — é = = > ( v B) <)) = a é , 4> e F
a
v Ta
a
a
a
c
(104)
Por tanto, el problema queda reducido a calcular los valores propios a., y
las funciones propias íjj ,• $
e F de los operadores V C y v B .
III -25-
Las ecuaciones (102 y 10 3) corresponden al caso de un reactor virtualmente crítico con a, cuya criticidad se ha conseguido incrementando las sec_
ciones eficaces de captura en cx/v.
6.2.1.1.- ANÁLISIS DE LA ECUACIÓN DE VALORES PROPIOS.
Análogamente al caso de la ecuación de valores propios en k, §6.1, interesa determinar la clase de espectro del operador v B , la existencia y uni_
cidad de soluciones pertenecientes a F, y en que caso las funciones propias
forman un conjunto completo respecto a las funciones en F .
Respecto a los valores y funciones propias se ha obtenido
(1 2 3'+)
' ' '
en
general que:
i) Existe un valor propio ctn, real y simple tal que OL. > Re a , n/0, al
cual corresponde una función propia <j) e
F, para todo r, vfi e R
«
0
x 1/ x Q, Además, (j>
es la única función propia de signo constante
en R x V x ü. Por tanto, todas las cj)a e F , y únicamente <}>a e F.
ii) Si el reactor es finito, el espectro de valores propios es discreto,
existiendo un límite inferior de a n dado por a n > -lim (v ¿ + (v)).
0
u — ^+Q
t
Si el reactor se extiende al infinito, al menos en una dirección, el
espectro tiene una parte discreta para a
>_ -(v ^,(v)) . , y el res-
to es continuo.
iii) Si el reactor es finito, las funciones propias forman un conjunto
completo, respecto a las funciones pertenecientes a F .
La sección eficaz ¿ (v) se considera promediada en todas las cuerdas
del reactor.
En casos extremos, algunos de los resultados anteriores pueden dejar de
cumplirse. A medida que el tamaño del reactor disminuye, a
tiende a dismi-
nuir, luego para reactores suficientemente pequeños, pudiera ocurrir que no
exista ningún valor propio a
U
(5)
sin embargo
que cumpla la condición a
> -lim (v ¿,(v));
t
~ v-X)
, en estas circunstancias, este limite inferior deja probable-
mente de existir. En el caso de que el reactor esté formado por dos regiones
separadas por una totalmente negra, el valor propio a_ puede dejar de ser sim
pie.
(1) Habetler, G.J. y Martino, M.A. - Proc. Symp. Appl. Math. XI, Am. Math.
Soc. (1962).
(2) Henry, A. - Véase ref 6, pág 22.
(3) Davison, B. - Véase ref. 2, pág. 8,1.
(4) Bell, G.I. y Glasstone, S. - Nuclear Reactor Theory - Van Nostrand (1970)
(5) Albertoni, S. y Montagnini, B. - J. Math. Anal. Applic. 13, 19 (1966).
III -26-
Generalmente se tiene que lim (v £ Cv)) = (.v £+Cv)l - , y los dos límites
de ii) y iii) coinciden. Según i) los valores propios pueden ordenarse según
valores decrecientes de su parte real a. > Re o, > Re a....
La existencia de estos límites de a, puede obtenerse partiendo de la
ecuación integral del transporte de neutrones. Para que T(r!-*-r,v), dado en
(24,IV), sea finito
i) Si el reactor se extiende al infinito, como en este caso
r-r' puede
hacerse infinito, deberá ser ^.(v) + — >_0—Xa >_ -(v £.(v)) . .
ii) Si el reactor es finito, cuando v -> 0, £ (v) + — se hace infinito,
luego deberá ser an>_-lim (v £.(v)).
v-HD
6.2.1.2.- DETERMINACIÓN DEL FLUJO.
Si <f>a
(r ,vú) es una de las funciones propias correspondiente al valor
n' n
propio degenerado a , la solución general de (103 ó 104), será
<
>
j (r,vfi,a)=a
<
>
j (v ,vñ)
a
a
a
0
0
ó(a-an) +
0
n
S a
<j>
(r,vQ) ó ( a - a ) (105)
¿
a ,m Ya ,m
n
?un
n n
n n
mn
cuya transformada inversa de Laplace, da el flujo obtenido bajo las condiciones i) y ii) del §6.2, y las i ) , ii) y iii) del §6.2.1.
$(r,vñ,t)
= a
(f>
a
0
(r,v!5) e
0
+
S a
n/0 a n ' m n
mn
<j>
(r ,vfi) e
a
n'mn
n
(106)
habiendo ordenado los valores propios, según se indico en el párrafo anterior.
Como a > Re a , n^0, al cabo de un tiempo suficientemente grande, todos los
términos serán despreciables frente al primero, con lo que (106) toma la forma asintótica
(j)(r,ví2,t) = a
, t » 0= ^ > an = —
(107)
é (?,vfl,t)
0
Análogamente, cuando se consideran los neutrones retardados, se obtiene
a
0
<j) (r,vfi) e
%
a t
\¡) = a
i> e
a. van
0
0
+
S
nn ¿ nu
a
a ,m
n n
^
m
n
tendiendo asintoticamente como
y<f>
a ,m
n n
e
a t
"
(108)
V
4i - a
a
o
tjj
a
e
(109)
o
En (86 V y 92 V) se obtendrán estos desarrollos siguiendo otro procedimiento .
6.2.1.3.- RELACIÓN ENTRE REACTOR CRITICO Y REACTOR VIRTUALMENTE CRITICO.
En el caso de que se cumplan las condiciones de los §6.2 y §6.2.1,
III - 2 7 -
si el reactor es crítico, según (81) tendrá por ecuación B = 0, que compara
da con la (103), dará el valor propio a = 0, y el reactor virtual coincidirá con el real. Pero no recíprocamente, ya que si a>= 0, como la ecuación
-1 8
B <j>
= 0 es distinta de la (39) v
— <j> = B<j>, será $a f <J>, no teniendo
0
,
. .
,
0
porque verificar § la condición de criticidad (79).
Comparando estos resultados con los del §6.1.2, se obtiene que si el
reactor es crítico a n = 0, p = 0, k_ = 1.
6.3.-REACTOR VIRTUALMENTE CRITICO CON X.
Se define como reactor virtualmente crítico con X, en el instante t ,
al reactor que tiene la misma configuración y composición que tiene el reac
tor real en el instante t , excepto que el numero de neutrones secundarios
emitidos por colisión queda dividido por un factor constante X, de tal modo
que el reactor virtual así obtenido sea crítico, o sea, tenga un flujo que
cumpla la condición (87).
La diferencia entre un reactor virtualmente crítico con X y uno con k,
radica en que en el primer caso la criticidad se alcanza modificando el número de neutrones secundarios emitidos por colisión, es decir, por dispersión
y por fisión, mientras que en el segundo caso se alcanza modificando solamen_
te los de fisión.
La ecuación integrodiferencial de Boltzmann del reactor virtualmente
crítico, sera (28)
;t(?,v,t0: h(íM) +
-Ü-V
v(v')
{
(r ,
= 0,
)dv'
(110)
o en forma operacional (39)
(L+Rt)
~ (S+F)
= o,
(lil)
La ecuación de valores propios generalizada (111), puede transformarse
en una ordinaria, teniendo en cuenta que el operador (L+R,) no es singular,
por lo que admitirá inverso (L+R )
, el cual es un operador integral cuyo
núcleo es la función de Green del problema de contorno del §5,IV. De esta for
ma, se obtiene la ecuación integral
-(L+R.)
T
(S+F)
= X
(112)
III - 2 8 -
El problema queda reducido a calcular los valores propios X. y las
^
funciones propias (j>^ e F
r
-i
)
-(L+R )
del operador
1
i
(S+F)
6.3.1.- ANÁLISIS DE LA ECUACIÓN DE VALORES PROPIOS.
El análisis de la ecuación de valores propios en A es análogo al
efectuado en el §6.1.2, resultando
i) Existe un valor propio X~ , positivo y simple tal que Xfi > |x |,
n^O , al cual corresponde una función propia <j>, £ F para todo
r,?!Í £ R x 1/ x Q, Además, <j>, es la única función propia de sig0
no constante en R x 1/ x fi. Por tanto, todas las <ji^ e F , y únicamente <j)-\ 6 F.
0
6.3.2.- RELACIÓN ENTRE REACTOR CRITICO Y VIRTUALMENTE CRITICO.
Comparando los resultados anteriores, se obtiene que si el reactor
es crítico aQ= 0, p Q = 0, k Q = 1, XQ= 1.
6.4.-COMPARACIÓN ENTRE LAS ECUACIONES DE VALORES PROPIOS CON k, a y A.
El empleo de la ecuación de valores propios con k~ tiene la ventaja
frente a las correspondientes con a_ y \~ , en que para k_^ 1 lo único que
se hace es modificar convenientemente el número de neutrones emitidos por
fisión, lo cual afecta poco al espectro neutrónico, mientras que para a^¿
t 0, lo que se hace es introducir núcleos cuya sección eficaz de captura
siga la ley 1/v, lo cual afecta considerablemente al espectro neutrónico,
y para \~f 0, se modifica el número de neutrones emitidos por dispersión
y
J
£•
•-
i-.
> r,
-y
J -, J--, •
•
-,
J ^
-endurecido^
rision. Para a. < 0, el espectro
del fluno
virtual quedara ( , , , ,
v
J
0 ^ '
ablandado
respecto al del flujo real.
Debido
a
)
lo anterior, el caso de empleo más frecuente, es el de
reactor virtualmente crítico con k, empleándose también, en cinética de
reactores, el virtualmente crítico con a.
6.4.1.- Teniendo en cuenta que las únicas funciones propias pertenecientes
a F son las <L , <ji , <K , se empleará indistintamente la condición <f>. ,
k0
aQ
AQ
k
e F, o bien el subíndice 0. Respecto a las restantes funciones pro
A
—
pias pertenecientes a F , y correspondientes a los valores propios k., ct.,
X., se representarán por <j>
i
ki
gar a confusión.
= (j>., <j>a
i
±
= <¡»., (}>. =<!>•, mientras no de lux
Ai
i
ITT
-29-
Fig. 1,111
Ap.I - 1 -
APENDICE I.
1.- ECUACIONES CONJUGADAS Y ADJUNTAS.
Empleando el formalismo de Dirac, sea O un operador lineal, y
x> y
y>
dos kets cualesquiera pertenecientes al espacio donde 0 está definido, de mo
do que
0 x> =
y>
(1)
En álgebra lineal, a cada espacio vectorial le corresponde un espacio
vectorial dual, es decir, al espacio de los kets |x> le corresponde el espacio dual de los bra <x , diciéndose que <x
Análogamente, <y
es el bra conjugado del ket ix>.
será el bra conjugado del ket ¡y>. Como los kets |x> y ¡y>
están relacionados por el operador lineal 0, los bra <x| y <y , estarán relacionados por un operador lineal 0
<x 0
llamado hermítico conjugado o adjunto de 0,
(2)
= <y
y como <y| es el bra conjugado del ket |y>, <x¡0'
será el bra conjugado del
ket 0|x> y las ecuaciones (1 y 2) serán conjugadas una de la otra.
Multiplicando (1) por el bra arbitrario <z| perteneciente al espacio don
de 0 está definido, y (2) por el ket conjugado |z> del bra anterior, y tenien
do en cuenta la propiedad del producto escalar <z|y> = <y z> , resulta
<z O x> = <x
= <o'z|x>
(3)
ecuación que sirve también, para obtener el operador adjunto.
Recíprocamente, si se define como operador adjunto del 0, el 0' obtenido
por (3), como |x> y
z> son kets arbitrarios, se obtiene que <xjo
es el bra
conjugado del ket 0|x>, según se consideró al pasar de (1) a (2)
Nótese que los kets |x> y |z> son arbitrarios, y si el medio es finito,
satisfarán, en general, condiciones de contorno distintas.
2.- ECUACIONES DE VALORES PROPIOS.
Si |y> = o|x>, se tiene que <y| = <x o , y las ecuaciones (1 y 2) se trans
forman en ecuaciones de valores propios,
Velarde, G. - Véase ref. 1, pág. 1, I.
Ap.I -2-
0|x> = o|x>
===> <x | O ' = <x|o
siendo una conjugada de la otra, y |x> los kets propios de 0 y <x| los bras
propios de 0' .
Prescindiendo de que 0' sea el adjunto de 0, la ecuación de valores
propios de 0
piendo |x'> sus kets propios, y la de 0 siendo <x'| sus bras
propios, serán
0 ! I x ' > = o ' j x ' > = = > <x' I 0 = <x ' I o '
siendo una conjugada de la otra, y o ' y o :
( 5)
los valores propios correspon-
dientes .
-primera,
.,.,,,.,
..
.^
- , - ^ J T
,primera.
La (
, ) ecuación de (5) se llama ecuación adjunta
de la ('
, )
J
segunda
^ segunda
de (4-), por lo cual se dice que las condiciones de contorno de |x'> son adjuntas de las de |x>, y al problema correspondiente a la ecuación (5) con
sus condiciones de contorno, problema adjunto del correspondiente a la ecua
cion'(4) con sus propias condiciones de contorno.
2.1.-ORTONORMALIZACION.
Particularizando la primera ecuación (4-) para el valor propio o., y la
segunda ecuación (5) para el o'., al multiplicar la primera por <x^ | y la se
gunda por |x.>, y restar los resultados, se obtiene
— 5'i
4-
(o . - o '. ) <x . | x.> = 0
(6)
Si los kets propios |x.> forman un conjunto completo, todos los o', es
tan entre los o. ,y si los kets propios |x".> forman un conjunto completo, todos
los o. están entre los o. ; ya que por ejemplo, si los |x.> forman un conjun
to completo, y o
k
no está entre los o., de (6) se obtiene que <x¿|x.> = 0,
^
i
es decir,el ket propio |x, > es ortogonal a cada ket
K
i
x.> de un conjunto com
pleto, luego debe ser idénticamente nulo contra lo supuesto.
2.1.1.- En mecánica cuántica, los operadores asociados a observables son auto
adjuntos o hermíticos O1 = 0, luego |x'>= |x>, <x'| = < x | , o' = o'
= o =
= o , y de (6) se obtiene que los kets propios pueden ortonormalizarse,
<x. |xi> = 5(i-j)
(7)
BIBLIOGRAFÍA DE LIBROS CONSULTADOS SOBRE TEORÍA Y
CALCULO DE REACTORES
1.- Bell, 6.1. y Glasstone, S. NUCLEAR REACTOR THEORY
Van Nostrand (1970).
2.- Case, K.M. y Zweifel, P.F. LINEAR TRANSPORT THEORY
Addison Wesley (1967).
3.- Henry, A. NUCLEAR REACTOR ANALYSIS. The MIT Press (1975).
4.- Akcasu, Z., Lellouche, G.S. y Shotkin, L.M. MATHEMATICAL
METHODS IN NUCLEAR REACTOR DYNAMICS. Academic Press (1971),
5.- Velarde, G. TEORÍA DE REACTORES. IEN, JEN (1960).
6.- Greenspan H., Kelber, G.N. y Okrent, D. COMPUTING METHODS
IN REACTOR PHYSICS. Gordon and Breach (1968).
7.- Clark, M. y Hansen, K.F. NUMERICAL METHODS OF REACTOR
ANALYSIS. Academic Press (1964).
8.- Davison, B. NEUTRÓN TRANSPORT THEORY. Oxford (1957).
J.E.N. 334
Junta de Energía Nuclear, División de Tecnología de Reactores, Madrid.
"Ecuaciones integrodiferenciales e integrales
normales y adjuntas del transporte de neutrones"
(Parte I)
VELARE, G. (1976) 60 pp. 3 f i g s . 8 refs.
J.E.N. 334
Junta de Energía Nuclear, División de Tecnología de Reactores, Madrid.
"Ecuaciones integrodiferenciales e integrales
normales y adjuntas del transporte de neutrones"
(Parte I) -
Basándose en diversas hipótesis simplificativas se obtienen las diferentes
ecuaciones integrodiferenciales de Botlzmann del transporte de neutrones, a p l i cándolas posteriormente a algunos casos particulares: moderación, termal i zación,
muí t i grupos, y reactores críticos y virtualmente críticos con k, ©c y X
VELARE, G. (1976) 60 pp. 3 f i g s . 8 refs.
Basándose en diversas hipótesis simplificativas se obtienen las diferentes
ecuaciones integrodiferenciales de Botlzmann del transporte de neutrones, a p l i cándolas posteriormente a algunos casos particulares: moderación, termal ización,
multigrupos, y reactores críticos y virtualmente críticos con k, o¿- y 'X.
CLASIFICACIÓN INIS Y ESCRIPTORES.- E-21; Neutrón Transport Theory; Boltzmann
Equation; Integral Equations; Slowing-Down; Muliigroup Theory; Eigenvalues;
Eigenfunctions,,
CLASIFICACIÓN INIS Y DESCRIPTORES.- E-21; Neutrón Transport Theory; Boltzmann
Equation; Integral Equations; Slowing-Down; Multigroup Theory; Eigenvalues;
Eigenfunctions.
J.E.N. 334
Junta de Energía Nuclear, División de Tecnología de Reactores, Madrid.
"Ecuaciones integrodiferenciales e integrales
normales y adjuntas del transporte de neutrones"
(Parte I)
J.E.N. 334
Junta de Energía Nuclear, División de Tecnología de Reactores, Madrid.
"Ecuaciones integrodiferenciales e integrales
normales y adjuntas del transporte de neutrones"
(Parte I)
VELARE, G. (1976) 60 pp. 3 figs. 8 refs.
VELARE, G. (1976) 60 pp. 3 figs. 8 refs.
Basándose en diversas hipótesis simplifi cativas se obtienen las diferentes
ecuaciones integrodiferenciales de Botlzmann del transporte de neutrones, a p l i cándolas posteriormente a algunos casos particulares: moderación, termal i zación,
multigrupos, y reactores críticos y virtualmente críticos con k, aC y X
Basándose en diversas hipótesis simplificalívas se obtienen las diferentes
ecuaciones integrodiferenciales de Botlzmann del transporte de neutrones, a p l i cándolas posteriormente a algunos casos particulares: moderación, termal i zación,
multigrupos, y reactores críticos y virtualmente críticos con k, o¿" y JL
CLASIFICACIÓN INIS Y DESCRIPTORES.- E-21; Neutrón Transport Theory; Boltzmann
CLASIFICACIÓN INIS Y DESCRIPTORES.- E-21; Neutrón Transport Theory; Boltzmann
Equation; Integral Equations; Slowing-Down; Multigroup Theory; Eigenvalues;
Equation; Integral Equations; Slowing-Down; Multigroup Theory; Eigenvalues;
Eigenfunctions.
Eigenfunctions.
J . E . N . 334
J . E . N . 334
Junta de Energía Nuclear, División de Tecnología de Reactores, Madrid.
Junta de Energía Nuclear, División de Tecnología de Reactores, Madrid.
"Normal and adjoint integral and integrodifferential neutrón transport equations" (Part I)
VELÁRDE, Q. (1976) 60 pp. 3 figs. 8 refs.
"Normal and adjoint integral and integrodifferential neutrón transport equations" (Part I)
VELARDE, 6 . (1976) 60 pp. 3 f i g s . 8 refs.
Using some simplifying hypotheses, different expressions of the BoHzraarin
1 ntegrodifferential equation are obtained. Posterior! 1 /, they are applied to
some particular cases: slowing down, themia'iization, niultigroups, c r i t i c a ! reactors and virtual c r i t i c a ! reactors with k, o C and X
Using some simplifying hypotheses, different expressions of the Boltzniann
integrodiíferential equation are obtained. Posteriorly, they are appüed t o
some particular cases: slowing down, thermalization, multigroups, c r i t i c a l reactors and virtual c r i t i c a l reactors with k, .^C and Á.
INIS CLASSIFICATION AND DESCRIPTORS.- E-21; Neutrón Transport Theory; Boltzniann
Equations; Integral Equations; Slowing-Down; Hultigroup Theory; Eigenvalues;
Eigenfunctions.
INIS CLASSIFICATION AND DESCRIPTORS.- E-21; Neutrón Transport Theory; Bclizmann
Equations; Integral Equations; Slov/ing-Down; Multigroup Theory; Eigenvalues;
Eigenfunctions.
J . E . N . 334
J . E . N . 334
Junta de Energía Nuclear, División de Tecnología de Reactores, Hadrid.
Junta de Energía Nuclear, División de Tecnología de Reactores, Hadrid.
"Normal and adjoint integral and integrodifferen tial neutrón transport equations" (Part I)
;
" N o r m a l a n d adjoint i n t e g r a l a n d i n t e g r o d i f f e r e n tial neutrón transport equations" (Part I)
VELARE, 6. (1976) 60 pp. 3 f i g s . 8 refs.
Using some simpllfying hypotheses, different expressions of the Boltzmann
i ntegrodif ferenti al equation are obtained. Posteriorly, they are applied t o
some particular cases: slowing down, thermalizaiion, muHigroups, c r i t i c a l reactors and virtual c r i t i c a l reactors with k, oC and A .
i
VELARE, G. (1976) 60 pp. 3 f i g s . 8 refs.
i
J
i
Using some simpligying hypotheses, different expressions of the Boltzniann
integrodifferential equation are obtained. Posteriorly, they are applied to
some particular cases: slowing down, thermalization, multigroups, c r i t i c a l reactors and virtual c r i t i c a l reactors with k, o £ and X
i
INIS CLASSIFICATION AND DESCRIPTORS¡- E-21; Neutrón Transport Theory; Boltzmann
;
Equations; Integral Equations; Slowing-Down; Multigroup Theory; Eigenvalues;
i
Eigenfunctions.
INIS CLASSIFICATION AND DESCRIPTORS.» E-Zi; Neutrón Transport Theory; Boltzmann
Equations; Integral Equations; Slowing-Down; Multigroup Theory; Eigenvalues;
Eigenfunctions.