Suelo Pa red d l = λ/4 5

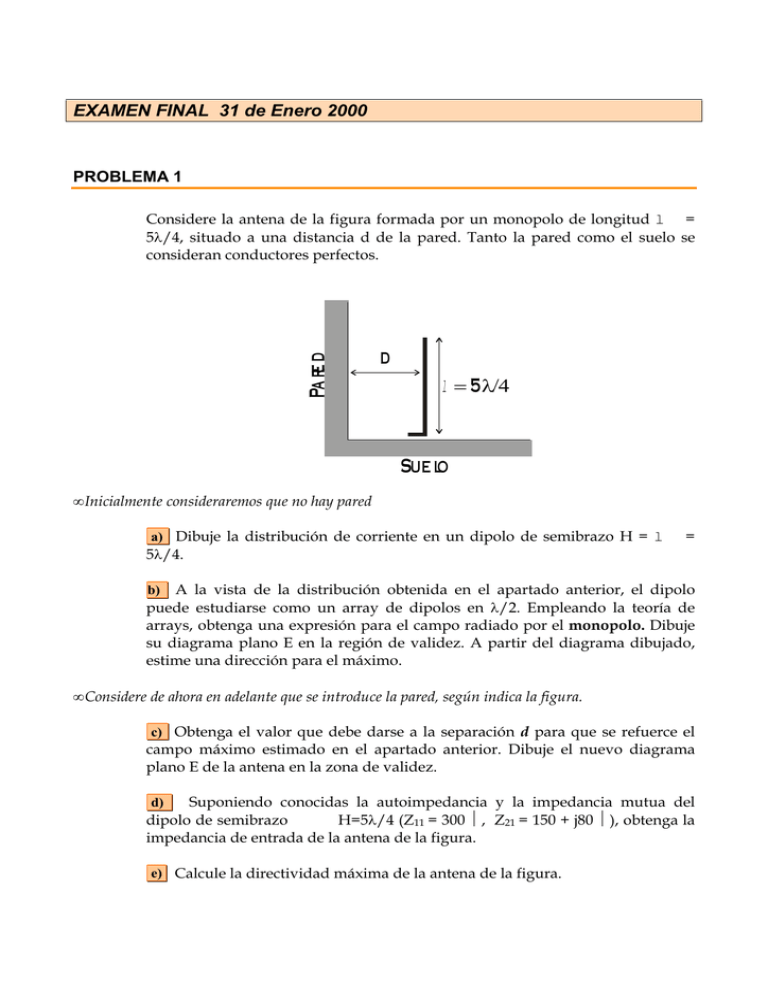
EXAMEN FINAL 31 de Enero 2000
PROBLEMA 1
Pa re d
Considere la antena de la figura formada por un monopolo de longitud l =
5λ/4, situado a una distancia d de la pared. Tanto la pared como el suelo se
consideran conductores perfectos.
d
l = 5 λ/4
Sue lo
• Inicialmente consideraremos que no hay pared
a) Dibuje la distribución de corriente en un dipolo de semibrazo H = l
=
5λ/4.
A la vista de la distribución obtenida en el apartado anterior, el dipolo
puede estudiarse como un array de dipolos en λ/2. Empleando la teoría de
arrays, obtenga una expresión para el campo radiado por el monopolo. Dibuje
su diagrama plano E en la región de validez. A partir del diagrama dibujado,
estime una dirección para el máximo.
b)
• Considere de ahora en adelante que se introduce la pared, según indica la figura.
c) Obtenga el valor que debe darse a la separación d para que se refuerce el
campo máximo estimado en el apartado anterior. Dibuje el nuevo diagrama
plano E de la antena en la zona de validez.
Suponiendo conocidas la autoimpedancia y la impedancia mutua del
dipolo de semibrazo
H=5λ/4 (Z11 = 300 Ω, Z21 = 150 + j80 Ω), obtenga la
impedancia de entrada de la antena de la figura.
d)
e) Calcule la directividad máxima de la antena de la figura.
PROBLEMA 2
Un reflector centrado tiene una apertura equivalente rectangular como se
muestra en la figura. La distribución de campo en ella puede aproximarse por
!

y 

una expresión de la forma Eap ( x, y ) = E0 C + (1 − C ) 1 −
  yˆ , siendo C < 1
L
/
2

1

 
a) Obtenga una expresión para la eficiencia de iluminación de la apertura,
ηil en función de C.
b) Se desea que el nivel en bordes del reflector en el plano E sea de –10.6
dB. Calcule la directividad resultante de la antena. Suponga que no hay
pérdidas por desbordamiento.
c) En el foco se sitúa una bocina sectorial plano E óptima. Diseñe sus
dimensiones eléctricas para que el nivel en bordes del reflector en el plano
E, debido al diagrama de la bocina sea τdiagrama (plano E) = -10 dB.
d) Obtenga la distancia focal del reflector.
e) Si la potencia radiada por el alimentador es 5 w, calcule el valor del
campo máximo Emáx radiado por el reflector (en V/m) a una distancia de 1
km y a la frecuencia de 10 GHz. Las dimensiones de la guía normalizada
para banda X son a=2.286 cm y b=1.016 cm.
y
L1 = 20λ
x
f
L2 = 5λ
b1
sen θ
λ
SOLUCIÓN AL PROBLEMA 1
Apartado a
I( z) := sin [ k⋅ ( H − z ) ]
1
I( z)
0
1
1
0.5
0
0.5
1
z
Apartado b
El monopolo, al aplicar la teoría de imágenes se puede analizar como un dipolo
de semibrazo H=5λ/4
La expresión para el vector de radiación de un dipolo de H=λ/4 es:
N=
2kI m ( cos ( k z H ) − cos ( kH ))
k 2 − k z2
El diagrama de radiación de un dipolo de semibrazo H=λ/4 es
E(θ ) :=
 π cos (θ ) 

2

cos 
sin (θ )
90
120
150
E( θ )
60
0.8
0.6
0.4
0.2
0
180
30
0
210
330
240
300
270
θ
El array tiene un diagrama de radiación que vendrá dado por las siguientes
expresiones y gráfica correspondiente.
 ψ

 2
F(ψ ) :=
ψ
sin  
 2
sin  5
6
4
F( ψ )
2
0
3
2
1
0
1
2
3
ψ
El producto del diagrama del elemento por el diagrama del array es el siguiente
90
120
1.754
60
1.5
150
1
30
0.5
E( θ ) ⋅A( θ )
180
0
0
210
−3
8.385×10
330
240
300
270
θ
Los nulos del diagrama de radiación se encuentran en Ψ=2π/5,4π/5, que
corresponden a las siguientes direcciones del diagrama
ψ −α

 k⋅ d 
θ0(ψ ) := acos 
 8π  ⋅ 180 = 53.13

 5  π
 6π  ⋅ 180 = 78.463

 5  π
θ0
θ0
 4π  ⋅ 180 = 101.537

 5  π
 2π  ⋅ 180 = 126.87

 5  π
θ0
θ0
Una buena estimación para el primer máximo es suponer que se encuentra
entre los dos primeros ceros, es decir entre 0 y 53,13, es decir 26.5º. Se puede
observar que en realidad el máximo aparece para un ángulo ligeramente
superior a 30º. Vamos a considerar el máximo en la dirección 30º
Apartado c
La imagen del dipolo, debido al efecto de la pared hace que aparezca un nuevo
array uniforme de dos elementos, alimentados con corrientes +I y –I
Para que la función tenga un máximo en la dirección 30º las señales se deben
sumar en fase en dicha dirección, o bien el argumento de la función array debe
ser π/2
k d sin(30) debe valer π/2, es decir d=0,5 λ
En el plano YZ
φ :=
π
2
d = 0.5
B(θ ) := 2⋅ sin (k⋅ d ⋅ sin (θ )⋅ sin (φ))
90
120
60
1.5
150
B( θ )
30
1
0.5
180
0
0
210
330
240
300
270
θ
El diagrama en el plano YZ , que incluye todos los efectos es
90
120
3.497
60
3
150
E( θ ) ⋅A( θ ) ⋅B ( θ )
30
2
1
180
0
0
210
− 15
1.924×10
330
240
300
270
θ
Apartado d
La impedancia del dipolo aislado es z11=300. La impedancia mutua es
z12=150-80j.
Teniendo en cuenta el efecto de la pared y que se trata de un monopolo
z=
z11 − z21
= 75 + 40 j
2
Apartado e
En la dirección del máximo el campo de un dipolo será proporcional a
I
E (r ) = 60 2 ⋅1.737
r
La potencia radiada se calcula como
W = I 2 ⋅ Re( Z )
Y la directividad
E2
η
D=
= 19.31 = 12.85dB
W
4π r 2
SOLUCIÓN AL PROBLEMA 2
Apartado a
La eficiencia de iluminación se calcula a partir de
!il $
1
L1L2
! %%
S
%%S
Eap (x , y )ds
2
"
2
Eap (x , y ) ds
$
3(1 # C )2
4(C 2 # C # 1)
Apartado b
El nivel en bordes del reflector nos indica el valor del pedestal en la distribución
de campo en la apertura dada. Basta con pasarlo a lineal
"E $ &10.6 dB $ 20 log C
C= 0.29
Conocido C, es inmediato calcular la eficiencia de iluminación y la directividad:
ηil = 0.91
D=30.6 dB
Apartado c
El nivel de iluminación del borde respecto al centro es –10.6 dB, de ellos, -10 dB
se deben al diagrama del alimentador y por tanto –0.6 son debidos a la
diferencia de caminos recorridos por los rayos. Esto implica que
'
'#
"c(plano E ) $ &0.6 $ 40 log *** cos *** E
+
+ 2
((
))
))
)) ,
,,
de donde βE=30º
Esto nos indica que la bocina debe proporcionar una iluminación de –10 dB en
la dirección βE. Con este dato podemos diseñar la bocina con ayuda de los
diagramas universales plano E. Seleccionamos la curva correspondiente a la
bocina óptima (s=1/4) y para un nivel de –10 dB obtenemos que
B
sen #E $ 1.5 .
$
Las dimensiones de la bocina son B=3λ y RE=4.5λ
Apartado d
La distancia focal se obtiene de forma inmediata a partir de
f
1
,
$
L1
4 tan(#E / 2)
f = 18.6λ
Apartado e
La directividad calculada en el apartado b) está relacionada con la potencia y el
campo máximo radiado a través de
2
D $
Emáx / !
WT / 4%r 2
, despejando el campo máximo se obtiene Emáx $ 0.4 V / m