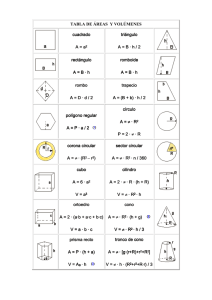
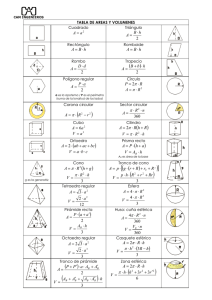
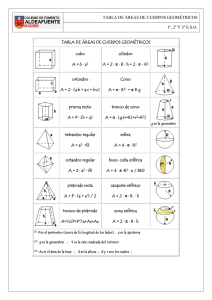
2º ESO Matemáticas

Organización de la unidad
El libro comienza con una unidad de repaso a modo de resumen con los conceptos que debes recordar para
abordar con éxito este curso . La estructura de esta unidad es algo diferente al resto . Tras la primera página con
un sumario de los conceptos a repasar, empieza el desarrollo de contenidos estructurado de la siguiente manera: cada epígrafe contiene un breve resumen de los conceptos, algunos ejemplos a modo de aclaración y
por último, una batería de actividades para practicar lo repasado .
Presentación
3 Números
decimales.
Sistema sexagesimal
La doble página inicial de la unidad
presenta un esquema-resumen conceptual que organiza previamente
tus ideas y guía tu estudio posterior,
un texto introductorio y el apartado
¿Qué necesitas saber?, una preparación teórico-práctica que orienta hacia los contenidos previos que debes
dominar para afrontar en buenas
condiciones la unidad . Este apartado está estructurado a su vez en dos
secciones: Recuerda, con un listado
con los conceptos teóricos previos
fundamentales y Resuelve, actividades que trabajan estos conceptos y
cuyo resultado final se facilita .
¿Qué necesitas saber??
Recuerda
•
•
•
•
Sistem
Sist
emaa de n
num
umer
erac
ació
ión
n de
deci
ciim
maal.
l.
Núme
Nú
mero
ross de
deci
cima
male
lees.
Jera
Je
rarq
rquí
uíaa de oope
pera
raci
cion
ones
es y uso de paré
rént
ré
ntes
esis
is.
Util
Ut
iliz
izac
ació
ión
n de est
stra
r te
ra
t gias per
errsoona
n les para
ra eell cáálc
l ullo
ment
me
ntal
al,, appro
roxi
xima
mado y con calcu
ula
lado
dora.
do
Resuellve
Jera
Je
rarquía de operacion
ones
es
Los números decimales
Sistema sexagesimal
Oper
O
Op
pe a:
a) 3 – (5 + 6 · 4))
c) 8 : ( 9 – 5)
5)
b 5 · (4 – 3 + 6)
b)
d)) 7 · ( 5 – 3 · 22)) · 2
Solu
So
luci
ción
ó : a)) –26;
–226;
6; bb)) 35
35;; c)
c) 2; d) –14
1
Formas compleja
e incompleja
Calcul
Calc
ula:
a:
a) 3324
24 : 110.
0.00
0000 b) 45 · 1.
1.00
0 0
c)) 56 : 00’’00
0001
01
1
Solu
So
luci
ción
ó : a) 0’
ón
0 03
0 24
4; bb)) 45.
5 0000; c) 56
560.
0 000
0000
Multip
ip
plicaaci
c ión
ó y div
ivis
issió
ón po
por laa uni
nida
daad se
d
segu
egu
guid
id a
ida
de cer
eros
oss
Tipos
Aproximación
R so
Re
solu
luci
ción
ón d
de proble
lema
maas
mas
• Decimal exacto
• Redondeo
• Decimal periódico puro
• Truncamiento
An
ndr
d éss com
o pr
p a 3 kg
kg de pa
p ta
t ta
tass a 0’
0’20
2 €/k
20
/ g.
g. Si ll
llev
evaa 2’
2 35
35 €,
¿cuá
¿c
uánt
uá
ntoo lee sob
obra
rará
rá??
rá
S lu
So
l ci
ción
ón:: 2’3
ón
’355 – 3 · 0’
0’20
’200 =1’
1’75
75 € llee soobr
75
b aarrá.
á
Operaciones
• Decimal periódico mixto
• Decimal no periódico
Operaciones
Fracción de un número decimal
El sistema de numeración sexagesimal tiene su principal aplicación en el uso horario. Este sistema es casi tan antiguo como el decimal y, en cierto sentido, se
podría decir que es un sistema más completo. Fíjate en que al contar de 60 en 60
utilizamos múltiplos de 10, 20, 30 y 60.
Desarrollo De conteniDos
A continuación comienza el desarrollo
de contenidos, con un lenguaje sencillo, comprensible y riguroso y siempre
acompañado donde se requiera de
gráficos para mejorar la comprensión .
00 Mate_2oESO.indd 4
Eltroncodecono
5.3. Áreadeltroncodecono
Paracalculareláreadeuntroncodeconoobservemossudesarrollo.Como
hemosvistoenelapartadoanterior,estáformadopordoscírculosyuntrapeciocircular.Portanto,eláreadeltroncodeconoserálasumadeláreade
esastresfiguras.
Sicortamosunconoconunplanoparaleloalabaseobtenemoslasiguiente
figura:
• Á rea lateral:eseláreadeltrapeciocircularqueengendralageneratriz.
2πR + 2πr
⋅ g ⇒ Alateral = π( R + r ) ⋅ g
2
Alateral =
• Á rea de la base mayor:eseláreadelcírculomásgrande.
Lafiguratieneunaformasimilaraladeuntrapecio.
Abase mayor=πR 2
Abase menor=πr2
• Á rea de la base menor:eseláreadelcírculomáspequeño.
Untronco de conoesuncuerpoderevoluciónqueseobtienealgirarun
trapeciorectángulosobreelladoqueformaelángulorecto.
•Calcular el área lateral y total del siguiente tronco de cono.
2 cm
Radio
Generatriz
tángulo.
• R adios:sonlosradiosdelasbases,esdecir,laslongitudesdelasbasesdel
Bases
Eje de giro
Abase mayor = π ⋅ 32  3’14 ⋅ 9 = 28’26 cm2
Abase menor = π ⋅ 22  3’14 ⋅ 4 = 12’56 cm2
3 cm
Atronco cono  62’ 8 + 28’26 + 12’56 = 103’ 62 cm2
5.4. Relaciónentreeltroncodeconoyelcono
trapecio.
Observemoslafigura.Vemosquetenemosdostriángulosrectángulosen
posicióndeTales.Portanto,secumplenlassiguientesproporciones:
5.2. Desarrollodeltroncodecono
• D os círculos distintos, quesonlasbasesmayorymenordeltroncodecono.
• U n trapecio circular, queeslasuperficielateraldeltronco.
Alateral = π ⋅ (3 + 2) ⋅ 4  3’14 ⋅ 5 ⋅ 4 = 62’ 8 cm2
4 cm
Altura
Radio
• S uperficie lateral:eslasuperficiequeengendralageneratrizalgirar.
Eldesarrollodeltroncodeconoestáformadoportresfigurasplanas:
R
ejemplo
mantienefijo.
• G eneratriz:eselsegmentoquedelimitaelladoopuestoalejedegiro.
• B ases:sonloscírculosquesegeneranalgirarlasbasesdeltrapeciorectrapecioquenogira.
g
2πr
Atronco cono=π(R+r)·g+πR 2+πr2
• E je de giro:eslarectaquecontieneelladodeltrapeciorectánguloquese
• A ltura: es la distancia entre las bases, es decir, la longitud del lado del
r
2πR
• Á rea total:eselárealateralmáseláreadelasbases.
5.1. Elementosdeltroncodecono
r
a’
=
R a + a’
Trapecio circular
Un trapecio circular es
unsectordeunacorona
circular.
r
h’
=
R h + h’
a’
r
h’
a
h
R
r
a’
h’
=
=
R a + a ’ h + h’
17. Un cono de 20 cm de altura y 6 cm de radio de la base se corta con un plano
a una altura de 15 cm de la base. Calcula las dimensiones del tronco de cono
resultante.
18.Calcula el área lateral y el área total del tronco del cono del ejercicio anterior.
182
14.Dibuja en tu cuaderno un tronco de cono que mida 4 cm de radio de la base
mayor, 2 cm de radio de la base menor y 3 cm de altura.
15.¿Qué altura tiene un tronco de cono si los radios de sus bases mayor y menor miden 6 y 4 cm y su generatriz mide 8 cm?
16.Dibuja el desarrollo del tronco de cono del ejercicio 14.
UNIDAD 9
ACTIVIDADES
19. Calcula el área total del cuerpo de revolución resultante de la siguiente figura plana:
ACTIVIDADES
Intercalados entre los contenidos y para
aclarar las posibles dudas surgidas, aparecen gran cantidad de Ejemplos y Actividades resueltas. Para que amplíes
conocimientos y compruebes si has
comprendido los conceptos desarrollados con anterioridad se plantean a lo
largo del texto gran número de Actividades, que hacen las veces de extensión práctica de la teoría tratada .
5
1 cm
6 cm
7 cm
Cuerpos de revolución
183
16/01/12 13:10
IMPORTANTE
Todas las actividades propuestas en este libro deben realizarse en un cuaderno de trabajo, nunca en el propio libro.
activiDaDes
La página de Actividades resueltas contiene cada una de las tipologías de actividades fundamentales de la
unidad . A continuación y para que afianzar los conocimientos aparecen tres páginas de actividades finales con
Ejercicios y Problemas. Los ejercicios
Actividades resueltas
Actividades finales
están agrupados por contenidos .
1. Representa los cuerpos de revolución que engendran
las siguientes figuras planas:
Las actividades finales están clasificadas
en tres niveles de dificultad mediante los
siguientes símbolos:
b) a) 5. Dibuja en tu cuaderno un cono que tenga 2 cm de ra­
dio y 4 cm de altura.
Solución
EJERCICIOS
Cuerpos de revolución
◐ 40.Calculaelárealateralytotaldelossiguientescilindros:
◐ 34.Representaloscuerposderevoluciónquegeneranlas
a) Radio=10m, altura=25m
siguientesfiguras,asícomoloselementosquelascom­
ponen:
b) Base=3’5cm, altura=0’5dm
c) Generatriz=5km, radio=2.500m
a) ○ 41.¿Cuáldelassiguientesfigurasrepresentaeldesarrollo
2 cm
4 cm
b) c) deuncilindro?
2 cm
4 cm
Solución
a) b) 6. Dibuja en tu cuaderno un tronco de cono generado
por un trapecio rectángulo con una base mayor de
3 cm, una base menor de 1 cm y una altura de 4 cm.
a)
b)
c)
◐ 35.¿Quéfiguraplanadacomoresultadoelsiguientecuer­
poderevolución?
Solución
◐ 42.Calculaeláreadelasiguientefigura:
1 cm
○ Sencilla .
1’5 cm
4 cm
2. Representa un cilindro con las siguientes característi­
cas y dibuja su desarrollo:
base = 1 cm de radio
7. Calcula la superficie esférica de una pelota de 10 cm
de radio.
1’5 cm
6’28 cm
1’5 cm
3. Calcula el área lateral y total de un cilindro con las di­
mensiones siguientes:
base = 2 cm de radio
altura = 3 cm
Solución
Alateral = 2πr ⋅ a  2 ⋅ 3’14 ⋅ 2 ⋅ 3 = 37’ 68 cm2
Abase = πr 2  3’14 · 22 = 12’56 cm2
Acilindro = Alateral + 2 ⋅ Abase  37’ 68 + 2 ⋅ 12’56 = 62’ 8 cm2
4. Calcula el área lateral de un cono que tiene 2 cm de
radio y cuya generatriz mide 7 cm.
Solución
El cono
◐ 36.Buscaentudormitoriodosfigurasqueseancuerpos
○ 43.Representa en tu cuaderno conos con las siguientes
derevolución,dibújalaseindicasuselementos.
Aesfera=4πr2≃4·3’14·102=1.256cm2
8. Calcula la superficie de la siguiente figura:
● Difícil .
188
Cuerpos de revolución en nuestro entorno
Solución
1 cm
Se concluye con una Autoevaluación
formada por diez actividades pensadas
para que valores tus conocimientos . Al
final del libro puedes encontrar las soluciones de dichas Autoevaluaciones .
altura = 1’5 cm
Solución
◐ Media .
5 cm
3 cm
1 cm
características:
◐ 37.Dibujacomocuerposderevoluciónlossiguientesob­
jetos:
a) Unlapicero.
b) Untarrodemermelada. e) Unarosquilla.
c) Unjarrón.
d) Ungorrodepayaso.
f) Unbalónderugby.
○ 45.¿Cuáldelossiguientesdesarrollossecorrespondecon
características:
eldeuncono?
a) Radio=2cm, altura=1cm
Podemosobservarquelafiguraestácompuestaporuna
semiesferayuncilindro.Vamosacalcularlasáreasde
estasdossuperficiesyluegolassumaremos:
b) Radio=altura=1’5cm
c) Generatriz=2’5cm, radio=1’5cm
d) Uncilindrogeneradoporunrectángulode2cmde
basey3cmdealtura.
Aesfera 4 πr 2 4 π12
=
=
= 2π  6’28 cm2
2
2
2
Abase cilindro = πr 2 = π ⋅ 12  3’14 cm2
a) c) b) d) PROBLEMAS
e) Uncilindrogeneradoporunrectángulode6cmde
basey5cmdediagonal.
◐ 69. Las nuevas botellas de la empresa donde trabaja Ángela tienen una boquilla de 12 mm de radio y la rosca
abarca una altura de 25 mm. Ángela es la encargada
◐ 46.Cde
alculaelárealateralytotaldelosconosconlassi­
tescilindros:
diseñar los tapones y necesita saber la cantidad de plásguientescaracterísticas:
a) Base=altura=3cm
tico que hará falta para fabricarlos. ¿Podrías ayudarla?
a) Generatriz=55dam, radio=0’2km
b) Radio=2cm, altura=4cm
b) Radio=2cm, altura=4cm
● 70. En una heladería han comprado un surtido de conos
c) Uncilindrogeneradoporunrectángulode1’5cm
de 15 cm de altura y 164’85 cm2 de superficie. Comoc) Base=altura=3cm
es
debasey5cmdealtura.
un tipo de cono nuevo, la heladera necesita comprar
d) Unconogeneradoporuntriángulorectángulode
d)Generatriz=5cm,
unaradio=3cm
herramienta para hacer las bolas de helado de un1’5mmdebasey5mmdealtura.
diámetro apropiado para este cono. ¿Podrías calcular
este dato?
◐ 39.Representaentucuadernoeldesarrollodelossiguien­
Comolapartesuperiordelcilindrolaocupalasemiesfe­
rasolotenemosquecontarunabase.Sumamos:
Alateral = πhr  3’14 ⋅ 7 ⋅ 2 = 43’96 cm2
Abase = πr 2  3’14 ⋅ 22 = 12’56 cm2
Afigura = Asemiesfera + Alateral cilindro + Abase cilindro
Acono = Alateral + Abase  43’96 + 12’56 = 56’52 cm2
Afigura  6’28 + 9’ 42 + 3’14 = 18’ 84 cm2
UNIDAD 9
c) Unconogeneradoporuntriángulorectángulode
1 cmdebasey3cmdealtura.
d) Unconogeneradoporuntriángulorectángulode
2 cmdebasey4cmdehipotenusa.
alturacuyabasetieneundiámetrode10cm?
○ 38.Representaentucuadernocilindrosconlassiguientes
Alateral cilindro = 2πra = 2π ⋅ 1 ⋅ 1’5  9’ 42 cm2
b) Generatriz=2’5cm, radio=1’5cm
◐ 44.¿Cuántomedirálageneratrizdeunconode12cmde
El cilindro
Solución
Asemiesfera =
a) Radio=20m, altura=11m
189
Cuerpos de revolución
● 71. En una fábrica de vidrio van a empezar a fabricar un
modelo de vaso con forma de tronco de cono. Los
nuevos vasos tienen una base de 2’5 cm de radio, su
abertura es de 7 cm de diámetro y su altura 3 cm. ¿Qué
cantidad de vidrio hará falta para fabricar 5.000 unidades de este tipo?
● 72. Andrea y Luis se han comido 4 paquetes de galletas.
Informática matemática
Construir un dodecaedro con Cabri 3D
En esta ocasión utilizaremos un nuevo software que se llama Cabri 3D. Puedes descargarte una versión de prueba de la página: <www.cabri.com>
Una vez instalado ejecutamos y nos aparece la siguiente ventana:
Hacemos click en el icono de representar poliedros y marcamos Dodecaedro regular.
Marcamos dos puntos en el plano y se representa un Dodecaedro con
una cara en el plano.
Podemos abrir el dodecaedro haciendo click en el desplegable según
aparece en la siguiente imagen.
Matemáticas recreativas
¿Cómo llegar de un cilindro a un
cono pasando por un tronco
de cono?
1. Tomamos una recta que usaremos de eje.
2. Tomamos un segmento paralelo al eje. Lo hacemos girar y obtenemos un cilindro.
3. Inclinamos el segmento ligeramente, pero sin tocar el eje. Lo hacemos girar y obtenemos un tronco de cono.
4. Seguimos inclinando el segmento hasta que toque el eje. Lo hacemos girar y obtenemos un cono.
192
¿Y de dónde vienen los nombres
de los cuerpos de revolución?
•
•
•
Cilindro: proviene del término griego kunlindros,
que significa arroyo, envuelto, es decir, figura de
rollo.
Cono: proviene del término griego konos, que
significa piña, es decir, con forma de piña. Por esa
misma razón a la familia de los pinos se le llama
coníferas.
Esfera: proviene del término griego sphaira, que
significa globo, cuerpo redondo.
UNIDAD 9
Cuando han terminado, se les ha ocurrido desenrollar
los envoltorios y pintarlos cada uno de un color para
hacer un mural y enmarcarlo. Como ven que las bases
no quedan bien, se las han quitado, y ahora están pensando en el tamaño del marco. Si saben que los paquetes tienen forma de cilindro de 15 cm de altura y 6
cm de diámetro, ¿qué superficie necesitarán para enmarcar el mural?
informática matemática
En este apartado se explica cómo utilizar distintas aplicaciones informáticas,
seleccionadas de entre las más útiles y
empleadas . Con esta sección aprenderás a resolver los problemas planteados
en la unidad con ayuda de las nuevas
tecnologías .
AUTOEVALUACIÓN
1. Representa el cuerpo de revolución que genera la siguiente figura plana al girar sobre el eje indicado:
Dado un cono con las siguientes dimensiones:
radio = 1’5 cm
generatriz = 4 cm
5. Represéntalo.
6. Dibuja su desarrollo.
7. Calcula sus áreas lateral y total.
8. Calcula las áreas lateral y total del tronco de cono con
las siguientes dimensiones:
R = 3’5 cm, r = 1’5 cm, altura = 2 cm
9. Calcula el área de la zona esférica resultante de cortar
una esfera de 8 cm de radio con dos planos paralelos
separados cada uno 2’5 cm del centro.
Dado un cilindro con las siguientes dimensiones:
diámetro base = 3 cm
altura = 2 cm
10. En una esfera terrestre, representa los siguientes elementos:
2. Represéntalo.
3. Dibuja su desarrollo.
a) Polo norte.
4. Calcula sus áreas lateral y total.
b) Eje de rotación.
c) Ecuador.
d) Paralelo.
Cuerpos de revolución
matemáticas recreativas
Desafío matemático
Vamos a medir la Tierra
En esta sección puedes encontrar una
miscelánea de curiosidades, actividades interesantes, cultura matemática . . . una manera alternativa de acercamiento a las Matemáticas .
Desafío matemático
Como ya sabes el planeta Tierra tiene la forma
ma de una
esfera casi perfecta, te recordamos que el Ecuador
cuador
es el paralelo máximo y divide a la Tierra en dos
hemisferios aproximadamente del mismo taamaño. El diámetro de la Tierra en el Ecuador
mide 12.756 km.
1
¿Qué longitud tiene la circunferencia
de la Tierra en el Ecuador?
2
¿Qué superficie tiene la Tierra?
3
Si sabemos que las ¾ partes de la
superficie terrestre están cubiertas
de agua, ¿cuántos km2 son agua y
cuántos tierra firme?
Los trópicos son paralelos que se encuentran a una latitud de 23° 26’ al norte y al sur
del Ecuador. El trópico que se encuentra all
cer,
norte del Ecuador se llama Trópico de Cáncer,
mientras que el que se encuentra al sur se llama
o de cada
Trópico de Capricornio. La longitud del rádio
trópico es de 5.851 km.
4
¿Qué longitud tiene la circunferencia de cada trópico?
5
¿Qué distancia hay desde el centro de la circunferencia del
Trópico de Cáncer
Cánce al Polo Norte?
6
¿Qu
¿Qué distancia separa los dos trópicos?
7
Esta sección plantea una tarea organizada en diversas actividades cuyo
hilo conductor es el texto a partir del que podrás poner en práctica diferentes competencias básicas. El diseño de estos desafíos está inspirado
en las pruebas PISA.
¿Qué superficie terreste hay entre el Ecuador y Trópico de Capricornio?
8
Busca en internet cómo se calcula el
volumen de un casquete esférico y
calcula el volumen que ocupa el casquete limitado por el Trópico de
Cancer y el Polo Norte.
En todos los apartados anteriores puedes dar el resultado en km, km2 o km3
aunque si te resulta más cómodo puedes utilizar la notación científica usando
potencias de 10.
Cuerpos de revolución
00 Mate_2oESO.indd 5
191
193
16/01/12 13:10