Problemas Tema2

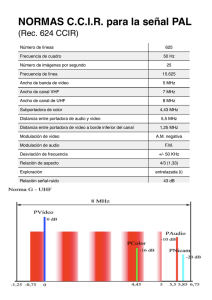
TEMA2: Técnicas de filtrado en RF.
Curso 2003-2004
PROBLEMAS TEMA 2
1.
Diseña un filtro Butterworth para fc =100 MHz que proporcione una atenuación de al menos 48 dB a
fx =500 MHz, entre un generador de 250 Ω con un condensador en paralelo de 1.55pF y una carga de
50 Ω. Asume componentes reales y absorbe la capacidad de la fuente con la estructura del filtro.
NOTA: Ver tabla1 y tabla2.
2.
Diseñar un filtro Chebychev de 5 secciones con 0.01 dB de rizado en la banda de paso hasta
fR = 400 MHz, (asume BW igual al rizado) para una resistencia de generador y carga de 50 Ω. Una vez
finalizado el diseño determina la frecuencia de corte 3 dB y realiza una estimación de la atenuación del
filtro a 1 GHz.
NOTA: Ver tabla 3 y pagina 18 de los apuntes.
3.
Se tiene un circuito resonante paralelo como el de la figura1. A la hora de realizar el filtro no se
pueden obtener los valores de bobina y condensador necesarios y entonces se decide realizar un
escalado del filtro 10:1 . Realice el escalado basado en el tapping.
4.
En el mismo problema anterior se llega, por algún camino .a la estructura mostrada en la figura 2.
Obtener el valor de los condensadores Cs 2, Cp2.
Figura 1
Figura 2
5.
En algunas aplicaciones se suele utilizar una combinación de 2 filtros complementarios enparalelo
para obtener adaptación a la entrada en todas las frecuencias incluida la banda de atenuación.. En este
ejercicio vamos a diseñar un filtro de este tipo. Para ello, al conectarlos en paralelo deben comenzar por
un elemento en serie. Una vez tomada esta decisión calcularemos el prototipo paso bajo, obtendremos
su equivalente paso alto y asociaremos ambos filtros. Las impedancias de generador y carga a las que
se conectaran los filtros serán de 75 Ω.
RF
HP
OL
IF
LP
Ro
Topología Butterworth
fc = 40 MHz
ALP = 30 dB @ 100 MHz
AHP = 20 dB @ 20 MHz
RL=75Ω
NOTA: Ambos filtros suelen de tener el mismo número de elementos por lo que se escogerá como orden el mayor que resulte
Electrónica de comunicaciones
1
TEMA2: Técnicas de filtrado en RF.
Curso 2003-2004
6.
Se quiere construir un filtro paso bajo con una frecuencia de corte de 25 MHz y que sea capaz de
proporcionar por lo menos una atenuación mínima de 20 dB en toda la banda de atenuación que
comienza en 32.5 MHz. El máximo rizado permitido en banda es de 0.3 dB y el filtro puede tener como
máximo 5 secciones. Las resistencias de generador y carga son de 50 Ω. Escoger la topología adecuada
del filtro y diseñarlo según la teoría moderna de filtros. Utilice el programa de software gratuito de la
web. (http://www.aade.com/filter.htm)
7.
A continuación se presentan las características de frecuencia central y ancho de banda de una serie
de filtros paso banda. Indicar, teniendo en cuenta estos parámetros exclusivamente, cuales serian
realizables mediante la teoría aproximada (síntesis) de filtros y cuales necesitan otra solución tecnológica
como por ejemplo filtros resonantes o combinaciones de filtros.
F1
fo = 100 MHz
Bw = 15 MHz
F3
fo = 1 GHz
Bw = 800 MHz
F2
fo = 500 MHz
Bw = 125 MHz
F4
fo = 700 MHz
Bw = 420 MHz
F5
F6
fo = 10 MHz
Bw = 200 KHz
f0 = 455 KHz
Bw = 2,5 KHz
8.
Diseñar un filtro Butterworth paso banda centrado en 500 MHz, con un ancho de banda de 150 MHz
y que sea capaz de proporcionar al menos una atenuación de 20 dB a 850 MHz. RG = RL= 50 Ω.
NOTA: Ver tabla 4.
8.
Diseñar un filtro Butterworth rechazo de banda centrado en 500 MHz con un Bw = 150 MHz y que
sea capaz de proporcionar al menos una atenuación de 20 dB a 550 MHz. RG = RL= 50 Ω.
NOTA: Ver tabla 4.
9.
Queremos utilizar el filtro paso banda de la figura 1 , diseñado para 75 Ω (entrada y salida) para
conectarlo a una impedancia de salida de 50 Ω. Se decide utilizar una transformación de Norton para
escalar dicha impedancia. Realiza el escalado paso a paso utilizando este procedimiento.
Figura 1
Tablas
ρ (%)
2
5
10
25
Rizado (dB)
0.001
0.01
0.04
0.28
Tabla 3. Equivalencia entre el rizado y la ρ.
Electrónica de comunicaciones
2
TEMA2: Técnicas de filtrado en RF.
Curso 2003-2004
Tabla 4. Tabla de cálculo para filtros Butterworth con RL = RS
Tabla 1. Atenuación de un filtro Butterworth en función del orden del mismo.
Electrónica de comunicaciones
3
TEMA2: Técnicas de filtrado en RF.
Curso 2003-2004
Tabla 2. Tabla de cálculo de un filtro Butterworth c uando RL ≠ RS
Electrónica de comunicaciones
4