sesión 04

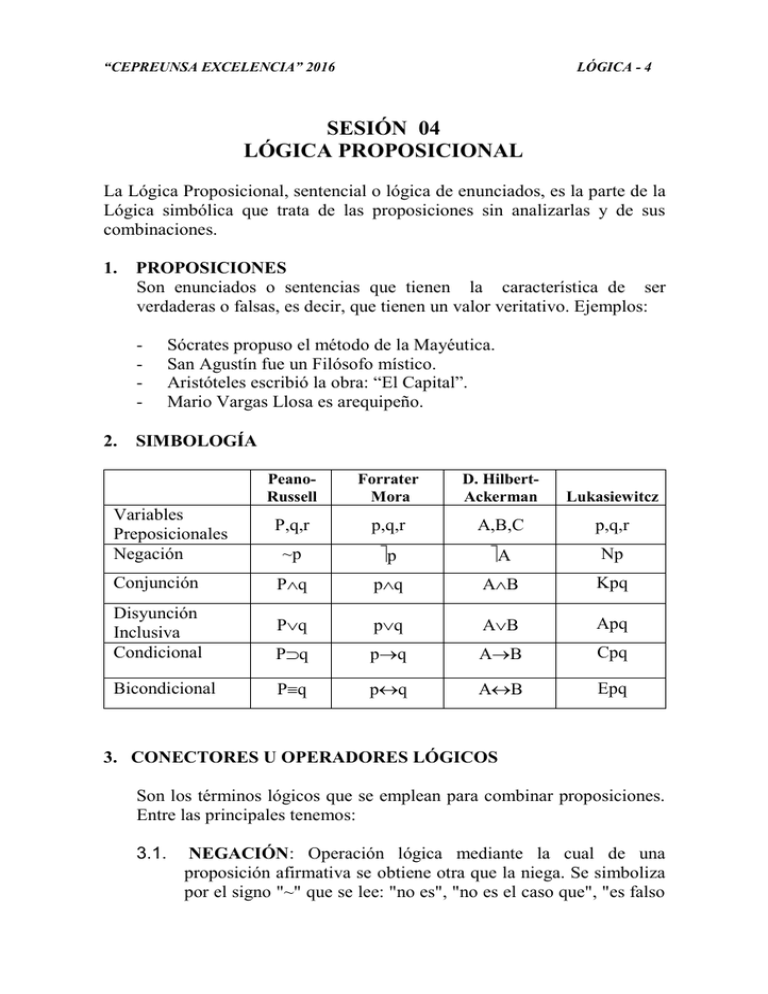
“CEPREUNSA EXCELENCIA” 2016
LÓGICA - 4
SESIÓN 04
LÓGICA PROPOSICIONAL
La Lógica Proposicional, sentencial o lógica de enunciados, es la parte de la
Lógica simbólica que trata de las proposiciones sin analizarlas y de sus
combinaciones.
1.
PROPOSICIONES
Son enunciados o sentencias que tienen la característica de ser
verdaderas o falsas, es decir, que tienen un valor veritativo. Ejemplos:
-
2.
Sócrates propuso el método de la Mayéutica.
San Agustín fue un Filósofo místico.
Aristóteles escribió la obra: “El Capital”.
Mario Vargas Llosa es arequipeño.
SIMBOLOGÍA
PeanoRussell
Forrater
Mora
D. HilbertAckerman
Lukasiewitcz
P,q,r
p,q,r
A,B,C
p,q,r
~p
p
A
Np
Conjunción
Pq
pq
AB
Kpq
Disyunción
Inclusiva
Condicional
Pq
pq
AB
Apq
Pq
pq
AB
Cpq
Bicondicional
Pq
pq
AB
Epq
Variables
Preposicionales
Negación
3. CONECTORES U OPERADORES LÓGICOS
Son los términos lógicos que se emplean para combinar proposiciones.
Entre las principales tenemos:
3.1.
NEGACIÓN: Operación lógica mediante la cual de una
proposición afirmativa se obtiene otra que la niega. Se simboliza
por el signo "~" que se lee: "no es", "no es el caso que", "es falso
“CEPREUNSA EXCELENCIA” 2016
LÓGICA - 4
que", "se niega que". Ejemplo: "Sócrates es filósofo" "p" tiene su
negación: "Sócrates no es filósofo" "~p".
3.2.
CONJUNCIÓN: Combina dos proposiciones mediante la
conectiva "y" entre ellas. Se simboliza por el signo "" que se
coloca entre las proposiciones. Ejemplo: "Aristóteles es el padre
de la lógica clásica y Frege el padre de la lógica moderna" "p^q".
3.3.
DISYUNCIÓN INCLUSIVA: Combina dos proposiciones
mediante la inserción de las conectiva "o" entre ellas. Se
simboliza por el signo "" que se coloca entre las proposiciones
conectadas y que se lee: "p ó q" (p ambas). Ejemplo: "Platón es
sabio o filósofo" "pq".
3.4.
DISYUNCIÓN EXCLUSIVA: Combina dos proposiciones
mediante la inserción de las conectivas "o...o..." que se anteponen
a cada proposición respectivamente. Se simboliza por el signo *
que colocado entre ellas, se lee: "o p o q" (pero o ambas).
Ejemplo: "O Pedro es peruano o Pedro es argentino" "pq".
3.5.
EL CONDICIONAL O IMPLICACIÓN MATERIAL
Combina dos proposiciones mediante la inserción de los
términos. "Si... entonces" o "Implica". Se simboliza por el signo
"" o "" insertado entre las dos proposiciones; siendo la
primera el "antecedente" y la segunda el "consecuente" y que se
lee: "si p, entonces q" o "p implica q". Ejemplo: "Si estudias
metódicamente, entonces ingresarás a la universidad" "pq".
3.6.
LA REPLICACIÓN MATERIAL. Combina dos proposiciones
mediante la inserción de los términos "Sólo si... entonces..." o
"replica". Se simboliza por el signo "" que colocado entre las
proposiciones, se lee: "Sólo si p, entonces q" o "p replica q".
Ejemplo: "Sólo si practicas, entonces aprenderás" "pq".
3.7.
EL BICONDICIONAL O EQUIVALENCIA: Combina dos
proposiciones mediante la inserción de los términos "...si y sólo
si..." o "...es equivalente..." se simboliza mediante el signo "" o
"o" que colocado entre las proposiciones, se lee: "p si y sólo si q"
o "p es equivalente a q", que puede significar: "Ingresarás a la
universidad, si y sólo si te esfuerzas" "pq".
“CEPREUNSA EXCELENCIA” 2016
LÓGICA - 4
3.8.
NEGACIÓN ALTERNA. Combina dos proposiciones mediante
los términos "no ...o no..." o "...excluye..." o "...incompatible...".
Se simboliza con el signo "" que colocado entre las dos
proposiciones, se lee: "no p o no q" o "p es incompatible con q" o
"p excluye a q" y puede significar: "No está en lo cierto Juan, o
no conoce el asunto" "pq".
3.9.
NEGACIÓN CONJUNTA: Combina dos proposiciones
mediante los términos "ni...ni..." antes de las proposiciones
respectivamente. Se simboliza mediante el signo "" que
colocado entre las proposiciones, se lee: "ni p ni q". Ejemplo: "Ni
Aristóteles fue alemán, ni Frege fue griego" "pq".
4. MATRICES VERITATIVAS O TABLAS DE VERDAD
La matriz veritativa o tabla de verdad es un procedimiento gráfico para,
averiguar mecánicamente los valores de verdad (V) y falsedad (F) de
las proposiciones moleculares, en base a los valores veritativos de sus
componentes.
Si se trata de una sola proposición sus valores son V-F, si se trata de dos
sus valores son cuatro, si de tres, sus valores son ocho, si de cuatro,
dieciséis, etc.
Tabla de verdad de la negación. Si p es verdadera, -p es falsa; si p es
falsa, -p es verdadera.
(margen)
p
-p
V
F
F
V
(cuerpo)
“CEPREUNSA EXCELENCIA” 2016
LÓGICA - 4
Tablas de verdad de las conectivas lógicas:
pq
pq
pq
pq
pq pq
pq
p/q
pq
v
v
V
V
F
V
V
V
F
F
v
f
F
V
V
F
V
F
V
F
f
v
F
V
V
V
F
F
V
F
f
f
F
F
F
V
V
V
V
V
ESQUEMAS MOLECULARES
Son las combinaciones de variables u operadores preposicionales que
permiten conformar y veritar operaciones lógicas complejas, y pueden ser:
CONSISTENTE O CONTINGENTE. Es aquél que, al aplicarle las tablas
de verdad, se obtiene en el resultado final tanto valores de verdad como de
falsedad. Por ejemplo:
p
q
~
(pvq)

q
V
V
F
V
V
V
V
F
F
V
V
F
F
V
F
V
V
V
F
F
V
F
F
F
CONTRADICTORIO, INCONSISTENTE O INCONTINGENTE. Es
aquel que, al aplicarle las tablas de verdad, se obtiene en el resultado final
todos los valores falsos.
(p~q) 
p
q
V
V
F F
F
V
V
F
F
V
V V
F F
F
F
F
V
F
F
F V
F
V
(pq)
“CEPREUNSA EXCELENCIA” 2016
LÓGICA - 4
TAUTOLÓGICO: Es aquel que, al aplicarle las tablas de verdad, en el
resultado final se obtiene todos los valores verdaderos. Ejemplo:
p
q
(pq)

q
V
V
V
V
V
V
F
F
V
F
F
V
F
V
V
F
F
F
V
F
PRÁCTICA 4
A. Diga si les siguientes enunciados son o no proposiciones, y
fundamente el por qué:
1. Horas dramáticas de la humanidad.
2. Sería fascinante viajar a Marte.
3. Es probable que ocurra grandes desastres este 2016.
4. Arequipa, sufre la contaminación de la Minera Cerro Verde.
5. La UNSA tiene un prestigio bien ganado en base a trabajo y lealtad.
B. Diga si las proposiciones son atómicas, o moleculares y qué conector
usa:
1. La lógica es una ciencia formal y la química una ciencia fáctica.
2. Las inferencias son procesos de razonamiento.
3. Si viajas a Macchu Pichu, tendrás una inolvidable experiencia.
4. La lógica se entiende si y sólo si se tiene un pensamiento crítico.
5. Los ejercicios en lógica facilitan el aprendizaje.
6. Tener el Título de Filósofo, equivale a ser egresado de la
“CEPREUNSA EXCELENCIA” 2016
LÓGICA - 4
Universidad.
C. Simbolizar las siguientes proposiciones:
1.
No es el caso que el campeonato mundial de fútbol 2016 y el
campeonato nacional caminos del Inca estén exentos de peligros.
2.
Si se deja de lado la Filosofía y se opta por la ciencia entonces es
previsible una sociedad más deshumanizada.
3.
O empezamos el cambio por nosotros o hemos de asistir a la auto
extinción de la humanidad.
4.
El cáncer es el mal de este tiempo y su tratamiento es costoso. Por
lo que debemos tomar conciencia de ello para evitarlo y tener la
cultura de la consulta médica.
5.
Cuando el cielo esta nublado el alma del arequipeño se entristece y
añora fervientemente su cielo azul.
D. Aplicar las tablas de verdad a los siguientes esquemas moleculares:
1. Aplicando las tablas de verdad al ejercicio, obtenernos un esquema
molecular:
((pq) (~rq))  (r~p)
a) Contradictorio
b) Contingente
c) Probabilístico
d) Sintético
e) Tautológico
2.
Aplicando las tablas de verdad al ejercicio siguiente obtenemos
una:
(p  (q  r))  ((p ~r)  p)
a) Tautología
b) Contingencia
c) Contradictoria
d) Síntesis
e) Probabilísmo
“CEPREUNSA EXCELENCIA” 2016
LÓGICA - 4