1º INGENIERIA INDUSTRIAL FUNDAMENTOS FISICOS DE LA

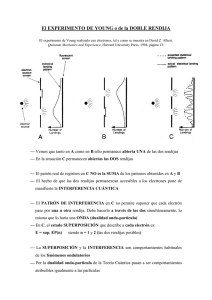
1º INGENIERIA INDUSTRIAL
FUNDAMENTOS FISICOS DE LA INGENIERIA
PRIMER PARCIAL
22 DE ENERO DE 2008
PARTE TEORICA: Esta parte del examen vale cinco puntos. Los tres ejercicios
tienen el mismo valor.
TIEMPO: 75 MINUTOS.
ESCRIBID LAS TRES PREGUNTAS EN HOJAS SEPARADAS.
1. Ondas estacionarias.
2. El sistema de la figura está formado por un depósito cerrado de gran sección lleno de
un fluido hasta un nivel H y en cuya parte superior hay aire comprimido. El fluido sale a
la atmósfera por la abertura 4. Las secciones s1, s2 y s4 son iguales. Los tubos verticales
sobre las posiciones 2 y 3 están abiertos a la atmósfera. Decir si las siguientes
afirmaciones son verdaderas o falsas, razonando la respuesta de forma precisa:
(a) El caudal que circula por el punto 1 es mayor que el caudal que circula por 3.
(b) La altura h es mayor que la altura h’.
(c) La velocidad en el punto 1 es menor que en el punto 4.
(d) Si abrimos un agujero en la parte superior del depósito el caudal de vaciado del
sistema es el mismo que en la situación inicial.
(e) Si con el depósito abierto sustituimos el fluido del sistema por otro de mayor
densidad el caudal circulante cambia.
3. La bandera que ondea en el mástil de un barco forma un ángulo de 45º respecto a la
dirección oeste, hacia el sur. Por otra parte, otra bandera que está en la costa forma un
ángulo de 30 º con respecto al oeste, también hacia el sur.
a. Si el barco va hacia el norte a 10 Km/h respecto a tierra, ¿cuál es la velocidad del
viento con respecto a la costa?
b. ¿Cuál es la velocidad del viento para el observador que está en el barco?
1º INGENIERIA INDUSTRIAL
FUNDAMENTOS FISICOS DE LA INGENIERIA
PRIMER PARCIAL
22 DE ENERO DE 2008
PROBLEMAS. Esta parte del examen vale cinco puntos. Los tres problemas tienen
el mismo valor.
TIEMPO: 90 MINUTOS.
ESCRIBID LAS TRES PREGUNTAS EN HOJAS SEPARADAS.
1. Una niña se deja caer resbalando sin rozamiento desde una altura h a lo largo de un
tobogán, tal y como muestra la figura. Sale lanzada desde una altura h/5 sobre una
piscina. Determinar, en función de h y θ:
a) la velocidad de la niña a la salida del tobogán
b) el tiempo, a partir de la salida del tobogán, que tarda en alcanzar la altura máxima
sobre el nivel del agua
c) la altura máxima alcanzada
d) Dar los resultados numéricos para estos datos: h=15 m, θ = 30o, g=10 m/s2.
2. Con la polea de la figura se eleva la masa M=100 Kg a velocidad constante v = 1.5
m/s. El momento de inercia de la polea respecto del eje perpendicular que pasa por su
centro de masas es I=mR2/2, siendo m=10 Kg la masa de la polea y R=0.5 m su radio
mayor. Las cuerdas no deslizan sobre las poleas. Calcular:
a) La tensión T y la reacción en el eje de la polea, siendo r=0.2 m el radio menor de
la polea.
b) Verificar que la potencia que la polea entrega a la masa M es la misma que la
que recibe del cable horizontal. ¿Cuánto vale esa potencia?
c) Si ahora el cable horizontal deja de hacer fuerza, ¿con qué aceleración
descenderá la masa M?
R
r
M
T
3. Un cilindro de volumen V0 y sección S está cerrado por un émbolo. El sistema está en
contacto térmico con un foco a temperatura T0. En el interior del cilindro hay nitrógeno
a una presión P0. Se comprime el nitrógeno bruscamente mediante una fuerza externa de
valor Fext=2P0S.
Calcular para ese proceso:
a) El estado final del gas.
b) El trabajo realizado por el gas, el calor absorbido por el gas y el cambio de
energía interna del gas.
c) El cambio de entropía del gas, del foco y del universo.
Desde éste último estado de equilibrio, se deja ahora expandir el gas espontáneamente
frente a una fuerza externa Fext=P0S. Responder a los apartados (a) (b) y (c) para el
nuevo proceso.
¿Cuál es el cambio total de la entropía del gas en los dos procesos? ¿Y el cambio total
de la entropía del foco? Comentar el resultado.
1º INGENIERÍA INDUSTRIAL
FUNDAMENTOS FÍSICOS DE LA INGENIERÍA
PRIMER PARCIAL
23 DE JUNIO DE 2008
PARTE TEÓRICA: Esta parte del examen vale cinco puntos. Los tres ejercicios
tienen el mismo valor.
TIEMPO: 75 MINUTOS.
ESCRIBID LAS TRES PREGUNTAS EN HOJAS SEPARADAS.
1. Oscilador armónico amortiguado. Sistema subamortiguado.
2. Decir si las siguientes afirmaciones son verdaderas o falsas, razonando las respuestas
de forma precisa:
a) En un tiro vertical hacia arriba el movimiento es primero desacelerado y luego
acelerado, y por lo tanto la aceleración cambia de signo.
b) Si la aceleración de un móvil es constante, entonces la trayectoria del móvil es
siempre una línea recta.
c) Un móvil puede cambiar la dirección de su velocidad cuando su aceleración es
constante.
d) Un móvil puede cambiar la dirección de su aceleración cuando la dirección de su
velocidad se mantiene constante.
e) Todas las partes de una rueda en rotación poseen la misma velocidad lineal.
3. Un disco de momento de inercia I1 gira con velocidad angular ω0 en torno a un eje
vertical sin rozamiento (ver figura). Un segundo disco, con momento de inercia I2, que
inicialmente no gira, cae sobre el primero. Como las superficies de los discos son
rugosas, los dos cilindros adquieren la misma velocidad angular ω. Determinar:
a) La velocidad angular común con la que girarán los dos discos.
b) La pérdida relativa de energía cinética.
1º INGENIERÍA INDUSTRIAL
FUNDAMENTOS FÍSICOS DE LA INGENIERÍA
PRIMER PARCIAL
23 DE JUNIO DE 2008
PROBLEMAS. Esta parte del examen vale cinco puntos. Los tres problemas tienen
el mismo valor.
TIEMPO: 90 MINUTOS.
ESCRIBID LAS TRES PREGUNTAS EN HOJAS SEPARADAS.
1. Una estudiante de 50kg es impulsada desde el suelo con una velocidad inicial de 5
m/s en una dirección que forma 60º con la horizontal. Según está en el aire, un
compañero le lanza un balón muy denso de 10kg de masa. Cuando la estudiante se
encuentra en el punto más alto de su trayectoria recoge el balón, agarrándolo
firmemente. Sabiendo que la velocidad del balón justo antes de ser recogido es de 4 m/s
vertical hacia arriba:
a) Calcular el vector velocidad de la estudiante en el instante inmediatamente anterior al
impacto.
b) Calcular el vector velocidad de la estudiante y el balón en el instante inmediatamente
posterior al impacto.
c) ¿A qué distancia desde donde saltó caerá?
d) ¿Se ha conservado el momento lineal y la energía cinética del sistema estudiantebalón desde que ella captura el balón hasta que llega al suelo? Razonarlo.
2. Una pieza esférica de aluminio de 200gr. se encuentra completamente sumergida
dentro de un depósito lleno de agua y apoyado en el fondo del mismo. ¿Cuál será la
fuerza que ejerce la pieza sobre el suelo del recipiente? (indicando módulo, dirección y
sentido).
Colgamos ahora la pieza de un muelle, de forma que sigue completamente sumergida
pero ya no está apoyada en el fondo. ¿Cuál será la elongación del muelle?.
Calcular el periodo de las pequeñas oscilaciones del sistema ignorando la fricción entre
la pieza y el agua. ¿Es esta aproximación razonable?
Datos: Densidad del aluminio:2.7 103Kg/m3;
Constante del muelle: 10N/m;
Coeficiente de fricción entre el agua y la esfera de aluminio: 5·10-3Ns/m
Continúa a la vuelta.
3. Sea un mol de un gas ideal diatómico que ocupa un volumen de 2 litros a la
temperatura de 300K. Sometemos el gas al siguiente proceso cíclico: En primer lugar,
se expande adiabática y cuasiestáticamente hasta que el volumen sea el doble. A
continuación, se comprime bruscamente a presión constante en contacto con un foco de
temperatura 150K. Una vez alcanzado el equilibrio se sigue comprimiendo cuasiestática
e isotérmicamente hasta alcanzar el volumen del primer estado. Por último, se va
subiendo cuasiestáticamente la presión manteniendo el volumen constante hasta
alcanzar el estado de partida.
a) Dibujar el ciclo. ¿Es reversible o irreversible? Justificarlo.
b) Calcular la variación de energía interna y de entropía totales del gas en el proceso.
c) Calcular el trabajo realizado en cada proceso y trabajo total.
d) Calcular el calor intercambiado en cada proceso. Indicar explícitamente en qué
procesos el gas absorbe o cede calor.
Dato: R=0.082 atm.l/mol K= 8.31 J/mol K
1º INGENIERÍA INDUSTRIAL
FUNDAMENTOS FISICOS DE LA INGENIERÍA
SEGUNDO PARCIAL
23 DE JUNIO DE 2008
PARTE TEÓRICA: Esta parte del examen vale cinco puntos. Los tres ejercicios
tienen el mismo valor.
TIEMPO: 75 MINUTOS.
ESCRIBID LAS TRES PREGUNTAS EN HOJAS SEPARADAS.
1. Asociación de resistencias eléctricas
2. Responde razonadamente si las siguientes afirmaciones son verdaderas o falsas:
Considérese un experimento de doble rendija de Young cuyas rendijas están separadas
por una distancia d y la fuente luminosa monocromática emite a una longitud de onda λ
= d/5
a) El último orden de interferencia que podremos observar será el tercero.
Si abrimos una nueva rendija a una distancia d, de forma que tenemos tres rendijas
equidistantes entre sí:
b) La separación angular entre dos máximos principales consecutivos será la
misma que con sólo dos rendijas
c) La irradiancia en los máximos principales es la misma que con sólo dos rendijas.
Si tapamos ahora la rendija central, quedando dos rendijas, separadas una distancia 2d
d) La separación angular entre dos máximos principales consecutivos será la
misma que en el apartado (a)
e) Si sumergimos la doble rendija en un medio material con índice de refracción
n=1.5, los máximos principales se encontrarán más cercanos entre sí.
3. Observa el circuito de la figura.
a) Calcula el campo magnético en el punto P.
b) ¿Cómo sería la fuerza que sufriría un electrón situado en el punto P que se
mueve horizontalmente hacia la derecha con velocidad v?
c) ¿Cómo sería la fuerza que sufriría un electrón situado en el punto P que se
mueve con la misma velocidad pero perpendicular al plano de la hoja y hacia
adentro?
R1
R2
P
1º INGENIERÍA INDUSTRIAL
FUNDAMENTOS FÍSICOS DE LA INGENIERÍA
SEGUNDO PARCIAL
23 DE JUNIO DE 2008
PROBLEMAS. Esta parte del examen vale cinco puntos. Los tres problemas tienen
el mismo valor.
TIEMPO: 90 MINUTOS.
ESCRIBID LAS TRES PREGUNTAS EN HOJAS SEPARADAS.
1. Un hilo delgado de longitud L cargado uniformemente con una carga Q se encuentra
doblado formando un arco de circunferencia de 90º (ver el dibujo). Calcular el campo
eléctrico y el potencial electrostático en el punto O (el centro de la circunferencia)
¿Qué trabajo mínimo tendremos que realizar para llevar a una partícula de carga -q
inicialmente en reposo desde un punto situado muy lejos del hilo hasta el punto O?
¿Qué fuerza habrá que ejercer para que la partícula cargada permanezca en reposo en el
punto O?
90º
O
2. Una barra conductora de masa m está situada sobre dos raíles horizontales, separados
una distancia l , entre los que se conecta una batería de f.e.m. ε 0 , tal y como se
representa en la figura. La resistencia eléctrica del conjunto es R y no existe rozamiento
al deslizamiento entre la barra y los raíles. El conjunto se encuentra en una región donde
existe un campo magnético B constante y de sentido entrante, perpendicular al plano del
papel. Determinar:
a) Aceleración inicial de la barra, teniendo en cuenta que parte del reposo.
b) f.e.m inducida en el circuito cuando la barra se mueve con velocidad v.
En cuanto la barra comienza a moverse la fuerza electromotriz total será la suma de la
fuerza electromotriz de la batería y la fuerza electromotriz inducida por el movimiento
de la varilla. Calcular:
c) Intensidad de corriente en el circuito y fuerza magnética sobre la barra cuando la
velocidad de la misma es v. ¿Existe algún valor de v para el cual la fuerza magnética es
cero? ¿Cuál es el valor de la intensidad es ese caso?
ε0
Continúa a la vuelta.
l0
3. Se coloca un objeto a 30cm a la izquierda de una lente y se observa que se forma una
imagen real de éste a 60cm de la lente. (a) Calcular la potencia de la lente.
Se coloca entonces otra lente de potencia de -8 dioptrías a 10cm a la derecha de la
primera lente.
(b) Calcular donde se formará la imagen final, su carácter real o virtual y el aumento
lateral total. Trazar los diagramas de rayos correspondientes.
(c) Calcular dónde habría que colocar la lente divergente para que la imagen final se
forme en el infinito.