LEER MÁS... - Instituto Tecnologico de San Luis Potosí
Anuncio

CURSO DE SELECCIÓN 2016
INSTITUTO TECNOLÓGICO DE SAN LUIS POTOSÍ
ANTOLOGÍA DE MATEMÁTICAS 2016
“Un gran descubrimiento resuelve un gran problema, pero es un grano de descubrimiento en la solución
de cualquier problema. Usted puede ser modesto, pero si desafía su curiosidad y pone en juego sus
facultades inventivas, y si lo resuelve por sus propios medios, puede experimentar la tensión y disfrutar del
triunfo del descubrimiento.”
George Polya (1887-1985)
ITSLP
I
CURSO DE SELECCIÓN 2016
AL ESTUDIANTE
Bienvenido al Curso de Selección del Instituto Tecnológico de San Luis Potosí, cuyo propósito es el
de contribuir con unos cuantos de ustedes a recuperar algunos conceptos matemáticos básicos
que se les hayan extraviado en el a veces sinuoso camino que les trajo hasta aquí, y con otros;
ofrecerles la oportunidad de reafirmar los antecedentes mínimos necesarios para iniciarse en el
fascinante estudio del cálculo diferencial e integral.
Este material ha sido escrito como una guía para ayudarte a sacar el máximo provecho de este
curso, antes de intentar resolver los problemas que se plantean, es conveniente que tengas en
cuenta las siguientes recomendaciones:
La actitud inicial es importante. Cuando nos enfrentamos a un problema es muy importante la
actitud que tienes ante él. ¿Estás ansioso por resolverlo o no tienes gana ninguna? ¿Tus
condiciones físicas (cansancio, sueño, etc.) son las adecuadas? ¿Tienes curiosidad, disposición de
aprender, gusto por el reto?
Ten confianza en tus capacidades. Con frecuencia, no es necesario saber mucho para resolver
bien un problema. Basta con pensar correctamente. Actúa, pues, sin miedo, con tranquilidad,
convencido de que está a tu alcance.
Sé paciente y constante. No abandones a la menor dificultad. Si te quedas atascado, no te des por
vencido; piensa un nuevo enfoque del problema. Cada problema requiere su tiempo.
Concéntrate en lo que haces. Resolver problemas es una actividad mental compleja. Requiere
poner en tensión todos nuestros resortes mentales.
Busca el éxito a largo plazo. Un joven vive muchas frustraciones, muchos desencantos, pero
tienes que aprender siempre a sobreponerte a esas cosas. Lo que más duele a un profesor es
cuando un joven estudiante viene a tratar de justificar su fracaso, aquí no hay fracasos, debe
haber siempre el intento permanente de superar cualquier dificultad y para eso estamos también
nosotros para ayudarte. Aprender a resolver problemas es un proceso lento. Los frutos tardarán
un cierto tiempo en llegar pero cuando notes los progresos sentirás una gran satisfacción
Bienvenido, mucho trabajo y mucho éxito.
ITSLP
II
CURSO DE SELECCIÓN 2016
Contenido
1.
Geometría ............................................................................................................................. 2
1.1.
Triángulo rectángulo..................................................................................................... 2
1.2.
Área, Perímetro ............................................................................................................ 3
1.3.
Teorema de Pitágoras ................................................................................................... 3
1.4.
Funciones trigonométricas: seno, coseno y tangente ................................................... 4
Problemas ................................................................................................................................. 6
2.
Matemáticas y resolución de problemas .............................................................................. 7
2.1 Estrategia para resolver problemas ................................................................................... 8
2.1.1 Estrategia: Búsqueda de un patrón ............................................................................. 8
2.1.2 Estrategia: Examinar un problema relacionado ........................................................ 13
2.1.3 Estrategia; hacer una tabla ........................................................................................ 13
2.1.4 Estrategia: trabajar regresivamente .......................................................................... 14
2.1.5 Razonamiento directo................................................................................................ 15
Problemas................................................................................................................................ 16
2.2 Sucesiones aritméticas ..................................................................................................... 19
Generalización de sucesiones aritméticas .................................................................................... 20
Problemas ............................................................................................................................... 22
2.3. Sucesiones geométricas ................................................................................................... 23
Problemas de sucesiones: ...................................................................................................... 25
Problemas de patrones, sucesiones ....................................................................................... 27
2.1.3. Ideas intuitivas del significado función ............................................................................ 30
Problemas de aplicación ............................................................................................................ 31
Problemas (Razonamiento algebraico) .................................................................................. 34
Aritmética ................................................................................................................................... 36
3.1
Jerarquía de operaciones ............................................................................................ 36
3.2
Elevación a Potencias .................................................................................................. 36
3.3
Radicación ................................................................................................................... 38
Potenciación y Radicación ................................................................................................... 43
ITSLP
III
CURSO DE SELECCIÓN 2016
3.4 Sistema de numeración .................................................................................................... 45
3.4.1El sistema de numeración decimal ................................................................................ 45
3.4.2Divisibilidad y números primos ................................................................................. 47
Problemas ............................................................................................................................... 48
3.4.4 Números primos ........................................................................................................ 49
3.4.5 Máximo común divisor .............................................................................................. 50
3.4.6 Mínimo común múltiplo ............................................................................................ 51
Problemas MCD, MCM ............................................................................................................ 52
3.5 Números racionales .......................................................................................................... 54
3.5.1Fracciones equivalentes ............................................................................................. 56
Problemas ............................................................................................................................... 58
3.5.2 Suma y resta de números racionales ......................................................................... 62
3.5.3Números mixtos .......................................................................................................... 63
Problemas con fracciones....................................................................................................... 66
3.5.4 Multiplicación y división de números racionales ...................................................... 69
Problemas con fracciones....................................................................................................... 74
3.6 Razonamiento proporcional ............................................................................................. 78
Problemas con fracciones y proporciones ............................................................................. 81
3.7 Porcentajes ....................................................................................................................... 83
Problemas de porcentajes ...................................................................................................... 86
4 Ecuaciones ............................................................................................................................... 88
4.1
Ecuaciones de primer grado con una incógnita. ........................................................ 88
4.2
Sistemas de ecuaciones .............................................................................................. 90
4.2.1 Método de suma y resta ........................................................................................... 90
4.2.2
Método de sustitución ........................................................................................... 91
4.2.3
Método de determinantes ..................................................................................... 91
4.2.4 Método de igualación ................................................................................................ 92
5
Álgebra ................................................................................................................................ 99
5.1
Operaciones algebraicas ............................................................................................. 99
5.1.1
Suma o adición .................................................................................................... 99
5.1.2
Resta o sustracción ............................................................................................... 99
ITSLP
IV
CURSO DE SELECCIÓN 2016
4.1.3
Multiplicación de polinomios .............................................................................. 100
5.1.4
División de polinomios ........................................................................................ 101
5.2
Productos notables y Factorización ............................................................................. 102
5.2.1
Productos notables ............................................................................................. 102
5.2.2
Factorización....................................................................................................... 103
5.3
Fracciones algebraicas ................................................................................................ 108
5.3.1
Operaciones con fracciones (operaciones básicas) .............................................. 108
5.4 Ecuaciones cuadráticas .................................................................................................. 111
Parábola................................................................................................................................. 111
5.4.1 Gráfica: Eje de simetría, foco, vértice y concavidad .................................................... 111
5.4.1Forma estándar .......................................................................................................... 111
BIBLIOGRAFIA ............................................................................................................................ 118
ITSLP
V
CURSO DE SELECCIÓN 2016
1. Geometría
La Geometría es una ciencia formativa que nos ayuda a razonar. Está presente en la naturaleza y es utilizada en
diversas actividades del hombre. Puede ser muy atractiva si se logra hacerla próxima a los alumnos; pero, también
puede ser muy difícil, si predomina en su enseñanza la abstracción.
Las reglas de la geometría se remontan a los antiguos egipcios y griegos, quienes usaron la geometría para medir la
altura de pirámides, la circunferencia de la tierra y la distancia a la luna.
1.1.
Triángulo rectángulo
La importancia de los triángulos en todas las ciencias es grande, por eso es necesario tener presente las
características fundamentales de ellos.
Las principales propiedades que tienen los triángulos son:
- La suma de los ángulos interiores de un triángulo es igual a 180°.
- Cada lado de un triángulo es menor que la suma de los otros dos.
- El ángulo que se opone al lado mayor es el mayor ángulo.
- Tipos de triángulos: escaleno, isósceles, equilátero, rectángulo.
Cuando se trata con triángulos es habitual el convenio de denotar con letras mayúsculas los vértices y los ángulos
(la misma letra para el vértice y el correspondiente ángulo). Para indicar un lado (o lo que mide) se usa la misma
letra que la del ángulo opuesto pero escrita en minúscula.
A. Si dos ángulos suman 90°, se dice que son _________________.
Los dos ángulos agudos de un triángulo rectángulo suman ______.
Por tanto, los dos ángulos agudos de un triángulo rectángulo son _________________.
B. Construye un triángulo cuyos lados midan:
,
y
. Mide los ángulos:
¿Qué tipo de triángulo resultó? ____________________________________.
2
CURSO DE SELECCIÓN 2016
C. Analizar para los datos que se dan a continuación si todos los triángulos pueden ser construidos. En caso
negativo analizar por qué no lo son y en caso positivo determinar la cantidad de soluciones posibles:
- un triángulo equilátero cuyos ángulos sean de
,
y
,
- un triángulo cuyos ángulos sean
,
y
,
- un triángulo cuyos lados midan
,
y
respectivamente.
1.2. Área, Perímetro
A. ¿Cuál es el área del siguiente triángulo? ¿Cuál es su perímetro?
1.3. Teorema de Pitágoras
El cuadrado de la hipotenusa del triángulo rectángulo es igual a la suma de los cuadrados de los catetos:
.
B. Encuentra el lado que falta en los siguientes triángulos rectángulos y dibújalos:
a)
b)
c)
d)
C. Considere un cuadrado cuya diagonal mide 10 unidades. Determine el área del cuadrado.
D. Determina el área de un triángulo equilátero cuyo lado mide
.
3
CURSO DE SELECCIÓN 2016
1.4. Funciones trigonométricas: seno, coseno y tangente
Hay seis funciones trigonométricas, también conocidas como funciones circulares, sin embargo en este apartado
solo discutiremos las siguientes tres: seno, coseno, tangente.
Definición de las funciones trigonométricas
Grados y radianes
La variable de entrada de una función trigonométrica es la medida del ángulo; la variable de salida es un número
real.
Definición de radián: un ángulo central de un círculo mide 1 radián si interseca un arco cuya longitud mide lo mismo
que el radio.
La siguiente relación es útil para realizar conversiones entre las diferentes unidades de ángulo:
A. Use el triángulo para completar la tabla.
B. Use el triángulo del problema anterior para completar la tabla.
C. Use el triángulo para completar la tabla.
4
CURSO DE SELECCIÓN 2016
D. ¿Cuántos radianes hay en 120°?
E. ¿Cuántos grados hay en
radianes?
F. Convierta los siguientes ángulos de grados a radianes y viceversa.
radianes
radianes
radianes
radianes
G. Use la calculadora para completar la siguiente tabla.
5
CURSO DE SELECCIÓN 2016
Problemas
H. Determine los lados del siguiente triángulo.
I. ¿Cuál es el área del pentágono? ¿Cuál es su perímetro?
J. Desde un punto a 340 pies de la base de un edificio, el ángulo de elevación hasta la parte alta del edificio es de
65°. Encuentre la altura
del edificio.
K. Desde la parte superior de un puente que mide 100 pies de altura, un hombre observa un automóvil que se
desplaza frente al edificio. Si el ángulo de depresión del automóvil cambia de 22° a 46° durante el periodo de
observación, ¿cuánto se ha trasladado el automóvil?
6
CURSO DE SELECCIÓN 2016
2. Matemáticas y resolución de problemas
Proceso de cuatro pasos para resolver problemas
1.
Entender el problema
a) ¿Puedes enunciar el problema con tus propias palabras?
b) ¿Qué tratas de hallar o de hacer?
c) ¿Cuáles son las incógnitas?
d) ¿De qué información dispones?
e) ¿Qué información, si es el caso, falta o cuál no se necesita?
2.
Trazar un plan
La siguiente listas de estrategias, aunque no es completa resulta muy útil:
a) Buscar un patrón.
b) Examinar problemas relacionados y determinar si las técnicas aplicadas para resolverlos se pueden
aplicar en este caso.
c) Examinar un caso más sencillo, o un caso particular del problema, para comprender mejor la solución
del problema original.
d) Hacer una tabla o lista.
e) Hacer un diagrama.
f) Plantear una ecuación.
g) Proponer y verificar.
h) Trabajar regresivamente.
i) Identificar un objeto parcial.
j) Usar razonamiento indirecto.
k) Usar razonamiento directo.
3. Realiza el plan
a) Llevar a cabo la estrategia o estrategias del paso 2 y efectuar las acciones y los cálculos necesarios.
b) Verificar cada pasó del plan conforme se avanza. La verificación puede ser intuitiva o una demostración
formal de cada paso.
c) Llevar un registro preciso del trabajo.
4.
Mirar hacia atrás
a) Verificar los resultados en el problema original. (en algunos casos se requerirá una demostración).
b) Interpretar la solución en términos del problema original. ¿Tiene sentido tu respuesta?, ¿es
razonable?, ¿responde la pregunta hecha originalmente?
c) Averiguar si hay otro método para hallar la solución.
d) Si es posible, determinar otros problemas relacionados, o más generales, para los cuales funcione la
técnica usada.
7
CURSO DE SELECCIÓN 2016
2.1 Estrategia para resolver problemas
Las estrategias son herramientas que puedes usar para descubrir o construir los medios para alcanzar un objetivo.
Para cada estrategia descrita a continuación, damos un problema que puede resolverse en más de una manera. Tú
puedes diseñar una estrategia diferente para resolver los problemas de muestra. No existe una estrategia que sea
la mejor.
2.1.1 Estrategia: Búsqueda de un patrón
Exploración con patrones
Las matemáticas se han descrito como el estudio de los patrones. Hay patrones donde sea –en papel tapiz,
mosaicos, tráfico y aún en los horarios de la televisión-. Cuando se cometen crímenes en series, los investigadores
policiacos estudian los archivos de cada caso en busca del modus operandi o patrón de operación. Los científicos
buscan patrones para aislar variables de manera que se logren conclusiones válidas en su investigación.
En matemática el estudio de patrones que surgen de situaciones simples constituyen fundamento para los
conceptos posteriores de funciones, ecuaciones y sucesiones. Desde situaciones muy sencillas los estudiantes
pueden aprender a identificar regularidades, reconocer un mismo patrón bajo diferentes formas y usar patrones
para predecir valores.
El trabajo con patrones aritméticos permite integrar estrategias de conteo, operatoria, divisibilidad,
proporcionalidad, etc. a la vez que exige razonamiento lógico y comunicabilidad matemática.
El estudiante ha de comprender el valor de descubrir patrones y expresarlos verbal y simbólicamente mediante
fórmulas que le ayudan a generalizar economizando esfuerzos.
El desarrollo de las habilidades en la generalización de patrones es el preámbulo necesario para el estudio del
álgebra. Cuando los estudiantes exploran patrones, se dedican a detectar similitudes y diferencias, clasificar,
etiquetar, buscar algoritmos, conjeturar, argumentar, establecer relaciones numéricas entre componentes o bien, a
generalizar los datos y relaciones matemáticas, desarrollan habilidades que son fundamentales para el aprendizaje
del álgebra.
a)
Describe los patrones que ves en lo siguiente:
1+0·9=1
2 + 1 · 9 = 11
3 + 12 · 9 = 111
4 + 123 · 9 = 1111
5 + 1234 · 9 = 11111
b) ¿Continúa el patrón anterior? Expresa por qué si o por qué no.
8
CURSO DE SELECCIÓN 2016
Solución
a) Hay varios patrones posibles. Por ejemplo, los números en el extremo izquierdo son os números naturales,
esto es, números del conjunto {1, 2, 3, 4, 5, …}. El patrón comienza con 1 y continúa en el siguiente número
natural mayor en cada línea sucesiva. Los números de “en medio” son el producto de dos números, el segundo
de los cuales es 9. El primer número en el primer producto es 0. Después ese primer número se forma usando
los números naturales y añadiendo uno más en cada línea sucesiva. Los números resultantes de lado derecho
se forman usando números 1 y añadiendo 1 en cada línea sucesiva.
b) el patrón en la ecuación completa parece continuar varios casos más, pero no continúa en general; por
ejemplo:
13 + 123456789101112 · 9 = 1,111,111,101,910,021
El patrón se rompe cuando el número multiplicado por 9 contiene dígitos usados previamente.
Como vimos en el ejemplo anterior, no es confiable determinar un patrón basados en unos cuantos casos. Cuando
hallemos patrones, debemos explicar por qué pensamos que van, o no, a continuar.
Intente este:
a)
Hallar tres términos más de manera que se continúe el patrón.
▪ ◊ ▪▪◊◊▪▪▪◊◊◊▪▪▪▪◊◊◊◊▪▪▪▪▪◊◊◊◊◊
b) Describa con palabras el patrón hallado.
A continuación vemos un patrón que si funciona y nos ayuda a resolver un problema. ¿Cómo puedes hallar la suma
de tres números naturales consecutivos sin efectuar la operación? Damos varios ejemplos. Busca un patrón en
estos ejemplos
14 + 15 + 16
(45)
19 + 20 + 21
(60)
99 + 100 + 101
(300)
9
CURSO DE SELECCIÓN 2016
Después de estudiar las sumas, se revela el patrón de multiplicar por 3 el número de en medio. Se pueden probar
otros números para ver si podemos exhibir un contraejemplo. El patrón sugiere otros planteamientos matemáticos
a considerar. Por ejemplo:
1.
2.
3.
¿Esto funciona con cualesquier tres números naturales consecutivos?
¿Cómo puedes hallar la suma de un número impar de números naturales consecutivos?
¿Qué sucede si hay un número par de números naturales consecutivos?
Damos a continuación una demostración (1), de que la suma de tres números naturales consecutivos es igual a 3
por el número de en medio.
Demostración
Sea n el primero de tres números naturales consecutivos. Entonces los tres números son n, n +1, y n + 2. La suma
de estos tres números es n + (n + 1) + (n + 2) = 3n + 3 = 3(n + 1). Por lo tanto, la suma de los tres números naturales
consecutivos es tres veces el número de en medio.
Problema de Gauss
Cuando Carl Gauss era niño, su maestro pidió a los alumnos que hallara la suma de los primeros 100 números
naturales, esperando así mantener la clase ocupada un buen rato. Gauss dio la respuesta casi de inmediato.
¿Puedes hacerlo tú?
Comprender los problemas. Los números naturales son 1, 2, 3, 4,….Así, el problema es hallar la suma 1 + 2 + 3 + 4
+… + 100.
Trazar un plan. Una estrategia posible es buscar un patrón. Una versión dela historia acerca del joven Gauss dice
que listó los números según se muestra en la siguiente figura. Para descubrir la suma original, Gauss dividió entra 2
la suma obteniendo:
1 + 2 + 3 + 4 + 5 +……….… + 98 + 99 + 100
100 + 99 + 98 + 97 + 96 +……………. + 3 +
101 + 101 +101 + 101+101 +……..
2 +
1
101 + 101 + 101
Realiza el plan. Hay 100 sumas de 101. Entonces el total se puede hallar al calcular:
100 101
ó 5050
2
Mirar hacia atrás. El método es matemáticamente correcto pues la sumase puede efectuar en cualquier orden, y la
multiplicación es una suma repetida. Además, la suma en cada en cada par siempre es 101 pues al movernos de un
10
CURSO DE SELECCIÓN 2016
par al siguiente, sumamos 1 al de arriba y restamos 1 al de abajo, lo cual no cambia la suma; por ejemplo, 2 + 99 =
(1 +1) + (100 - 1) = 100, 3 + 98 = (2 + 1) + (99 - 1) = 2 + 99 = 101, y así sucesivamente.
Un problema más general es hallar la suma de los primeros n números naturales, que antes y notamos la relación
en la siguiente figura. Hay n sumas de n +1 que dan un total de n(n + 1). Por lo tanto, la suma 1 + 2 +3 + 4+ 5+ 6 +…
+ n, está dada por:
n(n 1)
2
1 +
n
+
2 +
3
+
4
+ ….+
(n -1) + (n- 2) + (n - 3) +….
(n + 1) + (n + 1) + (n + 1) + (n +1) +…
+
n
1
+ (n + 1)
Ahora intente este:
Un corte en un tronco produce dos piezas, dos cortes produce tres piezas, y tres cortes producen cuatro piezas.
¿Cuántas piezas se producen con 10 cortes?. Supón que los cortes se realizan de la misma manera que los tres
primeros. ¿Cuántas piezas se producen con n cortes?
Resolver problema. Cuadros mágicos
Arreglar los números del 1 al 9 en un cuadro subdividido en 9 cuadros menores como el mostrado en la siguiente
figura, de manera que cada renglón, cada columna y cada diagonal principal sumen lo mismo. (El resultado se llama
cuadro mágico).
Comprender el problema. Necesitamos colocar cada uno de los 9 números 1, 2, 3, , …. 9 en los cuadros pequeños,
un número diferente en cada cuadrado de diferente manera que la suma de los números en cada renglón, columna
y diagonal principal sea la misma.
Trazar un plan. Si conociéramos el número fijo que deben sumar los renglones, las columnas y las diagonales,
tendríamos una mejor idea de qué números deben de ir juntos en un renglón, o columna, o diagonal, así, nuestro
objetivo parcial, es hallar esa suma fija. La suma de los 9 números 1 + 2 + 3 + … +9, es igual a tres veces la suma en
un renglón (¿por qué?). en consecuencia, la suma fija se obtiene al dividir 1 + 2 + 3 + … +9 entre tres. Usando el
procedimiento desarrollado por Gauss [n(n + 1) ]/2, tenemos que [9(9 + 1) ]/2 = 90/2 = 45, esta cantidad se divide
11
CURSO DE SELECCIÓN 2016
entre 3, y obtenemos 15, de modo que la suma en cada renglón, columna y diagonal debe ser 15. A continuación,
necesitamos decidir qué números podrían ocupar qué lugares. El número en el centro debe aparecer en cuatro
sumas de 15 (en dos diagonales, en el segundo renglón en la segunda columna). Cada número en las esquinas debe
aparecer entres sumas de 15.(¿puedes ver por qué?). si escribimos el 15 como suma de tres números diferentes de
1 al 9 de todas las maneras posibles, podríamos contar cuántas sumas contienen a cada uno de los números del 1 al
9. Los números que aparezcan en al menos cuatro sumas son candidatos para ocupar el cuadrado del centro,
mientras que los números que aparezcan en al menos tres sumas son candidatos para los cuadrados de las
esquinas. Nuestro nuevo objetivo parcial es escribir el número 15 de todas las maneras posibles, como suma de
tres números diferentes tomados del conjunto {1. 2, 3, 4, …9}.
Realizar el plan. La suma de 15 se puede escribir, de manera sistemática:
9+5+1
9+4+2
8+6+1
8+5+2
8+4+3
7+6+2
7+5+3
6+5+4
Nota que el 1 aparece sólo en dos sumas, el 2 aparece en tres sumas, el tres aparece en dos sumas. El único
número que aparece en cuatro sumas es el 5; por lo tanto, el 5 debe estar en el centro del cuadrado. Como el 2, 4,
6, y 8 aparecen tres veces cada uno, deben ir en las esquinas.
2
6
5
4
8
2
7
6
9
5
1
4
3
8
Mirar hacia atrás. Hemos visto que el 5 fue el único número, de los dados, que podía ocupar el centro. Sin embargo,
tuvimos varios candidatos para las esquinas y, por lo tanto, parece que el cuadrado mágico que hayamos no es el
único posible. ¿Puedes encontrar los demás?
12
CURSO DE SELECCIÓN 2016
2.1.2 Estrategia: Examinar un problema relacionado
Suma de números naturales pares
Hallar la suma de los números naturales pares menores o iguales a 100. Diseña una estrategia para hallar esa suma
y generaliza el resultado.
Comprender el problema. El problema es obtener la suma de los números naturales pares: 2 + 4 + 6 + 8 + … +
100
Trazar un plan. Reconocer que la suma se puede separar en dos partes más sencillas relacionadas con el problema
original de Gauss, nos ayuda a trazar un plan. Considerar lo siguiente:
2 + 4 + 6 + 8 + … + 100 = 2 · 1 + 2 · 2 + 2 · 3 + 2 · 4 + …. + 2 · 50
= 2 (1 + 2 + 3 + 4 + ……… + 50)
Así, podemos usar el método de Gauss para hallar la suma de los primeros 50 números naturales y después tomar
el doble.
Realizar el plan. Realizamos el plan como sigue:
2 + 4 + 6 + 8 + … + 100 = 2(1 + 2 + 3 + 4 + ……… + 50)
= 2 · [50(50 +1)/2]
= 2550;
Así, la suma es 2550
Ahora intente este:
Hallar la suma de los números naturales impares menores que 100.
2.1.3 Estrategia; hacer una tabla
Una estrategia que se usa a menudo es hacer una tabla. Se puede usar una tabla para buscar patrones que emerjan
en el problema, que a su vez puedan conducirnos a una solución.
Problema
A Carolina le ofrecieron un empleo de cuidado de bebes durante la tarde, por 10 días, los padres que la quieren
contratar le ofrecieron dos planes de pago. ¿Cuál de ellos deberá de aceptar Carolina?
Plan I. un pago único de $100 por 10 días de trabajo.
Plan II. El pago por el primer día de trabajo será de $0.25. Después, por cada día de trabajo se doblará el pago.
Comprender el problema. Hay dos planes diferentes, en el plan I el pago total es de $100, en el plan II, hay que
trazar un plan para hallar el pago total por los 10 días.
13
CURSO DE SELECCIÓN 2016
Trazar un plan: para determinar el pago por los 10 días se hará una taba de días y cantidad de dinero:
Días
Cantidad $
1
0.25
2
3
0.50 1
4
2
5
4
6
8
7
8
9
10
16
32
64
128
Respuesta: Carolina debe aceptar el plan II que paga $128
¿Es razonable?
Sí, la respuesta debe ser un número par pues las cantidades en la tabla se duplicaron.
Ahora intente este:
Mónica y Carla se iniciaron en un nuevo empleo el mismo día. Después de comenzar, Mónica debe visitar la oficina
central cada 15 días y Carla debe ir a la oficina central cada 18 días. ¿Cuántos días van a transcurrir antes de que
vallan el mismo día a la oficina central?
2.1.4 Estrategia: trabajar regresivamente
En algunos problemas es mejor comenzar por el resultado y trabajar hacia atrás (regresivamente).
Problema: Después de reparar un elevador, el ingeniero de mantenimiento verificó su trabajo enviando el elevador
12 pisos hacia arriba, 18 pisos hacia abajo y, de nuevo, 20 pisos hacia arriba. Si el elevador terminó en el piso 30
¿en qué piso comenzó sus pruebas el ingeniero?
Estrategia. Trabajar regresivamente
Cómo trabajar hacia atrás
1. Identifique lo que quiere hallar
2. Trazar un diagrama para mostrar cada cambio, comenzando en lo no conocido
3. Comienza por el final. Trabaja hacia atrás usando el inverso de cada cambio.
Diagrama:
El elevador subió 12 pisos =
+ 12
Después bajó 18 pisos =
- 18
Luego subió 20 =
+ 20
+ 14
Terminó en el 30
Si subió 14 pisos y está en el piso 30 significa que se encontraba en el piso 16 (16 + 14 = 30) cuando inició hacer sus
pruebas.
14
CURSO DE SELECCIÓN 2016
Problema: Luisa tiene un promedio (media) de 80 en sus 11 exámenes de matemáticas, su maestra le dice que va a
eliminar la calificación más baja, que es de 50. ¿Cuál es su nuevo promedio?
Comprender el problema
11 exámenes dan un promedio de 80,
Trazar un plan: significa que la multiplicación del promedio de 80 por el número de exámenes dará la puntuación
total obtenida:
(80)(11) = 880, si se elimina la calificación mínima de 50, se obtendrá la calificación de 10 exámenes: 880 – 50 =
830, para obtener el nuevo promedio dividimos 830/10 = 8.3 es el promedio eliminando la calificación mínima.
2.1.5 Razonamiento directo
Problema:
Alex, Beto, Carina y Dani participan ya sea en natación, beisbol, baloncesto o tenis. Beto juega béisbol, Alex no
puede nadar, Carina juega baloncesto. ¿en qué deportes participa cada persona?
Comprender el problema
Alex: (no nada): ¿?
Beto: beisbol
Carina: baloncesto
Dani: ¿?
Trazar un plan: solamente queda por asignarle deporte Alex y Dani, como Alx no nada, entonces debe de jugar
tenis, y para Dani sólo queda el natación.
Problema: Dos personas jugaron Damas entre si y cada una ganó tres partidas. ¿Es posible que sólo hayan jugado
cinco partidas?
Comprender el problema
Cada persona ganó tres partidas. Si cada uno ganó tres partidas y jugaron entre ellos, entonces se tuvieron que
jugar seis partidas; de otra manera no podrían haber tenido tres victorias cada uno. La respuesta es no, la situación
es imposible.
15
CURSO DE SELECCIÓN 2016
Problemas
1. Usa el enfoque del problema de Gauss para hallar las sumas de 36 + 37 + 38 + 39 + … + 146 + 147.
2. Acabas de salir de Oaxaca hacia el Istmo. El Camarón está a 120 km y Tehuantepec está a 200 km, hay
un descanso a la mitad del camino entre El Camarón y Tehuantepec. ¿A qué distancia de Oaxaca está el
punto de descanso?
3. Rayo, Chocolata, Trueno y Marisolita están en una carrera de caballos. Chocolata es la más lenta,
Trueno es más veloz que Rayo pero más lento que Marisolita. Da el orden de los caballos.
4. Pancho y Juanito comienzan a leer una novela el mismo día. Pancho lee 8 páginas diarias y Juanito 5
páginas diarias. Si Pancho va en la página 72, ¿en qué página va Juanito?
5. ¿Cuántos cuadros diferentes hay en la siguiente figura?
6. a) Sin calcular cada suma, determinar cuál es el más grande, O o E, y por cuánto.
O = 1 + 3 + 5 + 7 + … + 97
E = 2 + 4 + 6 + 8 + … + 98
b) Si P = 1 + 3 + 5 + 7 + … + 99, ¿Cuál es el más grande, E o P, y por cuánto?
7. a) Colocar los dígitos1, 2, 4, 5 y 7 en los cuadros siguientes de manera que en i) se obtenga el mayor producto y
en ii) se obtenga el mayor cociente:
i)
X
ii)
b) Usar los mismos dígitos para obtener (i) el menor producto y (ii)el menor cociente.
16
CURSO DE SELECCIÓN 2016
8. ¿Cuántos términos hay en la siguiente sucesión? 1, 8, 15, 22, …113.
9. Con base en el siguiente patrón, responde las preguntas (a) a (b)
1 = 21 - 1
1 + 2 = 22 – 1
1 + 2 + 22 = 23 - 1
1+ 2 + 2 2 + 23 = 24 – 1
1+ 2 + 2 2 + 23 + 24 = 25 – 1
a)
Escribir una expresión más sencilla para
1+ 2 + 2 2 + 23 + 24 + 25.
Justifica tu respuesta
b) Escribe una expresión más sencilla para la suma de de n-ésimo renglón del patrón.
10. ¿Cuántos números de cuatro dígitos tienen los mismos dígitos que 1993?
11. Un compás y una regla, juntos, cuestan $40. El compás cuesta $9 más que la regla. ¿Cuánto cuesta el compás?
12. Cata está parada a la mitad de una escalera. Sube tres escalones, baja cinco y, luego sube siete escalones. Por
último sube los restantes seis escalones para llegar al final de la escalera. ¿Cuántos peldaños tiene la escalera?
13. Dada la siguiente representación
a) ¿Cuántos puntos tendrá el sexto término de la sucesión? ¿y el séptimo? (Trata de responder sin dibujarlos)
c) ¿Es posible que un triángulo tenga 100 puntos?
17
CURSO DE SELECCIÓN 2016
14. Un granjero necesita cercar un terreno rectangular y quiere que el largo del campo sea 80 metros mayor que el
ancho. Si tiene 1080 metros de material para la cerca, ¿Cuáles deberán ser la longitud y el ancho del campo?
15. halla un cuadro mágico de 3 x 3 usando los números 3, 5, 7, 9, 11, 13, 15, 17 y 19.
16. halla las sumas siguientes:
a) 1 + 6 + 11+ 16 + 21 + … + 1001
b) 3 + 7 + 11+ 15 + 19 + … + 403
17. Tenemos ocho canicas de igual apariencia, pero una es un poco más pesada que las otras. Usando una balanza
explica cómo se puede descubrir la canica más pesada en exactamente.
a) 3 pesadas.
b) 2 pesadas.
18. a) Halla la suma de todos los números en el arreglo siguiente:
1 + 2 + 3 + 4 + 5 + 6 + … + 100
2 + 4 + 6 + 8 +10 + 12 + … + 200
3 + 6 + 9 + 12 + 15 + 18 + … + 300
b) Generaliza la parte (a) para un arreglo similar en donde cada renglón tenga n números y haya n renglones.
19. en los cuadros a continuación se escriben los 14 dígitos de una tarjeta de crédito si la suma de tres dígitos
consecutivos cualesquiera es 20, ¿Cuál es el valor de A?
A
7
7
4
20. Si 8 personas se dan la mano entre sí, ¿Cuántos apretones hubo?
a) generalizar la solución para n personas.
21. La distancia alrededor del mundo es aproximadamente de 40, 000 km, ¿Aproximadamente cuántas personas
de tamaña promedio de tu grupo se requerirán para rodear el mundo tomadas de la mano?
22. Un carro tiene un tanque de gasolina con capacidad de 45 litros. El carro consume 8.5 litros de gasolina por
cada 100 km. Se inició un viaje de 350 km con el tanque lleno. ¿Cuánto quedará en el tanque al final del viaje?
18
CURSO DE SELECCIÓN 2016
2.2 Sucesiones aritméticas
Una sucesión es un arreglo ordenado de números figuras u objetos. Una sucesión tiene términos identificados
como el 1o, 2o, 3o, y así sucesivamente. A veces es posible clasificar las sucesiones por medio de sus propiedades.
Por ejemplo, ¿qué propiedades tienen las primeras tres sucesiones que no tiene la cuarta?
a)
b)
c)
d)
1, 2, 3, 4, 5, 6, …
0, 5, 10, 15, 20, 25, …
2, 6, 10, 14, 18, 22, …
1, 11, 111, 1111, 1111, 11111, 111111, …
En cada una de las primeras sucesiones, cada término, comenzando desde el segundo, se obtiene del anterior
sumando un número fijo. Es decir, la diferencia entre un número consecutivo de la sucesión siempre es igual. En el
inciso d) la diferencia entre los primeros dos términos es 11-1= 10; la segunda deferencia es 111 – 11 = 100, la
tercera deferencia es 1111 – 111 = 1000; y así sucesivamente. Sucesiones como las tres primeras son sucesiones
aritméticas. Una sucesión aritmética es aquella en cada termino se obtiene del anterior mediante la suma o resta
de un número fijo, llamado diferencia, en el inciso b) la diferencia es 5, pues es el número fijo que se suma cada vez
para obtener el número siguiente, en el inciso c) la diferencia es 4.
También se pueden generar sucesiones aritméticas a partir de objetos, como en el ejemplo que sigue. Hallar un
patrón en el número de líneas de cada arreglo
Número de término (n)
Número de líneas
1
4
2
7=4+3=4+1·3
3
10 = (4 + 3) + 3 = 4 + 2 · 3
4
13 = (4 + 2 · 3) + 3 = 4 + 3 · 3
·
·
·
·
.
·
n
4 + (n - 1)3
Observa que al añadir una figura a un arreglo es una suma de 4 más cierto número de 3; vemos que el número de 3
es 1 menos que el número del término. Este patrón deberá continuar pues el primer término es 4 + 0 · 3 y cada vez
19
CURSO DE SELECCIÓN 2016
que el incremento es 1 el número de término, añadimos un 3 más. Así, se ve que el término 100-ésimo es 4 + (100 1)3 y, en general, el término n-ésimo an es 4 + (4 -1)3.
El n-ésimotérmino, que se denota con an puede escribirse como 3n + 1
Si nos dieran el valor de un término, podríamos usar la fórmula del término n-ésimo de la tabla anterior para
trabajar hacia atrás, o de manera regresiva, para hallar el número de términos. Por ejemplo, para esta sucesión,
queremos saber qué número de termino es 1798; sabemos que 3n + 1= 1798. Por lo tanto, 3n = 1797 y n = 599. Por
lo tanto el término número 599 es 1798.
EJEMPLO
Hallar los primeros cinco términos de una sucesión cuyo término n-ésimo está dado, y mencionar en qué caso la
sucesión es aritmética.
a) an= 4n + 3
b) an = n2 – 1
Solución:
a) Para hallar los primeros cinco términos sustituimos 1, 2, 3, 4 y 5 en a n = 4n + 3. Obtenemos: 7, 11, 15 y 19; esta
es una sucesión aritmética, con diferencia de 4.
b) Al sustituir 1, 2, 3, 4 y 5 en an = n2 – 1. Obtenemos 0, 3, 8,15 y 24, observamos que no es una sucesión aritmética,
ya que no hay una diferencia común.
Generalización de sucesiones aritméticas
Para generalizar el trabajo que se ha hecho hasta este momento con sucesiones aritméticas, suponemos que el
primer término en la sucesión es a1 y que la diferencia es d, se puede usar la estrategia de hacer una tabla para
investigar el término general de la sucesión, a1, a1 + d , a1 + 2d, a1 + 3d, …, como se muestra a continuación:
Número de término
1
2
3
4
·
·
·
n
Término
a1
a1 + d
a1 + 2d
a1 + 3d
a1 + (n - 1)d
20
CURSO DE SELECCIÓN 2016
De esta manera en cualquier sucesión aritmética el término n-ésimo con primer término a1 y
deferencia d está dado por
a1 + (n - 1)d
Ejemplo
En la sucesión aritmética 5, 9, 13, 17, 21, 25, …, el primer término es 5 y la diferencia es 4podemos verificar para n
= 1, 2, 3, 4, 5 y 6; genera la sucesión mencionada.
EJEMPLO
Un teatro está construido de manera que hay 20 asientos en la primera fila y 4 asientos adicionales en cada fila
consecutiva. La última fila tiene 144 asientos. ¿Cuántas filas tiene el teatro?
Solución:
Es una sucesión aritmética con a1 = 20, diferencia d = 4 y n es el número de términos.
Queremos hallar el número de términos cuando an = 20 + (n - 1) es igual a 144.
20 +(n - 1)4 = 144
(n - 1)4 = 124
n – 1 = 31
n = 32
Esto nos dice que cuando n = 32, el valor del término es 144, lo cual implica que hay 32 filas en el teatro. En lugar
de usar una fórmula, se puede hacer una tabla y buscar un patrón.
21
CURSO DE SELECCIÓN 2016
Problemas
1. Determinar cuáles de las siguientes sucesiones son aritméticas.
a)
1, 3, 5, 7, 9,…. __________________________________
b) 3, 5, 13, 21, … __________________________________
c)
0, 2, 4, 6, 7, … __________________________________
d) 2, 4, 8, 16, 32, __________________________________
e) 0. 5, 10, 15, 20, …_______________________________
f)
0.25, 0.5, 0.75, 1, … ______________________________
g)
½, 1/6, 1/6, 1/3, … ________________________________
h) 73/12, 41/6, 91/12, 25/3, … _________________________
2. Para celebrar el inicio de clases, los estudiantes de sexto año organizarán la fiesta en la casa de Judith. Su
hermano observa que al abrir la puerta por primera vez llega 1 invitado, la segunda vez llegan 3 invitados, al abrirla
por tercera vez 5 y así sucesivamente.
a) ¿Cuántos invitados entrarán en la novena vez que abren la puerta?
b) ¿Cuántas veces se ha abierto la puerta si en la fiesta hay 100 invitados?
3. Hallar el octavo término de la progresión -1, 6, 13, 20, ….
4. Un programa de ejercicios recomienda hacer 20 abdominales en la primera sesión de ejercicios e ir aumentando
7 abdominales por sesión, ¿cuántos abdominales tendrán que hacerse en la trigésima sesión?
5. El cuarto término de una progresión aritmética es 10, y el sexto es 16. Escribir la progresión.
6. El primer término de una progresión aritmética es -1, y el décimoquinto es 27. Hallar la
diferencia y la suma de los quince primeros términos.
22
CURSO DE SELECCIÓN 2016
2.3. Sucesiones geométricas
Para ilustrar una progresión geométrica se expondrá el siguiente caso:
Un sistema de ventas multinivel, basa sus ventas en productos de consumo para el hogar y de uso personal. Los
trabajadores de nivel más bajo se dedican a reclutar gente como distribuidores “independientes” comprando unos
$1500 en mercancía a los quienes reclutaron.
Su meta es reclutar cada vez más distribuidores. El ingreso es generado por la ventas de esa mercancía del
distribuidor más los “subdividendos” de las ventas de aquellos a quienes reclutaron (jerárquicamente sus
descendientes). Este método de ventas es y reclutamiento es una pirámide.
La estructura de ventas se basa en 6, si eres invitado a participar como cliente (no como vendedor) y aceptas le
harás un bien a la humanidad, pues usarás productos que no dañan al medio ambiente, sino productos
biodegradables, el requisito es que cada mes consumas $1500, lo cual no te hará ganar más que la satisfacción de
hacer algo por tu medio ambiente.
Si deseas ganar dinero debes invitar a seis amigos, no a vender, sino a consumir cada mes $1500 de mercancía de
limpieza y uso personal, y si éste a su vez hace lo mismo, él gana un pequeño porcentaje y tu ganas más.
Supongamos que Juan participa como consumidor, él a su vez invita a seis de sus amigos los cuales se convierten en
consumidores, y como ellos tienen más de seis amigos es sencillo que encuentren a seis más cada uno y estos a su
vez como son tan populares es sencillo que encuentre seis más cada uno, y como cada uno de estos comienza a
ganar sólo si encuentra seis más, pues se motiva cada día para encontrar seis “amigos” del medio ambiente.
Este evento se observa así:
1(Juan), 6(amigos de Juan), 36(amigos de los amigos de Juan), 216(amigos de los amigos de los amigos de Juan),
1296(consumidores).O bien así
1, 6, 62, 63, 64, 65, 66…
Te imaginas el número de personas a la red, después de 10 pasos, y cuánto gana Juan si por cada uno de los que
están en su pirámide él gana un 3% de lo que consuman todos los “amigos del medio ambiente”
Una progresión o sucesión geométrica, está constituida por una secuencia de elementos, en la que cada uno de
ellos se obtiene multiplicando el anterior por una constante denominada razón o factor de progresión. En forma
general se observa así
1
2
3
4
5
a, ar , ar , ar , ar , ar , …a ≠ 0, r ≠ 0
Se puede observar que si dividimos un término entre el anterior, el resultado siempre es r, a la cual se le llama
razón o factor.
ar n
r n1
ar
23
CURSO DE SELECCIÓN 2016
En base a la definición, determinar si las siguientes sucesiones son geométricas:
a)
1, 2, 4, 16, …
b) 2, 1, ½, ¼, …
c)
2, 3, 9/2, 27/4, …
Para encontrar el enésimo término de una sucesión geométrica es:
an = a1rn - 1
Problema: Si el 1º y el 10º término de una sucesión geométrica son 1 y 2 respectivamente, encontrar la razón
común de esta serie.
a n = a 1 rn - 1
Conociendo
Se tiene a10 = 2
a1 = 1
a10 = a1r9
Solución:
2 = 1r9
2 = r9
r = 21/9 = 1.08
Problema: Determinar r y a1 para la sucesión geométrica con a2 = 12 y a6 = 972
Solución:
Tenemos que de a1, a2, a3, a4, a5, a6
Conocemos a2 = 12 y a6 = 972 y que
a2 = a1r
12 = a1r
a6 = a1r5
972 = a1r5
12/r = a1
972/r5 = a1
24
CURSO DE SELECCIÓN 2016
Entonces:
12/r = 972/r
5
Dejando las r en el miso miembro obtenemos r5/r = 972/12
4
Tenemos
r = 81
Por lo tanto
r=3
Como a2 = a1r
y
a2 =12
12 = a1·3
a1 = 12/4
a1 = 4
Problemas de sucesiones:
1. Determinar cuáles de las siguientes sucesiones son geométricas, aritméticas o ninguna de las dos:
a)
b)
c)
d)
e)
f)
g)
h)
i)
8, 4, 2, 1
100(1.05), 100(1.07),100(1.09),100(1.11),…
4, 1.2, 0.36, 0.103, …
4, - 6, .13.5, …
-11, -16, -21, …
130, 65, 32.5, …
½, 1/6, 1/18,…
12, 4, 4/3,…
1, 3, 6, 10,…
2. Hallar el sexto término de la sucesión geométrica cuyos dos primeros términos son 4 y 6.
3. Longina es una chica algo pasada de peso y ha decidido someterse a una rigurosa dieta, le aseguraron que en los
dos primeros meses bajará 6 kilos y si continúa la dieta, en los próximos dos meses bajará el 75% del bimestre
anterior. Si Longina continúa esta dieta por dos años ¿cuántos kilos perderá Longina?
4. El disco de un péndulo se balancea en un arco de 24 cm de largo en su primera oscilación. Si cada balanceo
sucesivo es aproximadamente cinco sextos de la longitud del anterior, usa una serie geométrica para determinar la
distancia total aproximada que recorre antes de detenerse.
25
CURSO DE SELECCIÓN 2016
5. Un cultivo de bacterias se incrementó 20% cada hora, si el cultivo original tenía 10 000 bacterias, determinar el
número que hay después de 10 hrs.
6. Cuando usted compra alimento en una tienda, éstos han pasado a través de muchos intermediarios antes de
llegar a usted. Por ejemplo, el granjero se los vende a un transportista, quien se los vende a un comerciante, quien
se los vende a un distribuidor, y éste a su vez los vende a un tendero, quien los vende a usted. Suponga que el
granjero gastó $3.25 por kilo de carne de res.
a) Si el granjero y los cuatro intermediarios tienen una ganancia de 30%, ¿cuánto pagaría usted por kilo de carne de
res?
b) ¿Cuál es la ganancia del granjero?, ¿cuál es la ganancia de los cuatro intermediarios?
7. La cantidad de luz que se filtra a través de un lago disminuye en ½ por cada metro de profundidad.
a) Expresa una sucesión que indica la luz restante a la profundidad de 1, 2, 3, 4, y 5 m.
b) ¿Cuál es el sobrante de luz a una profundidad de 7 metros?
8. Asumiendo que el valor de un automóvil se deprecia un 10% cada año, si el precio de un automóvil es de $40 000
¿cuál sería su valor al cabo de 10 años?
9. En una ciudad de 200 000 habitantes, la población crece a razón de 1.2% cada año, estima la población dentro de
30 años.
10. Un tinte indicador se inyecta a Eduardo por razones médicas. Después de cada hora, permanecen 2/3 del tinte
de la hora anterior. ¿Cuánto tinte permanecerá en el sistema de Eduardo después de 10 hrs?
26
CURSO DE SELECCIÓN 2016
Problemas de patrones, sucesiones
1.
Para cada una de las siguientes sucesiones de figuras, determina un patrón posible y traza la que seguiría,
de acuerdo con el patrón:
a.
b.
2.
En cada uno de los incisos siguientes, lista términos que continúen en posible patrón. ¿Cuáles de las
siguientes sucesiones son aritméticas, cuales son geométricas y cuáles no son ni una ni otra?
a) 1, 3, 5, 7, 9
b) 0, 50, 100, 150, 200
c) 3, 6, 12, 24, 48
d) 10, 100, 1000, 10000, 100000
e) 9, 13, 17, 21, 25, 29
f) 1, 8, 27, 64, 125
3.
Halla el 10-enesimo término y el n-esimo termino de cada una de las sucesiones del problema 2 anterior.
4. Observa el siguiente patrón:
1+3=22
1+3+5=32
1+3+5+7=42
a.
b.
Establece una generalización basada en este patrón.
Con base en la generalización enunciada en (a), halla
1+3+5+7+…+35.
5. Los siguientes arreglos geométricos sugieren una sucesión de números:
2
6
12
20
27
CURSO DE SELECCIÓN 2016
a. Halla los siguientes tres términos.
b. Halla el término 100-enesimo
c. Halla el termino n-esimo
6. En el siguiente patrón, se necesitan 6 palillos para formar un hexágono, 11 palillos para formar dos
hexágonos y así sucesivamente. ¿Cuántos palillos se necesitarían para construir (a) 10 hexágonos? (b) n
hexágonos?
7.
Ricardo está construyendo sucesiones de cuadrados con cerillos. Uso 67 cerillos para formar la última
figura de su sucesión. ¿Cuántos cerillos usara para todo el proyecto?
8.
En cierto plantel se predijo que la población escolar se incrementaría en 50 estudiantes al año durante 10
años siguientes. Si la matricula actual es de 700 estudiantes, ¿cuál será la matricula al cabo de 10 años?
9.
Un tanque contiene 15,360 L de agua. Al final de cada día queda la mitad de agua, y no se repone. ¿Cuánta
agua quedara en el tanque al cabo de 10 días?
10. El ingreso anual de pepe se ha incrementado cada año en la misma cantidad. En el primer año su ingreso
fue de $24,000 y en el noveno año fue $31,680. ¿en qué año tuvo un ingreso de $45,120?
11. La primera diferencia de una sucesión es 2, 4, 6, 8… halla los primeros seis términos de la sucesión original
en cada uno de los casos siguientes:
a. El primer términos de la sucesión original es 3
b. La suma de los primeros dos términos de la sucesión original es 10
c.
El quinto término de la sucesión original es 35
28
CURSO DE SELECCIÓN 2016
12. Lista los siguientes tres términos para continuar con el patrón en cada uno de los siguientes incisos. (hallar
diferencias puede ser útil)
a. 5, 6, 14, 32, 64, 115, 191
b. 0, 2, 6, 12, 20, 30, 42
13. ¿Cuántos términos hay en cada una de las siguientes sucesiones?
a. 51, 52, 53, 54…151
3
60
b. 1, 2, 2 …2
c. 10, 20, 30, 40…2000
d. 9, 13, 17, 21, 25…353
e. 1, 2, 4, 8, 16, 32…1024
14. Halla los primeros cinco términos de las sucesiones cuyos términos n-ésimos son:
a. an= n2+2
b. an= 5n-1
c.
n
an=10 -1
d. an=3n+2
15. Supón que el patrón de figuras formadas con cuadros, presentado a continuación, continúa. Ahora
responde las siguientes preguntas:
A1
a.
b.
c.
A2
A3
A4
¿Cuántos cuadrados hay en la sexta figura, A6?
¿Cuál es la fórmula para An es el número de cuadrados en la figura n-ésima?
¿Existe una figura que tenga exactamente 449 cuadrados? De ser así, ¿Cuál es?
16. Corta una hoja de papel en 5 trozos. Toma cualquiera de los trozos y córtalos de nuevo en 5 piezas, y así
sucesivamente.
a. ¿Qué cantidad de trozos se puede obtener de esta manera?
b. ¿Qué cantidad de trozos se obtuvo en el n-ésimo corte?
17. La sucesión 32, a, b, c, 512 es una sucesión geométrica. Halla a, b, c.
18. Halla la suma de los primeros 43 términos de una sucesión aritmética en la que el termino número 11 es
83 y el termino número 62 es 440.
29
CURSO DE SELECCIÓN 2016
2.4. Razonamiento algebraico y el uso de las variables
La principal diferencia entre el aritmética y el Álgebra es que la aritmética efectúa operaciones con números reales,
mientras que el álgebra utiliza además de estos números las letras del alfabeto para representar cantidades
desconocidas.
Una de las más grandes ideas del razonamiento algebraico es el concepto de variable. Comprender el concepto de
variable es fundamental en matemáticas. Sin embargo, “variable” puede significar muchas cosas, puede usarse
como un elemento faltante o desconocido, como en x + 2 = 5.
Por lo general en álgebra se usan las últimas letras del alfabeto (x, y, z) para las variables, y para la parte numérica o
constante definidas usamos las primeras (a, b, c).
Si tenemos cualquier colección de variables y números reales, al aplicarles sumas, restas, multiplicaciones,
divisiones, potencias o extracciones de raíces, entonces, obtenemos una expresión algebraica.
Para resolver problemas matemáticos se requiere escribir una expresión algebraica que represente un enunciado, a
esto se le llama lenguaje algebraico.
Veamos algunos ejemplos de cómo se traducen enunciados a expresiones algebraicas:
2.1.3. Ideas intuitivas del significado función
No.
Enunciado
Expresión
1
El triple de un número más seis
3x + 6
2
Siete metros de tela cuestan 420
7x = 420
3
El costo de viajar en taxi es 14 pesos del banderazo más tres pesos
c = 14 + 3x
por km
4
La edad de un padre es el doble de la de su hijo y juntas suman 54
2x + x = 54
5
El número de mi casa más mi edad suman 222
x + y = 222
6
Un artículo más el iva vale 100 pesos
x + 0.16x = 100
7
La suma de dos números consecutivos es 45
x + (x + 1) = 45
8
Un número es 4 unidades mayor que el otro
x–y=4
9
El largo es el triple del ancho
10
La suma del doble de un número y el cubo del otro es 16
11
La velocidad es igual a distancia sobre tiempo
12
El área de un triángulo es base por altura sobre dos
l = 3a
3
2x + y = 16
v = d/t
A = (b · h)/2
30
CURSO DE SELECCIÓN 2016
13
La mitad de un número más el doble de otro es 100
x/2 + 2y = 100
14
La suma de los cuadrados de dos números es 100
x + y = 100
15
Juan vendió el triple de dulces de los que vendió Pepe
2
2
3x = y
Una de las estrategias de la sección anterior fue plantear una ecuación. Esta estrategia es parte del aspecto más
amplio del razonamiento algebraico.
Ejemplo
Una maestra dijo a sus alumnos: Tomen cualquier número y súmenle 15. Ahora multipliquen esa suma por 4. A
continuación resten 8 y dividan la diferencia entre 4. Ahora resten 12 del cociente y díganme la respuesta. Yo les
diré el número original.
Instrucciones
Expresión
Toma cualquier número
n
Súmale 15
n + 15
Multiplica esa suma por 4
4(n + 15)
Resta 8
4(n + 15) – 8
Divide la diferencia entre 4
[4(n + 15) – 8] / 4
Reste 12 del cociente a
[[4(n + 15) – 8] / 4 ] - 12
y de la respuesta
n+ 1
Problemas de aplicación
Un método para resolver problemas de aplicación es primero formular el problema como un problema
matemático, enseguida resolver el problema matemático y después interpretar la solución en términos del
problema original:
Problema de aplicación
Modelo matemático
Solución matemática
Interpretación del problema original
31
CURSO DE SELECCIÓN 2016
Ejemplo:
Problema de aplicación:
Modelo matemático:
Solución matemática:
Amelia ganó $120 de
niñera y $50 lavando el
carro. ¿Cuánto ganó en
total?
120 + 50 = x
120 + 50 = 170
Las ganancias de Amelia suman $ 170.
Podemos aplicar el procedimiento de los cuatro pasos para resolver problemas
1) Entender el problema: identificamos los datos que tenemos y lo que hay que hallar.
2) Trazar un plan: asignamos letras a las cantidades desconocidas y traducimos la información dada en el
problema a un modelo que incluya ecuaciones.
3) Realizar el plan: resolvemos la ecuación.
4) Mirar hacia atrás: interpretamos y verificamos la solución en términos del problema original.
Problema:
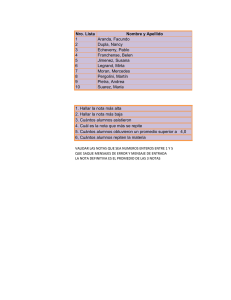
Bruno tiene cinco libros de la biblioteca vencidos. La multa para los libros vencidos es de 10 centavos diarios. Él
recuerda que sacó un libro de astronomía una semana antes que cuatro novelas. Si la multa total fue de $8.70,
¿cuánto tiempo estuvo vencido cada libro?
1) Entender el problema:
Bruno tiene cinco libros vencidos. Sacó uno de astronomía siete días antes que las cuatro novelas, por lo tanto, el
libro de astronomía está vencido siete días más que las novelas. La multa diaria por libro es de 10 centavos y la
multa total fue de $8.70. Necesitamos hallar cuántos días estuvo vencido cada libro.
2) Trazar un plan:
Sea d el número de días que estuvo vencida cada una de las novelas. El libro de astronomía estuvo vencido siete
días más, esto es d + 7 días. La multa total es igual a la multa del libro de astronomía más la multa de las cuatro
novelas que es igual a 870 centavos.
Multa por las cuatro novelas
= 4d
= 4(10)d = 40d
Multa por el libro de astronomía = 10 (d + 7)
Multa de las cuatro novelas + multa del libro de astronomía= Multa total
40d + 10 (d + 7) = 870
32
CURSO DE SELECCIÓN 2016
3) Realizar el plan: despejar d en la ecuación
40d + 10 d + 70 = 870
50d + 70 = 870
50d = 800
d = 16
4) Mirar hacia atrás
Para verificar las respuestas, sigamos la información original. Cada una de la novelas está vencida 16 días y el libro
de astronomía estuvo vencido d + 7 = 23 días.
Se pagó 40 centavos por cada novela cada día, en 16 días pagó 640; 23 días por 10 centavos por el libro de
astronomía es 230, da un total de 870 centavos que es igual a $8.70
Problema
En un pueblo, tres niños entregan todos los periódicos. Abel entrega tres veces la cantidad que entrega Brenda, y
Carla entrega 13 más que Abel. Si entre los tres niños entregan un total de 496 periódicos, ¿Cuántos periódicos
entregó cada uno?
Trazar un plan:
Abel = a
Brenda = b
Carla = c
Abel entrega tres veces la cantidad que entrega Brenda: a = 3b ó b = a/3
Carla entrega 13 periódicos más que Abel: c = 13 + a
La entrega total es de 496: a + b + c = 496
Dejamos la ecuación en términos de una sola variable:
a + a/3 + (13 + a) = 496
(3ª + a + 3a)/3 = 496 – 13
7a/3 = 483
7a = 1449
a = 207
Sustituimos a en b = a/3
b = 207/3
b = 69
Sustituimos a en c = 13 + a
c = 13 + 207
c = 220
Mirar hacia atrás
Para verificar la respuesta se sigue la información original, en la primera frase, “Abel entrega tres veces la cantidad
que entrega Brenda” 3 · 69 = 207. La segunda frase “Carla entrega 13 más que Abel”, 207 + 13 = 220. La
información en la entrega total se verifica: 207 + 69 + 220 = 496.
33
CURSO DE SELECCIÓN 2016
Problemas (Razonamiento algebraico)
1.
Tres naves salen de un puerto. La primera lleva
1
del total de pasajeros, la segunda la mitad del total de
3
pasajeros y la ultima 20 pasajeros. ¿Cuántos pasajeros había en total?
2.
Carlos, Adrián y Beto fueron a cenar y pagaron la cuenta entre los tres. Carlos pagó el 60% del total,
Adrián pagó el 40% de lo que restaba y Beto pagó $30, ¿Cuál era el monto total de la cuenta?
3.
En la tumba del matemático famoso Diofanto se encuentra la siguiente inscripción:
“La sexta parte de la vida de Diofanto constituyó su infancia. Luego pasó una doceava parte de su vida
cuando de vello cubriose su barbilla. La séptima parte la vivió en un matrimonio estéril. Pero 5 años más
tarde Diofanto se volvió dichoso al nacer su primogénito, el cual solo tuvo como edad la mitad que la de su
padre. Y con profunda pena, Diofanto descendió a la sepultura habiendo sobrevivido cuatro años luego
del deceso de su hijo.”
¿Cuántos años vivió Diofanto?
4.
Un triángulo isósceles tiene 14 cm de perímetro, el lado desigual es tres veces menor que cada uno de los
otros. ¿Cuánto miden los lados?
5.
El perímetro de un rectángulo es 28 cm. Calcula su área sabiendo que uno de sus lados tiene cuatro
centímetros más que el otro.
34
CURSO DE SELECCIÓN 2016
6.
La fórmula para convertir grados Celsius (C) a grados Fahrenheit (F) es F= (9/5)C+32. Sandra, en México, ve
que la temperatura es de 32°C. ¿Cuál es la temperatura en grados Fahrenheit?
7.
Para convertir de la escala Celsius (C) a la escala de Kelvin (K), se necesita sumar 273.15 a la temperatura
Celsius.
a. Escribe la fórmula para K en términos de C
b. Escribe una fórmula para convertir de la escala de Kelvin a la escala de Celsius
8.
Escribe la ecuación relacionando las variables descritas en cada una de las siguientes situaciones.
a. La paga P por t horas si se pagan a 80$ la hora
b. La paga P por t horas si se pagan $150 por la primera hora y $100 por cada hora adicional.
c. La paga total P por t horas de jardinería si te pagan $200 por ir y $100 por cada hora de trabajo
d. El costo total C de una membrecía en un club que cobra $3000 iniciales y $40 por cada n días de
asistencia
e. El costo C de rentar un auto de tamaño medio por 1 día recorriendo m millas si la renta es de $300
diarios más $3.50 por milla.
9.
Resuelve las ecuaciones siguientes:
a. 3-x=-15
b. –x-3=15
c. 3x-5=16
d. 2x+5=3x-4
10. Una maestra dijo a su grupo: tomen un número y multiplíquenlo por 3. Súmenle 49 y dividan el resultado
entre 7. Resten 7 del cociente, dividan el nuevo resultado entre 3 y díganme su respuesta; yo les diré su
número original. Para determinar el número original de cada alumno, la maestra multiplico cada respuesta
por 7. Explica cómo pudo saber la maestra el número original de cada estudiante.
11. David tiene tres veces más dinero que Ricardo. Juntos tienen $400. ¿Cuánto tiene cada uno?
12. Un hombre dejo un legado de $640000 a tres niñas. La mayor recibió tres veces más que la menor y la de
en medio recibió $140000 más que la menor, ¿Cuánto recibió cada niña?
35
CURSO DE SELECCIÓN 2016
Aritmética
3.1
Jerarquía de operaciones
El orden en que se realizan las operaciones es: potenciación y radicación; después multiplicación y división, y por
último sumas y restas.
Signos de agrupación:
Son empleados para asociar dos o más términos y que las expresiones sean claras al indicar la jerarquización de las
operaciones, se utilizan los siguientes signos:
a) Paréntesis ordinario
()
Ejemplo:
(2x+3)
b) Paréntesis rectangular o corchete
[]
Ejemplo:
[2 + (3-x)]
c) Paréntesis de llave
{}
Ejemplo:
{1- [2 + (3-x)}
.
Y nos indican que las operaciones colocadas dentro de ellas deben de ser realizadas primero.
Efectuar la operación indicada
1.
2.
3.
4.
5.
3.2
Elevación a Potencias
Si n es un número entero positivo y b es cualquier número real entonces:
b se le llama base y a n se le da el nombre de exponente.
,n factores. Al número
Regla 1.
Si se multiplican números de igual base los exponentes se suman:
Regla 2.
Si se dividen dos números de igual base los exponentes se restan:
Regla 3.
En las potencias los exponentes se multiplican:
Regla 4.
Propiedad distributiva para la multiplicación:
Regla 5.
Propiedad distributiva para la división:
Definición del exponente cero: Si b es un número real diferente de cero, entonces:
Definición del exponente entero negativo (
: Si n es un entero y
entonces
.
.
36
CURSO DE SELECCIÓN 2016
POTENCIAS SUCESIVAS
Hallar el valor de:
PRODUCTO DE POTENCIAS DE IGUAL
BASE
(Para multiplicar potencias de la misma
base se suman los exponentes)
Encontrar:
COCIENTE DE POTENCIAS DE IGUAL
BASE
(Para dividir potencias de la misma
base se restan los exponentes)
Encontrar:
1.
1.
1.
2.
2.
2.
3.
3.
3.
4.
4.
4.
5.
5.
5.
6.
1.
7.
2.
8.
3.
Simplificar
1.
2.
3.
4.
5.
6.
7.
37
CURSO DE SELECCIÓN 2016
3.3
Radicación
Las raíces impares de una cantidad, tienen el mismo signo que la cantidad subradical.
Ejemplo:
1.
2.
Las raíces pares de una cantidad negativa no se pueden extraer porque toda cantidad ya sea positiva o negativa
elevada a una potencia par da un resultado positivo.
Raíz de una potencia, para extraer una raíz a una potencia se divide el exponente de la potencia por índice de la
raíz.
Propiedades de los radicales: para k, n, m números naturales mayores o iguales a 2, a y b números reales.
Ejemplo:
Raíz de un Producto
Raíz de un Cociente
Raíz de una Potencia
Raíz de una Raíz
38
CURSO DE SELECCIÓN 2016
Ejemplo:
Forma
radical
32 x
Forma
exponencial
3
2
4
4
10
y 20
1
5
-
Realizar:
Hallar el valor de:
Determine la cantidad subradical en:
1.
1.
2.
2.
3.
3.
4.
4.
Hallar el valor de:
Resultado
Resultado expresado con
exponente fraccionario
+
*
39
CURSO DE SELECCIÓN 2016
Potenciación y Radicación
Efectuar las operaciones y simplificar
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
43
CURSO DE SELECCIÓN 2016
17.
18.
19.
*
*
20.
21.
22.
23.
*
*
+
+
-
24.
25.
44
CURSO DE SELECCIÓN 2016
3.4 Sistema de numeración
El sistema de numeración indoarábigo que usamos actualmente fue desarrollado por los hindúes y
transportado a Europa por los árabes; de ahí el nombre indoarábigo., este sistema de numeración se basa
en las propiedades siguientes:
13. Todos los números se construyen a partir de diez dígitos
14. El valor posicional está basado en las potencias de 10, en número base del sistema.
3.4.1El sistema de numeración decimal
Debido a que el sistema indoarábigo está basado en potencias de 10, a veces se le llama sistema de base
diez, o decimal. El valor posicional asigna un valor a un dígito dependiendo de su colocación en un numeral.
Por ejemplo, en el numeral 5984, el 5 tiene el valor posicional de “millares”, el 9 tiene el valor posicional de
“centenas”, el 8 tiene el valor posicional de “decenas” y el 4 tiene el valor posicional de “unidades”.
Podíamos escribir 5984 en forma expandida como: 5 ·103 + 9 · 102 + 8 · 10 + 4 ·1. En la forma expandida de
5984 hemos usado exponentes. Por ejemplo 1000, ó 10 ·10 · 10, se escribe 103. En este caso 10 es un factor
del producto. En general, tenemos la siguiente definición.
Si a es cualquier número, y n es cualquier número natural, entonces
an = a · a · a · a . . . a
n factores
Problemas
1.
Para cada uno de los numerales decimales siguientes, da el valor posicional del numeral subrayado:
a)
827 367
b) 8 421 234
c)
436 567
d) 67 890
2.
Escribe en forma expandida los siguientes numerales.
a) 347
b) 8 653
c)
5 467 856
d) 45 328 904
45
CURSO DE SELECCIÓN 2016
3.
Un cierto número completo de tres dígitos tiene las propiedades siguientes: el dígito de las
centenas es mayor que 7, el dígito de las decenas es un número impar, y la suma de los dígitos es
10. ¿Qué número podría ser?
4.
Julia está leyendo un libro, su hermano le pregunta en qué página va. Julia, a quien le gustan los
acertijos, le dice que la suma de los números de las páginas en donde está abierto el libro es 243 y
que está a punto de dar vuelta a la página. ¿En qué número de página va Julia?
5.
Los niños aprenden el significado de diez, cien, mil y, más adelante, de un millón. Algunos aprenden
que el nombre para un millón de millones es un billón y que un millón de billones es un trillón.
Escribe lo siguiente con numeración indoarábigo (notación en base diez).
a) Seis millones seiscientos mil cuarenta y cinco.
b) Nueve mil cuatro millones cinco mil seiscientos cuarenta y cinco.
c) Tres billones nueve mil cuatro millones cuatrocientos mil setenta.
d) Cien billones.
6.
En una calculadora, usa sólo las teclas 1, 2, 3, 4, 5, 6, 7, 8, y 9, llena la pantalla de la calculadora
para mostrar lo siguiente:
a) El mayor número posible si cada tecla se puede usar una sola vez.
b) El menor número posible si cada tecla se puede usar solo una vez.
c) El mayor número posible si una tecla se puede usar más de una vez.
d) El menor número posible si una tecla se puede usar más de una vez.
46
CURSO DE SELECCIÓN 2016
3.4.2Divisibilidad y números primos
Los divisores de un número son los que dividen exactamente, es decir, con los que el cociente entero y el
residuo cero.
Si a y b son enteros cualesquiera, entonces b divide a a, que se escribe b|a, si, y sólo si, existe un entero
único c tal que a = bc
Si b|a, entonces b es un factor, o un divisor, de a, y a es un múltiplo de b.
Reglas de divisibilidad
En ocasiones conviene saber si un número es divisible entre otro sólo con verlo o mediante una prueba
sencilla.
Criterios de divisibilidad para 2, 5, 10, 3, 9, 4, 8 y 6
Un entero es divisible entre 2 si, y sólo si, su dígito de las unidades es divisible entre 2.
Un entero es divisible entre 5 si, y sólo si, su dígito de las unidades es divisible entre 5 ó 0.
Un entero es divisible entre 10 si, y sólo si, su dígito de las unidades es divisible entre 10, esto es, si,
y solo si, el dígito de las unidades es 0.
Un entero es divisible entre 3 si, y sólo si, la suma de sus dígitos es divisible entre 3.
Un entero es divisible entre 9 si, y sólo si, la suma de sus dígitos es divisible entre 9.
Un entero es divisible entre 4 si, y sólo si, los dos dígito del entero representa un número divisible
entre 4.
Un entero es divisible entre 8 si, y sólo si, los tres dígito del entero representa un número divisible
entre 8.
Un entero es divisible entre 6 si, y sólo si el entero es divisible entre 2 y 3.
47
CURSO DE SELECCIÓN 2016
Problemas
1.
Clasifica cada caso como verdadero o falso. Si es falso, di por qué:
a) 6 es un factor de 30
b) 6 es un divisor de 30
c) 30 es factor de 6
d) 30 es divisor entre 6
e) 30 es un múltiplo de 6
f) 6 es un múltiplo de 30
2.
Usa los criterios de divisibilidad para responder lo siguiente:
a) Hay 1379 niños inscritos para jugar en la liga de beisbol, si se van a asignar exactamente 9
jugadores a cada equipo, ¿habrá algún equipo al que le falten jugadores?
b) Hay 261 estudiantes que se asignarán a 9 maestras de modo que cada maestra tenga el mismo
número de estudiantes. ¿Es ello posible?
c)
3.
Seis amigos ganaron un boleto de lotería. El pago es $242 800. ¿Se puede dividir el dinero
equitativamente?
Sin usar calculadora, prueba cada uno de los números siguientes para ver si son divisibles entre 2,
3, 4, 5, 6, 8, 9, y 10:
a) 746 988
b) 81 342
c)
15 810
d) 4 201 012
e) 1 001
e) 10 001
4.
Si es posible, coloca un dígito en el cuadro de modo que el número , sea divisible entre
527 4
a)
2
2
b) 3
c) 4
d) 9
48
CURSO DE SELECCIÓN 2016
3.4.4 Números primos
Cualquier entero positivo con exactamente dos distintos divisores positivos es un número primo, o un
primo. El número 1 tiene sólo un factor positivo, de modo que no es primo. Los primeros 12 primos son: 2,
3, 5, 7, 11, 13, 17, 19, 23, 29, 31 y 37.
Factorización en primos
Una expresión como producto en factores es una factorización en primos. Para hallar una factorización en
primos de un número dado, primero reescribimos el número como un producto de dos números primos más
pequeños mayores que 1.
El teorema fundamental de la aritmética nos asegura que una vez hallada una factorización en primos de un
número, no puede hallarse, de ese mismo número, una factorización en primos diferente por ejemplo,
considera 260. Comenzamos con en menor primo, 2, y vemos si divide a 260. De no ser así, tratamos que el
siguiente primo mayor y verificamos la divisibilidad entre ese primo. Una vez que hayamos un primo que
divida al número en cuestión debemos de hallar el cociente del número dividido entre el primo. Este paso de
la factorización en primos de 260 se muestra a continuación. Después verificamos si el primo divide al
cociente. Si sucede así, repetimos el proceso; de no ser así, pasamos al siguiente primo mayor, 3, y vemos si
divide al cociente. Vemos que 260 dividido entre dos da 130, como se muestra. Continuamos el
procedimiento, usando primos cada vez mayores, hasta alcanzar el cociente
1. El número original es el
producto de todos los divisores primos usados.
260
2
130
2
65
5
13
13
1
La factorización de 260 se escribe como 22· 5 · 13.
La factorización en primos se utiliza para encontrar el máximo común divisor y el mínimo común múltiplo.
49
CURSO DE SELECCIÓN 2016
3.4.5 Máximo común divisor
El máximo divisor común (MCD) de dos enteros a y b es el mayor entero que divide tanto a a como a b
El máximo divisor común (MCD) de dos enteros a y b es el mayor entero que divide tanto a a como a b.
Para hallar el MDC de dos o más enteros positivos, halla primero las factorizaciones en primos de los
números dados y después identifica cada factor primo común de los números dados. El MDC es el producto
de los factores comunes. Para hallar el MDC (180, 168), factorizamos en primos:
180 = 2 · 2 · 3 · 3 · 5
168 = 2 · 2 · 2 · 3 · 7
Vemos que 180 y 168 tienen en común dos factores de 2 y uno de 3. Estos primos comunes dividen tanto a
2
180 como a 168. Por lo tanto, el máximo divisor común de 180 y 168 es 2 · 3. El procedimiento para hallar el
MDC de dos o más números usando el método de factorización en primos se resume a continuación:
Para hallar el MDC de dos o más enteros positivos, halla primero las factorizaciones en primos de los
números dados y después identifica cada factor primo común de los números dados. El MDC es el
producto de los factores comunes.
Problema: Carmelita está haciendo paquetes de aperitivos para un grupo de excursionistas; para esto
dispone de 60 bolsas de granola y 90 botellas de agua. Cada paquete deberá de tener el mismo número de
bolsas de granola y de botellas de agua. ¿Cuál es el mayor número de paquetes que puede hacerse sin que
sobren bolsas de granola ni botellas de agua?
Solución:
Para resolver este problema necesitamos hallar los factores comunes de 60 y 90. El máximo factor común
(MFC) es el mayor número que es factor de 60 y 90. Usamos la factorización en primos.
60
90
2
factor común
30
45
2
15
45
3
factor común
5
15
5
factor común
1
3
3
1
Los factores comunes son 2, 3 y 5; por lo tanto su producto nos dará su MDC; 2 · 3 · 5 = 30. El mayor número
de paquetes de aperitivos que ella puede hacer es 30.
50
CURSO DE SELECCIÓN 2016
3.4.6 Mínimo común múltiplo
Si a y b son positivos. Entonces el mínimo múltiplo común (MCM) de a y b es el número entero positivo que
es simultáneamente un múltiplo de a y un múltiplo de b.
Las salchichas se vende usualmente en paquetes de 10 y el pan para hacer hot-dogs suele venderse en
paquetes de 8 piezas. Esta disparidad causa problemas cuando uno trata de hacer corresponder salchichas y
panes. ¿Cuál es el menor número de paquetes de cada uno que podrías ordenar de modo que haya igual
número de salchichas que de pan? Las cantidades de salchichas que podemos tener son simplemente
múltiplos de 10 (10, 20, 30, 40, 50) y múltiplos de 8 (8, 16, 24, 32, 40, 48) y buscar los múltiplos comunes;
esto sucede en 40, 80, 120,…y como en este problema estamos interesados en el menor de estos múltiplos,
es 40.
Un método para hallar múltiplos comunes es el de división entre primos,
Método de la división entre primos
Este método consiste en dividir entre el menor número primo que divide a por lo menos uno de los números
dados.
Ejemplo: hallar el MCM de 12, 75 y 120.
Iniciamos dividiendo con el menor primo que es 2, y volvemos a dividir entre dos si algún número tiene
mitad y así seguimos hasta que todos los números tienen de residuo 1.
12
75
120
2
6
75
60
2
3
75
30
2
3
75
15
3
1
25
5
5
5
1
5
1
Así el MCM (12, 75 120) = 2 · 2 · 2 · 3 · 5 · 5 = 600
51
CURSO DE SELECCIÓN 2016
Problemas MCD, MCM
1.
Hallar el MCD y el MCM para cada uno de los casos siguientes, usando el método de
factorización de primos.
a) 18 y 10
la
b) 24 y 36
c)
8, 24 y 52
d) 132 y 504
e) 65 y 1690
f)
900, 96 y 630
g) 108 y 360
h) 11 y 19
2.
En el dormitorio de Patricia hay tres relojes de alarma, cada uno programado para activarse en
tiempos diferentes. El reloj A se activa cada 15 min, el reloj B se activa cada 40 min y el reloj C se
activa cada 60 min. Si los tres relojes se activan a las 6:00 A.M, contesta lo siguiente:
a. ¿Cuánto tiempo transcurrirá antes de que las alarmas se activen juntas de nuevo, después
de las 6:00 A.M?
b.
¿La respuesta a (a) sería diferente si el reloj B se activara cada 15 min y el reloj A se
activara cada 40 min?
3.
Midas tenía 120 monedas de oro y 144 monedas de plata. Quiere colocar sus monedas de oro y sus
monedas de plata en pilas de modo que haya el mismo número de monedas en cada pila. ¿Cuál es
el mayor número de monedas que puede colocar en cada pila?
4.
Beto y Sofía trabajan de noche. Beto tiene libre cada sexta noche y Sofía tiene libre cada octava
noche. Si ambos tienen noche libre hoy, ¿Cuántas noches pasaran antes de que vuelvan a tener la
noche libre juntos?
5.
Los Cinemas I y II comienzan sus funciones a las 7:00 P.M. La película en el Cinema I dura 75 min
mientras que la película en el Cinema II dura 90 min. Si la proyección es continua, ¿Cuándo
comenzaran de nuevo a la misma hora?
6.
Dos ciclistas recorren un trayecto circular. El primer ciclista completa una vuelta en 12 min y el
segundo ciclista la completa en 18 min. Si comienzan en el mismo lugar, al mismo tiempo y en la
misma dirección, ¿Después de cuantos minutos se encontraran de nuevo en el lugar de partida?
52
CURSO DE SELECCIÓN 2016
7.
a.
Un terreno rectangular de 75 pies por 625 pies se va a dividir en porciones cuadradas del mismo
tamaño. Si los lados de los cuadrados han de ser números completos de pies:
¿Cuáles son los mayores cuadrados posibles y cuantos cuadrados cabrán en el terreno?
b.
¿Cuáles son los cuadrados más pequeños posibles?
c.
¿Qué otro tamaño de cuadrados es posible?.
8.
La directora de una escuela primaria quiere dividir cada uno de los tres grupos de cuarto grado en
grupos iguales más pequeños con al menos 2 estudiantes en cada uno. Si los grupos tienen 18, 24 y
36 estudiantes, respectivamente, ¿Qué tamaños de grupos son posibles?
9.
Susana gasto la misma cantidad de dinero en DVD que en discos compactos. Si el DVD cuesta $12 y
el CD $16, ¿Cuál es la mínima cantidad que pudo haber gastado en cada uno?
10. En una tienda de artículos para fiestas, los platos de papel vienen en paquetes de 30, las tazas de
papel en paquetes de 15 y las servilletas en paquetes de 20. ¿Cuál es el menor número de platos,
tazas y servilletas que pueden comprarse de modo que se tenga el mismo número de cada uno?
11. En una bodega hay tres toneles de vino, cuya capacidades son 250 litros, 360 litros y 540 litros. Su
contenido se quiere envasar en cierto número de garrafas iguales. Calcular las capacidades
máximas de estas garrafas para que en ellas se pueda envasar el vino contenido en cada uno de los
toneles y el número de garrafas que se necesitan.
12. Tres avisos luminosos encienden sus luces de la siguiente manera: el primero cada 6 segundos, el
segundo cada 9 segundos y el tercero cada 15 segundos. A las 7 de la noche se encienden
simultáneamente los tres avisos. ¿cuántas veces coinciden encendidas los avisos en los 9 min.
siguientes?
53
CURSO DE SELECCIÓN 2016
3.5 Números racionales
El conjunto de números de la forma
a
, donde b ≠ 0 y ay b son enteros, es el conjunto de los números
b
racionales, que se denota con Q que proviene de la palabra inglesa quotient, que significa cociente; se
define de la manera siguiente:
a
son enteros y b ≠ 0
b
Q=
Q es un subconjunto de otro conjunto de números llamado fracciones. Las fracciones son de la forma
donde b ≠ 0 pero a y b no son necesariamente enteros. Por ejemplo,
1
2
a
,
b
es una fracción pero no es un
número racional, (en este curso nos restringiremos a fracciones donde a y b son números reales, pero esta
restricción no es necesaria). El hecho de que b ≠ 0 siempre es necesaria, pues es imposible dividir entre 0.
El conjunto de los números racionales
En el número racional
a
a
, a es un numerador y b es el denominador. El número racional
también se
b
b
puede representar como a/b o como a
b.
Las siguientes figuras ilustran el uso de los números racionales como parte de un todo y como parte de un
conjunto dado. Por ejemplo, en el modelo de área de la figura, en (a) una de las tres partes congruente, ó
1/3 del rectángulo grande está sombreado; en (b) dos de tres partes congruentes, dos de tres partes
congruentes, ó 2/3 del segmento unitario, están sombreadas; en (c) tres de cinco círculo congruentes, ó 3/5
de los círculos, están sombreados.
a)
b)
0
c)
1
54
CURSO DE SELECCIÓN 2016
Uso de los números racionales
Uso
Problema de división o solución de un
problema de multiplicación
Partición, o parte de un todo
Razón
Probabilidad
Porcentaje
Ejemplos
La solución de 2x = 3 es 3/2
José recibió ½ de salario mensual de
María como pensión alimenticia.
La razón de los republicanos a los
demócratas en el senado de Estados
Unidos es de tres a cinco.
Cuando echas una moneda ideal, la
probabilidad de obtener cara es ½.
Porque el resultado de la división se
multiplica por cien, de aquí que 35%
sea mismo que
35
100
Nuestra primera relación con fracciones, con números racionales, usualmente es como una descripción más
que como una notación matemática. Escuchamos frases como “media pizza”, “un tercio del pastes” ó “tres
cuartos de una tarta”. Nos encontramos preguntas como “si tres barras idénticas de fruta se distribuyen
equitativamente entre cuatro amigos, ¿Cuánto obtiene cada uno?” la respuesta es que cada uno recibe ¾ de
barra.
Para entender el significado de cualquier fracción,
a
, usando el modelo parte todo, debemos tomar en
b
cuenta los siguiente:
1.
2.
3.
El todo en consideración.
El número b de partes iguales en Las que se divide el todo.
El número a de partes del todo que estamos seleccionando.
Los números racionales se pueden representar sobre una recta numérica. Una vez asignados los enteros 0 y
1 a punto sobre una recta, se ha definido el segmento unitario y cualquier otro número racional está
asignado a punto específico. Por ejemplo, para representar ¾ sobre la recta numérica, dividimos el
segmento de 0 a 1 en cuatro segmentos de igual longitud.
-1
0
¾
1
55
CURSO DE SELECCIÓN 2016
Una fracción
a
, donde 0≤|a|≤|b|, es una fracción propia.
b
Una fracción
a
donde si |a|≥ |b|> es una fracción impropia.
b
Por ejemplo, 4/7 es una fracción propia.
7/4, 4/4, y – 9/4 son fracciones impropias.
3.5.1Fracciones equivalentes
Las fracciones equivalentes o iguales, son números que representan el mismo número en la recta numérica.
Como representan cantidades iguales, como
1 2
=
3 6
Las fracciones que representan la misma cantidad se llaman fracciones equivalentes.
1
1
2
1
6
1
12
1 3 6
= =
2 6 12
¿Cómo hallar fracciones equivalentes?
Usa la multiplicación
Para hallar fracciones equivalentes se multiplica el numerador y el denominador por el mismo número
distinto de cero.
18 2 36
x =
24 2 48
56
CURSO DE SELECCIÓN 2016
Usa la división
18 3 6
=
24 3 8
De modo que,
18 36 6
,
y
son fracciones equivalentes.
24 48 8
Para simplificar fracciones deberemos de encontrar un factor común del numerador y denominador y dividir
ambos miembros entre su máximo divisor común, para escribir la fracción en su mínima expresión o forma
más simple.
Un número racional
a
está en su forma más simple si, sólo si, a y b no tienen un factor común mayor que 1,
b
esto es, si a y b son primos relativos.
Comparar fracciones con denominadores distintos
Comparar fracciones con denominadores iguales no implica dificultad porque a mayor numerador mayor es
valor de la fracción; mientras que comparar fracciones con denominadores distintos puede lograrse
reescribiendo las fracciones con el mismo denominador usando el denominador común, o multiplicando
tanto numerador como denominador por un número que iguale los denominadores de las fracciones que se
están comparando.
Determinar cuál de las siguientes fracciones es mayor:
3 3
ó
4 10
La primera fracción multiplicamos numerador y denominador por 10 y la segunda por 4
3 10 30
x
=
4 10 40
y la segunda
De esta forma observamos claramente que
Ordenar las fracciones
3 4 12
x
=
10 4 40
30 12
3 3
>
es decir: >
40 40
4 10
3 9 5 2
,
, y
de menor a mayor.
4 16 8 3
57
CURSO DE SELECCIÓN 2016
Problemas
7
de cada una de las maneras siguientes:
8
1.
Escribe una frase que ilustre el uso de
2.
a) Como un problema de división
b) Como parte de un todo
c) Como una razón
Para cada uno de los casos siguientes, escribe una fracción que represente la parte sombreada:
a)
b)
c)
d)
3.
Para cada uno de los cuatro cuadrados siguientes, escribe una fracción que represente la parte
sombreada, ¿Qué propiedad de las fracciones ilustra el diagrama?
a)
c)
b)
d)
58
CURSO DE SELECCIÓN 2016
4.
Completa cada una de las figuras siguientes de modo que ilustre
3
.
5
a)
b)
c)
d)
e)
f)
5.
Si cada uno de los modelos siguientes representa la fracción dada, traza un modelo que represente
todo
a.
b.
¾
4/3
59
CURSO DE SELECCIÓN 2016
c.
d.
1/5
¼
6.
Escribe una fracción que represente la parte sombreada.
7.
Usa la figura como referencia para representar cada caso como una fracción:
8.
En cada caso, escribe tres fracciones iguales a la fracción dada:
a.
2
9
9.
Halla la forma más simple para cada una de las fracciones siguientes:
156
93
10
d.
68
a.
b.
2
5
c.
b.
e.
0
3
27
45
84
91
d.
c.
f.
a
2
65
91
663
703
10. Determina si los pares siguientes son iguales:
a.
c.
3
375
y
8
1000
6
600
y
10
1000
b.
d.
18
23
y
69
54
17 25
y
27 45
60
CURSO DE SELECCIÓN 2016
11. Se necesita una tabla exactamente
tabla de
11
pulg de ancho para tapar un hoyo. ¿Puede rebajarse una
32
3
pulg para tapar el hoy? Si es asi, ¿Cuánto debe rebajarse la tabla?
8
12. Traza un modelo de área para mostrar que
3 6
=
4 8
13. En el grupo de algebra de Ana, 6 de 31 estudiantes obtuvieron A en un examen. El mismo examen
se aplicó al grupo de Beto y 5 de 23 estudiantes obtuvieron A. ¿Qué clase tiene mayor de A?
14. Para cada uno de los siguientes pares de fracciones, reemplaza la coma con el símbolo correcto (<,
=, >) para obtener una proposición verdadera:
a)
d)
7 5
,
8 6
1
1
,
7 8
4 3
2 ,2
5 6
2 4
e)
,
5 10
b)
c)
f)
7
2
,
8
5
10 10
,
7 17
61
CURSO DE SELECCIÓN 2016
3.5.2 Suma y resta de números racionales
La suma y la resta de números racionales es muy parecida a la suma y la resta de números enteros.
Ilustraremos la suma de dos números racionales con denominadores iguales,
2
1
+ , usando el
6
6
modelo del área de una figura, tenemos:
2
6
+
1
6
=
3
6
Definición de suma de números racionales con denominadores iguales
Si
a c
a c ac
y son números racionales, entonces
+
=
b b
b
b b
Definición de suma de números racionales con denominadores diferentes
Si
a c
a c ad bc
y son dos números racionales cualesquiera, entonces
+
=
db
b d
b d
Para la suma de números racionales con denominadores diferentes, se obtiene el MCM de éstos
números.
Ejemplo:
Hallar las sumas siguientes:
a)
2
4
+
15 21
62
CURSO DE SELECCIÓN 2016
2
1
+
3 5
3
1 1
c)
+
+
4
5 6
3 4
d)
+
y
x
b)
Solución:
a)
como MMC (15, 21) = 3· 5· 7 = 105, entonces:
2
4
34
14 20
+
=
=
105
15 21
105
b)
2 1 10 3 7
+ =
=
3 5
15
15
c)
3 1 1 30(3) 1(24) 1(20) 90 24 20 134 67
+ + =
=
=
=
4 5 6
120
120
120 60
d)
3 4 3 y 4x
+ =
x y
xy
3.5.3Números mixtos
Números mixtos, estos es, números formados por un entero y una parte fraccionaria de un
3
3
3
3
2
entero. Por ejemplo 4 significa 2 + 4 . A veces se infiere que 4 significa 2 por 4 , pero esto
2
no es correcto.
0
1
2
3
4
63
CURSO DE SELECCIÓN 2016
a
Un número mixto es un número racional y, por lo tanto, siempre se puede escribir en la forma b .
Para cambiar un número mixto a una fracción (impropia), se multiplica el entero por el
denominador y se suma con el numerador de la fracción, quedando como nuevo numerador y el
denominador se conserva.
Por ejemplo: cambiar los siguientes números mixtos.
a)
1 13
4
3 3
2 17
3
5
5
b)
Para cambiar una fracción (impropia) a un número mixto se divide el numerador entre el
denominador, el cociente es el número entero, el residuo es el nuevo numerador y se conserva
el mismo denominador.
Ejemplo:
29
Transformar 5 a un número mixto.
5
5 29
25
04
Por lo tanto
29
4
5
5
5
64
CURSO DE SELECCIÓN 2016
Resta de números racionales
Si
a c
a c ad bc
y son números racionales cualesquiera, entonces
=
b d
b d
bd
Ejemplo: Halla cada una de las diferencias:
5 1
a) 8 4
1
3
5 2
3
4
b)
Solución:
a) Un enfoque es hallar el MCM para las resta de fracciones. Como MCM (8, 4) = 8, tenemos
5 1 52 3
=
=
8 4
8
8
b) pasamos los números mixtos fracciones impropias, hallamos el MCM y restamos los
numeradores:
1
3 16 11 64 33 31
7
+
=
=
=2
5 2 =
3
4 3
4
12
12
12
65
CURSO DE SELECCIÓN 2016
Problemas con fracciones
1.
Calcula cada caso usando cualquier método:
a.
1 2
2 3
g.
6 8 13
7 15 5
b.
14 2
12 3
h.
3 11 5
4 6 10
c.
5 3
x y
i.
7 3 8
8 11 6
d.
3
5
7
2
2
2
2 x y 2 xy
x
j.
5 6 15
3 8 4
e.
5
1
2
6
8
k.
7 12 4
2 5 7
f.
1
1
4 3
2
6
l.
8 5 19
7 25 5
2.
Transforma cada una de las fracciones siguientes a números mixtos:
a.
56
3
c.
293
100
b.
14
5
d.
47
8
3.
Transforma cada uno de los siguientes números mixtos en fracciones de la forma
a
, donde a y b
b
son enteros:
a.
6
3
4
c.
3
93
100
b.
2
14
5
d.
4
47
8
66
CURSO DE SELECCIÓN 2016
4.
Usa información de la tabla para responder cada una de las preguntas siguientes:
Equipo
Patos
Castores
Tigres
Osos
Leones
Gatos
Tejones
a.
b.
c.
d.
e.
f.
5.
Partidos Jugados
22
19
28
23
27
25
21
Partidos Ganados
10
10
9
8
7
6
5
1
de sus partidos?
2
1
¿Qué equipo gano menos de de sus partidos?
2
1
¿Qué equipo gano más de de sus partidos?
3
1
¿Qué equipo gano menos de de sus partidos?
3
1
¿Qué equipo gano más de de sus partidos?
4
1
¿Qué equipo gano menos de de sus partidos?
4
2
1
1
Un grupo consta de
de primer año,
de segundo año,
de tercer año y el resto son
5
4
10
¿Qué equipo gano más de
especialidad. ¿Qué fracción del grupo son los alumnos de especialidad?
6.
Un dependiente vendió tres piezas de un tipo de cinta a tres clientes distintos. Una pieza tenía
yardas de longitud, otra tenia 2
1
3
3
1
yd de longitud y la tercera tenia 3 yd de longitud. ¿Cuál es la
4
2
longitud total vendida de este tipo de cinta?
67
CURSO DE SELECCIÓN 2016
7.
a.
b.
c.
d.
La compañía Naturales vende sus productos en muchos países. Las dos graficas circulares siguientes
muestran las fracciones de las ganancias de la compañía para los años 2000 y 2005. Con base en
esta información, responde las siguientes preguntas:
En el año 2000, ¿En cuánto excedió la fracción de ventas en Japón a la de Canadá?
En 2005, ¿Cuánto falto para la fracción de ventasen Inglaterra fuera de la de Estados Unidos?
¿En cuánto excedió la fracción de ventas totales para Estados Unidos en 2005 a la de 2000?
¿Es cierto que la cantidad total de ventas en dólares en Australia fue menos en 2000 que en 2005?
¿Por qué?
Fracciones de ventas totales, 2000
1
3
Estados
EstadosUnidos
Unidos
Australia
1
20
1
5
1
6
Canadá
Canadá
1
4
Inglaterra
Japón
Fracciones de ventas totales, 2005
1
6
7
20
Estados Unidos
Australia
2
5
1
10
1
4
Canadá
Inglaterra
Japón
68
CURSO DE SELECCIÓN 2016
8.
Una receta requiere 3
1
3
tazas de leche. Ramón puso 1 tazas y vacio el recipiente. ¿Cuánta mas
2
4
leche necesita agregar?
9.
3
7
yardas de tela. Piensa hacer una falda usando 1 yd, unos pantalones
4
8
3
2
usando 2 yd y un chaleco usando 1 yd, ¿Cuánta tela le va a sobrar?
8
3
Martina compro 8
3
1
3
pulg se corta de una tabla de 38 pulg. La sierra se lleva pulg. ¿Cuánto
8
4
4
1
queda de la tabla de 38 pulg después del corte?
4
10. Una tabla de 15
1
1
de su ingreso el sábado de lo que le quedo, el domingo. ¿Puede modelarse esta
2
3
1 1
situación como ? Explica porque si o porque no.
2 3
11. Carla gasto
3.5.4 Multiplicación y división de números racionales
Para ilustrar la definición de multiplicación de números naturales, usamos la interpretación de multiplicación
como suma repetida. Usando la suma repetida podemos interpretar 3 ·
3·
3
4
como sigue:
3 3 3 3 9
= +
+
=
4 4 4 4 4
A continuación consideramos lo que sucede cuando ningún factor del producto es un entero: si la
vegetación alguna vez cubrió alrededor de
3
1
de la tierra y ahora sólo queda
de esta vegetación, ¿qué
5
2
fracción de tierra está cubierta de vegetación hoy día?
1
3
de , usaremos un modelo de área, mediante un rectángulo que representa todo separado
2
5
3
en quintos, con
sombreado, dividimos la porción sombreada del rectángulo en dos partes congruentes y
5
Para hallar
69
CURSO DE SELECCIÓN 2016
tomamos una de esas partes .el resultado será la porción verde que queda de la tierra, la cual corresponde 3
partes de 10, ó
3
del todo.
10
3
5
1
2
3
5
Así tenemos:
1 3 3
=
2 5 10
Definición de multiplicación de números racionales
Si
a c
a c ac
y son números racionales cualesquiera, entonces =
b d
b d bd
Ejemplo:
Si
5
7
de la población de cierta ciudad completó el bachillerato y
de quienes lo completaron son mujeres,
6
11
¿qué fracción de la población de esa ciudad son mujeres y terminaron el bachillerato?
Solución:
La fracción deberá ser
7
5
7 5 7 5 35
de , ó
· =
=
11
6
11 6 11 6 66
La fracción de la población que son mujeres y que terminaron el bachillerato es
35
.
66
70
CURSO DE SELECCIÓN 2016
Propiedades
Inverso multiplicativo para números racionales
a b
a b
,
es el único número racional tal que
· = 1. El
b a
b a
a
a
inverso multiplicativo de
también se llama recíproco de
b
b
Para cualquier número racional distinto de cero,
Propiedad distributiva de la multiplicación sobre la suma de números racionales
Si
a c e
,
y
son números racionales cualesquiera, entonces
f
b d
a c e
+
b d f
=
a c
b d
+
a e
b f
Propiedad multiplicativa del cero para números racionales
Si
a
a
es cualquier número racional, entonces · 0 = 0
b
b
Ejemplo:
Una bicicleta está en venta a
3
de su precio original. Si el precio de venta es de $330, ¿Cuál era el precio
4
original?
Solución:
Sea x el precio original. Entonces
3
3
3
del pecio original es x. como el precio de venta es $330, tenemos
4
4
4
x = 330. Despejando x tenemos
3x = (330) (4)
3x = 1320
x = 440
El precio original de la bicicleta fue de $440
71
CURSO DE SELECCIÓN 2016
División de números racionales
Considera 3
1
, que es equivalente a encontrar cuántas mitades hay en 3. Observamos del modelo de
2
área en la siguiente figura que hay 6 mitades en las tres piezas completas.
1
2
1
2
1
2
1
+
1
Registramos esto como 3
1
2
+
1
1
2
=
1
2
3
1
1
= 6, lo cual es cierto porque · 6 = 3
2
2
Algoritmo para la división de fracciones
Si
a c
y
son números racionales cualesquiera y , entonces
b d
a c ad
=
b d bc
Es lo mismo si invertimos numerador y denominador de la segunda fracción y realizar una multiplicación:
a d ad
=
b c bc
Ejemplo:
Una estación de radio proporciona un servicio público de anuncios de 36 minutos cada 24 horas de
transmisión.
a) ¿Qué parte de la transmisión diaria está asignada al servicio público de anuncios?
b) ¿Cuántos anuncios del servicio público con duración de 3/4 min se permiten en los 36 minutos?
Solución:
a)
Hay 60 minutos en una hora y 60 · 24 minutos en un día. Así
36
36
1
ó
=
60 24 1440 40
72
CURSO DE SELECCIÓN 2016
144
36
= 34(4/3), ó
= 48 anuncios están permitidos
3
3
4
b)
Ejemplo:
Tenemos 35 ½ yardas de material disponible para fabricar toallas. Cada toalla requiere 3/8 de yarda de
material.
a) ¿Cuántas toallas puede hacerse?
b) ¿Cuánto material sobrará?
Solución:
a)
Necesitamos hallar la parte entera de la respuesta a 35 ½
35 ½
3
, la división es:
8
3 71 8 284
2
=
= 94
=
8
2 3
3
3
Por lo tanto pueden hacerse 94 toallas.
b) Como la división en a) fue entre 3/8, la cantidad de material que sobra es 2/3 de 3/8, ó 2/3 · 3/8 =
6/24 = ¼ de yarda. Esto también se puede responder notando que los 2/3 de la parte (a) son dos
tercios de una toalla, que requiere 2/3 de 3/8 de yarda de material.
73
CURSO DE SELECCIÓN 2016
Problemas con fracciones
1.
Usa una región rectangular para ilustrar cada uno de los productos siguientes:
a)
2.
3.
b)
c)
2 1
5 3
e.
22 2
4
7
3
a.
49 26
65 98
c.
xy z 2 a
z x3 y 2
b.
a b2
b a2
d.
1 3
2 3
3 4
Despejar x en cada caso:
b.
2
7
x
3
6
3
1
x
4
2
c.
d.
1
3 8
4
1
b. 7 4
4
1
c. 9 10
5
d.
e.
f.
1
4
1
3
2
1 1
3
2 2
82
g.
3
h.
4
1
3
1
2
2
Estima los siguiente:
4
1
5 3
5 10
10 1
b. 4
5
11 8
8
20
9
c.
1
3
12
a.
6.
5 2
3
x
6 3
4
2x 1 x 1
3 4 6 2
Calcular mentalmente lo siguiente. Obtén la respuesta exacta.
a.
5.
2 1
3 5
Halla cada uno de los productos siguientes.
a.
4.
1 3
3 4
1
3
7
1
8
12
d.
1
8
Un trabajo de costura requiere 6 yardas de material que cuesta 62 centavos la yarda, y
3
1
4
yardas que cuestan 81 centavos la yarda. Escoge entre los siguientes el mejor estimado del costo
del trabajo:
a. Entre $2 y $4
b. Entre $4 y $6
c. Entre $6 y $8
d. Entre $8 y $10
74
CURSO DE SELECCIÓN 2016
7.
Cinco octavos de los estudiantes de una secundaria viven en dormitorios. Si 6000 estudiantes de la
secundaria viven en dormitorios, ¿Cuántos estudiantes hay en la secundaria?
8.
Una universidad tuvo una reducción de personal académico y perdió
1
de sus profesores. Si
5
quedaron 320 profesores después de la reducción. ¿Cuántos profesores había originalmente?
9.
Alberto pose
5
de las acciones de una compañía. Su hermana Renata posee la mitad de número de
9
acciones de Alberto. ¿Qué parte de las acciones no pertenecen ni a Alberto ni a Renata?
10. Una persona tiene 29
uniforme requiere
a.
b.
1
yardas de material disponible para hacer uniformes para muñecas. Cada
2
3
yardas de material.
4
¿Cuántos uniformes puede hacer?
¿Cuánto material le va a sobrar?
11. Se vende un traje por $180. ¿Cuál es el precio original del traje si el descuento fue
1
del precio
4
original?
12. Todos los salarios de una compañía de software se incrementa en cada año un
1
del salario de
10
cada empleado del año anterior.
a. Si el salario anual actual de Marta es de $100000, ¿Cuál será su salario en 2 años?
b. Si el salario actual de Arturo es de 99000 ¿Cuál era su salario hace un año?
c. Si el salario actual de Juanita es de 363000, ¿Cuál era su salario hace 2 años?
13. Jazmín está leyendo un libro. Ha terminado
3
del libro y le faltan 82 páginas. ¿Cuántas páginas ha
4
leído?
14. Juan sacó el dinero de su cuenta de ahorro. Gastó $50 en un radio y
3
de lo que quedó en regalos.
5
La mitad de lo que quedó, lo regresó a su cuenta y le restan $35, los donó a una institución de
beneficencia. ¿Cuánto dinero tenía Juan originalmente en su cuenta de ahorro?
75
CURSO DE SELECCIÓN 2016
15. Pedro, Pablo y María comenzaron al mismo tiempo a caminar alrededor de una senda circular en la
misma dirección. Pedro tardó
1
5
de hora en dar una vuelta. Pablo tardó
de hora y María tardó
2
12
1
de hora.
3
a) ¿Cuántos minutos tarda cada persona en caminar alrededor de la senda?
b) ¿Cuántas vueltas dará cada persona alrededor de la senda antes de encontrarse los tres de
nuevo en el punto de inicio?
16. La fórmula para convertir grados Celsius (oC) a grados Fahrenheit (F) es
9
5
F= · C + 32
a)
Si Sandra lee que en Veracruz la temperatura es de es de 32ºC, ¿cuál es la temperatura en
grados Fahrenheit?
b) Si la temperatura desciende a -40ºF en West Yellowstone, ¿Cuál es la temperatura en grados
Celsius?
17. Alex da
1
1
1
de sus canicas a Beto. Beto da de éstas a Carina. Carina da
de éstas a Dani. Si Dani
2
2
2
tiene cuatro canicas, ¿cuántas canicas tenía Alex originalmente?
18. El peso normal del cerebro de un elefante africano es de 9
1
lb. ¿Aproximadamente cuál será el
4
peso del cerebro de 13 elefantes?
19. Escribe cada una de las expresiones siguientes en la forma más sencilla, usando exponentes
positivos en la respuesta final:
3
a.
1 1
2 2
7
9
1 1
b.
2 2
5
c.
2 4
3 9
7
6
2
3 3
d.
5 5
7
3 5
e.
5 3
f.
5 7
6
4
3
7
76
CURSO DE SELECCIÓN 2016
SUMA Y RESTA
MULTIPLICACIÓN Y DIVISIÓN
SIMPLIFICACIÓN DE UNA
FRACCIÓN COMPLEJA
1.
1.
1.
2.
2.
2.
3.
3.
3.
4.
4.
4.
5.
5.
5.
6.
6.
6.
7.
7.
8.
8.
9.
9.
10.
10.
7.
8.
9.
10.
77
CURSO DE SELECCIÓN 2016
3.6 Razonamiento proporcional
En la vida diaria encontramos razones, por ejemplo, puede haber una razón de 2 a 3 demócratas a
republicanos en cierto comité legislativo, un amigo pudo haber recibido una multa de exceso de velocidad
por conducir a 120 kilómetros por hora, o las rosas pueden costar 20 pesos la docena. Cada uno de estos
casos ilustra una razón. Las razones se escriben
a
o a : b y se usa para comparar cantidades.
b
Una razón de 1: 3 de niños a niñas en una clase, significa que el número de niños es
1
del de niñas; esto es,
3
hay 1 niño por cada 3 niñas. También se puede decir que la razón de niñas a niños es de 3 : 1, o que hay 3
veces más niñas que niños. Algunas razones dan comparación parte a parte, como la razón del número de
niños a niñas.
Las razones también pueden representar comparaciones parte a todo o de todo a parte. Por ejemplo, si la
razón de niños aniñas en una clase es de 1: 3 entonces la razón de niños (parte) a todos los niños y niñas (el
todo) es 1: 4.
Nota que la razón de 1:3de niños a niñas en una clase no nos dice cuántos niños y cuántas niñas hay en esa
clase, sólo nos dice el tamaño relativo de los grupos. Puede haber 2 niños y 6 niñas, ó 3 niños y 9 niñas, o 4
niños y 12 niñas, o algún otro número que de una fracción equivalente a
1
.
3
Ejemplo:
Hay 7 varones y 12 mujeres en una cafetería el lunes en la tarde, y en la sala de juegos contigua había 14
varones y 24 mujeres.
a) Expresa el número de varones a mujeres en la cafetería (parte a parte).
b) Expresa el número de varones a mujeres en la sala de juegos (parte a parte).
c) Expresa el número de varones en la sala de juegos al número de personal en la sala de juegos como
una razón (parte a todo).
Solución
7
12
14
7
b) La razón es
ó
.
24 12
a)
La razón es
c) La razón es
14
7
ó
38 19
78
CURSO DE SELECCIÓN 2016
Proporciones
En general, dos razones son proporcionales, si, y sólo si, las fracciones que las representan son iguales. Dos
razones iguales forman una proporción.
Propiedades de las proporciones
Si a, b, c y d son números reales y b 0 y d 0, entonces la proporción
a c
=
es verdadera si, y sólo si, ad = bc
b d
Ejemplo:
Cali puede escribir 8 páginas por cada 4 páginas que escribe Dani, si Dani ha escrito 12 páginas, ¿cuántas
páginas ha escrito Cali?
Solución:
La proporción es
8
x
=
, donde x es el número de páginas que escribirá Cali, al despejar x = 24.
4 12
Ejemplo:
Si con tres paquetes de cacao se hacen 15 tazas de chocolate caliente, ¿Cuántos paquetes se necesitan para
preparar sesenta tazas?
Solución:
La proporción es
3
x
=
, donde x = 12.
15 60
Por lo tanto, se necesitan 12 paquetes de cacao que se necesitan para preparar sesenta tazas de chocolate
caliente.
Ejemplo:
Si hay 3 carros por cada 8 estudiantes de una preparatoria, ¿Cuántos carros hay para 1200 estudiantes?
Solución:
Usamos la estrategia formar una tabla:
Número de carros
Número de estudiantes
3
8
x
1 200
La razón de carros a estudiantes siempre deberá ser la misma
79
CURSO DE SELECCIÓN 2016
3
x
=
8 1200
3· 1200 = 8 · x
3600 = 8x
450 = x
Por lo tanto hay 450 carros.
Una proporción establece que dos razones son iguales
Los productos cruzados de los términos de una proporción son iguales.
Ejemplo.
Determina si las razones
3 pies 9 pies
y
forman una proporción.
24 s
8s
Solución:
Observamos que las unidades son las mismas los numeradores y en los denominadores.
3·24 = 9· 6
72 = 72
Como las unidades son las mismas y los productos cruzados son iguales, las razones forman una proporción.
Si las variables x y y están relacionadas por la igualdad y = kx, k =
y
, entonces se dice que y es
x
proporcional a x y k es la constante de proporcionalidad entre y yx.
Ejemplo:
Carlos, Pablo y Susana obtuvieron $ 2520 por pintar una casa. Carlos trabajó 30 h, Pablo trabajó 50 h y
Susana 60 h. Ellos se dividieron el dinero en proporción al número de horas trabajadas. ¿Cuánto ganó cada
uno?
Solución:
Sea x la razón unitaria de la razón de pago por hora. Entonces 30x denota la cantidad de dinero que recibió
Carlos, y Pablo recibió 50x, y Susana recibió 60x. como la cantidad total de dinero recibido es
30x + 50x + 60x = 2 520
140x = 2 520
x = 18
Por lo tanto Carlos recibió 30 x = 30(18) = $ 540
Pablo recibió
50x = 50(18) = $ 900
Susana recibió 60x = 60(18) = $ 1 080
Dividiendo cada una de las cantidades entre 18 se demuestra que la proporción es la requerida.
80
CURSO DE SELECCIÓN 2016
Problemas con fracciones y proporciones
1.
Despejar x en cada una de las proporciones siguientes:
a)
12 18
=
x
45
b)
x 10
=
7
21
c)
5 3x
=
7 98
2.
Hay aproximadamente 2 lb de músculo por cada 5 lb de peso. ¿cuánto peso muscular tiene una
persona de 90 lb?
3.
En Acaxao hay 5 adultos por cada adolescente que conduce. Si hay 12 345 conductores adultos en
Acaxao, ¿Cuántos conductores adolescentes hay?
4.
En un mapa, 1/3 de pulgada representa 5 millas, si Nueva York y Acaxao distan 18 pulgadas en el
mapa, ¿cuál es la distancia real entre ellas?
5.
David lee 40 páginas de un libro en 50 minutos ¿cuántas páginas podrá leer en 80 minutos si lee a
una velocidad constante?
6.
Una vela tiene 30 pulg de largo. Después de consumirse durante 12 minutos la vela tiene 25
pulgadas de largo. ¿en cuánto tiempo se consumirá la vela a la misma tasa?
7.
Un jardín rectangular tiene una razón de ancho a largo de 5 : 9. Si la distancia alrededor del jardín
es de 2 800 pies, ¿cuáles son las dimensiones del jardín?
81
CURSO DE SELECCIÓN 2016
8.
Gabriel, Marcelo y Carmelita invirtieron en una compañía a razón de 2 : 4 : 5, respectivamente. Si se
dividen las ganancias de $2 8000 proporcionalmente a su inversión, ¿cuánto recibirá cada uno?
9.
Susana y Dora trabajaron 3
1
1
h y 4 h respectivamente en un proyecto de programación. Les
2
2
pagaron $176 por el proyecto. ¿Cuánto ganó cada una?
10. Esther logró 75 anotaciones en su práctica de tiro a gol. Si su taza de acierto-falla es de 5 :4,
¿cuántos tiros realizó?
11. Juanita pesa 160 lb en la tierra y 416 lb en Júpiter. Hallar el peso de Ana en Júpiter si ella pesa 120
lb en la tierra.
12. La cantidad de oro para joyería y para otros productos se mide en quilates (K), donde 24K
representa el oro puro. La marca 14K es una cadena indica que la razón entre la masa del oro en la
cadena es de 14 : 24. Si un anillo de oro tiene la marca 18K y pesa 0.4 oz, ¿cuál es el valor del oro en
el anillo si el oro puro está valuado en $300 la oz?
82
CURSO DE SELECCIÓN 2016
3.7 Porcentajes
Los problemas de aplicación que incluyen porcentajes usualmente toman una de las formas siguientes.
1.
2.
3.
Hallar el porcentaje de un número.
Hallar qué porcentaje es un número de otro.
Hallar un número cuando se conoce el porcentaje de ese número.
Antes de considerar ejemplos que ilustren estas formas, recuerda lo que significa hallar una fracción “de” un
2
2
40
de 70 significa ·70. De manera análoga, para hallar 40% de 70 tenemos
de
3
3
100
40
70, lo cual significa
·100, ó 0.40 (70) = 28.
100
número por ejemplo,
Ejemplo:
Una casa que se vende por $92 000, se requiere un 20% de enganche, ¿Cuál es el monto del enganche?
Solución:
El enganche es el 20% de $92 000, ó 0.2 * $92 000 = $18 400. Por lo tanto, el monto del enganche es de $18
400
Ejemplo:
Si Alberto tiene 45 respuestas correctas de un examen de 80 preguntas, ¿qué porcentaje de sus respuestas
son correctas?
Solución:
45
de las respuestas correctas, para hallar el porcentaje de las respuestas correctas,
80
45
necesitamos convertir
a un porcentaje. Podemos hacerlo multiplicando la fracción por 100 y añadiendo
80
Alberto tiene
el símbolo % como sigue:
45
45
= 100 ·
= 56.25%
80
80
Así el 56.25% de las respuestas fueron correctas.
Una solución alternativa usa proporciones. Sea n el porcentaje de respuestas correctas y procedemos como
sigue:
45
n
=
80 100
83
CURSO DE SELECCIÓN 2016
n =
45
· 100
80
n =
4500
= 56.25
80
Ejemplo:
Cuarenta y dos por ciento de los padres de los niños que asisten a la escuela pública de cierta población
trabajan en la universidad local. Si el número de padres empleados por la universidad es de 168, ¿cuántos
padres tienen a sus hijos en la escuela pública?
Solución.
Sea n el número de de padres que trabajan en la universidad y tienen a sus hijos en la escuela pública.
Entonces, 42% de n es 168. Podemos traducir esta información a una ecuación y despejar n.
42% de n = 168
42
·n = 168
100
0.42 ·n = 168
n =
168
= 400
0.42
También se puede resolver usando una proporción:
42 168
=
100
n
42n = 100 * 168
n=
16800
= 400
42
Hay 400 padres en la escuela pública.
Ejemplo:
Queta compró una bicicleta y un año después la vendió por 20% menos de lo que ella pagó. Si la vendió en
$144, ¿cuánto pagó por ella?
Solución:
Buscamos el precio original, P, que Queta pagó por la bicicleta. Sabemos que la vendió en $144 y que esto
incluye una pérdida del 20%. Por lo tanto ella la vendió al 80 % del valor original, nosotros buscamos el 100%
del valor.
84
CURSO DE SELECCIÓN 2016
144
n
=
80 100
n=
144 100
= 180
80
Así ella pagó $180 por la bicicleta.
Ejemplo:
La tienda de vaqueros anuncia un traje con un descuento del 10%, para un ahorro de $ 15. Más adelante, el
gerente anuncia el traje con un 30% de descuento del pecio original. ¿Cuál es la cantidad del descuento
actual?
Solución:
Un 10% equivale a $15, para encontrar el precio original usamos una proporción:
$15
n
=
; n = $150
10% 100
Para hallar el último descuento que fue del 30% sobre el precio original, tenemos:
$150
n
=
; n = $45 de descuento
30%
100%
Conocer fracciones equivalentes para algunos porcentajes pude facilitar cálculos. La siguiente tabla presenta
varias fracciones equivalentes y decimal correspondiente:
Porcentaje
Fracción
equivalente
25%
50%
75%
20%
10%
5%
1%
1
4
1
2
3
4
1
5
1
10
1
20
1
100
Decimal
0.25
0.5
0.75
0.2
0.1
0.05
0.01
85
CURSO DE SELECCIÓN 2016
Problemas de porcentajes
1.
Marcos tenía 84 cajas de caramelo para vender. Él vendió el 75% de las cajas, ¿Cuántas cajas vendió?
2.
Gabriela ganó $16 000 el año pasado y recibió un aumento del 6%. ¿Cuánto gana ella ahora?
3.
Juan recibió un aumento del 7% el año pasado. Si su salario es ahora de $ 27 285 ¿cuál era su salario el
año pasado?
4.
José vendió 180 periódicos de 200; Beto vendió 85% de sus 260 periódicos. Rafa vendió 212, 80% de
los que tenía.
a) ¿Quién vendió más periódicos? ¿Cuántos?
b) ¿Quién vendió el mayor porcentaje de sus periódicos de sus periódicos?
c)
¿Quién vendió el mayor número de periódicos? ¿Cuántos?
5.
Si un vestido que normalmente cuesta $35 está en oferta por $28, ¿cuál es el porcentaje de
descuento?
6.
Un carro usado costaba $1700. Un año después valía $1 400. ¿Cuál es el porcentaje de depreciación?
7.
En cierto parque se contaron un día 728 águilas. Cinco años después se contaron 594. ¿Cuál fue el
porcentaje de merma en el número de águilas contadas?
8.
Dora compró un vestido marcado con el 20% de descuento. Si el precio normal era de $28.00, ¿cuál
fue el precio de venta?
9.
Si ¼ de taza de cereal para el desayuno tiene el 0.5% de los requerimientos mínimos diarios de
vitamina C, ¿cuántas tazas deberían comer para obtener el requerimiento mínimo diario de vitamina
C?
86
CURSO DE SELECCIÓN 2016
10. Una encuesta reporta que 66
2
% de 1800 empleados favorece un nuevo programa de seguros.
3
¿Cuántos empleados están a favor del nuevo programa?
11. Roberto pagó $330 por una nueva bicicleta de montaña para venderla en su tienda. Quiere que el
precio sea tal que él pueda ofrecerla en su tienda con un descuento del 10% y aun así ganar el 20% del
precio que pagó. ¿En qué precio debe venderse la bicicleta?
12. El precio de un traje de $200 se redujo en 25%. ¿En qué porcentaje debe incrementarse el precio del
traje para volver al precio de $200?
13. El carro que se compró Elisa hace 1 año se depreció en $1 116.88, que es el 12.13% del precio que ella
pagó. ¿Cuánto pagó por el carro?
14. Un equipo de trabajo consta de 1 aprendiz, 1 cabo y un maestro carpintero. El equipo recibe un
cheque por $4 200 por un trabajo recién terminado. Un cabo gana el 200% de lo que gana el aprendiz,
y el maestro carpintero gana el 150% de lo que gana el cabo. ¿Cuánto ganó cada persona del equipo?
15. En una fábrica de frascos hay dos máquinas que producen 1000 frascos. La máquina A produce el 70%
de los frascos, mientras que la máquina B produce el 30% restante. El 5% de los artículos producidos
por la máquina A, y el 8% de los productos producidos por la máquina B, resultan con algún defecto.
a) ¿Qué porcentaje de los frascos producidos en la fábrica resultan defectuosos?
b) ¿Qué porcentaje de los artículos defectuosos provienen de la máquina B?
87
CURSO DE SELECCIÓN 2016
4 Ecuaciones
4.1
Ecuaciones de primer grado con una incógnita.
Ecuación es una igualdad condicionada que está compuesta por términos, cuyos valores no conocemos,
denominados variables o incógnitas de la ecuación, por lo general representados por las últimas letras del
abecedario, y por términos cuyos valores no cambian, denominados constantes.
Existen varios tipos de ecuaciones, dependiendo de su grado y número de incógnitas. El grado de una
ecuación con una incógnita nos lo indica el mayor exponente que tenga la variable, habiendo ecuaciones de
primer grado o lineales como
, ecuaciones de segundo grado como
, ecuación
de tercer grado o ecuación cúbica
.
Resolver una ecuación lineal con una incógnita consiste en encontrar el valor de la variable que al sustituir
en la ecuación original mantiene la igualdad. Para llegar a la solución es necesario dejar en el primer
miembro de la ecuación a todos los términos que contengan a la variable, y en el segundo miembro los
términos que no lo contengan, de modo que cuando algo está sumando lo restamos en ambos miembros de
la ecuación para que no se altere la igualdad, esto implica que dos términos se cancelarán en uno de los
miembros. Simplificando podemos decir que al trasladar términos de un miembro a otro de la ecuación
equivale a cambiarle el signo a la operación; así mismo cuando un miembro está multiplicando pasará al
otro miembro dividiendo.
Ejemplo:
Resolver la ecuación
Resolver la ecuación indicada:
1.
2.
3.
4.
5.
6.
88
CURSO DE SELECCIÓN 2016
7.
8.
9.
10.
11.
12.
13.
14.
15.
89
CURSO DE SELECCIÓN 2016
4.2
Sistemas de ecuaciones
Se da el nombre de sistema de ecuaciones a un conjunto de dos o más ecuaciones que tienen idénticas
soluciones, por lo que también se les llama ecuaciones simultáneas.
Estos sistemas pueden ser de tres clases:
1)
2)
3)
Consistentes, es decir, tienen una sola respuesta.
Equivalentes o dependientes, es decir, tienen varias soluciones.
Inconsistentes o incompatibles, es decir, no tienen solución.
4.2.1 Método de suma y resta
2x 3y 7 1
2x y 4 2
2x 3y 7
() 2 x y 4
2 y 3
3
y
2
3
2 x 3
7
2
9
2x 7
2
2x 7
9 14 9 5
2
2
2
5
5
x 2
2 4
5
x
4
Prueba
5 3
2 3
7
4 2
10 9
7
4 2
10 18
7
4
28
7
4
77
90
CURSO DE SELECCIÓN 2016
4.2.2
Método de sustitución
2 x 3 y 7 de 1 2 x 7 3 y
7 3y
3x y 7
x
2
7 3y
3
y 7
2
21 9 y
y7
2 x 3(1) 7
2
21 9 y 2 y
7
2x 7 3 4
2
4
21 7 y 14
x 2
2
7 y 14 21 7
x2
7
y
1
7
y 1
4.2.3
Método de determinantes
2x 3y 7
3x y 7
73
7 1
7 21 14
x
2
23
29
7
3 1
x2
y
2 7
37
7
y 1
14 21
1
7
91
CURSO DE SELECCIÓN 2016
4.2.4 Método de igualación
2x 3y 7 1
3x y 7 2
de ecuación 1
2x 7 3y x
7 3y
2
de ecuación 2
3x 7 y x
7y
3
xx
7 3y 7 y
2
3
3(7 3 y ) 2(7 y )
21 9 y 14 2 y
9 y 2 y 14 21 7
7
7 y 7 y
7
y 1
sust.en 1
2 x-3 y 7
2 x-3(-1 ) 7
2x 7 3 4
x2
.
Diga si los sistemas que siguen son consistentes, inconsistentes o dependientes.
1)
4 x 12 y 3 1
1
1
x y 32
3
3
4 x 12 y 3
12( x y 9)
4 x 12 y 3
12 x 12 y 108
16 x 111 x
111
16
111
4
12 y 3
16
111
99
12 y 3
4
4
33
y
16
El sistema es consistente.
92
CURSO DE SELECCIÓN 2016
2)
2
y x 5 1
2 x 3 y 15
3
2 x 3 y 15 2 2 x 3 y 15 El valor de x depende de y
Por lo que el sistema es dependiente o equivalente.
3)
x y 3 1
x y 3
1
1
1
1
x y 1 23 x y 1
3
3
3
3
x y 3
x y 3
______________
00 6
Inconsistente
Despeje de los sistemas el par común (x, y), en términos de c.
9
x c 3c
2
9
6c 9c 3
x 3c c
c
2
2
2
x y 6c 1
3
x c
x
y
3
c
2
2
4)
2 y 9c
9
y c
2
93
CURSO DE SELECCIÓN 2016
Resolver cada una de los siguientes
sistemas de ecuaciones lineales
1. 2x + y = 6
-3x + 2y = 5
2. 2x + 3y = 12
3x + 2y = 12
3. 1/3x + 2/5y = 4
7x + 3y = 27
4. x + 2y = 5
-3x + 10y = -7
5.
4x - y = 6
2x + 3y = 10
6. 16x - 5y = 103
7x + 19y = -188
7. x/2 + y/6 = ½
0.2x – 0.3 = 0.2
8. 2(x-y-1) = 1 – 2x
6(x – y) = 4 – 3(3y – x)
9. 2x - y = 19
-x = -5 - 2y
10. a – 6b = 11
5a – 15b = 10
11. 7x + 21y = 10
14x -7y = -1
12. 3a + 5b = 21
a – b = -5
13. 6a + 2b = 14
-2a – b = 7
94
CURSO DE SELECCIÓN 2016
PROBLEMAS DE ECUACIONES
1. ¿Cuál es el valor de cada figura?
12
18
10
2. Paty y Ramón tenían la misma cantidad de dinero, pero compraron revistas de igual precio. Si Paty
adquirió 5 revistas y le quedaron $15 y Ramón compró 3 y le sobraron $29, ¿Cuánto cuesta cada revista?
3. En la panadería, Pablo pagó $ 500 por 5 barras de pan y 3 donas. Si Carina pagó $ 190 por 2 barras de
pan y 1 donas, ¿cuál es el precio de la barra de pan y el de las donas?
4. En el país del trueque, 1 auto y 1 velero se cambian por 1 casa; 1 velero se cambia por 1 auto y 1
departamento, 2 casas se cambian por 3 departamentos. ¿A cuántos autos equivale 1 velero?
95
CURSO DE SELECCIÓN 2016
5. Un hotel tiene habitaciones dobles y sencillas. En total hay 50 habitaciones y 87 camas. ¿Cuántas
habitaciones tiene de cada tipo?
6. En una tienda de anticuario hay 12 candelabros de 2 y 3 brazos. Para usarlos se necesitan 31 velas,
¿cuántos hay de cada tipo?
7. Hoy la edad de un hijo es 1 año menos que 1/3 de la de su madre. Si dentro de 5 años, la edad de la
madre será 10 años mayor que el doble de la de su hijo, ¿qué edad tienen?
8. Una alberca rectangular de ancho igual a 2/3 de su largo está rodeada por una barda. Entre la barda y la
alberca hay 1 metro de jardín alrededor de todo el perímetro de la alberca. Si el perímetro de la barda
es de 58 m, ¿Cuáles son las dimensiones de la alberca?
9. Un ejercicio realizado en clase consta de 16 cuestiones. El profesor suma 5 puntos por cada respuesta
correcta y resta 3 puntos por cada cuestión incorrecta o sin contestar. Si un alumno ha obtenido 32
puntos en el ejercicio, ¿cuántas cuestiones ha contestado correctamente?
10. Dos números suman 51. Si el primero lo dividimos entre 3 y el segundo entre 6, los cocientes se
diferencian en 1. Halla los números.
96
CURSO DE SELECCIÓN 2016
11. Un comerciante compró dos relojes distintos por $ 3.000. y los vendió por $ 3.225. ¿Cuánto pagó por
cada reloj si en la venta del primero ganó un 20% y en la del segundo perdió un 5 %?
12. Calcular las edades de un abuelo, un padre y un hijo. La edad del padre es el triple que la del hijo, las
edades del padre y del abuelo suman 102, y 5 veces la edad del hijo excede en 10 años la del abuelo.
13. Un hombre cercó un terreno cuyo perímetro es de 400 m y por el cual pagó $ 3720. El frente del terreno
mide 60 m. El precio por cada metro de la cerca frontal es $2 más caro que el precio por cada metro del
resto de la cerca. ¿Cuál es el precio de cada metro para la cerca frontal y para el resto de la cerca?
14. En una canasta hay manzanas, peras, naranjas y plátanos. Hay 44 frutas en la canasta. Hay 2 manzanas
más que peras. Hay 8 peras más que plátanos. Hay dos plátanos más que naranjas. ¿Cuántas manzanas
hay en la canasta?
15. Un oficinista compra 30 objetos entre lápices y bolígrafos con un costo de $ 124 Si los lápices cuestan $
2.5 y los bolígrafos $ 6 ¿cuántos bolígrafos y lápices compró?
16. Encuentra dos números sabiendo que la mitad de su suma es 218 y el doble de su diferencia es 116.
97
CURSO DE SELECCIÓN 2016
17. Escribe un sistema lineal de dos ecuaciones y dos incógnitas que tenga como soluciones x = 5; y = -2.
18. Un padre quiere repartir el dinero que lleva en el bolsillo entre sus hijos. Si a cada hijo le da $ 700 le
sobran $ 200 pero si le da a cada uno $ 800 le faltan $ 200. ¿Cuánto dinero lleva en el bolsillo y cuántos
hijos tiene?
19. Calcula el valor de una cinta de vídeo y un CD si 2 cintas de vídeo y un CD valen $70 y 4 cintas de vídeo y
2 CD valen $100.
20. María y Juan fueron a la tienda. María pagó $17 por 5 dulces, 1 chocolate y 3 galletas. Juan pagó $16
por 2 dulces, 2 chocolates y 1 galleta. Si el precio de cada chocolate es el triple que el de una galleta,
¿Cuánto cuestan los dulces, los chocolates y las galletas?
21. Una caja contiene clavos, tornillos y tuercas. El número de clavos es el triple que el de tornillos y la
cantidad de tornillos es tres veces el de tuercas. ¿Cuántos clavos tornillos y tuercas hay en la caja si en
total existen 1872 objetos?
98
CURSO DE SELECCIÓN 2016
5
5.1
Operaciones algebraicas
5.1.1
Álgebra
Suma o adición
Es una operación algebraica que tiene por objeto reunir dos o más expresiones. En la práctica los polinomios
se pueden solucionar colocándose uno debajo del otro en columna.
Ejemplo:
5.1.2
Resta o sustracción
Es una operación que tiene por objeto, dada una suma de dos sumandos (minuendo) y uno de ellos
(sustraendo), hallar el otro sumando (resta o diferencia). En la resta algebraica hay que restar del minuendo
cada uno de los términos del sustraendo.
Ejemplo: de
restar
Efectuar la operación indicada:
Suma de monomios y polinomios
1.
2.
3.
Sustracción de monomios y polinomios
4.
5.
6.
99
CURSO DE SELECCIÓN 2016
4.1.3
Multiplicación de polinomios
Es una operación que tiene por objeto, dadas las cantidades llamadas multiplicando y multiplicador, hallar
una tercera cantidad llamada producto.
El producto de dos o más monomios es otro monomio obtenido a través de:
1) La ley de los signos
2) El producto de los coeficientes.
3) El producto de las variables de acuerdo con las leyes de los exponentes.
Ejemplo:
Multiplicar
Para encontrar el producto de un monomio por un polinomio, se multiplica el monomio por todos y cada
uno de los términos de polinomio.
Ejemplo:
Multiplicar
Para determinar productos entre polinomios, se aplica la propiedad distributiva. Esto es, se multiplica cada
término de uno de los polinomios por los términos del otro.
Ejemplo:
Multiplicar
Efectúa la operación indicada:
1.
2.
3.
4.
5.
6.
100
CURSO DE SELECCIÓN 2016
5.1.4
División de polinomios
Es una operación que tiene por objeto dado el producto de dos factores (dividendo) y uno de los factores
(divisor) hallar el otro factor (cociente).
Ejemplo:
1)
Dividir
3a 3 6a 2 b 9ab 2 entre 3a
3a 3 6a 2 b 9ab 2
a 2 2ab 3b 2
3a
2)
Dividir
11a 3 3a 5 46a 2 32 entre 8 3a 2 6a
Se ordenan los polinomios y se efectúa la división
3a 2 6a 8 3a 5
a 3 2a 2 3a 4
11a 3 46a 2
32
3a 5 6a 4 8a 3
6a 4 3a 3 46a 2
6a 4 12a 3 16a 2
9a 3 30a 2
32
9a 18a 24a
3
2
12a 2 24a 32
12a 2 24a 32
0
Efectúa la operación indicada:
1.
2.
3.
4.
101
CURSO DE SELECCIÓN 2016
5.
6.
7.
5.2
Productos notables y Factorización
5.2.1
Productos notables
Se llama productos notables a ciertos productos que cumplen reglas fijas y cuyo resultado puede ser escrito
por simple inspección; es decir sin efectuar la multiplicación.
Cuadrado de un binomio:
Es el cuadrado del primero más el doble producto del primero por el segundo más el cuadrado del segundo.
Cubo de un binomio:
El cubo de la primera cantidad más el triple producto del cuadrado del primero por el segundo más el triple producto del
Efectúa los
notables
siguientes
productos
1.
2.
3.
4.
5.
6.
102
CURSO DE SELECCIÓN 2016
5.2.2
Factorización
El proceso de escribir un número o una expresión algebraica como el producto de otros números o
expresiones algebraicas se denomina factorización.
Ejemplos:
1.
2.
Fórmulas especiales:
. Se usa para factorizar trinomios de la forma
, para lo cual, se buscan dos números que sumados den el coeficiente de x y multiplicados den
el término constante.
Ejemplos:
Trinomio cuadrado perfecto: Una cantidad es trinomio cuadrado perfecto si es producto de dos factores
iguales,
Ejemplo:
Diferencia de cuadrados: Es el producto de los binomios conjugados,
Ejemplos:
Factoriza las siguientes expresiones
algebraicas
1.
2.
3.
4.
5.
6.
7.
103
CURSO DE SELECCIÓN 2016
Diferencia de cubos:
Ejemplos:
1.
2.
3.
Suma de cubos:
Ejemplo:
4.
Diferencia de dos enésimas potencias:
Ejemplos:
5.
6.
Factorización por factores comunes
Ejemplos:
7.
Factorización por agrupamiento
Ejemplos:
Factorización por el método de completar el cuadrado: se completa el cuadrado sumando y restando
el mismo término algebraico y se resuelve por diferencia de cuadrados
Ejemplo:
104
CURSO DE SELECCIÓN 2016
Factoriza las siguientes expresiones
algebraicas
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Trinomios de la forma
, se diferencia al trinomio cuadrado perfecto en el coeficiente de x.
Para Factorizar se multiplica el trinomio por el coeficiente del término cuadrático, posteriormente se buscan
dos números que multiplicados den el término constante
y sumados den el término lineal
Finalmente se divide entre el número descompuesto en n factores y que son divisibles entre ellos.
Ejemplo:
Factorizar
Efectúa las siguientes factorizaciones:
1.
2.
3.
4.
5.
105
CURSO DE SELECCIÓN 2016
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23. –y – x +1 + xy
24. ax + by + ay + bx
25.
26.
27.
28.
a 3 x b3 y b3 x a 3 y
29.
106
CURSO DE SELECCIÓN 2016
30.
31.
32.
33.
34.
35.
36. 2( x 2) 2 2 x 13x 2
2
37.
38.
39.
40.
41.
107
CURSO DE SELECCIÓN 2016
5.3
5.3.1
Fracciones algebraicas
Operaciones con fracciones (operaciones básicas)
Suma y resta (regla general):
1.
Se simplifican las fracciones dadas si es posible.
2.
Se obtiene el mínimo común denominador.
3.
Se efectúan las operaciones indicadas.
4.
Se suman los numeradores de las fracciones que resulten y se parte esta suma por el denominador
común.
5.
Se reducen términos semejantes en el numerador.
6.
Se simplifica la fracción si es posible.
Ejemplo:
Fracciones con denominadores compuestos, para encontrar el mínimo común denominador se factoriza
cada fracción.
Ejemplo:
El factor común proviene de la factorización de cada uno de los denominadores:
108
CURSO DE SELECCIÓN 2016
Efectúa la operación indicada:
1.
2.
3.
4.
5.
6.
Efectuar la operación indicada:
Multiplicación
Ejemplo:
División
Ejemplo:
109
CURSO DE SELECCIÓN 2016
Efectúa la operación indicada:
1.
2.
3.
4.
5.
6.
7.
110
CURSO DE SELECCIÓN 2016
5.4 Ecuaciones cuadráticas
Una ecuación cuadrática en una variable es cualquier ecuación que se pueda escribir de la forma:
ax 2 bx c 0
Por ejemplo: f(x) = -3x2 + 4x + 1
a0
g(x) = 7x2 - 4
h(x) = x2
La ecuación cuadrática más simple es f(x) = x2 . la gráfica de ella servirá como base para trazar la
gráfica de cualquier función cuadrática como ax2 + bx + c. cuando se ubican esos puntos en un
sistema de coordenadas rectangulares y se unen con una curva uniforme, se obtiene la gráfica de
f(x) = x2.la curva se llama parábola y toda ecuación cuadrática ax2 + bx + c tiene una parábola
como gráfica.
Parábola
Definición
La parábola es el conjunto de puntos en un plano que equidistan de una línea particular (la
directriz) y un punto particular (el foco) en el plano.
5.4.1 Gráfica: Eje de simetría, foco, vértice y concavidad
1. Gráfica de la parábola
1. Eje de simetría, foco, vértice y concavidad
5.4.1Forma estándar
2. Forma estándar:
, vértice en
, eje de simetría en
.
Cuando una función cuadrática está expresada en la forma ax2 + bx + c, algunas de las
propiedades de sus gráficas no son evidentes. Sin embargo, si se convierte esa función a la forma
estándar se puede trazar la parábola.
Ejemplo
y = x2 + 4x + 3
La reformulamos para obtener un trinomio cuadrado perfecto:
y = (x + 4x + __?__) + 3
en el signo de interrogación escribimos (para completar el cuadrado perfecto) el cuadrado de la
mitad de b, y lo restamos fuera del paréntesis y con esto obtenemos la forma estándar.
y = (x2 + 4x + 4) + 3 - 4
y = (x + 2)2 - 1
forma estándar
111
CURSO DE SELECCIÓN 2016
A esta técnica se le llama completar el cuadrado.
La gráfica de e la ecuación anterior es una parábola con vértice en (-2, -1) y su eje de simetría es x
= -2
Para determinar las abscisa al origen de la parábola, se obtienen los valores de x, o raíces de la
ecuación f(x) = 0, también se les llama ceros de la función f(x).
Ejemplo:
Determinar las abscisas al origen de la parábola:
6 x 2 19 x 7 0
Se puede resolver por factorización de la siguiente forma:
36 x 2 196 x 42 0
6 x 21 6 x 2
3
2
2 x 7 3x 1 0
2x 7
7
x
2
3 x 1
1
x
3
Se puede resolver por la fórmula general
b b 2 4ac
2a
x
x
19
19 486)8 7) 19
2
26
x1
19 23 42 7
12
12 2
x2
19 23 4
1
12
12
3
361 168 19 23
12
12
112
CURSO DE SELECCIÓN 2016
Resolverlos siguientes ejercicios usando la fórmula general
1)
2)
2 x 2 8x 3 0
x 2 10 x 3 0
Solución por raíz cuadrada
Para ecuaciones de la forma
ax 2 c 0
1)
2x 2 3 0
2x 2 3
3
x2
2
x
3
2
Resolver los siguientes ejercicios
1) 3 x 2 27 0
Sol. 3
2
1
5
2) x
2
4
3) 3 x 2 5 0
x
Sol.
Sol. x
1 5
2
5
3
Pasar a la forma estándar y ax h k
2
y x 2 2 x 5 x 2 2 x 1 6 x 1 6
2
4) Identificar coordenadas del vértice, ecuaciones del eje de simetría y la ordenada en el origen.
y x 2 2 x 1 y x 2 2 x 1 2 V 1,2 ; eje x 1
y x 1 2
2
p / x 0 y 1 2 1
ordenada en el origen 1
113
CURSO DE SELECCIÓN 2016
5) Resuelva por factorización
x 2 5 x 6 0 x 2 x 3 0
x1 2 & x2 3
6) Resuelva completando el cuadrado
x 2 4 x 1 0 x 2 4 x 4 1 4 0 x 2 3 0
x 2 2
2
3
x2 3
x 2 3
7) Determine las abscisas al origen.
y 2 x 2 5x 3
( x 3)(2 x 1) 0 x1 3; x 2
1
2
4 x 2 5 x(2) 6
(2 x 6) (2 x 1)
2
1
8) Encontrar el tipo de solución de las siguientes ecuaciones
a) Número real
b) Dos números racionales
c) Dos números irracionales
a) x 2 8 x 16 0
( x 4)( x 4) 0 x 4 solución ( a)
b) x 2 2 x 15 0
x 2 2 x 15 0
( x 5)( x 3) x1 5 x2 3 solución b)
c)
x 2 3x 1 0
x
3 9 4 3 13
2
2
solución (c)
114
CURSO DE SELECCIÓN 2016
Determinar el vértice y el eje de
simetría de la siguiente función
1. f(x) = x2 - 6x + 7
2. f(x) = x2 - 2x + 9
3. f(x) = 2x2 + 8x - 1
4. f(x) = -x2 + x – 2
5. f(x) = - x2 - 6x + 2
6. f(x) = 2x2-4x +3
7. f(x) = x2 + 5x – 2
8. f(x) = - 3x2 - 6x + 5
9. f(x) = x2 - 9x
Determinar las abscisas al origen
1. y = 2x2 – 2x – 4
2. y = x2 + 3x – 10
3. y = x2 – x – 12
4. y = x2 – 5x + 6
5. y = x2 – 10x – 4
6. y = 2x2 – 5x – 3
7. y = x2 – 10x
8. y = 4x2 – 32x + 64
9. y = x2 - 9x
115
CURSO DE SELECCIÓN 2016
Realizar los siguientes ejercicios:
1. Considere la siguiente fórmula
hacia ____________________.
Obtenga su gráfica. Es una _________________ abierta
2. Considere la siguiente fórmula
Obtenga su gráfica. La __________________es
cóncava hacia ____________________.
3. Considere la siguiente fórmula
____________________. Obtenga su gráfica.
Es una parábola abierta hacia
4. Considere la siguiente fórmula
____________________. Obtenga su gráfica.
La parábola es cóncava hacia
5. Determine las coordenadas del vértice de la parábola
Completar el cuadrado de
.
, se suma el cuadrado de la mitad de :
. Por consiguiente
Completando el cuadrado:
eje de simetría esta en
, vértice
, su
.
6. Determinar la concavidad de la parábola, su vértice y su eje de simetría si
.
.
Vértice:
. Eje de simetría en
.
7. Determine las intersecciones con el eje
de la parábola
.
Las intersecciones con el eje son -2 y 3. A estos puntos también se les llama raíces de la
ecuación
, y también se les llama ceros de la función
.
8. Localizar el vértice y el eje de simetría, y grafique la curva de la parábola
¿Cuál es su concavidad?
.
Completando el cuadrado:
Vértice:
116
CURSO DE SELECCIÓN 2016
Eje de simetría:
, la curva es cóncava hacia arriba.
9. Determine las intersecciones con el eje
de la parábola
Las coordenadas del punto de intersección son:
10. Encuentre los puntos de intersección con el eje
c) Grafique .
11. Resuelva
12. Grafique
.
.
de
.
.
, y determine los valores de tal que
13. Muestre de forma gráfica que la ecuación cuadrática
números reales.
.
notiene solución en los
La gráfica de
está por arriba del eje para todos los valores de . Por
consiguiente la ecuación no tiene solución en los números reales.
117
CURSO DE SELECCIÓN 2016
BIBLIOGRAFIA
[1] Sobel Max y Lerner N. Precálculo.5ª ed. Pearson, Álgebra y trigonometría con Geometría
Analítica. Walter Fleming. Dale Varberg. 3ª ed. Prentice- Hall
[2] Ramírez A. Margarito (2010).Matemáticas I para el desarrollo de competencias. México:B.SLP
[3] Courand Richard, Robins, Herbert ¿Qué son las matemáticas? FCE 2002.
[4] Florence M. Lovaglia, Merritt A. Elmore, Donald Conway, Algebra, ed, Harla, 1a edicion, 1972
[5] Santos, Trigo Luz Manuel., Principios y métodos de la resolución de problemas en el
aprendizaje de las matemáticas, editorial Iberoamérica 2000.
[6] Rivaud, Morayta Juan José. Trigonometría. Editorial Limusa, 2001.
[7] Rivaud, Morayta Juan José. Geometría Intuitiva 2, Áreas, Volúmenes y Centros de Gravedad.
Editorial Limusa, 1988.
[8] Enzerberger, Hans Magnus. El Diablo de los Números. 7ª Ed. España, Sirvela, 1999
[9] Stanley L. Grossman, Matemáticas algebra lineal, ed. Mac Graw Hill, 2011, ISBN: 978-970-106517-4.
118