practica de mecanica 1

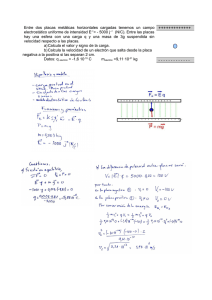
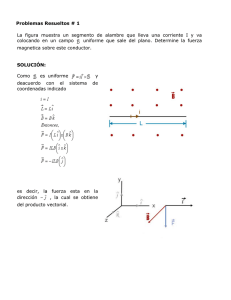
Física III
( Lic.en Física )
http://www.fceia.unr.edu.ar/~fisica3
Práctica de problemas
1
INTERACCIÓN ELÉCTRICA
César A. Ramírez
1) Tres cargas puntuales q1, q2 y q3 (q2 = -q1 con q1>0) están equiespaciadas a lo largo
de una línea con q2 en el centro. Calcular el signo y el valor de q3 a fin de que la
fuerza resultante sobre q1 sea nula.
2) Encontrar la fuerza eléctrica de repulsión, entre dos protones, en una molécula de
-10
hidrógeno, siendo la separación entre los mismos 0.74 x 10 m. Compararla con la
fuerza de atracción gravitacional correspondiente.
3) Cuatro cargas se encuentran ubicadas en los vértices de un cuadrado de 5 cm de
lado. Calcular la fuerza resultante sobre la carga q3 si
q1=10-7 coulomb, q2 = 2q1, q3 = -2q1 y q4 = -q1
4) Dos esferas idénticas de masa m y con igual carga q están suspendidas del mismo
punto por medio de dos cuerdas de longitud l. Encontrar el ángulo que las cuerdas
forman con la vertical, una vez logrado el equilibrio. Obtener el resultado que
corresponde a un ángulo pequeño, respecto a la vertical (aproximar la tg del ángulo
por el seno del mismo ángulo).
5) Entre dos placas planas paralelas, muy próximas, cargadas con cargas iguales pero
de signo opuesto, se forma un campo eléctrico uniforme. De la superficie con carga
negativa se libera un electrón que luego choca con la placa positiva, distante 2cm
de la primera. El tiempo empleado en recorrer esa distancia es de 1.5 x 10 -8
segundos. a) Calcular el campo eléctrico , b) Calcular la velocidad del electrón al
chocar con la placa.
6) Un electrón se lanza con una velocidad inicial de 2 x 10 6 m/s desde un punto
equidistante a las placas deflectoras de un tubo de rayos catódicos, en dirección
paralela a las placas. Entre las placas hay un campo eléctrico uniforme de 200 N/c.
Calcular : a) la distancia perpendicular al eje que ha recorrido el electrón cuando
pasa por el extremo de las placas. b) el ángulo que forma su velocidad con la
dirección de partida, cuando abandona las placas. c) La distancia por debajo de la
dirección de partida, a la que choca con una pantalla fluorescente F. La longitud de
las placas es de 10cm y la distancia de la pantalla a las placas es de 70cm.
7) Dos carga puntuales q1=10-6c y q2=3q1 están ubicadas sobre el eje x a una distancia
entre ambas de 10 cm. Calcular el campo eléctrico sobre el eje x , en función de x.
Considerar el campo positivo cuando apunta hacia la derecha y negativo cuando
apunta hacia la izquierda.
8) Calcular el campo eléctrico en los puntos del eje x, producido por un alambre de
longitud L, con un distribución uniforme de carga, ubicado sobre ese eje de
coordenadas. Repetir el cálculo para una distribución de carga no uniforme
dependiente de la variable x.
9) Calcular el campo eléctrico en todo el espacio, producido por un alambre recto de
longitud L con una distribución de carga uniforme λ , ubicado sobre el lado positivo
del eje x desde el origen de coordenadas. Demostrar que las componentes de dicho
campo son:

E x (x,y)  (cos 2 -cos1 )
4 0 y

4 0 y
Donde θ1 es el ángulo que forma la línea vertical que va desde el punto (x,y)
hasta el eje x, y la recta que va desde ese punto al origen de coordenadas y θ 2 es el
ángulo que forma con la recta que va desde ese punto al otro extremo del alambre
cargado.
Un alambre semicircular está cargado con una carga Q distribuida uniforme. Hallar
el campo eléctrico en el punto central de la circunferencia donde se apoya.
Calcular el campo eléctrico en un punto del eje de un anillo cargado uniformemente.
Calcular el campo eléctrico en un punto del eje de una corona circular de radio
interior R1 y radio exterior R2. Deducir del resultado el campo eléctrico de un círculo
de radio R.
A partir del campo eléctrico de un círculo de radio R obtener el campo eléctrico
producido por una superficie plana cargada uniformemente en un punto muy
próximo a la superficie.
Calcular el campo eléctrico en la zona central de dos planos muy próximos
cargados uniformemente, dentro y fuera de las placas, con a) cargas iguales y b)
opuestas.
El potencial a una distancia r de una carga puntual q es de 600V y el campo
eléctrico es de 200 N/c. a) Cuál es la distancia r, b) Cuál es la carga q.
Una pequeña esfera de 0,2 g cuelga de un hilo entre dos placas paralelas verticales
separadas por 5 cm. La esfera tiene una carga de 6x10-9c. ¿Cuál es la diferencia
de potencial entre las placas si el hilo forma un ángulo de 10º con la vertical?.
Indicar en un esquema cuál es la placa con mayor potencial.
Dos cargas puntuales de 2x10-7c y 3x10-7c están separadas por una distancia de
0,1 m. Calcular el campo eléctrico que producen y el potencial eléctrico, en: a) el
punto medio de la distancia que las separa, b) un punto situado a 0,04 m de la
primera, sobre la recta que pasa por ambas pero fuera del segmento que las une. c)
¿En qué punto el campo eléctrico es cero?. Graficar en forma cualitativa las líneas
de campo y las líneas equipotenciales.
Dos cargas positivas iguales están fijas sobre el eje y en los puntos
correspondientes a y=a , y=-a. a) Trazar un diagrama y calcular el potencial en el
origen. b) Probar que el potencial en cualquier punto del eje x es
2q
V
4 0 a2  b 2
y graficarlo entre –5a y 5a . c) ¿Para qué valor de x el potencial tiene la mitad de su
valor en el origen?. d) A partir del potencial obtener el campo eléctrico sobre el eje
x.
Dos cargas de signos opuestos, separadas una distancia d forman un dipolo
eléctrico. Expresar el potencial eléctrico y el campo en cualquier punto del espacio a
distancias del dipolo mucho mayores que d. Emplear coordenadas polares.
Una corona circular de radio interior R1 y radio exterior R2 tiene una carga total Q.
Calcular el potencial eléctrico en un punto cualquiera el eje perpendicular al plano
de la corona. A partir del resultado obtener el campo eléctrico sobre esos puntos.
Obtener el potencial y el campo eléctrico sobre los puntos del eje de un disco de
radio R a partir del problema anterior.
Una carga –q de masa m se libera a una distancia z de un plano cargado
positivamente con una densidad de carga σ. Calcular: a) su aceleración, b) la
velocidad con que incidirá en el plano y c) el tiempo transcurrido.
Tres cargas positivas de 2x10-7c, 1x10-7c y 3x10-7c están alineadas sobre una recta
separadas 0,1 m, con la segunda carga en el centro. Calcular: a) la energía
E y (x,y)  -(sen 2 -sen1 )
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
21)
22)
23)
24)
25)
26)
27)
potencial de cada carga debida a las otras. b) La energía potencial interna del
sistema. Comparar ambos resultados e interpretar físicamente.
Dos cargas puntuales positivas y de igual magnitud están fijas sobre el eje y en los
puntos con y=a, y=-a. Una tercera partícula de masa m y carga q ubicada en el
origen se separa ligeramente de su posición de equilibrio, en la dirección del eje x, y
se suelta. a) ¿Cuál es su velocidad cuando alcanza una distancia mucho más
grande que a? , b) Obtener una expresión de la velocidad en función de la
coordenada x, y graficarla. c) Buscar el punto de máxima aceleración. d) Si la
partícula es lanzada desde una gran distancia sobre el eje x en dirección al origen
con la mitad de la velocidad obtenida en el primer punto, ¿a qué distancia del origen
se detiene?. e) Si una partícula con carga –q es liberada en un punto muy
distanciado del eje x, ¿con qué velocidad llega al origen de coordenadas?.
En un modelo aproximado puede suponerse que el electrón del átomo de hidrógeno
se mueve alrededor del núcleo (un protón) sobre una órbita circular de radio 0,53 x
10-10m. Calcular: a) La energía potencial del electrón, su energía cinética y su
energía mecánica total. b) El número de vueltas por segundo y la frecuencia angular
de su movimiento.
Un triodo consiste en dos placas paralelas separadas 15 cm con una grilla plana
ubicada entre ellas a 3 cm de una de ellas. Desde una de las placas (cátodo) se
emiten electrones con velocidades despreciables. La otra placa (ánodo) se
encuentra a un potencial de 15V respecto al cátodo y la grilla se encuentra a 18 V
respecto al cátodo. a) Trazar un diagrama del potencial y calcular el campo eléctrico
en cada zona, dentro del triodo, b) Calcular las velocidades de los electrones
emitidos al atravesar la grilla y al chocar con el ánodo.
Un acelerador lineal con una diferencia de potencial de 800 KV produce una
corriente de protones de 1mA. Calcular: a) El número de protones por segundo
emitidos, b) La potencia requerida, c) La velocidad final de los protones.
Suponiendo que los protones pierden el 80% de su energía al chocar con el blanco,
calcular la rapidez con que debe removerse la energía del blanco (refrigerarse).