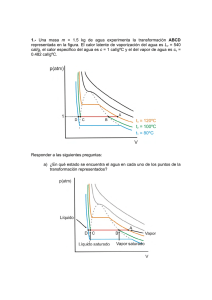
sugerencias relacionadas con el desarrollo de balances de

1
UNIDAD 2
BALANCE DE ENERGÍA
Ing. VICTOR JAIRO FONSECA V.
2
Objetivos
Conocer las leyes fundamentales de la termodinámica, definir los conceptos de
energía y establecer el balance general de la energía.
Definir los conceptos de energía.
Definir los conceptos de calor sensible y calor latente.
Definir los conceptos de calor de formación, calor de reacción, calor de
disolución, calor de mezcla y calor de combustión.
Establecer los balances de energía para un sistema.
Resolver problemas relativos a los balances de energía en proceso alimenticios
3
4 Introducción
Para un científico el concepto más importante lo constituye la energía. En todos
los fenómenos científicos y en todo lo que ocurre, interviene la energía.
Los acontecimientos físicos, desde el desarrollo de una nebulosa, hasta los
movimientos de una bacteria, consisten fundamentalmente en transformaciones
de energía.
Si bien la energía no puede ser tocada ni vista, su presencia es detectada a cada
instante. El hombre, desde sus orígenes hasta el presente, ha logrado
sorprendentes progresos, desde el fuego hasta la fisión nuclear.
La vida del ser humano depende directamente de las transformaciones que se
producen en los procesos energéticos de la respiración y del metabolismo de los
alimentos.
El estudio de la energía abarca el mecanismo motor del universo en
innumerables aspectos.
sus
El concepto de energía está íntimamente ligado al de trabajo. Se puede, incluso,
decir que energía es la magnitud que mide la capacidad que tiene un sistema para
realizar un trabajo. La definición científica de trabajo expresa bien el concepto
intuitivo que todos tenemos: para ejecutar un trabajo es necesario aplicar una
fuerza sobre un cuerpo y desplazarlo. Se actúa de ese modo para levantar un
cuerpo cualquiera, o incluso para aserrar el tronco de un árbol.
Las aguas de una catarata tienen energía; después del impacto contra el fondo
pierden velocidad y se mueven lentamente al transformarse parte de su energía;
el efecto de esta transformación se aprecia en lo erosión de las rocas contra las
cuales choca el agua.
Un proyectil en movimiento tiene energía y esta puede ser de tal magnitud que al
chocar contra una coraza, la perfora.
En un trozo de hierro calentado al rojo hay energía y, si se le sumerge en un
líquido, este se caliente y, en ocasiones, parte del líquido se transforma en vapor.
Un rayo de luz transporte energía y puede aumentar la energía calórica de un
cuerpo elevando su temperatura. Una corriente eléctrica mueve un motor y éste
produce un trabajo, o al pasar por una resistencia genera calor.
Los procesos de adecuación de alimentos, desde su fuente primaria en la
naturaleza hasta su presentación para consumo inmediato, obedecen a
transformaciones de orden físico y/o químico, en los cuales ocurre intercambios
de masa y energía.
El crecimiento de las plantas, su floración y fructificación obedecen a fenómenos
en los que interviene la energía, en su forma lumínica. Todo vegetal de consumo
humano o animal contiene almacenada y en la cadena alimenticio plantas-animalhombre, ocurren intercambios de energía.
Ing. VICTOR JAIRO FONSECA V.
4
Una de las formas más elementales de preparación de alimentos tiene lugar en
los sencillos procesos de cocción, en donde los alimentos se hacen más digeribles
o se mejora su sabor, igualmente se esterilizan o se preservan.
En todos los hogares del mundo se acostumbra a cocer determinados alimentos:
la energía en su forma de calor constituye el mecanismo de transformación más
importante para los alimentos, ya a nivel doméstico, ya a escala industrial.
El calor interviene en la industria de enlatados, tanto para cocer como para
esterilizar los alimentos.
En la industria láctea pasos importantes son la pasterización lograda con el calor;
multitud de alimentos se preservan secándolos, empleando calor para retirar la
humedad presente.
Inmensos gastos se evitan transportando productos concentrados obtenidos en
evaporadores o cristalizadores.
Licores se obtienen por destilación de mostos y en la industria de bebidas
fermentadas los mostos se obtienen por cocción de las materias primas
farináceas.
La industria panificadora demanda inmensas cantidades de calor, en fin, salvo los
productos de origen vegetal y de consumo inmediato, todos los alimentos están
íntimamente asociados a fenómenos caloríficos o energéticos, producidos o
dirigidos por el hombre.
Los procesos no solamente demandan calor, en muchos casos se requiere
retirarlo, como en el enfriamiento de alimentos pasterizados, la liofilización
(evaporación por congelación y disminución rápida de la presión, lo que causa la
sublimación del agua); bajas temperaturas se requieren para madurar cervezas y
vinos e igualmente, para preservar lácteos y carnes.
Los fenómenos caloríficos son los de mayor concurrencia en la industria de
alimentos, pues permiten las transformaciones de orden químico, están
acompañados con intercambio o consumo de otros tipos de energía; inicialmente
la mecánica, para el movimiento y trabajo de los más variados y diversos equipos
de la industria. La energía eléctrica es, en su mayor parte, la responsable de los
trabajos mecánicos.
Procesos de esterilización, y para concluir procesos bioquímicos, emplean otras
formas de energía como los rayos ultravioleta o las microondas. Hasta la energía
nuclear se emplea hoy en la industria de alimentos. Interminable sería la lista de
procesos en los cuales interviene la energía en cualquiera de sus formas.
Debe usted, por lo tanto, tener un conocimiento adecuado de la energía y
disponer de las bases científicas para su correcto manejo. La crisis energética, por
el agotamiento de las fuentes de suministro, día tras día encarece los costos de
un proceso; tan solo un correcto uso de la energía permite optimizar las
operaciones básicas y economizar en los costos; cada vez más onerosos, que
5
tiene la industria de alimentos, igualmente permite competir con los países
industrializados, hacer accequibles a la población muchos alimentos de los que
hoy no se dispone, conservar los recursos del país, en fin, mejorar la calidad
humana sin detrimento del medio ambiente.
Estudios muy profundos se han efectuado sobre la energía; en el presente
capítulo, usted conocerá básicamente los aspectos de la energía que conciernen
a los balances energéticos y de masa; determinará las relaciones más importantes
de las propiedades termodinámicas de la materia, efectuará balances térmicos y
adquirirá las bases para desarrollarlos a nivel de las principales operaciones
unitarias que tienen cabida en la Industria de Alimentos.
Hasta principios del siglo XIX solo se entendía por energía la energía mecánica,
es decir cinética y potencial. La comprobación de que la energía cinética puede
transformarse en calor abrió el camino para nueva ideas acerca de tan importante
tema.
Al mezclar dos sustancias a temperaturas diferentes, la mezcla llega a una
temperatura de equilibrio situada entre las dos temperaturas iniciales. Los
científicos de ese entonces explicaban el fenómeno, atribuyendo en los cuerpos la
existencia de una sustancia llamada “Calórico”. De acuerdo a tal teoría, una
sustancia de elevada temperatura tienen mucho calórico, mientras otro cuerpo
cuya temperatura fuese baja, tendría poco calórico.
Según el razonamiento de aquellos científicos, cuando dos cuerpos se ponen en
contacto, el más rico en calórico transfiere una parte de sus reservas al otro.
La teoría del “calórico” fue desplazada por aquella otra, válida hoy en día, que
considera el calor como una forma de energía. Benjamín Thompson conde de
Rumford, natural de Baviera, Alemania, contribuyó con sus observaciones, en una
fábrica de cañones, a plantear esta nueva teoría, que fue desarrollada años
después por los trabajos de Julius Von Meyer, Hermann Von Helmholtz y James
P. Joule.
Joule, con sus trabajo, contribuyó en 1843, a establecer la ley de conservación de
la energía tal como la conocemos. Sus experimentos con sistemas aislados,
demostraron que la relación entre la cantidad de calor producida en un proceso y
la cantidad de trabajo realizado era constante. A medida que se progresaba en los
procesos de la transformación de la energía, se encontraban limitaciones en lo
referente a la dirección en que un proceso tiene lugar, o cual lejos puede un
proceso llegar a ser completo.
El desarrollo de una ley limitante nació en 1824, con los trabajos teóricos de Sadi
Carnot relacionados con la conversión de calor en trabajo en una máquina térmica
y con los desarrollados por Lord Kelvin en sus experiencias sobre calor y trabajo.
Kelvin expresó lo que conoce como segundo principio o segunda Ley de la
Termodinámica. “No es posible, sin permanentes alteraciones en el sistema o en
el ambiente, transformar totalmente cierta cantidad de calor en trabajo”.
Ing. VICTOR JAIRO FONSECA V.
6
Otro de los enunciados del segundo principio se debe a Clausius:” El calor de los
cuerpos que están a mayor temperatura pasa espontáneamente a aquellos cuya
temperatura es menor”.
En virtud de ese principio, cuando dos cuerpos, inicialmente a temperaturas
diferentes son puestos en contacto tienden a alcanzar la misma temperatura; lo
contrario es decir que cuerpos cuyas temperaturas iniciales sean las mismas
evolucionen
hasta
adquirir
temperaturas
diferentes,
nunca
ocurre
espontáneamente.
La mayoría de las leyes en las ciencias, se nombran acorde al científico que las
ha formulado, pero en la termodinámica, ellas simplemente se numeran en razón
de la gran cantidad de científicos que han contribuido a su formulación. La
numeración no corresponde al orden cronológico de su desarrollo, la segunda ley
fue postulada antes que la primera.
La ley de conservación de la energía, se conoce como la primera ley de la
termodinámica y su aplicación conlleva cálculos de energía, relacionados con toda
clase de procesos.
La tercera ley de la termodinámica se refiere a las propiedades de los sistemas
para el cero absoluto de temperatura. En la mayoría de los casos, es posible
emplear la primera y segunda Ley para calcular solo las cantidades relativas o
cambios en las propiedades durante un proceso. El uso directo de la tercer ley es
raramente necesario en trabajos de ingeniería.
4.1. Primera ley de la termodinámica
La Primera Ley de la Termodinámica o ley de conservación de la energía, se
expresa en forma similar a la ley de conservación de la materia: “En cualquier
proceso ordinario físico o químico, la energía no se crea ni se destruye”.
En forma similar a la ley de conservación de la materia, la primera ley de la
termodinámica se relaciona con cantidades que son complejas de describir. Esta
primera ley versa sobre energía, la cual puede tomar diversas formas; entonces,
se hace necesario definir varios conceptos antes de entrar a los procedimientos
matemáticos que son usados en los cálculos numéricos.
Un sistema es cualquier parte del Universo que se ha escogido para un estudio
en particular, y dependerá, desde luego, del problema particular a resolver y de
los datos disponibles. Una vez el sistema se ha escogido, el resto del universo se
denomina alrededores.
El uso de la palabra Universo es común en la terminología Termodinámica, se
interpreta para significar que los contornos serán tan inmensos que cualquier
efecto de la energía a estudiar estará confinado al sistema y sus alrededores.
Un sistema se describe especificando que está en un cierto estado, lo cual es otra
7
manera de decir que tiene ciertas propiedades. Así como un punto puede ser
localizado en el espacio por sus coordenadas matemáticas; el estado de un
sistema es descrito por parámetros termodinámicos, los que son valores
numéricos de cantidades mensurables o deducidas.
Dependiendo de la naturaleza del sistema, un determinado número de
propiedades deben ser dadas para especificar el estado del mismo. Con los gases
se requiere conocer su composición, la presión y temperatura para definir su
estado. También son significativas para el gas, aparte de su composición, la
presión del volumen o el volumen y la temperatura para igualmente, conocer su
estado.
Un sistema en un estado, puede ser cambiado a otro estado variando sus
propiedades.
Ejemplo 25
El agua a presión atmosférica y a temperatura de 60C está en estado líquido,
cuando la presión es la mitad de la atmosférica y su temperatura es de 80C el
agua se encuentra en forma de vapor o gas.
En este sistema se tiene un estado líquido, con propiedades iniciales: presión, una
atmósfera y temperatura de 60C, el líquido se cambia a vapor variando ambas
propiedades.
Ejemplo 26
El metano, en condiciones naturales, se encuentra en estado gaseoso,
conociéndose como condiciones naturales, la presión y temperatura ambiente; a
presión de 20 atmósferas el metano es líquido. Se ha variado la presión para el
cambio de estado.
Volviendo a la Primera Ley de la Termodinámica, es conveniente que se tenga un
concepto muy claro de la energía. Ya definíamos a la energía como la capacidad
de hacer un trabajo y el trabajo se define matemáticamente como el producto de
una fuerza por el desplazamiento.
Empleándose la fórmula diferencial:
dw = Fdx
y
W =  Fdx
[5]
donde W es el trabajo, F la fuerza aplicada y dx el desplazamiento.
Cuando el desplazamiento dx es función de alguna variable y la fuerza es
constante, para el trayecto recorrido entre a y b.
W = F ab dx
La unidad de trabajo es el sistema m.k.s. es el Julio (j) o Newton-metro (N-m). En
el sistema internacional la unidad es la misma.
Solamente cuando la fuerza F actúa sobre la distancia dx, ocurre un trabajo.
Ing. VICTOR JAIRO FONSECA V.
8
Cuando un sistema efectúa un trabajo, disminuye, pues, su capacidad de hacerlo
y, por consiguiente, su energía.
Un sistema puede poseer energía de acuerdo a su movimiento, a su posición o a
la interacción de sus partes.
4.1.1 Energía potencial (Ep)
Cuando un sistema está colocado a una altura h de un plano de referencia, por
ejemplo la superficie de la tierra, posee una energía, denominada por muchos
científicos como energía potencial, algunos la llaman energía potencial mecánica
y otros energía potencial gravitacional.
Si el cuerpo 1 , de masa m colocada a la altura dh del nivel 00’, está unido
mediante una cuerda imponderable que pasa a través de una polea sin fricción a
otro sistema 2, de masa igual m, colocada en el nivel 00’, tal como se representa
en la siguiente figura.
Figura 29
Es obvio que al bajar el sistema 1 al nivel 00’, el sistema 2 se elevará una
distancia dh y, en consecuencia, se está efectuando un trabajo para mover el
sistema 2.
9
Figura 30
El trabajo efectuado será el equivalente a vencer, durante el recorrido de la altura
dh, la fuerza de gravedad que actúa sobre el sistema 2, esta fuerza es equivalente
al peso P del sistema y se debe recordar que el peso de un cuerpo es igual al
producto de la masa m, por la aceleración de la gravedad d, luego el trabajo
realizado sobre el sistema 2 es:
dw = F dh
W=
yo
m g dh
[6]
[7]
W=mgy
Este trabajo se ha realizado a costa de una energía producida a partir del sistema
1, por el hecho de encontrarse este sistema a una altura Y del nivel de referencia.
El sistema 1 posee, por lo tanto, una energía que depende de su posición y altura.
Es la energía potencial.
Solamente diferencias de energía potencial, referidas a dos niveles tienen
significado físico. En el ejemplo de la figura 78 se tomó como nivel de referencia la
superficie 00’y como nivel para determinar la energía potencial la línea YY’. Son
necesario, por lo tanto, dos niveles para establecer un valor de energía potencial.
4.1.2. Energía cinética (Ec):
Otra forma de energía poseía por un sistema es la energía cinética, igualmente
llamada energía mecánica cinética.
Suponiendo que un sistema de masa m lleva una velocidad v o’ puede lograr una
Ing. VICTOR JAIRO FONSECA V.
10
aceleración a cuando sobre él actúa una fuerza F; transcurrido un tiempo, el
sistema ha adquirido una nueva velocidad v1 y ha recorrido una distancia x; usted
puede escribir la ecuación general para el movimiento uniformemente acelerado.
v21 - v02 = 2 a x
v21
-
v02
v02 = 2 a x
recordamos que F = m a
F
= 2 ---- x
m
concluimos F. x = ½ m ( v12 - v02 )
[8]
La cantidad , ½ m v2 , corresponde a un trabajo Fx y se denomina energía
cinética. La ecuación [8] expresa que el trabajo efectuado por la fuerza total es
igual al cambio de energía cinética del sistema.
Ejemplo 27. Un proyectil de masa 2 kg. Es lanzado verticalmente con una
velocidad de 600 m/s determinar:
a) El trabajo que ha realizado el elemento impulsor para elevarlo.
b) La máxima altura que alcanza dicho proyectil.
Solución:
a. El trabajo desarrollado por el elemento impulsor hace que el proyectil recorra
una distancia h, y a la vez este trabajo se convierte en la energía cinetica del
proyectil, así
W = F x h = Ec = ½
m ( v12 - v02 ), reemplazando valores, con unidades
consistentes
W = ½ x 2 x (6002 - 02) = 360.000 julios,
b) La altura se calcula tomando F = m g = 2 x 9,8 = 18,6 kg
y h = W /F = 360.000/ 18,6 = 18.367 m
4.1.3 Energía mecánica (Em)
De las diversas formas con que la energía se presenta, la más visible y evidente
es la conocida como energía mecánica, que depende de las condiciones externas
del sistema y de su masa.
Tanto la energía potencial como la cinética pertenecen a este tipo de energía y
por ello también tienen la denominación de mecánica. Se define como energía
mecánica a la suma de las energías potencial y cinética.
Em = E p + Ec
[9]
Un cuerpo de una determinada masa, y bajo condiciones dadas de altura y
11
velocidad, posee una energía mecánica igual a la de otro cuerpo de igual masa y
bajo iguales condiciones.
Sin embargo, existen otras formas de energía que dependen de la naturaleza
misma del cuerpo; así, una pila cargada tiene más energía que una descargada
cuando las dos, teniendo igual masa, están en las mismas condiciones de
velocidad y altura.
4.1..4 Energía interna (U)
La energía que posee un sistema dependiente de su naturaleza misma, se conoce
como energía interna y normalmente, es debida a los movimientos y
configuraciones moleculares de los cuerpos. Puede formularse:
U = m Ui
[10]
Donde Ui es la energía Interna Unitaria.
Dentro del balance de energía no es necesario conocer el valor absoluto de la
energía interna; pues se trabajará con los cambios de ella, que pueden ser
calculados a partir de las propiedades medibles que posee el sistema, por ejemplo
temperaturas, estado físico, presión, etc.
Existen otros tipos de energía que puede poseer un sistema dependientes de los
materiales del sistema mismo, por ejemplo la magnética, la electrostática y la
superficial pero, desde el punto de vista de la tecnología de alimentos, ellas no se
consideran en los balances de energía.
Resumiendo, se establece que un sistema posee tres tipos de energía, la
potencial, la cinética y la interna y podemos decir que, para un instante y, el
sistema posee una energía total:
v12
E1 = m ( g y + -------- + U1)
[11]
2
Si consideramos que el sistema ha sufrido un cambio en su estado, es decir su
altura, velocidad, o energía interna han sido modificadas, permaneciendo
constante su masa, la energía para el nuevo estado será:
v21
E1 = m ( g y + -------- + U1)
2
Y el sistema ha sufrido un cambio de energía:
E = E2 - E1
[12]
La energía total de un sistema es desconocida, pero el cambio de energía
ocurrido en varios procesos sufridos por el sistema puede ser determinada. Pero
¿Cómo ha cambiado la energía del sistema? La primera ley de la termodinámica
establece que la energía no se crea ni se destruye, luego el cambio de energía de
Ing. VICTOR JAIRO FONSECA V.
12
los alrededores, es una cantidad exactamente igual pero de sentido o signo
contrario, el único medio por el cual el sistema y sus alrededores pueden
intercambiar energía es por trabajo y calor. Llamando Q al calor que entra o sale
del sistema:
La Primera Ley de la Termodinámica expresa: (para el sistema)
E = Q - W
[13
Para los alrededores
E’= Q’- W’
[14]
E = - E’
[15]
Entonces
E = E2 - E1 = -E’= Q + W’
E2 = E 1 + Q - W
[16]
[17]
4.1.5. Energía P.V
En sistemas donde ocurre una expansión o compresión (cambio de volumen, dV)
a presión P constante, generalmente gases y líquidos, se requiere de un trabajo
para lograrla.
Observando la figura 3, en un cilindro de longitud l y área seccional A, actúa un
pistón sobre el cual se ejerce una fuerza F, el trabajo para desplazar el pistón una
distancia dl será:
dW = Fdl
Compresión de un gas en un cilindro
FIGURA 31
Al desplazarse el pistón un dl, el gas contenido en el cilindro se está
comprimiendo y su volumen V está cambiando, luego el trabajo ejercido se gasta
en comprimir el gas.
Multiplicando y dividiendo la ecuación anterior por el área seccional A, obtenemos:
13
F
d W = ----- A dl
A
En esta expresión, F/A es la presión P del sistema y A dl es dV.
Luego:
d W = P dV
W = PdV
[18]
Situación similar ocurre cuando el gas se expande y, en ese caso, el gas está
ejerciendo el trabajo.
El trabajo de expansión o compresión se logra, bien a costa de la energía del
sistema o de la energía de los alrededores.
Cuando el sistema opera a volumen constante y tienen condiciones estáticas o de
no flujo (no hay Cambio de altura, ni el sistema tiene velocidad), como el caso de
los procesos llamados de cochada, el trabajo del sistema es nulo, dado que dV =
0 y no hay cambios en las energías potencial y cinética.
Recordamos que en la gráfica P vs V, la integral definida es igual al área bajo la
curva entre los valores V1 y V2
Ejemplo 28. En un refrigerador, el compresor comprime 10 litros refrigerante a la
mitad, a una presión de 100 kg/cm2. Tomando un rendimiento del 32%,
determinar la cantidad de calor que se extrae en el refrigerador.
Solución. El compresor realiza un trabajo para comprimir el gas de 10 a 5 litros a
la presión establecida, luego
W = P x (V2 - V1 ) y tomando unidades consistentes
100 k/cm2 x 10.000 cm2 / m2
= 1.000.000 kg / m2
3
10 - 5 litros = 0,010 – 0,005 m
W = 1.000.000 x ( 0,010 -0,005) =…5.000 kg –m
W = 5.000 kg –m x 9.8 ( N / kg) = 49.000 N-m = 49.000 J
Dado que la eficiencia (  )es del 32% y que el calor se expresa en calorías
Ing. VICTOR JAIRO FONSECA V.
14
Q =  x W = 0,32 x 49.000 J / 4.186 J/cal = 3.745,82 cal.
4.2. Balance total de energía
Si a las ecuaciones de energía adicionamos el trabajo debido a la energía P.V, se
tiene:
V12
E1 = m ( g y1 + ---- + U1) + PV
[19]
2
Y, para los estados 1 y 2, la ecuación [19] se convierte:
v12
v22
m g y1 + m ---- + mU1 + P1V1 + Q´ - W´ = m g y2 + m ---- + mU2 + P2V2
2
2
[20]
La ecuación [20] se denomina ecuación del balance total de energía y es la
expresión general matemática de la primera ley de la termodinámica.
También es generalizado el uso de la ecuación:
Q’- W’=  (mu + PV) + (mgy) + (mv2/2)
[21]
de amplio empleo en operaciones de flujo de fluidos y balances de calor y
energía.
En la tercera unidad se presentará la aplicación en fluidos con
ecuación de Bernoulli.
la llamada
Para emplear las ecuaciones [20] y [21] en balances de energía o aplicaciones
prácticas de la primera ley de la termodinámica, deben definirse algunos términos:
4.2.1 Calor de índole física
Operaciones de carácter puramente físico están a menudo acompañadas de
cambios de energía térmica, los cuales son causados por la adición o remoción de
calor y/o trabajo.
Cuando se adiciona calor a una sustancia, ésta puede cambiar su temperatura o
cambiar su estado físico (sólido o líquido a gas o directamente sólido a gas).
Para el anterior caso, la energía adicionada en forma de calor, cuyo efecto es
únicamente elevar la temperatura sin que ocurra un cambio de estado, se
denomina calor sensible o calor especifico.
Cuando la adición de calor causa un cambio de estado físico, sin que ocurra un
cambio de temperatura, se llama Calor latente.
15
4.2.2. Calor específico: Se define como calor específico de una sustancia, C., la
cantidad de calor requerida por un gramo de dicha sustancia para ser elevada su
temperatura en un grado centígrado y se expresa:
C = dQ/dT
[22]
El calor específico es una función de la temperatura; para condiciones de presión
constante, cada sustancia tiene un calor específico Cp y, para volumen constante,
igualmente, un calor específico Cv’
La unidad de calor se llama, en el sistema c.g.s., caloría (cal) y su definición es:
una caloría es la cantidad de calor necesaria para elevar la temperatura de un
gramo de agua a presión atmosférica y temperatura de 14,5C. En el sistema
inglés se tiene como unidad la BTU. (Bristish Thermal Unit) o cantidad de calor
necesaria para elevar la temperatura de una libra de agua de 63 a 64 Farenheit,
a presión atmosférica
En el sistema c.g.s. el calor específico, también llamado capacidad calorífica,
tiene como unidades, de acuerdo a su definición, caloría por gramo - grado
centígrado (cal/gC).
La cantidad de trabajo se define por medio de un sistema mecánico y sus
unidades son Newton - metro (N-m) o Julio (J) ; similarmente se define la cantidad
de calor en términos de calorías y, lógicamente, no se pueden adicionar o sustraer
cantidades que tengan diferentes unidades. Fue Joule quien obtuvo la relación
entre el BTU y la libra - pie, al encontrar experimentalmente el factor de
conversión entre las unidades de trabajo y calor, conocido como Equivalente
Mecánico del Calor. (E.M.C.)
En el sistema m.k.s. una caloría equivale a 4,186 Newton metro o a 4,186 joules.
Para el sistema inglés, un BTU. equivale a 778 libra - pie.
Ejemplo 29
¿Qué cantidad de calor requiere una sustancia para elevar su temperatura en
10C, si su calor específico es de 1,2 cal/gC?.
Solución. Tomando como base de cálculo 1 gramo, la cantidad de calor es :
Q = 1 gramo X 1,2 cal/gC x 10C = 12 calorías.
Ejemplo 30
¿Qué cantidad de calor se necesita extraer de 125 gramos de agua, para enfriarla
en 1C?.
Ing. VICTOR JAIRO FONSECA V.
16
Solución. Recuerde usted que el calor específico del agua es 1,0 cal/gC
(definición de caloría).
Luego la cantidad de calor que se debe retirar de los 125 gramos es:
Q’= 125 gramos X 1,0 cal/gC X (-1C) = -125 calorías.
Aparece el signo negativo; nos significa que el calor se extrae del sistema.
Ejemplo 31
En el experimento para determinar el E.M.C., Joule describía en 1843 “ El trabajo
realizado por un peso de una libra que desciende 772 pies , si se emplea en
producir calor por el rozamiento del agua, elevará la temperatura de una libra de
agua en un grado Fahrenheit”.
Acorde a estos datos, determine usted el E.M.C. obtenido experimentalmente, en
el sistema m.k.s.
El trabajo realizado al caer el peso será:
W = 1 lb. X 772 pies = 772 lb. Pies.
W = 772 lbs (0,452 kg/lb) x pie (0,3058 m/pie)
= 106,358 kg - m = 106,358 kg - m x 9,8 nw/kg
= 1.042,3 Nw - m.
La cantidad de calor cedida al agua es Q = 1 BTU, pues se elevó en un grado
Farenheit la temperatura de 1 lb. de agua.
Q = 1 BTU = 252 calorías
entonces E.M.C. = 1042,3084 / 252
= 4,136 Julio/cal.
Mediante el empleo de aparatos de gran exactitud, actualmente se ha encontrado
que el E.M.C. es 4,186 julios/cal. y este es el valor que se toma como factor de
conversión.
Ejemplo 32
Un alimento líquido con calor específico de 0,8 cal/gramo C (1), entra a un
pasteurizador a una temperatura de 10C (2) y sale 2 metros (3) encima del nivel
de entrada a una temperatura de 80 C (4); su velocidad de entrada es de 10 m/s
(5) y la salida es de 18 m/s. (6) Se pregunta:
a) ¿Cuánto calor se necesita para calentar el líquido?
b) ¿Cuántos Julios son necesarios para elevar el líquido?
c) ¿Cuántos julios son necesarios para aumentar la velocidad?
d) ¿Qué % de trabajo total requerido, expresado como calor, constituye la energía
mecánica?
17
Solución
Para el sistema de pasterización no se tiene el elemento que produzca trabajo y
existe el que cede calor. Para efectos de cálculo, tomamos como base 1
kilogramo masa (7) del líquido.
Recordamos que los números en ( ) son las referencias para la hoja de cálculo
La Ecuación del Balance de Energía es:
Q’= (mu + Pv) + (mgy) + (mv2/2)
a) Acorde a la ecuación, el término (mu + Pv) representa el calor usado para
cambiar la temperatura, luego
(mu + Pv) = C(T2 - T1),
el peso de líquido es m x g = 1x 9,81 = 9,81 kg (9)
(mu + PV) = 9,81x0,8 (cal -gramo/ C ) (80-10)C x 1000 g/kg = 549.360 cal (10)
b) El trabajo para elevar el líquido será:
Wy = (mgy) = 1 kg X 9,8 m/s2 X 2m = 19,62 Joules (11)
c) El trabajo para aumentar la velocidad
Wv = (m v2 / 2) = 1 kg x ( 10 8 - 102 ) / 2 m2/s2 = 112 Joules (12)
El trabajo total expresado como calor, será:
Q’= 549.360 cal + 19,6 Jl / 4,186 J/ cal + 112/ 4,186 jJ/ cal.
Q’= 549.360 + 4,68 + 26,78 = 549.391 cal. (13)
La energía mecánica, suma de la potencial y la cinética, expresada como calor es
4,68 + 26,76 = 31,44 cal., lo que representa: 31,44 / 549.391 x 100 = 0,0056%
Del calor total requerido por el sistema, el trabajo que se ha realizado sobre el
sistema es realmente despreciable (0,0056%) respecto al calor requerido para
elevar la temperatura del kilogramo masa de líquido.
Se presenta a continuación la respectiva hoja de calculo ( ver anexo )
La hoja de cálculo de este ejemplo permite hacer un análisis inmediato sobre las
cantidades de energía que se modifican o transfieren en un proceso que implique
operaciones unitarias.
Ing. VICTOR JAIRO FONSECA V.
18
EJEMPLO 32
BALANCE DE ENERGIA
BALANCE TOTAL DE UN PASTERIZADOR
PARAMETROS
SIMB.
Presentación del problema
Calor Específico
c
Temperatura de entrada
T1
Temperatura de salida
T2
Velocidad de entrada
V1
Velocidad de salida
v2
Diferencial de altura
H
UNID.
FUENTE
REF.
0
kcl / kg C
0
C
0
C
m/s
m/s
m
VALORES
S.I
1
2
4
5
6
3
MKS
0,8
10
80
10
18
2
REPRESENTACION GRAFICA
v2
18
m/s
0
T2
80
C
E 2.299.752,58 julios
H 2
m
V1
T1
1
10
10
kg
m/s
0
C
Solución
PARAMETROS
Base de Cálculo, masa de líquido
Constante de gravedad
Peso del líquido
Calor de calentamiento
Trabajo para Energia Potencial
Trabajo para Incremento de velocidad
Total de energía requerida
SIMB.
m
g
P
Qc
Ep
Ev
E
UNID.
kg*
2
m/s
kg
kcal, cal
J, cal
J, cal
J, cal
FUENTE REF.
Dato
7
Tablas
8
Cálculo
9
Calculo
10
Calculo
11
Cálculo
12
Cálculo
13
VALORES
1
9,81
9,81
549,36 549.360
19,62
4,69
112
26,76
2.299.753 549.391
En la hoja se han colocado unidades en los sistemas mks e Internacional
Realizando la simulación hojas 2 y 3, se varían la altura y la velocidad de salida
en altos porcentajes y en un muy pequeño valor se modifica la temperatura de
salida del líquido. En los dos primeros casos el cambio en la energía total
involucrada en el proceso es prácticamente despreciable en tanto que en el
19
tercero, el cambio es significativo.
Por esta razón en la industria de alimentos los balances de energía se realizan
únicamente sobre la energía térmica o calor dejando de lado las otras energías.
Algunas se involucran cuando en el proceso se transforman en calor , como la
energía eléctrica empleada, a través de resistencias, para generar calor.
Solución para altura de 6 metros y V2 40 m/s
PARAMETROS
SIMB.
UNID.
Base de Cálculo, masa de líquido m
kg*
2
Constante de gravedad
g
m/s
Peso del líquido
P
kg
Calor de calentamiento
Qc
kcal, cal
Trabajo para Energia Potencial
Ep
J, cal
Trabajo Incremento de velocidad Ev
J, cal
Total de energía requerida
E
J, cal
FUENTE REF. VALOR
1
9,81
9,81
549,36 549.360
58,86
14,06
750 179,17
2.300.430 549.553
Solución para temperatura de salida de 82 oC
PARAMETROS
Solución
Base de Cálculo, masa de líquido
Constante de gravedad
Peso del líquido
Calor de calentamiento
Trabajo para Energia Potencial
Trabajo Incremento de velocidad
Total de energía requerida
SIMB.
UNID.
m
g
P
Qc
Ep
Ev
E
Kg*
2
m/s
Kg
Kcal, cal
J, cal
J, cal
J, cal
FUENTE REF.
VALORES
1
9,81
9,81
565,056 565.056
19,62
4,69
112
26,76
2.365.456 565.087
Debe recordarse la diferencia entre masa, m y peso, p para la correcta aplicación
de los formulismos.
Nuevamente se aprecia la magnitud de cambio en la energía térmica respecto al
cambio de energía potencial y de la energía mecánica del movimiento
Ejemplo 33
Un material en reposo con masa de l kg y calor específico 0,8 cal/gC cae al vacío
y al chocar contra una superficie sólida eleva su temperatura 1C.
a) ¿De qué altura cayó el material?
b) ¿Qué velocidad alcanzó el material justo antes de chocar?
El ejemplo indica que no hay interacción entre el sistema (el material) y sus
alrededores. No hay trabajo desarrollado por el sistema y no se adiciona calor al
mismo.
Ing. VICTOR JAIRO FONSECA V.
20
a) Toda la energía es retenida por el sistema y suponemos que después del
impacto el material queda en reposo.
De la ecuación para el balance total de energía:
(mu + Pv) + (mgy) + ( (m v2 / 2)
= Q’= E
Es igual a cero o Q’= E = 0
El material parte del reposo y termina igualmente en reposo luego
( (m v2 / 2)
=0
entonces (mu + Pv) = -(mgy)
Esta ecuación nos significa que el resultado del proceso (caída una distancia y) es
incrementar la energía interna del material. Pero a la vez el cambio en la energía
interna ha elevado la temperatura en 1C así:
- (mgy) = (mu + Pv) = CT = 0,8 cal/gC X 1C X 1000 g
- (mgy) = 800 cal ó 3349 J
y = - 3349 J/(1 kg X 9,8 m/s2) = - 341,7 m.
El signo negativo significa que el material ha descendido.
b) Como el material inicialmente está en reposo, su velocidad inicial es cero. Justo
antes de chocar la energía interna del material permanece sin cambio alguno y es
durante el choque cuando varía, luego (mu + Pv) = 0 y el balance total de energía
para este caso es:
(mgy) + (mv2/2) = Q’= E’= 0
Y como la velocidad inicial es cero
(mv2/2) = m v21/2 = - (mgy) = 3349 J ==== v = ( 2 x 3349 / 1) 1/2
v1 = 81,84 m/s
Es notorio establecer como una energía interna ( térmica ) relativamente pequeña
puede transformarse en una energía mecánica relativamente grande.
Tanto el ejemplo 34 como el 35 demuestran que en procesos físico o químicos, en
los cuales están presentes loes efectos del calor, los efectos potenciales y
cinéticos pueden ser despreciables, dados sus valores comparativamente
pequeños respecto a los de la energía interna, y la ecuación del balance total de
energía puede escribirse
Q’- W’= (mu + PV)
[23]
Llamando U la energía interna de una unidad de masa, la ecuación se nos
transforma en:
Q’- W’= (U + PV)
[24]
En la mayoría de los procesos donde los balances de calor son efectuados sin
21
incluir aparatos productores de trabajo, como bombas o similares, la ecuación se
convierte en:
Q = (U + PV)
[25]
Las magnitudes U y PV son de común ocurrencia en muchos procesos y tienen
más una conveniencia matemática que un significado físico.
Dada la frecuencia con que se manejan estos términos, se han agrupado en un
concepto llamado Entalpía cuyo símbolo es H y sus unidades, igual que las de Q y
U, son el Julio, la caloría o la BTU.; la ecuación [25] se nos transforma en:
Q = H
[26]
Debe recordarse que, para procesos estacionarios con volumen constante
E = Q
y
Q = U
[27]
Y para presión constante
E = Q - (PV) y Q = H
[28]
Igualmente se recuerda que, en la forma original de la primera ley, la energía
interna, la potencial, la cinética y la energía PV se consideran importantes, otras
formas de energía como la magnética, la eléctrica y la superficial son
insignificantes; y, cuando existen efectos calóricos, los efectos de las energías
potencial y cinética son despreciables.
El calor generado o consumido en un proceso se clasifica de acuerdo a si el
proceso es físico o químico.
Se ha establecido que la cantidad de calor asociada con un proceso, puede ser
encontrada conociéndose el valor de ciertas funciones termodinámicas como la
energía interna, energía PV o entalpía.
Al conocer usted como se evalúan estas funciones, es posible calcular las
cantidades de calor asociadas.
El calor puede ser absorbido o emanado, por un sistema de diversas maneras.
Existe el calor asociado a una reacción química y se denomina calor de reacción.
Por ejemplo, al reaccionar la cal viva (CaO) con agua, forma la cal apagada
Ca(OH)2 y se desprende calor.
Otro calor es el asociado a la naturaleza físico-química del sistema, como el calor
de dilución o de mezcla. Por ejemplo el producido al disolver ácido sulfúrico en
agua.
4.2.3. Calor específico a presión constante (Cp)
Cuando se caliente una sustancia a presión constante, para un cambio
infinitesimal de temperatura, la ecuación [29] se convierte:
Ing. VICTOR JAIRO FONSECA V.
22
dQ
=
CpdT
[30]
dQ
=
dH
[31]
Cp
=
dH/dt
[32]
Y también
Luego
El calor específico a presión constante, Cp’ es igual a la tasa de cambio de la
entalpía respecto a la temperatura para presión constante.
El calor específico a presión constante es una función de la temperatura, y es
propio para cada sustancia. Se determina experimentalmente y ecuaciones de
diverso tipo se han desarrollado para expresarlo. La más común es la forma
polinomial.
Cp = a + bt + ct2 + dt3 .....
[33]
Para muchas sustancias y en un amplio rango de temperatura, el calor específico
es constante.
Otras, especialmente líquidos y gases, tienen una variación lineal y la ecuación es
expresada con dos términos. Solamente para gases, y dentro de un muy amplio
rango de temperatura, se emplean tres términos de la ecuación [30].
Las expresiones matemáticas para el calor específico se pueden graficar, al final
del capitulo se presentan gráficas para algunos alimentos.
Ejemplo 34
Experimentalmente se determinó que, para un gas, el calor específico C p se rige
por la ecuación:
Cp = 3,27 + 0,42 X 10-3 T, cal/g-molK; siendo T la temperatura absoluta en K...
Hállese el calor específico Cp para 0, 100 y 200C.
Solución
La ecuación emplea la temperatura absoluta T en K, entonces para:
t
= 0C
T = 273K y Cp = 3,27 + 0,42 X 10-3 X 273 cal/molK
t
=100C
T = 373K y C p = 3,27 + 0,42 X 10-3 X 373 cal/gmolK
t
=200C
T = 473K y Cp = 3,27 + 0,42 X 10-3 X 473 cal/gmolK
Cp 0C = 3,38 cal/gmolK
Cp 100C = 3,42 cal/gmolK
Cp 200C = 3.47 cal/gmolK
23
Por razones de orden práctico, las unidades del calor específico para los gases
son caloría/g molK.
Para determinar la cantidad de calor que requiere una sustancia de masa m, para
elevar su temperatura de t1 a t2’ la ecuación [32] se convierte:
dQ = mCp dT
T1
Q = m  T2 CP dT
[34]
Para el caso de N moles de un gas:
T1
Q = N  T2 CP dT
[35]
Ejemplo 35
Para el gas del ejemplo 51, determine usted la cantidad de calor necesaria para
elevar la temperatura de 12 moles de 0 a 100.
Solución
Para aplicar la ecuación (31), se tiene N = 12 moles
Cp = 3,27 + 0,42 X 10-3 T
T1 = 273L T2 = 373K
Luego
T1
T1
Q = N  T2 CP dT = N  T2 ( 3,27 + 0,42 x 10-3 T) dT
-3
373
2
Q = N(3,27 T + 0,42 x 10 T /2) ]273
Q= 123,27 (373 - 273) + (0,42 x 10-3 / 2)( 3732 - 2732) = 4086,8 cal.
Como se refería anteriormente, para sólidos y líquidos el calor específico, Cp, es
constante o tiene variación lineal. En estos casos se emplea el calor específico
promedio y la ecuación [34] se transforma en:
Q = M Cp ( T2 - T1)
[36]
De amplísimo uso en balances de energía y en general, en la termodinámica.
Si bien, el calor específico puede asumirse, en ciertos casos, constante para cada
sustancia, cada una tiene un calor específico propio, de acuerdo a la fase ó
estado físico en que se encuentre. Por ejemplo, para el agua:
Ing. VICTOR JAIRO FONSECA V.
24
0,47 cal/gr oC
1,0 cal/gr oC
0,50 cal/gr oC
El calor específico del vapor es
El calor específico del agua líquida es
El calor específico del hielo
Ejemplo 36
En el rango de 0 a 98 oC, el alcohol etílico tiene un calor específico de 0,68 cal/gr
o
C,. Determine usted la cantidad de calor requerida para calentar un litro de 10 a
48 oC, siendo su peso específico de 0,79.
Solución
Debe recordarse que en los sistema SI y mks el peso específico tiene un valor
numérico igual a la densidad, así que el peso a calentar es
Peso p = 0,79 x 1.000 = 790 gramos y teniendo unidades consistentes
Calor requerido Q = 790 x 0,68 x ( 48 -10 ) = 20.414 cal.
Ejemplo 37
El calor específico promedio Cp de un alimento es 1,18 cal/gr oC. Qué cantidad
de calor se requiere extraer para enfriar una cochada de 300 kgs. a 10 oC, si ella
se encuentra en ebullición a 118oC
Solución
Empleando la ecuación (32) Q = M Cp ( T2 -T1)
Q = 300 kg x 1000 g / kg x 1,18 cal /g 0C ( 10 -118 ) 0C
Q = - 3,82 x 10 7 calorías
Se puede emplear igualmente el calor especifico 1,18 kcal / kg 0C y
Q = 300 kg x 1 kg x 1,18 kcal / kg 0C ( 10 -118 ) 0C
Q = - 3,82 x 10 4 kilocalorías
Recuerde el significado del signo negativo
En el manejo de ecuaciones en las que intervienen cambios físicos se debe tener
presente el sentido físico o matemático del cambio o gradiente también llamado
diferencial. Matemáticamente un gradiente puede ser positivo o negativo en tanto
que un gradiente físico no puede ser negativo.
En el caso de temperaturas físicamente no puede existir un gradiente negativo, al
aplicar el gradiente matemático puede aparecer el signo negativo que significa
extracción de calor.
El gradiente físico T = 118 - 10 =
108 0 C
El gradiente matemático T = 10 - 118 = - 108 0 C
A nivel de balances térmicos es conveniente, emplear los gradientes físicos y
tener presente si en el proceso se retira o se suministra calor , de tal forma que se
sea consecuente con la operación realizada, como enfriamiento, calentamiento,
condensación etc.
25
Dada la magnitud en los valores de Q, se acostumbra a usar como unidad la
kilocaloría (kcal).
FIGURA 32
4.2.4 Calor específico a volumen constante (CV)
Cuando se calienta una sustancia a volumen constante, proceso de cochada, para
un cambio infinitesimal de temperatura, la ecuación [29] se convierte en:
dQ = CV dT
[37]
Recordando lo explicado en la energía PV. Tenemos que la ecuación [27] puede
escribirse:
dQ = dU luego dU = CVdT
Ing. VICTOR JAIRO FONSECA V.
[38]
26
FIGURA 33
Las unidades y el tratamiento del CV son similares a los del Cp; y usted puede
considerar que para sólidos y la mayoría de los líquidos, el valor de CV es igual al
de Cp; pero para el caso de los gases ellos difieren.
Considerando un gas perfecto y tomando como base una unidad molar:
d ( U +PV )
dU
d (PV)
Cp = dH / dT = ------------------- = ------- + -----------dT
dT
dT
A la vez CV = dU/dT y, de la ecuación de los gases perfectos PV = RT,
reemplazando estos valores:
27
Cp =
d( RT )
Cv + --------------- = CV + R
dT
[39]
En la práctica el comportamiento de los gases se aparta de la ecuación de estado;
sin embargo, para efectos de problemas puede ser empleada con bastante
seguridad.
En la tabla 3 se observan los valores de Cp - Cv para algunos gases, es
aproximadamente igual a R: (1.987 cal/gmolC).
Ejemplo 38
El gas Carbónico CO2 tiene,, a 25C, un calor específico Cp de 8,96 cal/g molC.
Se caliente de 15 a 40C; calcular Q, W, U y H para el proceso: (a) presión
constante y (b) a volumen constante, (Cv = 6.92 cal/g molC)
Solución
Tomamos como base 1 mol de gas y
a) Calentamiento a presión constante
Qp = Mcp T = H
Qp = 1 X 8,96 cal/g molC X (40 - 15) C = 224 calorías
W p = PdV = P V = R T
W p = 1.987 cal/g molC X (40 - 15) C = 49,68 calorías
Up = Qp - W p = 224 - 49,68 = 174,32 calorías
b) Calentamiento a volumen constante. Para este caso U y H dependen de la
temperatura únicamente y
Q = U = 174,32 calorías = H
W p = PdV = P x 0 = 0
Q también puede calcularse tomando Cvy
QV= M CV T
QV = 1 mol x 6,92 cal/g molC x 25C = 173 calorías
Ejemplo 39
El ácido clorhídrico gaseoso tiene calor específico Cp aproximado a 6,60 + 0,98 X
10-3 T cal/g molK.
Determine la cantidad de calor necesario para calentar 15 moles de 100 a 200C,
a presión de 1 atmósfera, empleando:
Ing. VICTOR JAIRO FONSECA V.
28
a) Valor de Cp de la Tabla 3
b) La ecuación de Cp en función de T.
c) La diferencia en % que se presenta, respecto al primer valor obtenido.
Solución
a) Con el valor de Cp de la Tabla 3
Q = N Cp T = 15 mol X 7,05 cal/g molC X 100C
= 10575 calorías
b) Empleando la ecuación, las temperaturas son 373 y 473K
T1
473
Q = N  T2 CP dT = N 373 ( 6,60 + 0,98 x 10-3 T) dT
Q = 15  6,60 (473 - 373) + ( 0,98 x 10 -3 ) /2 (4732 - 3732)
Q = 15 6,60 x 100 + 0,49 x 10-3 x 84600 = 10.522 calorías
c) La diferencia en % es:
( 10.575 - 10.522 ) / 10.575 x 100 = 0,5%
¿Qué conclusión saca de este %?
4.2.5. Calor latente
El calor latente es el calor implicado en un cambio de estado físico, o fase, sin que
ocurra un cambio en la temperatura (generalmente el proceso ocurre a presión
constante) y se denomina de acuerdo al cambio de fase ocurrido.
El calor latente de fusión es el requerido para que una sustancia pase del estado
sólido al líquido.
El calor latente de vaporización es el necesario para que una sustancia pase del
estado líquido al gaseoso.
El calor latente de sublimación es el requerido para que una sustancia pase del
estado sólido al gaseoso.
Algunos sólidos presentan cambios en su estructura cristalina, debido a efectos
caloríficos. Se denomina Calor de Transición al necesario para que una sustancia
pase de un estado cristalino a otro; por ejemplo, en el azufre los cristales
monoclínicos pasan a rómbicos por la adición de calor.
Como en el caso de los calores específicos, los calores latentes son propios de
cada sustancia. Son, similarmente, funciones pero, a diferencia del específico, el
calor latente es función de una sola variable, es decir, o bien función de la
temperatura o bien función de la presión; pero no simultáneamente de las dos.
29
Una variable excluya la otra. Por ejemplo, el agua a nivel del mar ebulle a 100C ,
siendo la presión de 760 mm de Hg, igualmente hierve a 92C cuando la presión
es de 560 mm. No ocurre que el agua hierva a 92C con presión de 1 atmósfera o
tenga una presión de 560 mm cuando ebulle a 100C.
Estas circunstancias llevan a establecer que un cambio de fase ocurre a
temperatura y presión constante. Luego, para esta clase de procesos, se aplica la
ecuación del balance de energía [28] y se establece que el efecto del calor está
representado por un cambio de la entalpía.
Q = H
[28]
De acuerdo a la clase de calor latente, la entalpía correspondiente lleva un
subíndice así:
H1
Hv
H3
Ht
para calor latente de fusión
para calor latente de vaporización
para calor latente de sublimación y
para calor latente de transición
Como los calores específicos, los calores latentes son hallados
experimentalmente y son propios para cada sustancia. Para los sólidos y líquidos
tienen como unidad cal/g en tanto que para los gases se emplea cal/g mol.
Ejemplo 40
Determinar el calor requerido para fundir 470 gramos de hielo. H1 del hielo es 80
cal/g.
Solución
Q = MH1 = 470g x 80 cal/g = 37.600 cal.
Ejemplo 41
Calcular el calor requerido para evaporar 7.300 kg de agua que se encuentran a
19C y una presión de 760 mm. De Hg.
Solución
Para la presión de 760 mm de Hg, el agua ebulle a 100C; dentro del proceso,
inicialmente se debe calentar el agua de 19C a 100C; y luego evaporarla a
temperatura constante.
Para calentarla de 19C a 100C
Q = MCPT = 7.300g x 1 cal/gC x (100-19) C
Q = 591.300 cal ó 591 kcal.
Ing. VICTOR JAIRO FONSECA V.
30
Para evaporarla, se toma Hv = 540 cal/g
O
Temperatura
Ebullición
Calentamiento
Calentamiento, Ebullición
y vaporización a partir de 19 o C
P = 760 mm.
19OC
Tiempo
Figura 34
Temperatura en función de tiempo
Q
Q
M Hv = 7.300g x 540 cal/g
3.942.000 cal ó 3.942 kcal.
=
=
Luego :
Qtotal = 591 + 3.942 kcal = 4.533 kcal
Ejemplo 42.
Es necesario congelar a - 80C, 30 moles de un gas que se encuentra a 93C y
presión atmosférica.
Su temperatura de condensación es de 37C y Hv es 4,21 kcal/gmol, su
temperatura de fusión es de -42C y H1 es 0,379 kcal/gmol. Por otra parte Cp del
gas es 6,74 cal/gmol, Cp del líquido 0,38 cal/mol y Cp del sólido 8,5 cal/gmolC.
Solución.
La figura 35 que relaciona la temperatura de la sustancia con el estado y el tiempo
de proceso nos permite visualizar el problema y determinar que los pasos a seguir
93
Enfriamiento del gas
Condensación
37
Enfriamiento del líquido
Congelación
-42
Subenfriamiento
-80
Tiempo
31
FIGURA 35
Temperatura en función de tiempo
para llevar el gas de 93C a -80C son:
a) Enfriamiento del gas de 93C (temperatura de condensación).
b) Condensación del gas a temperatura constante de 37C.
c) Enfriamiento del líquido de 37 a -42C.
d) Solidificación o congelamiento del líquido a -42C y
e) Enfriamiento del sólido a -42a -80C.
El calor extraído para cada uno de los pasos es:
a) Q3 = Ncp T = 30 mol X 6,74 (cal/gmolC) X (93-37) C
Q3 = 11.323 Cal.
b) Qb = N Hv = 30 mol X 4,21 (kcal/g mol)
Qb = 126,3 kcal
c) Qc = Ncp T = 30 mol X 0,38(cal/g molC) X (37--42)C
Qc = 901 cal.
d) Qd = N Hf = 30 mol X 0,379 (kcal/g mol)
Qd = 11,37 kcal
d) Qe = Ncp T = 30 mol X 8,5 (cal/g molC) -42-(-80) C
Qe = 9.690 cal
Q = 11323 + 126300 + 900 + 11370 +9690 cal
Q = 159.584 calorías
El problema puede resolverse directamente así:
Q = 30 mol (6m74(cal/g molC) X 56C + 4.210 (cal/g mol) + 0,38 (cal/g molC)
X 79C + 379 (cal/g mol) + 8,5 (cal/g molC) X 38C)
= 30 mol ( 377n44 X 4.210 + 30,02 + 379 + 323) cal/g mol
= 159.584 calorías
En el anterior ejemplo, también es posible determinar el calor cedido, conociendo
la entalpía del mismo compuesto a 93C y a -80C, para condiciones de presión
constante a 1 atmósfera en temas propios de la Termodinámica.
El anterior
problema se resuelve mediante los procedimientos comunes
(memorias de cálculo ) y mediante la Hoja de Cálculo.
En la hoja de cálculo, en la solución se transcriben únicamente los cálculos, ya no
se transcriben o repiten datos consignados en el planteamiento del problema.
Ing. VICTOR JAIRO FONSECA V.
32
Mientras se adquiere la destreza adecuada se puede incluir la columna de
ecuaciones, empleando la simbología correspondiente como se observa en la
columna FORMULAS
EJEMPLO 42
BALANCE DE CALOR
ENFRIAMIENTO DE UN
GAS
PARAMETROS
Presentación del problema
Gas
Temperatura inicial
Temperatura Final
Temp. de condensación
Entalpía de Condensación
Temperatura de Fusión
Entalpía de fusión
Calor específico del gas
Calor específico del
líquido
Calor específico del sólido
Solución
Calor de enfr.
Calor de condensación
Calor enfriamiento líquido
Calor de solidificación
Calor de enfri. del sólido
Calor Total
SIMB UNID.
FUEN.
REF.
FORMULAS
N
T1
Tf
Tc
Hv
Ts
Hf
Cpg
Cpl
mol
o
C
o
C
o
C
kcal/mol
o
C
kcal/mol
o
Cal/mol C
o
Cal/mol C
Datos
Datos
Datos
Datos
Datos
Datos
Datos
Datos
Datos
30
93
-80
37
4,21
-42
0,379
6,74
0,38
Cps
Cal/mol C Datos
8,50
Qa
Qb
Qc
Qd
Qe
Qt
cal
kcal, cal
cal
kcal, cal
cal
cal
o
Cálculo
Cálculo
Cálculo
Cálculo
Cálculo
Cálculo
N x Cpg x (T1-Tc)
N x Hv
N x Cpl x (Tc-Ts)
N x Hf
N x Cps x (Tc-Ts)
 Qi
VALORES
11.323
126,30 126.300
901
11,4 11.370
9.690
159.584
En operaciones industriales el balance de calor sobre flujos es muy importante
para establecer no solamente la cantidad de calor requerido en un proceso sino
también la magnitud del servicio que provee o retira calor .
Cabe unas preguntas respecto al problema anterior, cuánto tiempo se gastó para
cada una de las etapas del enfriamiento y cambio de fase?.
Un mismo equipo puede realizar esta operación en una hora o en un día?.
Realmente no, la capacidad del equipo es función del flujo de calor que se
requiera y a la vez este es función del tiempo de cada etapa.
Al estudiar la llamada transferencia de calor se establecen los principios que
permiten determinar los tiempos de proceso térmico.
Para evaluar flujos se toman tiempos representativos. Como se aprecia en el
ejemplo 18
33
Ejemplo 43
100 kilogramos de vapor de agua a 250C y 38,8 atmósferas de presión se enfrían
y condensan a 40C y P = 1 atm, determinar el calor cedido.
.
Temperatura o C
250
Enfriamiento
Condensación
Enfriamiento
100
40
Tiempo
FIGURA 36
Condensación y enfriamiento de vapor
Solución.
Una representación gráfica ayuda en la resolución del ejemplo
La entalpía del vapor a 250C y 38,8 atmósferas es 2.166 kcal/kg.
La entalpía del agua a 40C y presión atmosférica es 122 kcal/kg.
Q = mH = 100 kg (2166 - 122) kcal/kg = 204.400 cal.
Ejemplo 44.
Una unidad de medida comercial empleada en refrigeración es la tonelada de frío
y esta definida como la cantidad de calor que se ha de retirar a una tonelada de
agua que se encuentra a 0°C para convertirla en hielo, en un periodo de 24 horas.
Establecer una tonelada de frío a cuantas kilocalorías /hora y BTU/hora equivale.
Solución
El calor latente de congelación del agua es de 80 kilocalorías /kilogramo, de tal
forma que para congelar en un día, 1 tonelada ó 1.000 kilos de agua se requiere
extraer:
Q = 1.000 x 80 = 80.000 kcal
El calor que se retira por hora o flujo de calor, q, es:
Ing. VICTOR JAIRO FONSECA V.
34
q = 80.000 /24 = 3.333 Kcal/ hr
en BTU, tomando 1 BTU = 0,252 Kcal
BTU/hr = 3.333 /0.252 = 13.227 BTU/hr
Ejemplo 45.En el proceso de elaboración de cerveza, inicialmente se prepara en una olla, un
mosto por infusión o maceración (cocción) de una masa compuesta de malta
molida y agua.
Durante este proceso, en primer lugar se hace necesario calentar el agua de
temperatura ambiente hasta 35 0C en 10 minutos, esta temperatura favorece la
dispersión de las harinas en el agua.
Luego en 5 minutos disolver las harinas de malta en el agua , llevar la masa
agitándola durante 15 minutos a una temperatura de 52 0C a esta temperatura
efectuar un proceso llamado descanso de proteólisis, durante 10 minutos.
Terminada la proteólisis se lleva la masa a 72 0C en 10 minutos para hacer la
hidrólisis de almidones, llamado también descanso de amilólisis, este descanso
se hace durante 10 minutos.
Finalmente la masa se sube a 80 0C en 3 minutos, para luego ser enviada a otra
etapa del proceso.
Determinar las cantidades de calor suministradas en cada operación, asumiendo
que no hay pérdida de calor. E igualmente establecer los flujos de calor teniendo
los siguientes parámetros:
Peso de Agua
2.400 kilos
Calor específico promedio 1,0 kcal/kg 0 C.
Peso de harinas de malta 600 kilos
Calor especifico promedio de la malta 0,8 kcal/kg 0 C.
Solución
La solución se hará directamente en la hoja de cálculo, con la ayuda del
diagrama de temperaturas-tiempos y con las siguientes consideraciones:
El agua se encuentra a temperatura ambiente , 15 0 C. Inicialmente se calienta el
agua y al adicionar la malta se forma una masa cuyo calor especifico es diferente
al del agua y al de la malta.
Se calcula tomando en cuenta de que es una propiedad extensiva
Cpm = ( Pa x Cp a + Pb x Cpb ) / Pm
Siendo a el compuesto a es decir agua, b el compuesto b ó harinas y m la mezcla
de los dos componentes.
35
Temperatura
0C
Descansos
Temperatura
80
72
Amilólisis
Proteólisis
52
Disolución de
malta
36
Calentamientos
15
Maceración de la malta
FIGURA 37
Para determinar el flujo se emplea como unidad de tiempo la hora, que es una
unidad comercial ampliamente usada en cálculos de flujos de calor. Al transcribir
los datos se divide el tiempo en minutos por 60.
En la hoja de cálculo se resuelve el problema con las condiciones dadas en el
enunciado.
EJEMPLO 45
MACERACION DE UNA MASA DE
MALTA Y AGUA
PARAMETROS
Agua
Calor especifico del agua
Harinas de malta
Calor especifico de la malta
Masa
Calor especifico de la masa
Temperatuta inicial
Temperatura de calentamiento agua
Tiempo de calentamiento
Tiempo de disolución de harinas
Temperatura de proteólisis
Tiempo de Calentamiento a proteolisis
Descanso de proteólisis
Temperatura de hidrólisis de almidones
Tiempo de calentamiento
Ing. VICTOR JAIRO FONSECA V.
SIMB.
A
Cpa
B
Cpm
UNID.
kg
0
kcal/kg C
kg
0
kcal/kg C
Cp
T1
T2
tc
td
T3
tcp
tp
T4
tch
kcal/kg C
o
C
o
C
hr
hr
0
C
hr
hr
o
C
hr
0
FUENTE
Dato
Dato
Cálculo
Cálculo
Cálculo
Dato
Dato
Dato
Dato
Dato
Dato
Dato
Dato
Dato
REF. VALORES
2.400,00
1,00
600,00
0,80
3.000,00
0,96
15
36,00
0,17
0,08
52,00
0,25
0,17
72,0
0,17
36
Descanso de hidrólisis
Temperatura final
Tiempo final de calentamiento
PARAMETROS
Calor para agua
Flujo de calor
Calor para proteolisis
Flujo de calor
Calor para hidrólisis
Flujo de calor
Calor para calentamiento final
Flujo de calor
Calor total suministrado
th
Tf
tf
SIMB.
Q1
q1
Q2
q2
Q3
q3
Q4
q4
hr
o
C
hr
UNID.
kcal
kcal / hr
kcal
kcal / hr
kcal
kcal / hr
kcal
kcal / hr
kcal
Dato
Dato
Dato
FUENTE
Dato
Dato
Dato
Dato
Dato
Dato
Dato
Dato
Dato
0,17
80,0
0,05
REF. VALORES
50.400
302.400
46.080
184.320
57.600
345.600
23.040
460.800
177.120
En la hoja 2 se presenta una simulación empleando únicamente 1.800 kilos de
agua, en la practica esto significa que la masa es más concentrada o más espesa.
Como se observa el consumo de calor y el flujo son mucho menores que en el
primer caso, 138.120 contra 177.720 kcal. Resultando en un ahorro del 22 %
que en términos económicos es muy significativo.
PARAMETROS
Calor para agua
Flujo de calor
Calor para proteolisis
Flujo de calor
Calor para hidrólisis
Flujo de calor
Calor para calentamiento final
Flujo de calor
Calor total suministrado
SIMB.
Q1
q1
Q2
q2
Q3
q3
Q4
q4
UNID.
kcal
kcal / hr
kcal
kcal / hr
kcal
kcal / hr
kcal
kcal / hr
kcal
FUENTE REF.
Dato
Dato
Dato
Dato
Dato
Dato
Dato
Dato
Dato
VALORES
37.800
226.800
36.480
145.920
45.600
273.600
18.240
364.800
138.120
Debe tenerse presente que cuando se calientan masas concentradas existe una
tendencia a formar incrustaciones o a pegarse a las paredes de los equipos en los
cuales se hace la transferencia de calor. omúnmente, y de no tener cuidados en el
flujo de calor, esto se traduce en que el alimento se quema o se ahuma, ante ello
el ingeniero debe evaluar el grado de concentración al riesgo de la incrustación. El
agitar vigorosamente la masa favorece el flujo de calor disminuyendo los riesgos
de que el producto sufra daños.
En, el archivo excel, hoja3, se presenta dos gráficas en la que se representa el
calor suministrado para cada etapa y el flujo de calor en cada etapa.
Puede observarse:
37
70000
Calor suministrado
60000
50000
40000
30000
20000
10000
0
1
2
3
4
Etapa
FIGURA 38
para este problema como la etapa en la que se transfiere menor cantidad de
calor, la etapa 4, con 23.040 kcal, requiere del mayor flujo de calor, 460.800 kcal
/hr.
Al establecer qué equipo se requiere para el suministro de calor, se debe tomar
como base de calculo el mayor flujo y en el presente caso las 460.800 kcal / hr.
Flujo de Calor
500000
450000
400000
350000
300000
250000
200000
150000
100000
50000
0
1
2
3
4
Etapa
FIGURA 39
Se puede entrar a considerar lo estricto del tiempo para subir a los 80 0 C, el
hecho de incrementar 2 minutos, es decir llevar el tiempo del calentamiento a 5
minutos, rebaja considerablemente el flujo de calor como se presenta en la hoja 4.
Ing. VICTOR JAIRO FONSECA V.
38
En este ejemplo se ha introducido la ayuda de los gráficos de variables que
permite visualizar el comportamiento de ellas para estudiar alternativas y tener
bases para toma de decisiones.
En la hoja 5 se ha copiado el problema y en esta hoja cambie los tiempos de cada
etapa y observe las variaciones que se tienen en los flujos.
Cambie en muy pequeños valores, las temperaturas de proceso y observe los
cambios en las cantidades de calor transferidos. Debe observarse que para
algunos cambios en los valores del tiempo, la escala de los flujos cambia y
consecuencialmente las figuras también.
4.3 Calor de índole química
4.3.1 Calor de formación
Hasta ahora, se han estudiado procesos que involucran estrictamente cambios
físicos; se han efectuado balances térmicos en los que se determinan calor o
trabajos asociados con cambios de temperatura, cambios de presión o cambios
de fase de sustancias puras o mezcla de sustancias.
Los calores o entalpías de índole química siempre van acompañadas de
transferencia de masa y por ello se involucran balances de materiales salvo
cuando a nivel de las reacciones se hacen los balances estequiometricos y la
energía se relaciona a moles
En un número considerable de procesos ocurren cambios químicos que conllevan
a cambios o intercambios en una o más clases de energía, considerada como
calor o trabajo del sistema.
En un problema cualquiera se plantea un proceso físico como es el de calentar el
agua y esto se lleva a cabo a costa de un proceso químico, como es el de la
combustión del carbón.
Resuelto el problema, se determinó que el agua para su calentamiento requería
de 6000 kcal, y este calor proviene de la combustión de 1 kg de carbón,
asumimos que existe una combustión es decir:
C + 02

CO2 + calor
Y ella se está llevando a cabo a presión constante. La ecuación químicamente es
adecuada pero, desde el punto de vista energético o termodinámico, surgen
interrogantes como:
a) Cuáles son las temperaturas del Carbono y el Oxígeno?
b) ¿Cuál es la temperatura del CO2 formado y en qué estado se encuentra.
c) ¿El oxígeno es puro o proviene de una mezcla de gases (aire por ejemplo) y en
qué estado se encuentra?
39
d) Igualmente ¿el Carbón es puro, de qué clase es? ó ¿proviene de una mezcla?
e) ¿Cómo se establecen las cantidades en que intervienen los reactantes en el
proceso y cuál la correspondiente al producto?
La suposición establecida, y los interrogantes que han surgido, llevan a formular
unos parámetros básicos para analizar y desarrollar los procesos químicos y
desde el punto de vista balances de energía. Para el problema en mención, el
planteamiento para la combustión del carbón puede ser:
Ejemplo 46
¿Qué cantidad de calor se desprende por la combustión de 1 kg. de grafito (una
forma de carbón), usando una cantidad estequiométrica de oxígeno puro y
estando los reactantes, así como el producto final, en condiciones estándar?.
Recordando como condiciones estándar 1 atmósfera de presión y 25C de
temperatura, la ecuación química puede escribirse;
C (sól, 1 atm, 25C) + O2(g,1 atm, 25C) + calor
Para el Balance de Energía se dispone de la ecuación:
E=Q-W
[13]
Y para procesos a volumen constante y proceso a presión constante
Q = U
[27]
y Q =H
[28] respectivamente
La combustión del carbón se lleva a cabo a presión constante, por lo tanto se
emplea la ecuación [28] así, el calor generado Q es igual al cambio de entalpía del
sistema.
Dicho de otra forma, el calor generado es igual a la entalpía final o de los
productos menos la entalpía inicial o de los reactantes.
Ya para determinar el calor generado en la combustión del grafito, el problema
consiste en determinar las entalpías del CO2 del C y del O2 a condiciones
estándar y efectuar el balance correspondiente.
H = H del CO2(g,1 atm, 25C)- H del C(s, 1 atm, 25C) - H del O2(g, 1 atm,
25C)
Ejemplo 47
El gas de cocina propano (C3H8) combuste completamente según la ecuación:
C3H8 + 5 O2 
3CO2 + 4H2O + h
Para condiciones estándar (c.s)) la reacción se escribe:
C3H8 (gas, c.s.) + 5 O2 (gas, c.s.) 
Ing. VICTOR JAIRO FONSECA V.
3CO2 (gas, c.s.) + 4H2O (gas, c.s.) + H
40
El calor generado en la combustión, H, se determina:
H = H1H2O (g.c.) + 3H1 CO2(gas, c,s.) - H1
H1O2(gas,c.s.)
C3H8(gas,c-s.)
-
5
En los dos ejemplos, 44 y 45, el balance de energía se estableció con base las
entalpías de las sustancias.
Las entalpías de las sustancias a condiciones estándar se denominan Calor
Estándar de Formación y su correcta definición es: Calor de Formación de una
sustancia H0fs es el cambio de entalpía que ocurre en la reacción, cuando los
reactantes están inicialmente en su forma elemental a presión y temperatura.
La determinación para algunas sustancias se hace en forma experimental en los
laboratorios y a condiciones de presión y temperaturas estándar, de ahí que
usualmente se emplee el término Calor Estándar de Formación.
Para otras sustancias se emplean métodos indirectos, que se verán más
adelante.
En la Tabla 7 se encuentran los valores para algunas sustancias.
Es importante tener presente que los elementos químicos en su estado natural y
forma más común de existencia, no tienen Calor de Formación. La razón se
encuentra en la misma definición de Calor de Formación.
En el ejemplo 47, en el balance de Energía se toma la Entalpía o Calor de
Formación del agua a condiciones estándar y en el estado gaseoso H1 H2O
(gas, c.s.); se debe recordar que el agua a condiciones normales (25C y 1
atmósfera de presión) se encuentra en el estado líquido.
Entonces salta la pregunta. ¿El calor de formación del agua líquida es el mismo
calor de formación del vapor?. La respuesta es ¡no! H, del agua líquida, es -68,3
kcal/g mol y la de vapor es -57,8 kcal/g mol, esto nos significa que el calor de
formación del líquido es menor que el del vapor (se debe tener en cuenta el signo
menos); dicho de otra forma, se desprende más calor cuando se forma el líquido
que cuando se forma el gas, y es lógico porque en la formación del gas este
requiere consumir calor para cambiar de fase (líquido a gas), o sea el calor de
vaporización.
Algunas sustancias presentan situaciones similares a la del agua, como el ácido
nítrico, ácido cianhídrico, anhídrido sulfúrico y muchos compuestos orgánicos del
orden de los aromáticos o cíclicos: benceno, tolueno, xileno, etc.
Habíamos referido que los Hf de los compuestos que a condiciones normales
están en fase líquida pero también se forman en fase gaseosa, el Hf para el
compuesto en fase gaseosa se calcula tomando el del líquido y se le adiciona el
valor de vaporización a la temperatura estándar (25C) y presión correspondiente
a la presión de vapor para la temperatura estándar.
41
Para el agua, el calor molar de vaporización a 25C es de + 10.519 cal/mol, el
calor de formación del agua líquida es - 68.317 cal/gmol, luego el calor de
formación del agua en fase vapor será (-68.317 + 10.519) cal/gmol = 57.798
cal/gmol.
4.3.2. Calor de reacción
Ejemplo 48
Determine la cantidad de calor desprendida al combustir en condiciones normales
y cantidades estequiométricas un kilogramo de grafito, empleando el calor
estándar de formación del mismo, dado en la Tabla 7.
Solución:
Del balance de Energía, ecuación final del ejemplo 62:
H = - 94.052 cal/gmol - 0 - 0 = - 94.052 Cal/gmol
Pudiéndose escribir

C + O2
CO2 - 94.052 cal/gmol
Para un kilogramo de grafito el número de moles es:
N
= 1.000 g/12 g/gmol = 83,33 g mol
H
= -94.052 cal/gmol X 83,33 g mol
= 7.837.353 calorías
Se recuerda que el valor negativo significa calor extraído del sistema, que para el
presente ejemplo significa calor cedido por el sistema o calor desprendido en el
proceso.
Ejemplo 49.
Determine el calor generado al combustir en condiciones normales y en
cantidades estequiométricas 1 mol de CO.
Solución
La reacción química es
C0 + ½ O2

CO2 + calor
Y, para condiciones normales con P = cte.
H = -
H0f
Q = H
CO2
De la Tabla 7.
H CO = -26.416 cal/gmol
Ing. VICTOR JAIRO FONSECA V.
42
H = -94.052 - (-26.416)- 0 = -67.636 cal/g mol
La ecuación química se puede escribir
CO + ½ O2 
CO2
- 67.636 cal.
Nuevamente aparece el valor negativo para la Entalpía, luego hay calor cedido o
generado.
Ejemplo 50
Determine el cambio de calor, cuando se combuste incompleta o parcialmente, en
condiciones normales y cantidades estequiométricas, 1 gmol de carbón.
Solución:
La reacción química es
C + ½ O2

CO2 + calor
H = H1CO - HFC - HFO2
H = (-26.416 - 0 - 0) cal g/mol = - 26.416 cal g/mol
La ecuación química puede escribirse:
C + ½ O2

CO - 26.416
Los anteriores ejemplos han permitido ilustrar el manejo de los calores de
formación. Si consideramos las ecuaciones químicas de los ejemplos 48 y 49 y las
sumamos tenemos:
C + O2

CO2 - 67.636 cal/gmol
C + ½ O2

CO - 26.416 cal/gmol
CO + ½ O2 + C + ½ O2 
CO2 + CO - 67636 - 26.416 cal/gmol
C + O2

CO2 - 94.052 cal g/mol.
Ecuación que se obtuvo en el ejemplo 48 Observando los anteriores
procedimientos, las ecuaciones de los ejemplos 49 y 50 son pasos intermedios
para la ecuación del ejemplo 48.
Concluyendo: cuando una reacción química puede ser considerada como la suma
de dos o más reacciones parciales, el cambio de entalpía para la reacción total es
igual a la suma de los cambios de entalpías de las reacciones parciales.
Este enunciado constituye un principio fundamental de la Termodinámica y su
empleo permite calcular los calores de formación de sustancias que, por algunas
circunstancias, no pueden determinarse en el laboratorio.
A través de los ejemplos, se ha calculado un cambio de entalpía cuando existe
una reacción química y este cambio se denomina calor de reacción.
43
Calor estándar de reacción Hf’ - Es el cambio de entalpía estándar cuando existe
una reacción química y este cambio se denomina calor de reacción.
Existen reacciones químicas tales como la combustión, neutralización,
isomerización y formación, donde, generalizando, los calores asociados a esas
reacciones se llaman Calores de Reacción.
Llamando nr los coeficientes estequiométricos de los reactantes y n p los
coeficientes estequiométricos de los productos, el balance de energía para una
reacción química es:
Hr =  np Hf productos -  nf Hof reactante
(36)
Ejemplo 51
Determinar el calor de reacción para las siguientes reacciones:
a)
b)
c)
4 NH3(g) + 5 O2 (g)
2 Na(s) + 2 H2O(g)
SO3 (g)
+ H2O(g)



Solución:
a) Hr = nr Hof productos -  np Ho f reactivos
De la tabla 7:
Hf NO(g) = 21.600 calg/mol
Hf H2O(g) = - 57.798 cal/gmol
Hf NH3(g) = - 11.040 cal/gmol
Hr = 4(21.600) + 6(-57.798) - 4(-11.040)cal.
Hr = - 216.228 cal.
b) De la tabla 7:
Hf NaOH(s) = - 101990 cal/gmol
Hf H2O(g) = - 57798 cal/gmol
Hr = 2(-101990) - 2 (-57798) cal
Hr = - 88384 cal.
c) De la tabla 7
Hf H2SO4 (1) = - 193.910 cal/gmol
HfSO3 (G) = - 94.450
Hf H2O(g) = - 57.798
Hr = - 193.910 - (-94.450) 1 (-57.798)
Hr = - 157.258 cal.
Ing. VICTOR JAIRO FONSECA V.
4 NO(g) + 6H20 (g)
2 NaOH (s) + H2(g)
H2SO4 (y)
44
4.3.3 Calor de disolución (H8)
Un efecto calorífico particular, asociado con la composición de algunas
sustancias, es el llamado Calor de Disolución.
Varios ácidos, hidróxidos y aún sales inorgánicas, al disolverse en agua generan
calor; otros absorben calor y se presentan fenómenos en los que, para el primer
caso la solución se calienta y para el segundo se enfría.
El calor generado o absorbido en el proceso, es función de la concentración final
de la solución. En la tabla 4 se establecen los calores de solución de algunos
solutos, en agua y a 25C.
Puede apreciase en ella que para algunos compuesto, como el HCl, a medida que
incrementa la disolución el calor de solución o entalpía de solución o entalpía de
solución aumenta.
El proceso de disolución puede ser representado por una ecuación química; así, al
disolver una mol de ácido clorhídrico puro en doscientas moles de agua, puede
escribirse, tomando el dato de la Tabla 8.
HCl(g) + 200 H2O (|)

HCl (200 H2O)- 17,74 kcal/gmol
Igualmente existen gráficas que relacionan el calor de disolución por mol de soluto
con las moles del solvente agua,
45
FIGURA 40
Ing. VICTOR JAIRO FONSECA V.
46
FIGURA 41
47
Ejemplo 52
¿Cuánto calor se genera al disolver una mol de ácido sulfúrico puro en 10 moles
de agua?
Solución
La ecuación se plantea:
H2SO4 (I,c,n) + 10 H2O(I,c,n)

H2SO4 (10H2O)(I,c,n) - Hd
Y de la figura 39
Hd = - 15.800 cal/gmol (H2SO4)
Ejemplo 53
Determine la cantidad de calor generado al disolver una solución de 1 a 1 molar
de ácido sulfúrico en 9 moles de agua.
Solución
El problema puede resolverse en dos formas:
a) Una directa, ya del ácido disuelto 1 a 1 para llevarlo al ácido 1 a 10, con la
ecuación:
H2SO4 (1 H2O)(I, c, n) + 9(H2O)(I,c,n)  H2SO4 (10H2O)(I,c-n) - Hd
y Hd = Hd H2SO4(10H2O)(I,c,-n) - Hd H2SO4 (1 H2O)(I,c-n)
Hd = - 15.800 - (-6.900) cal/gmol
Hd = - 8.900 cal/gmol
El balance de energía corresponde al de una reacción en la cual el calor de
disolución del agua (como reactante) es cero.
b) Una indirecta partiendo del ácido puro para llevarlo a soluciones 1 a 10 y 1 a 1
molar, luego :
H2SO4 (I,c.n) 10 H2O (Imc.n)
cal/gmol
H2SO4 (I,c.n) + H2O(I,c.n) 
Ing. VICTOR JAIRO FONSECA V.

H2SO4 (10H2O) (I,c.n) - 15.800
H2SO4 (H2O) (I.c.n) - 6.900 cal/gmol
48
Restando tenemos:
9H2O (I,c.n) 
H2SO4 (10 H2O)(I,c.n) - H2SO4 (H2O)(I,c.n) - 8.900 cal/gmol
ó H2SO4 (H2O)(I,c.n) + 9 H2O(I,c.n)
cal/gmol

H2SO4
(10H2O)(I,c.n)
-
8.900
El ejemplo 53, nos permite establecer un principio para calcular el calor de
disolución en soluciones.
El cambio de entalpía para diluir una solución es igual al calor de disolución a la
concentración final menos el calor de disolución a la concentración inicial.
Este principio es similar al que rige para los cambios de entalpía en las reacciones
químicas y en reacciones que implican procesos de disolución, se hace aplicación
general del mismo.
Ejemplo 54
El calor de formación del Cloruro de Potasio es de -104.348 calorías/mol y el calor
de formación del Cloruro de Potasio en 400 moles de agua es de - 100.164
calorías. Determine el calor de disolución del KCl en 400 moles de agua.
Solución
La reacción de formación para el KCl es:
K + ½ Cl2

KCl - 104.348
Para el KCl (400 H2O) su ecuación es:
K + ½ Cl2 + 400 H2O

KCl (400 H2O) - 100.164
Para la disolución del KCl en 400 mol de agua se tiene:
KCl + 400 H2O

KCl (400 H2O) + Hd
Y Hd lo obtenemos restando de la segunda ecuación la primera y
Hd = - 100.164 - (-104.348) = 4184 cal.
Ejemplo 55
Calcular el calor de formación del Cloruro de Potasio en 400 moles de agua. El
calor de formación del KCl es - 104.348 cal y el calor de disolución es de 4.184
cal.
49
Solución
Las ecuaciones que representan el proceso son:
K + ½ Cl2

KCl + 400 H2O
KCl - 104.348

KCl (400H2O) + 4.184
y
K + ½ Cl2 + 400 H2O

KCl(400 H2O) = 100.164 cal/gmol
Este ejemplo puede considerarse inverso al anterior, pero nos complementa el
manejo de los calores en disolución.
Es muy importante tener presente que el agua, en los procesos que impliquen
dilución se toma como un elemento y en los cálculos de cambio de entalpía, no se
tiene en cuenta el calor de formación del agua.
Usted debe determinar, dentro de una reacción que implique disolución, cuando
hay formación de agua para, en este caso, así tener en cuenta el calor de
formación del agua.
Ejemplo 56
Determine el cambio de Entalpía para la reacción
KOH + HCl (400 H2O)

KCl (400 H2O) + H2O (|)
Teniendo las siguientes entalpías:
Hf KOH = - 102.020 cal/gmol
Hf HCl(400 H2O) = 39.850 cal/gmol
Hf HCl (400 H2O) = - 100.164 cal/gmol
Hf H2O(l) = - 68.317 cal/gmol
Solución
El ejemplo nos muestra que en la reacción hay formación del agua líquida.
Aplicando la regla para el calor de reacción
Hf = Hf KCl(400 H2O), H2O(e) - Hf KOH, HC (400 H2O)
Luego Hf = - 26.611 calorías.
4.3.4. Calor de mezcla
Ing. VICTOR JAIRO FONSECA V.
50
Cuando dos sustancias puras se mezclan, el calor de mezcla se define como los
cambios de Entalpía que ocurren cuando las sustancias puras son mezcladas
para formar una solución a temperatura constante y presión de una atmósfera.
Al mezclar las sustancias A y B, el calor de mezcla Hm será:
Hm = HA + HB + Hs
[41]
Este calor de mezcla Hm es en realidad el Calor de Formación de la solución, en
el cual se toman los calores de formación de las sustancias A, B y el calor de
disolución de ellas.
El valor Hm para un sistema dado depende de las cantidades de A y B que
intervienen en la mezcla; para reportar valores normalmente se toma 1 mol del
compuesto A para mezclar con n moles del Compuesto B que se constituye en el
solvente, así:
Hm = HA + n HB + Hs
[42]
Otra forma de reportar valores y que es más conveniente, es el llamado Diagrama
de Entalpía - concentración (H - x).
Los diagramas de entalpía concentración, son gráficos de la entalpía de una
solución binaria como una función de la composición de la misma, con la
temperatura como parámetro y teniendo una presión constante de una atmósfera.
Los valores de entalpía se basan en unidades de peso o en una mol de solución.
Si una mol de solución tiene XA moles del compuesto A y XB moles del compuesto
B, la ecuación (38) se convierte en:
Hm = XA HA + XB HB + Hs
[39]
De esta ecuación se deduce que el valor de Hm depende de los calores de
formación de los compuestos puros y del calor de disolución de los mismos.
Como HA y HB son conocidos, Hs es mensurable a medida que se mezclan A
y B pudiéndose obtener así los valores de Hm’
Como base del diagrama entalpía- concentración se toma un HA igual a cero
para un estado específico del componente A y HB igual a cero para un estado
específico del componente B, sin que esto signifique que se ha escogido la misma
temperatura para los dos compuestos.
En el caso del diagrama H2SO4 - H2O se ha encontrado conveniente fijar que H
H2O sea cero para el agua pura líquida a 0C e igualmente H H2SO4 sea cero
para el ácido puro a 25C.
Para sistemas que tienen agua como uno de los componentes, se debe tomar la
entalpía del agua pura líquida como cero, a 0C, porque esta es la base usada en
51
las tablas de vapor.
Cuando el calor de disolución H3 es cero, la ecuación nos muestra que la
entalpía de una solución es igual a la suma de las entalpías de los componentes
puros que la forman.
Hm = XAHA + XBHB
[44]
Entalpia
En este caso especial es válido para las soluciones ideales, término muy similar al
de los gases ideales. En un concepto muy amplio, un gran número de soluciones
se aproximan al comportamiento de la solución ideal y ecuaciones simplificadas
pueden ser usadas para los cálculos requeridos.
Concentración
Figura 42
Diagrama Entalpía-Concentración
Para una solución ideal en el diagrama Entalpía-concentración, la isoterma es una
recta que une los puntos de la entalpía HA para XA = 1 con HB para XB = 1; las
isotermas reales son curvas, como se indica en la figura 11, la distancia vertical
entre la curva ideal y la curva real es la entalpía de disolución Hs’ cuyo valor
para la gráfica es negativo en todo el rango de composición y significa que la
disolución es exotérmica. Cuando la curva real está por encima de la ideal Hs es
positivo y el proceso de disolución es endotérmico.
Ejemplo 57
Un evaporador al vacío y baja temperatura, debe concentrar 5000 kilos de una
solución de NaOH del 10% al 50%. La solución entra al evaporador a una
temperatura de 25C.
La presión es de 0,1 atmósferas y bajo estas condiciones el punto de ebullición de
Ing. VICTOR JAIRO FONSECA V.
52
la soda al 50% es de 88C. Determine la cantidad de calor consumida por hora.
Solución
El diagrama de flujo representado en la Figura 50 nos indica esquemáticamente el
proceso.
Vapor de Agua
Y kgs/ hr
0,1 Atm.
O
88
C
NAOH10%
Y kg /hr
NaOH 50%
XC kg / hr
Evaporación al vacío
FIGURA 43
Efectuando el balance de materiales tenemos:
Q
Con base en el hidróxido de sodio:
5.000 X 0,10 = X x 0,50  X = 1.000 kg/hr.
Con base en el agua:
5.000 X 0,90 = X x 0,350 + Y  Y = 4.000 kg/hr
El balance de Energía se establece globalmente
Hs = Q = Hx + Hy - Hr
El cambio de entalpía es igual a la entalpía final, o de productos, menos la
entalpía inicial
Hx, entalpía para solución al 50% y 88C
= 119 kcal/kg
53
Hy, entalpía del vapor a 0,1 atm y 88C
= 638 kcal/kg
HA, entalpía de la solución al 10% y 25C = 19 kcal/kg
Q = 119 X 1.000 + 637 X 4.000 + 19 x 5.000 kcal
Q = 2.572.000 kcal
4.3.5. Calor de combustión
Una de las reacciones químicas más comunes es la oxidación rápida de algunas
sustancias conocidas como combustibles, esta reacción constituye el fenómeno
de la combustión, recibiendo tratamiento especial por parte de algunos autores.
El calor desprendido en una combustión es fácil de determinar en aparatos
llamados bombas calorimétricas, de las cuales la más usada es la Parr.
Ella consiste de un recipiente cilíndrico metálico con una camisa que se llena de
agua. Todo el recipiente se encuentra cuidadosamente aislado del ambiente.
La muestra se coloca dentro del recipiente el cual se llena de oxígeno puro a 20
atmósferas de presión.
Por medio de una bujía, una chispa produce la ignición del material.
Al combustir la muestra todo el sistema se calienta; como se conocen los
volúmenes del recipiente y del agua, así como los calores específicos de los
materiales, se determina el calor desprendido en la combustión por la elevación
que ha ocurrido en la temperatura del sistema.
Se busca que la elevación de temperatura sea pequeña, empleando pequeños
pesos de muestras y se puede asumir que el proceso ocurre a volúmenes y
temperaturas constantes.
El efecto calorífico medido en la bomba corresponde al cambio interno de energía
ocurrido durante la combustión, luego:
H = U + PV
Por la medición del calor generado en la bomba podemos determinar U y, como
el cambio de temperatura es muy bajo comparado con la temperatura del sistema
(1 ó 2%), teniendo en cuenta que T está en K), el término PV., que realmente es
VP, puede tomarse como despreciable.
Consideraciones más profundas sobre el comportamiento de VP en las
condiciones dadas, son objeto de la Termodinámica.
H = U + PV
.
Ing. VICTOR JAIRO FONSECA V.
54
Figura 44
Bomba calorimétrica de Parr - esquema
La gran importancia que merece la bomba de combustión radica en que, mediante
su uso, es posible determinar el calor de Formación de gran cantidad de
sustancias.
Aquí debemos recordar que en toda reacción química el calor de reacción es igual
al calor de formación de los productos menos el calor de formación de los
reactantes, en una combustión el calor de reacción es el de combustión, los
productos son CO2 Y H2O cuyos valores de formación se conocen, luego por las
ecuaciones correspondientes se calcula el calor de formación de los productos.
Ejemplo 58
Determine el calor de formación del Benceno líquido (C6H6). Si su calor de
combustión es de 780980 cal/mol
Solución:
El benceno combuste así:
C6 H6(l) + 7 ½ O2(g) 
3H2O(l) + 6 CO2(g) + Hc
Hc = 3H f (H2O) + 6 Hf (CO2)g - Hf (C6H6) cal/gmol
o
= -204951 - 564312 + 780980 cal/gmol
= 11717 cal/gmol
En algunas tablas se encuentran dos valores del calor de combustión para los
compuestos:
El llamado bruto o alto (gross or higher) y toma en cuenta la formación del agua
55
(producto de combustión) en la fase líquida y el llamado neto o largo (net o lower)
tiene en cuenta el agua formada en la fase gaseosa.
Ejemplo 59
Una bomba de Parr pesa 8 kilos y está hecha con un material cuyo C p es 0,3
cal/gC, su volumen es de 1 litro y tiene una camisa con 2 litros de agua.
Efectuada la combustión de 2 gramos de grafito, de densidad 2,25 g/cm 3, con
oxígeno puro a 25 atm se eleva la temperatura del sistema de 25 a 28,56C.
Determine el calor de combustión del grafito.
Solución:
La reacción de combustión es
Cs
O2(g) 
CO2(G) + HC
El calor de combustión lo calculamos aplicando
Hc = U y U = mCp T, tomándose en cuenta la elevación de la temperatura
del recipiente, del agua y del producto.
Ordenando las cifras y tomando datos de las Tablas tenemos:
Grafito
gramos
(0,167 gmol)
2,673 cal/gmol
Oxígeno
1
0,083 gmol)
8,270 cal/gmol
Agua
2.000 g
1.000 cal/g
Metal (bomba)
8.000 g
CO2
Aplicando la ecuación para U
0,30 cal/g
(0,167 gmol)
7,0 cal/g
U = (0,167 X 2,673 + 0,083 X 8,270 + 2000 X 1 + 8.000 X 0,3) 3,56
U = 15.668 cal.
Esta generación o producción de calor, fue dada por la combustión de 2 gramos
de grafito, teniendo la mol de grafito 12 gramos de carbón
Hc = 12/2 X 15.588 = 94.008 cal
En las tablas se tienen valores de 94.052, la pequeña diferencia de 44 calorías
(0,046%,) obedece a las correcciones de V.P.
Ejemplo 60
Calcúlese el calor de formación del n-Butanof C4 H10’ gaseoso a partir de los
Ing. VICTOR JAIRO FONSECA V.
56
calores de formación del agua y del CO2’
Solución
La ecuación teórica de formación es:
4C + 5H2

C4 H10 + Hf
Esta reacción no tiene ocurrencia en la práctica, pero se tiene otro tipo de
reacciones, como las de combustión, cuyos calores pueden determinarse en la
bomba de Parr.

C + O2
y
H2 + ½O2
C4 H10 + 13/2 O2


CO2 + Hc
H2O + Hc
5 H2O + 4CO2 Hc
Estableciendo el balance de las ecuaciones y reordenando tenemos:
4C(s) 4 O2(g)
5H2(g) + 5/2 O2(g)
5H20(g) + 4CO2(g)



4CO2(g) + 4(-94.052) Cal
5H20(g) + 5 -57.798) Cal
C4H10(g) + 13.202 + 635.384 Cal
4C + 5H2

C4H10(g) - 29814 cal/gmol
Sumando
Hemos usado como Hc del C4H10(g) el valor neto o bajo, ya que el agua, está en
la fase gaseosa.
Los ejemplos nos han indicado la importancia de los calores de combustión para
poder calcular los calores de formación de muchos compuestos existentes en la
naturaleza y que aún no se han podido determinar, pero igual o mayor importancia
ocupa en los procesos energéticos que tienen lugar en el metabolismo, bien sea
para la formación de alimentos o bien para su digestión.
Los procedimientos anteriores los hemos llevado a cabo trabajando en las
llamadas condiciones estándar pero, en la práctica, debido a la misma ubicación
de las industrias y a las condiciones de un proceso, las presiones y temperaturas
son muy diferentes a las normales.
4.4. Balance estequiométrico de masa y energía
Hemos apreciado cómo los efectos y fenómenos asociados con el calor conllevan
balances de ecuaciones químicas y/o físicas, provenientes de cambios químicos
y/o físicos, sin tener en cuenta el tiempo en que ocurren las transformaciones, ni
las condiciones de operación.
Por esta razón, debe tenerse en cuenta un procedimiento que permita establecer
los cambios de energía que ocurran en un proceso con condiciones iniciales y
57
finales dadas en un tiempo dado.
El procedimiento realmente es una secuencia de cambios
termodinámico y por tal razón se denomina proceso termodinámico.
de
orden
El proceso consta básicamente de tres pasos:
a) Reducir las condiciones iniciales de P1’ T1 a Pn, Tn.
b) Llevar a cabo el proceso químico o físico (reacción), incluyendo diluciones y
concentraciones, a condiciones normales y
c) Llevar las condiciones normales (Pn, Tn) a T 2 y P2 los productos obtenidos.
Para aquellos estudiantes que no dominen el manejo de la reacción química, así
como las transformaciones simultáneas de presión y temperatura, los pasos
anteriores se desglosan y se establecen:
a) Reducir la presión de P1 a Pn
b) Reducir la temperatura de T1 a Tn
c) Separar los reactantes en sustancias puras.
d) Llevar a cabo las reacciones químicas en condiciones normales.
e) Mezclar los productos.
f) Calentar los productos de Tn a T2 y
g) Comprimir (o expandir) el producto de Pn a P2
En ocasiones, algunos procesos exigen operaciones muy especiales, lo que
obliga a emplear diferentes pasos, tanto en el número como en el orden, dentro
del proceso termodinámico.
Realmente los ejemplos son los que mejor pueden ayudar para la comprensión y
manejo de los conceptos que intervienen en el proceso.
Recomendamos al estudiante acudir a la bibliografía aconsejada, ya que en ella
encontramos buenos y numerosos ejemplos.
Igualmente es aconsejable ayudarse con diagrama o gráficos, pues ellos permiten
visualizar un proceso y facilitan el planteamiento del problema.
Para los ejemplos siguientes sugerimos que el estudiante resuelva el problema
empleando otra alternativa, es decir realice otros pasos o los mismos en diferente
orden.
Ejemplo 61
Determine el calor de formación del HCl, para una temperatura de 800C.
Ing. VICTOR JAIRO FONSECA V.
58
Solución
Recuerde usted, que la ecuación química para la formación del ácido clorhídrico
es
½H2(g) + ½ Cl2(g)

Hcl(g) + Hf
Y de las tablas el Hf = - 22063 calorías. (Condiciones Normales). En el gráfico se
puede visualizar el proceso.
Para emplear datos disponibles en tablas, el proceso lo efectuaremos en tres
etapas:
a) Llevar los reactantes de 800C a 25C
b) Efectuar la reacción.
C) Llevar el producto de 25 a 800C.
FIGURA 45
Formación del HCl a 800°C
De las tablas se tiene:
Cp Hcl = 6,70 + 0,00084 T cal/molC
CpCl2 = 7,58 + 0,00064 T cal/gmolC
Cp H2 = 6,62 + 0,00081 T cal/gmolC
Hof (Hcl) = - 22063 cal
Para los procesos de cambios de temperaturas podemos emplear los C p para H2
59
a 800 Cp
a 25 Cp
Cp
Para Cl2
a 800 Cp
a 25 Cp
Cp
Para Hcl
a 800 Cp
25 Cp
Cp
=
=
=
7,489 cal/molC
6,681 cal/molC
7,175 cal/molC
=
=
=
8,26 cal/molC
7,770 cal/molC
8,015 cal/molC
=
=
=
7,600 cal/molC
6,950 cal/molC
7,275 cal/molC
a) Para llevar el H2 y Cl2 de 800 a 25C.
=
=
=
7,175 (25 - 800) + 8,015 (25 - 800) cal
-5.561 - 6.211
= - 11.772 cal (por mol de H2 y Cl2 )
- 5.561 cal ( por ½ mol de H2 y Cl 2 )
b) El calor de reacción Hf es - 22.063 ( por mol de Hcl)
c) Para llevar el Hcl de 25 a 800 
Q = mCp T = 7.275 (800 - 25) = 5.638 cal
Luego Q1 = - 5.886 - 22.063 + 5.638 = - 22.311 cal.
Ejemplo 62
Calcule el calor de combustión del metano a 600C si los productos de
combustión son CO2 + H2O
Como en el caso anterior, tenemos tres pasos:
a) Enfriar metano y Oxígeno a 25C
b) Combustir
c) Calentar productos a 600C
La combustión a condiciones normales se efectúa acorde a
CH4(g) + 2 O2(g)

Ing. VICTOR JAIRO FONSECA V.
CO2(g) + 2H2O(|) - 212.800
60
C H 4 600 C
2O2 1 Atm.
C H4
2O2
600 C
1 Atm.
FIGURA 46
Formación del CH4 a 600°C
Los valores comprendidos de los Cp se pueden tomar:
CH4
10,0
cal/gmolK
O2
7,3
CO2
9,9
H2O
8,2
a) Q1 = 1 X 10,0(25-600) + 2 X 7,3 (25 - 600)
=
b) Hf = - 212.800
=
c) Q2 = 1 X 9,9 (600 - 25) + 2 X 8,2 (600 - 25)
=
C H4
2O2
- 14.145 cal
- 212.800 cal
+ 15.123 cal
Los dos ejemplos nos ilustran casos de común ocurrencia en la industria y son
aplicación de los conocimientos que el estudiante ha adquirido en este capítulo.
Observando con detenimiento el desarrollo y resultados obtenidos, llegamos a
conclusiones importantes.
a) Los calores de formación y/o combustión dentro de un rango amplio de
temperatura (600 a 800C) varían muy poco, 1,12% para el primer y 0,46% para el
segundo caso.
b) La diferencia anterior es la diferencia entre las cantidades de calor de la etapa
final (o de cambio de temperatura de los productos) y la cantidad de calor de la
etapa inicial (o de cambio de temperatura de los reactantes).
Volviendo al ejemplo 61, el paso a) lo podemos reordenar así:
C O2
H O2
61
Q1 =
- ( 7.175 + 8.015 )
----------------------------(800-25)
2
= - 5.886 cal/gmol
Como Q2 = 7,275 (800 - 25)= 5.638 cal/gmol
7,175
8,015
Sumando Q1 + Q2 = (7,175 - -------- + ---------- ) (800 - 25) = - 248 cal/gmol
2
2
que es el cambio neto de energía respecto al calor de formación a 25C (- 22311 22063 = - 248 cal/gmol)
Observando los valores que se encuentran dentro del paréntesis, ellos son: el
calor específico del producto menos el calor específico de los reactantes,
multiplicando cada uno de ellos por el número de moles correspondientes de la
reacción química. (Recordamos ½ H2 + ½ Cl = Hcl las moles del producto son 1 y
de los reactantes ½ y ½).
En el ejemplo 62 el paso (a) nos queda:
Q1 = - (10.0 + 2 x 7,3) ( 600 - 25 ) = 14,5
Como
Q2 = ( 9,9 + 2 x 8,2 ) - 10,0 + 2 x 7,3 ) (600 - 25)
Q1 + Q1 = 978 kcal / mol
Que es el cambio neto de energía respecto al calor de combustión a 25 0 C
Para determinar los calores o entalpías de reacción, a condiciones diferentes a las
normales, podemos generalizar lo planteado en los ejemplos diciendo que el calor
de reacción a condiciones diferentes de las normales es igual al calor de reacción
a condiciones normales más el cambio de entalpía de los reactantes y de los
productos entre las condiciones dadas y las normales, es decir:
H t
ó
= H f n
H t
+ 
= H f n
T
T
( nr  298 CP dT ) -  ( np  298 CP dT )
+ 
(30)
T
( nr  298  CP dT )
donde  CP = ( CP ) prod - ( CP ) react
Estas ecuaciones pueden visualizarse objetivamente en los ejemplos anteriores.
Ejemplo 63
Ing. VICTOR JAIRO FONSECA V.
62
Determine el calor de formación del Benceno líquido a 70C, si su calor de
combustión es de - 780 980 cak/mol-g
Solución
La reacción química es:
C6 H6 (l) +15/2 O2 (g)
------
3 H 2 O (g)
+ 6 CO 2 (g) - 780.980
Se tiene
H c
= 3H f ( H 2 O ) + 6H f ( CO 2 ) - H f ( C6 H6 )
H f ( C6 H6 )
= 3H f ( H 2 O ) + 6H f ( CO 2 ) - H c
Y tomando valores de tablas tenemos que
H f ( C6 H6 ) = 3 (- 68.317 ) + 6 ( -94.052) + 780.980 = 11.717 cal /mol ( ver
ejemplo 22)
La ecuación nos queda directamente:
3 H 2 + 6C = C6 H6 + 11.717 cal / mol
Debemos advertir que en la práctica y aún a nivel experimental, no se ha logrado
la reacción anterior.
Sin embargo el empleo de pasos termodinámicos en un proceso teórico, nos
permite determinar propiedades de las sustancias que son imposibles de conocer
prácticamente, tal como lo mencionábamos en la sección sobre calor de
combustión.
Con la ayuda del diagrama, planteamos los pasos.
a) Llevar H2 y C de 70C a 25C
b) Hacer la reacción
c) Subir el C6 H6 de 25 a 70C
Los valores de Cp son:
H2
= 7,175 cal/ mol
C
= 2,820 cal/ mol
C6 H6 = 32.500 cal/ mol
Pero al efectuar directamente el proceso, acorde a la ecuación (42)
63
3H2
C6
70 C
1 Atm.
C
A
3H2
FIGURA 47
Formación del benceno
B a 70°C
Q = 11.717 +C(6 32, 5 - 6 x2,820 - 3 x 7,175 ) ( 70 - 25 )
Q = 11,449 calorías
Ing. VICTOR JAIRO FONSECA V.
70 C
1 Atm.
64
Calor Espécifico, J/kg°k
CALOR ESPECIFICO, Cp
Leche Entera Pasteurizada
3930
3920
3910
y = 0,422x 20,4452x + 3863,7 +
3900
3890
3880
3870
3860
0
10 20 30 40
50 60 70 80 90 100
Temperatura, °C
Calor Espécifico, J/kg°k
CALOR ESPECIFICO, Cp
Mantequilla
2400
y = -0,3164x 213,049x + 2287,3 +
2380
2360
2340
2320
2300
2280
0
10
20
30
40
50
60
70
Temperatura, °C
80
90 100
65
Ing. VICTOR JAIRO FONSECA V.
66
67
Ing. VICTOR JAIRO FONSECA V.
68
69
Ing. VICTOR JAIRO FONSECA V.
70
71
Ing. VICTOR JAIRO FONSECA V.
72
73
Ing. VICTOR JAIRO FONSECA V.
74
75
Ing. VICTOR JAIRO FONSECA V.
76