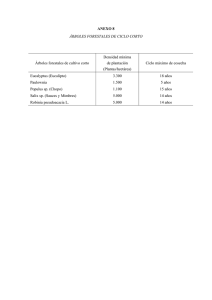
Tabla de volumen para Populus nigra cv Italica en plantaciones

Tabla de volumen para Populus nigra cv ‘Italica’ en plantaciones lineales en el noroeste
de Chubut.
AMICO I.1; BAVA J.2,3, CALDERÓN A.4
1
Técnico INTA EEA Esquel. Chacabuco 513. Esquel. Chubut. [email protected]
Investigador CIEFAP. Ruta 259. Esquel. Chubut. [email protected]
3
Profesor adjunto Cátedra Dasometría. Facultad de Ingeniería Forestal. Universidad
Nacional de la Patagonia. San Juan Bosco
4
Profesor titular Cátedra Dasonomía. FCA. UNCuyo. [email protected]
2
Resumen
En el noroeste de Chubut se encuentran establecidas cortinas rompevientos de álamo con el
objetivo de proteger los cultivos y brindar abrigo al ganado. Los sitios donde se encuentran las
alamedas son predios destinados al cultivo de pasturas, forrajes o al pastoreo de vacunos y
ovinos. La especie más difundida es el álamo negro o criollo (Populus nigra cv ‘Italica’). Estas
plantaciones se establecieron con fines ambientales y de protección, pero en algunos casos,
son cortadas y aprovechadas una vez que los árboles alcanzan su madurez. Su madera es
utilizada para tirantería de techos, machimbre, muebles, postes y leña. El presente trabajo tiene
como objetivo presentar una herramienta para la estimación del volumen total con corteza, de
aplicación en el noroeste de la provincia de Chubut. Se presenta una función para el cálculo de
volúmenes de árboles individuales para Populus nigra cv ‘Italica’ en cortinas rompevientos. La
muestra consistió en 40 árboles con los cuales se ajustaron modelos lineales y no lineales de
simple y doble entrada. Se usaron como variables independientes la altura (H), el diámetro a la
altura del pecho (Dap) y la variable combinada Dap2*H. El modelo elegido fue el de
Schumacher-Hall (V = a . Dapb Hc ) por presentar mejor ajuste y menores residuos.
Palabras clave: Populus nigra cv ‘Italica’ – tabla volumen – Chubut.
1
Introducción
En el noroeste de Chubut se encuentran establecidas cortinas rompevientos de álamo con
el objetivo de proteger los cultivos y brindar abrigo al ganado. Los sitios donde se encuentran
las alamedas son predios destinados principalmente al cultivo de pasturas, forrajes y/o al
pastoreo de vacunos y ovinos. La mayoría de estas alamedas son plantaciones lineales de una
sola fila y la especie más difundida es el álamo negro o criollo (Populus nigra cv ‘Italica’).
A pesar que la zona tiene buenas condiciones ecológicas para el cultivo de álamos, existen
pocas forestaciones y muchas ellas son muy viejas. Las alamedas se establecieron con fines
ambientales y paisajísticos, pero eventualmente, son cortadas una vez que los árboles
alcanzan la madurez. La madera es utilizada para tirantería de techos, encofrado, machimbre,
muebles, postes y leña.
En la Región Andino Patagónica, no existen modelos de predicción de volumen para
álamos. Para la provincia de Santa Cruz, Peri (1994) y Peri et al. (1998) crearon algunos
modelos de predicción, pero estos no se ajustan a la zona debido a que fueron realizados en
sitios con condiciones ambientales muy diferentes.
Con el fin de elaborar una tabla de volumen para el noroeste de la provincia de Chubut, se
ajustaron distintos modelos de predicción en función del diámetro a la altura de pecho y la
altura.
Materiales y Métodos
Se trabajó con material proveniente seis plantaciones lineales en secano ubicadas en
las localidades de Trevelin y El Hoyo. Se apearon 40 árboles abarcando distintos rangos de
diámetros y alturas. Los árboles eran adultos, pero se desconocía la edad de las plantaciones.
Los árboles se seleccionaron teniendo en cuenta la calidad del fuste, evaluando la presencia
de daño y todo signo externo como grietas, rajaduras o agallas que pueda ser indicador de
anomalías internas en la madera. A cada individuo se le midió el diámetro al tocón (a 30 cm del
suelo), Dap (diámetro a altura del pecho), diámetros cada dos ó tres metros según el caso y la
altura total. La edad se determinó contando los anillos en rodelas extraídas a la altura del tocón
y del Dap. El volumen de las trozas se calculó usando la fórmula de Smalian y para la troza
apical se utilizó la fórmula del volumen del cono.
Utilizando el diámetro y la altura como variables predictoras, se ajustaron modelos
lineales con una o dos variables, simple o combinada y un modelo no lineal con las dos
variables predictoras. Para el ajuste de los modelos y el análisis estadístico se utilizó el
programa InfoStat versión 2008. Mediante el análisis de regresión, utilizando el método de los
mínimos cuadrados se obtuvieron los estimadores de los parámetros de los modelos. En el
modelo no lineal (Ecuación de Schumacher - Hall) se probaron distintos valores iniciales para
estimar los parámetros en base a la bibliografía (Prodan et al, 1997; Peri y Martinez Pastur,
1998; Peri et al, 1998). El análisis de la varianza y la representación gráfica de los residuales
permitió evaluar los modelos ajustados.
En la Tabla nº 1 se presentan los modelos ajustados con una o dos variables. De estos
modelos, los más usados en dasometría son el conocido como de variable combinada de Spurr
y el de Schumacher - Hall (Bava, 2005).
2
Tabla nº 1:
Modelos preseleccionados para la estimación de volumen en plantaciones lineales
de Populus nigra cv ‘Italica’
Tipo de Modelo
V= a + bDap
V= a + bDap + cDap2
V= a + bDap + cH
V= a + bDap + cDap2 + dH + eH2
V= a + bDap 2+ cH + dH2
V= a + b Dap2H (Modelo de Spurr)
V= a DapbHc (Modelo de Schumacher Hall)
V: Volumen en m3
Dap: Diámetro a la altura del pecho en cm
H: altura en m
Resultados
Los árboles muestra presentaron amplitud de Dap, altura y edad. Los árboles eran
adultos y de edad avanzada. El volumen real promedio de fuste de la muestra fue de 1,7719
m3, el Dap promedio de 48,73 cm y la altura promedio 27,04 m. En la Tabla nº 2 pueden
observarse las características de los árboles muestreados.
Tabla 2: Características de los árboles muestra
Variable
Media
Mín
Máx
Edad al tocon
32
22
55
Edad al dap
30,5
21
52
Dap
48,73
31,75
71,50
H
27,04
15,40
36,80
Volumen
1,7719
0,4851
3,4976
Para la elección del modelo más apropiado, la evaluación estadística se basó en el
coeficiente de determinación ajustado (r2 ajust), el cuadrado medio del error (CME), el error
estándar de las estimaciones de los parámetros, el análisis de los residuales de la regresión,
las medias aritméticas de los residuos en valor absoluto (Media Res abs), la representación
gráfica de los residuales y la representación gráfica de los volúmenes observados en función
de los estimados (los predichos por el modelo). En la Tabla nº 3 se presentan las funciones de
volumen ajustadas y sus estadísticos.
3
Tabla nº 3: Funciones de volumen ajustadas y sus estadísticos
r2
ajust
CME
V= -1,522459+0,0067606*DAP
0,8661
0,1124
0,2796
V= -1,018342+0,0466590*DAP+0,00204644*DAP2
0,8661
0,1146
0,2766
V= -2,398742+0,056144*DAP+0,053061*H
0,9574
0,0346
0,1202
V= 0,170899+0,016614*DAP+0,000414*DAP2*0,080891*H+0,002528*H2
0,9699
0,0244
0,1109
V= 0,474228+0,000571*DAP2-0,073235 *H+0,002400*H2
0,9701
0,0242
0,1114
V= 0.662747+0,000080*DAp2*H
0,8360
0,1331
0,2822
V= 0,000123*DAP1,459329*H1,165000
0,9730
0,0218
0,1088
Función ajustada
Media
Res abs
Varios modelos mostraron un buen comportamiento de los indicadores estadísticos. La
comparación de modelos se basó en el criterio de buscar que el cuadrado medio del error
(CME) sea lo menor posible, que el error estándar de las estimaciones de los parámetros sea
lo más pequeño posible, que el coeficiente de determinación ajustado (r2 ajust) sea alto, que las
medias aritméticas de los residuos en valor absoluto sea pequeña (Media Res abs) y que los
coeficientes estimados no se encuentren altamente correlacionados. Para la selección
definitiva se hizo prevalecer el análisis de los residuales y la observación de los gráficos de
dispersión de los residuos versus los valores estimados por los modelos (que no presentaran
sesgo ni tendencia).
El modelo seleccionado fue el siguiente:
V=0,000123*DAP1,459329*H1,165000
El volumen real promedio de fuste de la muestra fue de 1,7719 m3 y el estimado por el
modelo 1.7717 m3. El error estándar de la función seleccionada fue 0,1407 m3 y el promedio
del valor absoluto de los residuos de 0,1088 m3.
En la Figura nº.1.puede observarse que los residuales de los valores predichos por el
modelo elegido se concentran en torno al valor cero –donde la mayor congregación se aprecia
entre +0,2 m3 y –0,2 m3–, con una tendencia a tomar una forma de megáfono, con mayores
residuos cuando los valores de volumen son mayores. En teoría esto indicaría que se está
violando el supuesto de homoscedasticidad de varianzas. Sin embargo, pueden hacerse dos
consideraciones importantes: una de ellas es que la tendencia es leve y la mayor parte de los
valores predichos se distribuye en forma bastante uniforme. En segunda instancia, en la
práctica los ajustes de funciones a través de técnicas de regresión cumplen sólo
excepcionalmente con este supuesto. En la Figura nº 2 se muestra la relación entre los
volúmenes observados y los estimados con la función de Schumacher y Hall.
4
Figura nº 1: Residuos de los valores predichos por el modelo elegido
0,40
0,30
Residuos_Volumen
0,20
0,10
0,00
-0,10
-0,20
-0,30
-0,40
0,00 0,50 1,00 1,50 2,00 2,50 3,00 3,50 4,00
Predichos_Volumen
Figura nº 2: Volumen observado y estimado por árbol con la Ecuación de Schumacher – Hall.
4,00
3,50
3,00
Volumen
2,50
2,00
1,50
1,00
0,50
0,00
0,00 0,50 1,00 1,50 2,00 2,50 3,00 3,50 4,00
Predichos_Volumen
Con los datos de la muestra se trató de validar la ecuación de volumen presentada por
Peri y Martinez Pastur (1998) para la provincia de Santa Cruz. Se observó que a igualdad de
diámetro y altura, la función ajustada por estos autores sobreestima el volumen. Por lo tanto,
esta función no se adapta para los árboles del noroeste del Chubut, que para diámetro
semejantes, los árboles son más altos.
En la Tabla nº 4 se presenta la tabla para determinar el volumen por árbol en función del
diámetro a la altura del pecho (Dap) y la altura total con el modelo seleccionado de
Schumacher y Hall.
5
Tabla nº 4: Tabla de volumen para Populus nigra cv ‘Italica’ en función del Dap y la Altura.
Tabla de Volumen total m3
Altura Total (m)
Dap
(cm)
30
32
34
36
38
40
42
44
46
48
50
52
54
56
58
60
62
64
66
68
70
72
14
0,3808
0,4185
0,4572
0,4969
0,5377
0,5795
0,6223
16
0,4449
0,4889
0,5341
0,5806
0,6282
0,6771
0,7270
0,7781
0,8303
0,8835
18
0,5104
0,5608
0,6127
0,6660
0,7206
0,7767
0,8340
0,8926
0,9524
1,0134
20
0,5770
0,6340
0,6927
0,7529
0,8148
0,8781
0,9429
1,0091
1,0768
1,1457
1,2161
1,2877
1,3606
1,4348
1,5102
1,5868
22
0,6448
0,7085
0,7740
0,8414
0,9104
0,9812
1,0536
1,1276
1,2032
1,2803
1,3589
1,4389
1,5204
1,6033
1,6875
1,7731
24
0,7136
0,7841
0,8566
0,9311
1,0076
1,0859
1,1660
1,2479
1,3316
1,4169
1,5039
1,5924
1,6826
1,7743
1,8676
1,9623
2,0585
2,1561
26
0,7833
0,8607
0,9403
1,0221
1,1060
1,1920
1,2800
1,3699
1,4617
1,5554
1,6508
1,7481
1,8471
1,9477
2,0501
2,1541
2,2596
2,3668
2,4755
2,5857
2,6975
6
28
0,8540
0,9383
1,0251
1,1143
1,2058
1,2995
1,3954
1,4934
1,5935
1,6956
1,7997
1,9057
2,0136
2,1234
2,2349
2,3483
2,4634
2,5802
2,6987
2,8189
2,9407
30
0,9255
1,0169
1,1109
1,2076
1,3067
1,4083
1,5122
1,6184
1,7269
1,8375
1,9503
2,0652
2,1821
2,3011
2,4220
2,5448
2,6696
2,7962
2,9246
3,0548
3,1868
3,3206
32
0,9977
1,0963
1,1977
1,3019
1,4087
1,5182
1,6303
1,7448
1,8617
1,9810
2,1026
2,2265
2,3525
2,4808
2,6111
2,7435
2,8780
3,0145
3,1530
3,2934
3,4357
3,5798
34
1,0707
1,1765
1,2853
1,3971
1,5118
1,6293
1,7496
1,8725
1,9980
2,1260
2,2565
2,3894
2,5247
2,6623
2,8022
2,9443
3,0886
3,2351
3,3837
3,5344
3,6871
3,8418
36
1,1445
1,2575
1,3738
1,4933
1,6159
1,7415
1,8700
2,0014
2,1355
2,2724
2,4119
2,5539
2,6985
2,8456
2,9952
3,1471
3,3013
3,4579
3,6167
3,7777
3,9410
4,1064
38
1,2189
1,3393
1,4631
1,5904
1,7210
1,8548
1,9916
2,1315
2,2744
2,4201
2,5687
2,7200
2,8740
3,0306
3,1899
3,3517
3,5159
3,6827
3,8518
4,0233
4,1972
4,3733
Conclusiones
El modelo propuesto por Schumacher y Hall resultó ser el más conveniente de los que se
probaron en este trabajo.
Los valores de los estadísticos utilizados en el análisis de la varianza, nos permiten aceptar
la existencia de un buen ajuste entre las variables consideradas, mientras que el análisis gráfico
de los residuales comprobó la ausencia de sesgo del modelo.
Bibliografía
- Bava, J. 2005. Apuntes de Cátedra Dasometría. Facultad de Ingeniería Forestal. Universidad
Nacional de la Patagonia San Juan Bosco. Sede Esquel. 99 p.
- InfoStat, 2008. Software InfoStat versión 2008. Manual del Usuario Grupo InfoStat, FCA,
Universidad Nacional de Córdoba, Argentina.
- Peri, P.L 1994. Ecuaciones de volumen total para tres especies de Salicáceas en Ea. "La Julia",
provincia de Santa Cruz, Argentina. Publicación Técnica Forestal Nº 2 Convenio UNPA-INTACAP.
- Peri P.; Martinez Pastur G. 1998 Crecimiento en cortinas cortaviento de Populus nigra cv Italica
en Patagonia, Argentina. Investigación Agraria: Sistemas y Recursos Forestales 7 (1-2): 73-83.
- Peri, P.; Battro P.; Sendín, M. 1998 Uso de modelos de crecimiento en cortinas cortaviento de
Populus nigra cv Italica, relacionado a las características de suelos y al inventario de existencias,
en el valle inferior del río Chubut. Publicación Técnica Forestal Nº 10 UNPA - EEA Santa CruzEEA Chubut. 18 pp.
- Prodan, M.; Peters, R.; Cox, F.; Real, P. 1997. Mensura Forestal. Serie de Investigación y
Educación en el desarrollo sostenible. BMZ/GTZ; IICA: san José, Costa Rica. 586 pp.
7