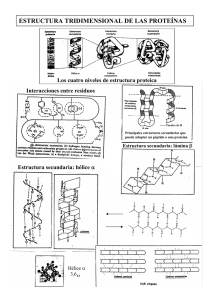
Separación y procesos biotecnológicos - U

Universidad De Chile
Facultad de Ciencias Físicas y Matemáticas
Departamento de Ingeniería Química y Biotecnología
Profesora: María Elena Lienqueo
Auxiliar: Ana Quiroga
Ayudante: Diego Díaz P.
Separación de Proteína y Procesos Biotecnológicos
Ejercicio 3
Primavera de 2010
Una muestra de la proteína A ha sido inyectada a una columna de HIC, el perfil obtenido
se muestra en la siguiente tabla:
Volumen
[ml]
410
445
500
550
575
600
625
650
Proteína A
[g/L]
0,03
0,28
0,91
0,35
0,05
Contaminante
[g/L]
0,03
0,25
0,5
0,25
0,03
a) Determine los perfiles cromatográficos tanto para la proteína A como para el contaminante.
Recomendación: Dibuje los perfiles. (3,0 puntos)
b) Determine la concentración de proteína A y contaminante en la muestra que se inyecta a la
columna (yf) (1,5 puntos)
c) Suponiendo que la fracción de huecos es de un 40%, y sabiendo que se ha determinado la
constante de adsorción de la proteína A que es 10. Determine el volumen total de la columna
y la constante de adsorción del contaminante. Comente. (1,5 puntos)
Pauta
a) A partir de los datos y graficando se tiene:
De allí se desprende que la ecuación de un perfil cromatográfico es:
𝑡
−1
𝑡0
𝑦 = 𝑦0 ∙ 𝑒𝑥𝑝 −
2 ∙ 𝜎𝐴2
2
Del gráfico:
𝒚0 (g/L)
Vo (mL)
Proteína A
0,91
500
Contaminante
0,5
600
El valor de  se obtiene al calcular la pendiente de:
𝑡
𝑦
1 − 𝑡0 − 1
𝐿𝑛
= 2∙
𝑦0
𝜎
2
2
Linealización Proteína A
-3,5
-3
-2,5
-2
-1,5
-1
ln(Y/Yo)
-4
-(V/Vo - 1 )^2/2
0
-0,002 0
-0,5
-0,004
-0,006
-0,008
-0,01
-0,012
-0,014
-0,016
-0,018
0,5
y = 0,004x - 0,000
R² = 0,969
Linealización Contaminante
0
-3
-2,5
-2
-1,5
-1
-0,5-0,0005 0
0,5
-0,001
ln(Y/Yo)
-0,0015
-0,002
-0,0025
-0,003
-0,0035
-0,004
-(V/Vo - 1 )^2/2
De allí se desprende que:


2
Proteína A Contaminante
0,004
0,001
0,0632
0,0316
Luego los perfiles serían:
Proteína A:
2
 V


 1 


500
ml
 
y = 0,91gr / lt   exp   


2  0,004




y = 0,001x - 9E-06
R² = 1
Contaminante:
2
 V



 1 


600
ml
 
y = 0,5gr / lt   exp   


2  0,001




b) Calculo de yf, para ello se utiliza las ecuaciones
yo =
yF
2N
N=
Combinando se tiene
yF =
1
2
yo 2

Proteína A Contaminante
Yf (g/L)
36,1
39,7
c) Usando la ecuación:
k=
Vo  Vc
(1   )Vc
 =0,4 y k=10 según enunciado.
Despejando Vc con los datos para la proteína A:
Vc =
Vo
500[ml]

(  (1   )k ) (0,4  (1  0,4)10)
Vc = 78, 125 [ml]
Calculo de k del contaminante:
k=
Vo  Vc 600[ml]  0,4  78,125[ml]

(1   )Vc
(1  0,4)  78,125[ml]
K_contaminante = 12,13
Comentario:
La matriz tiene más afinidad por el contaminante, se recomendaría utilizar otra matriz.