1º de Bachillero SOLUCIONES A LOS EJERCICIOS Y PROBLEMAS

MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I
Unidad 9: Aplicaciones de la derivada
SOLUCIONES A LOS EJERCICIOS Y PROBLEMAS BÁSICOS
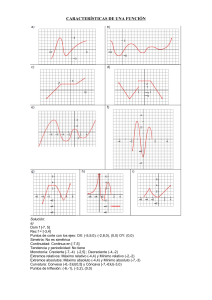
1. Determina los intervalos de crecimiento, decrecimiento, concavidad y
convexidad; y los puntos de máximo relativo, mínimo relativo, máximo
absoluto, mínimo absoluto y puntos de inflexión de la función f(x) cuya gráfica
es:
SOLUCIÓN
Creciente: (-2, 0) ∪ (2, + ∞ )
Decreciente: (- ∞ , -2) ∪ (0, 2)
Concava: (-2, 2)
Convexa: (- ∞ , -2) ∪ (2, + ∞ )
Máximo relativo en x=0 M(0, 12)
Mínimos relativos en x= -2 y x=2 m1(-2, 0) y m2(2, 0)
Máximo absoluto: No existe
Mínimos absolutos: m1(-2, 0) y m2(2, 0)
2. Dibuja las gráficas de las siguientes funciones y, a partir de ellas, determina los
intervalos de crecimiento, decrecimiento, concavidad y convexidad; y los
puntos de máximo relativo, mínimo relativo, máximo absoluto, mínimo
absoluto y puntos de inflexión.
−2
a) y=-x+2 en [-2, 3]
b) y=-2x2+8x en [0, 5] c) y=
en (- ∞ , + ∞ )
x
SOLUCIÓN
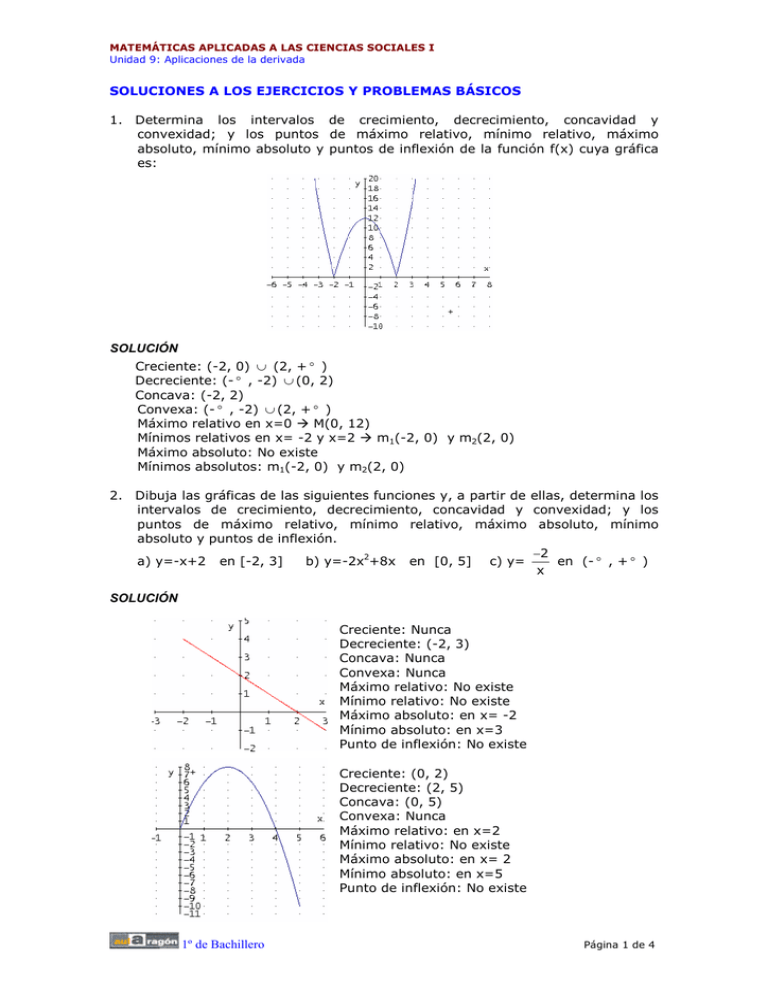
Creciente: Nunca
Decreciente: (-2, 3)
Concava: Nunca
Convexa: Nunca
Máximo relativo: No existe
Mínimo relativo: No existe
Máximo absoluto: en x= -2
Mínimo absoluto: en x=3
Punto de inflexión: No existe
Creciente: (0, 2)
Decreciente: (2, 5)
Concava: (0, 5)
Convexa: Nunca
Máximo relativo: en x=2
Mínimo relativo: No existe
Máximo absoluto: en x= 2
Mínimo absoluto: en x=5
Punto de inflexión: No existe
1º de Bachillero
Página 1 de 4
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I
Unidad 9: Aplicaciones de la derivada
Creciente: (- ∞ , + ∞ )-{0}
Decreciente: Nunca
Concava: (0, + ∞ )
Convexa: (- ∞ , 0)
Máximo relativo: No existe
Mínimo relativo: No existe
Máximo absoluto: No existe
Mínimo absoluto: No existe
Punto de inflexión: No existe
3. Utiliza las derivadas para hallar los intervalos de crecimiento, decrecimiento,
concavidad y convexidad; y los puntos de máximo relativo, mínimo relativo, e
inflexión, en las siguientes funciones:
a) y =2x-1
b) y=(x-2)2
c) y = -2x3
SOLUCIÓN
a)
y’ = 2>0 en (- ∞ , + ∞ )
Creciente en (- ∞ , + ∞ ) no hay máximo ni mínimo relativos
y’’=0 en (- ∞ , + ∞ )
No hay concavidad, ni convexidad, ni tiene puntos de inflexión
b)
y’ = 2(x-2)
y’ =0 ⇒ x-2=0 ⇒ x=2
Si x<2 ⇒ y’<0 ⇒ decreciente en (- ∞ , 2)
Si x>2 ⇒ y’>0 ⇒ creciente en (2, + ∞ )
En x=2 y’ =0 y la función pasa de decreciente a creciente ⇒ mínimo
relativo en x=2
y’’= 2>0 siempre ⇒ convexa en (- ∞ , + ∞ ) No existen puntos de
inflexión
c)
y’ = -6x2 <0 siempre ⇒ decreciente en (- ∞ , + ∞ )
y’’ =-12x
y’’=0 ⇒ -12x=0 ⇒ x=0
Si x<0 ⇒ y’’>0 ⇒ convexa en (- ∞ , 0)
Si x>0 ⇒ y’’<0 ⇒ cóncava en (0, + ∞ )
En x=0 y’’ =0 y la función pasa de convexa a concava ⇒ Punto de
inflexión en x=0
4. Las funciones de ingresos y costes anuales por la fabricación y venta de q
unidades de un determinado producto vienen dadas por:
I(q) = 2000q – 0’04q2 ;
C(q) = 1000000+100q+0’001q2
Halla:
a) La función que da el beneficio anual.
b) ¿Cuántas unidades hay que producir y vender para que el beneficio sea
máximo? ¿Cuál es ese beneficio?
1º de Bachillero
Página 2 de 4
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I
Unidad 9: Aplicaciones de la derivada
SOLUCIÓN
a) El beneficio es igual a los ingresos menos los costes:
B(q) = I(q) - C(q) = 2000q – 0’04q2 – (1000000+100q+0’001q2) ⇒
B(q) = – 1000000+1900q - 0’041q2
b) Para hallar el beneficio máximo buscaremos el máximo relativo ya que la
función corresponde a una parábola cóncava y, en ese caso, el máximo
absoluto corresponde con el máximo relativo.
B’(q) = 1900 - 0’082q=0 ⇒ q ≈ 23171 unidades
Como B’’(q) = -0’082 ⇒ B’’(23171) = -0’082 < 0
Por tanto el beneficio máximo se obtiene con la venta de 23171 unidades.
El beneficio será:
B(23171) = – 1000000+1900—23171 - 0’041—231712 ≈ 21012195 €
5. Representa gráficamente las siguientes funciones, indicando los puntos más
representativos:
y = x3 –3x2 +2x
a)
b) y = x4 – 8x2 +16
SOLUCIÓN
a)
Cortes con los ejes: A(0,0) , B(1, 0) , C(2, 0)
Máximo relativo en x=0’4226
Mínimo relativo en x= 1’5774
Punto de inflexión en x= 1
1º de Bachillero
Página 3 de 4
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I
Unidad 9: Aplicaciones de la derivada
b)
Cortes con los ejes: A(-2,0) , B(0, 16) , C(2, 0)
Máximo relativo en x=0
Mínimo relativo en x= -2 , x= 2
Punto de inflexión en x= -1’15 , x=1’15
1º de Bachillero
Página 4 de 4