Braquistócrona

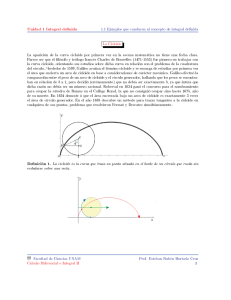
BRAQUISTÓCRONA
INTRODUCCIÓN
Si preguntamos a cualquier persona que grafique la trayectoria que un cuerpo hace cuando se desplaza de un
punto a otro de menor altura, en un campo gravitatorio, es probable que éste diga que la trayectoria es una
recta que una esos puntos. En contra de lo que parecería a primera vista, la línea recta no es la que permite el
descenso más rápido, sino una curva que se llama braquistócrona (del griego braquis, corto, y cronos,
tiempo), también conocida como cicloide.
La braquistocrona fue encontrada a fines del Siglo XVII y su historia es muy interesante, ya que involucró a
los más grandes matemáticos de esa época.
HISTORIA
El 29 de enero de 1697 Newton recibía una carta procedente de Basilea que contenía dos problemas. Aunque
también había sido enviada, además de a Newton, a otros cuantos matemáticos del continente.
El remitente de la misiva era Johann Bernoulli (1667−1748) aunque Gottfried Leibniz(1646−1716), que
mantenía con Newton varias disputas, también había influido en su envío. El reto tenía aparentemente
intención de desafiar a Newton, quien se había alejado de las actividades científicas; y es que el problema
requería del cálculo diferencial e integral, cuya paternidad se discutía entre Newton y Leibniz, ya que se lo
descubrieron de forma simultánea e independiente.
La carta llego a manos de Newton a las 6 de la tarde y a las cuatro de la mañana ya había resuelto ambos
problemas. A la mañana siguiente Newton envió las soluciónes al presidente de la Royal Society. Las
soluciones fueron publicadas de forma anónima en el número de febrero de 1697 de Philosophical
Transactions. Newton resolvió en unas horas lo que a muchos matemáticos de la época le hubiese costado
todas una vida. Varignon, L´Hôpital o David Gregory que también habían recibido los problemas fueron
incapaces de resolverlos.
Pese al anonimato con que se publicaron las soluciones, por la elegancia de las mismas Bernoulli reconoció de
inmediato a su autor y al leer el artículo en Philosophical Transactions exclamo: "Ex ungue leonis" ("De las
garras del león").
En mayo de 1697, el Acta Eruditorum publicó cuatro soluciones, cuyos autores eran Leibniz, el mismo
Bernoulli y su hermano mayor Jacob, y la anónima de Newton.
El problema de la braquistocrona y otros semejantes, hicieron que se desarrollara lo que ahora se conoce como
cálculo de variaciones en mecánica racional o teórica.
PROBLEMA
El primero de los problemas propuestos por Johann Bernoulli a Newton es el denominado problema de la
braquistócrona. Consiste en determinar la curva a través de la que el tiempo que tarde un objeto en caer de un
punto a otro sea mínimo.
Esta curva resulto ser un arco de cicloide. La cicloide es la curva que describe un punto de una circunferencia
que rueda sobre una recta sin deslizar. Para darnos una mejor idea proponemos una experiencia: colocamos un
marcador en la periferia de un aro, hacemos rodar éste, sin deslizar, de manera que el marcador marque en una
1
superficie su movimiento, el marcador trazará una cicloide con su parte cóncava hacia abajo. Si este dibujo se
da vuelta, obtendrá una braquistocrona. El dibujo tendrá un aspecto como el de la figura, donde la forma de la
cicloide corresponde a la curva envolvente exterior.
ALGUNAS DEMOSTRACIONES DE PROPIEDADES DE LA BRAQUISTOCRONA
Tomemos unos ejes coordenados convenientes, sobre la superficie donde se apoya esta rueda y coincidente
con la rueda se establecerá el eje x y el eje y será la perpendicular a ella por el punto que se ha señalado en la
rueda cuando éste está en el suelo.
Si hacemos que la rueda ruede un poco y veamos dónde va a parar el punto P de la circunferencia. Cuando el
centro del círculo C ha pasado a C´, el punto P ha pasado a P´. Este es el punto cuya ecuación queremos.
Llamamos a sus coordenadas (x,y). Como la rueda no resbala sobre el suelo, lo que sabemos es que la
longitud del arco LP sobre la circunferencia es igual a la longitud del segmento rectilíneo OL. Si llamamos
al ángulo LC´P´ medido en radianes, resulta OL = LP´ = r. Por otra parte, las coordenadas de P´ en nuestro
sistema son:
2
x = OL − P´S = r − rsen
y = SL = C´L − C´S = r − rcos
Así obtenemos la ecuación en coordenadas paramétricas de la cicloide
x = r − rsen
y= r − rcos
3
La cicloide tiene propiedades geométricas muy interesantes. Por ejemplo, la longitud de la cicloide es 8 veces
la del radio de la rueda que la genera y el área bajo la cicloide es tres veces la del círculo que engendra la
curva; por tanto las áreas de las tres regiones señaladas en la figura inicial, marcadas con los números 1, 2 y 3
son iguales.
BIBLIOGRAFÍA
•
• http://bib0.unsl.edu.ar/baea/prof−cs/nro1−03/pcs−nro1.htm#art4
• http://www.geocities.com/capecanaveral/lab/1719/anecdotas.html#newton
4